Classification Algorithms for Fast Retrieval of Atmospheric Vertical Columns of CO in the Interferogram Domain
Abstract
1. Introduction
2. Background
2.1. Measurements from Space
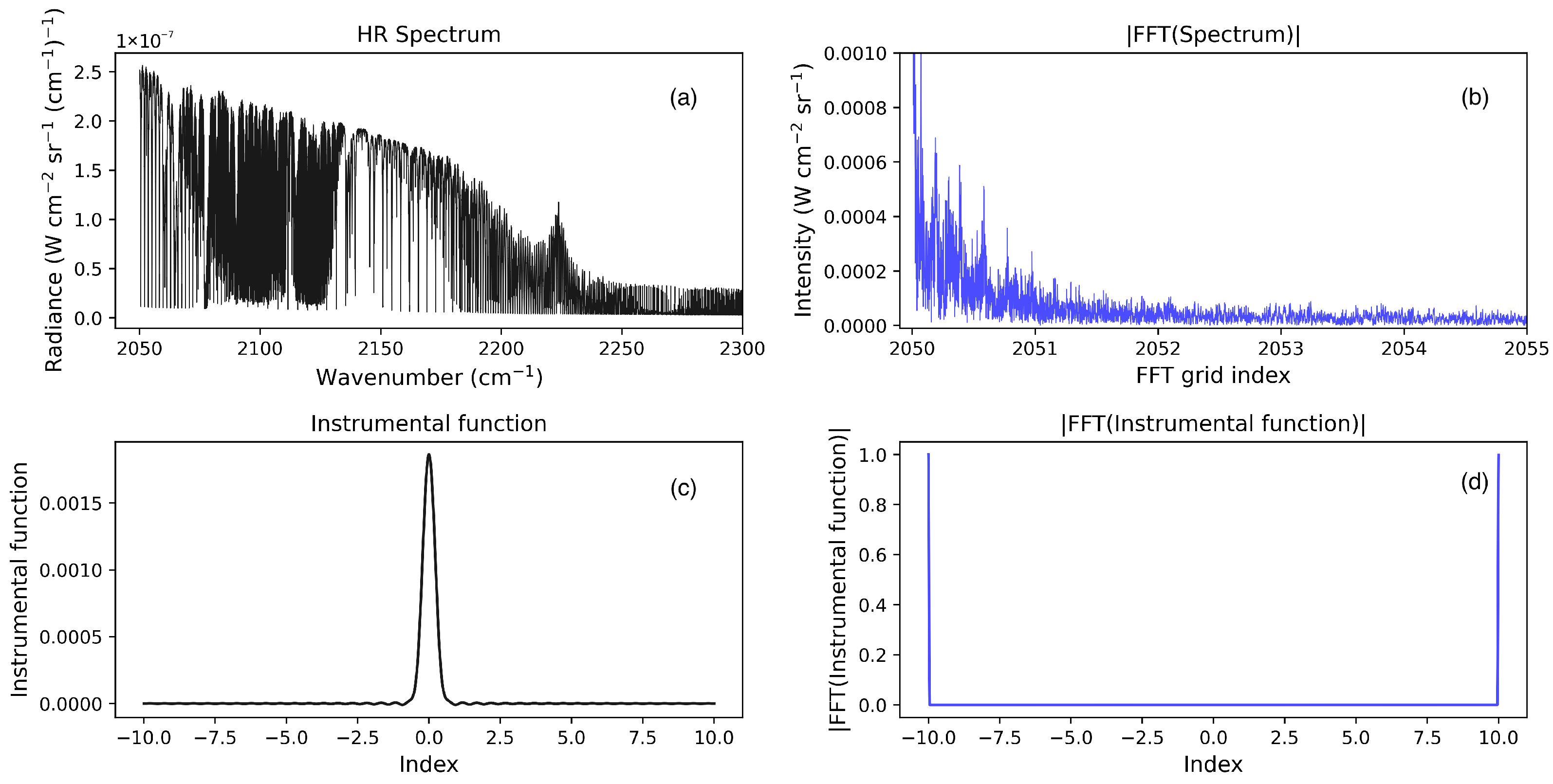
2.2. Interferogram Versus Spectrum
2.3. Existing Fast Retrieval in Spectral Domain
3. Methodology
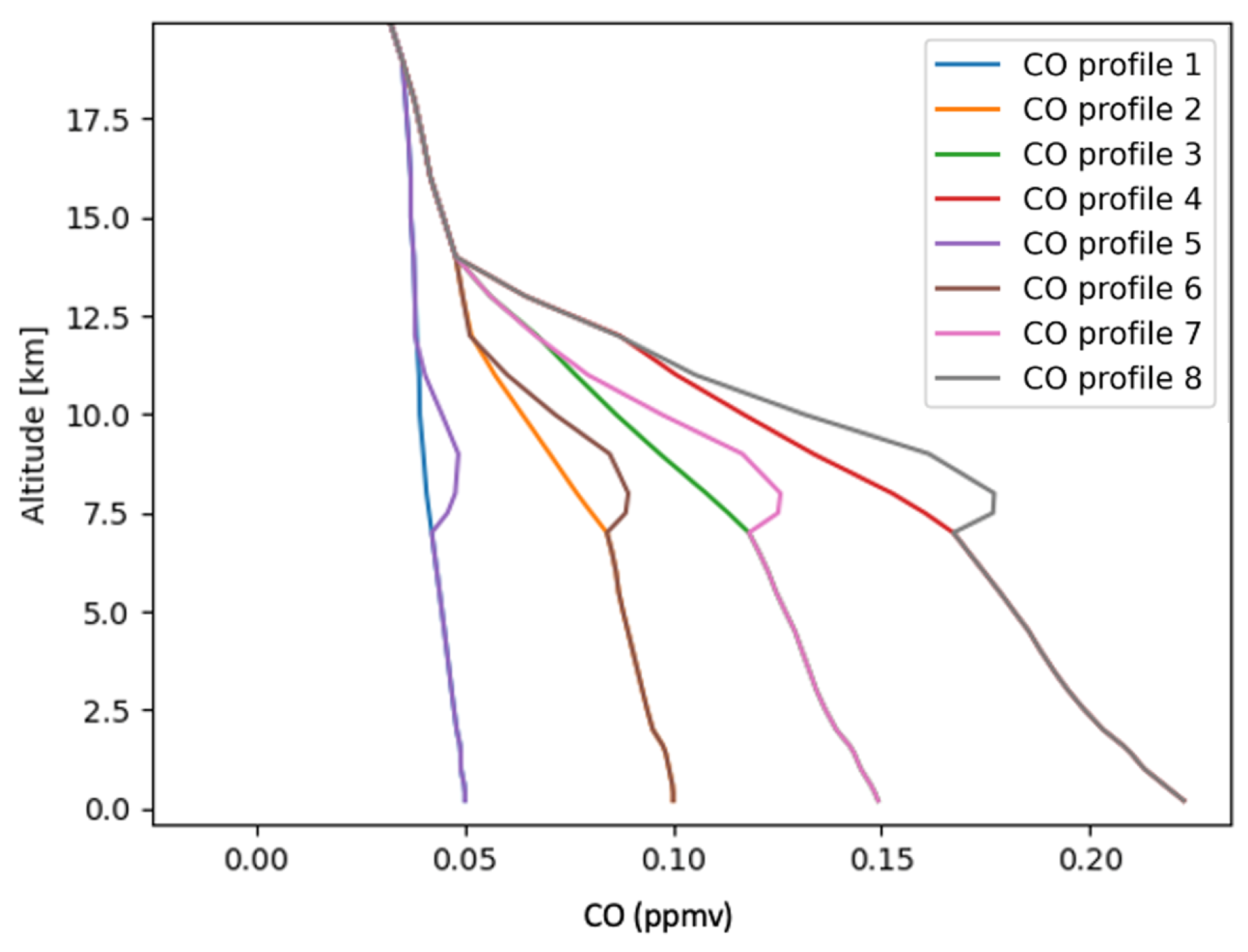
3.1. Reference Dataset
3.1.1. Radiative Transfer Computation
3.1.2. Interferogram Generation
3.2. Selection of Optical Path Differences
3.3. Algorithm 1: Classification from Geophysical Parameters
3.4. Algorithm 2: Radiance Classification
3.5. Algorithm 3: Neural Networks
4. Results
4.1. Algorithm 1: Starting with Geophysical Parameters
4.2. Algorithm 2: Radiance Classes
4.3. Algorithm 3: Neural Networks
Bias in the Neural Networks Approach
5. Discussion

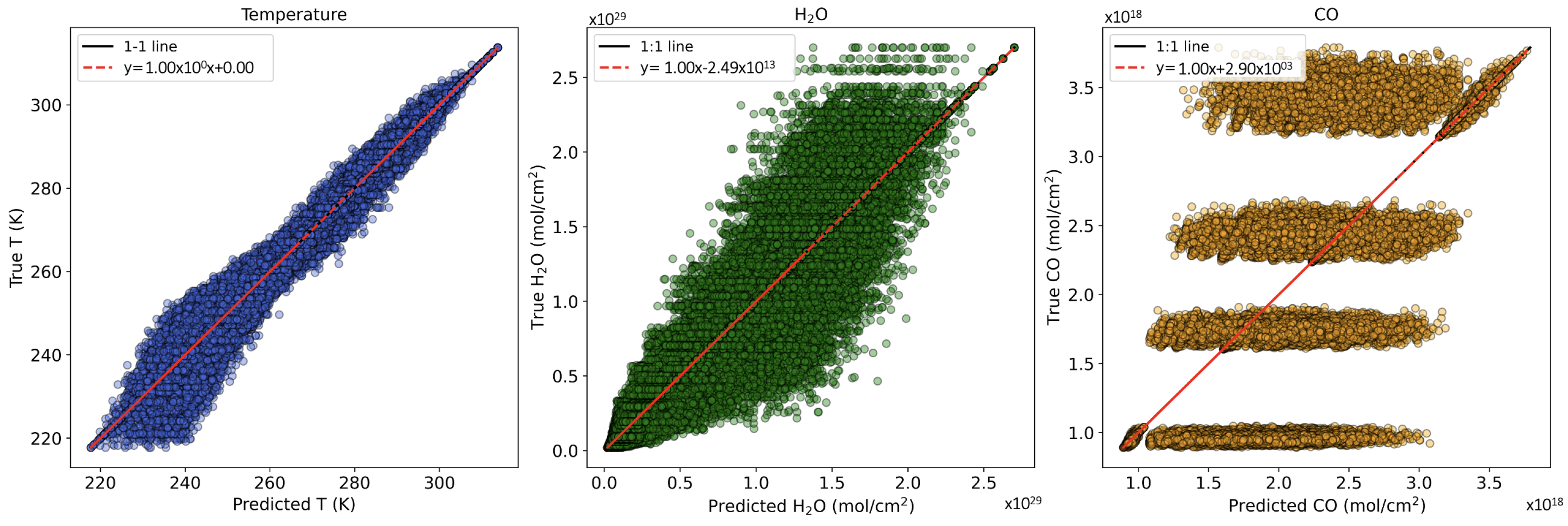
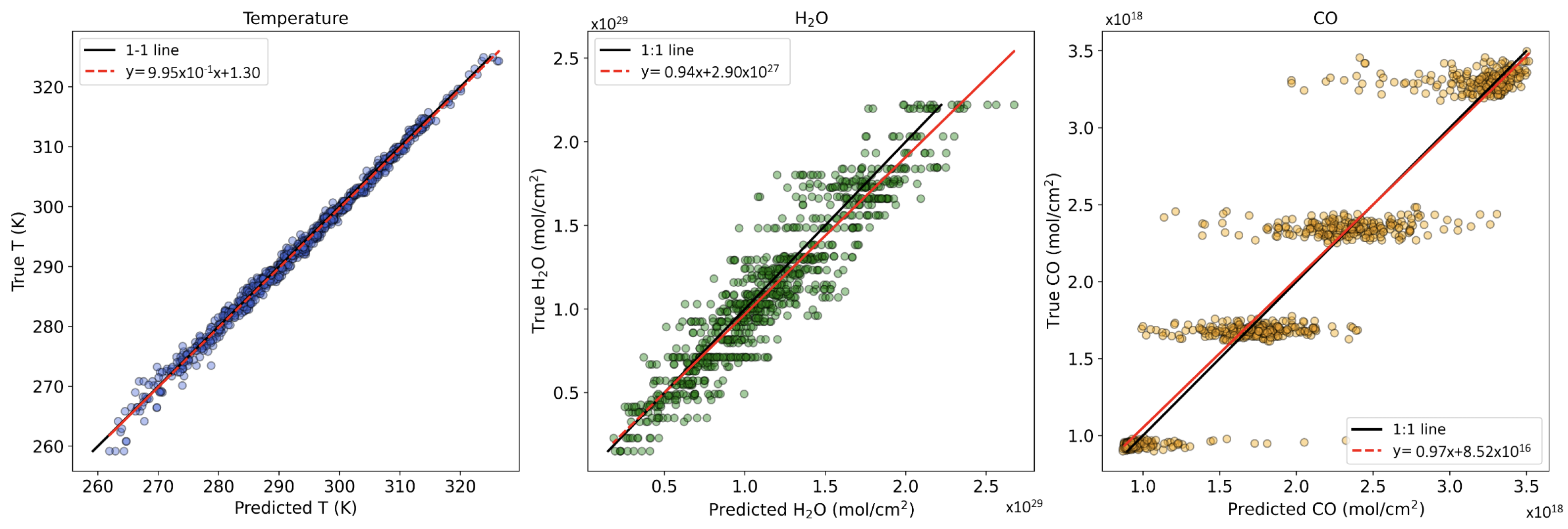
6. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OPD | Optical Path Difference |
| TIGR | Thermodynamic Initial Guess Retrieval |
| IASI | Infrared Atmospheric Sounding Interferometer |
| NN | Neural Network |
| NRT | Near-real-time |
| LARA | LATMOS Atmospheric Retrieval Algorithm |
| LATMOS | Laboratoire atmosphères, milieux, observations spatiales |
Appendix A

References
- George, M.; Clerbaux, C.; Hurtmans, D.; Turquety, S.; Coheur, P.-F.; Pommier, M.; Hadji-Lazaro, J.; Edwards, D.P.; Worden, H.; Luo, M.; et al. Carbon monoxide distributions from the IASI/METOP mission. Atmos. Chem. Phys. 2009, 9, 8317–8330. [Google Scholar] [CrossRef]
- Müller, J.F.; Stavrakou, T.; Bauwens, M.; George, M.; Hurtmans, D.; Coheur, P.F.; Clerbaux, C.; Sweeney, C. Top-Down CO Emissions Based on IASI Observations and Hemispheric Constraints on OH Levels. Geophys. Res. Lett. 2018, 45, 1621–1629. [Google Scholar] [CrossRef]
- George, M.; Clerbaux, C.; Bouarar, I.; Coheur, P.; Deeter, M.N.; Edwards, D.P.; Francis, G.; Gille, J.C.; Hadji-Lazaro, J.; Hurtmans, D.; et al. An examination of the long-term CO records from MOPITT and IASI: Comparison of retrieval methodology. Atmos. Meas. Tech. 2015, 8, 4313–4328. [Google Scholar] [CrossRef]
- Blumstein, D.; Chalon, G.; Carlier, T.; Buil, C.; Hébert, P.; Maciaszek, T.; Ponce, G.; Phulpin, T.; Tournier, B.; Simeoni, D.; et al. IASI instrument: Technical overview and measured performances. Proc. SPIE 2004, 5543, 196–207. [Google Scholar] [CrossRef]
- Crevoisier, C.; Clerbaux, C.; Guidard, V.; Phulpin, T.; Armante, R.; Barret, B.; Camy-Peyret, C.; Chaboureau, J.-P.; Coheur, P.-F.; Crépeau, L.; et al. Towards IASI-New Generation (IASI-NG): Impact of improved spectral resolution and radiometric noise on the retrieval of thermodynamic, chemistry and climate variables. Atm. Meas. Techniq. 2014, 12, 4367–4385. [Google Scholar] [CrossRef]
- Stuhlmann, R.; Rodriguez, A.; Tjemkes, S.; König, M. MTG-IRS: A Highly Advanced Infrared Sounder for Meteosat Third Generation. In Proceedings of the EUMETSAT Meteorological Satellite Conference, Vienna, Austria, 16–20 September 2013; EUMETSAT: Darmstadt, Germany, 2013. [Google Scholar]
- EUMETSAT. MTG-IRS Level 1 Algorithm Theoretical Basis Document. 2019. Available online: https://user.eumetsat.int/s3/eup-strapi-media/MTG_IRS_Level_1_Algorithm_Theoretical_Basis_Document_v2_7b42d5efaa.pdf (accessed on 16 December 2024).
- ESA. Meteosat Third Generation: Infrared Sounder (MTG-IRS). 2023. Available online: https://www.eumetsat.int/meteosat-third-generation-sounder-1-and-copernicus-sentinel-4 (accessed on 16 December 2024).
- Gousset, S.; Croize, L.; Le Coarer, E.; Ferrec, Y.; Rodrigo-Rodrigo, J.; Brooker, L. NanoCarb hyperspectral sensor: On performance optimization and analysis for greenhouse gas monitoring from a constellation of small satellites. CEAS Space J. 2019, 11, 507–524. [Google Scholar] [CrossRef]
- Brooker Lizon-Tati, L.; Serra, S.V.; Bovensman, H.; Crevoisier, C.; Dogniaux, M.; Croiz’e, L.; Ferrec, Y.; Le Coarer, E.; Gousset, S.; Sic, B.; et al. SCARBO: A constellation of small satellites for the monitoring of anthropogenic greenhouse gases. In Proceedings of the 73rd International Astronautical Congress (IAC), Paris, France, 18–22 September 2022. [Google Scholar]
- Dogniaux, M.; Crevoisier, C.; Gousset, S.; Le Coarer, E.; Ferrec, Y.; Croizé, L.; Wu, L.; Hasekamp, O.; Sic, B.; Brooker, L. The Space Carbon Observatory (SCARBO) concept: Assessment of XCO2 and XCH4 retrieval performance. Atmos. Meas. Tech. 2022, 15, 4835–4858. [Google Scholar] [CrossRef]
- Croizé, L. Performance Assessment for Total CO2 and CH4 Column Monitoring Using a Miniaturized Static Spectrometer; EGU, European Geosciences Union: Vienna, Austria, 2019; Available online: https://meetingorganizer.copernicus.org/EGU2019/EGU2019-13333.pdf (accessed on 16 December 2024).
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000. [Google Scholar] [CrossRef]
- Michelson, A.A. On the Application of Interference Methods to Spectroscopic Measurements.—I. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1891, 31, 338–346. [Google Scholar] [CrossRef]
- Beer, R. Remote Sensing by Fourier Transform Spectrometry; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Bracewell, R.N. The Fourier Transform and Its Applications, 2nd ed.; McGraw-Hill Book Company: Columbus, OH, USA, 1986. [Google Scholar]
- Bell, R. Introductory Fourier Transform Spectroscopy; Academic Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Kyle, T.G. Temperature soundings with partially scanned interferograms. Appl. Opt. 1977, 16, 326–333. [Google Scholar] [CrossRef]
- Fortunato, G. Application of interferential correlation of spectrum to the detection of atmospheric pollutants. J. Opt. 1978, 9, 281. [Google Scholar] [CrossRef]
- Goldstein, H.W.; Grenda, R.N.; Bortner, M.H.; Dick, R. CIMATS—A correlation interferometer for the measurement of atmospheric trace species. In Proceedings of the Joint Conference on Sensing of Environmental Pollutants, New Orleans, LA, USA, 6–11 November 1977; American Chemical Society: Washington, DC, USA, 1978; pp. 586–589. [Google Scholar]
- Smith, W.L.; Howell, H.B.; Woolf, H.M. The Use of Interferometric Radiance Measurements for Sounding the Atmosphere. J. Atmos. Sci. 1979, 36, 566–575. [Google Scholar] [CrossRef]
- Serio, C.; Masiello, G.; Grieco, G. Fourier Transform Spectroscopy with Partially Scanned Interferograms as a Tool to Retrieve Atmospheric Gases Concentrations from High Spectral Resolution Satellite Observations—Methodological Aspects and Application to IASI. In Atmospheric Model Applications; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef][Green Version]
- Grieco, G.; Masiello, G.; Matricardi, M.; Serio, C. Partially scanned interferogram methodology applied to IASI for the retrieval of CO, CO2, CH4 and N2O. Opt. Express 2013, 21, 24753–24769. [Google Scholar] [CrossRef] [PubMed]
- Chevallier, F.; Chéruy, F.; Scott, N.A.; Chédin, A. A regularized neural network approach for retrieval of atmospheric and surface temperatures with the IASI instrument. J. Appl. Meteorol. 2002, 41, 144–159. [Google Scholar] [CrossRef]
- Whitburn, S.; Van Damme, M.; Clarisse, L.; Clerbaux, C.; Hurtmans, D.; Coheur, P.F. A new neural network-based methane retrieval algorithm for IASI: Analysis of sensitivity to spectroscopy and ancillary data. Atmos. Meas. Tech. 2016, 9, 4955–4977. [Google Scholar] [CrossRef]
- Van Damme, M.; Whitburn, S.; Clarisse, L.; Clerbaux, C.; Hurtmans, D.; Coheur, P.F. An improved NH3 retrieval algorithm for IASI using the neural network-based ANNI-NH3-v2.1 framework. Atmos. Meas. Tech. 2017, 10, 4905–4914. [Google Scholar] [CrossRef]
- Susskind, J.; Barnet, C.D.; Blaisdell, J.M. Improved Determination of Surface and Atmospheric Temperatures Using Only Shortwave AIRS Channels: The AIRS Version 6 Retrieval Algorithm. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Paper ID 20100014828. 2010. Available online: https://ntrs.nasa.gov/api/citations/20100014828/downloads/20100014828.pdf?utm_source=chatgpt.com (accessed on 16 December 2024).[Green Version]
- Liu, X.; Chance, K.; Sioris, C.E.; Kurosu, T.P.; Spurr, R.J.D. Tropospheric ozone profiles from the Tropospheric Emission Spectrometer (TES): Characterization of the optimal estimation retrievals. J. Geophys. Res. Atmos. 2006, 111, D22S08. [Google Scholar] [CrossRef]
- Murty, D.; Barnet, C.; Xu, L.; Gu, D.; Wilson, M.; Kizer, S.; Xiong, X.; Maddy, E.; Ferraro, R.; Knuteson, R.; et al. The CrIMSS EDR Algorithm: Characterization, Optimization, and Validation. JGR Atmos. 2014. [Google Scholar] [CrossRef]
- Bauduin, S.; Clarisse, L.; Theunissen, M.; George, M.; Hurtmans, D.; Clerbaux, C.; Coheur, P.F. IASI’s sensitivity to near-surface carbon monoxide (CO): Theoretical analyses and retrievals on test cases. J. Quant. Spectrosc. Radiat. Transf. 2017, 189, 428–440. [Google Scholar] [CrossRef]
- AERIS Data Center. Thermodynamical Initial Guess Retrieval (TIGR); AERIS Data Center: Paris, France, 2025. [Google Scholar]
- Chédin, A.; Scott, N.A.; Wahiche, C.; Moulinier, P. The Improved Initialization Inversion Method: A High-Resolution Physical Method for Temperature Retrievals from Satellites of the TIROS-N Series. J. Clim. Appl. Meteorol. 1985, 24, 1283–1299. [Google Scholar] [CrossRef]
- Achard, V. A statistical method for selecting a representative set of atmospheric situations for satellite simulations. J. Appl. Meteorol. 1991, 30, 476–490. [Google Scholar]
- Chevallier, F.; Chédin, A.; Chéruy, F.; Morcrette, J.J. TIGR-like atmospheric-profile databases for accurate radiative-flux computation. Q. J. R. Meteorol. Soc. 1998, 124, 1431–1454. [Google Scholar]
- Payan, S.; Camy-Peyret, C.; Jeseck, P.; Hawat, T.; Durry, G.; Lefèvre, F. First direct simultaneous HCl and ClONO2 profile measurements in the Arctic Vortex. Geophys. Res. Lett. 1998, 25, 2663–2666. [Google Scholar] [CrossRef]
- Payan, S.; Camy-Peyret, C.; Bureau, J. Comparison of Retrieved L2 Products from Four Successive Versions of L1B Spectra in the Thermal Infrared Band of TANSO-FTS over the Arctic Ocean. Remote Sens. 2017, 9, 1167. [Google Scholar] [CrossRef]
- Mondelain, D.; Payan, S.; Deng, W.; Camy-Peyret, C.; Hurtmans, D.; Mantz, A.W. Measurement of the temperature dependence of line mixing and pressure broadening parameters between 296 and 90 K in the ν3 band of 12CH4 and their influence on atmospheric methane retrievals. J. Mol. Spectrosc. 2007, 244, 130–137. [Google Scholar] [CrossRef]
- Butz, A.; Bösch, H.; Camy-Peyret, C.; Dorf, M.; Engel, A.; Payan, S.; Pfeilsticker, K. Observational constraints on the kinetics of the ClO-BrO and ClO-ClO ozone loss cycles in the Arctic winter stratosphere. Geophys. Res. Lett. 2007, 34, L05801. [Google Scholar] [CrossRef]
- Payan, S.; Camy-Peyret, C.; Oelhaf, H.; Wetzel, G.; Maucher, G.; Keim, C.; Pirre, M.; Huret, N.; Engel, A.; Volk, M.C.; et al. Validation of version-4.61 methane and nitrous oxide observed by MIPAS. Atmos. Chem. Phys. 2009, 9, 413–442. [Google Scholar] [CrossRef]
- Keim, C.; Eremenko, M.; Orphal, J.; Dufour, G.; Flaud, J.M.; Höpfner, M.; Boynard, A.; Clerbaux, C.; Payan, S.; Coheur, P.F.; et al. Tropospheric ozone from IASI: Comparison of different inversion algorithms and validation with ozone sondes in the northern middle latitudes. Atmos. Chem. Phys. 2009, 9, 9329–9347. [Google Scholar] [CrossRef]
- Razavi, A.; Clerbaux, C.; Wespes, C.; Clarisse, L.; Hurtmans, D.; Payan, S.; Camy-Peyret, C.; Coheur, P.F. Characterization of methane retrievals from the IASI space-borne sounder. Atmos. Chem. Phys. 2009, 9, 7889–7899. [Google Scholar] [CrossRef]
- Segonne, C.; Huret, N.; Payan, S.; Gouhier, M.; Catoire, V. A Spectra Classification Methodology of Hyperspectral Infrared Images for Near Real-Time Estimation of the SO2 Emission Flux from Mount Etna with LARA Radiative Transfer Retrieval Model. Remote Sens. 2020, 12, 4107. [Google Scholar] [CrossRef]
- Huret, N.; Segonne, C.; Payan, S.; Salerno, G.; Catoire, V.; Ferrec, Y.; Roberts, T.; Pola Fossi, A.; Rodriguez, D.; Croizé, L.; et al. Infrared hyperspectral and ultraviolet remote measurements of volcanic gas plume at Mt Etna during IMAGETNA campaign. Remote Sens. 2019, 11, 1175. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hargreaves, E.R.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Conway, E.K.; Hill, C.; Kochanov, R.V.; Tan, Y.; et al. The HITRAN2020 Molecular Spectroscopic Database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Clough, S.A.; Shephard, M.W.; Mlawer, E.; Delamere, J.S.; Iacono, M.; Cady-Pereira, K.; Boukabara, S.; Brown, P.D. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Strang, G. Calculus; Wellesley-Cambridge Press: Wellesley, MA, USA, 1999. [Google Scholar]
- Smith, F.; Armante, R.; August, T.; Barnet, C.; Bouchard, A.; Camy-Peyret, C.; Capelle, V.; Clarisse, L.; Clerbaux, C.; Coheur, P.F.; et al. Hyperspectral Earth Observation from IASI: Five Years of Accomplishments. Bull. Am. Meteorol. Soc. 2012, 93, 347–370. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, X.; Zhang, L. A hybrid deep learning approach for hyperspectral image classification using convolutional and recurrent neural networks. ISPRS J. Photogramm. Remote Sens. 2020, 165, 182–192. [Google Scholar]
- Niemeyer, T.; Ustinov, E.; Burrows, J.P. Convolutional neural networks for atmospheric trace gas retrievals from hyperspectral remote sensing data. Remote Sens. 2020, 12, 1998. [Google Scholar]
- Kadowaki, Y.; Tanaka, Y.; Takamura, E. Cloud property retrievals using deep learning and LSTM networks from MODIS and VIIRS observations. Atmos. Res. 2021, 250, 105366. [Google Scholar]
- Sun, H.; Chen, X.; Wu, J. LSTM-based spectral inversion for atmospheric trace gas retrievals from TROPOMI satellite data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4108711. [Google Scholar]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28, pp. 802–810. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Giuseppe, G.; Masiello, G.; Serio, C. Interferometric vs Spectral IASI Radiances: Effective Data-Reduction Approaches for the Satellite Sounding of Atmospheric Thermodynamical Parameters. Remote Sens. 2010, 2, 2323–2346. [Google Scholar] [CrossRef]
- AERIS Data Infrastructure. AERIS Data and Services for the Atmosphere. 2025. Available online: https://www.aeris-data.fr (accessed on 14 January 2025).


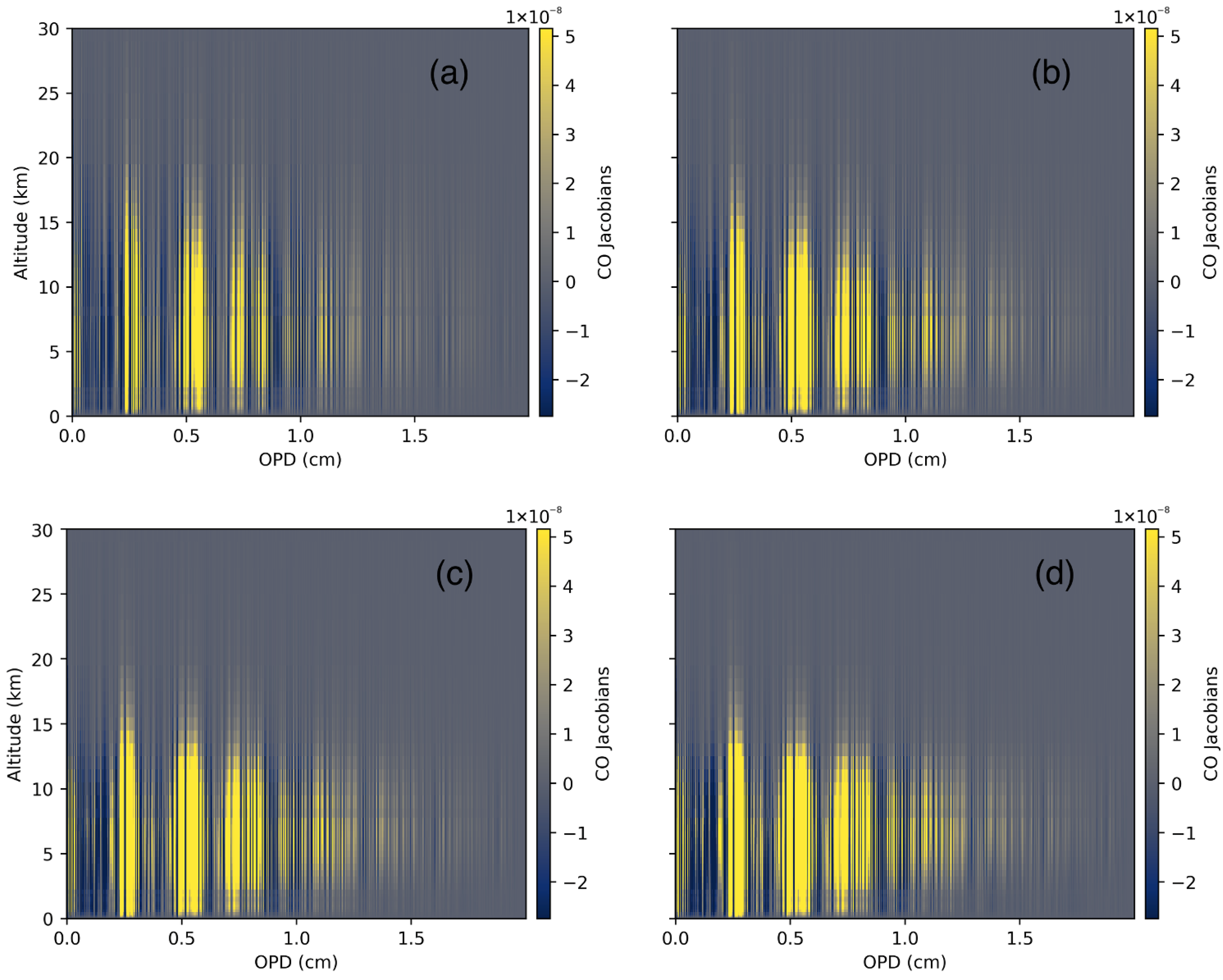
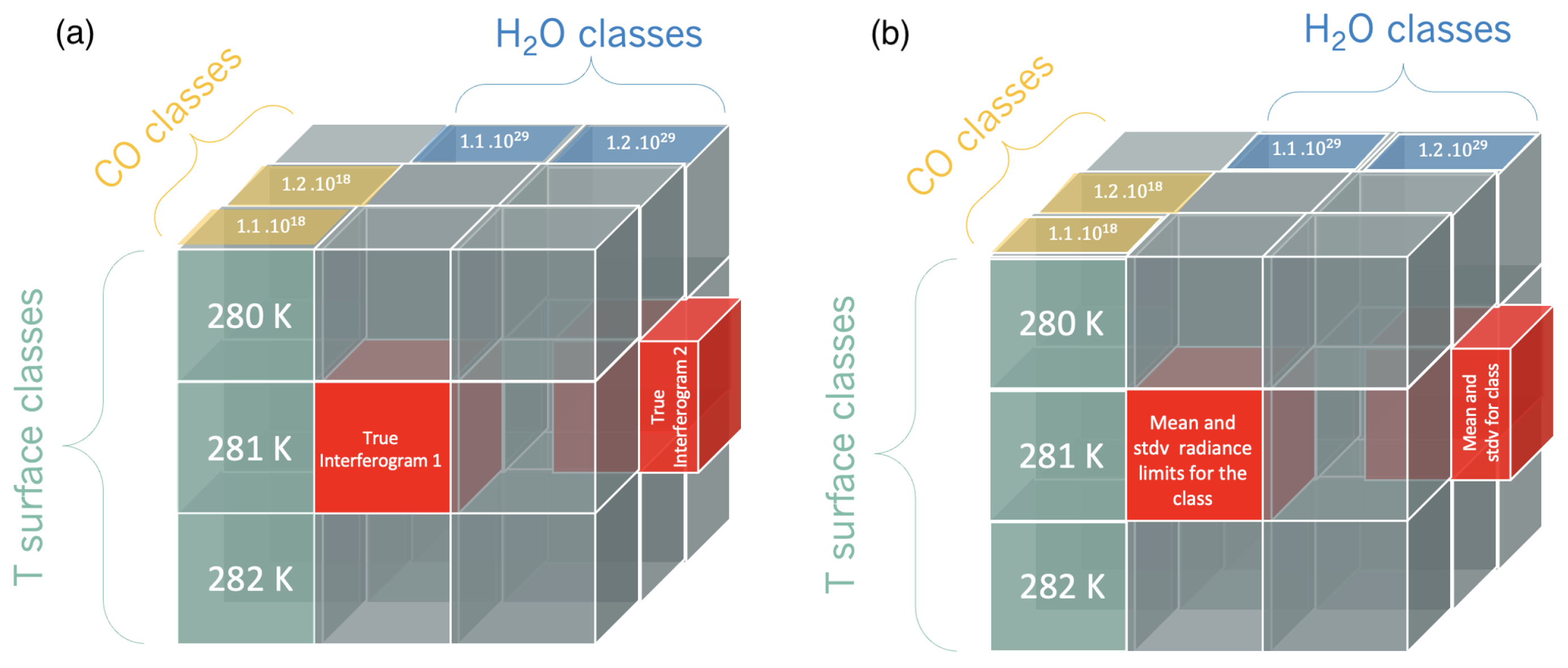
| Case | No. of OPDs | No. of T Classes | No. of H2O Classes | No. of CO Classes | T Surface (K) MSE | H2O (mol/cm2) MSE | CO (mol/cm2) MSE |
|---|---|---|---|---|---|---|---|
| A | 2 | 112 | 20 | — | 57% | 89% | — |
| B | 3 | 112 | 20 | — | 43% | 77% | — |
| C | 3 | 300 | 50 | — | 13% | 46% | — |
| D | 3 | 112 | 20 | 20 | 0.48% | 42% | 31% |
| E | 3 | 300 | 50 | 50 | 0.47% | 41% | 31% |
| F | 3 | 112 | 20 | 20 | 0.41% | 39% | 30% |
| Case—OPD Ranges | No. of Interferograms | T Surface (K) MSE | H2O (mol/cm2) MSE | CO (mol/cm2) MSE | Training Time |
|---|---|---|---|---|---|
| A | 4616 | 0.28% | 12% | 23% | ∼5 h |
| B | 4616 | 0.31% | 14% | 14% | ∼5 h |
| B | 100,000 | 0.34% | 18% | 16% | ∼7 days |
| C | 4616 | 0.33% | 14% | 9% | ∼5 h |
| C | 100,000 | 0.25% | 18% | 13% | ∼7 days |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ećo, N.; Payan, S.; Croizé, L. Classification Algorithms for Fast Retrieval of Atmospheric Vertical Columns of CO in the Interferogram Domain. Remote Sens. 2025, 17, 2804. https://doi.org/10.3390/rs17162804
Ećo N, Payan S, Croizé L. Classification Algorithms for Fast Retrieval of Atmospheric Vertical Columns of CO in the Interferogram Domain. Remote Sensing. 2025; 17(16):2804. https://doi.org/10.3390/rs17162804
Chicago/Turabian StyleEćo, Nejla, Sébastien Payan, and Laurence Croizé. 2025. "Classification Algorithms for Fast Retrieval of Atmospheric Vertical Columns of CO in the Interferogram Domain" Remote Sensing 17, no. 16: 2804. https://doi.org/10.3390/rs17162804
APA StyleEćo, N., Payan, S., & Croizé, L. (2025). Classification Algorithms for Fast Retrieval of Atmospheric Vertical Columns of CO in the Interferogram Domain. Remote Sensing, 17(16), 2804. https://doi.org/10.3390/rs17162804






