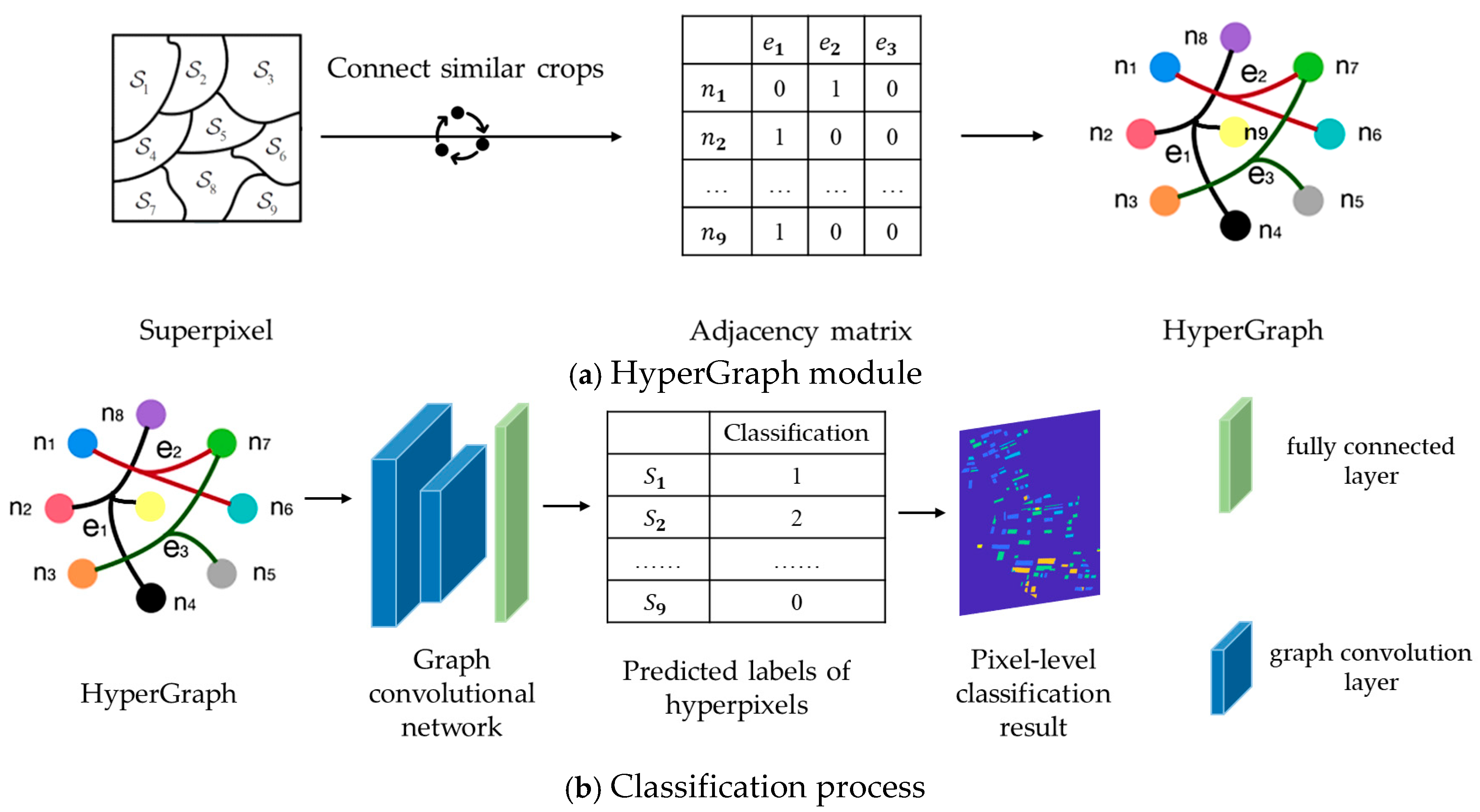
1. Introduction
Synthetic Aperture Radar (SAR) is an active microwave remote sensing technology. Due to its unique working principle, it has the capability of all-day, all-weather observation and high-resolution imaging [
1]. It is able to penetrate the cloud layer and part of the vegetation cover to obtain information on the scattering characteristics of terrains. Among the existing space-borne SAR systems, dual polarimetric SAR has become an important data source in the field of agricultural monitoring due to its comprehensive performance, considering the aspects of resolution, observation width, scattering representation and timely acquisition. By transmitting one polarization wave and receiving two orthogonally polarization waves, dual polarimetric SAR enhances the information dimension by about two times compared with single PolSAR. Compared with fully PolSAR systems, it can achieve a balance between data information and acquisition efficiency.
Although dual polarimetric data can provide certain polarimetric information, it only contains information from two channels, which limits its ability to comprehensively characterize crops to a certain extent, and there is a problem of missing information. Multi-temporal observation data has a unique advantage in that it can continuously and dynamically record the change process of crops during the growth cycle, including the evolution of morphology, structure, physiological characteristics and other aspects. This time-dimensional information can effectively complement the insufficiency of dual polarimetric data. Different crops will show significantly different characteristics at their respective growth stages [
2]. Combining multi-temporal data with dual polarization can make full use of the advantages of both [
3], and it can more accurately identify and classify different types of crops and improve the classification accuracy of PolSAR [
4].
In the literature, multi-temporal dual PolSAR crop classification methods use the pixel of images as the processing unit and mainly rely on the polarimetric features and texture properties of the pixel. Salma et al. used the K-means unsupervised method for the clustering of
and
, then analyzed the changes in scattering mechanisms of ginger, tobacco, rice, cabbage and pumpkin crops in the plane during their respective growth stages [
5]; Wang et al. extracted 12 polarimetric parameters based on the covariance matrix and
decomposition, evaluated the sensitivity of each parameter to crop phenology, and constructed a classification model using the best combination [
6]. Machine learning algorithms have been gradually applied to make better use of polarimetric features. Common machine learning algorithms include maximum likelihood classification, decision tree [
7], random forest (RF) [
8,
9], Support Vector Machine (SVM) [
10,
11], etc. Machine learning technology shows obvious advantages with its powerful data processing capabilities. It can efficiently analyze and process massive amounts of data to achieve high-precision crop identification. Liu Rui et al. took Xinjiang Shihezi city as the study area and used multi-temporal Sentinel-1A SAR data with three classification algorithms, RF, CART decision tree and SVM. The classification results have shown that the RF classification method had the highest classification accuracy [
12]. Dobrinić et al. also used RF for a classification task and used Sentinel-1 multi-temporal data for a classification study of crop categories [
13]. At the same time, deep learning technology is gradually showing its powerful advantages in the field of crop classification. By constructing neural network models, deep learning can more accurately capture the subtle changes in the crop growth process, thus improving the classification accuracy. Xiao et al. investigated the application of multi-temporal SAR images in crop classification in rural areas of China, using a pixel-based Kth nearest neighbor algorithm in subspace, with an overall accuracy of up to 98.2% for ten categories [
14]. Xue et al. proposed a sequence SAR target classification method based on the spatial–temporal ensemble convolutional network; this network has shown a higher classification accuracy [
15]. Teimouri et al. classified 14 categories of crops in the Danish region based on a combination of FCN and ConvLSTM, which achieved a higher accuracy [
16]; Wei et al. proposed a classification method based on the U-Net model for multi-temporal dual polarimetric crop data, which was able to achieve high classification accuracy in complex crop growing environments [
17].
However, with the increasing resolution of dual polarimetric SAR systems, for high-resolution images, pixel-based image classification algorithms usually produce speckle noise effects [
18] and degrade the image classification accuracy due to the high intraclass variability and low interclass separability of image pixels. So some scholars jumped out of the pixel-based framework and developed object-based methods, which are realized by aggregating neighboring pixels with similar features [
19,
20,
21,
22]. Object-level image processing means are more in line with the actual situation of farmland distributed in plots. For example, when classifying a large area of wheat cultivation, the object-based method is able to recognize the contiguous wheat area as a whole object, instead of the fragmented and scattered classification results as in the case of image element-based classification. Unlike pixel-level methods that ignore spatial context, superpixels group pixels into locally homogeneous regions that align well with agricultural field boundaries. Using superpixels as the basic processing unit allows the model to leverage these inherent spatial relationships for more accurate classification.
In practice, Clauss et al. segmented the Sentinel-1 time series using Simple Linear Iterative Clustering (SLIC), followed by extracting the VH-averaged backscatter coefficients for each superpixel, which has been used in six different rice growing regions with an average overall accuracy of 83% [
23]. Some scholars have utilized Simple Non-Iterative Clustering (SNIC) for segmentation and have shown that object-based algorithms have higher accuracy than pixel-based algorithms. Xiang et al. combined backscatter coefficients with texture, elevation, and slope information, then used an object-oriented approach to combine these features to improve land cover classification accuracy [
24]. Emilie et al. used an object-level random forest classifier to classify crops based on Sentinel-1 time series from January to August 2020 [
25]. Gao et al. proposed a root-mean-square-based temporal polarization similarity metric and generated superpixels using an edge detection method with stacked two-dimensional Gaussian-type windows, which demonstrated better performance than the traditional method on Sentinel-1 dual polarimetric SAR data [
26]. Huang Chong et al. proposed an Object-Based Dynamic Time Warping (OBDTW) algorithm to better improve rice classification accuracy by utilizing the features of long-term Sentinel-1 SAR data [
27].
However, effectively fusing these datasets remains challenging. First, crop scattering properties change dynamically, making simple feature concatenation ineffective. Second, the high-dimensional data contains both redundant and complementary information, requiring a model that can selectively leverage useful features while suppressing noise and redundancy.
Although there have been a number of scholars who have conducted relevant studies and innovations on the classification of crops for multi-temporal dual polarimetric SAR data, there are still some problems that need to be further investigated: The first question is that for SAR data of different temporals, the polarimetric scattering features of crops may change, which may easily lead to inconsistent superpixel boundaries across temporals when single time segmentation is performed. The second is that most of the existing classification algorithms are based on local features or neighborhood information, which makes it difficult to effectively capture the similarities and associations between distant plots.
To address the above problems, this article designed a multi-temporal dual polarimetric SAR crop classification method based on plot distribution information, with specific main research components.
(1) A superpixel segmentation model based on multi-temporal data was constructed. By performing superpixel formation on the covariance matrices combined from multi-temporal data, the consistency and stability of superpixel boundaries were achieved by utilizing the constraints of the temporal covariance matrix. This strategy not only fully integrated the information of all temporal data during the long time period, but also effectively alleviated the boundary mismatch problem caused by single time segmentation.
(2) A HyperGraph neural network was used to connect far-distant crop plots with others of the same type. Considering that although the same crop plots may be spatially dispersed, their scattering characteristics have certain similarities and correlations, this article utilized a HyperGraph neural network to establish higher-order relationships among multiple superpixels to effectively capture potential feature correlations and category consistency, so as to improve the accuracy and robustness of PolSAR data in crop classification.
(3) Different scattering features were extracted and combined to explore their classification performances in complex scenes. Four typical dual polarimetric features of superpixels, , , and , were extracted, and the classification was verified for each scattering feature one by one to explore its feasibility for crop classification. The classification accuracy was further investigated by feature combination; the classification of feature combination achieved the optimal accuracy on the experimental dataset.
3. Results and Discussion
3.1. Experimental Settings
To ensure the accuracy of the training data, about 6% of the labeled superpixels of the total superpixel data volume are selected from the segmentation results, and these superpixels are used to construct the adjacency matrix, and as the model training set. In the testing step, all the superpixels are used for the test in order to comprehensively assess the performance of the model. In the HyperGraph classification model, the Adam optimizer is used to train 200 epochs at a learning rate of 0.01.
To achieve a more intuitive and accurate presentation of the classification results, the pixel location information contained in each superpixel is recorded during the process of segmentation. After the HGNN completes the task of classifying, the predicted category labels of each superpixel are converted back to pixel labels. Through this reverse conversion process, the classification results at the superpixel level can be refined to the pixel level, thus obtaining the final, higher-resolution classification results.
3.2. Experimental Results
In this article, the method is validated and discussed through experiments in three aspects: (1) Firstly, in the step of superpixel segmentation, the effects of different parameters on the superpixel segmentation results are analyzed. At the same time, in order to show the advantages of multi-temporal information in superpixel segmentation, the effects of single-temporal and multi-temporal superpixel segmentation are compared. (2) Secondly, in the research of superpixel classification features, the classification effects of different polarimetric features for dual polarimetric data under the HGNN are compared, as well as the possible feature combinations, to examine the influence of input features and, further, to obtain the optimal feature combinations. (3) Finally, in terms of classification model performance evaluation, the performance of the HGNN, GNN, and RF are compared in the superpixel classification task, in order to validate the advantages of combining superpixels and the HyperGraph in crop classification.
3.2.1. Analysis of Superpixel Segmentation Results
- ➢
Effect of seed points on superpixel segmentation
As a key step, the setting of different seed points can obviously change the effect of superpixel segmentation. This section describes experiments conducted for different seed points. The seed point directly affects the step length of superpixel segmentation; it has an inverse relationship with the step length. The step length determines the size and density of the superpixels, with a smaller step length typically generating more pairs of smaller-sized and finer superpixels, while a larger step length generates fewer but larger superpixels. This tuning helps to balance the computational complexity of segmentation with accuracy.
In the experiments, the number of seed points was set to 1000, 1500, 2000, 2500, 3000 and 3500, and the superpixel segmentation edges with different seed points are shown in
Figure 5. It was found that when the number of seed points is 2500, the generated superpixels are of moderate number and reasonable size, which can effectively capture the boundary of the parcel in the image, avoiding the problem of excessive refinement or too much roughness.
In contrast, when the numbers of seed points were 1000, 1500 and 2000, the segmentation results appeared too coarse to accurately distinguish the boundaries of different parcels due to the large step length. Especially when the number of seed points was 1000, the generated superpixel area was too large, resulting in the neighboring regions being unable to be effectively distinguished, and the superpixel merged several different plots into one large parcel. When the numbers of seed points were 3000 and 3500, the step length was smaller, and although the superpixels became more detailed, the over-refined superpixels not only increased the computational complexity and prolonged the processing time, but also made the segmentation results too redundant, which affected the efficiency of the subsequent processing.
Combining the above experimental results and analysis, the 2500 seed point number is considered optimal for this experiment, which provides a good balance between segmentation accuracy and computational complexity.
- ➢
Comparative analysis of single-temporal with multi-temporal superpixel segmentation
The experiment further compared the effect of single-temporal with multi-temporal superpixel segmentation to verify the effect of temporal information on the superpixel segmentation results.
For single-temporal superpixel segmentation, the same SLIC method was used for superpixel generation by replacing the color distance with the Wishart distance. The single-temporal superpixel segmentation algorithm acted independently on the data of each temporal to ensure that the segmentation processes did not interfere with each other. To ensure the comparability of the experiments, the experimental process kept the number of seed points at 2500, and the results are shown in
Figure 6. Observing the results presented in
Figure 6a–c, it can be seen that there were obvious differences in the size and shape of the region obtained from the segmentation of each temporal, and different types of plots are not effectively distinguished in the segmentation image.
Simultaneously, for comparison, we also performed superpixel segmentation on single-time data using the traditional SLIC algorithm based on RGB distance under the same parameter setting of 2500 seed points. As shown in
Figure 7, the traditional SLIC method was unable to distinguish between different crop regions.
Obviously different from single-temporal segmentation, multi-temporal superpixel segmentation exhibited better results, as shown in
Figure 5d and
Figure 6d. The algorithm was able to identify the features that change over time, which enabled the parcels that behave similarly at different time points to be classified into the same superpixel region, improving the consistency and accuracy of segmentation. Multi-temporal segmentation not only takes into account spatial information, but it is also able to capture subtle changes due to temporal variations.
During the crop growth cycle, the differences in the plots at different stages in SAR images may be subtle, and are difficult to accurately distinguish by traditional single-time segmentation methods. In contrast, temporal union segmentation can clearly distinguish these subtle changes and use them as the basis for superpixel division by comprehensively analyzing multi-temporal data, so that crop plots at different growth stages can be more accurately divided.
3.2.2. Classification Results of HGNN
The extracted scattering features for each superpixel were input into the HGNN. Based on the information of the superpixels, the network set a hyperedge for each category and grouped all similar superpixels into one group, and the node–hyperedge adjacency matrix could be constructed using the set of hyperedges.
In order to verify the effectiveness of the object-oriented HGNN, four types of scattering features obtained at different seed points were selected for comparison experiments in this study.
The classification accuracies of the four superpixel scattering features in the HGNN network of this experiment are shown in
Table 1. In general, the classification accuracy of each superpixel scattering feature shows a trend of first increasing and then leveling off with the increase in the number of seed points. Specifically, when the number of seed points was 1000, the classification accuracy of
,
and
was relatively low, and the classification accuracy of
was relatively high. When the number of seed points was increased to 2500, the classification accuracies of the four superpixel scattering features
,
,
and
reached 85.08%, 90.15%, 85.40%, and 92.07%, respectively. When the number of seed points increased from 2500 to 3500, the improvement in classification accuracy was marginal, while the computational cost for superpixel segmentation rose significantly. Therefore, a setting of 2500 seed points effectively controls computational cost while ensuring high accuracy, achieving the best trade-off between precision and efficiency. Thus, in this experiment, it is considered that the overall classification effect reaches an optimal state with this setting. After this, the classification accuracy tended to stabilize by continuing to increase the number of seed points. By comparing the classification accuracies of these four scattering features, it can be found that
shows better results than the other three under different seed points. When the seed point number was 2500, the classification effect corresponded to the effect of superpixel segmentation.
Next, the effectiveness of multi-temporal superpixel classification was verified, as shown in
Table 2. This indicated that integrating data from multi-temporal data can effectively overcome the limitations of single-time data. By using complementary information along the temporal dimension, this approach reduced random errors and the influence of environmental factors, enabling a more comprehensive characterization of crop changes, and led to a substantial improvement in classification accuracy.
On the basis of single-feature classification, we further developed multi-feature combination classification under the condition of the optimal parameter of 2500 seed points, which has been verified by previous experiments.
Table 3 compares the overall classification performance of different superpixel feature combinations. The experimental results show that the classification effect of the feature combination with
is improved. The classification accuracy of
is 95.74%, and its classification result is shown in
Figure 8b. It is worth mentioning that when the feature combination is
, its classification accuracy is not as high as that of the
. This performance degradation is likely because
does not contribute new and valuable scattering information. As shown in
Table 1, the classification performance of
alone is poor. The scattering mechanism information provided by
lacks sufficient discriminative power for the crop types in this study. During the growth stages, the scattering mechanism for most of these crops is predominantly volume scattering. Consequently, their
values are concentrated within a range of approximately 45° to 90°, which cannot provide the distinctive information needed to differentiate among these categories.
To further evaluate the model’s classification performance under the optimal parameter settings, 2500 seed points and the
feature combination, we analyze the classification accuracy for each crop class in detail.
Table 4 presents the classification confusion matrix, while
Table 5 lists the Producer’s Accuracy (PA) and User’s Accuracy (UA) for each category.
The model demonstrates strong discriminative ability for wheat, beet, potato, and grass, but its classification performance for corn is comparatively poor. It is noteworthy that while the PA for corn reaches a perfect 1.0000, its UA is only 0.6146. Upon analysis, this discrepancy does not stem from issues in the model’s algorithmic design, architecture, or training optimization. Instead, it is attributed to the significantly low proportion of corn samples in the dataset. Out of a total of 32,922 labeled pixels in the entire dataset, only 1248 are labeled as corn, accounting for just 3.79%. After superpixel segmentation, the number of superpixels corresponding to corn becomes even smaller. This scarcity means that during the training phase, the model’s learning of corn features is concentrated on an extremely limited set of examples. It becomes highly proficient at identifying these few specific samples in the training set, leading to the high PA. However, in practical scenarios where sample distribution is more diverse and complex, the model lacks learning experience from a sufficient variety of corn samples. This makes it difficult to effectively distinguish other classes from corn, causing a large number of non-corn samples to be misclassified as corn. Consequently, the UA value is substantially lower.
3.2.3. Comparative Performance Analysis of HGNN and Other Classification Models
In order to evaluate the effectiveness of the HGNN, experiments were conducted to compare and analyze the classification performance of the other two typical classification models, namely, the random forest (RF) and the graph neural network (GNN), based on different scattering features. The relevant experiments were conducted with seed points of 2500 and the same superpixel features as the input. From the experimental results in
Table 6, it can be seen that the different models show obvious differences. The RF classifier has a lower accuracy compared to the other two models, with its classification accuracy only ranging from about 74.54% to 80.45%. This is due to its structure based on decision tree integration, which has some limitations in dealing with complex feature information, and it does not consider spatial relationships, making it difficult to fully explore the potential relationships in the data. The classification accuracy of the GNN model is obviously improved compared to the RF, with its classification accuracy ranging from 82.45% to 93.17%. This is due to its ability to effectively capture the graph structure information in the data and better utilize the correlation relationship between the data when dealing with features. The HGNN model performs better, with a classification accuracy ranging from 85% to 95.74%. As a more advanced model architecture, the HGNN has a unique advantage in dealing with higher-order relationships and complex structured data, and it can extract the key information of scattering features with greater accuracy, thus achieving higher accuracy and better performance.
3.3. Methodological Applicability, Limitations and Future Research
This method is suitable for dealing with complex crop classification with multi-temporal dual polarimetric SAR data, especially for solving the fine classification problem of crops with uneven spatial distribution, such as broken farmland and mixed planting areas. By improving SLIC superpixel segmentation through the united multi-temporal dual polarimetric covariance matrix, it can effectively resist the interference of temporal differences and capture the crop boundaries. Combined with the HGNN, when constructing the higher-order spatial correlation among the obtained superpixels, the classification accuracy of farmland parcels is obviously improved. However, its performance relies on high-quality and continuous temporal polarimetric SAR data.
In the future, the superpixel segmentation algorithm can be adaptively adjusted in real time according to the crop growth state, so that the segmentation process not only considers the spatial characteristics, but also dynamically combines the temporal changes and crop physiological parameters to realize on-demand and accurate segmentation.