MSRGAN: A Multi-Scale Residual GAN for High-Resolution Precipitation Downscaling
Abstract
1. Introduction
- We propose MSRGAN, a generative adversarial network that integrates multi-source meteorological data and high-resolution topographic priors. Through the joint design of deep convolution, attention mechanisms, and residual connections, MSRGAN effectively enhances the spatial resolution and predictive consistency of precipitation maps.
- We design a Deep Multi-Scale Perception Module (DeepInception) and a Multi-Scale Feature Modulation Module (MSFM), which can simultaneously model both local and global precipitation features. These modules address the limitations of traditional models in terms of receptive field size and their difficulty in identifying long-range precipitation structures.
- We introduce a Spatial-Channel Collaborative Attention Network (SCAN) and a conditional feature fusion mechanism to enable joint modeling across spatial and channel dimensions. This design improves the model’s capability to capture complex precipitation distribution patterns and enhances the fidelity of fine-scale details.
- We conduct both quantitative and qualitative experiments on real WRF simulation data under multiple precipitation intensity thresholds. The results demonstrate the superiority of the proposed model in extreme precipitation detection, spatial structure reconstruction, and false alarm suppression.
2. Methods
2.1. Definition of the Problem
2.2. Overall Architecture Design
2.2.1. Deep Multi-Scale Perception Module (DeepInception)
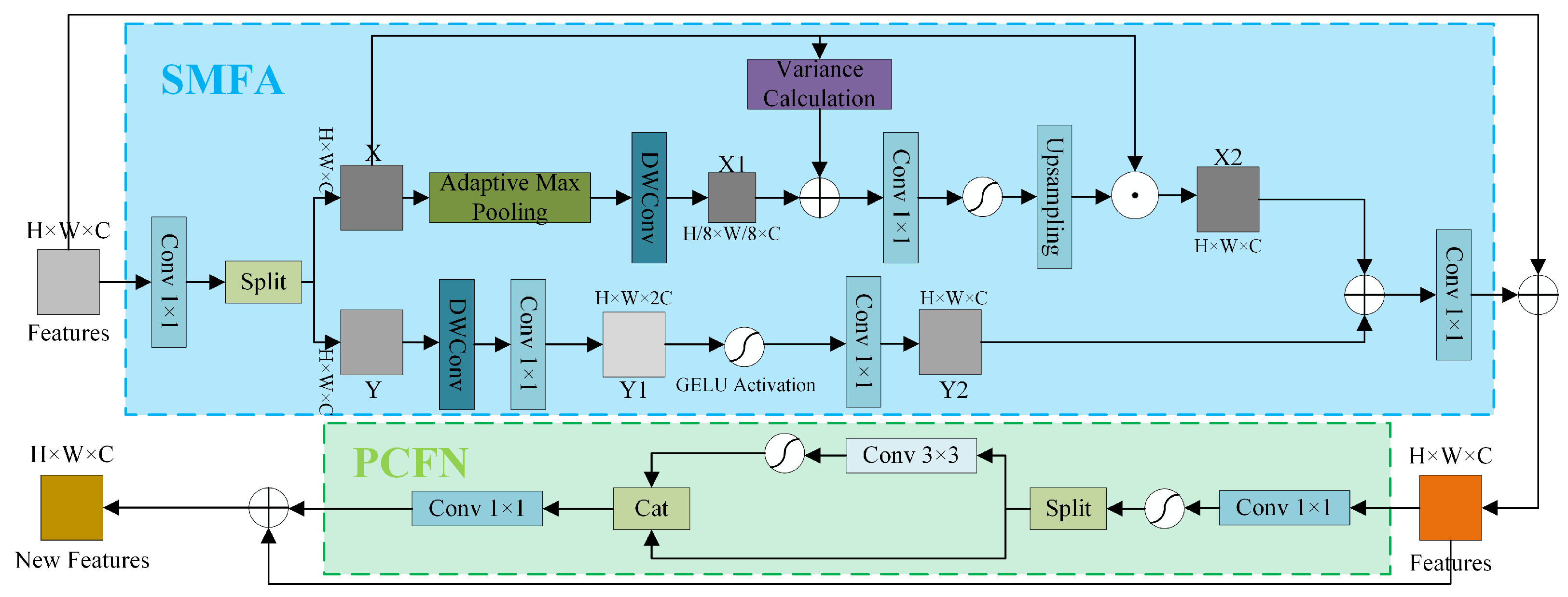
2.2.2. Multi-Scale Feature Modulation (MSFM) Module
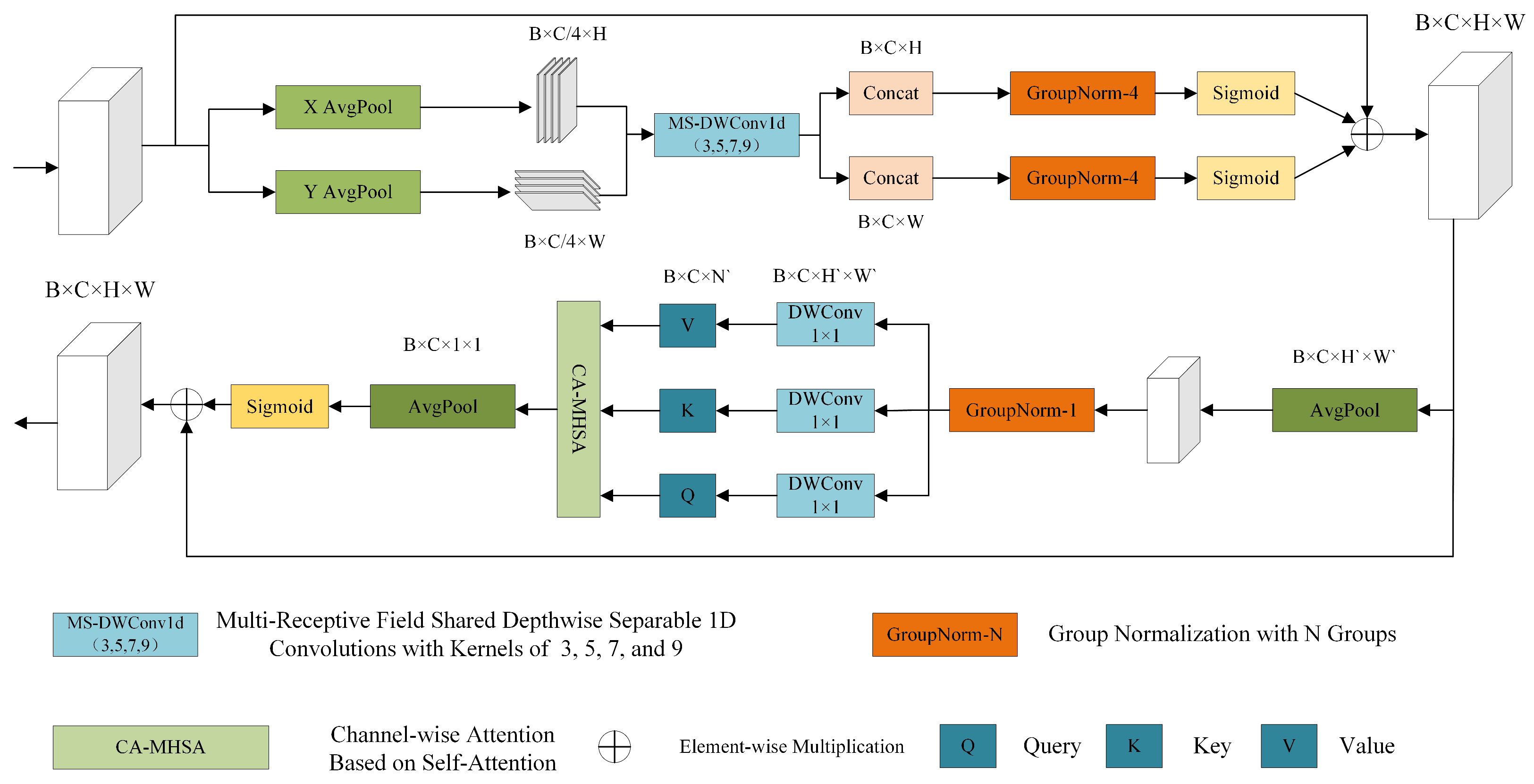
2.2.3. Spatial-Channel Attention Network (SCAN)
3. Data and Experimental Configuration
3.1. Dateset
3.2. Implementation Details
3.3. Evaluation Metrics
4. Experimental Results and Analysis
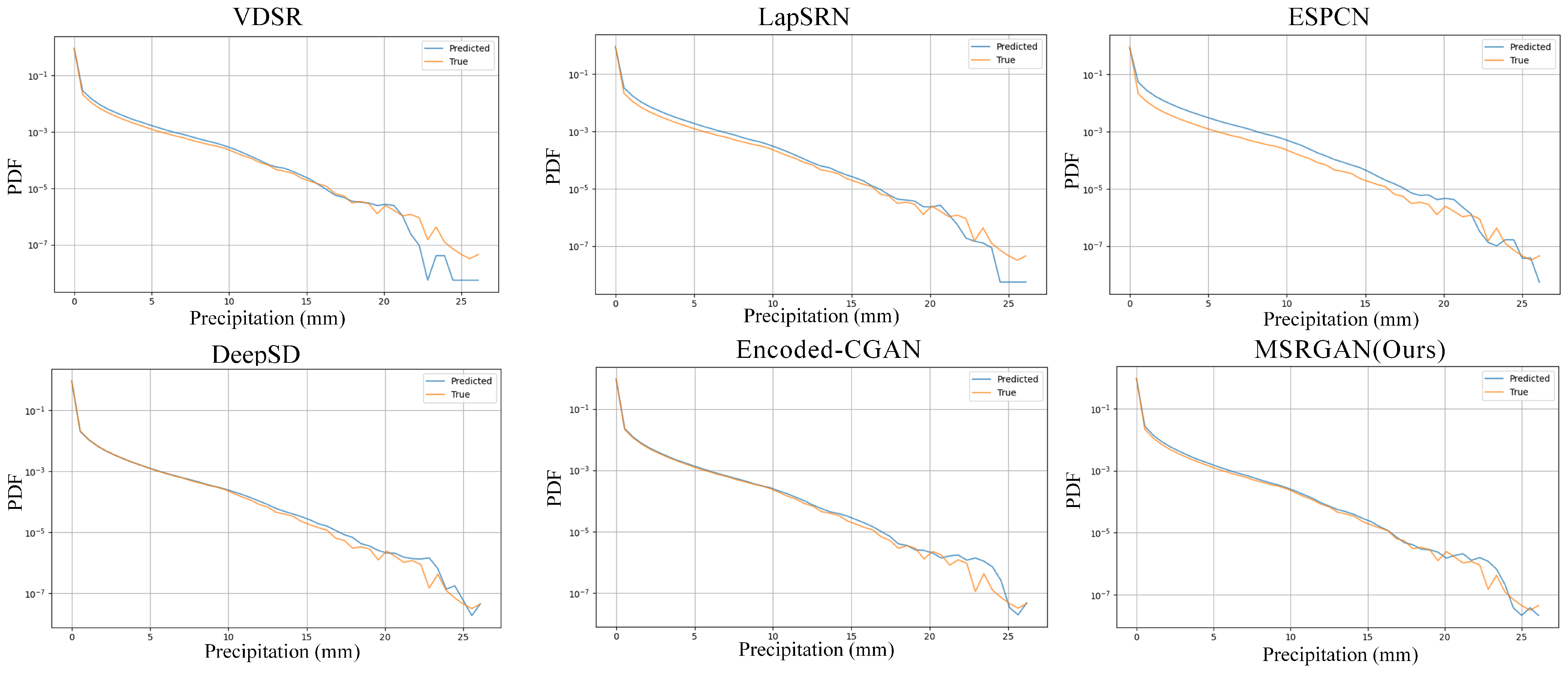
4.1. Evaluation of Downscaling Methods Using the Probability Density Function (PDF)
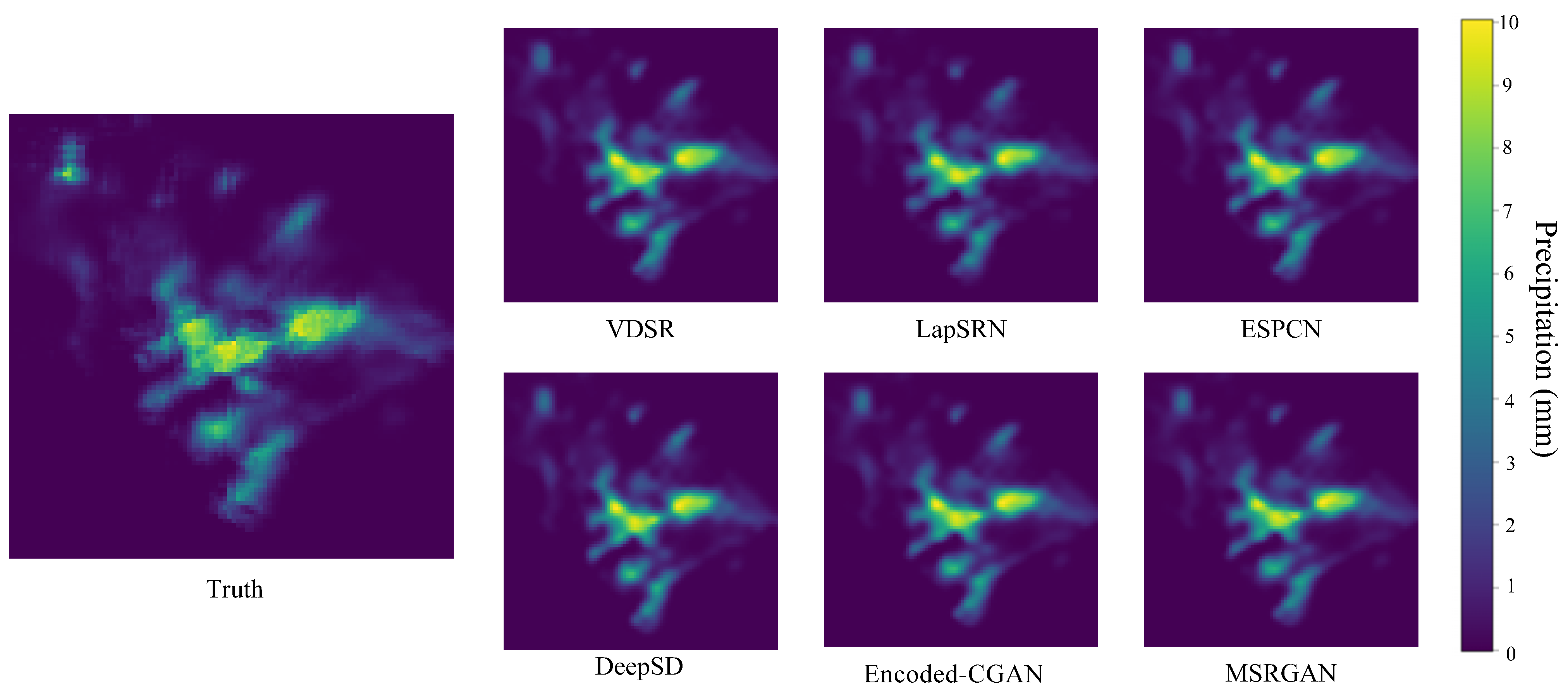
4.2. Model Evaluation Analysis
4.3. Ablation Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kotz, M.; Levermann, A.; Wenz, L. The effect of rainfall changes on economic production. Nature 2022, 601, 223–227. [Google Scholar] [CrossRef]
- Lesk, C.; Coffel, E.; Horton, R. Net benefits to US soy and maize yields from intensifying hourly rainfall. Nat. Clim. Change 2020, 10, 819–822. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the dependence of satellite rainfall uncertainty on topography and climate for hydrologic model simulation. IEEE Trans. Geosci. Remote Sens. 2012, 51, 704–718. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust responses of the hydrological cycle to global warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Koizumi, K.; Ishikawa, Y.; Tsuyuki, T. Assimilation of precipitation data to the JMA mesoscale model with a four-dimensional variational method and its impact on precipitation forecasts. Sola 2005, 1, 45–48. [Google Scholar] [CrossRef]
- Ricciardelli, E.; Di Paola, F.; Gentile, S.; Cersosimo, A.; Cimini, D.; Gallucci, D.; Geraldi, E.; Larosa, S.; Nilo, S.T.; Ripepi, E.; et al. Analysis of Livorno heavy rainfall event: Examples of satellite-based observation techniques in support of numerical weather prediction. Remote Sens. 2018, 10, 1549. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, C.; Chen, S.; Zha, X.; Ma, Q. Review of post-processing research for remote-sensing precipitation products. Adv. Water Sci. 2021, 32, 627–637. [Google Scholar]
- Wang, H.; Wang, G.; Liu, L. Climatological beam propagation conditions for China’s weather radar network. J. Appl. Meteorol. Climatol. 2018, 57, 3–14. [Google Scholar] [CrossRef]
- Stevens, B.; Satoh, M.; Auger, L.; Biercamp, J.; Bretherton, C.S.; Chen, X.; Düben, P.; Judt, F.; Khairoutdinov, M.; Klocke, D.; et al. DYAMOND: The DYnamics of the Atmospheric general circulation Modeled On Non-hydrostatic Domains. Prog. Earth Planet. Sci. 2019, 6, 1–17. [Google Scholar] [CrossRef]
- Vandal, T.; Kodra, E.; Ganguly, S.; Michaelis, A.; Nemani, R.; Ganguly, A.R. Deepsd: Generating high resolution climate change projections through single image super-resolution. In Proceedings of the 23rd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1663–1672. [Google Scholar]
- Wang, J.; Liu, Z.; Foster, I.; Chang, W.; Kettimuthu, R.; Kotamarthi, V.R. Fast and accurate learned multiresolution dynamical downscaling for precipitation. Geosci. Model Dev. Discuss. 2021, 2021, 1–24. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, J.; Kuang, Q.; Xu, Z.; Shen, C.; Liu, W.; Zhou, K. DeepDT: Generative adversarial network for high-resolution climate prediction. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1001105. [Google Scholar] [CrossRef]
- Li, Z.; Lu, Z.; Zhang, Y.; Li, Y. PSRGAN: Generative Adversarial Networks for Precipitation Downscaling. IEEE Geosci. Remote Sens. Lett. 2025, 22, 1001005. [Google Scholar] [CrossRef]
- Tang, J.; Niu, X.; Wang, S.; Gao, H.; Wang, X.; Wu, J. Statistical downscaling and dynamical downscaling of regional climate in China: Present climate evaluations and future climate projections. J. Geophys. Res. Atmos. 2016, 121, 2110–2129. [Google Scholar] [CrossRef]
- Taillardat, M.; Mestre, O.; Zamo, M.; Naveau, P. Calibrated ensemble forecasts using quantile regression forests and ensemble model output statistics. Mon. Weather Rev. 2016, 144, 2375–2393. [Google Scholar] [CrossRef]
- Chaney, N.W.; Herman, J.D.; Ek, M.B.; Wood, E.F. Deriving global parameter estimates for the Noah land surface model using FLUXNET and machine learning. J. Geophys. Res. Atmos. 2016, 121, 13–218. [Google Scholar] [CrossRef]
- He, X.; Chaney, N.W.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A comparison of different regression algorithms for downscaling monthly satellite-based precipitation over North China. Remote Sens. 2016, 8, 835. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Qin, B.; Zhao, S.; Duan, Z. Comparison of different methods for spatial downscaling of GPM IMERG V06B satellite precipitation product over a typical arid to semi-arid area. Front. Earth Sci. 2020, 8, 536337. [Google Scholar] [CrossRef]
- Ebrahimy, H.; Aghighi, H.; Azadbakht, M.; Amani, M.; Mahdavi, S.; Matkan, A.A. Downscaling MODIS land surface temperature product using an adaptive random forest regression method and Google Earth Engine for a 19-years spatiotemporal trend analysis over Iran. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2103–2112. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
- Sharma, S.C.M.; Mitra, A. ResDeepD: A residual super-resolution network for deep downscaling of daily precipitation over India. Environ. Data Sci. 2022, 1, e19. [Google Scholar] [CrossRef]
- Tu, T.; Ishida, K.; Ercan, A.; Kiyama, M.; Amagasaki, M.; Zhao, T. Hybrid precipitation downscaling over coastal watersheds in Japan using WRF and CNN. J. Hydrol. Reg. Stud. 2021, 37, 100921. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, K.; Shao, C.; Zhou, X.; Zhao, L.; Chen, Y.; Wu, H. A downscaling approach for constructing high-resolution precipitation dataset over the Tibetan Plateau from ERA5 reanalysis. Atmos. Res. 2021, 256, 105574. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Price, I.; Rasp, S. Increasing the accuracy and resolution of precipitation forecasts using deep generative models. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Virtual, 28–30 March 2022; pp. 10555–10571. [Google Scholar]
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-enhanced GAN for remote sensing image superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Yang, F.; Ye, Q.; Wang, K.; Sun, L. Successful Precipitation Downscaling Through an Innovative Transformer-Based Model. Remote Sens. 2024, 16, 4292. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 624–632. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Hu, Y.; Tian, S.; Ge, J. Hybrid convolutional network combining multiscale 3D depthwise separable convolution and CBAM residual dilated convolution for hyperspectral image classification. Remote Sens. 2023, 15, 4796. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]


| Variable Description (Units) | Value Range |
|---|---|
| 50 km, 3-hourly precipitation (mm/3 h) | [0.05, 29.30] |
| 50 km, 3-hourly SLP (hPa) | [990.97, 1039.34] |
| 50 km, 3-hourly IWV (cm) | [1.56, 116.46] |
| 50 km, 3-hourly T2 (K) | [241.75, 310.35] |
| 12 km, topographic height (m) | [0, 3204.51] |
| Output | |
| 12 km, 3-hourly precipitation (mm/3 h) | [0.05, 31.62] |
| Method | CSI | HSS | FAR | J-S | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 5 | 10 | 0.5 | 5 | 10 | 0.5 | 5 | 10 | ||||
| Interpolator | 0.8125 | 0.7171 | 0.5741 | 0.8894 | 0.8341 | 0.7292 | 0.1147 | 0.1573 | 0.2422 | 0.0622 | ||
| VDSR | 0.8697 | 0.6669 | 0.3418 | 0.4626 | 0.3785 | 0.2144 | 0.0764 | 0.1135 | 0.1343 | 0.0303 | ||
| LapSRN | 0.8544 | 0.6441 | 0.3313 | 0.9157 | 0.7390 | 0.4160 | 0.0779 | 0.1071 | 0.1478 | 0.0436 | ||
| ESPCN | 0.8663 | 0.6825 | 0.3640 | 0.4616 | 0.3828 | 0.2229 | 0.0857 | 0.0967 | 0.1459 | 0.1065 | ||
| DeepSD | 0.8790 | 0.8056 | 0.6437 | 0.9321 | 0.8916 | 0.7830 | 0.0537 | 0.1251 | 0.2798 | 0.0033 | ||
| Encoded-CGAN | 0.8847 | 0.8038 | 0.6507 | 0.9347 | 0.8905 | 0.7882 | 0.0490 | 0.0648 | 0.1239 | 0.0064 | ||
| MSRGAN (Ours) | 0.8859 | 0.8088 | 0.6521 | 0.9353 | 0.8935 | 0.7892 | 0.0599 | 0.0911 | 0.1582 | 0.0200 | ||
| Ablation Setting | CSI | HSS | FAR |
|---|---|---|---|
| Replace DeepInception with Inception | 0.8789 | 0.9312 | 0.0484 |
| Without DeepInception | 0.8833 | 0.9339 | 0.0531 |
| Without MSFM | 0.8791 | 0.9312 | 0.0668 |
| Use 1 MSFM per stage | 0.8772 | 0.9302 | 0.0436 |
| Use 2 MSFMs per stage | 0.8817 | 0.9329 | 0.0489 |
| Replace SCAN with CBAM | 0.8820 | 0.9331 | 0.0487 |
| Ours (Full MSRGAN) | 0.8859 | 0.9353 | 0.0599 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, Z.; Cao, G.; Wang, Q.; Li, Y.; Lu, Z. MSRGAN: A Multi-Scale Residual GAN for High-Resolution Precipitation Downscaling. Remote Sens. 2025, 17, 2281. https://doi.org/10.3390/rs17132281
Liu Y, Li Z, Cao G, Wang Q, Li Y, Lu Z. MSRGAN: A Multi-Scale Residual GAN for High-Resolution Precipitation Downscaling. Remote Sensing. 2025; 17(13):2281. https://doi.org/10.3390/rs17132281
Chicago/Turabian StyleLiu, Yida, Zhuang Li, Guangzhen Cao, Qiong Wang, Yizhe Li, and Zhenyu Lu. 2025. "MSRGAN: A Multi-Scale Residual GAN for High-Resolution Precipitation Downscaling" Remote Sensing 17, no. 13: 2281. https://doi.org/10.3390/rs17132281
APA StyleLiu, Y., Li, Z., Cao, G., Wang, Q., Li, Y., & Lu, Z. (2025). MSRGAN: A Multi-Scale Residual GAN for High-Resolution Precipitation Downscaling. Remote Sensing, 17(13), 2281. https://doi.org/10.3390/rs17132281





