Physically Based and Data-Driven Models for Landslide Susceptibility Assessment: Principles, Applications, and Challenges
Abstract
1. Introduction
2. Construction and Analysis of the Literature Database
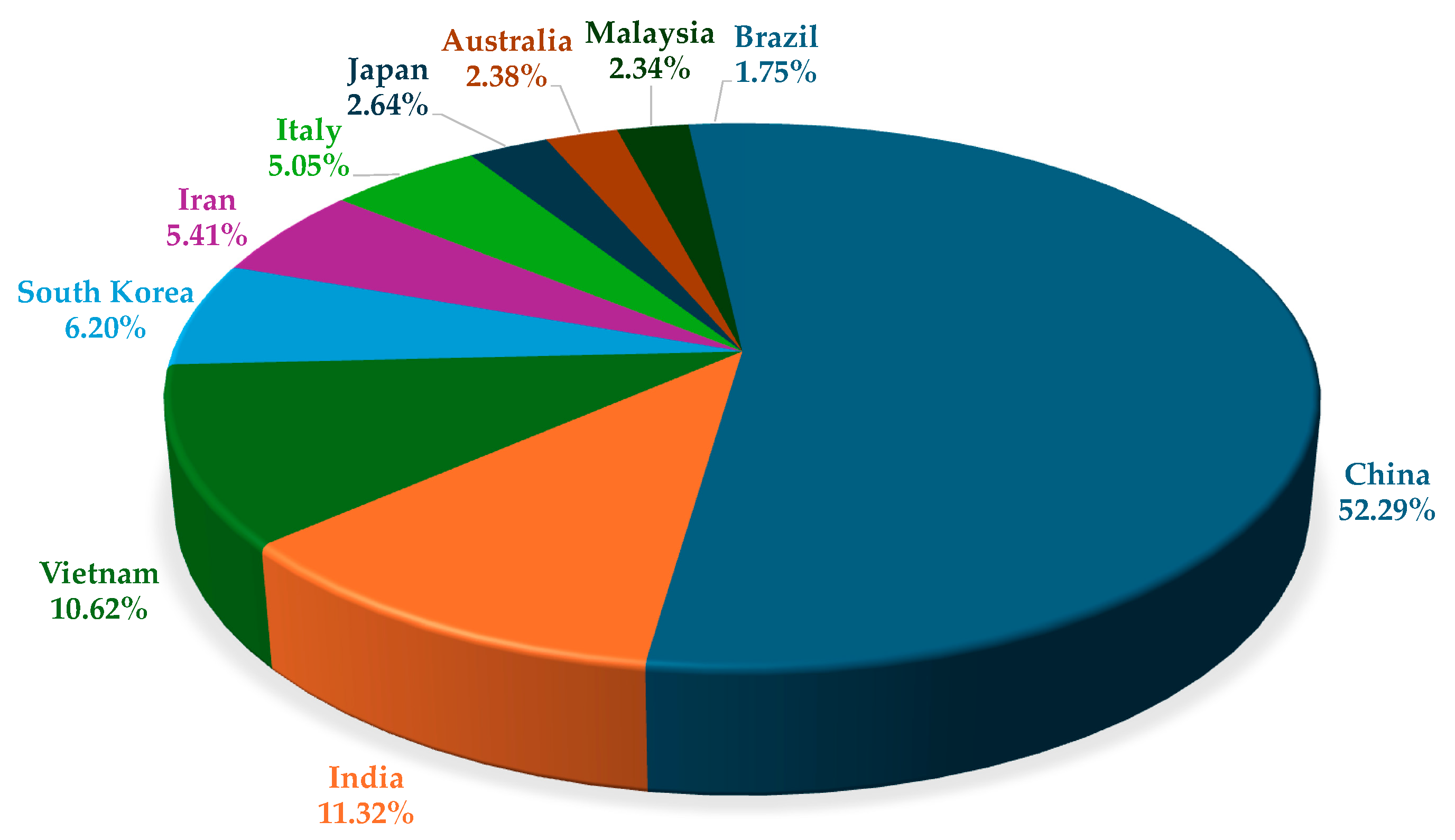
2.1. Information on Articles
2.2. Overview of Whole Landslide Susceptibility Studies
2.3. Overview of Studies Using Physically Based Models
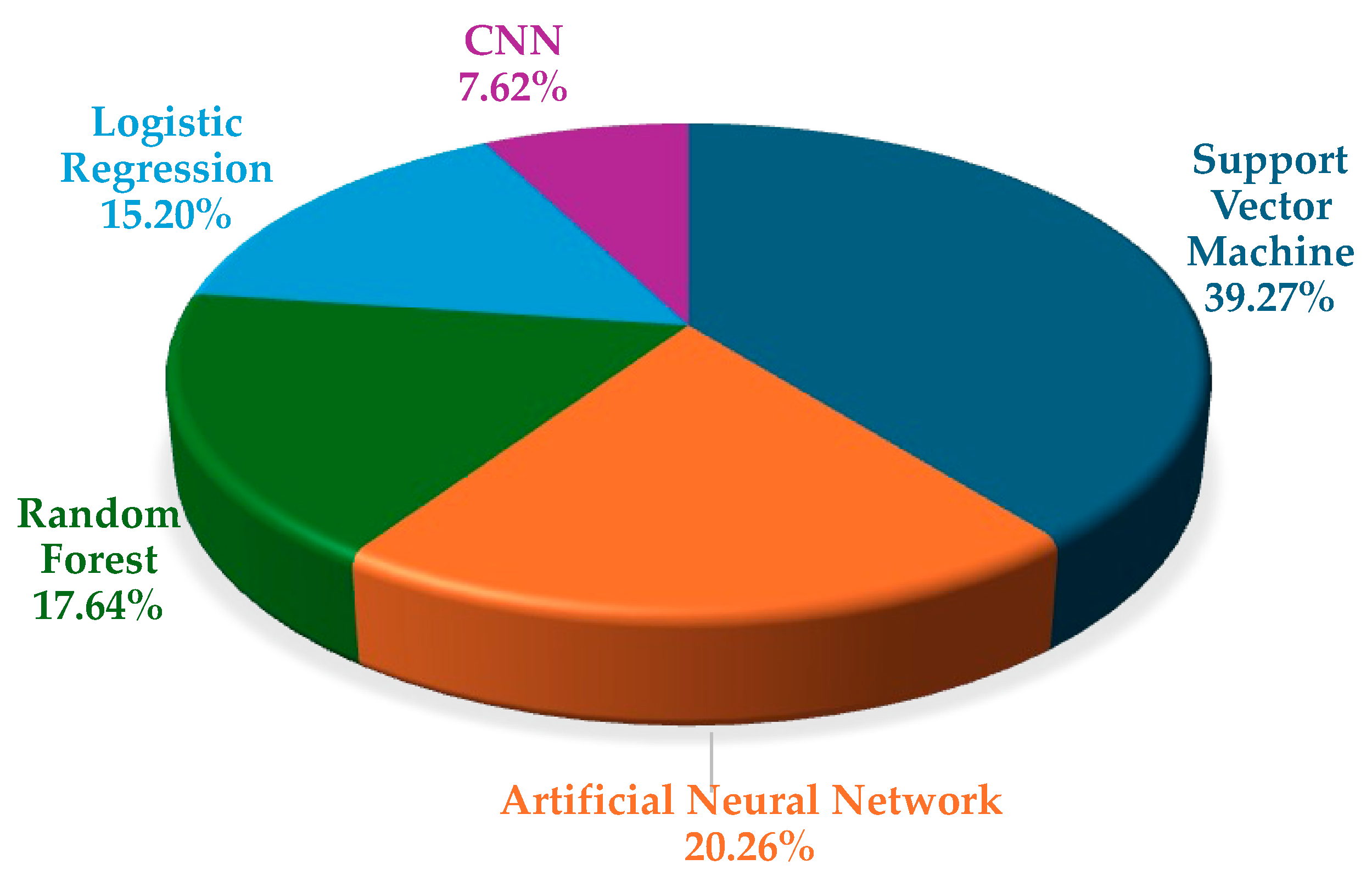
2.4. Overview of Landslide Susceptibility Studies Related to Data-Driven Models
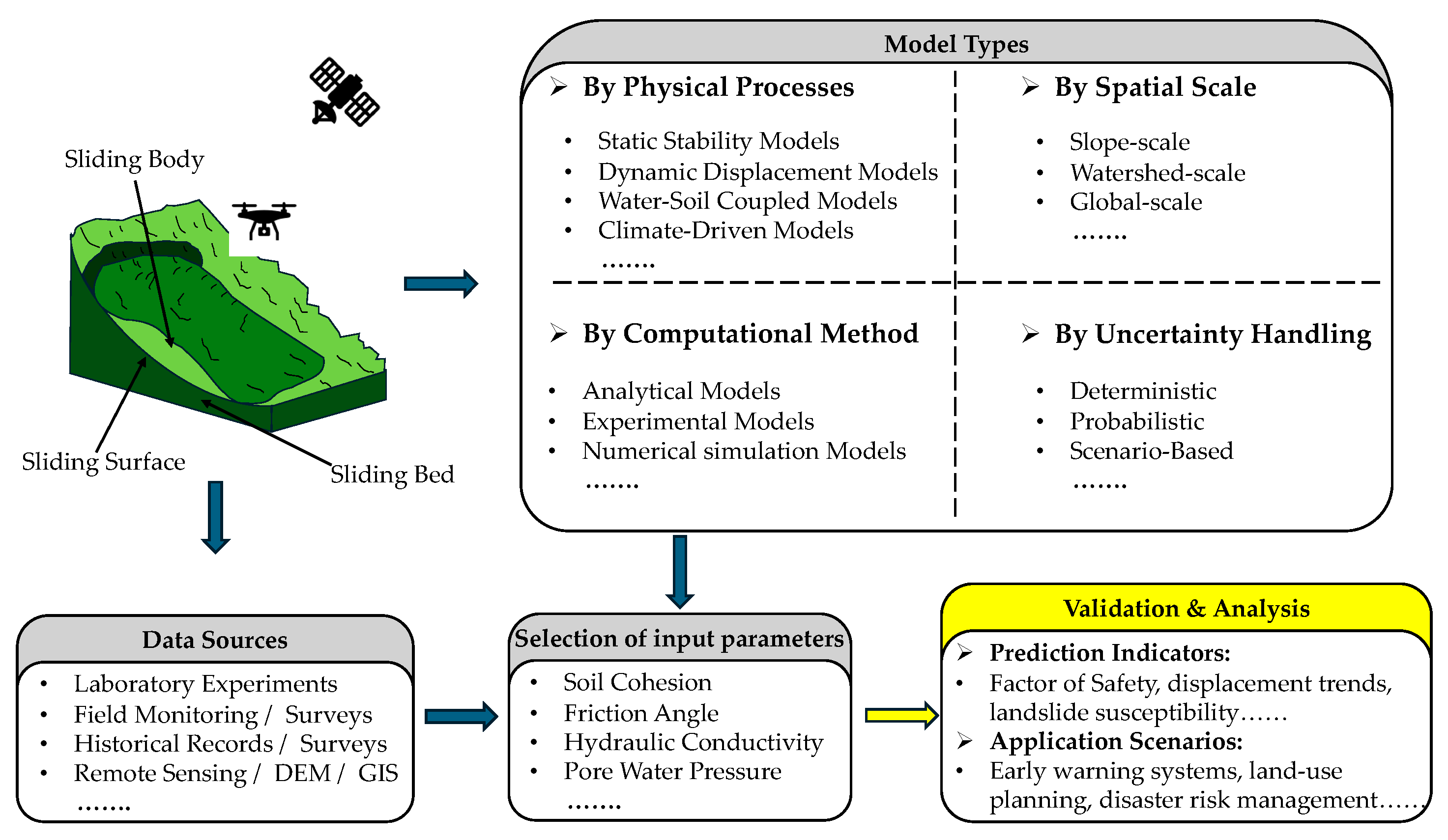
3. Physically Based Models for Landslide Susceptibility Assessment
3.1. Principles for Physically Based Models
3.2. Selection of Input Parameters in Physically Based Models
3.3. Classification of Physically Based Models by Processes
3.3.1. Static Stability Models
3.3.2. Dynamic Displacement Prediction Models
3.3.3. Water–Soil Coupled Models
3.3.4. Climate-Driven Models
3.4. Classification of Physically Based Models by Spatial Scales
3.5. Classification of Physically Based Models by Computational Methods
3.5.1. Analytical Models
3.5.2. Numerical Models
3.5.3. Experimental Models
3.6. Classification of Physically Based Models by Uncertainty Handling Methods
3.6.1. Deterministic Models
3.6.2. Probabilistic Models
3.6.3. Scenario-Based Models
3.7. Strengths and Limitations of Physically Based Models
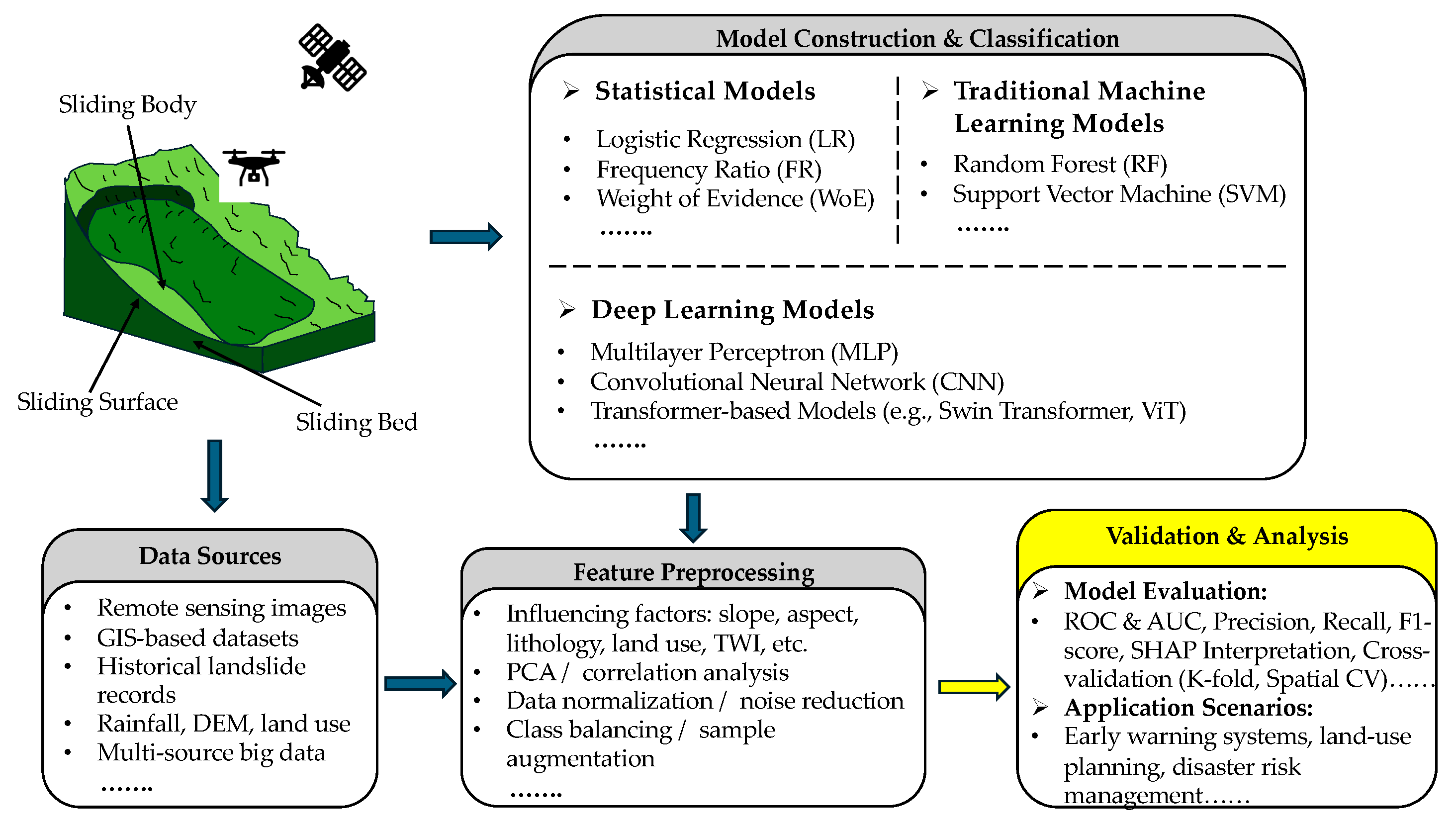
4. Data-Driven Models for Landslide Susceptibility Assessment
4.1. Principles for Data-Driven Models
4.2. Selection of Input Parameters in Data-Driven Models
4.3. Classification of Statistical Models for Landslide Susceptibility
4.3.1. Logistic Regression
4.3.2. Frequency Ratio
4.3.3. Weight of Evidence
4.4. Classification of Traditional Machine Learning Models for Landslide Susceptibility
4.4.1. Support Vector Machines
4.4.2. Random Forest
4.5. Classification of Deep Learning Models for Landslide Susceptibility
4.5.1. Multilayer Perceptron
4.5.2. Convolutional Neural Network
4.5.3. Transformer-Based Model
4.6. Evaluation Metrics and Methods
4.7. Strengths and Limitations of Data-Driven Models
5. Discussion and Prospect for Future Research
5.1. Multi-Level Integration Framework for Landslide Susceptibility Prediction
5.2. Multi-Source and Multi-Scale Data Fusion for Physically Based and Data-Driven Models
5.3. Parameter Optimization and Uncertainty Quantification in Physically Based and Data-Driven Models
5.4. Enhancing Regional Transferability of Physically Based and Data-Driven Models
5.5. Improving Interpretability in Physically Based and Data-Driven Models
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Turner, A.K.; Schuster, R.L. Landslides: Investigation and Mitigation; Special Report 247; National Academy Press: Washington, DC, USA, 1996; ISBN 9780309061513. [Google Scholar]
- Zhao, C.; Lu, Z. Remote sensing of landslides—A review. Remote Sens. 2018, 10, 279. [Google Scholar] [CrossRef]
- Metternicht, G.; Hurni, L.; Gogu, R. Remote sensing of landslides: An analysis of the potential contribution to geo-spatial systems for hazard assessment in mountainous environments. Remote Sens. Environ. 2005, 98, 284–303. [Google Scholar] [CrossRef]
- Lan, H.; Liu, X.; Li, L.; Li, Q.; Tian, N.; Peng, J. Remote sensing precursors analysis for giant landslides. Remote Sens. 2022, 14, 4399. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Risk Reduction (UNDRR). Available online: https://www.undrr.org/ (accessed on 27 February 2025).
- Van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, J. Regional Landslide Susceptibility Assessment and Model Adaptability Research. Remote Sens. 2024, 16, 2305. [Google Scholar] [CrossRef]
- Ge, R.; Chen, J.; Ma, S.; Tan, H. Inventory and Spatial Distribution of Landslides on the Eastern Slope of Gongga Mountain, Southwest China. Remote Sens. 2024, 16, 3360. [Google Scholar] [CrossRef]
- Liu, S.; Du, J.; Yin, K.; Zhou, C.; Huang, C.; Jiang, J.; Yu, J. Regional early warning model for rainfall induced landslide based on slope unit in Chongqing, China. Eng. Geol. 2024, 333, 107464. [Google Scholar] [CrossRef]
- Zheng, W.; Cao, Y.; Fan, W.; Liang, X.; Yuan, S.; Guo, Q.; Zhang, J. Influence of faults on landslide formation and distribution: Insights from the Hanwang Fault Zone in the Qinling-Daba Mountains, China. Geomorphology 2025, 472, 109603. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, L.M.; Chen, H.X.; Fei, K.; Hong, Y. Topography and geology effects on travel distances of natural terrain landslides: Evidence from a large multi-temporal landslide inventory in Hong Kong. Eng. Geol. 2021, 292, 106266. [Google Scholar] [CrossRef]
- Liu, Q.; Jian, W.; Nie, W. Rainstorm-induced landslides early warning system in mountainous cities based on groundwater level change fast prediction. Sustain. Cities Soc. 2021, 69, 102817. [Google Scholar] [CrossRef]
- Miklin, L.; Podolszki, L.; Gulam, V.; Markotić, I. The Impact of Climate Changes on Slope Stability and Landslide Conditioning Factors: An Example from Kravarsko, Croatia. Remote Sens. 2022, 14, 1794. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Mao, H. Influence of human activity on landslide susceptibility development in the Three Gorges area. Nat. Hazards 2020, 104, 2115–2151. [Google Scholar] [CrossRef]
- Kaushal, S.; Thanveer, J.; ul Islam, S.M.; Negi, A.; Dhanshyan, A.; Beetan, Y.; Subramanian, S.S.; Sajinkumar, K.S.; Yunus, A.P. Unveiling the amplifying impact: Anthropogenic activities and the two-fold surge in landslides in the Lesser Himalayas. CATENA 2025, 250, 108771. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, C.; Nie, R.; Zhang, W.; Zhang, L.; Zhang, Z.; Li, W.; Liu, G.; Dai, X.; Zhang, D.; et al. Research on uncertainty of landslide susceptibility prediction—Bibliometrics and knowledge graph analysis. Remote Sens. 2022, 14, 3879. [Google Scholar] [CrossRef]
- Bao, H.; Zeng, C.; Peng, Y.; Wu, S. The use of digital technologies for landslide disaster risk research and disaster risk management: Progress and prospects. Environ. Earth Sci. 2022, 81, 446. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z.; JTC-1 Joint Technical Committee on Landslides and Engineered Slopes. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef]
- Kumari, S.; Agarwal, S.; Agrawal, N.K.; Agarwal, A.; Garg, M.C. A Comprehensive Review of Remote Sensing Technologies for Improved Geological Disaster Management. Geol. J. 2025, 60, 223–235. [Google Scholar] [CrossRef]
- Ali, R.A.; Mannakkara, S. Phased post-disaster recovery challenges: 2016–2017 floods and landslides in Colombo and Kalutara, Sri Lanka. Int. J. Disaster Risk Reduct. 2024, 111, 104728. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, L.; Gardoni, P.; Chen, Y.; Tan, L.; Liu, D.; Du, C.; Li, H. Comparison of hybrid data-driven and physical models for landslide susceptibility mapping at regional scales. Acta Geotech. 2023, 18, 4453–4476. [Google Scholar] [CrossRef]
- Yu, L.; Zhou, C.; Wang, Y.; Cao, Y.; Peres, D.J. Coupling data- and knowledge-driven methods for landslide susceptibility mapping in human-modified environments: A case study from Wanzhou County, Three Gorges Reservoir Area, China. Remote Sens. 2022, 14, 774. [Google Scholar] [CrossRef]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.K.A.; Gerber, W.; Jaboyedoff, M. Rockfall characterisation and structural protection—A review. Nat. Hazards Earth Syst. Sci. 2011, 11, 2617–2651. [Google Scholar] [CrossRef]
- Terlien, M.T. The determination of statistical and deterministic hydrological landslide-triggering thresholds. Environ. Geol. 1998, 35, 124–130. [Google Scholar] [CrossRef]
- Van Asch, T.W.; Malet, J.P.; van Beek, L.P.; Amitrano, D. Techniques, issues and advances in numerical modelling of landslide hazard. Bull. Soc. Géol. Fr. 2007, 178, 65–88. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Xie, Y.; Yu, F.; Peng, L. Research on progressive failure process of Baishuihe landslide based on Monte Carlo model. Stoch. Environ. Res. Risk Assess. 2017, 31, 1683–1696. [Google Scholar] [CrossRef]
- do Pinho, T.M.; Augusto Filho, O. Landslide susceptibility mapping using the infinite slope, SHALSTAB, SINMAP, and TRIGRS models in Serra do Mar, Brazil. J. Mt. Sci. 2022, 19, 1018–1036. [Google Scholar] [CrossRef]
- Dietrich, W.E.; Bellugi, D.; Real de Asua, R. Validation of the shallow landslide model, SHALSTAB, for forest management. Land Use Watersheds Hum. Influ. Hydrol. Geomorphol. Urban For. Areas 2001, 2, 195–227. [Google Scholar] [CrossRef]
- Pack, R.T.; Tarboton, D.G.; Goodwin, C.N. The SINMAP Approach to Terrain Stability Mapping. Available online: https://digitalcommons.usu.edu/cee_facpub/2583/ (accessed on 27 February 2025).
- Alvioli, M.; Baum, R.L. Parallelization of the TRIGRS model for rainfall-induced landslides using the message passing interface. Environ. Model. Softw. 2016, 81, 122–135. [Google Scholar] [CrossRef]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. CATENA 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Chen, Q.; Ge, Y.; Tang, H. Rock discontinuities characterization from large-scale point clouds using a point-based deep learning method. Eng. Geol. 2024, 337, 107585. [Google Scholar] [CrossRef]
- Yang, X.; Liu, R.; Yang, M.; Chen, J.; Liu, T.; Yang, Y.; Chen, W.; Wang, Y. Incorporating landslide spatial information and correlated features among conditioning factors for landslide susceptibility mapping. Remote Sens. 2021, 13, 2166. [Google Scholar] [CrossRef]
- Chen, X.W.; Lin, X. Big data deep learning: Challenges and perspectives. IEEE Access 2014, 2, 514–525. [Google Scholar] [CrossRef]
- Chen, L.; Ma, P.; Fan, X.; Wang, X.; Ng, C.W.W. A knowledge-aware deep learning model for landslide susceptibility assessment in Hong Kong. Sci. Total Environ. 2024, 941, 173557. [Google Scholar] [CrossRef] [PubMed]
- Feng, D.; Beck, H.; Lawson, K.; Shen, C. The suitability of differentiable, physics-informed machine learning hydrologic models for ungauged regions and climate change impact assessment. Hydrol. Earth Syst. Sci. 2023, 27, 2357–2373. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Goetz, J.N.; Guthrie, R.H.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Salciarini, D.; Godt, J.W.; Savage, W.Z.; Conversini, P.; Baum, R.L.; Michael, J.A. Modeling regional initiation of rainfall-induced shallow landslides in the eastern Umbria Region of central Italy. Landslides 2006, 3, 181–194. [Google Scholar] [CrossRef]
- Cervi, F.; Berti, M.; Borgatti, L.; Ronchetti, F.; Manenti, F.; Corsini, A. Comparing predictive capability of statistical and deterministic methods for landslide susceptibility mapping: A case study in the northern Apennines (Reggio Emilia Province, Italy). Landslides 2010, 7, 433–444. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Gessler, P.E.; Boll, J.; Elliot, W.J.; Foltz, R.B. Spatially and temporally distributed modeling of landslide susceptibility. Geomorphology 2006, 80, 178–198. [Google Scholar] [CrossRef]
- Ciurleo, M.; Cascini, L.; Calvello, M. A comparison of statistical and deterministic methods for shallow landslide susceptibility zoning in clayey soils. Eng. Geol. 2017, 223, 71–81. [Google Scholar] [CrossRef]
- Bogaard, T.A.; Greco, R. Landslide hydrology: From hydrology to pore pressure. Wiley Interdiscip. Rev. Water 2016, 3, 439–459. [Google Scholar] [CrossRef]
- Gallen, S.F.; Clark, M.K.; Godt, J.W.; Roback, K.; Niemi, N.A. Application and evaluation of a rapid response earthquake-triggered landslide model to the 25 April 2015 Mw 7.8 Gorkha earthquake, Nepal. Tectonophysics 2017, 714, 173–187. [Google Scholar] [CrossRef]
- Sun, X.; Chen, G.; Yang, X.; Xu, Z.; Yang, J.; Lin, Z.; Liu, Y. A process-oriented approach for identifying potential landslides considering time-dependent behaviors beyond geomorphological features. J. Rock Mech. Geotech. Eng. 2024, 16, 961–978. [Google Scholar] [CrossRef]
- Labuz, J.F.; Zang, A. Mohr–Coulomb Failure Criterion. Rock Mech. Rock Eng. 2012, 45, 975–979. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P. Distributed modelling of shallow landslides triggered by intense rainfall. Nat. Hazards Earth Syst. Sci. 2003, 3, 81–93. [Google Scholar] [CrossRef]
- Rossi, G.; Catani, F.; Leoni, L.; Segoni, S.; Tofani, V. HIRESSS: A physically based slope stability simulator for HPC applications. Nat. Hazards Earth Syst. Sci. 2013, 13, 151–166. [Google Scholar] [CrossRef]
- Wu, H.; Ye, C.; Pei, X.; Oguchi, T.; He, Z.; Yang, H.; Huang, R. Incorporating Effects of Slope Units and Sliding Areas into Seismically Induced Landslide Risk Modeling in Tectonically Active Mountainous Areas. Remote Sens. 2024, 16, 3517. [Google Scholar] [CrossRef]
- Zeng, P.; Feng, B.; Dai, K.; Li, T.; Fan, X.; Sun, X. Can satellite InSAR innovate the way of large landslide early warning? Eng. Geol. 2024, 342, 107771. [Google Scholar] [CrossRef]
- Saade, A.; Abou-Jaoude, G.; Wartman, J. Regional-scale co-seismic landslide assessment using limit equilibrium analysis. Eng. Geol. 2016, 204, 53–64. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, H.; An, P.; Fang, K.; Lu, S.; Xia, D. A physical model test on a seepage-initiation-braking-type (SIBT) landslide under the coupling of rainfall and water level fluctuation. Acta Geotech. 2025, 20, 37–54. [Google Scholar] [CrossRef]
- Ding, H.; Xue, L.; Shang, J.; Guo, S.; Liu, H.; Li, L.; Wang, H. Study on synergistic action of tap-like arbor root system and anti-slide piles by physical model experiment of landslides. Landslides 2024, 21, 1707–1717. [Google Scholar] [CrossRef]
- Cui, H.; Ji, J.; Hürlimann, M.; Medina, V. Probabilistic and physically-based modelling of rainfall-induced landslide susceptibility using integrated GIS-FORM algorithm. Landslides 2024, 21, 1461–1481. [Google Scholar] [CrossRef]
- Escobar-Wolf, R.; Sanders, J.D.; Vishnu, C.L.; Oommen, T.; Sajinkumar, K.S. A GIS tool for infinite slope stability analysis (GIS-TISSA). Geosci. Front. 2021, 12, 756–768. [Google Scholar] [CrossRef]
- Du, J.; Yin, K.; Lacasse, S. Displacement prediction in colluvial landslides, Three Gorges Reservoir, China. Landslides 2013, 10, 203–218. [Google Scholar] [CrossRef]
- Agliardi, F.; Scuderi, M.M.; Fusi, N.; Collettini, C. Slow-to-fast transition of giant creeping rockslides modulated by undrained loading in basal shear zones. Nat. Commun. 2020, 11, 1352. [Google Scholar] [CrossRef]
- Xu, J. Failure process of saturated granite residual soil slope: A 3D viscoelastic-plastic finite element modeling approach with nonstationary parameter creep. Bull. Eng. Geol. Environ. 2023, 82, 276. [Google Scholar] [CrossRef]
- Li, Y.; Feng, X.; Yao, A.; Zhang, Z.; Li, K.; Wang, Q.; Song, S. Progressive evolution and failure behavior of a Holocene river-damming landslide in the SE Tibetan Plateau, China. Landslides 2022, 19, 1069–1086. [Google Scholar] [CrossRef]
- Alam, M.J.B.; Manzano, L.S.; Debnath, R.; Ahmed, A.A. Monitoring slope movement and soil hydrologic behavior using IoT and AI technologies: A systematic review. Hydrology 2024, 11, 111. [Google Scholar] [CrossRef]
- Xiong, X.; Shi, Z.M.; Guan, S.G.; Zhang, F. Failure mechanism of unsaturated landslide dam under seepage loading–Model tests and corresponding numerical simulations. Soils Found. 2018, 58, 1133–1152. [Google Scholar] [CrossRef]
- Zhao, Y. Transient stability analysis method and sensitivity study of unsaturated soil slopes under consideration of rainfall conditions. Arab. J. Geosci. 2021, 14, 1179. [Google Scholar] [CrossRef]
- Jakob, M.; Lambert, S. Climate change effects on landslides along the southwest coast of British Columbia. Geomorphology 2009, 107, 275–284. [Google Scholar] [CrossRef]
- Ardestani, A.; Amini, M.; Esmaeili, K. A two-dimensional limit equilibrium computer code for analysis of complex toppling slope failures. J. Rock Mech. Geotech. Eng. 2021, 13, 114–130. [Google Scholar] [CrossRef]
- De Sy, V.; Schoorl, J.M.; Keesstra, S.D.; Jones, K.E.; Claessens, L. Landslide model performance in a high resolution small-scale landscape. Geomorphology 2013, 190, 73–81. [Google Scholar] [CrossRef]
- Alvioli, M.; Guzzetti, F.; Rossi, M. Scaling properties of rainfall induced landslides predicted by a physically based model. Geomorphology 2014, 213, 38–47. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Stanley, T.; Amatya, P.; Emberson, R.; Khan, S.; Tanyaș, H. Global landslide hazard assessment for situational awareness (LHASA) Version 2: New activities and future plans. In EGU-General Assembly 2020: Sharing Geoscience Online; NASA: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Lian, J.; Wu, J. Surficial stability analysis of soil slope under seepage based on a novel failure mode. Front. Struct. Civ. Eng. 2021, 15, 712–726. [Google Scholar] [CrossRef]
- Fernandez, J.C.J.; Castanon-Jano, L.; Gaute Alonso, A.; Blanco-Fernandez, E.; Fernandez, J.C.G.; Gonzalez, V.C.; Castro-Fresno, D.; Garcia-Sanchez, D. 3D numerical simulation of slope-flexible system interaction using a mixed FEM-SPH model. Ain Shams Eng. J. 2022, 13, 101592. [Google Scholar] [CrossRef]
- Kumar, P.R.; Muthukkumaran, K.; Sharma, C. Sustainability Considerations in Recent Advances of Numerical Techniques for Investigating Slope Stability. Sustain. Dev. Geospat. Technol. 2024, 2, 127–138. [Google Scholar] [CrossRef]
- Li, Q.; Huang, D.; Pei, S.; Qiao, J.; Wang, M. Using physical model experiments for hazards assessment of rainfall-induced debris landslides. J. Earth Sci. 2021, 32, 1113–1128. [Google Scholar] [CrossRef]
- Jiang, X.; Jiang, L.; Zhou, W. Monitoring and Early Warning Technologies on Karst Lands; Springer: Cham, Switzerland, 2024; ISBN 978-3-031-59045-0. [Google Scholar]
- Lombardo, L.; Tanyas, H. From scenario-based seismic hazard to scenario-based landslide hazard: Fast-forwarding to the future via statistical simulations. Stoch. Environ. Res. Risk Assess. 2022, 36, 2229–2242. [Google Scholar] [CrossRef]
- Bednarik, M.; Yilmaz, I.; Kralovičová, L. Deterministic approach to assess landslide susceptibility and landslide activity in the Central-Western Region of Slovakia. Bull. Eng. Geol. Environ. 2024, 83, 327. [Google Scholar] [CrossRef]
- Lari, S.; Frattini, P.; Crosta, G.B. A probabilistic approach for landslide hazard analysis. Eng. Geol. 2014, 182, 3–14. [Google Scholar] [CrossRef]
- Cao, C.; Zhu, K.; Xu, P.; Shan, B.; Yang, G.; Song, S. Refined landslide susceptibility analysis based on InSAR technology and UAV multi-source data. J. Clean. Prod. 2022, 368, 133146. [Google Scholar] [CrossRef]
- Chen, T.; Wang, Q.; Zhao, Z.; Liu, G.; Dou, J.; Plaza, A. LCFSTE: Landslide conditioning factors and swin transformer ensemble for landslide susceptibility assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 6444–6454. [Google Scholar] [CrossRef]
- Huqqani, I.A.; Tay, L.T.; Mohamad-Saleh, J. Spatial landslide susceptibility modelling using metaheuristic-based machine learning algorithms. Eng. Comput. 2023, 39, 867–891. [Google Scholar] [CrossRef]
- Dey, S.; Das, S.; Roy, S.K. Landslide susceptibility assessment in Eastern Himalayas, India: A comprehensive exploration of four novel hybrid ensemble data driven techniques integrating explainable artificial intelligence approach. Environ. Earth Sci. 2024, 83, 641. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Ilia, I.; Tsangaratos, P. Applying weight of evidence method and sensitivity analysis to produce a landslide susceptibility map. Landslides 2016, 13, 379–397. [Google Scholar] [CrossRef]
- Vakhshoori, V.; Zare, M. Landslide susceptibility mapping by comparing weight of evidence, fuzzy logic, and frequency ratio methods. Geomat. Nat. Hazards Risk 2016, 7, 1731–1752. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, T.; Liu, S.; Zhang, W.; Yang, B.; Chen, L. Quantification of model uncertainty and variability for landslide displacement prediction based on Monte Carlo simulation. Gondwana Res. 2023, 123, 27–40. [Google Scholar] [CrossRef]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef]
- Chauhan, V.K.; Dahiya, K.; Sharma, A. Problem formulations and solvers in linear SVM: A review. Artif. Intell. Rev. 2019, 52, 803–855. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. CATENA 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Joachims, T. Making Large-Scale SVM Learning Practical. Technical Report No. 1998,28. Available online: https://www.econstor.eu/handle/10419/77178 (accessed on 27 February 2025).
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide susceptibility assessment in Vietnam using support vector machines, decision tree, and Naive Bayes Models. Math. Probl. Eng. 2012, 2012, 974638. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Y.; Liang, Y.; Sun, P.; Li, Y.; Su, X.; Wang, A.; Meng, X. Landslide risk assessment using a combined approach based on InSAR and random forest. Remote Sens. 2022, 14, 2131. [Google Scholar] [CrossRef]
- Peng, T.; Chen, Y.; Chen, W. Landslide susceptibility modeling using remote sensing data and Random Sub-Space-based functional tree classifier. Remote Sens. 2022, 14, 4803. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Behnia, P.; Blais-Stevens, A. Landslide susceptibility modelling using the quantitative random forest method along the northern portion of the Yukon Alaska Highway Corridor, Canada. Nat. Hazards 2018, 90, 1407–1426. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, H.; Liu, G.; Chen, Q.; Tang, H. Automated identification of rock discontinuities from 3D point clouds using a convolutional neural network. Rock Mech. Rock Eng. 2025, 1–18, in press. [Google Scholar] [CrossRef]
- Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), IEEE, Turin, Italy, 1–3 October 2018; pp. 80–89. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Considerations for evaluation and generalization in interpretable machine learning. In Explainable and Interpretable Models in Computer Vision and Machine Learning; Springer: Cham, Switzerland, 2018; pp. 3–17. [Google Scholar] [CrossRef]
- Akosah, S.; Gratchev, I.; Kim, D.H.; Ohn, S.Y. Application of artificial intelligence and remote sensing for landslide detection and prediction: Systematic review. Remote Sens. 2024, 16, 2947. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, T. Deep learning for exploring landslides with remote sensing and geo-environmental data: Frameworks, progress, challenges, and opportunities. Remote Sens. 2024, 16, 1344. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, L.; Ding, X.L.; Hu, J.; Li, Z.W.; Zhu, J.J. Slope deformation prior to Zhouqu, China landslide from InSAR time series analysis. Remote Sens. Environ. 2015, 156, 45–57. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Region-based convolutional networks for accurate object detection and segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 142–158. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China. Sci. Total Environ. 2019, 694, 133464. [Google Scholar] [CrossRef]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 15908–15919. Available online: https://proceedings.neurips.cc/paper/2021/hash/854d9fca60b4bd07f9bb215d59ef5561-Abstract.html (accessed on 27 February 2025).
- Wang, H.; Wang, L.; Zhang, L. Transfer learning improves landslide susceptibility assessment. Gondwana Res. 2023, 123, 238–254. [Google Scholar] [CrossRef]
- Tang, X.; Tu, Z.; Wang, Y.; Liu, M.; Li, D.; Fan, X. Automatic detection of coseismic landslides using a new transformer method. Remote Sens. 2022, 14, 2884. [Google Scholar] [CrossRef]
- Ge, Q.; Li, J.; Wang, X.; Deng, Y.; Zhang, K.; Sun, H. LiteTransNet: An interpretable approach for landslide displacement prediction using transformer model with attention mechanism. Eng. Geol. 2024, 331, 107446. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef]
- Bao, S.; Liu, J.; Wang, L.; Zhao, X. Application of transformer models to landslide susceptibility mapping. Sensors 2022, 22, 9104. [Google Scholar] [CrossRef]
- Carrington, A.M.; Manuel, D.G.; Fieguth, P.W.; Ramsay, T.; Osmani, V.; Wernly, B.; Bennett, C.; Hawken, S.; Magwood, O.; Sheikh, Y.; et al. Deep ROC analysis and AUC as balanced average accuracy, for improved classifier selection, audit and explanation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 329–341. [Google Scholar] [CrossRef]
- Alatorre, L.C.; Sánchez-Andrés, R.; Cirujano, S.; Beguería, S.; Sánchez-Carrillo, S. Identification of mangrove areas by remote sensing: The ROC curve technique applied to the northwestern Mexico coastal zone using Landsat imagery. Remote Sens. 2011, 3, 1568–1583. [Google Scholar] [CrossRef]
- Wang, S.; Chen, W.; Xie, S.M.; Azzari, G.; Lobell, D.B. Weakly supervised deep learning for segmentation of remote sensing imagery. Remote Sens. 2020, 12, 207. [Google Scholar] [CrossRef]
- Gøtzsche, P.C. Believability of relative risks and odds ratios in abstracts: Cross sectional study. BMJ 2006, 333, 231–234. [Google Scholar] [CrossRef]
- Van den Broeck, G.; Lykov, A.; Schleich, M.; Suciu, D. On the tractability of SHAP explanations. J. Artif. Intell. Res. 2022, 74, 851–886. [Google Scholar] [CrossRef]
- Liu, L.L.; Yang, C.; Wang, X.M. Landslide susceptibility assessment using feature selection-based machine learning models. Geomech. Eng. 2021, 25, 1–16. [Google Scholar] [CrossRef]
- Jenkins, L.T.; Creed, M.J.; Tarbali, K.; Muthusamy, M.; Trogrlić, R.Š.; Phillips, J.C.; Watson, C.S.; Sinclair, H.D.; Galasso, C.; McCloskey, J. Physics-based simulations of multiple natural hazards for risk-sensitive planning and decision making in expanding urban regions. Int. J. Disaster Risk Reduct. 2023, 84, 103338. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, S.; Ouyang, C.; Chen, M.; Liu, C.; Zhang, J.; Yu, L.; Wang, F.; Xie, Y.; Li, J.; et al. Artificial intelligence for geoscience: Progress, challenges, and perspectives. Innovation 2024, 5, 100691. [Google Scholar] [CrossRef]
- Ma, Z.; Mei, G.; Xu, N. Generative deep learning for data generation in natural hazard analysis: Motivations, advances, challenges, and opportunities. Artif. Intell. Rev. 2024, 57, 160. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]
- Rai, R.; Sahu, C.K. Driven by data or derived through physics? A review of hybrid physics guided machine learning techniques with cyber-physical system (CPS) focus. IEEE Access 2020, 8, 71050–71073. [Google Scholar] [CrossRef]
- Cui, H.; Tong, B.; Wang, T.; Dou, J.; Ji, J. A hybrid data-driven approach for rainfall-induced landslide susceptibility mapping: Physically-based probabilistic model with convolutional neural network. J. Rock Mech. Geotech. Eng. 2024, in press. [Google Scholar] [CrossRef]
- Hemalatha, T.; Ramesh, M.V.; Rangan, V.P. Adaptive learning techniques for landslide forecasting and the validation in a real world deployment. In Advancing Culture of Living with Landslides: Volume 5 Landslides in Different Environments; Springer International Publishing: Cham, Switzerland, 2017; pp. 439–447. [Google Scholar] [CrossRef]
- Xiang, X.; Wen, H.; Xiao, J.; Wang, X.; Yin, H.; Huang, J. Analyzing failure mechanisms and predicting step-like displacement: Rainfall and RWL dynamics in lock-unlock landslides. Geosci. Front. 2025, 16, 101959. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Zhang, J.; Sun, D.; Zhou, X.; Mi, C.; Wen, H. Insights into geospatial heterogeneity of landslide susceptibility based on the SHAP-XGBoost model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Scaioni, M.; Longoni, L.; Melillo, V.; Papini, M. Remote sensing for landslide investigations: An overview of recent achievements and perspectives. Remote Sens. 2014, 6, 9600–9652. [Google Scholar] [CrossRef]
- Zheng, F.; Tao, R.; Maier, H.R.; See, L.; Savic, D.; Zhang, T.; Chen, Q.; Assumpção, T.H.; Yang, P.; Heidari, B.; et al. Crowdsourcing methods for data collection in geophysics: State of the art, issues, and future directions. Rev. Geophys. 2018, 56, 698–740. [Google Scholar] [CrossRef]
- Gupta, K.; Satyam, N. Integrating real-time sensor data for improved hydrogeotechnical modelling in landslide early warning in Western Himalaya. Eng. Geol. 2024, 338, 107630. [Google Scholar] [CrossRef]
- Kang, Y.; Zhao, C.; Zhang, Q.; Lu, Z.; Li, B. Application of InSAR techniques to an analysis of the Guanling landslide. Remote Sens. 2017, 9, 1046. [Google Scholar] [CrossRef]
- Zhou, C.; Cao, Y.; Gan, L.; Wang, Y.; Motagh, M.; Roessner, S.; Hu, X.; Yin, K. A novel framework for landslide displacement prediction using MT-InSAR and machine learning techniques. Eng. Geol. 2024, 334, 107497. [Google Scholar] [CrossRef]
- Chen, W.; Li, X.; Wang, Y.; Chen, G.; Liu, S. Forested landslide detection using LiDAR data and the random forest algorithm: A case study of the Three Gorges, China. Remote Sens. Environ. 2014, 152, 291–301. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, C.; Liu, W.; Huang, J.; Su, Y.; Yang, Y.; Jiang, W.; Sun, W. Landslide identification method based on the FKGRNet model for remote sensing images. Remote Sens. 2023, 15, 3407. [Google Scholar] [CrossRef]
- Zhang, R.; Lv, J.; Yang, Y.; Wang, T.; Liu, G. Analysis of the impact of terrain factors and data fusion methods on uncertainty in intelligent landslide detection. Landslides 2024, 21, 1849–1864. [Google Scholar] [CrossRef]
- Murakami, A.; Fujisawa, K.; Shuku, T. Developments of inverse analysis by Kalman filters and Bayesian methods applied to geotechnical engineering. Proc. Jpn. Acad. Ser. B 2023, 99, 352–388. [Google Scholar] [CrossRef]
- Kuang, P.; Li, R.; Huang, Y.; Wu, J.; Luo, X.; Zhou, F. Landslide displacement prediction via attentive graph neural network. Remote Sens. 2022, 14, 1919. [Google Scholar] [CrossRef]
- Varela, P.; Medina-Cetina, Z.; Hernawan, B. Bayesian model calibration of submarine landslides. Landslides 2025, in press. [Google Scholar] [CrossRef]
- Zhao, T.; Peng, H.; Xu, L.; Sun, P. Statistical landslide susceptibility assessment using Bayesian logistic regression and Markov Chain Monte Carlo (MCMC) simulation with consideration of model class selection. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2024, 18, 211–227. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Z.; Jian, W.; Robledo, L.F. Landslide displacement prediction by using Bayesian optimization–temporal convolutional networks. Acta Geotech. 2024, 19, 4947–4965. [Google Scholar] [CrossRef]
- Wang, J.; Nie, G.; Gao, S.; Xue, C. Simultaneous state–parameter estimation of rainfall-induced landslide displacement using data assimilation. Nat. Hazards Earth Syst. Sci. 2019, 19, 1387–1398. [Google Scholar] [CrossRef]
- Dwivedi, R.; Dave, D.; Naik, H.; Singhal, S.; Omer, R.; Patel, P.; Qian, B.; Wen, Z.; Shah, T.; Morgan, G.; et al. Explainable AI (XAI): Core ideas, techniques, and solutions. ACM Comput. Surv. 2023, 55, 194. [Google Scholar] [CrossRef]







| Category | Sub-Category | Description |
|---|---|---|
| A. Bibliographic Information | A1 | Article ID/record number (unique identifier from the database) |
| A2 | Article title | |
| A3 | Author(s) | |
| A4 | Publication year | |
| A5 | Journal name | |
| A6 | Citation count (optional) | |
| A7 | Abstract | |
| B. Regional and Geographic Information | B1 | Continent (e.g., Asia, Europe, North America, South America) |
| B2 | Country (e.g., China, Italy, USA, Japan) | |
| B3 | Specific region (e.g., Himalayas, Alps, Yangtze River Basin) | |
| B4 | Coordinates (latitude/longitude, if available) | |
| C. Landslide Characteristics and Scenario | C1 | Triggering factor (e.g., rainfall, earthquake, human activities, reservoir discharge) |
| C2 | Study scale (e.g., local, regional, national, global) | |
| C3 | Data availability type (e.g., remote sensing, field monitoring, historical database) | |
| D. Methodological Information | D1 | Model type (physically based, data-driven, hybrid) |
| D1a | Physically based models (e.g., SHALSTAB, SINMAP, TRIGRS, infinite slope model) | |
| D1b | Data-driven models (e.g., LR, RF, ANN, SVM, CNN, Transformer) | |
| D1c | Hybrid models (e.g., physically informed ML, coupled models) | |
| D2 | Specific algorithm or model used (e.g., RF + SHALSTAB, TRIGRS–CNN, knowledge-based XGBoost) |
| First Author | Year | Citations | Article Title |
|---|---|---|---|
| Goetz, Jason N. (Canada) [39] | 2011 | 209 | Integrating physical and empirical landslide susceptibility models using generalized additive models |
| Salciarini, Diana (Italy) [40] | 2006 | 208 | Modeling regional initiation of rainfall-induced shallow landslides in the eastern Umbria Region of central Italy |
| Cervi, Federico (Italy) [41] | 2010 | 129 | Comparing predictive capability of statistical and deterministic methods for landslide susceptibility mapping: a case study in the northern Apennines (Reggio Emilia Province, Italy) |
| Gorsevski, Pece V. (North Macedonia) [42] | 2006 | 127 | Spatially and temporally distributed modeling of landslide susceptibility |
| Ciurleo, Mariantonietta (Italy) [43] | 2017 | 96 | A comparison of statistical and deterministic methods for shallow landslide susceptibility zoning in clayey soils |
| First Author | Year | Citations | Article Title |
|---|---|---|---|
| Reichenbach, Paola (Italy) [38] | 2018 | 1322 | A review of statistically based landslide susceptibility models |
| Pradhan, Biswajeet (India) [44] | 2013 | 998 | A comparative study on the predictive ability of the decision tree, support vector machine, and neuro-fuzzy models in landslide susceptibility mapping using GIS |
| Dieu Tien Bui (Vietnam) [45] | 2016 | 995 | Spatial prediction models for shallow landslide hazards: a comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree |
| Pradhan, Biswajeet (India) [46] | 2010 | 749 | Landslide susceptibility assessment and factor effect analysis: backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling |
| Chen, Wei (China) [32] | 2017 | 682 | A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, C.; Wu, H.; Oguchi, T.; Tang, Y.; Pei, X.; Wu, Y. Physically Based and Data-Driven Models for Landslide Susceptibility Assessment: Principles, Applications, and Challenges. Remote Sens. 2025, 17, 2280. https://doi.org/10.3390/rs17132280
Ye C, Wu H, Oguchi T, Tang Y, Pei X, Wu Y. Physically Based and Data-Driven Models for Landslide Susceptibility Assessment: Principles, Applications, and Challenges. Remote Sensing. 2025; 17(13):2280. https://doi.org/10.3390/rs17132280
Chicago/Turabian StyleYe, Chenzuo, Hao Wu, Takashi Oguchi, Yuting Tang, Xiangjun Pei, and Yufeng Wu. 2025. "Physically Based and Data-Driven Models for Landslide Susceptibility Assessment: Principles, Applications, and Challenges" Remote Sensing 17, no. 13: 2280. https://doi.org/10.3390/rs17132280
APA StyleYe, C., Wu, H., Oguchi, T., Tang, Y., Pei, X., & Wu, Y. (2025). Physically Based and Data-Driven Models for Landslide Susceptibility Assessment: Principles, Applications, and Challenges. Remote Sensing, 17(13), 2280. https://doi.org/10.3390/rs17132280






