Sparse Reconstruction-Based Target Localization with Distributed Waveform-Diverse Array Radars

Abstract

This paper addresses the problem of target localization in a distributed waveform diverse array radar system, exploiting the technique of sparse reconstruction. At the configuration stage, the distributed radar system consists of two individual Frequency Diverse Array Multiple-Input Multiple-Output (FDA-MIMO) radars and one single Element-Pulse Coding MIMO (EPC-MIMO) radar. To obtain the angle and incremental range (i.e., the range offset between the sampling point and actual position within the range bin) of the targets in each local radar, two sparse reconstruction-based algorithms, including the grid-based Iterative Adaptive Approach (IAA) and gridless Atomic Norm Minimization (ANM) algorithms, are implemented. Furthermore, multiple sets of local statistics are fused at the fusion center, where a Weighted Least Squares (WLS) method is performed to localize targets. At the analysis stage, the estimation performance of the proposed methods, encompassing both IAA and ANM algorithms, is evaluated in contrast to the Cramér–Rao Bound (CRB). Numerical results and parametric studies are provided to demonstrate the effectiveness of the proposed sparse reconstruction methods for target localization in the distributed waveform diverse array system.

1. Introduction

Target localization is an indispensable application that has raised significant attention within the radar scientific community [1,2,3]. However, the localization of weak targets has become a significant challenge in practical applications [4,5]. Typically, weak targets exhibit characteristics such as a low Radar Cross Section (RCS), meaning they are easily buried in the background of noise [6,7]. These characteristics make these targets difficult to detect accurately, which in turn has a negative impact on the overall performance of radar systems [8]. Traditional phased array radars are widely used for target localization, where high-precision target detection can be achieved by forming a beam in the intended direction using multiple antenna elements [9,10,11]. In [10], a novel adaptive sampling interval algorithm for multi-target tracking is introduced. Moreover, a joint target assignment and resource optimization strategy for multi-target tracking with the phased array radar is proposed [11]. However, for weak targets, the detection performance is reduced due to the low Signal-to-Noise Ratio (SNR) of weak targets [12,13,14]. To tackle the problem, a viable solution is to employ the distributed radar system by jointly operating multiple spatially separated radars, which leverages the spatial diversity to enhance target detection and localization performances for weak targets [15,16].

Currently, the localization methods with distributed radar systems are mainly divided into two categories, including direct positioning methods [17,18] and indirect positioning methods [19,20]. In particular, the former involves data acquisition in each individual station and data fusion in the fusion center without any a priori processing. In this regard, the fusion center aggregates the received data from all stations and performs unified signal processing to obtain the target’s information. Such a method enjoys the advantages of high-precision estimation. However, it results in a huge computational load [21,22]. In contrast, with the latter method, the data is processed in each individual station to obtain target parameters, including angle, incremental range, and range ambiguity index. Then, the information related to all stations is transmitted to the fusion center, where further processing is carried out to localize the target [23,24]. Hence, the processing efficiency is significantly improved compared with the direct processing methods. In this respect, a localization method for the target using distributed radar systems is presented in [25], in which a closed-form solution of target position is derived via a two-stage Weighted Least Squares (WLS) framework. Furthermore, an iterative-based target position refinement process is designed to alleviate the off-grid problem caused by spatial discretization using a significantly higher computational efficiency and a lower data communication burden compared with the direct positioning methods [26].

Recently, the concept of Frequency Diverse Array (FDA) has garnered widespread attention. In this context, a small frequency increment is introduced between adjacent transmit elements [27,28,29]. Furthermore, by integrating FDA with Multiple-Input Multiple-Output (MIMO) technology, it is possible to obtain the range–angle-dependent beampattern after digital mixing and separating the transmitted waveforms. Therefore, the additional Degrees of Freedom (DOFs) in the range dimension can be acquired, which enables the simultaneous estimation of target’s range and angle [30]. In this context, the incremental range, which denotes the range offset between the sampling and actual positions within the range bin, can be obtained [31]. To achieve more precise range estimation, three approximated maximum likelihood techniques are designed in [32]. Furthermore, by extending the FDA-MIMO into multiple pulses, an equivalent coding coefficient is introduced across the transmit elements and pulses, which leads to another alternative framework, i.e., the Element-Pulse Coding MIMO (EPC-MIMO) radar. In this respect, the equivalent pointing directions corresponding to different pulses in the EPC-MIMO radar are introduced, enabling the separation of range ambiguity [33]. Specifically, an enhanced parameter estimation approach is developed to obtain the angle and range region number index (also termed as the number of delayed pulses) of the target [34]. Moreover, a reweighted atomic norm minimization-based approach is developed to separate range-ambiguous clutter by leveraging transmit spatial frequencies from different range ambiguity regions [35].

Following the guidelines, by combining the waveform-diverse array radars and the distributed system, a potential detection advantage for weak targets can be obtained by exploiting both the spatial and waveform diversities [36]. In this paper, the target localization in a distributed waveform diverse array radar system consisting of two individual FDA-MIMO radars and a single EPC-MIMO radar is configured, exploiting the technique of sparse reconstruction [37,38]. The main contributions of this paper can be summarized as follows:

(i)

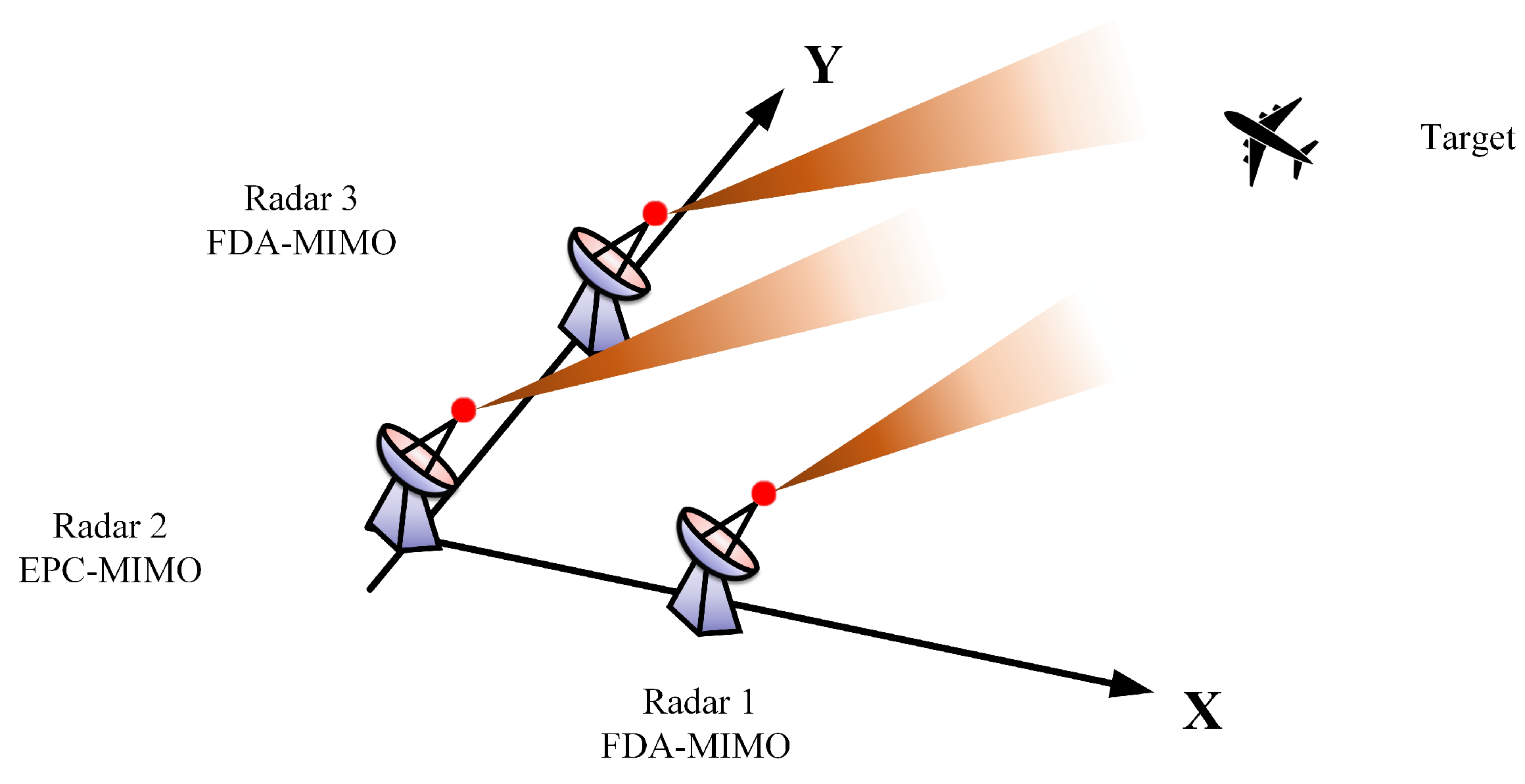
At the configuration stage, the distributed waveform diverse array radar system is formed by three local stations [39,40,41], including two individual FDA-MIMO radars and a single EPC-MIMO radar. Notably, both the FDA-MIMO and EPC-MIMO radars are configured in a colocated MIMO architecture. Specially, the incremental range and angle parameters are measured by the FDA-MIMO radar. In the meanwhile, the range ambiguity index and angle parameters are acquired by the EPC-MIMO radar.

(ii)

The Iterative Adaptive Approach (IAA) [42,43,44] and the Atomic Norm Minimization (ANM) [45,46,47] algorithms are employed at FDA-MIMO radar stations for parameter estimation. Simultaneously, the angle and range ambiguity index are acquired by the EPC-MIMO radar through the Coordinate Descent Multiple-Signal Classification (CD-MUSIC) method. Furthermore, based on the single-station estimation results, the WLS method is used by the fusion center to localize targets [48];

(iii)

At the analysis phase, both the Cramér–Rao Bounds (CRBs) for the FDA-MIMO and EPC-MIMO radars are derived. In addition, the Root Mean Square Errors (RMSEs) versus the SNRs are provided to verify the effectiveness of the methods. Furthermore, a comprehensive localization error analysis is carried out.

The organization of the paper proceeds as follows. Section 2 presents the signal model of the distributed waveform diverse radar system. In Section 3, multi-dimensional parameter estimation based on sparse reconstruction theory is studied. To demonstrate the efficacy of the proposed method, numerical results are provided in Section 4. Finally, Section 5 summarizes the article and explores potential directions for future research.

Notations: Boldface is utilized for vectors $\mathit{x}$ (in lowercase), where the n-th component is denoted as $\mathit{x}\left(n\right)$, and for matrices $\mathit{A}$ (in uppercase), where the $(m,n)$-th column is represented as ${\mathit{A}}_{m,n}$. A matrix $\mathit{A}\in {\mathbb{C}}^{N\times M}$ can be defined by the columns ${\mathit{a}}_m\in {\mathbb{C}}^N,m=1,\dots ,M$ (i.e., $\mathit{A}=[{\mathit{a}}_1,\dots ,{\mathit{a}}_M]$). The transpose and the conjugate transpose operators are denoted by the symbols ${\left(·\right)}^{\mathrm{T}}$ and ${\left(·\right)}^{\mathrm{H}}$, respectively. ${\mathbb{R}}^N$, ${\mathbb{C}}^N$ and ${\mathbb{C}}^{N\times M}$ are, respectively, the sets of N-dimensional vectors of complex numbers, N-dimensional vectors real numbers, and $N\times M$ complex matrices. ⊙, ⊗ and ∘ represent the Hadamard (elementwise) product, the Kronecker product and the Khatir–Rao product, respectively. The letter j represents the imaginary unit (i.e., $j=\sqrt{-1}$). The $\mathrm{diag}\left(\mathit{A}\right)$ refers to extracting the main diagonal elements of $\mathit{A}$ into a column vector, and ${\mathbf{1}}_N$ represents an $N\times 1$ column vector of ones. The $\inf \left(·\right)$ is the infimum operator. The determinant of the matrix $\mathit{A}\in {\mathbb{C}}^{N\times N}$ is indicated with $\det \left(\mathit{A}\right)$. For any $\mathit{x}\in {\mathbb{C}}^N$, $∥\mathit{x}∥$ denotes its Euclidian norm. The $\mathrm{diag}\left(\mathit{A},l\right)$ returns the l-th diagonal elements of $\mathit{A}$.

2. Signal Model of Distributed Waveform Diverse Array Radars

Consider a distributed radar system in Cartesian coordinates. The system is comprised of three local radar stations, including two FDA-MIMO radars and one EPC-MIMO radar, as illustrated in Figure 1. Notably, both the FDA-MIMO and EPC-MIMO radars are configured in a colocated MIMO arrangement using uniform linear arrays, which comprises M transmit and N receive antenna elements [49]. The spacing between the antenna elements is set at half-wavelength, with the first element designated as the reference.

2.1. FDA-MIMO Radar

The signal model for a specific FDA-MIMO radar is presented in this section. By employing a sequential frequency increment, which is termed $\Delta f$, to each element of the transmit array, the carrier frequency assigned to the m-th $(m=1,2,\dots ,M)$ element is thus expressed

$$f_m=f_0+\left(m-1\right)\Delta f,$$

(1)

where $f_0$ denotes the reference carrier. Subsequently, the transmit signal of the m-th transmit element is

$$s_m\left(t\right)=\sqrt{{\displaystyle \frac{E}{M}}}{\phi }_m\left(t\right){\mathrm{e}}^{j2\pi f_{m}t},0\le t\le T_p,$$

(2)

where E denotes the transmitted signal’s power, $T_p$ represents the radar pulse duration, and ${\phi }_m\left(t\right)$ is the baseband waveform assumed to satisfy the orthogonal condition, formulated as follows

$$\int {\phi }_m\left(t\right){\phi }_{m^{\prime }}^{*}(t-\tau )e^{j2\pi \Delta f(m-m^{\prime })t}dt=0,$$

(3)

where $\tau$ denotes an arbitrary time delay.

Considering a point-like target in the far field with range $r_0$ and angle ${\theta }_0$, the signal transmitted from the m-th element of the transmit array and received by the target can be described as follows

$$\begin{array}{cc}\hfill s_m\left(t,{\theta }_0\right)& =s_m\left(t-{\tau }_m\right)\hfill \\ \hfill & ={\phi }_m(t-{\tau }_m){\mathrm{e}}^{j2\pi f_m\left(t-{\tau }_m\right)},\hfill \end{array}$$

(4)

where ${\tau }_m={\displaystyle \frac{r_m}{c}}={\displaystyle \frac{r_0-\left(m-1\right)dsin{\theta }_0}{c}}$ and c denotes the speed of light.

To proceed, the signal received by the n-th element can be described as

$$\begin{array}{cc}\hfill y_n\left(t\right)=& \xi \sum _{m=1}^{\mathrm{M}}{\phi }_m(t-{\tau }_{n,m}){\mathrm{e}}^{j2\pi f_m(t-{\tau }_{n,m})}\hfill \\ \hfill \approx & \xi {\mathrm{e}}^{j2\pi f_0(t-{\tau }_0)}{\mathrm{e}}^{j2\pi f_0{\displaystyle \frac{d(n-1)sin{\theta }_0}{c}}}\hfill \\ \hfill & \sum _{m=1}^{\mathrm{M}}{\phi }_m(t-{\tau }_0){\mathrm{e}}^{j2\pi \Delta f(m-1)(t-{\tau }_0)}{e}^{j2\pi f_0{\displaystyle \frac{d(m-1)sin{\theta }_0}{c}}},\hfill \end{array}$$

(5)

where $\xi$ is the complex echo amplitude, ${\tau }_0={\displaystyle \frac{2r_0}{c}}$ denotes the envelope time delay, and this approximation underscores the narrowband assumptions, implying that $\phi \left(t-{\tau }_{n,m}\right)=\phi \left(t-{\tau }_0\right)$.

After undergoing the preprocessing steps, the signal can be characterized as follows

$${\tilde{y}}_{n,m}\left(t^{*}\right)={\xi }^{\prime }{e}^{j2\pi f_0{\displaystyle \frac{d\left(n-1\right)sin{\theta }_0}{c}}}{e}^{-j2\pi \left(m-1\right)\Delta f\Delta \tau }{e}^{j2\pi f_0{\displaystyle \frac{d\left(m-1\right)sin{\theta }_0}{c}}},$$

(6)

where ${\xi }^{\prime }=\xi e^{-j2\pi f_0{\tau }_0}$.

Then, the useful samples received from the cell under test can be aggregated to construct an $MN$ dimensional vector

$$\begin{array}{cc}\hfill {\mathit{y}}_s=& {\left[{\tilde{y}}_{1,1}\left(t^{*}\right),{\tilde{y}}_{1,2}\left(t^{*}\right),\dots ,{\tilde{y}}_{N,M}\left(t^{*}\right)\right]}^{\mathrm{T}}\hfill \\ \hfill =& {\xi }^{\prime }{\mathit{b}}_r\left({\theta }_0\right)\otimes \left[{\mathit{a}}_t\left({\theta }_0\right)\odot {\mathit{a}}_t\left(\Delta \tau \right)\right]\hfill \\ \hfill =& {\xi }^{\prime }\mathit{u}\left(\Delta \tau ,{\theta }_0\right),\hfill \end{array}$$

(7)

where

• $\mathit{u}\left(\Delta \tau ,{\theta }_0\right)={\mathit{b}}_r\left({\theta }_0\right)\otimes {\mathit{a}}_t\left(\Delta \tau ,{\theta }_0\right)\in {\mathbb{C}}^{MN}$ with $\Delta \tau$ the incremental delay w.r.t. the sampling time associated with the target range cell;
• ${\mathit{b}}_r\left({\theta }_0\right)={\left[1,e^{j2\pi f_0{\displaystyle \frac{dsin\left({\theta }_0\right)}{c}}},\dots ,e^{j2\pi f_0{\displaystyle \frac{d\left(N-1\right)sin\left({\theta }_0\right)}{c}}}\right]}^{\mathrm{T}}\in {\mathbb{C}}^N$ represents the angle-dependent receive steering vector;
• ${\mathit{a}}_t\left({\theta }_0\right)={\overline{\mathit{R}}}^{\mathrm{T}}\mathit{c}\left({\theta }_0\right)\in {\mathbb{C}}^M$ with $\overline{\mathit{R}}\in {\mathbb{C}}^{M\times M}$ the transmit waveforms correlation matrix, of which the $(m,n)$-th entry of $\overline{\mathit{R}}$, ${\overline{R}}_{m,n}={\int }_0^{T_p}{\phi }_m\left(s\right){\phi }_n^{*}\left(s\right)ds,\left(m,n\right)\in {\left\{1,\dots ,M\right\}}^2$, and $\mathit{c}\left({\theta }_0\right)={\left[1,e^{j2\pi f_0{\displaystyle \frac{dsin\left({\theta }_0\right)}{c}}},\dots ,e^{j2\pi f_0{\displaystyle \frac{d\left(M-1\right)sin\left({\theta }_0\right)}{c}}}\right]}^{\mathrm{T}}\in {\mathbb{C}}^M$ the angle-dependent transmit steering vector;
• ${\mathit{a}}_t\left(\Delta \tau \right)={\left[1,e^{-j2\pi \Delta f\Delta \tau },\dots ,e^{-j2\pi \left(M-1\right)\Delta f\Delta \tau }\right]}^{\mathrm{T}}\in {\mathbb{C}}^M$ denotes the range-dependent steering vector.

2.2. EPC-MIMO Radar

In this section, the signal model for the EPC-MIMO radar is established, with its two-dimensional coding schematic depicted as in Figure 2.

Given K pulses transmitted within each coherent processing interval, the signal emanating from the m-th element during the k-th $(k=1,2,\dots ,K)$ pulse can be described as

$$s_{m,k}\left(t\right)=\mathrm{rect}\left({\displaystyle \frac{t}{T_p}}\right)c_{m,k}{\phi }_m\left(t\right)e^{j2\pi f_{0}t},$$

(8)

where $\mathrm{rect}\left({\displaystyle \frac{\mathrm{t}}{{\mathrm{T}}_{\mathrm{p}}}}\right)=\left\{\begin{array}{c}1,0<t<T_p\hfill \\ 0,else\hfill \end{array}\right.$, B represents the bandwidth and $c_{m,k}$ is the EPC phase factor, i.e.,

$$c_{m,k}=e^{j2\pi \gamma \left(m-1\right)\left(k-1\right)},$$

(9)

where $\gamma \in \left(0,1\right)$ denotes a user-defined coding parameter. Consequently, the EPC vector corresponding to the k-th pulse can be expressed as

$${\mathit{c}}_k={\left[1,e^{j2\pi \gamma \left(k-1\right)},\dots ,e^{j2\pi \gamma \left(M-1\right)\left(K-1\right)}\right]}^{\mathrm{T}}.$$

(10)

Assume that a far-field target is located at $\left(r_0,{\theta }_0\right)$. The echo signal received by the n-th element, originating from the m-th element during the k-th pulse, can be formulated as

$$x_{n,m,k}\left(t\right)=\xi {\phi }_m(t-{\tau }_0)e^{j2\pi \gamma (m-1)(k-p_s-1)}{e}^{j2\pi f_0(t-{\tau }_{n,m})},$$

(11)

where $\xi$ signifies the complex amplitude and $p_s$ denotes the number of delayed pulses.

Subsequently, the signal undergoes mixing and matched filtering by employing the m-th filter defined as ${\tilde{r}}_m\left(t\right)={\phi }_m^{*}(-t)$, which yields

$${\tilde{x}}_{n,m,k}\left(t\right)=\xi {\tilde{r}}_m\left(t\right)e^{j2\pi \gamma (m-1)(k-p_s-1)}{e}^{-j2\pi f_0{\tau }_{n,m}}.$$

(12)

Hence, the signals corresponding to all transmit pulses and receive elements are formulated in the following expression

$${\mathit{x}}_k={\left[{\tilde{x}}_{1,1,k}\left(t\right),\cdots ,{\tilde{x}}_{n,m,k}\left(t\right),\cdots ,{\tilde{x}}_{N,M,k}\left(t\right)\right]}^{\mathrm{T}}.$$

(13)

Therefore, the decoding procedure is carried out as follows

$${\mathit{y}}_k\left(t\right)={\left(\mathrm{diag}\left\{{\mathit{g}}_k\right\}\right)}^{\mathrm{H}}{\mathit{x}}_k\left(t\right),$$

(14)

where ${\mathit{g}}_k={\mathbf{1}}_N\otimes {\mathit{c}}_k\in {\mathbb{C}}^{MN}$.

Thus, the echo signal gathered from the k-th pulses can be expressed as

$$\begin{array}{cc}\hfill {\mathbf{y}}_r=& {\beta }^{\prime }\left[\mathbf{b}\left({\theta }_0\right)\otimes \mathbf{a}\left({\gamma }_s,{\theta }_0\right)\right]\hfill \\ \hfill =& {\beta }^{\prime }\mathbf{u}\left({\gamma }_s,{\theta }_0\right),\hfill \end{array}$$

(15)

where

• $\mathit{a}\left({\gamma }_s,{\theta }_0\right)={\left[1,e^{-j2\pi {\gamma }_s},\dots ,e^{-j2\pi {\gamma }_s(M-1)}\right]}^{\mathrm{T}}\odot {\left[1,e^{j2\pi {\displaystyle \frac{d}{{\lambda }_0}}sin\left({\theta }_0\right)},\dots ,e^{j2\pi {\displaystyle \frac{d}{{\lambda }_0}}(M-1)sin\left({\theta }_0\right)}\right]}^{\mathrm{T}}\in {\mathbb{C}}^M$ denotes the transmit steering vector with ${\gamma }_s=\gamma p_s$;
• ${\beta }^{\prime }={\beta }_s{e}^{-j2\pi f_0{\tau }_0}$, with ${\beta }_s$ the amplitude coefficient of the target.

3. Target Localization Based on Sparse Reconstruction

3.1. Target Localization with a Distributed Radar System

In this subsection, the WLS method is applied at the fusion center to localize targets, utilizing statistical data gathered from the local stations. Notably, the number of radar stations is set to V. A specific localization scenario is considered where the SNR of the target is different across different local radar stations. Therefore, fusing these local statistics with equal weights for localization is impractical and could lead to significant localization inaccuracies.

To address this issue, a linear transformation is first applied to the SNRs obtained at each station, thus the v-th $(v=1,2,\cdots ,V)$ station is represented as

$${{\mathrm{SNR}}^{\prime }}_v={\displaystyle \frac{{\mathrm{SNR}}_v-min(\mathrm{SNR})}{max(\mathrm{SNR})-min(\mathrm{SNR})}}.$$

(16)

Subsequently, the weights are further refined based on the SNRs as

$$w_v={\displaystyle \frac{e^{{{\mathrm{SNR}}^{\prime }}_v/T}}{{\displaystyle \sum _{j=1}^V}{e}^{{{\mathrm{SNR}}^{\prime }}_j/T}}},$$

(17)

where T is the temperature coefficient.

Afterwards, multiple sets of parameters received from all local FDA-MIMO/EPC-MIMO radar stations are integrated by the fusion center of the distributed radar system. Therefore, the target’s observation position is represented as ${\mathit{p}}_v={\left[p_{vx},p_{vy}\right]}^{\mathrm{T}}$ and can be formulated accordingly

$$p_{vx}=u_{vx}+r_{v}sin\left({\theta }_v\right),$$

(18)

and

$$p_{vy}=u_{vy}+r_{v}cos\left({\theta }_v\right),$$

(19)

where the positions of distributed radars are denoted as ${\mathit{u}}_v={\left[u_{vx},u_{vy}\right]}^{\mathrm{T}}$, ${\theta }_v$ represents the angle of the target measured by the v-th radar station, and $r_v$ similarly denotes the range information.

The WLS method is applied to achieve target localization, and the objective function can be expressed as

$$\begin{array}{cc}\hfill f& =min\sum _{v=1}^V{w}_v{\left(\mathit{z}-{\mathit{p}}_v\right)}^{\mathrm{T}}\left(\mathit{z}-{\mathit{p}}_v\right)\hfill \\ \hfill & ={{\mathit{E}}_r}^{\mathrm{T}}\mathit{W}{\mathit{E}}_r\hfill \\ \hfill & ={\left(1_V\otimes \mathit{z}-\mathit{P}\right)}^{\mathrm{T}}\mathit{W}\left(1_V\otimes \mathit{z}-\mathit{P}\right),\hfill \end{array}$$

(20)

where $\mathit{z}={\left[x_s,y_s\right]}^{\mathrm{T}}$ represents the target position to be solved, $\mathit{P}={\left[{\mathit{p}}_1,{\mathit{p}}_2,\dots ,{\mathit{p}}_V\right]}^{\mathrm{T}}$ denotes the observation matrix, ${\mathit{E}}_r={\left[\mathit{z}-{\mathit{p}}_1,\mathit{z}-{\mathit{p}}_2,\dots \mathit{z}-{\mathit{p}}_V\right]}^{\mathrm{T}}$ is the error matrix, and $\mathit{W}=\mathrm{diag}\left(w_1,w_2,\dots ,w_V\right)$ represents the weight matrix. Therefore, the target location to be solved is

$$\mathit{z}={\displaystyle \frac{{1_V}^{\mathrm{T}}\mathit{W}P}{{1_V}^{\mathrm{T}}\mathit{W}{1}_V}}.$$

(21)

3.2. Iterative Adaptive Approach

In this subsection, the IAA algorithm is employed for parameter estimation problems in FDA-MIMO radar [50,51,52]. Now, letting $\delta =2\Delta f\Delta \tau$ (satisfying $\left|\delta \right|\le {\displaystyle \frac{\Delta f}{B}}$, $\mathit{u}\left(\Delta \tau ,{\theta }_0\right)$ can be further expressed as

$$\begin{array}{cc}\hfill \mathit{u}\left(\Delta \tau ,{\theta }_0\right)=& \mathit{u}\left(\delta ,{\theta }_0\right)\hfill \\ \hfill =& {\mathit{b}}_r\left({\theta }_0\right)\otimes {\mathit{a}}_t\left(\delta ,{\theta }_0\right)\hfill \\ \hfill =& {\mathit{b}}_r\left({\theta }_0\right)\otimes \left[{\mathit{a}}_t\left({\theta }_0\right)\odot {\mathit{a}}_t\left(\delta \right)\right],\hfill \end{array}$$

(22)

where ${\mathit{a}}_t\left(\delta \right)={\left[1,e^{-j\pi \delta },\dots ,e^{-j\pi \left(M-1\right)\delta }\right]}^{\mathrm{T}}$.

Assume that L targets are located in the far field of space. The received signal can be represented as

$$\mathit{x}\left(t\right)=\sum _{l=1}^{\mathrm{L}}{\mathit{b}}_{\mathit{r}}\left({\theta }_l\right)\otimes {\mathit{a}}_{\mathit{t}}\left({\delta }_l,{\theta }_l\right){\mathit{s}}_l\left(t\right)+\mathit{n}\left(t\right)=\mathit{As}\left(t\right)+\mathit{n}\left(t\right),$$

(23)

where $\mathit{A}=\left[{\mathit{b}}_{\mathit{r}}\left({\theta }_1\right)\otimes {\mathit{a}}_{\mathit{t}}\left({\delta }_1,{\theta }_1\right),{\mathit{b}}_{\mathit{r}}\left({\theta }_2\right)\otimes {\mathit{a}}_{\mathit{t}}\left({\delta }_2,{\theta }_2\right),\dots ,{\mathit{b}}_{\mathit{r}}\left({\theta }_L\right)\otimes {\mathit{a}}_{\mathit{t}}\left({\delta }_L,{\theta }_L\right)\right]\in {\mathbb{C}}^{MN\times L}$ denotes the steering vector matrix of targets, $\mathit{n}$ represents a zero-mean complex circularly symmetric Gaussian random vector, i.e., the Gaussian white noise, and $\mathit{s}\left(t\right)={\left[{\mathit{s}}_1\left(t\right),{\mathit{s}}_2\left(t\right),\dots ,{\mathit{s}}_L\left(t\right)\right]}^{\mathrm{T}}$.

The two-dimensional space formed by incremental range and angle domains is divided into Q grids. Notice that $Q\ge L$ is ensured for the sparsity of signals in the range domain. Therefore, the incremental range–angle corresponding to each grid is expressed as

$$\left(\tilde{\delta },\tilde{\theta }\right)=\left[\left({\tilde{\delta }}_1,{\tilde{\theta }}_1\right),\left({\tilde{\delta }}_1,{\tilde{\theta }}_2\right),\dots ,\left({\tilde{\delta }}_Q,{\tilde{\theta }}_Q\right)\right].$$

(24)

The received signal, subsequent to sparse processing, can be expressed as

$$\mathit{x}\left(t\right)={\mathit{A}}^{\prime }\mathit{s}\left(t\right)+\mathit{n}\left(t\right),$$

(25)

where ${\mathit{A}}^{\prime }=\left[\mathit{b}\left({\tilde{\theta }}_1\right)\otimes \mathit{a}\left({\tilde{\delta }}_1,{\tilde{\theta }}_1\right),\mathit{b}\left({\tilde{\theta }}_2\right)\otimes \mathit{a}\left({\tilde{\delta }}_2,{\tilde{\theta }}_2\right),\dots ,\mathit{b}\left({\tilde{\theta }}_Q\right)\otimes \mathit{a}\left({\tilde{\delta }}_Q,{\tilde{\theta }}_Q\right)\right]$.

Assume that $\mathit{G}=\mathrm{diag}\left(g_q\right)$ is a $Q\times Q$ dimensional diagonal matrix where its diagonal elements correspond to the power values of each grid point, of which the q-th value is

$$g_q={∥x_q∥}^2.$$

(26)

Then, the noise covariance matrix is defined, and it can be represented as follows at the q-th grid point

$${{\mathit{R}}^{\prime }}_q=\mathit{R}-g_q{\mathit{u}}_q\left(\delta ,\theta \right){{\mathit{u}}_q}^{\mathrm{H}}\left(\delta ,\theta \right),$$

(27)

where $\mathit{R}=\mathit{AG}{\mathit{A}}^{\mathrm{H}}$ denotes the covariance matrix of the received signal.

Therefore, the parameter estimation results are obtained through a WLS-based IAA algorithm as follows

$${\tilde{\alpha }}_q^k=\underset{{\alpha }_q^k}{min}{\left[{\mathit{x}}^k-{\mathit{u}}_q\left(\delta ,\theta \right){\alpha }_q^k\right]}^{\mathrm{H}}{{\mathit{R}}^{\prime }}_q\left[{\mathit{x}}^k-{\mathit{u}}_q\left(\delta ,\theta \right){\alpha }_q^k\right],$$

(28)

where ${\alpha }_q^k$ represents the complex amplitude of the signal at the q-th grid point during the k-th pulse.

The Equation (28) can be further expressed as

$${\tilde{\alpha }}_q^k={\displaystyle \frac{{{\mathit{u}}_q}^{\mathrm{H}}\left(\delta ,\theta \right){\mathit{R}}^{-1}{\mathit{x}}^k}{{{\mathit{u}}_q}^{\mathrm{H}}\left(\delta ,\theta \right){\mathit{R}}^{-1}{\mathit{u}}_q\left(\delta ,\theta \right)}}.$$

(29)

In order to activate the IAA, an initialization of $\mathit{G}$ is required, with an initial value assigned to $g_q$, namely

$${\tilde{g}}_q={\displaystyle \frac{{\displaystyle \sum _{k=1}^{\mathrm{K}}}{\left|{\mathit{u}}_q\left(\delta ,\theta \right){\mathit{x}}^k\right|}^2}{K{∥{\mathit{u}}_q\left(\delta ,\theta \right)∥}^2}}.$$

(30)

The above process is repeated iteratively until a specific condition is met or a preset number of iterations $\vartheta$ is reached. Subsequently, the signal power $g_q$ at the grid points is given. Thus, the parameter estimation of the target is achieved. The procedures of the mentioned IAA algorithm for the FDA-MIMO radar are summarized in Algorithm 1.

Algorithm 1 FDA-IAA

Input: $\mathit{A}$, $\mathit{x}$, ${\mathit{u}}_q$, $\delta$, $\theta$ and $\mathit{G}$. Output: $g_q$.   Initialization: Set ${\tilde{g}}_q$ via Equation (30);   repeat   1. Perform at most $\vartheta$ iterations;   2. For $q=1,2,\dots ,Q$;   3. Compute ${\tilde{\alpha }}_q^k$ via Equation (29);   4. Compute $g_q={∥x_q∥}^2$;   Output $g_q$.

3.3. Atomic Norm Minimization Approach

The ANM algorithm is introduced in this subsection [39,40,53]. As can be seen from Equation (23), the incremental range information ${\delta }_l$ and angle information ${\theta }_l$ are coupled within the steering vector ${\mathit{a}}_t\left({\delta }_l,{\theta }_l\right)$, which may lead to ambiguity in the parameter estimation results. Therefore, a decoupling model for the received signal in the k-th pulse is presented to separate the angle and incremental range information, which is written as

$$\begin{array}{cc}\hfill {\mathit{x}}_k=& \sum _{l=1}^{\mathrm{L}}{\xi }_{kl}{\mathit{b}}_r\left({\theta }_l\right)\otimes \left[{\mathit{a}}_t\left({\theta }_l\right)\odot {\mathit{a}}_t\left({\delta }_l\right)\right]+{\mathit{n}}_k\hfill \\ \hfill =& \sum _{l=1}^{\mathrm{L}}{\xi }_{kl}\left[{\mathbf{1}}_N\otimes {\mathit{a}}_t\left({\delta }_l\right)\right]\odot \left[{\mathit{b}}_r\left({\theta }_l\right)\otimes {\mathit{a}}_t\left({\theta }_l\right)\right]+{\mathit{n}}_k\hfill \\ \hfill =& \mathrm{diag}\left\{\sum _{l=1}^{\mathrm{L}}{\xi }_{kl}{\mathbf{1}}_N\otimes \left\{{\mathit{a}}_t\left({\delta }_l\right){\left[{\mathit{b}}_r\left({\theta }_l\right)\otimes {\mathit{a}}_t\left({\theta }_l\right)\right]}^{\mathrm{T}}\right\}\right\}+{\mathit{n}}_k,\hfill \end{array}$$

(31)

where ${\xi }_{kl}$ denotes the amplitude and phase of the l-th target at the k-th pulse.

Then, define $\mathrm{f}\left({\theta }_l\right)\stackrel{\Delta }{=}{\left[1,e^{j2\pi f_0{\displaystyle \frac{dsin\left({\theta }_l\right)}{c}}},\dots ,e^{j2\pi f_0{\displaystyle \frac{\left(M+N-2\right)dsin\left({\theta }_l\right)}{c}}}\right]}^{\mathrm{T}}\in {\mathbb{C}}^{M+N-1}$ as the set formed by extracting the non-redundant $M+N-1$ elements from ${\mathit{b}}_r\left({\theta }_l\right)\otimes {\mathit{a}}_t\left({\theta }_l\right)$. Hence, the Equation (31) can be rewritten as

$$\begin{array}{cc}\hfill {\mathit{x}}_k=& \mathrm{vec}\left\{\mathrm{diag}\left[\sum _{l=1}^{\mathrm{L}}{\xi }_{kl}{\mathit{a}}_t\left({\delta }_l\right){\mathrm{f}}^{\mathrm{T}}\left({\theta }_l\right),0\right],\mathrm{diag}\left[\sum _{l=1}^{\mathrm{L}}{\xi }_{kl}{\mathit{a}}_t\left({\delta }_l\right){\mathrm{f}}^{\mathrm{T}}\left({\theta }_l\right),1\right],\dots ,\right.\hfill \\ \hfill & \left.\mathrm{diag}\left[\sum _{l=1}^{\mathrm{L}}{\xi }_{kl}{\mathit{a}}_t\left({\delta }_l\right){\mathrm{f}}^{\mathrm{T}}\left({\theta }_l\right),N-1\right]\right\}+{\mathit{n}}_k.\hfill \end{array}$$

(32)

Next, the extracting matrix $\mathbf{\Gamma }=\left[{\mathbf{\Gamma }}_1;{\mathbf{\Gamma }}_2;\dots ;{\mathbf{\Gamma }}_N\right]\in {\mathbb{C}}^{MN\times M(M+N-1)}$ is constructed with ${\mathbf{\Gamma }}_n\in {\mathbb{C}}^{M\times M(M+N-1)}$. Notably, the $\left(1+\left(n-1\right)M+\left(m-1\right)\left(M+1\right)\right)$-th element in the m-th row of ${\mathbf{\Gamma }}_n$ is one, and other elements are zero. Therefore, the Equation (32) can be re-expressed as

$$\begin{array}{cc}\hfill {\mathit{x}}_k=& \sum _{l=1}^{\mathrm{L}}{\xi }_{kl}\mathbf{\Gamma }\left[\mathrm{f}\left({\theta }_l\right)\otimes {\mathit{a}}_t\left({\delta }_l\right)\right]+{\mathit{n}}_k\hfill \\ \hfill =& \mathbf{\Gamma }\left[\mathit{F}\left({\theta }_l\right)\circ {\mathit{A}}_t\left(\delta \right)\right]{\mathit{\xi }}_k+{\mathit{n}}_k,\hfill \end{array}$$

(33)

where $\mathit{F}\left(\theta \right)=\left[\mathrm{f}\left({\theta }_1\right),\mathrm{f}\left({\theta }_2\right),\dots ,\mathrm{f}\left({\theta }_L\right)\right]\in {\mathbb{C}}^{(M+N-1)\times L}$, ${\mathit{A}}_t\left(\delta \right)=\left[{\mathit{a}}_t\left({\delta }_1\right),{\mathit{a}}_t\left({\delta }_2\right),\dots ,{\mathit{a}}_t\left({\delta }_L\right)\right]\in {\mathbb{C}}^{MN\times L}$, and ${\mathit{\xi }}_k=\left[{\xi }_{k1},{\xi }_{k2},\dots {\xi }_{kL}\right]\in {\mathbb{C}}^L$.

Then, the received signals for K pulses can be presented as

$$\mathit{X}=\mathbf{\Gamma }\left[\mathit{F}\left(\theta \right)\circ {\mathit{A}}_t\left(\delta \right)\right]\mathit{\xi }+\mathit{N},$$

(34)

where $\mathit{X}=\left[{\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_K\right]\in {\mathbb{C}}^{MN\times K}$, $\mathit{\xi }=\left[{\mathit{\xi }}_1,{\mathit{\xi }}_2,\dots ,{\mathit{\xi }}_K\right]\in {\mathbb{C}}^{MN\times K}$, and $\mathit{N}=\left[{\mathit{n}}_1,{\mathit{n}}_2,\dots ,{\mathit{n}}_K\right]\in {\mathbb{C}}^{MN\times K}$. Thus, the decoupling model for angle-incremental range is obtained as in Equation (34).

The following defines a 2D atomic set as the target’s angle and incremental range

$$\begin{array}{c}\hfill \Im \stackrel{\Delta }{=}\left\{\mathrm{f}\left(\theta \right)\otimes {\mathit{a}}_t\left(\delta \right)\mathit{v}\left|\theta \in \left[-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right),\delta \in \left[-{\displaystyle \frac{\Delta f}{B}},{\displaystyle \frac{\Delta f}{B}}\right),{∥\mathit{v}∥}_2=1,\mathit{v}\in {\mathbb{C}}^{1\times K}\right.\right\}.\end{array}$$

(35)

According to Equation (34), a new matrix ${\mathit{X}}_s$ is defined as follows [54]

$$\begin{array}{cc}\hfill {\mathit{X}}_s\stackrel{\Delta }{=}& \mathit{F}\left(\theta \right)\circ {\mathit{A}}_t\left(\delta \right)\mathit{\xi }\hfill \\ \hfill =& \sum _{l=1}^{\mathrm{L}}{\rho }_l\mathrm{f}\left({\theta }_l\right)\otimes {\mathit{a}}_t\left({\delta }_l\right){\mathit{v}}_l,\hfill \end{array}$$

(36)

where $\mathrm{f}\left({\theta }_l\right)\otimes {\mathit{a}}_t\left({\delta }_l\right){\mathit{v}}_l\in \Im$, ${\rho }_l={∥{\mathit{\xi }}_{l,:}∥}_2$, and ${\mathit{v}}_l={\displaystyle \frac{{\mathit{\xi }}_{l,:}}{{∥{\mathit{\xi }}_{l,:}∥}_2}}$. Thus, matrix ${\mathit{X}}_s$ can be considered as a linear combination of L atoms in the atomic set ℑ.

According to compressed sensing theory, the sparsity of the received signal is characterized by its ${\ell }_0$ norm, defined as

$${∥{\mathit{X}}_s∥}_{\Im ,{\ell }_0}\stackrel{\Delta }{=}\inf \left\{L\left|{\mathit{X}}_s=\sum _{l=1}^{\mathrm{L}}{{\rho }^{\prime }}_l{\mathrm{h}}_l,{\mathrm{h}}_l=\mathrm{f}\left({\theta }_l\right)\otimes {\mathit{a}}_t\left({\delta }_l\right){\mathit{v}}_l,{\mathrm{h}}_l\in \Im ,{\rho }^{\prime }>0\right.\right\}.$$

(37)

Notably, the problem of ${\ell }_0$ norm minimization is NP-hard, and it is difficult to obtain an exact solution. Thus, the ${\ell }_1$ norm is usually used as a substitute in practice, represented as follows

$${∥{\mathit{X}}_s∥}_{\Im ,{\ell }_1}\stackrel{\Delta }{=}\inf \left\{\sum _{l=1}^{\mathrm{L}}{{\rho }^{\prime }}_l\left|{\mathit{X}}_s=\sum _{l=1}^{\mathrm{L}}{{\rho }^{\prime }}_l{\mathrm{h}}_l,{\mathrm{h}}_l=\mathrm{f}\left({\theta }_l\right)\otimes {\mathit{a}}_t\left({\delta }_l\right){\mathit{v}}_l,{\mathrm{h}}_l\in \Im ,{\rho }^{\prime }>0\right.\right\}.$$

(38)

Then, according to [55,56], by minimizing and convex relaxation, Equation (38) can be transformed into the following Semi-Definite Programming (SDP) problem

$${\mathcal{P}}_1:\left\{\begin{array}{c}\underset{\mathit{u},\mathit{V}}{\min }{\displaystyle \frac{1}{2\sqrt{MN}}}\left\{\mathrm{Tr}\left[T\left(\mathit{u}\right)\right]+\mathrm{Tr}\left(\mathit{V}\right)\right\}\hfill \\ \mathrm{s}.\mathrm{t}.\left[\begin{array}{c}T\left(\mathit{u}\right){\mathit{X}}_s\hfill \\ {{\mathit{X}}_s}^{\mathrm{H}}\mathit{V}\hfill \end{array}\right]\ge 0\hfill \end{array}\right.,$$

(39)

where $\mathit{u}={\left[u_{0,-\left(N-1\right)},u_{0,0},u_{0,\left(N-1\right)},u_{1,-\left(N-1\right)},\dots ,u_{1,\left(N-1\right)},\dots ,u_{M+N-2,\left(N-1\right)}\right]}^{\mathrm{T}}\in {\mathbb{C}}^{N_u}$ with $N_u=\left(M+N-1\right)\left(2N-1\right)$, $\mathit{V}\in {\mathbb{C}}^{K\times K}$ and $\mathit{u}$ and $\mathit{V}$ represent auxiliary variables. The $T\left(\mathit{u}\right)$ denotes the transformation of $\mathit{u}$ into a Hermitian matrix, which can be written as

$$T\left(\mathit{u}\right)=\left[\begin{array}{c}{\mathit{T}}_0{\mathit{T}}_1\dots {\mathit{T}}_{M+N-2}\hfill \\ {\mathit{T}}_1{\mathit{T}}_0\dots {\mathit{T}}_{M+N-3}\hfill \\ ⋮⋮\ddots ⋮\hfill \\ {{\mathit{T}}^{\mathrm{H}}}_{M+N-2}{{\mathit{T}}^{\mathrm{H}}}_{M+N-2}\dots {\mathit{T}}_0\hfill \end{array}\right],$$

(40)

where ${\mathit{T}}_i$ (for $i=0,1,\dots ,M+N-2$) is formulated as

$${\mathit{T}}_i=\left[\begin{array}{c}{u}_{i,0}{u_{i,}}_1\dots u_{i,N-1}\hfill \\ u_{i,N-1}{u}_{i,0}\dots u_{i,N-2}\hfill \\ ⋮⋮\ddots ⋮\hfill \\ u_{i,-\left(N-1\right)}{u}_{i,-\left(N-2\right)}\dots u_{i,0}\hfill \end{array}\right].$$

(41)

Considering the noise background, the objective function in Equation (39) is further modified as

$${\mathcal{P}}_2:\left\{\begin{array}{c}\underset{\mathit{u},\mathit{V}}{\min }{\displaystyle \frac{1}{2\sqrt{MN}}}\left\{\mathrm{Tr}\left[T\left(\mathit{u}\right)\right]+\mathrm{Tr}\left(\mathit{V}\right)\right\}+{\displaystyle \frac{\mu }{2}}{∥\mathit{X}-\mathbf{\Gamma }{\mathit{X}}_s∥}_F^2\hfill \\ \mathrm{s}.\mathrm{t}.\left[\begin{array}{c}T\left(\mathit{u}\right){\mathit{X}}_s\hfill \\ {{\mathit{X}}_s}^{\mathrm{H}}\mathit{V}\hfill \end{array}\right]\ge 0\hfill \end{array}\right.,$$

(42)

where $\mu$ represents the regularized parameter.

By solving Equation (42), it yields the $T\left(\mathit{u}\right)$. Subsequently, the estimated values of the target’s incremental range and angle can be obtained by applying the decomposition theorem to $T\left(\mathit{u}\right)$ [57]. The procedures of the mentioned ANM algorithm for the FDA-MIMO radar are summarized in Algorithm 2.

Algorithm 2 FDA-ANM

Input: M, N, ${\mathit{x}}_k$, $\mu$, ${\theta }_l$ and ${\delta }_l$. Output: A solution $T\left(\mathrm{u}\right)$ to (42).     1. Define $\mathrm{f}\left({\theta }_l\right)$ to separate ${\delta }_l$ and ${\theta }_l$ via Equations (31) and (32);     2. Construct $\mathbf{\Gamma }$ to obtain $\mathit{X}$ via Equations (33) and (34);     3. Define ℑ to acquire ${\mathit{X}}_s$ via Equations (35) and (36);     4. Formulate ${∥{\mathit{X}}_s∥}_{\Im ,{\ell }_1}$ according to Equation (38);     5. Construct a SDP problem as in Equation (39);     6. The objective function is formed as in Equation (42);     7. Calculate $T\left(u\right)$ via Equation (42);     Output $T\left(u\right)$.

3.4. Coordinate Descent Multiple Signal Classification Approach

In this subsection, the CD-MUSIC algorithm is employed for the parameter estimation (i.e., the angle and range ambiguity index) in the EPC-MIMO radar [58,59]. The MUSIC algorithm is leveraged by exploiting the eigenstructure of the signal covariance matrix, which is obtained through snapshots data, namely

$$\widehat{\mathit{R}}={\displaystyle \frac{1}{K}}\sum _{k=1}^{\mathrm{K}}{\mathit{y}}_{\mathit{r}}\left(k\right){{\mathit{y}}_{\mathit{r}}}^{\mathrm{H}}\left(k\right).$$

(43)

Notably, the noise subspace matrix ${\mathit{E}}_n\in {\mathbb{C}}^{MN-L}$ is constructed from the eigenvectors corresponding to the $MN-L$ smallest eigenvalues. In particular, the matrix is obtained through the eigenvalue decomposition of the sample covariance matrix $\widehat{\mathit{R}}$. Consequently, the spatial spectrum of the MUSIC algorithm is derived as follows

$$P={\displaystyle \frac{1}{{\mathit{u}}^{\mathrm{H}}\left({\gamma }_s,\theta \right){\mathit{E}}_n{\mathit{E}}_n^{\mathrm{H}}\mathit{u}\left({\gamma }_s,\theta \right)}},$$

(44)

where $\mathit{u}\left({\gamma }_s,\theta \right)=\mathit{b}\left(\theta \right)\otimes \mathit{a}\left({\gamma }_s,\theta \right)$ denotes the transceive steering vector.

The procedures of the mentioned CD-MUSIC algorithm for the EPC-MIMO radar are summarized in Algorithm 3. Notice that the exit condition is $\left|P^{n+1}-P^n\right|<\epsilon$, with $\epsilon$ a controllable small value. Therefore, the angle and range ambiguity index can be separately obtained by searching for the maximum value of P.

Algorithm 3 EPC-CD-MUSIC

Require:  ${\theta }_0$, ${\gamma }_s$, P, $\epsilon$. Ensure:  $\widehat{\theta }$, ${\widehat{\gamma }}_s$. Initialization: $n=0$, ${\widehat{\theta }}^0={\theta }_0$, ${{\widehat{\gamma }}_s}^0={\gamma }_s$, $P^0=P\left({{\widehat{\gamma }}_s}^0,{\widehat{\theta }}^0\right)$. repeat (optimization for initial search direction given by ${\gamma }_s$) 1. Find ${\widehat{\gamma }}_s^{n+1}=arg\underset{{\gamma }_s\in I_{{\gamma }_s}}{max}P\left({\gamma }_s,{\widehat{\theta }}^n\right)$; 2. Find ${\widehat{\theta }}^{n+1}=arg\underset{\theta \in I_{\theta }}{max}P\left({{\widehat{\gamma }}_s}^{n+1},\theta \right)$; 3. $n=n+1$ until $\left|P^{n+1}-P^n\right|<\epsilon$; $P_x=P^n$; ${\widehat{\gamma }}_{sx}={{\widehat{\gamma }}_s}^n$; ${\widehat{\theta }}_x={\widehat{\theta }}^n$; Initialization: $n=0$. repeat (optimization for initial search direction given by $\theta$) 1. Find ${\widehat{\theta }}^{n+1}=arg\underset{\theta \in I_{\theta }}{max}P\left({{\widehat{\gamma }}_s}^n,\theta \right)$; 2. Find ${{\widehat{\gamma }}_s}^{n+1}=arg\underset{{\gamma }_s\in I_{{\gamma }_s}}{max}P\left({\gamma }_s,{\widehat{\theta }}^{n+1}\right)$; 3. $n=n+1$ until $\left|P^{n+1}-P^n\right|<\epsilon$; $P_y=P^n$; ${\widehat{\gamma }}_{sy}={{\widehat{\gamma }}_s}^n$; ${\widehat{\theta }}_y={\widehat{\theta }}^n$; if $P_x>P_y$ then   Output ${\widehat{\gamma }}_s={\widehat{\gamma }}_{sx}$ and $\widehat{\theta }={\widehat{\theta }}_x$. else   Output ${\widehat{\gamma }}_s={\widehat{\gamma }}_{sy}$ and $\widehat{\theta }={\widehat{\theta }}_y$. end if

3.5. CRBs for the FDA-MIMO Radar and EPC-MIMO Radar

In this subsection, the CRBs for the FDA-MIMO radar and the EPC-MIMO radar are developed to characterize the statistical efficiency of the proposed methods.

3.5.1. FDA-MIMO Radar

Let us first define three auxiliary vectors, i.e., $\mathit{w}={\mathit{R}}_n^{-1/2}\mathit{u}\left(\delta ,\theta \right)\in {\mathbb{C}}^{MN}$, ${\mathit{w}}_{\delta }={\mathit{R}}_n^{-1/2}$${\mathit{u}}_{\delta }\left(\delta ,\theta \right)\in {\mathbb{C}}^{MN}$, and ${\mathit{w}}_{\theta }={\mathit{R}}_n^{-1/2}{\mathit{u}}_{\theta }\left(\delta ,\theta \right)\in {\mathbb{C}}^{MN}$, with ${\mathit{R}}_n$ the positive-definite covariance matrix of the noise. In this context, the real-valued vector $\mathit{\alpha }\in {\mathbb{R}}^4$, which encapsulates the unknown parameters $\theta$, $\delta$, $\overline{\xi }=\mathrm{Re}\left({\xi }^{\prime }\right)$, $\widehat{\xi }=\mathrm{Im}\left({\xi }^{\prime }\right)$, is introduced as

$$\mathit{\alpha }={\left[\theta ,\delta ,\overline{\xi },\widehat{\xi }\right]}^{\mathrm{T}}.$$

(45)

Subsequently, the CRBs for the angle and incremental range are derived under the assumption that ${\xi }^{\prime }$ remains unknown. Hence, the CRBs for the unknown parameters are provided by the diagonal elements of ${\mathit{D}}_{\mathit{\alpha }}={\mathit{F}}^{-1}\in {\mathbb{R}}^{4\times 4}$, where the Fisher Information Matrix (FIM) $\mathit{F}\in {\mathbb{R}}^{4\times 4}$ can be presented as

$$\begin{array}{cc}\hfill \mathit{F}=& 2\mathrm{Re}\left\{{\left[{\displaystyle \frac{\partial {\xi }^{\prime }\mathit{u}\left(\delta ,\theta \right)}{\partial \mathit{\alpha }}}\right]}^{\mathrm{H}}{\mathit{R}}_n^{-1}\left[{\displaystyle \frac{\partial {\xi }^{\prime }\mathit{u}\left(\delta ,\theta \right)}{\partial \mathit{\alpha }}}\right]\right\}\hfill \\ \hfill =& 2\mathrm{Re}\left\{{\left[{\xi }^{\prime }{\mathit{u}}_{\theta }\left(\delta ,\theta \right),{\xi }^{\prime }{\mathit{u}}_{\delta }\left(\delta ,\theta \right),\mathit{u}\left(\delta ,\theta \right),j\mathit{u}\left(\delta ,\theta \right)\right]}^{\mathrm{H}}{\mathit{R}}_n^{-1}\left[{\xi }^{\prime }{\mathit{u}}_{\theta }\left(\delta ,\theta \right),{\xi }^{\prime }{\mathit{u}}_{\delta }\left(\delta ,\theta \right),\mathit{u}\left(\delta ,\theta \right),j\mathit{u}\left(\delta ,\theta \right)\right]\right\}\hfill \\ \hfill =& 2\mathrm{Re}\left\{{\left[{\xi }^{\prime }{\mathit{w}}_{\theta },{\xi }^{\prime }{\mathit{w}}_{\delta },\mathit{w},j\mathit{w}\right]}^{\mathrm{H}}\left[{\xi }^{\prime }{\mathit{w}}_{\theta },{\xi }^{\prime }{\mathit{w}}_{\delta },\mathit{w},j\mathit{w}\right]\right\}.\hfill \end{array}$$

(46)

Therefore, the FIM can be expressed as

$$\mathit{F}=2\left[\begin{array}{c}{\mathit{F}}_{11}{\mathit{F}}_{12}\\ {\mathit{F}}_{21}{\mathit{F}}_{22}\end{array}\right],$$

(47)

where

• ${\mathit{F}}_{11}=\left[\begin{array}{cc}{\left|{\xi }^{\prime }\right|}^2{∥{\mathit{w}}_{\theta }∥}^2& {\left|{\xi }^{\prime }\right|}^2\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}{\mathit{w}}_{\delta }\right\}\\ {\left|{\xi }^{\prime }\right|}^2\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}{\mathit{w}}_{\delta }\right\}& {\left|{\xi }^{\prime }\right|}^2{∥{\mathit{w}}_{\delta }∥}^2\end{array}\right]$;
• ${\mathit{F}}_{12}=\left[\begin{array}{cc}\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}{\left({\xi }^{\prime }\right)}^{*}\right\}& -\mathrm{Im}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}{\left({\xi }^{\prime }\right)}^{*}\right\}\\ \mathrm{Re}\left\{{\mathit{w}}_{\delta }^{\mathrm{H}}\mathit{w}{\left({\xi }^{\prime }\right)}^{*}\right\}& -\mathrm{Im}\left\{{\mathit{w}}_{\delta }^{\mathrm{H}}\mathit{w}{\left({\xi }^{\prime }\right)}^{*}\right\}\end{array}\right]$;
• ${\mathit{F}}_{21}={\mathit{F}}_{12}^{\mathrm{T}}$;
• ${\mathit{F}}_{22}={∥\mathit{w}∥}^2{\mathit{I}}_2={∥\mathit{w}∥}^2\left[\begin{array}{c}10\\ 01\end{array}\right]$.

Hence, the ${\mathit{D}}_{\mathit{\alpha }}$ can be obtained as the inverse of $\mathit{F}$, i.e.,

$${\mathit{D}}_{\mathit{\alpha }}={\mathit{F}}^{-1}={\displaystyle \frac{1}{2}}\left[\begin{array}{c}{\mathit{G}}_1^{-1}{\mathit{G}}_2\hfill \\ {\mathit{G}}_3{\mathit{G}}_4^{-1}\hfill \end{array}\right],$$

(48)

where ${\mathit{G}}_1\in {\mathbb{R}}^{2\times 2}$ is expressed as

$$\begin{array}{cc}\hfill {\mathit{G}}_1=& {\mathit{F}}_{11}-{\mathit{F}}_{12}{\mathit{F}}_{22}^{-1}{\mathit{F}}_{21}\hfill \\ \hfill =& {\left|{\xi }^{\prime }\right|}^2\left[\begin{array}{cc}{∥{\mathit{w}}_{\theta }∥}^2-{\displaystyle \frac{{\left|{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}\right|}^2}{{∥\mathit{w}∥}^2}}& \mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}{\mathit{w}}_{\delta }\right\}-{\displaystyle \frac{\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}{\mathit{w}}^{\mathrm{H}}{\mathit{w}}_{\delta }\right\}}{{∥\mathit{w}∥}^2}}\\ \mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}{\mathit{w}}_{\delta }\right\}-{\displaystyle \frac{\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}{\mathit{w}}^{\mathrm{H}}{\mathit{w}}_{\delta }\right\}}{{∥\mathit{w}∥}^2}}& {∥{\mathit{w}}_{\delta }∥}^2-{\displaystyle \frac{{\left|{\mathit{w}}_{\delta }^{\mathrm{H}}\mathit{w}\right|}^2}{{∥\mathit{w}∥}^2}}.\end{array}\right].\hfill \end{array}$$

(49)

Therefore, the CRBs for $\delta$ and $\theta$ (analytical details are reported in Appendix A.1) are given by

$$D_{\delta }={\displaystyle \frac{{\left|{\xi }^{\prime }\right|}^2}{2\det \left({\mathit{G}}_1\right)}}\left({∥{\mathit{w}}_{\theta }∥}^2-{\displaystyle \frac{{\left|{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}\right|}^2}{{∥\mathit{w}∥}^2}}\right),$$

(50)

and

$$D_{\theta }={\displaystyle \frac{{\left|{\xi }^{\prime }\right|}^2}{2\det \left({\mathit{G}}_1\right)}}\left({∥{\mathit{w}}_{\delta }∥}^2-{\displaystyle \frac{{\left|{\mathit{w}}_{\delta }^{\mathrm{H}}\mathit{w}\right|}^2}{{∥\mathit{w}∥}^2}}\right).$$

(51)

3.5.2. EPC-MIMO Radar

Similarly, three auxiliary vectors are defined, i.e., $\mathit{w}={\mathit{R}}_n^{-1/2}\mathit{u}\left({\gamma }_s,\theta \right)\in {\mathbb{C}}^{MN}$, ${\mathit{w}}_{{\gamma }_s}={\mathit{R}}_n^{-1/2}$${\mathit{u}}_{{\gamma }_s}\left({\gamma }_s,\theta \right)\in {\mathbb{C}}^{MN}$, and ${\mathit{w}}_{\theta }={\mathit{R}}_n^{-1/2}{\mathit{u}}_{\theta }\left({\gamma }_s,\theta \right)\in {\mathbb{C}}^{MN}$. In this context, the real-valued vector ${\mathit{\alpha }}^{\prime }\in {\mathbb{R}}^4$, which encapsulates the unknown parameters $\theta$, ${\gamma }_s$ and $\overline{\xi }=\mathrm{Re}\left({\xi }^{\prime }\right)$, $\widehat{\xi }=\mathrm{Im}\left({\xi }^{\prime }\right)$, is introduced as

$${\mathit{\alpha }}^{\prime }={\left[\theta ,{\gamma }_s,\overline{\xi },\widehat{\xi }\right]}^{\mathrm{T}}.$$

(52)

Subsequently, the CRBs for angle and range ambiguity index are derived under the assumption that ${\xi }^{\prime }$ remains unknown. Hence, the CRBs for the unknown parameters are provided by the diagonal elements of ${\mathit{D}}_{\mathit{\alpha }}={\mathit{F}}^{-1}\in {\mathbb{R}}^{4\times 4}$, where the FIM $\mathit{F}\in {\mathbb{R}}^{4\times 4}$ can be presented as

$$\begin{array}{cc}\hfill \mathit{F}=& 2\mathrm{Re}\left\{{\left[{\displaystyle \frac{\partial {\xi }^{\prime }\mathit{u}\left({\gamma }_s,\theta \right)}{\partial {\mathit{\alpha }}^{\prime }}}\right]}^{\mathrm{H}}{\mathit{R}}_n^{-1}\left[{\displaystyle \frac{\partial {\xi }^{\prime }\mathit{u}\left({\gamma }_s,\theta \right)}{\partial {\mathit{\alpha }}^{\prime }}}\right]\right\}\hfill \\ \hfill =& 2\mathrm{Re}\left\{{\left[{\xi }^{\prime }{\mathit{u}}_{\theta },{\xi }^{\prime }{\mathit{u}}_{{\gamma }_s},\mathit{u},j\mathit{u}\right]}^{\mathrm{H}}{\mathit{R}}_n^{-1}\left[{\xi }^{\prime }{\mathit{u}}_{\theta },{\xi }^{\prime }{\mathit{u}}_{{\gamma }_s},\mathit{u},j\mathit{u}\right]\right\}\hfill \\ \hfill =& 2\mathrm{Re}\left\{{\left[{\xi }^{\prime }{\mathit{w}}_{\theta },{\xi }^{\prime }{\mathit{w}}_{{\gamma }_s},\mathit{w},j\mathit{w}\right]}^{\mathrm{H}}\left[{\xi }^{\prime }{\mathit{w}}_{\theta },{\xi }^{\prime }{\mathit{w}}_{{\gamma }_s},\mathit{w},j\mathit{w}\right]\right\}.\hfill \end{array}$$

(53)

Therefore, the FIM can be expressed as

$$\mathit{F}=2\left[\begin{array}{c}{\mathit{F}}_{11}{\mathit{F}}_{12}\\ {\mathit{F}}_{21}{\mathit{F}}_{22}\end{array}\right],$$

(54)

where

• ${\mathit{F}}_{11}=\left[\begin{array}{cc}{\left|{\xi }^{\prime }\right|}^2{∥{\mathit{w}}_{\theta }∥}^2& {\left|{\xi }^{\prime }\right|}^2\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}{\mathit{w}}_{{\gamma }_s}\right\}\\ {\left|{\xi }^{\prime }\right|}^2\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}{\mathit{w}}_{{\gamma }_s}\right\}& {\left|{\xi }^{\prime }\right|}^2{∥{\mathit{w}}_{{\gamma }_s}∥}^2\end{array}\right]$;
• ${\mathit{F}}_{12}=\left[\begin{array}{cc}\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}{\left({\xi }^{\prime }\right)}^{*}\right\}& -\mathrm{Im}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}{\left({\xi }^{\prime }\right)}^{*}\right\}\\ \mathrm{Re}\left\{{\mathit{w}}_{{\gamma }_s}^{\mathrm{H}}\mathit{w}{\left({\xi }^{\prime }\right)}^{*}\right\}& -\mathrm{Im}\left\{{\mathit{w}}_{{\gamma }_s}^{\mathrm{H}}\mathit{w}{\left({\xi }^{\prime }\right)}^{*}\right\}\end{array}\right]$;
• ${\mathit{F}}_{21}={\mathit{F}}_{12}^{\mathrm{T}}$;
• ${\mathit{F}}_{22}={∥\mathit{w}∥}^2{\mathit{I}}_2={∥\mathit{w}∥}^2\left[\begin{array}{c}10\\ 01\end{array}\right]$.

Hence, the ${\mathit{D}}_{\mathit{\alpha }}$ can be obtained as the inverse of $\mathit{F}$, i.e.,

$${\mathit{D}}_{\mathit{\alpha }}={\mathit{F}}^{-1}={\displaystyle \frac{1}{2}}\left[\begin{array}{c}{\mathit{G}}_1^{-1}{\mathit{G}}_2\hfill \\ {\mathit{G}}_3{\mathit{G}}_4^{-1}\hfill \end{array}\right],$$

(55)

where ${\mathit{G}}_1\in {\mathbb{R}}^{2\times 2}$ is expressed as

$$\begin{array}{cc}\hfill {\mathit{G}}_1=& {\mathit{F}}_{11}-{\mathit{F}}_{12}{\mathit{F}}_{22}^{-1}{\mathit{F}}_{21}\hfill \\ \hfill =& {\left|{\xi }^{\prime }\right|}^2\left[\begin{array}{cc}{∥{\mathit{w}}_{\theta }∥}^2-{\displaystyle \frac{{\left|{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}\right|}^2}{{∥\mathit{w}∥}^2}}& \mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}{\mathit{w}}_{{\gamma }_s}\right\}-{\displaystyle \frac{\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}{\mathit{w}}^{\mathrm{H}}{\mathit{w}}_{{\gamma }_s}\right\}}{{∥\mathit{w}∥}^2}}\\ \mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}{\mathit{w}}_{{\gamma }_s}\right\}-{\displaystyle \frac{\mathrm{Re}\left\{{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}{\mathit{w}}^{\mathrm{H}}{\mathit{w}}_{{\gamma }_s}\right\}}{{∥\mathit{w}∥}^2}}& {∥{\mathit{w}}_{{\gamma }_s}∥}^2-{\displaystyle \frac{{\left|{\mathit{w}}_{{\gamma }_s}^{\mathrm{H}}\mathit{w}\right|}^2}{{∥\mathit{w}∥}^2}}.\end{array}\right].\hfill \end{array}$$

(56)

Therefore, the CRBs for ${\gamma }_s$ and $\theta$ (analytical details are reported in Appendix A.2) are given by

$$D_{{\gamma }_s}={\displaystyle \frac{{\left|{\xi }^{\prime }\right|}^2}{2\det \left({\mathit{G}}_1\right)}}\left({∥{\mathit{w}}_{\theta }∥}^2-{\displaystyle \frac{{\left|{\mathit{w}}_{\theta }^{\mathrm{H}}\mathit{w}\right|}^2}{{∥\mathit{w}∥}^2}}\right),$$

(57)

and

$$D_{\theta }={\displaystyle \frac{{\left|{\xi }^{\prime }\right|}^2}{2\det \left({\mathit{G}}_1\right)}}\left({∥{\mathit{w}}_{{\gamma }_s}∥}^2-{\displaystyle \frac{{\left|{\mathit{w}}_{{\gamma }_s}^{\mathrm{H}}\mathit{w}\right|}^2}{{∥\mathit{w}∥}^2}}\right).$$

(58)

4. Numerical Results

In this section, numerical examples are presented to evaluate the localization performance of the proposed methods. The performance of the methods is evaluated across various SNR values, which are defined according to [60], as

$$\mathrm{SNR}={\left|{\xi }^{\prime }\right|}^2{\mathit{u}}^{\mathrm{H}}\left({\delta }_0,{\theta }_0\right){\mathit{R}}_n^{-1}\mathit{u}\left({\delta }_0,{\theta }_0\right).$$

(59)

Monte Carlo trials are executed to assess the performance. Moreover, the RMSEs in terms of angle and range are calculated as follows

$${\mathrm{RMSE}}_{\theta }=\sqrt{{\displaystyle \frac{1}{{\mathrm{M}}_{\mathrm{C}}}}{\sum }_{i=1}^{{\mathrm{M}}_{\mathrm{C}}}{\left|\theta -{\tilde{\theta }}_i\right|}^2},$$

(60)

$${\mathrm{RMSE}}_{\delta }=\sqrt{{\displaystyle \frac{1}{{\mathrm{M}}_{\mathrm{C}}}}{\sum }_{i=1}^{{\mathrm{M}}_{\mathrm{C}}}{\left|\delta -{\tilde{\delta }}_i\right|}^2},$$

(61)

and

$${\mathrm{RMSE}}_{\gamma }=\sqrt{{\displaystyle \frac{1}{{\mathrm{M}}_{\mathrm{C}}}}{\sum }_{i=1}^{{\mathrm{M}}_{\mathrm{C}}}{\left|\gamma -{\tilde{\gamma }}_i\right|}^2},$$

(62)

where ${\mathrm{M}}_{\mathrm{C}}=200$ denotes the number of independent experiments and ${\tilde{\theta }}_i$, ${\tilde{\delta }}_i$, and ${\tilde{\gamma }}_i$ represent the estimated angle, incremental range, and range ambiguity index in the i-th independent experiment, respectively. Furthermore, the simulation parameters involved the analyzed case are provided in

Table 1. Simulation parameters of the distributed waveform-diverse array radars.

Parameter	Value	Parameter	Value	Parameter	Value
M	10	N	10	K	6
B	10 MHz	$\Delta f$	5 MHz	$f_0$	10 GHz
$\gamma$	0.1	$PRF$	75 kHz

.

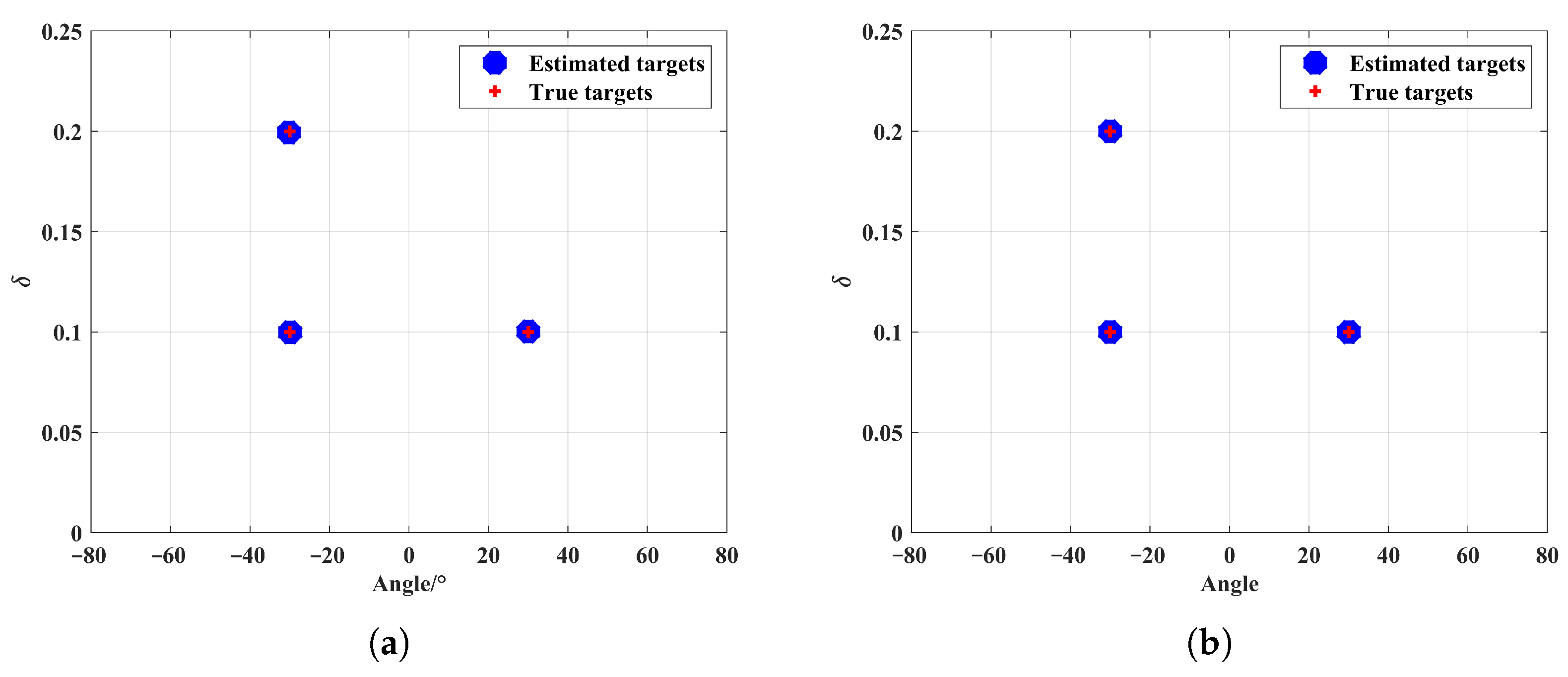
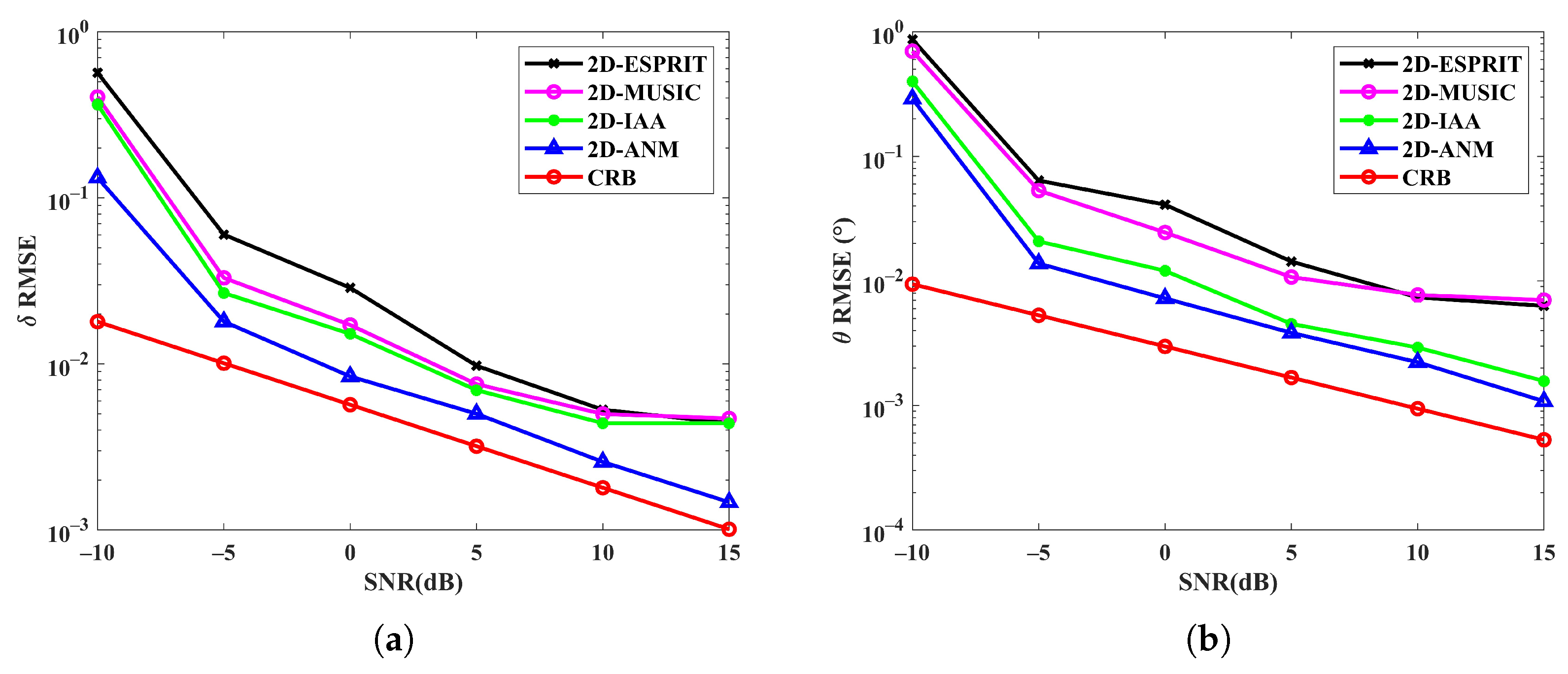
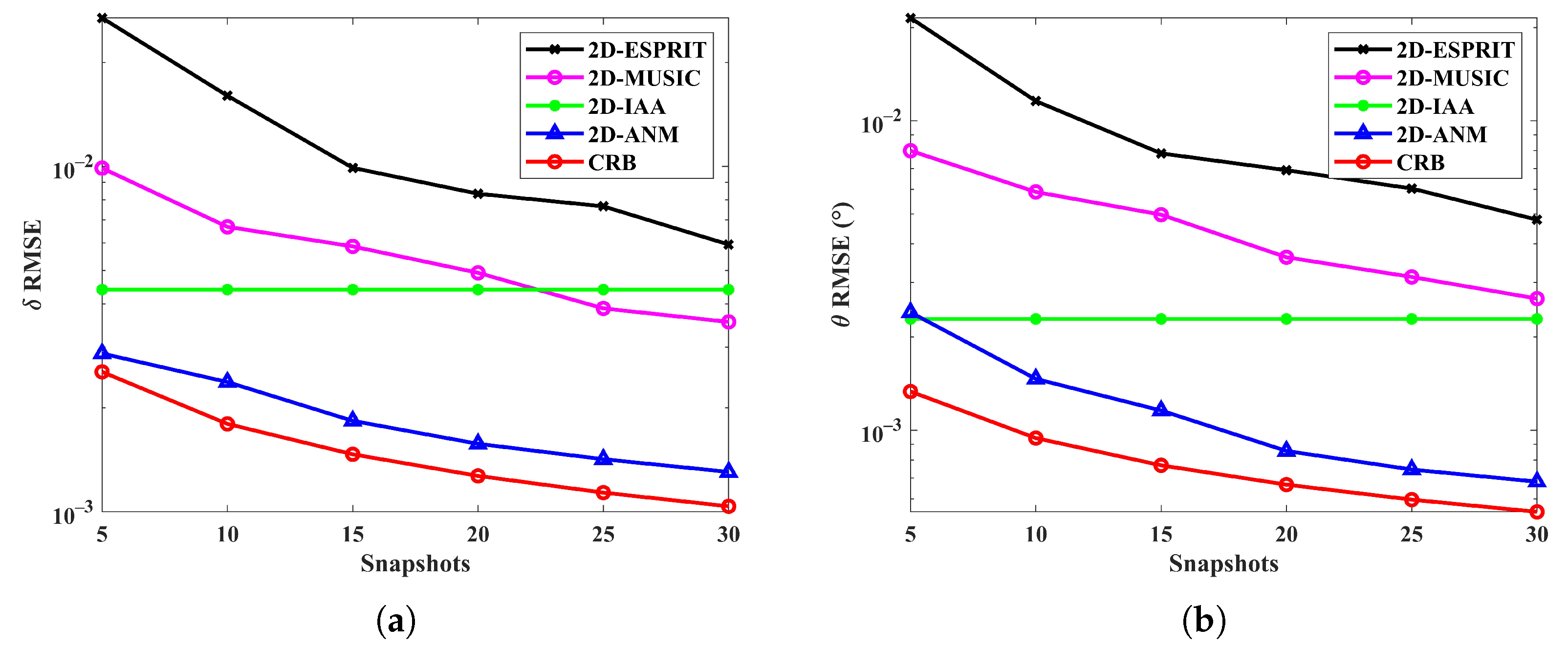
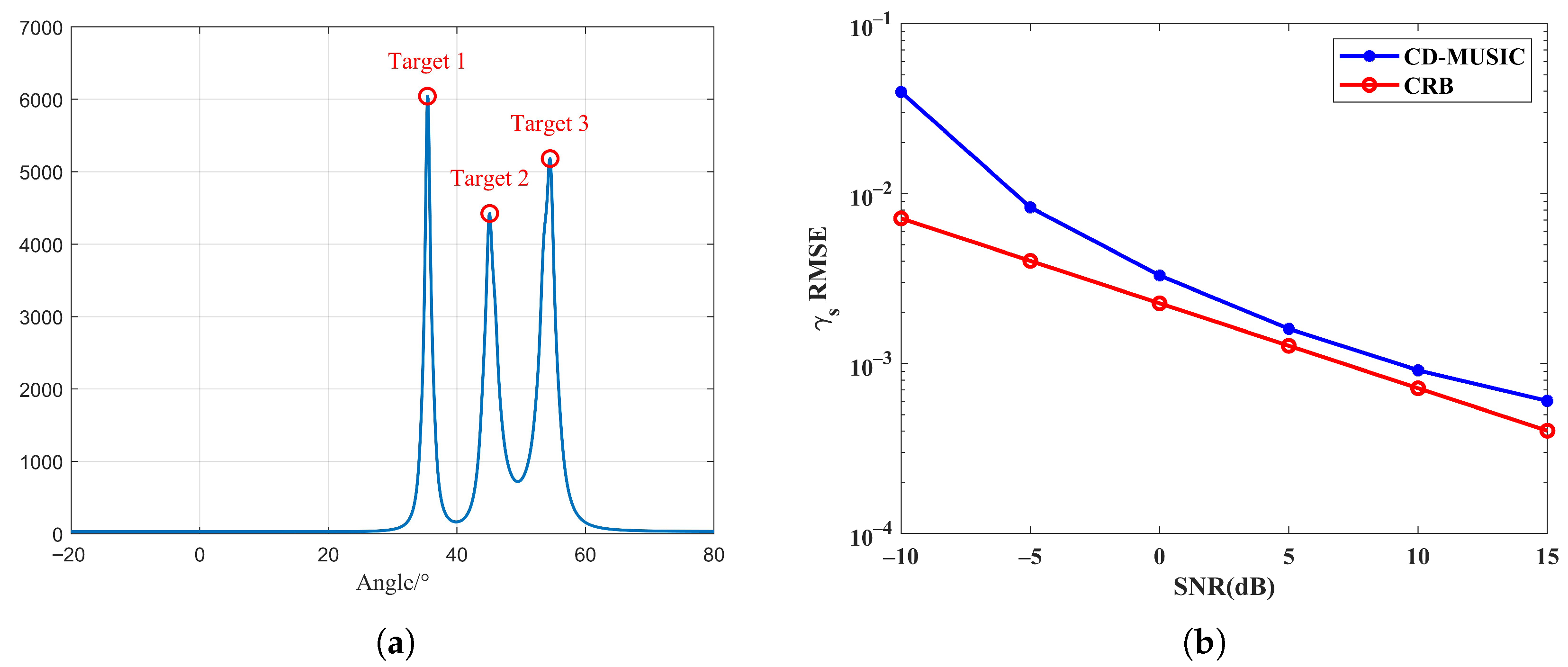
4.1. Performance Analysis of the Sparse Reconstruction Approach

In this subsection, numerical examples are presented to evaluate the effectiveness of the proposed methods to estimate the target’s incremental range and angle of arrival within the framework of an FDA-MIMO radar system. Specifically, the angle grid (−90°, 90°) containing 181 sample points is employed by the IAA algorithm. Meanwhile, the incremental range grid consisting of 501 sample points is also utilized in the following case. The actual target is set as $\left(\delta ,\theta \right)=\left(0.1,{30}^{\circ }\right)$. In this experiment, the effectiveness of the proposed methods is studied, considering two extra targets with $\left({\delta }_1,{\theta }_1\right)=\left(0.1,-{30}^{\circ }\right)$ and $\left({\delta }_2,{\theta }_2\right)=\left(0.2,-{30}^{\circ }\right)$. It can be observed that target $\left(\delta ,\theta \right)=\left(0.1,-{30}^{\circ }\right)$ shares the same angle with one target and the same incremental range with another.

The estimation outcomes of the two algorithms are provided in Figure 3. Apparently, the estimation results for the targets perfectly coincide with the actual positions. Additionally, targets located at the same angle but with different incremental ranges, or those with the same incremental range but different angles, can be clearly separated. The outcomes validate the effectiveness of the two proposed algorithms.

To further shed light on performance of the different methods, Figure 4 illustrates the RMSE versus SNR w.r.t the incremental range–angle estimation. It is evident that as the SNR increases, the estimation accuracy of both algorithms undergoes a notable improvement, ultimately achieving satisfactory performance at relatively high SNR levels. Moreover, when the SNR attains a sufficiently high level within the context of the given scenario, the performance of both algorithms converges relatively closely to the benchmark established by the CRB. Notably, when compared with the parameter estimation algorithms based on 2D subspaces in [58,59], the algorithms discussed in this context demonstrate significant advantages in parameter estimation performance. Furthermore, as evidenced by the numerical results in Figure 4, the estimation performance of the 2D-ANM at SNR = 15 dB demonstrates improvements of at least 1.6 dB, 8.1 dB, and 7.7 dB compared to the 2D-IAA, 2D-MUSIC, and 2D-ESPRIT algorithms, respectively.

To provide additional insight into the estimation performance of the proposed algorithms, consider setting SNR = 10 dB and varying both the number of array elements and the number of pulses independently, with the results shown in Figure 5 and Figure 6 below. Figure 5 illustrates the RMSE versus the number of array elements for incremental range–angle estimation. As the number of array elements increases, it is evident that the estimation accuracy of both methods enhances, achieving satisfactory performance at high numbers of array elements. However, once the number of array elements reaches a sufficiently high threshold, their performance starts to diverge from the CRB benchmark. Notably, the ANM maintains superior estimation performance. Specifically, with 10 array elements, the ANM achieves performance improvements of at least 1.2 dB, 3.2 dB, and 3.1 dB compared to the 2D-IAA, 2D-MUSIC, and 2D-ESPRIT algorithms, respectively.

Figure 6 presents the RMSE curves for angle and increment range estimation of the two algorithms, plotted versus K. Figure 6 illustrates that at low pulse counts, the sparse reconstruction algorithms exhibit notably superior performance compared to the subspace algorithms [58,59]. As K increases, the curve of the ANM algorithm consistently declines, maintaining a trend that aligns closely with the CRB. However, the IAA algorithm shows almost no improvement in estimation performance, and the performance gaps compared to subspace-based algorithms continue to decrease. Notably, when K = 20, the ANM algorithm achieves performance improvements of at least 4.5 dB, 5.0 dB, and 7.2 dB compared to the 2D-IAA, 2D-MUSIC, and 2D-ESPRIT algorithms, respectively.

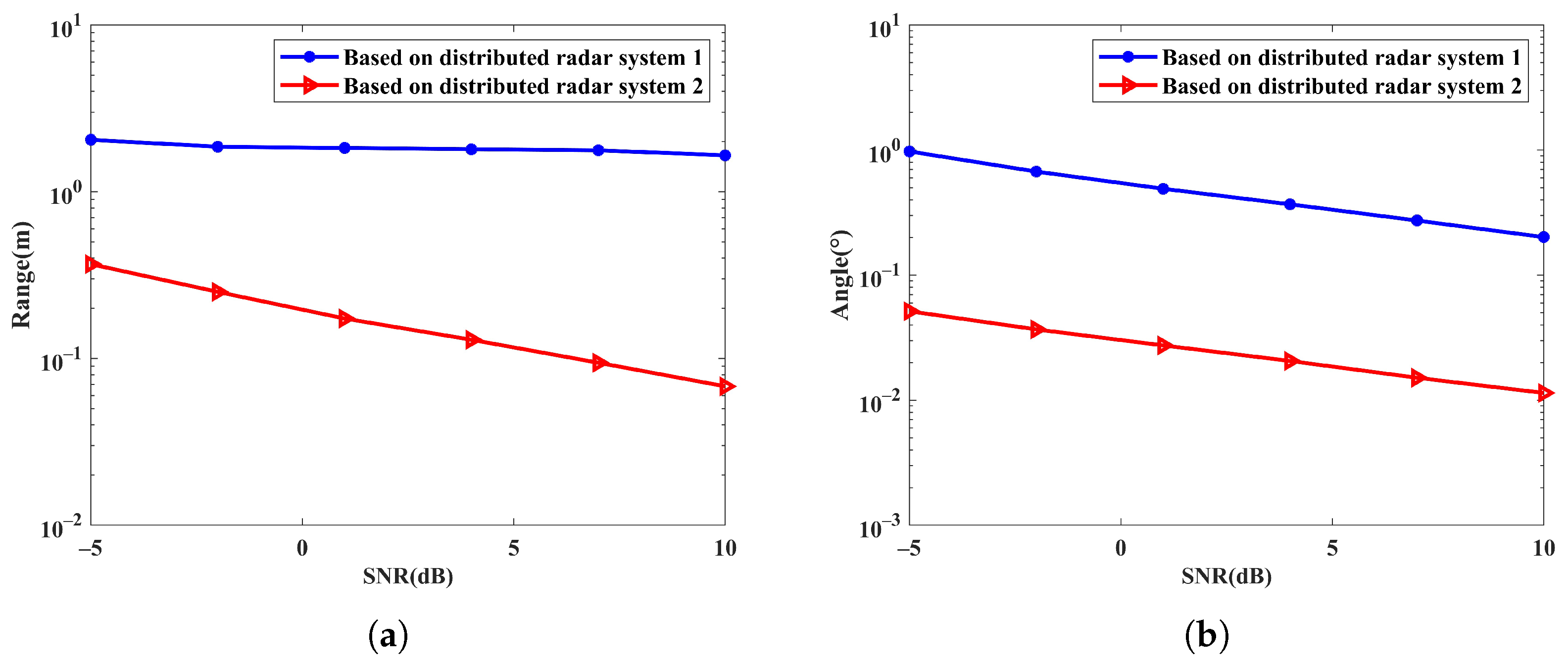
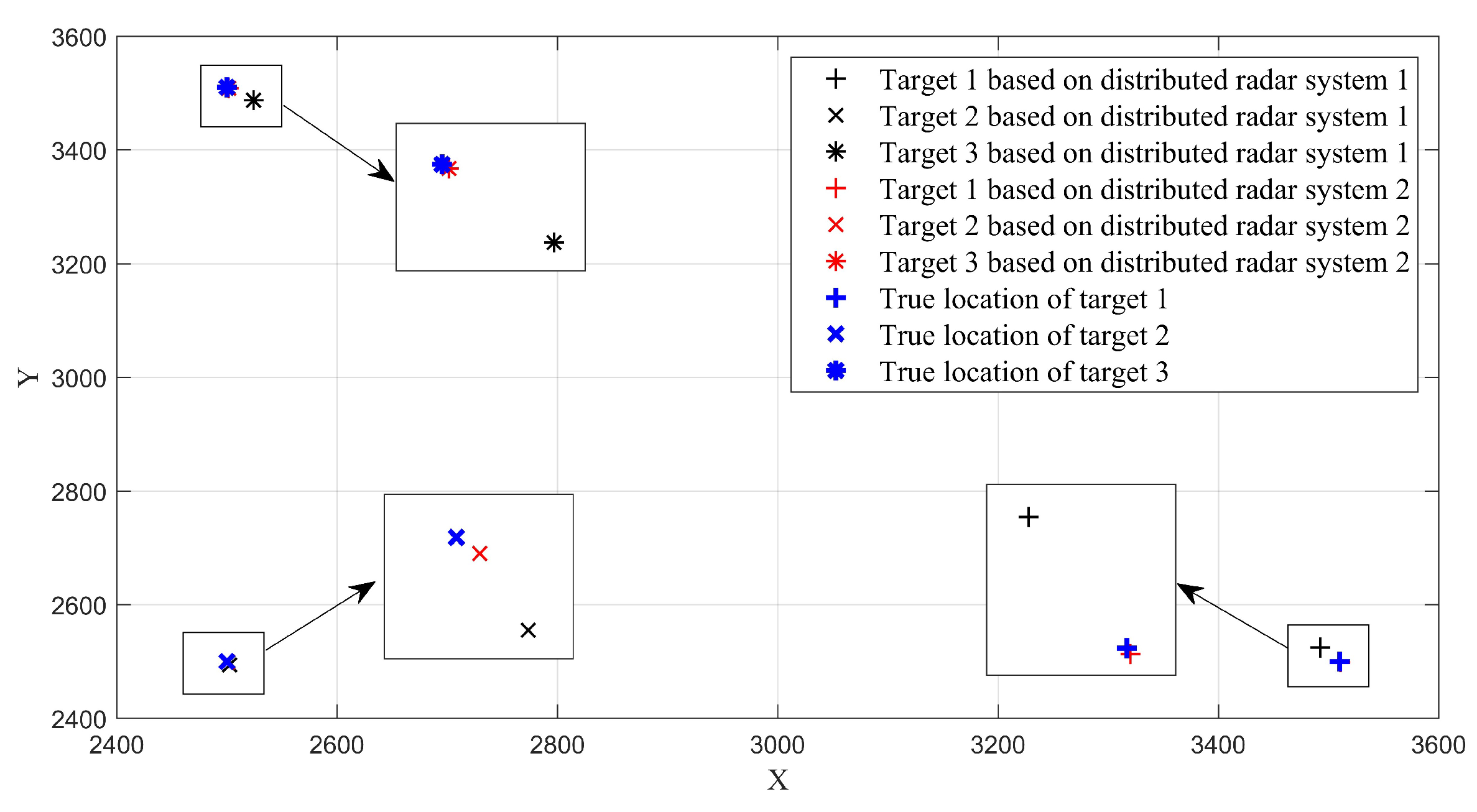
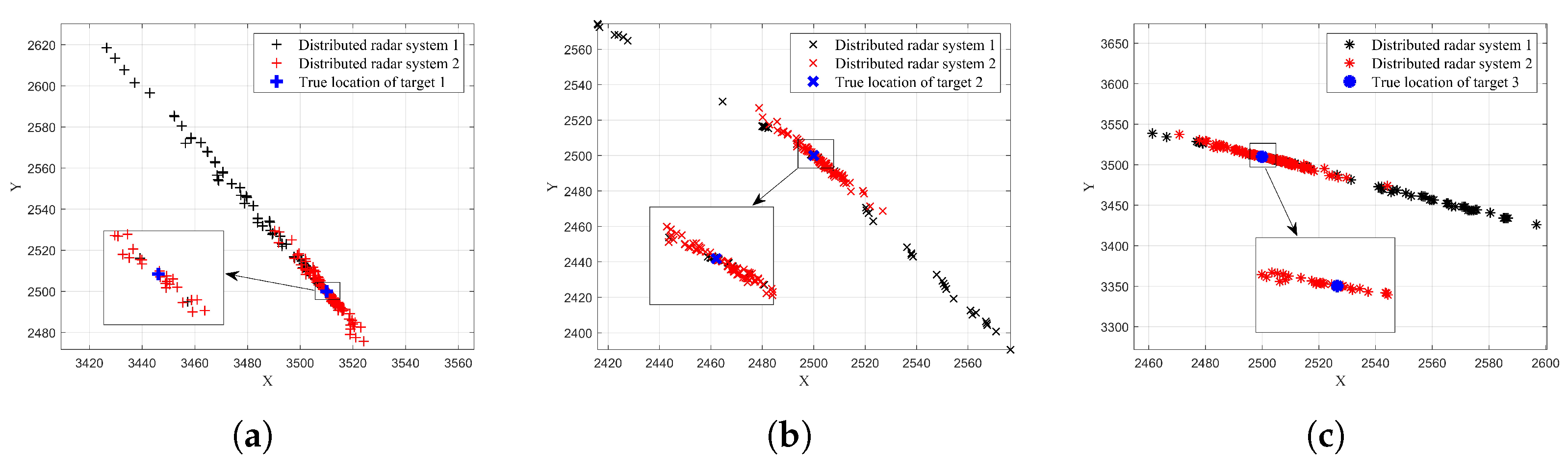
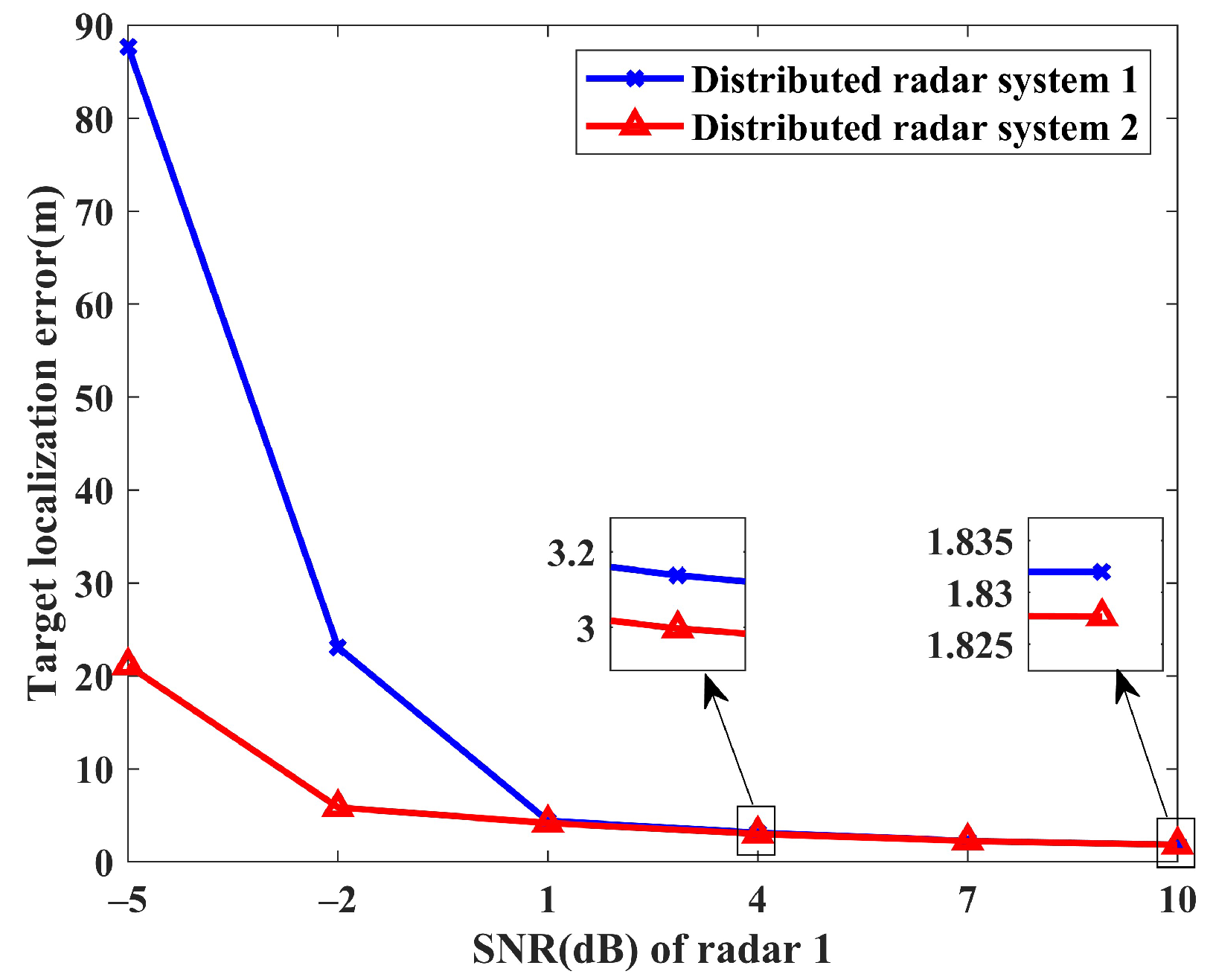
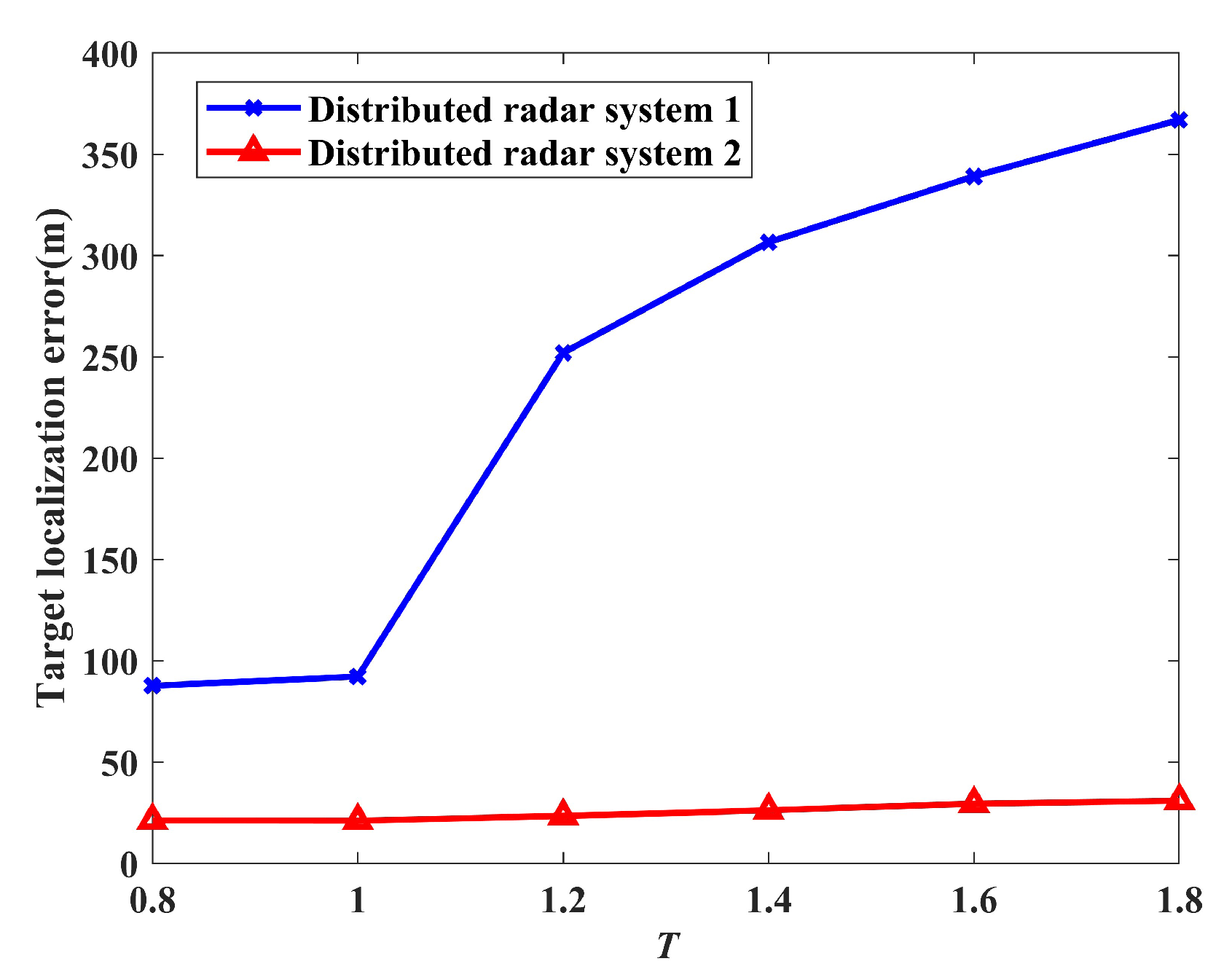
4.2. Performance Analysis of Target Localization Using Sparse Reconstruction with Distributed Waveform Diverse Array Radars

In this subsection, the localization performance of the distributed waveform diverse array radar system is evaluated. Specifically, the grid partitioning employed by the IAA algorithm aligns with the configurations established in Table 1. The Cartesian coordinates of the targets and radar stations are outlined in

Table 2. Location information in Cartesian coordinates.

Parameter	Value	Parameter	Value
Target 1	(3510, 2500)	Radar 1	(1000, 0)
Target 2	(2500, 2500)	Radar 2	(0, 0)
Target 3	(2500, 3510)	Radar 3	(0, 1000)

.

Specifically, the distributed waveform diverse array radar system employing the IAA algorithm on its FDA-MIMO radar is termed as distributed radar system 1, whereas the system using the ANM algorithm is termed as distributed radar system 2. Both EPC-MIMO radars in the two distributed systems employ the CD-MUSIC algorithm to obtain the target’s angle and range ambiguity index. Subsequently, the SNR values for the respective stations are configured as −5, 5, and 0, with 200 Monte Carlo trials.

Figure 7 illustrates the RMSEs versus SNR for angle and range estimation of three targets with a distributed waveform diverse array radar system. The RMSEs for range estimation in Figure 7a demonstrate that the two distributed waveform diverse array radar systems achieve excellent estimation performance. Specifically, the ANM-based system achieves a 7.4 dB improvement in estimation performance compared to the IAA-based system at SNR = −5 dB. The RMSE curves for angle estimation in Figure 7b show a continuous decrease as the SNR increases. Notably, the ANM-based system achieves at least a 12.4 dB performance improvement compared to the IAA-based system. In summary, both algorithms demonstrate excellent performance, but the ANM algorithm outperforms the IAA algorithm.

In Figure 8, the estimation results for the angle and range ambiguity index of three targets by distributed waveform diverse array radar systems have been provided. From Figure 8a, it is evident that the curves of the three targets exhibit relatively high peaks, allowing them to be clearly distinguished in the angle dimension. Furthermore, benefiting from the coding of EPC, the range ambiguity is effectively estimated in the distributed radar system, as shown in Figure 8b. It is evident from the numerical results that the RMSE curve is very close to the CRB, which shows that the system has an excellent capability for resolving range ambiguity. As a result, high-precision parameter estimation and resolution of range ambiguity can be achieved simultaneously, demonstrating the superiority of the distributed waveform diverse array radar system for target localization.

The localization results for three different targets, achieved by two distributed radar systems, are presented in Figure 9. These results represent the average values derived from 200 Monte Carlo experiments. It can be seen that the localization results of the two distributed radar systems are highly accurate, approaching the true target values and demonstrating the capability to localize multiple targets. Upon closer inspection of the enlarged block diagram, it becomes evident that the actual target locations are nearly perfectly aligned with the localization results of distributed radar system 2. As a comparison, the results of system 1 deviate slightly from the true values. Furthermore, considering the aforementioned experimental conditions, it is apparent that distributed radar system 2 exhibits superior localization performance at lower SNR levels. The advantage of the ANM algorithm, particularly in low-SNR environments, is underscored by this observation.

The distribution of localization results for three distinct targets is displayed in Figure 10. It is clear that the dot distributions for all three targets share similar characteristics. In particular, the red dots are close to the true values of each target. In contrast, the black dots are more widely dispersed around the true values, indicating a relatively significant deviation. Thus, in cases of a low SNR and limited snapshots, the superior localization accuracy and robustness of the distributed radar system based on the ANM algorithm are verified.

To further validate the localization performance of the methods, the localization results obtained under various SNR scenarios are presented. The baseline dataset, featuring SNR values of [−5, 5, 0], serves as our starting point. Subsequently, the SNR of radar station 1 undergoes adjustment and is systematically elevated. Furthermore, to maintain the SNR ratios observed in the initial dataset, the SNRs of the other two radar stations are also adjusted accordingly. Similarly, 200 Monte Carlo simulations are conducted to verify the estimation accuracy. The average error trends of the three targets versus the SNR variation at radar 1 are shown in Figure 11. Under the same conditions, distributed radar system 2 demonstrates excellent performance improvement compared to system 1. The performance gap between the two systems gradually decreases with an increasing SNR and stabilizes at higher SNRs. Specifically, system 2 achieves a 75.9% improvement in target localization accuracy compared to system 1 at SNR = −5 dB, maintaining this advantage across all evaluated SNR values.

An experimental study was conducted to evaluate the impact of temperature coefficients associated with the weights. The SNRs are set to [−5, 0, 5] dB, with 200 Monte Carlo trials performed. As shown in Figure 12, system 2 exhibits lower localization errors than system 1 under all temperature coefficient conditions, confirming its performance superiority. Specifically, at T = 0.8, the performance gap reaches its minimum, where system 2 achieves a 76% improvement over system 1. As T increases, the performance difference grows rapidly. In summary, the ANM-based system further demonstrates superior target localization accuracy and robust performance across all test conditions.

5. Conclusions

Target localization based on sparse reconstruction in distributed waveform-diverse array radars, particularly considering low-SNR scenarios, has been investigated. At the design stage, two sparse reconstruction methods are employed at FDA-MIMO radar stations to estimate parameters. Moreover, the WLS method is used by the fusion center to locate the target based on the single-station estimation results. At the analysis stage, the performance of the proposed methods has been assessed based on localization errors, CRBs, and RMSEs. Simulation results show that both single-station and distributed radar systems that employ sparse reconstruction algorithms can accurately localize targets. Significantly, the distributed radar system based on the ANM algorithm demonstrates outstanding localization performance, characterized by excellent accuracy and robustness. The results have shown the effectiveness of the provided methods for target localization in all the considered case studies.

Future research may encompass the introduction of various error conditions, such as spatial registration errors, within the framework of the distributed waveform-diverse array radar architecture. Furthermore, the impact of array errors and mutual coupling in distributed radar systems remains a noteworthy research concern.