Attitude Estimation of Spinning Space Targets Utilizing Multistatic ISAR Joint Observation
Abstract
1. Introduction
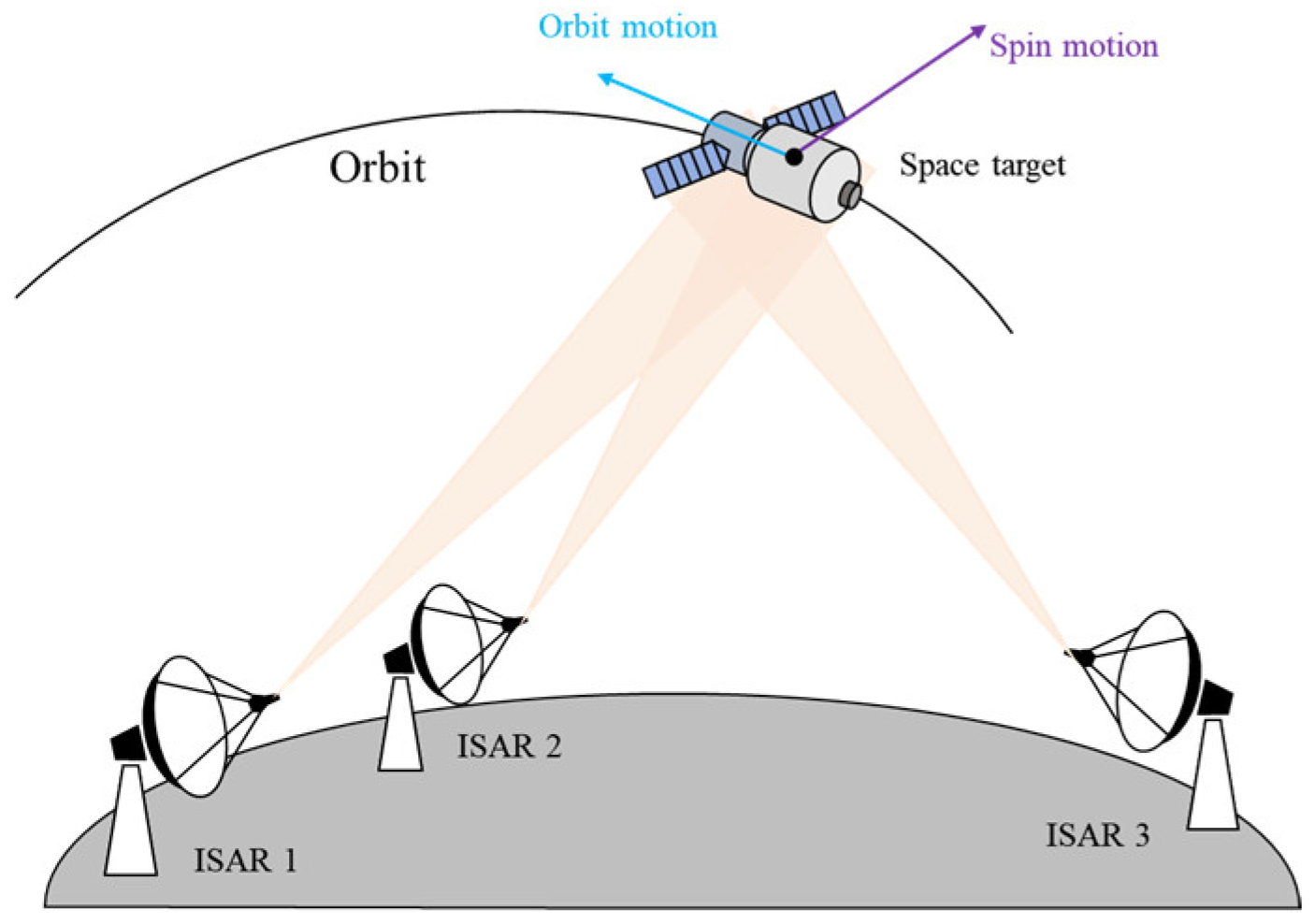
- Capability of Efficient Attitude Estimation for Spinning Targets: By deploying ISAR stations at three different locations to observe the target simultaneously, this method fully leverages the differences in observation perspectives from multiple stations, allowing accurate estimation of the attitude of spinning targets through a single observation, without the need for long-term target monitoring. This approach provides strong technical support for target surveillance in complex space environments.
- Automated Feature Extraction: In this paper, we propose ISAR-HRNet, a network capable of achieving automated extraction and precise association of key points in the ISAR images of space targets. By using the ISAR-HRNet, the proposed method significantly reduces manual intervention in the attitude estimation process and improves the algorithm’s automation level.
- Independent Target Model: The proposed method simultaneously optimizes the lengths and orientations of target components by leveraging the features extracted from ISAR images. Consequently, it eliminates the requirement for prior knowledge of the target’s 3D model, thereby significantly broadening the algorithm’s applicability across diverse scenarios.
- Analytical Solution of Spin Vector: The analytical expression of the target’s spin vector optimization model is derived and established. Compared with the existing algorithms, it can effectively avoid getting trapped in the local optimal value during the iterative solution process of the spin vector. This not only ensures the accuracy of the spin vector but also significantly shortens the estimation time.
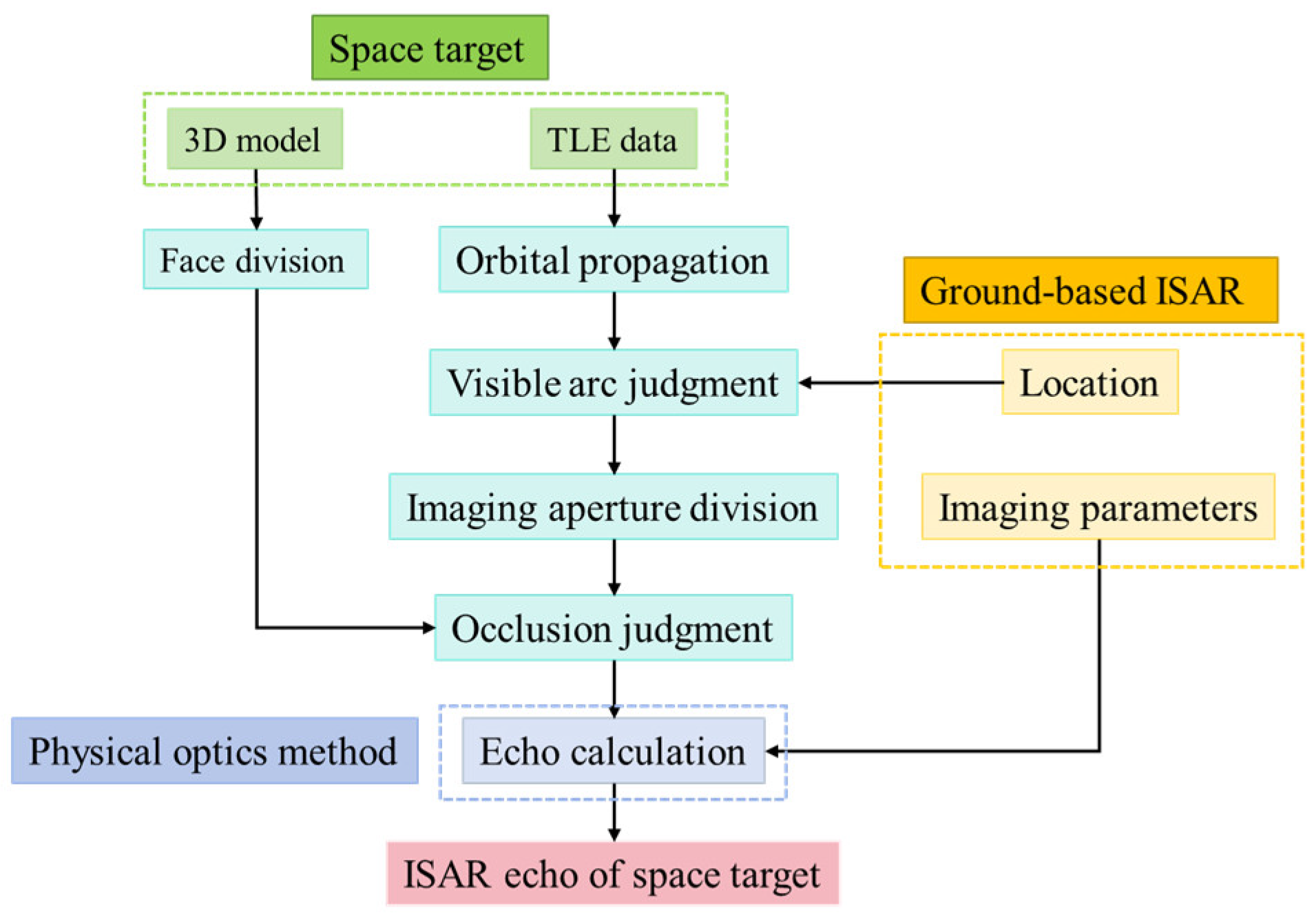
2. Fundamentals of Multi-Station ISAR Joint Observation for Space Targets
2.1. Imaging Geometry of Multi-Station ISAR Joint Observation System
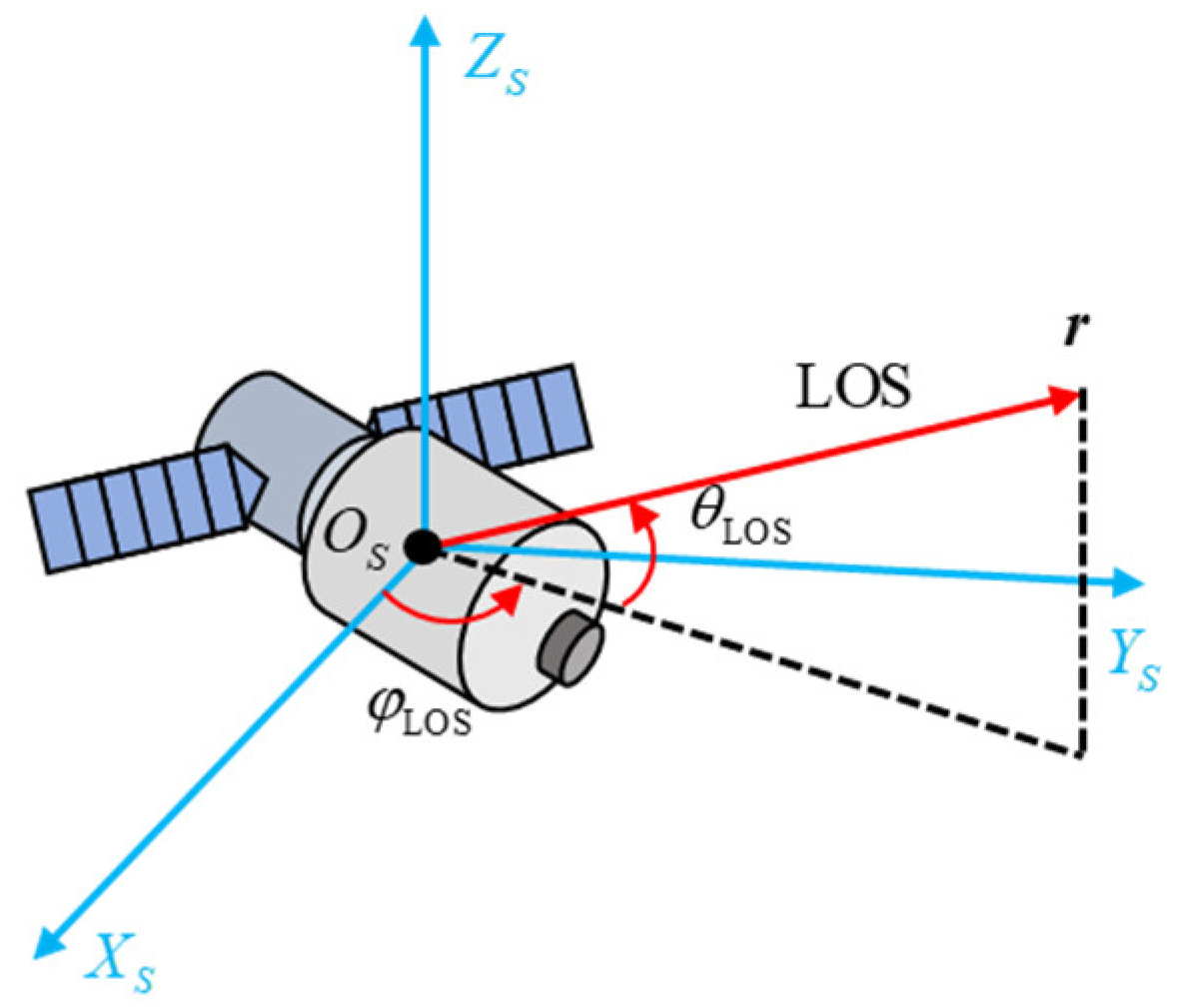
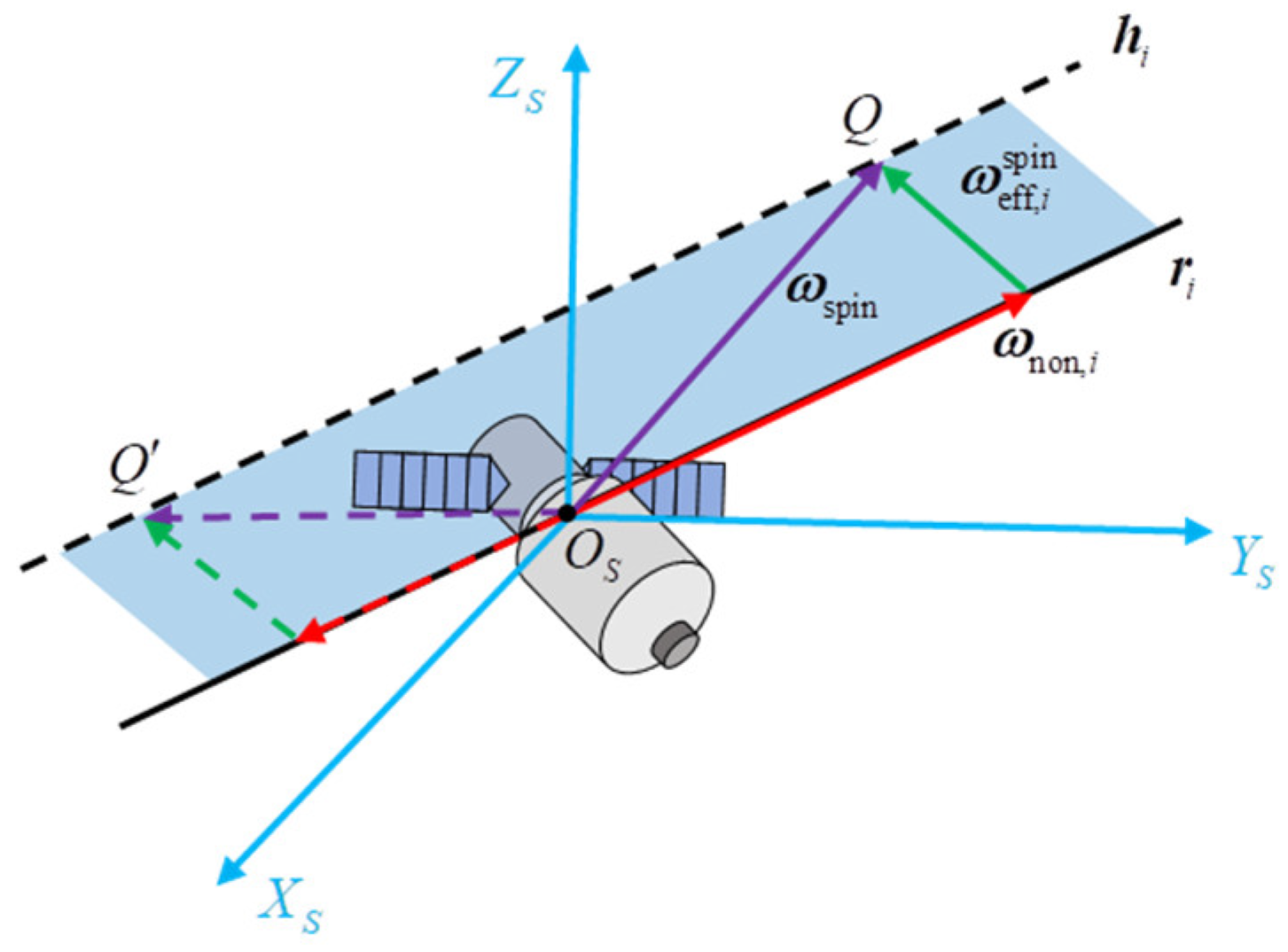
2.2. Motion Model of Spinning Space Targets
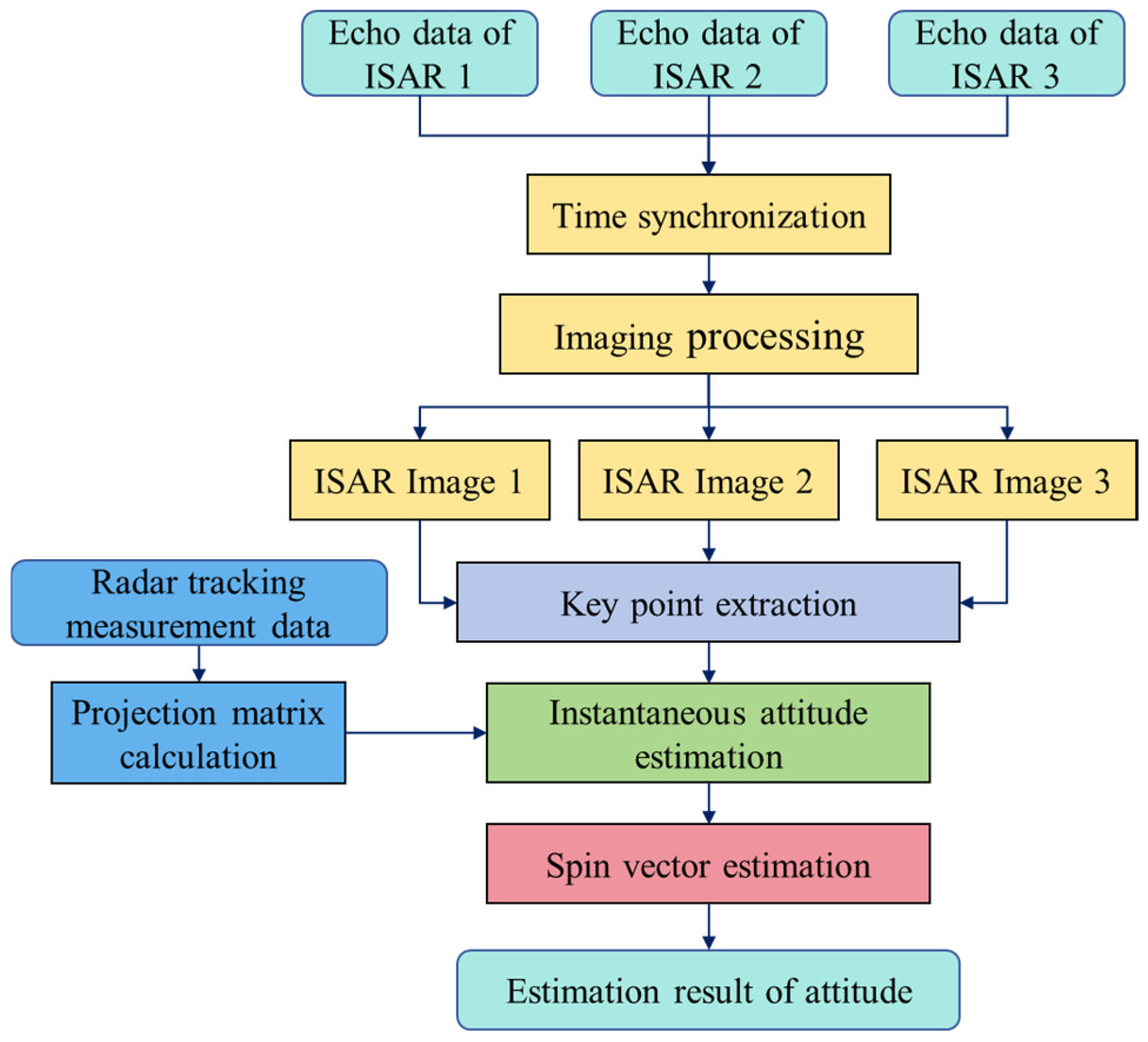
3. Attitude Estimation of Spinning Space Targets Utilizing Multistatic ISAR Joint Observation
3.1. Definition of Key Points
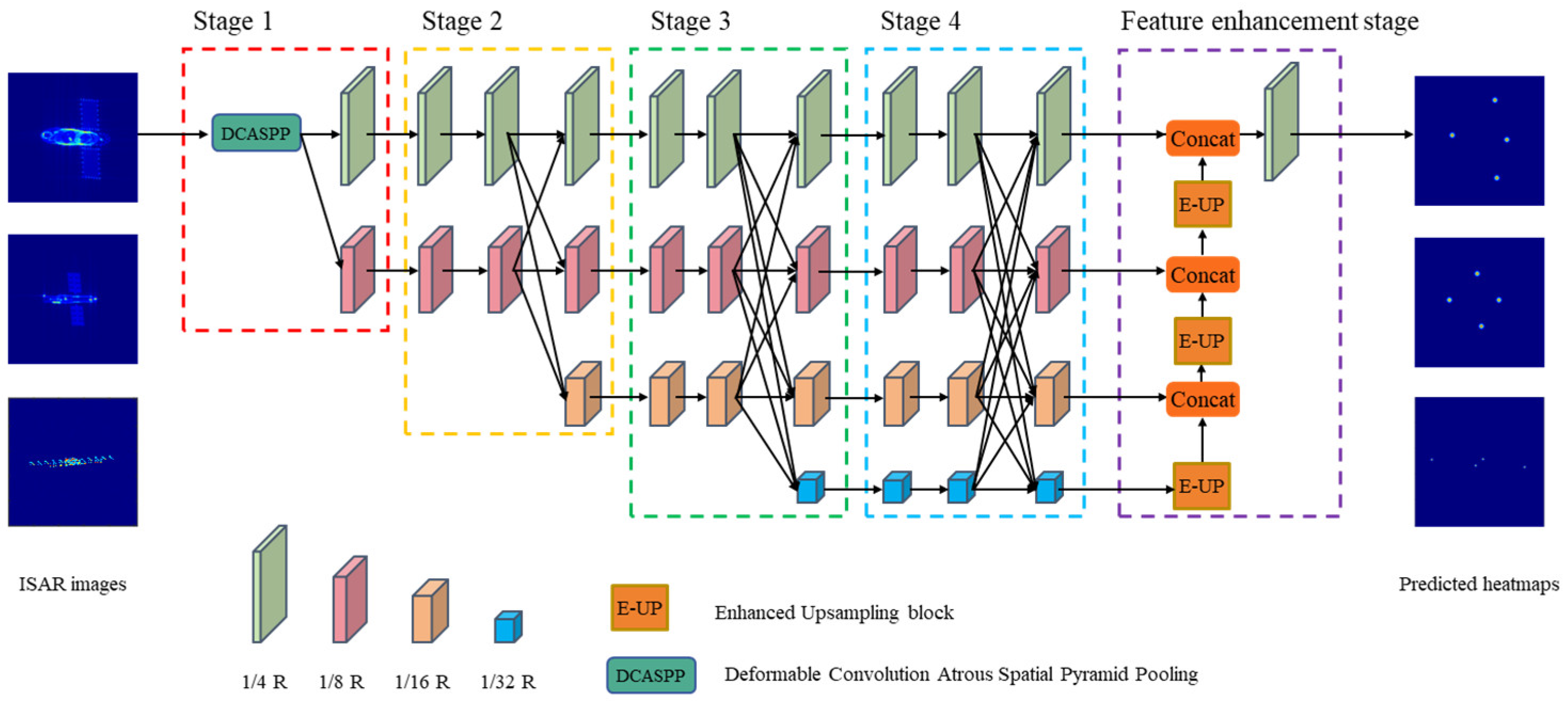
3.2. Key Point Extraction Using ISAR-HRNet
3.2.1. Structure of ISAR-HRNet
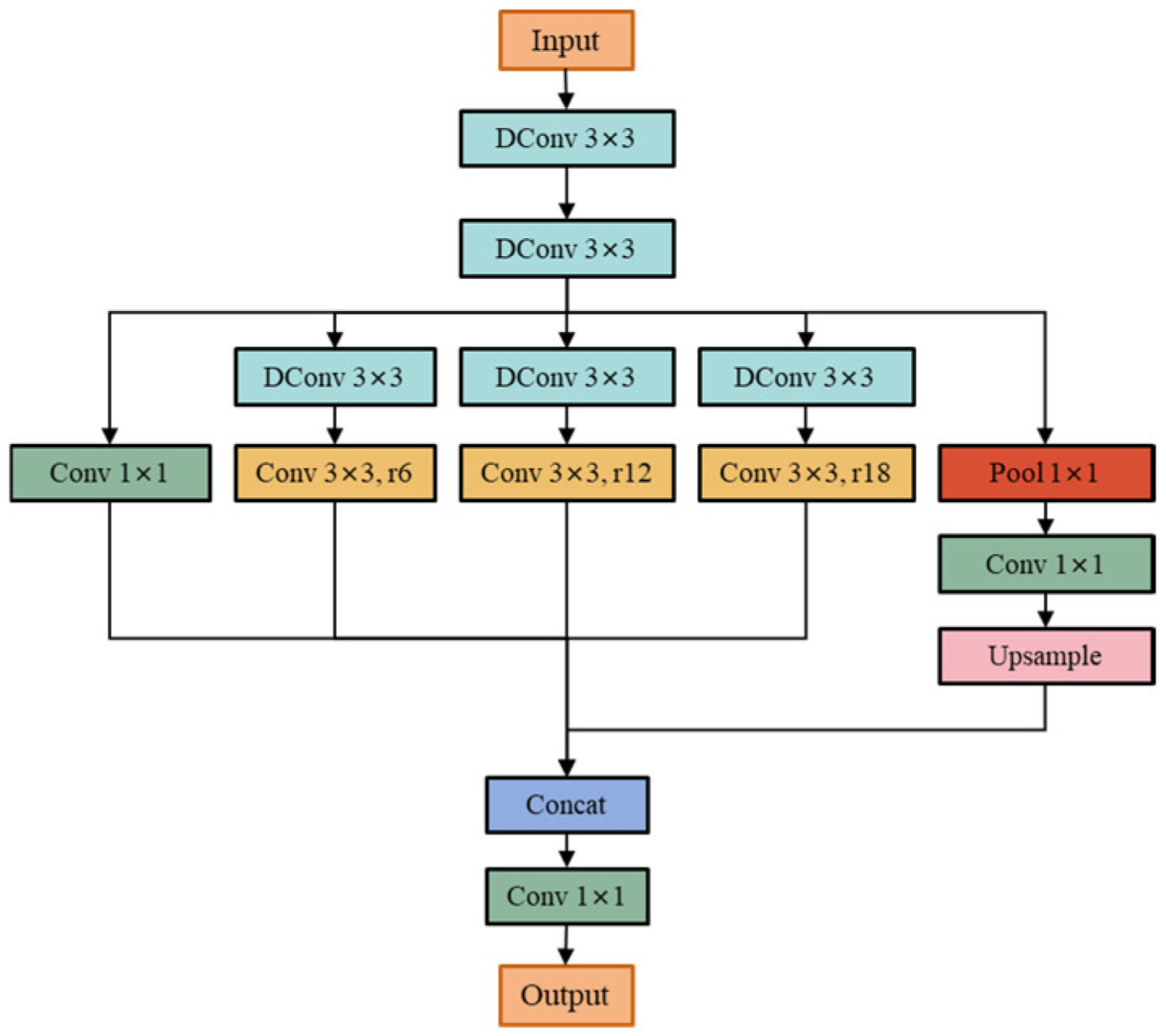
3.2.2. Deformable Convolution Atrous Spatial Pyramid Pooling
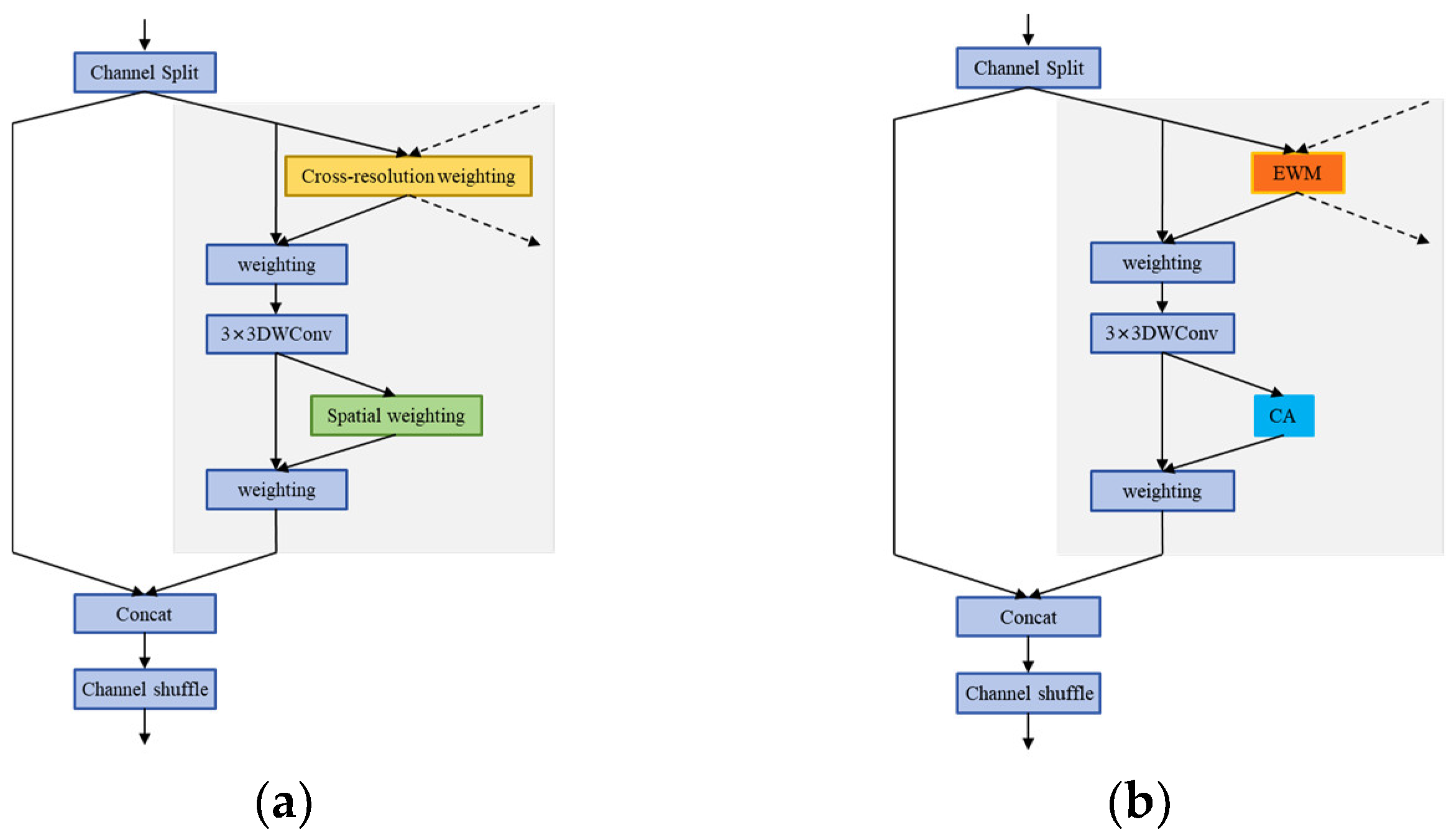
3.2.3. Feature Extraction Block
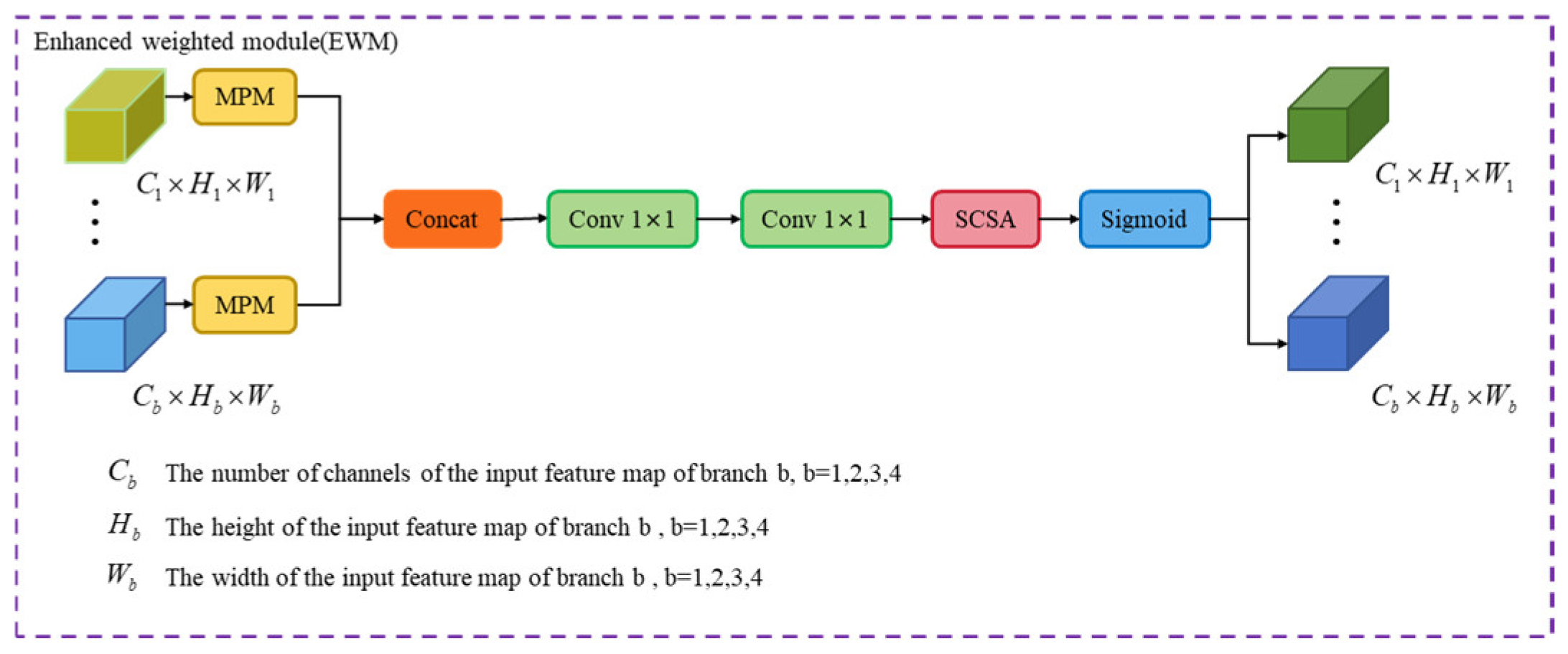
3.2.4. Feature Enhancement Stage
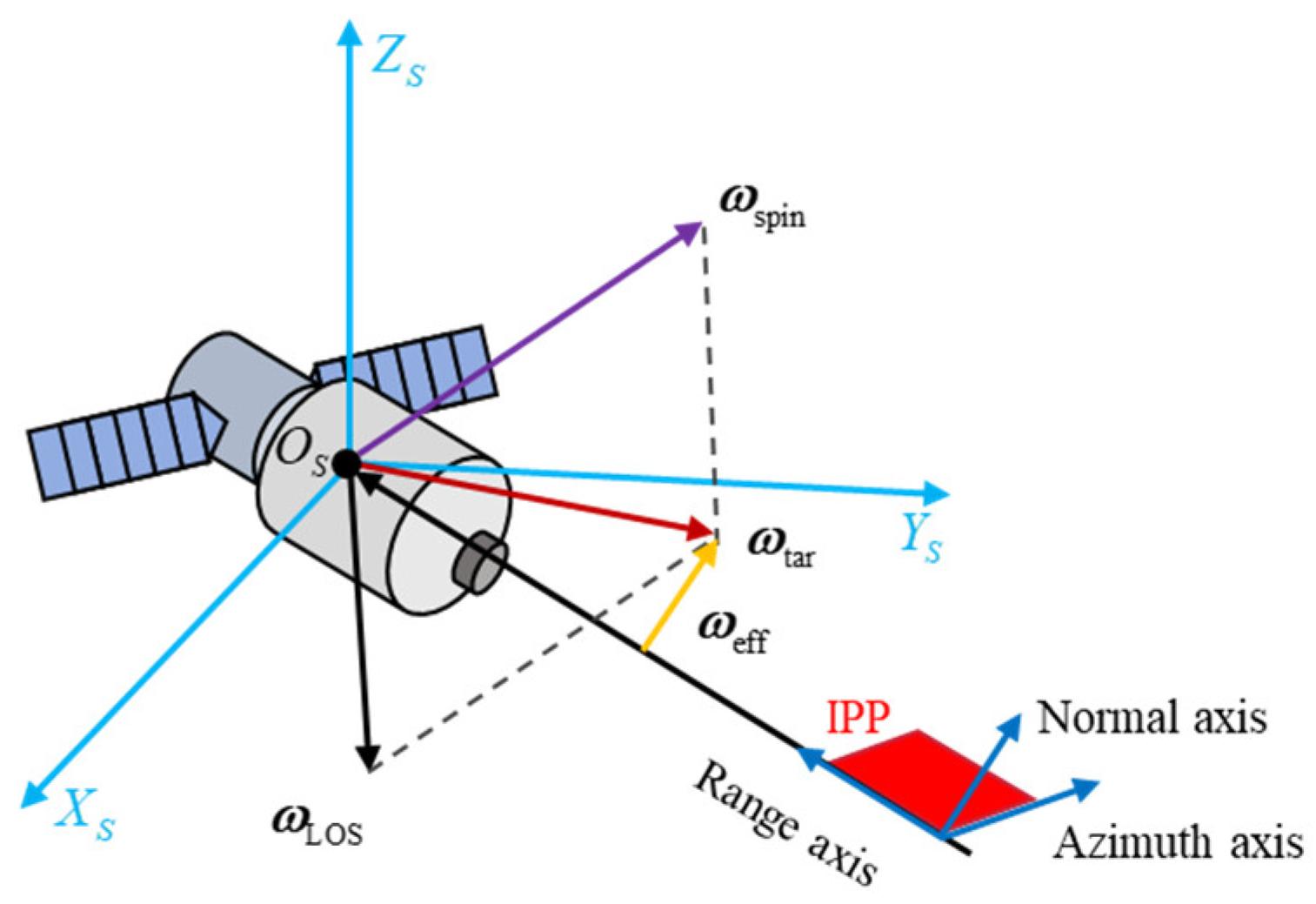
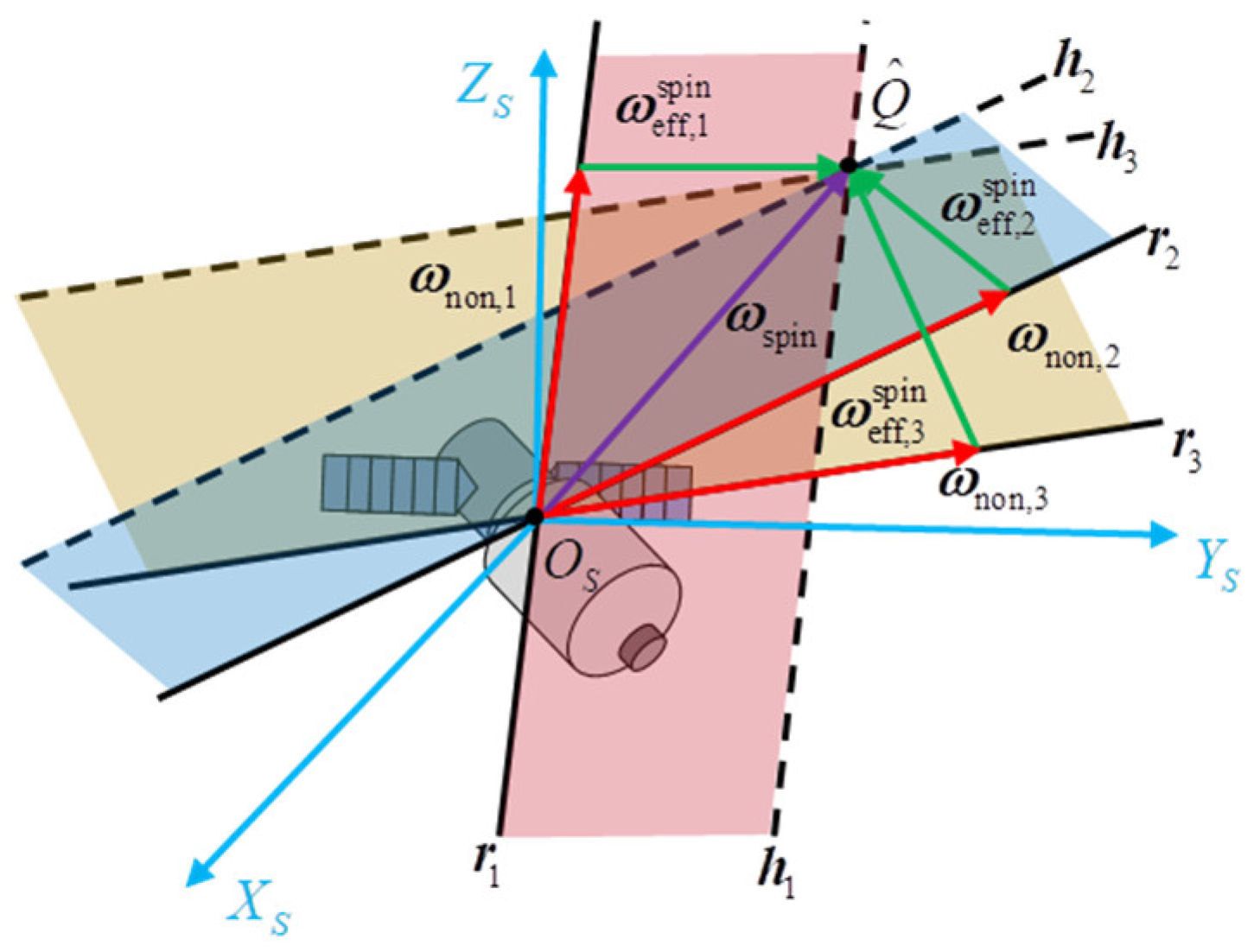
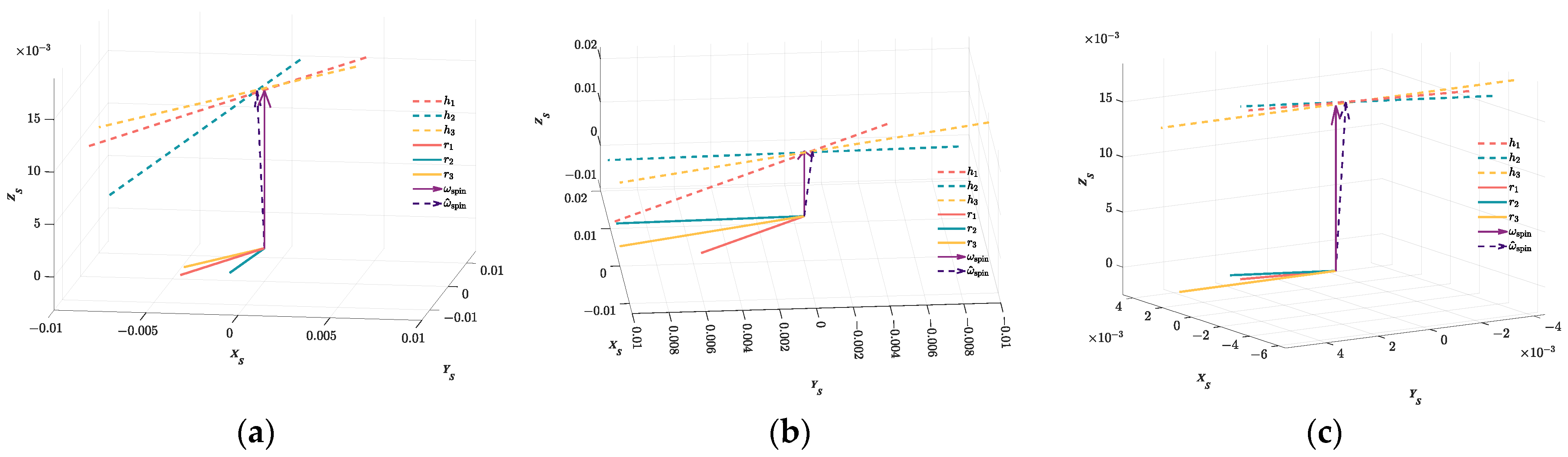
3.3. Instantaneous Attitude Estimation
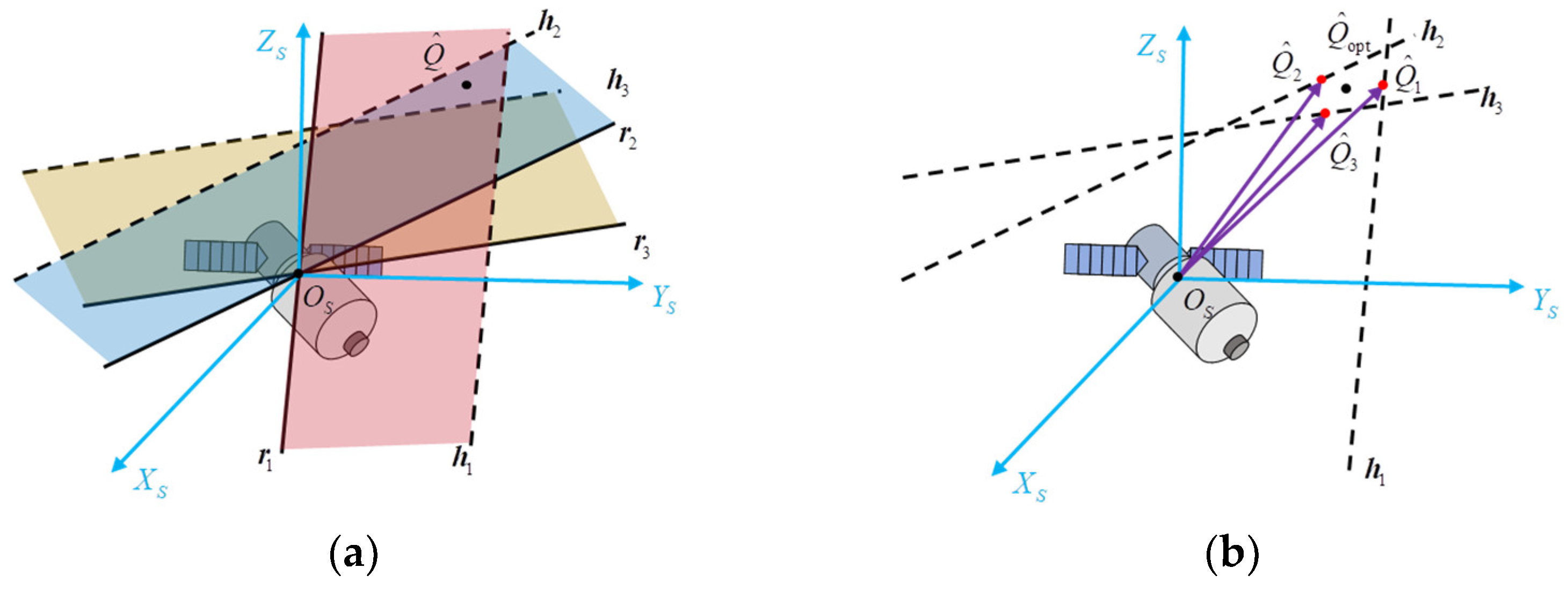
3.4. Spin Vector Estimation
3.5. Summary
| Algorithm 1: Attitude Estimation of Spinning Targets |
|
4. Experiments and Results
4.1. Data Description
4.2. Validation of Simulated Data
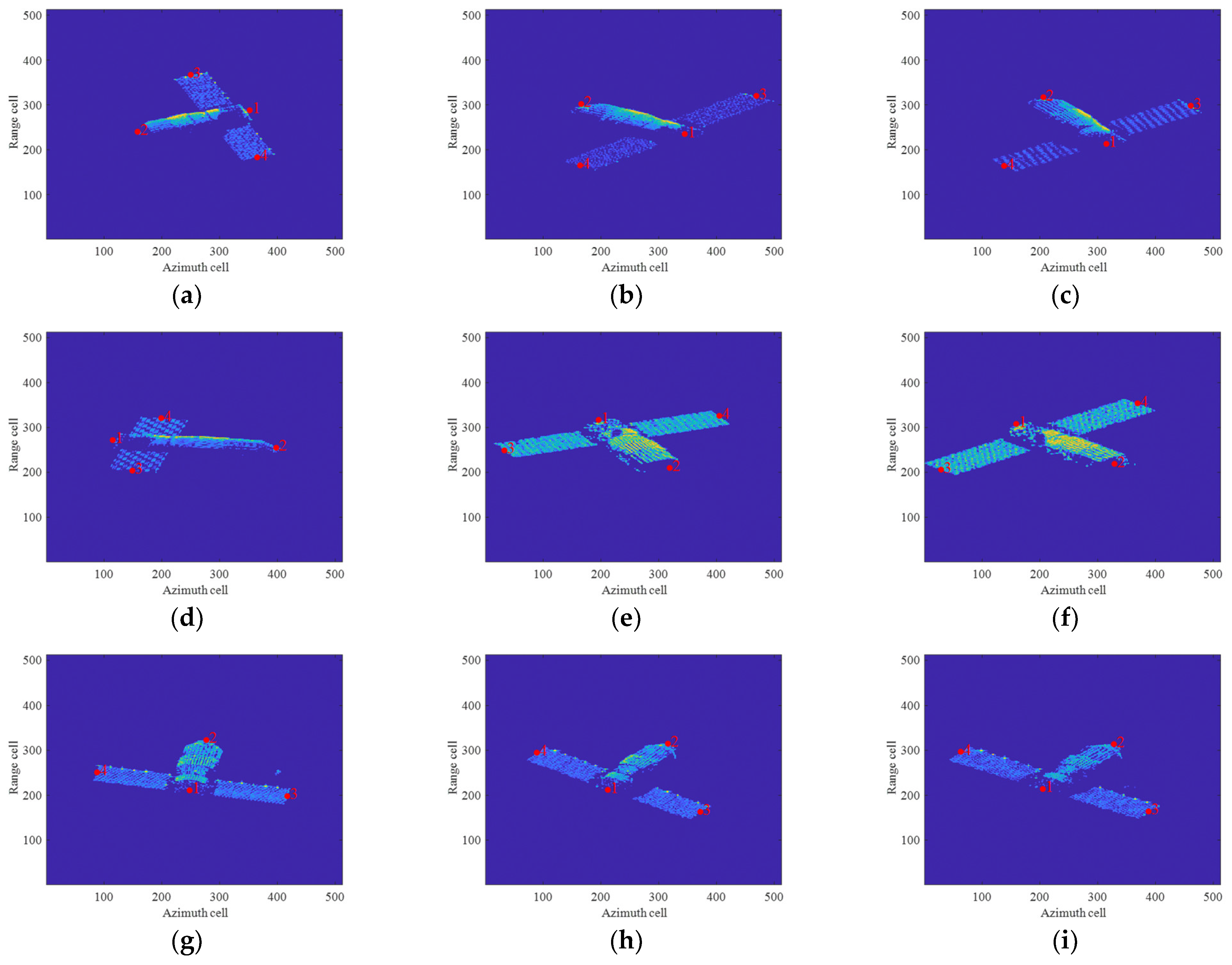
4.2.1. Effectiveness Validation
4.2.2. Comparison Analysis
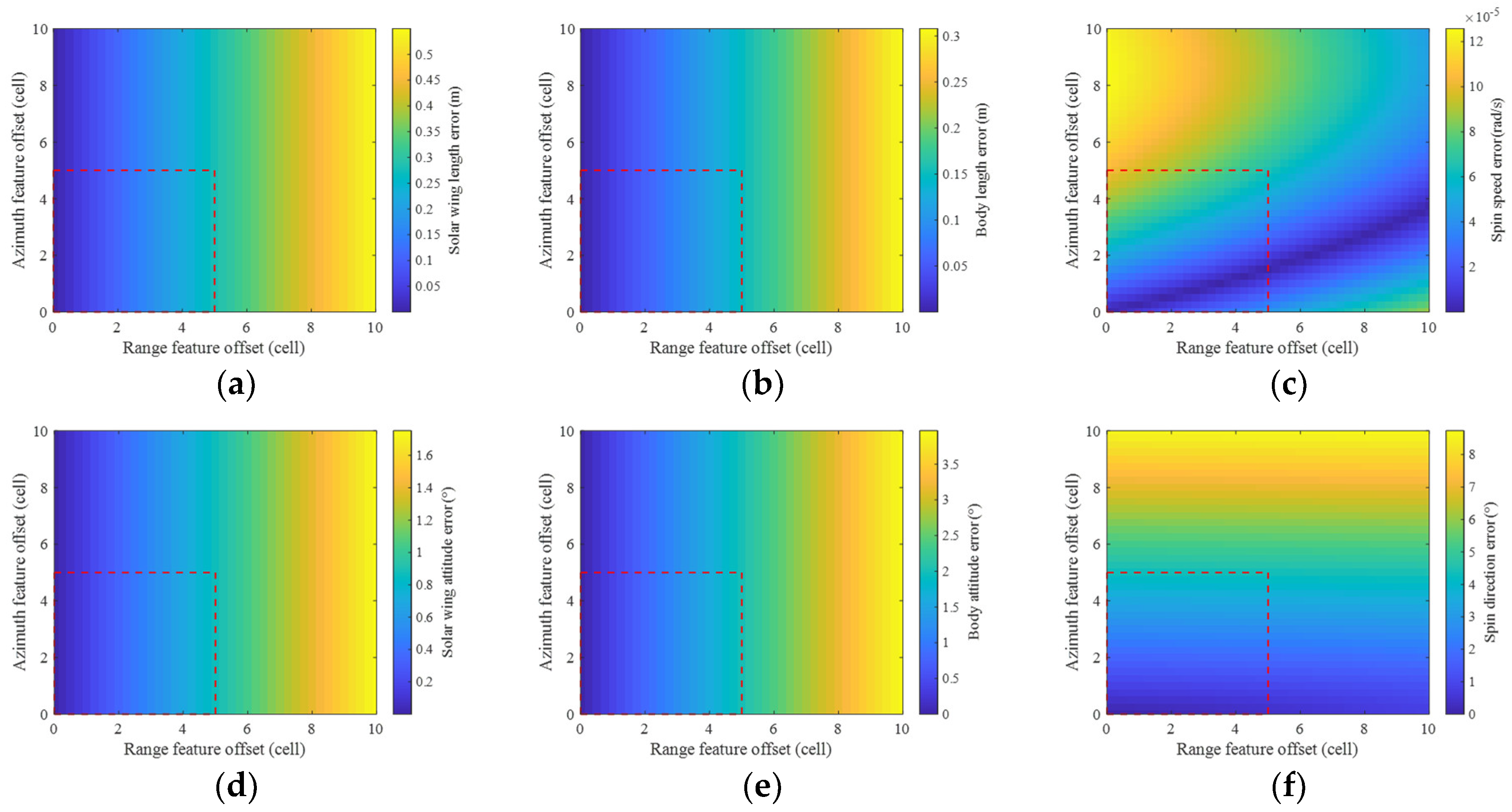
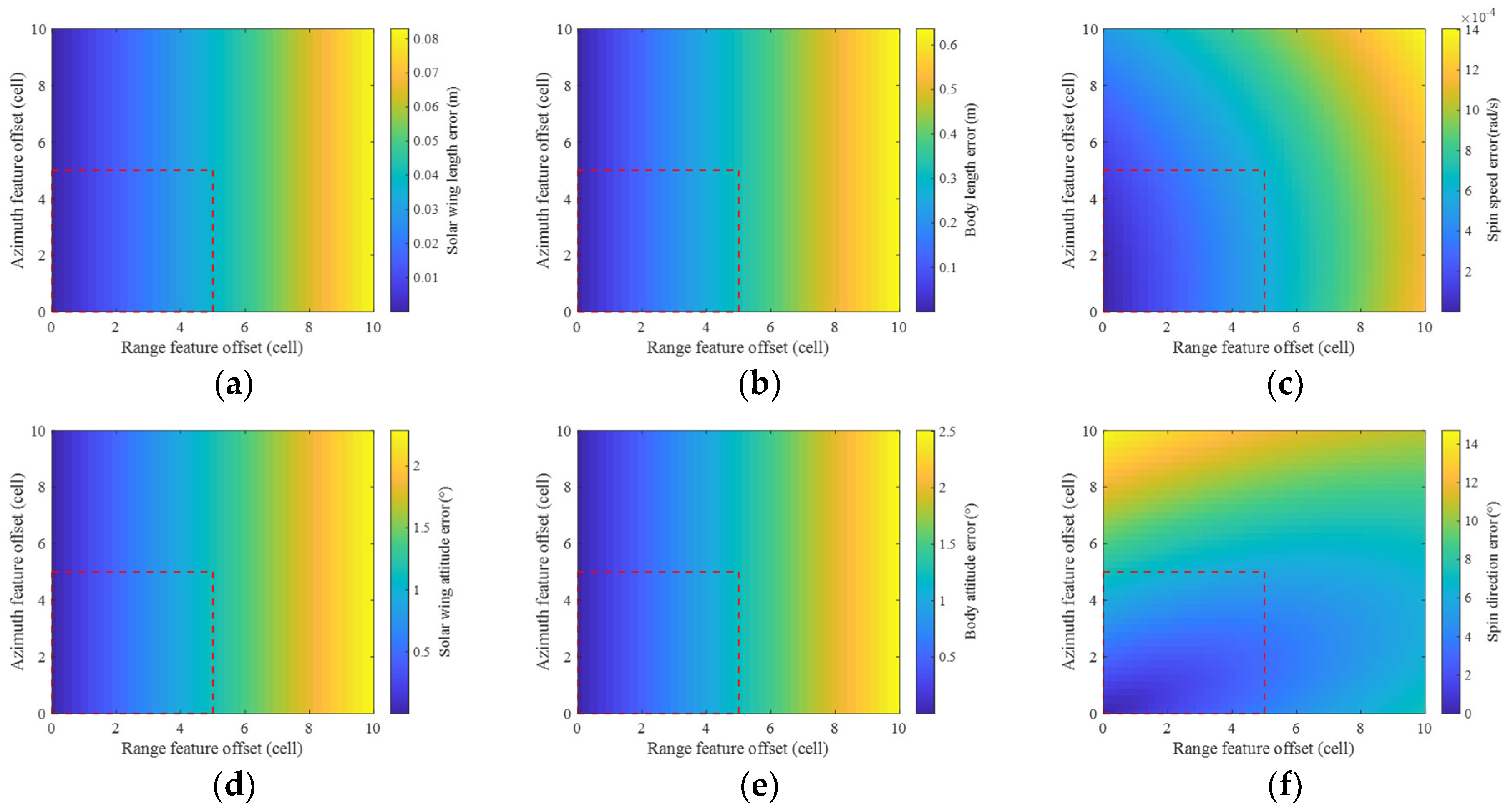
4.2.3. Robustness Analysis
4.3. Validation of Measured Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.Y.; Jiang, L.B.; Li, M.X.; Ren, X.Y.; Wang, Z. Slow-Spinning Spacecraft Cross-Range Scaling and Attitude Estimation Based on Sequential ISAR Images. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7469–7485. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, Z.B.; Zhou, F.; Shi, X.R. A New 3-D Geometry Reconstruction Method of Space Target Utilizing the Scatterer Energy Accumulation of ISAR Image Sequence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8345–8357. [Google Scholar] [CrossRef]
- Guo, W.J.; Yang, Q.; Wang, H.Q.; Luo, C.G. Axis Estimation of Spaceborne Targets via Inverse Synthetic Aperture Radar Image Sequence Based on Regression Network. Remote Sens. 2024, 16, 4148. [Google Scholar] [CrossRef]
- Li, B.; Wang, J.L.; Fu, T.; Zhao, L.Z.; Zhang, S.; Lv, P. Estimating the Hotspot Area Observed by Earth Imaging Satellite via ISAR Image Sequence. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5101917. [Google Scholar] [CrossRef]
- Deng, J.Y.; Xie, P.F.; Zhang, L.; Cong, Y.L. ISAR-NeRF: Neural Radiance Fields for 3-D Imaging of Space Target from Multiview ISAR Images. IEEE Sens. J. 2024, 24, 11705–11722. [Google Scholar] [CrossRef]
- Gong, R.; Wang, L.; Wu, B.; Zhang, G.; Zhu, D.Y. Optimal Space-Borne ISAR Imaging of Space Objects with Co-Maximization of Doppler Spread and Spacecraft Component Area. Remote Sens. 2024, 16, 1037. [Google Scholar] [CrossRef]
- Lemmens, S.; Krag, H. Sensitivity of automated attitude determination form ISAR radar mappings. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS 2013), Maui, HI, USA, 10–13 September 2013. [Google Scholar]
- Lemmens, S.; Krag, H.; Rosebrock, J.; Carnelli, I. Radar mappings for attitude analysis of objects in orbit. In Proceedings of the 6th European Conference on Space Debris, Darmstadt, Germany, 22–25 April 2013. [Google Scholar]
- Sommer, S.; Rosebrock, J.; Cerutti-Maori, D.J.E.; Leushacke, L. Temporal analysis of envisat’s rotational motion. In Proceedings of the 7th European Conference on Space Debris, Darmstadt, Germany, 18–21 April 2017. [Google Scholar]
- Du, R.Z.; Zhou, Z.B.; Liu, L.; Bai, X.R.; Zhou, F. A New Attitude Estimation Method of Space Target Utilizing ISAR Image Sequence Under Low SNR. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 57–61. [Google Scholar]
- Zhou, Y.J.; Zhang, L.; Wang, H.X.; Qiao, Z.J.; Hu, M.Q. Attitude estimation of space targets by extracting line features from ISAR image sequences. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–4. [Google Scholar]
- Zhou, Y.J.; Zhang, L.; Cao, Y.H.; Wu, Z.H. Attitude Estimation and Geometry Reconstruction of Satellite Targets Based on ISAR Image Sequence Interpretation. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1698–1711. [Google Scholar] [CrossRef]
- Wang, J.D.; Li, Y.C.; Du, L.; Song, M.; Xing, M. Joint Estimation of Satellite Attitude and Size Based on ISAR Image Interpretation and Parametric Optimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5103817. [Google Scholar] [CrossRef]
- Xie, P.F.; Zhang, L.; Du, C.; Wang, X.Q.; Zhong, W.J. Space Target Attitude Estimation from ISAR Image Sequences with Key Point Extraction Network. IEEE Signal Process. Lett. 2021, 28, 1041–1045. [Google Scholar] [CrossRef]
- Xie, P.F.; Zhang, L.; Ma, Y.; Zhou, Y.J.; Wang, X.Q. Attitude Estimation and Geometry Inversion of Satellite Based on Oriented Object Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4023505. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Zhang, L.; He, C.Y. Dynamic Estimation of Spin Spacecraft Based on Multiple-Station ISAR Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2977–2989. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Xie, P.F.; Li, C.W.; Jian, M.; Zhang, L.; An, Z.W. Automatic Dynamic Estimation of On-Orbit Satellites Through Spaceborne ISAR Imaging. IEEE Trans. Radar Syst. 2023, 1, 34–47. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Zhang, L.; Cao, Y.H.; Huang, Y. Optical-and-Radar Image Fusion for Dynamic Estimation of Spin Satellites. IEEE Trans. Image Process. 2020, 29, 2963–2976. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.T.; Liu, L.; Du, R.Z.; Wang, Z.; Shang, R.H.; Zhou, F. Three-Dimensional Reconstruction of Space Targets Utilizing Joint Optical-and-ISAR Co-Location Observation. Remote Sens. 2025, 17, 287. [Google Scholar] [CrossRef]
- Long, B.; Tang, P.; Wang, F.; Jin, Y.-Q. 3-D Reconstruction of Space Target Based on Silhouettes Fused ISAR-Optical Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5213919. [Google Scholar] [CrossRef]
- Du, R.Z.; Liu, L.; Bai, X.R.; Zhou, Z.B.; Zhou, F. Instantaneous Attitude Estimation of Spacecraft Utilizing Joint Optical-and-ISAR Observation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5112114. [Google Scholar] [CrossRef]
- Zhou, Z.B.; Jin, X.G.; Liu, L.; Zhou, F. Three-Dimensional Geometry Reconstruction Method from Multi-View ISAR Images Utilizing Deep Learning. Remote Sens. 2023, 15, 1882. [Google Scholar] [CrossRef]
- SGP4. Available online: https://www.mathworks.com/matlabcentral/fileexchange/62013-sgp4 (accessed on 18 April 2025).
- Pittet, J.-N.; Šilha, J.; Schildknecht, T. Spin motion determination of the Envisat satellite through laser ranging measurements from a single pass measured by a single station. Adv. Space Res. 2018, 61, 1121–1131. [Google Scholar] [CrossRef]
- Song, C.; Lin, H.-Y.; Zhao, C.-Y. Analysis of Envisat’s rotation state using epoch method. Adv. Space Res. 2020, 66, 2681–2688. [Google Scholar] [CrossRef]
- Li, J.S.; Zhang, Y.S.; Yin, C.B.; Xu, C.; Li, P.J.; He, J. A Novel Joint Motion Compensation Algorithm for ISAR Imaging Based on Entropy Minimization. Sensors 2024, 24, 4332. [Google Scholar] [CrossRef]
- Shao, S.; Liu, H.W.; Zhang, L.; Yan, J.K.; Wei, J.Q. Model-Data Co-Driven Integration of Detection and Imaging for Geosynchronous Targets with Wideband Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5235616. [Google Scholar] [CrossRef]
- Bezerra, F.D.M.; Santos, L.A. A new look at the Euler-Rodrigues formula for three-dimensional rotation. Palest. J. Math. 2024, 13, 243–248. [Google Scholar]
- Guo, X.R.; Liu, F.K.; Huang, D.R. Migration through Resolution Cell Correction and Sparse Aperture ISAR Imaging for Maneuvering Target Based on Whale Optimization Algorithm-Fast Iterative Shrinkage Thresholding Algorithm. Sensors 2024, 24, 2148. [Google Scholar] [CrossRef]
- Yang, J.X.; Wang, Y. Sparse Aperture Inverse Synthetic Aperture Radar Imaging for Maneuvering Targets with Migration Through Resolution Cells Correction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 4446–4472. [Google Scholar] [CrossRef]
- Liu, F.K.; Huang, D.R.; Guo, X.R.; Feng, C.Q. Joint Range Alignment and Autofocus Method Based on Combined Broyden-Fletcher-Goldfarb-Shanno Algorithm and Whale Optimization Algorithm. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5214617. [Google Scholar] [CrossRef]
- Cai, J.; Martorella, M.; Chang, S.Q.; Liu, Q.H.; Ding, Z.G.; Long, T. Efficient Nonparametric ISAR Autofocus Algorithm Based on Contrast Maximization and Newton’s Method. IEEE Sens. J. 2021, 21, 4474–4487. [Google Scholar] [CrossRef]
- Xu, D.; Wang, X.; Wu, Z.X.; Fu, J.X.; Zhang, Y.H.; Chen, J.L.; Xing, M.D. Space Target 3-D Reconstruction Using Votes Accumulation Method of ISAR Image Sequence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 9881–9893. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Zhang, L.; Xing, C.; Xie, P.F.; Cao, Y.H. Target Three-Dimensional Reconstruction from the Multi-View Radar Image Sequence. IEEE Access 2019, 7, 36722–36735. [Google Scholar] [CrossRef]
- Yu, C.Q.; Xiao, B.; Gao, C.X.; Yuan, L.; Zhang, L.; Sang, N.; Wang, J.D. Lite-HRNet: A Lightweight High-Resolution Network. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10435–10445. [Google Scholar]
- Kato, S.; Hotta, K.; Hatakeyama, Y.; Konishi, Y. Lite-HRNet Plus: Fast and Accurate Facial Landmark Detection. In Proceedings of the 2023 IEEE International Conference on Image Processing (ICIP), Kuala Lumpur, Malaysia, 8–11 October 2023. arXiv:2308.12133. [Google Scholar]
- Pang, S.C.; Peng, R.R.; Dong, Y.K.; Yuan, Q.; Wang, S.T.; Sun, J.Q. JointMETRO: A 3D reconstruction model for human figures in works of art based on transformer. Neural Comput. Appl. 2024, 36, 11711–11725. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, Z.; Li, C.; Zhou, F. An Enhanced Sequential ISAR Image Scatterer Trajectory Association Method Utilizing Modified Label Gaussian Mixture Probability Hypothesis Density Filter. Remote Sens. 2025, 17, 354. [Google Scholar] [CrossRef]
- Zhao, L.Z.; Wang, J.L.; Su, J.Y.; Luo, H.Y. Spatial Feature-Based ISAR Image Registration for Space Targets. Remote Sens. 2024, 16, 3625. [Google Scholar] [CrossRef]
- Ni, P.S.; Liu, Y.Y.; Pei, H.; Du, H.Z.; Li, H.L.; Xu, G. CLISAR-Net: A Deformation-Robust ISAR Image Classification Network Using Contrastive Learning. Remote Sens. 2023, 15, 33. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, Y.S.; Yin, C.B.; Lin, C.Y.; Xu, C.; Zhang, X. A Deformation Robust ISAR Image Satellite Target Recognition Method Based on PT-CCNN. IEEE Access 2021, 9, 23432–23453. [Google Scholar] [CrossRef]
- Si, Y.Z.; Xu, H.Y.; Zhu, X.Z.; Zhang, W.H.; Dong, Y.; Chen, Y.X.; Li, H.B. SCSA: Exploring the synergistic effects between spatial and channel attention. Neurocomputing 2025, 634, 129866. [Google Scholar] [CrossRef]
- Hou, Q.B.; Zhou, D.Q.; Feng, J.S. Coordinate Attention for Efficient Mobile Network Design. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13708–13717. [Google Scholar]
- Sunandini, G.; Sivanpillai, R.; Sowmya, V.; Variyar, V.V.S. Significance of Atrous Spatial Pyramid Pooling (ASPP) in Deeplabv3+ for Water Body Segmentation. In Proceedings of the 2023 10th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 23–24 March 2023; pp. 744–749. [Google Scholar]
- Ma, P.F.; Ma, J.; Wang, X.J.; Yang, L.C.; Wang, N.N. Deformable convolutional networks for multi-view 3D shape classification. Electron. Lett. 2018, 54, 1373–1374. [Google Scholar] [CrossRef]
- Xue, R.H.; Bai, X.R.; Zhou, F. SAISAR-Net: A Robust Sequential Adjustment ISAR Image Classification Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5214715. [Google Scholar] [CrossRef]
- Wang, J.Q.; Chen, K.; Xu, R.; Liu, Z.W.; Chen, C.L.; Lin, D. CARAFE: Content-Aware ReAssembly of FEatures. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3007–3016. [Google Scholar]
- Nearest Approaches to Multiple Lines in N-Dimensional Space. Available online: https://www.crewes.org/Documents/ResearchReports/2010/CRR201032.pdf (accessed on 17 April 2025).
- Franceschetti, G.; Lodice, A.; Rccio, D. A canonical problem in electromagnetic backscattering from buildings. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1787–1801. [Google Scholar] [CrossRef]
- Boag, A. A fast physical optics (FPO) algorithm for high frequency scattering. IEEE Trans. Antennas Propag. 2004, 52, 197–204. [Google Scholar] [CrossRef]
- NASA 3D Resources. Available online: https://nasa3d.arc.nasa.gov/models (accessed on 15 April 2025).
- Space-Track. Available online: https://www.space-track.org/ (accessed on 17 April 2025).
- Wang, C.Y.; Jiang, L.B.; Ren, X.Y.; Zhong, W.J.; Wang, Z. Automatic Instantaneous Attitude Estimation Framework for Spacecraft Based on Colocated Optical/ISAR Observation. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3502005. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, S.H.; Liu, A.F.; Li, R.Z. Automatic Instantaneous Attitude Estimation of Satellite Based on Optical and ISAR Image Fusion. In Proceedings of the 2024 9th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 12–14 July 2024; pp. 659–664. [Google Scholar]
- Monitoring the Re-Entry of the Chinese Space Station Tiangong-1 with TIRA. Available online: https://www.fhr.fraunhofer.de/en/businessunits/space/monitoring-the-re-entry-of-the-chinese-space-station-tiangong-1-with-tira.html (accessed on 1 April 2018).
- Sharper ISAR Images of Satellites and Other Space Objects. Available online: https://www.fhr.fraunhofer.de/en/sections/Radar-for-Space-Situational-Awareness-RWL/sharper-isar-images-of-satellites-and-other-space-objects-jb2019.html (accessed on 17 April 2025).
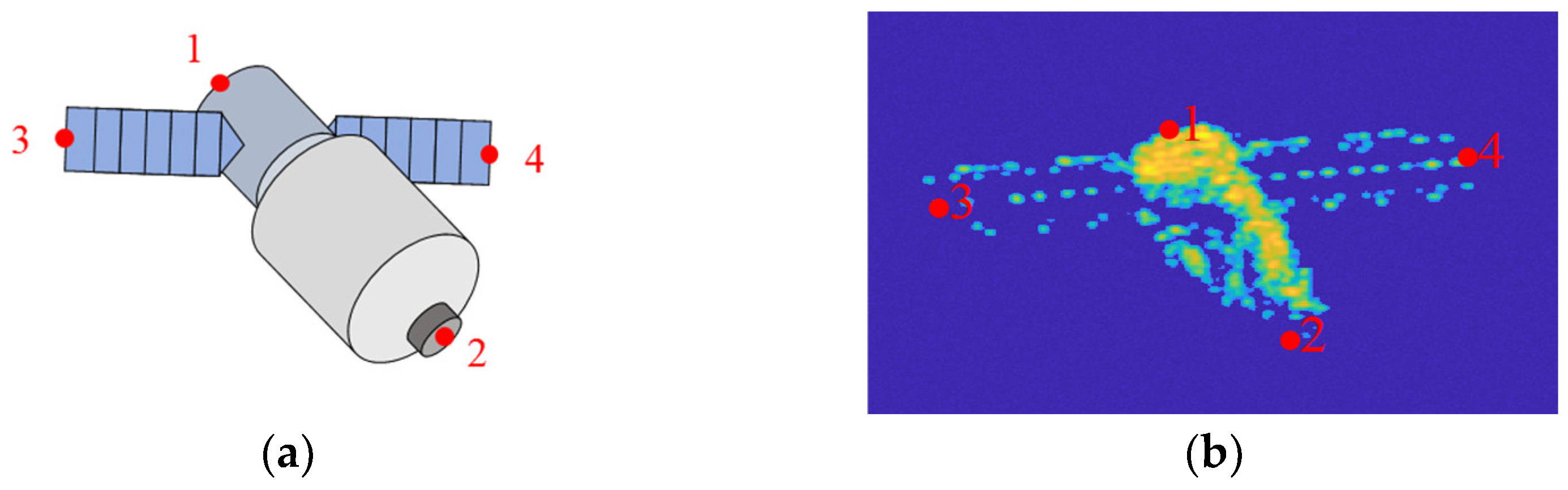


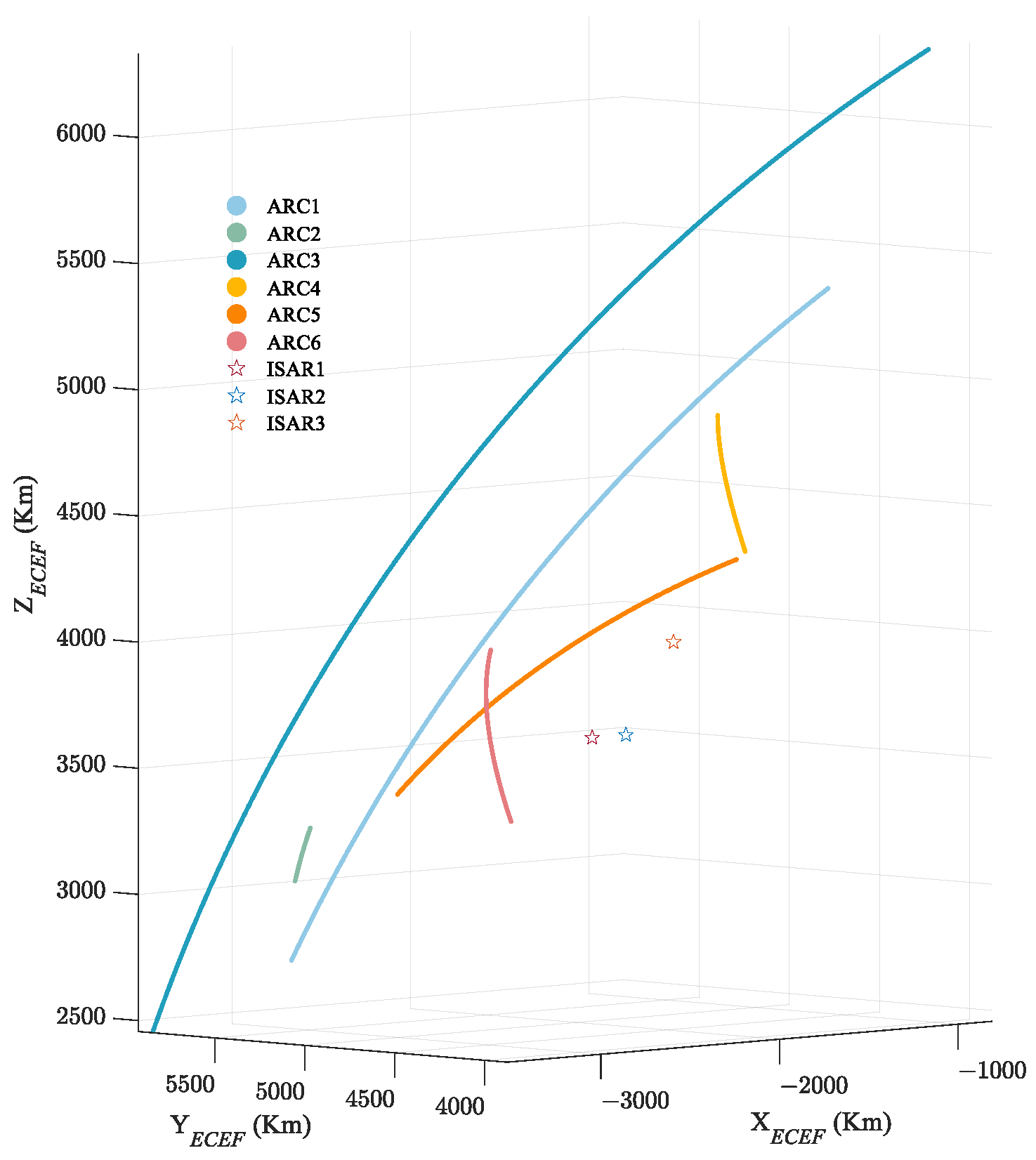


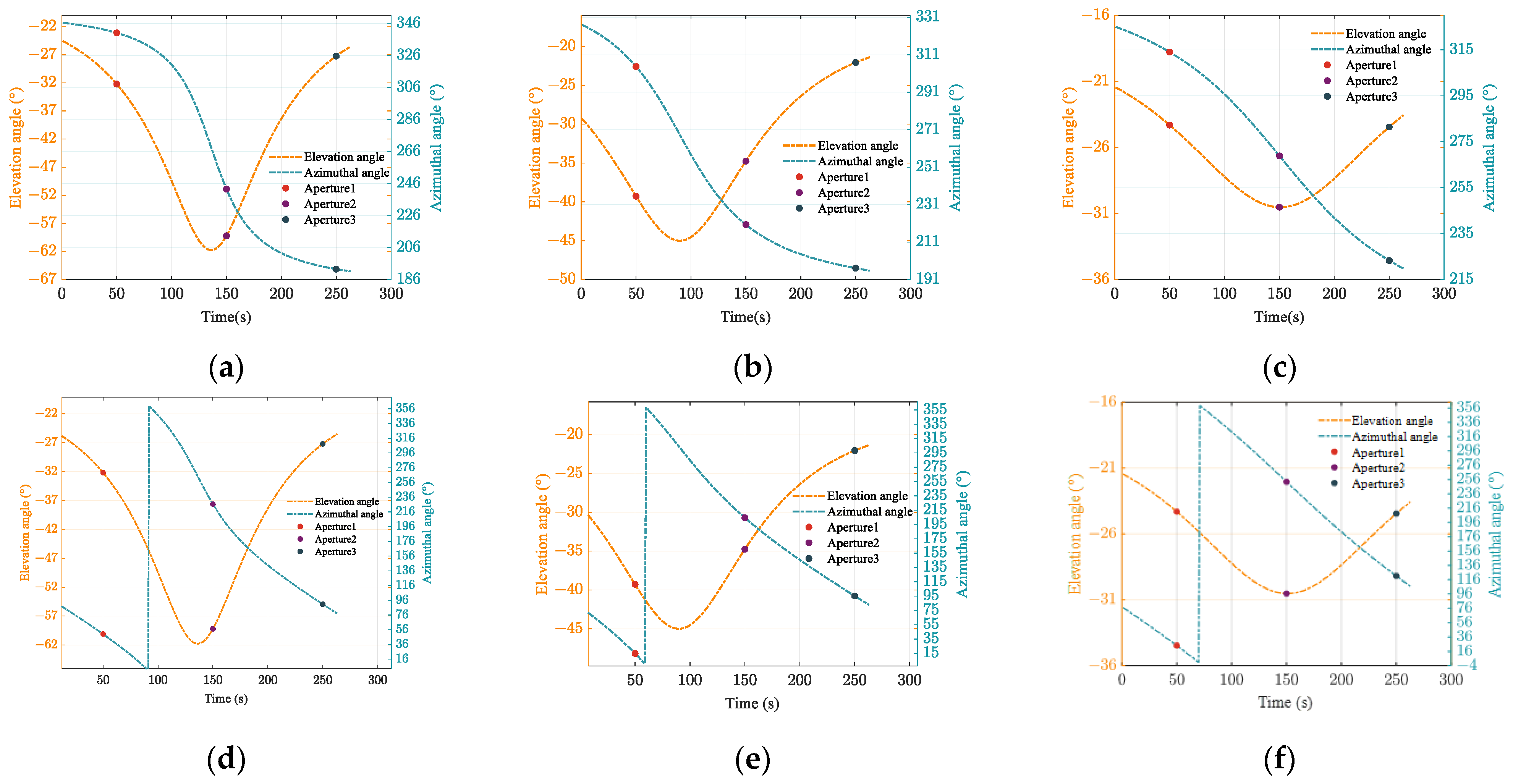





| TLE Name | TLE Parameters |
|---|---|
| TLE 1 | 1 39150U 13018A 23092.27047355 .00001617 00000-0 23877-3 0 9995 2 39150 98.0352 163.0146 0022971 76.1631 284.2129 14.76472717535358 |
| TLE 2 | 1 44310U 19032A 23092.17633197 .00006723 00000-0 52032-3 0 9993 2 44310 44.9832 194.7597 0009778 146.1448 288.1752 15.02106084209691 |
| TLE 3 | 1 51102U 22004A 23092.58401987 .00000276 00000-0 11131-3 0 9990 2 51102 98.5957 152.8512 0500395 303.1456 52.2629 13.83927097 62353 |
| TLE 4 | 1 25544U 98067A 23091.10374725 .00020749 00000-0 37896-3 0 9992 2 25544 51.6419 350.4695 0007223 140.3984 6.4707 15.49341873389833 |
| TLE 5 | 1 48274U 21035A 23091.59408903 .00036645 00000-0 37919-3 0 9995 2 48274 41.4735 262.9651 0005222 273.2786 165.3212 15.63969261109859 |
| TLE 6 | 1 37820U 11053A 16266.35688463 .00025497 00000-0 24137-3 0 9991 2 37820 42.7662 24.7762 0015742 351.0529 104.2087 15.66280400285808 |
| Radar Station | Position |
|---|---|
| ISAR1 | Xi’an (34.4 N, 109.5 E, 557 m) |
| ISAR2 | Zhengzhou (34.6 N, 113.5 E, 0 m) |
| ISAR3 | Taiyuan (38.8 N, 111.6 E, 1452 m) |
| Parameter | Value |
|---|---|
| Size of a Single Image | 512 × 512 |
| Signal Frequency | 10, 12 and 14 GHz |
| Bandwidth | 2, 3 and 4 GHz |
| Pulse Repetition Frequency | 80 Hz |
| Imaging Aperture | Key Point | Automatic Extraction (Cells) | Ground Truth (Cells) | Extraction Offset (Cells) | Mean Offset (Cells) |
|---|---|---|---|---|---|
| Aperture 1 | key point 1 | (354.5, 288.0) | (352.0, 288.0) | (2.5, 0) | (2.5, 1.0) |
| key point 2 | (159.0, 241.0) | (158.5, 240.5) | (0.5, 0.5) | ||
| key point 3 | (253.5, 368.5) | (250.0, 367.5) | (3.5, 1) | ||
| key point 4 | (368.5, 184.5) | (365.5, 183.0) | (3, 1.5) | ||
| Aperture 2 | key point 1 | (118.0, 272.5) | (115.0, 272.0) | (3.0, 0.5) | (2.5, 2.0) |
| key point 2 | (401.5, 259.0) | (398.5, 255.0) | (3.0, 4.0) | ||
| key point 3 | (151.0, 206.5) | (149.5, 204.5) | (1.5, 2.0) | ||
| key point 4 | (201.5, 322.0) | (199.0, 321.0) | (2.5, 1.0) | ||
| Aperture 3 | key point 1 | (251.5, 211.5) | (248.5, 211.5) | (3.0, 0) | (2.0, 1.0) |
| key point 2 | (280.0, 323.5) | (277.5, 323.0) | (2.5, 0.5) | ||
| key point 3 | (418.5, 201.5) | (417.5, 198.5) | (1.0, 3.0) | ||
| key point 4 | (89.0, 251.0) | (88.0, 251.0) | (1.0, 0) |
| Imaging Apertures | Parameter | Estimation Value | Truth Value | Estimation Error |
|---|---|---|---|---|
| Aperture 1 | The length of the main body | 10.5142 m | 10.5400 m | 0.0258 m |
| The orientation vector of the main body | (0.7217, 0.6921, −0.0110) | (0.7317, 0.6816, 0) | 1.0428° | |
| The length of the solar panel | 19.4929 m | 19.3400 m | 0.1529 m | |
| The orientation vector of the solar panel | (−0.6826, 0.7307, −0.0060) | (−0.6816, 0.7317, 0) | 0.3532° | |
| Spin speed | 0.0149 rad/s | 0.0150 rad/s | 0.0001 rad/s | |
| Spin direction vector | (−0.0281, 0.0098, 0.9996) | (0, 0, 1) | 1.7053° | |
| Aperture 2 | The length of the main body | 10.6125 m | 10.5400 m | 0.0725 m |
| The orientation vector of the main body | (−0.6178, 0.7862, −0.0118) | (−0.6282, 0.7781, 0) | 1.0137° | |
| The length of the solar panel | 19.2016 m | 19.3400 m | 0.1384 m | |
| The orientation vector of the solar panel | (−0.7804, −0.6253, −0.0065) | (−0.7781, −0.6282, 0) | 0.4286° | |
| Spin speed | 0.0150 rad/s | 0.0150 rad/s | 0.0000 rad/s | |
| Spin direction vector | (−0.0089, −0.0295, 0.9995) | (0, 0, 1) | 1.7658° | |
| Aperture 3 | The length of the main body | 10.4118 m | 10.5400 m | 0.1282 m |
| The orientation vector of the main body | (−0.8198, −0.5726, −0.0082) | (−0.8206, −0.5716, 0) | 0.4755° | |
| The length of the solar panel | 19.3552 m | 19.3400 m | 0.0152 m | |
| The orientation vector of the solar panel | (0.5770, −0.8167, −0.0044) | (0.5716, −0.8206, 0) | 0.4574° | |
| Spin speed | 0.0152 rad/s | 0.0150 rad/s | 0.0002 rad/s | |
| Spin direction vector | (−0.0022, −0.0242, 0.9997) | (0, 0, 1) | 1.3924° |
| Method | Key Point Extraction | Target Motion Modeling | Parameter Solving |
|---|---|---|---|
| Method 1 | RKPEN | spin | analytical method |
| Method 2 | KRCNN | spin | analytical method |
| Method 3 | PMKN | spin | analytical method |
| Method 4 | SHKEN | spin | analytical method |
| Method 5 | Lite-HRNet | spin | analytical method |
| Method 6 | ISAR-HRNet | three-axis stable | analytical method |
| Method 7 | ISAR-HRNet | spin | intelligent optimization algorithm |
| Ours | ISAR-HRNet | spin | analytical method |
| Imaging Aperture | Method | Mean Offset (Cells, Cells) | Estimation Error of the Length of the Main Body (m) | Estimation Error of the Orientation Vector of the Main Body (°) | Estimation Error of the Length of the Solar Panel (m) | Estimation Error of the Orientation Vector of the Solar Panel (°) | Estimation Error of Spin Speed (rad/s) | Estimation Error of Spin Orientation Vector (°) |
|---|---|---|---|---|---|---|---|---|
| Aperture 1 | Method 1 | (3.0, 2.0) | 0.0326 | 1.3605 | 0.1993 | 0.4545 | 0.0001 | 3.1720 |
| Method 2 | (3.5, 1.5) | 0.0371 | 1.5706 | 0.2301 | 0.5236 | 0.0001 | 2.8157 | |
| Method 3 | (3.0, 2.5) | 0.0289 | 1.1926 | 0.1747 | 0.3991 | 0.0001 | 3.3064 | |
| Method 4 | (3.5, 2.5) | 0.0344 | 1.4445 | 0.2116 | 0.4822 | 0.0001 | 3.6301 | |
| Method 5 | (4.0, 1.5) | 0.0389 | 1.6546 | 0.2424 | 0.5512 | 0.0001 | 2.5925 | |
| Ours | (2.5, 1.0) | 0.0256 | 1.0458 | 0.1532 | 0.3505 | 0.0000 | 1.7036 | |
| Aperture 2 | Method 1 | (3.5, 2.0) | 0.0989 | 1.3738 | 0.1890 | 0.5845 | 0.0000 | 2.0417 |
| Method 2 | (2.5, 2.5) | 0.0751 | 1.0529 | 0.1447 | 0.4459 | 0.0000 | 2.2797 | |
| Method 3 | (3.0, 3.5) | 0.0840 | 1.1734 | 0.1613 | 0.4978 | 0.0001 | 3.1427 | |
| Method 4 | (4.5, 1.5) | 0.1292 | 1.7730 | 0.2442 | 0.7586 | 0.0000 | 1.5622 | |
| Method 5 | (2.0, 3.5) | 0.0648 | 0.9120 | 0.1253 | 0.3855 | 0.0001 | 3.0017 | |
| Ours | (2.5, 2.0) | 0.0721 | 1.0127 | 0.1391 | 0.4287 | 0.0000 | 1.7650 | |
| Aperture 3 | Method 1 | (2.5, 2.5) | 0.1545 | 0.5741 | 0.0171 | 0.5506 | 0.0003 | 3.0750 |
| Method 2 | (3.0, 1.5) | 0.2058 | 0.7693 | 0.0232 | 0.7339 | 0.0004 | 2.1212 | |
| Method 3 | (3.5, 2.5) | 0.2186 | 0.8184 | 0.0247 | 0.7797 | 0.0004 | 2.7823 | |
| Method 4 | (2.5, 3.0) | 0.1673 | 0.6227 | 0.0186 | 0.5964 | 0.0003 | 3.8150 | |
| Method 5 | (2.5, 1.0) | 0.1628 | 0.6057 | 0.0180 | 0.5804 | 0.0003 | 1.7380 | |
| Ours | (2.0, 1.0) | 0.1288 | 0.4772 | 0.0141 | 0.4589 | 0.0002 | 1.3935 |
| Parameter | Method 6 (Single-Station Mode) | Method 6 (Multi-Station Mode) | Ours |
|---|---|---|---|
| Estimation error of the length of the main body (m) | 2.0267 | 0.0755 | 0.0755 |
| Estimation error of the orientation vector of the main body (°) | 5.3569 | 0.8452 | 0.8452 |
| Estimation error of the length of the solar panel (m) | 3.1493 | 0.1021 | 0.1021 |
| Estimation error of the orientation vector of the solar panel (°) | 10.5735 | 0.4127 | 0.4127 |
| Estimation error of spin speed (rad/s) | Not Available | Not Available | 0.0001 |
| Estimation error of spin vector (°) | Not Available | Not Available | 1.6207 |
| Imaging Aperture | Method | Estimation Error of Spin Speed (rad/s) | Estimation Error of the Orientation of the Spin Vector (°) | Average Time Consumption (s) |
|---|---|---|---|---|
| Aperture 1 | Method 7 | 0.0023 | 2.1725 | 0.2996 |
| Ours | 0.0001 | 1.7036 | 0.0025 | |
| Aperture 2 | Method 7 | 0.0012 | 2.5017 | 0.3253 |
| Ours | 0.0000 | 1.7650 | 0.0028 | |
| Aperture 3 | Method 7 | 0.0026 | 1.7381 | 0.2828 |
| Ours | 0.0002 | 1.3935 | 0.0020 |
| Key Point | Mean Offset (Cells, Cells) |
|---|---|
| Key point 1 | (3.5, 4.5) |
| Key point 2 | (4.0, 4.5) |
| Key point 3 | (4.5, 3.0) |
| Key point 4 | (3.0, 5.0) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yin, C.; Xu, C.; He, J.; Li, P.; Zhang, Y. Attitude Estimation of Spinning Space Targets Utilizing Multistatic ISAR Joint Observation. Remote Sens. 2025, 17, 2263. https://doi.org/10.3390/rs17132263
Li J, Yin C, Xu C, He J, Li P, Zhang Y. Attitude Estimation of Spinning Space Targets Utilizing Multistatic ISAR Joint Observation. Remote Sensing. 2025; 17(13):2263. https://doi.org/10.3390/rs17132263
Chicago/Turabian StyleLi, Jishun, Canbin Yin, Can Xu, Jun He, Pengju Li, and Yasheng Zhang. 2025. "Attitude Estimation of Spinning Space Targets Utilizing Multistatic ISAR Joint Observation" Remote Sensing 17, no. 13: 2263. https://doi.org/10.3390/rs17132263
APA StyleLi, J., Yin, C., Xu, C., He, J., Li, P., & Zhang, Y. (2025). Attitude Estimation of Spinning Space Targets Utilizing Multistatic ISAR Joint Observation. Remote Sensing, 17(13), 2263. https://doi.org/10.3390/rs17132263






