Multi-Modal Remote Sensing Image Registration Method Combining Scale-Invariant Feature Transform with Co-Occurrence Filter and Histogram of Oriented Gradients Features
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
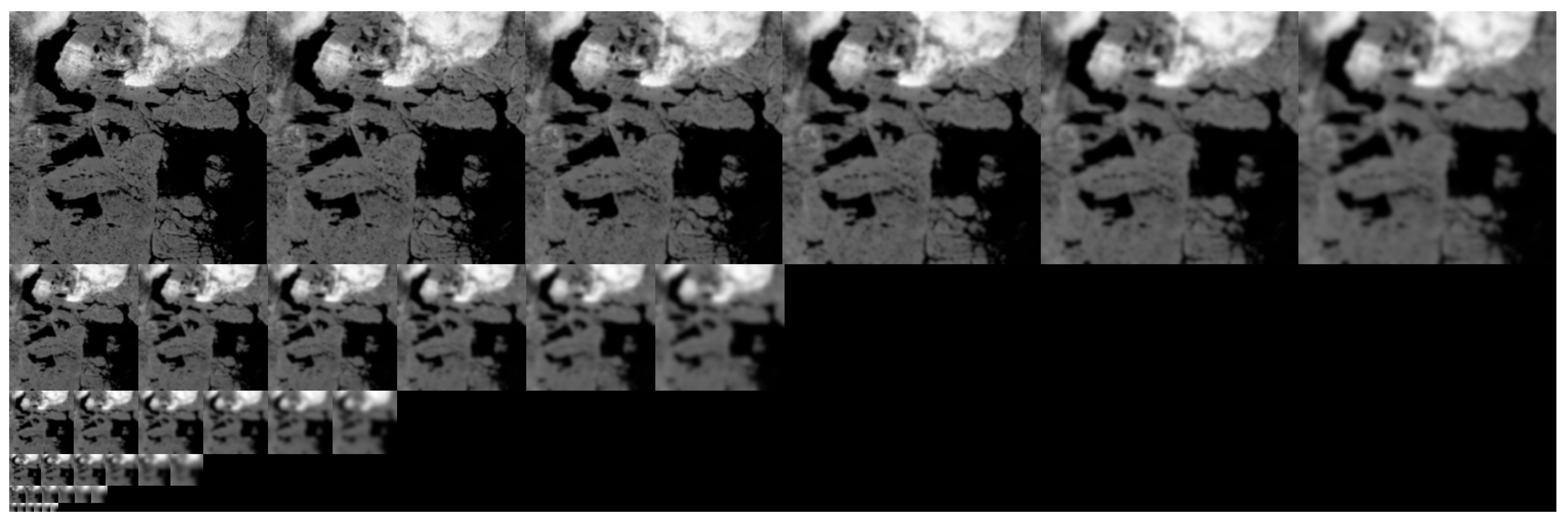
3.1. Image Pyramid Construction Based on the Co-Occurrence Filter
3.2. Feature Point Extraction
- (1)
- Scale space extreme detection: In contrast to the original SIFT feature point extraction method, our approach leverages an image pyramid based on co-occurrence filters to produce a series of difference images at various scales. A pixel is designated as a candidate feature point if its value in the difference image represents a local extremum—either a maximum or minimum—relative to its 26 neighbors across the current and adjacent scales in the scale space.
- (2)
- Feature point localization: We use the detailed model to correct the location of the candidate feature points. Then, candidate feature points are filtered by using the non-maximum suppression algorithm.
- (3)
- Orientation assignment: To achieve image rotation invariance, each feature point is assigned one or more dominant orientations using the gradient information of the image patch where the key point is located.
3.3. Image Gradient
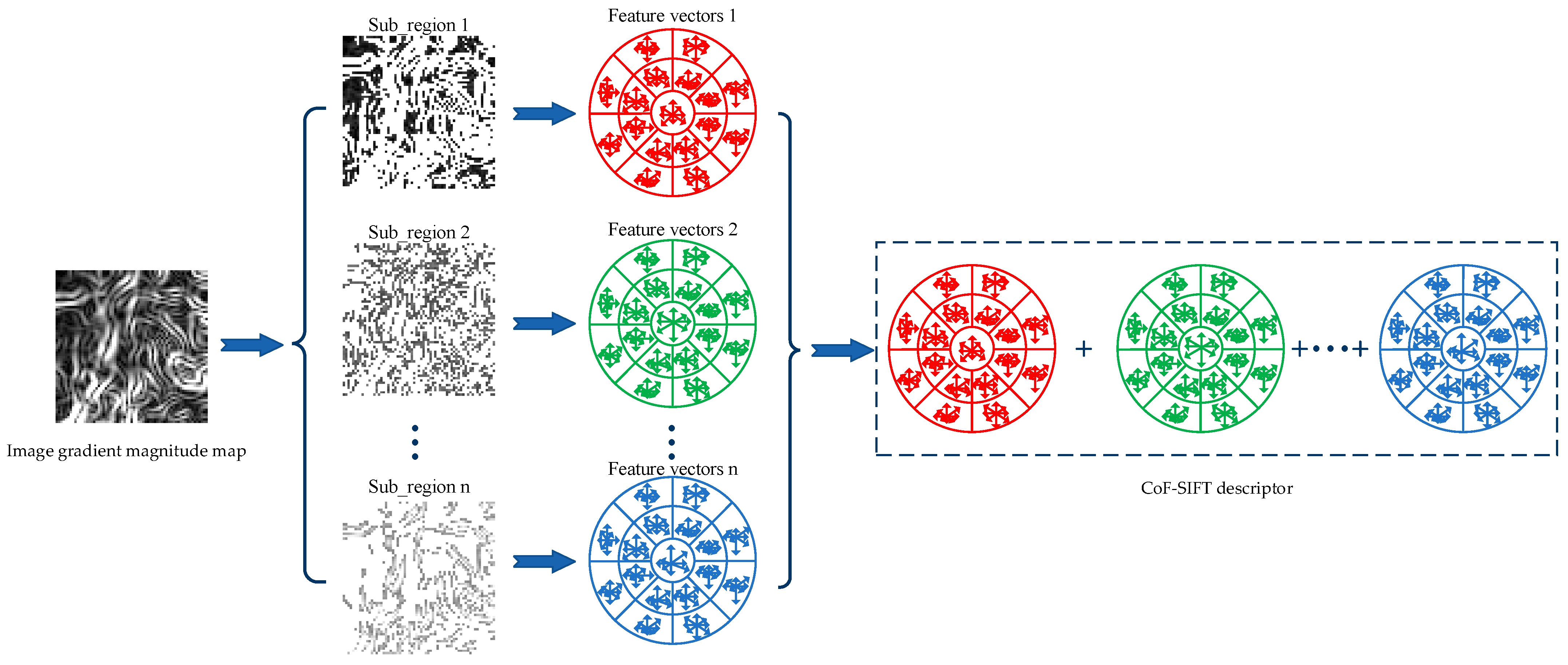
3.4. Image Gradient Magnitude Map Segmentation Based on Magnitude Order
3.5. Local Feature Descriptor Construction
3.6. Matching Strategy
3.6.1. Bidirectional Image Matching
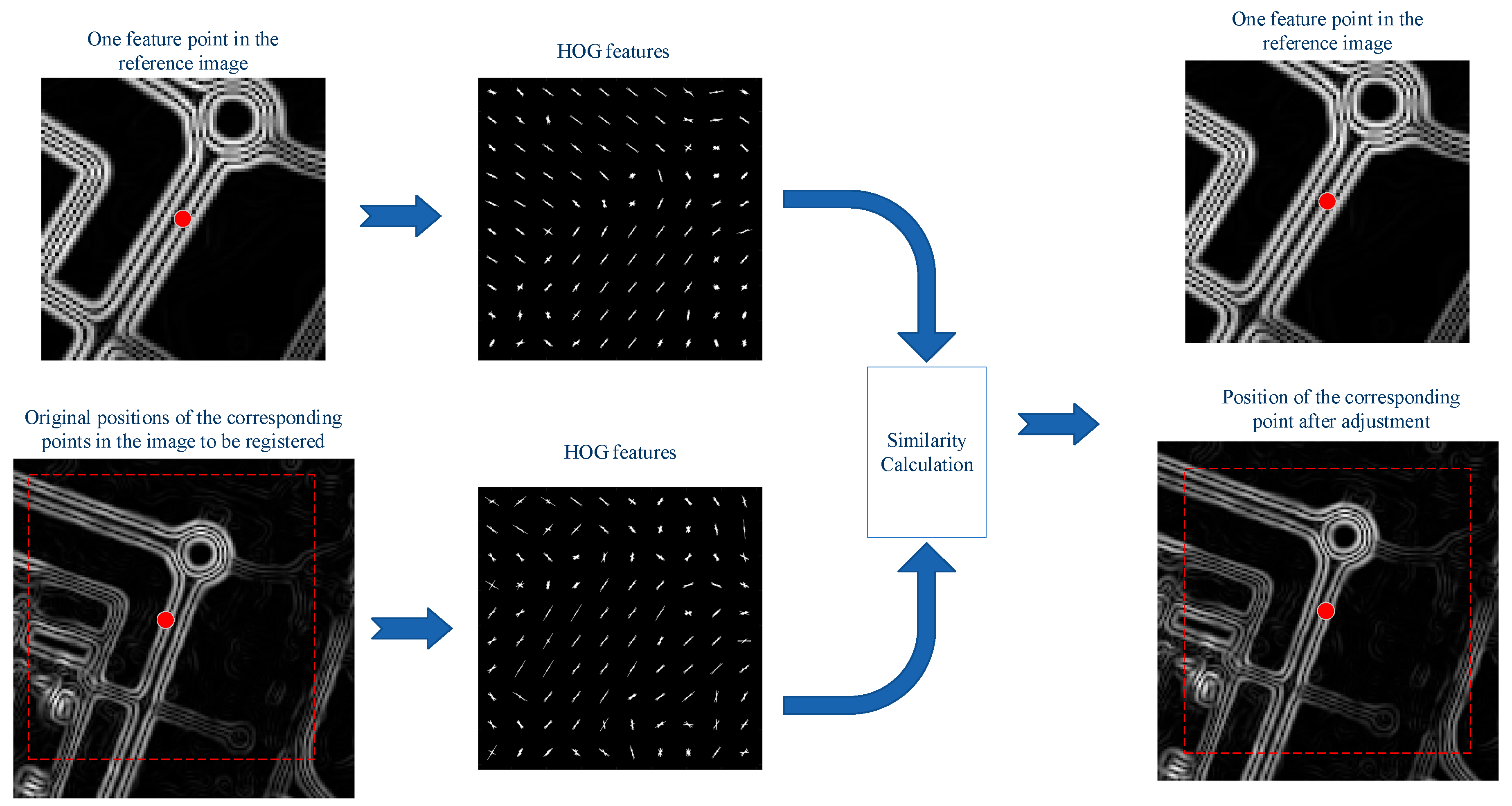
3.6.2. Corresponding Point Location Adjustment Using the Similarity of HOG Features
3.7. Multi-Modal Remote Sensing Datasets
- Depth images were derived from airborne LiDAR data;
- Infrared images were collected from airborne infrared sensors and the Landsat TM-5 satellite;
- Map images were obtained from Google Maps;
- SAR images were acquired from the GaoFen-3 (GF-3) satellite;
- Night–day images originated from National Aeronautics and Space Administration (NASA)’s Suomi National Polar-orbiting Partnership (Suomi-NPP) satellite and National Oceanic and Atmospheric Administration (NOAA) satellites.
4. Results and Discussion
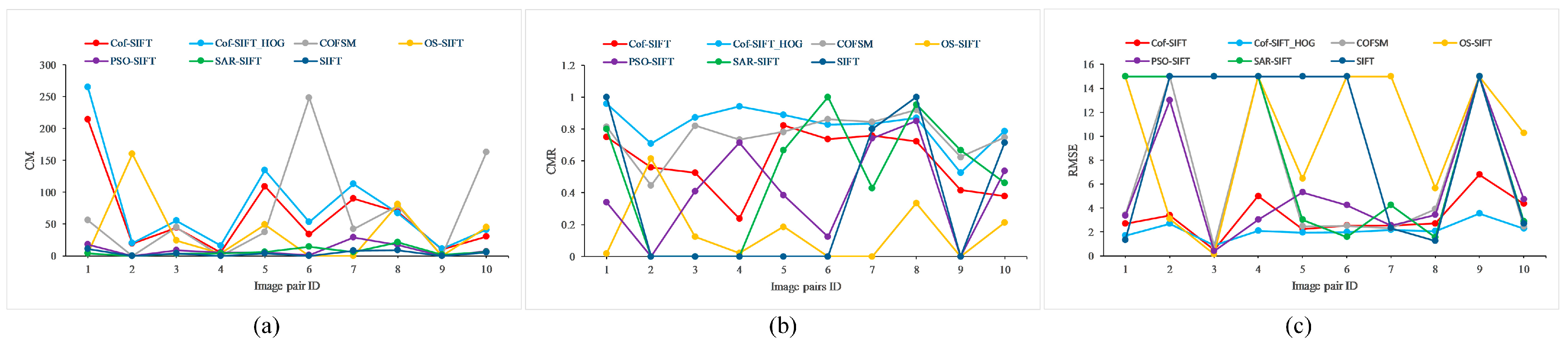
4.1. Evaluation Criterion
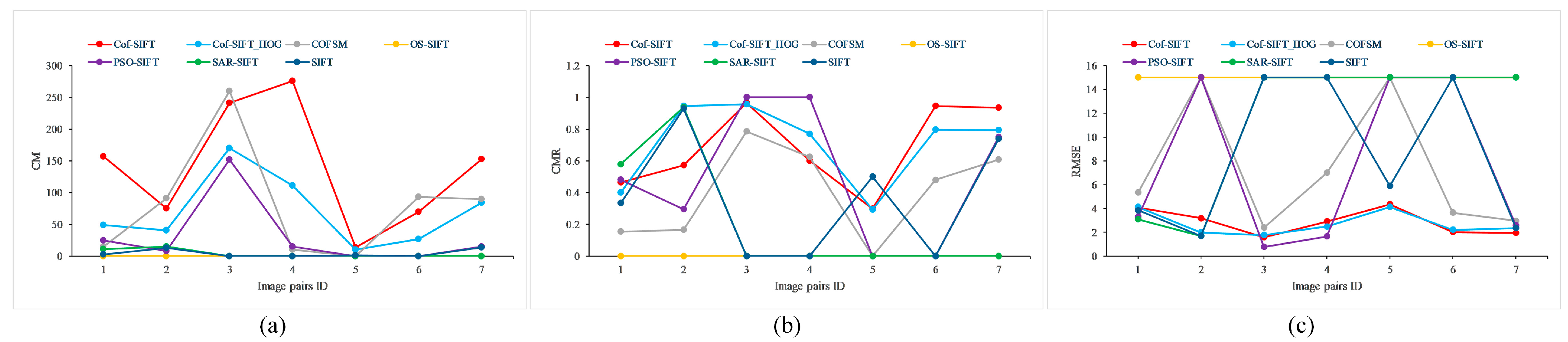
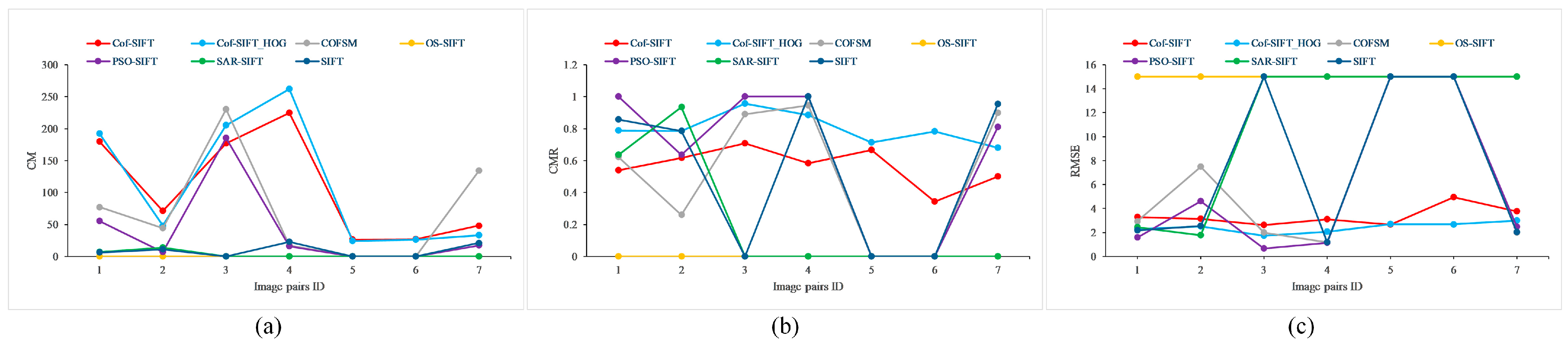
4.2. Image Matching Results on Multi-Modal Image Datasets
4.3. Checkerboard Mosaiced Images on Partial Multi-Modal Image Pairs
4.4. Evaluation of Image Pairs with Skew Transformations
4.5. Evaluation of Effect of Co-Occurrence Filter and HOG on Matching Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SAR | Synthetic Aperture Radar |
| SIFT | Scale-Invariant Feature Transform |
| MI | Mutual Information |
| HOPC | Histogram of Orientated Phase Congruency |
| CFOG | Channel Features of Orientated Gradients |
| DoG | Difference-of-Gaussians |
| GLOH | Gradient Location and Orientation Histogram |
| RANSAC | Random Sample Consensus |
| SR | Success Rate |
| CMR | Correct Match Ratio |
| RMSE | Root Mean Square Error |
| PC | Phase-Consistent |
| NCM | Number of Correct Matches |
| HOG | Histogram of Oriented Gradients |
| HOWP | Histogram of the Orientation of Weighted Phase |
| NOAA | National Oceanic and Atmospheric Administration |
| Suomi-NPP | Suomi National Polar-orbiting Partnership |
| CM | Correct Match |
| NASA | National Aeronautics and Space Administration |
| GF-3 | GaoFen-3 |
References
- Bruzzone, L.; Bovolo, F. A Novel Framework for the Design of Change-Detection Systems for Very-High-Resolution Remote Sensing Images. Proc. IEEE 2013, 101, 609–630. [Google Scholar] [CrossRef]
- Tuia, D.; Marcos, D.; Camps-Valls, G. Multi-Temporal and Multi-Source Remote Sensing Image Classification by Nonlinear Relative Normalization. ISPRS J. Photogramm. Remote Sens. 2016, 120, 1–12. [Google Scholar] [CrossRef]
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake Damage Assessment of Buildings Using VHR Optical and SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef]
- Yang, J.; Gong, P.; Fu, R.; Zhang, M.; Chen, J.; Liang, S.; Xu, B.; Shi, J.; Dickinson, R. The Role of Satellite Remote Sensing in Climate Change Studies. Nat. Clim. Change 2013, 3, 875–883. [Google Scholar] [CrossRef]
- Feng, R.; Shen, H.; Bai, J.; Li, X. Advances and Opportunities in Remote Sensing Image Geometric Registration: A Systematic Review of State-of-the-Art Approaches and Future Research Directions. IEEE Geosci. Remote Sens. Mag. 2021, 9, 120–142. [Google Scholar] [CrossRef]
- Zhu, B.; Ye, Y. Multimodal Remote Sensing Image Registration: A Survey. J. Image Graph. 2024, 29, 2137–2161. [Google Scholar] [CrossRef]
- Viola, P.; Wells, W.M. Alignment by Maximization of Mutual Information. J. Image Graph. 1997, 24, 137–154. [Google Scholar] [CrossRef]
- Ye, Y.; Shen, L. Hopc: A Novel Similarity Metric Based on Geometric Structural Properties for Multi-Modal Remote Sensing Image Matching. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-1, 9–16. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-Modal Image Matching Based on Radiation-Variation Insensitive Feature Transform. IEEE Trans. Image Process. 2020, 29, 3296–3310. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Y.; Wan, Y.; Liu, X.; Yan, X.; Li, J. Multi-Modal Remote Sensing Image Matching Considering Co-Occurrence Filter. IEEE Trans. Image Process. 2022, 31, 2584–2597. [Google Scholar] [CrossRef]
- Zhuang, J.; Chen, W.; Huang, X.; Yan, Y. Band Selection Algorithm Based on Multi-Feature and Affinity Propagation Clustering. Remote Sens. 2025, 17, 193. [Google Scholar] [CrossRef]
- Wan, G.; Ye, Z.; Xu, Y.; Huang, R.; Zhou, Y.; Xie, H.; Tong, X. Multimodal Remote Sensing Image Matching Based on Weighted Structure Saliency Feature. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4700816. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, Y.; Wan, Y.; Liu, W.; Yang, W.; Zheng, Z.; Xiao, R. Histogram of the Orientation of the Weighted Phase Descriptor for Multi-Modal Remote Sensing Image Matching. ISPRS J. Photogramm. Remote Sens. 2023, 196, 1–15. [Google Scholar] [CrossRef]
- Zampieri, A.; Charpiat, G.; Girard, N.; Tarabalka, Y. Multimodal Image Alignment Through a Multiscale Chain of Neural Networks with Application to Remote Sensing. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; Springer International Publishing: Cham, Switzerland, 2018; Volume 11220, pp. 679–696. [Google Scholar]
- Yang, Z.; Dan, T.; Yang, Y. Multi-Temporal Remote Sensing Image Registration Using Deep Convolutional Features. IEEE Access 2018, 6, 38544–38555. [Google Scholar] [CrossRef]
- Zhuang, J.; Zheng, Y.; Guo, B.; Yan, Y. Globally Deformable Information Selection Transformer for Underwater Image Enhancement. IEEE Trans. Circuits Syst. Video Technol. 2024, 35, 19–32. [Google Scholar] [CrossRef]
- Baruch, E.B.; Keller, Y. Joint Detection and Matching of Feature Points in Multimodal Images. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 6585–6593. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-Free Local Feature Matching with Transformers. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; Volume 4, pp. 8918–8927. [Google Scholar]
- Zhu, R.; Yu, D.; Ji, S.; Lu, M. Matching RGB and Infrared Remote Sensing Images with Densely-Connected Convolutional Neural Networks. Remote Sens. 2019, 11, 2836. [Google Scholar] [CrossRef]
- Li, L.; Han, L.; Ye, Y.; Xiang, Y.; Zhang, T. Deep Learning in Remote Sensing Image Matching: A Survey. ISPRS J. Photogramm. Remote Sens. 2025, 225, 88–112. [Google Scholar] [CrossRef]
- Han, S.; Liu, X.; Dong, J.; Liu, H. Remote Sensing Multimodal Image Matching Based on Structure Feature and Learnable Matching Network. Appl. Sci. 2023, 13, 7701. [Google Scholar] [CrossRef]
- Zhang, Y.; Lan, C.; Zhang, H.; Ma, G.; Li, H. Multimodal Remote Sensing Image Matching via Learning Features and Attention Mechanism. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5603620. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Jevnisek, R.J.; Avidan, S. Co-Occurrence Filter. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3184–3192. [Google Scholar]
- Dalal, N.; Triggs, W. Histograms of Oriented Gradients for Human Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-like Algorithm for SAR Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef]
- Ma, W.; Wen, Z.; Wu, Y.; Jiao, L.; Gong, M.; Zheng, Y.; Liu, L. Remote Sensing Image Registration with Modified Sift and Enhanced Feature Matching. IEEE Geosci. Remote Sens. Lett. 2017, 14, 3–7. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; You, H. OS-SIFT: A Robust SIFT-Like Algorithm for High-Resolution Optical-to-SAR Image Registration in Suburban Areas. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3078–3090. [Google Scholar] [CrossRef]
- Quan, D.; Wang, S.; Gu, Y.; Lei, R.; Yang, B.; Wei, S.; Hou, B.; Jiao, L. Deep Feature Correlation Learning for Multi-Modal Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4708216. [Google Scholar] [CrossRef]
- Ye, Y.; Yang, C.; Gong, G.; Yang, P.; Quan, D.; Li, J. Robust Optical and SAR Image Matching Using Attention-Enhanced Structural Features. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5610212. [Google Scholar] [CrossRef]
- Hou, Z.; Liu, Y.; Zhang, L. POS-GIFT: A Geometric and Intensity-Invariant Feature Transformation for Multimodal Images. Inf. Fusion 2024, 102, 102027. [Google Scholar] [CrossRef]
- Chen, H.M.; Arora, M.K.; Varshney, P.K. Mutual Information-Based Image Registration for Remote Sensing Data. Int. J. Remote Sens. 2003, 24, 3701–3706. [Google Scholar] [CrossRef]
- Ye, Y.; Bruzzone, L.; Shan, J.; Bovolo, F.; Zhu, Q. Fast and Robust Matching System for Multimodal Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9059–9070. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. A Performance Evaluation of Local Descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1615–1630. [Google Scholar] [CrossRef]
- Ye, Y.; Shan, J.; Hao, S.; Bruzzone, L.; Qin, Y. A Local Phase Based Invariant Feature for Remote Sensing Image Matching. ISPRS J. Photogramm. Remote Sens. 2018, 142, 205–221. [Google Scholar] [CrossRef]
- Liu, X.; Ai, Y.; Tian, B.; Cao, D. Robust and Fast Registration of Infrared and Visible Images for Electro-Optical Pod. IEEE Trans. Ind. Electron. 2019, 66, 1335–1344. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, Y.; Liu, Y.; Zhang, L.; Zhang, J.; Sun, Y.; Ai, H. 3MRS: An Effective Coarse-to-Fine Matching Method for Multimodal Remote Sensing Imagery. Remote Sens. 2022, 14, 478. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, B.; Wang, G.; Wu, F. Exploring Local and Overall Ordinal Information for Robust Feature Description. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2198–2211. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M.; Wang, S. A Geometric Estimation Technique Based on Adaptive M-Estimators: Algorithm and Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5613–5626. [Google Scholar] [CrossRef]






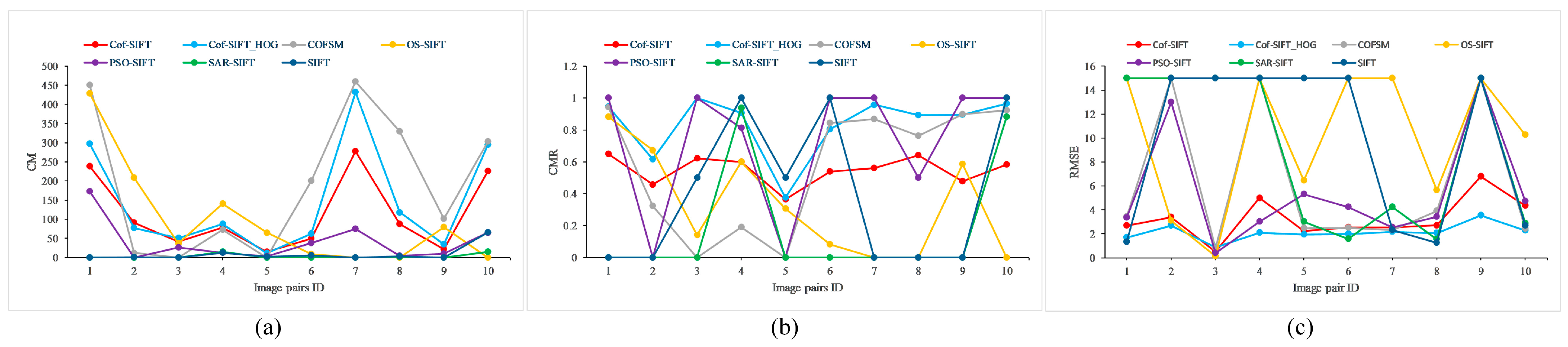

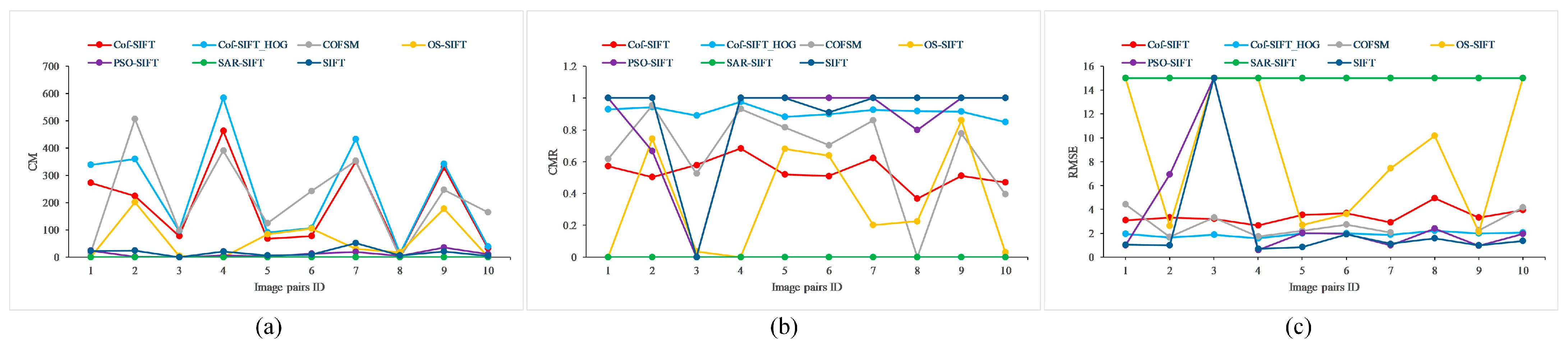

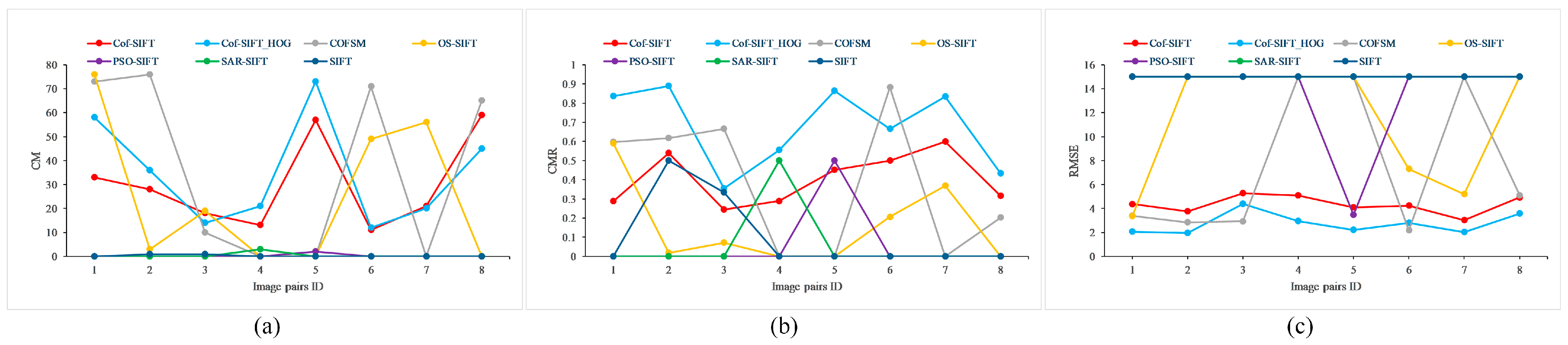

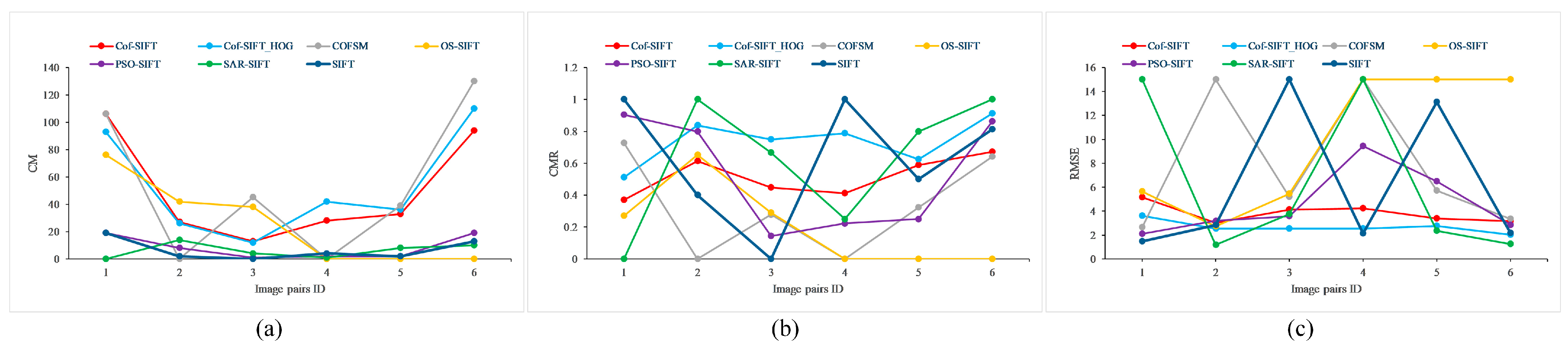







| Cof-SIFT | Cof-SIFT_HOG | COFSM | |
|---|---|---|---|
| SR | 100% | 100% | 72% |
| CM | 100 | 109 | 110 |
| CMR | 55% | 79% | 67% |
| RMSE | 3.54 | 2.37 | 3.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Liu, S.; Zhang, H.; Li, D.; Ma, L. Multi-Modal Remote Sensing Image Registration Method Combining Scale-Invariant Feature Transform with Co-Occurrence Filter and Histogram of Oriented Gradients Features. Remote Sens. 2025, 17, 2246. https://doi.org/10.3390/rs17132246
Yang Y, Liu S, Zhang H, Li D, Ma L. Multi-Modal Remote Sensing Image Registration Method Combining Scale-Invariant Feature Transform with Co-Occurrence Filter and Histogram of Oriented Gradients Features. Remote Sensing. 2025; 17(13):2246. https://doi.org/10.3390/rs17132246
Chicago/Turabian StyleYang, Yi, Shuo Liu, Haitao Zhang, Dacheng Li, and Ling Ma. 2025. "Multi-Modal Remote Sensing Image Registration Method Combining Scale-Invariant Feature Transform with Co-Occurrence Filter and Histogram of Oriented Gradients Features" Remote Sensing 17, no. 13: 2246. https://doi.org/10.3390/rs17132246
APA StyleYang, Y., Liu, S., Zhang, H., Li, D., & Ma, L. (2025). Multi-Modal Remote Sensing Image Registration Method Combining Scale-Invariant Feature Transform with Co-Occurrence Filter and Histogram of Oriented Gradients Features. Remote Sensing, 17(13), 2246. https://doi.org/10.3390/rs17132246






