HG-Mamba: A Hybrid Geometry-Aware Bidirectional Mamba Network for Hyperspectral Image Classification
Abstract
1. Introduction
- 1.
- HSpectral redundancy: high inter-band correlation compounded by noise not only elevates computational costs but also impairs the discriminability of features.
- 2.
- Spatial insensitivity: fixed convolutional kernels prove inadequate for modeling boundary regions, where spatial importance diminishes with increased distance.
- 3.
- Unidirectional bias: Mamba’s causal state transitions truncate the contextual dependencies that are essential in bidirectional hyperspectral imaging data.
- 1.
- We propose the first framework that unifies convolutional operations, geometry-aware filtering, and bidirectional state-space models (SSMs) into a hierarchical architecture. This design enables joint extraction of local spectral details and global contextual dependencies while reducing computational complexity to linear time.
- 2.
- We develop a sequential two-stage architecture, which comprises a bidirectional Spectral Mamba (SeBM) module for enhancing spectral discriminability and a bidirectional Spatial Mamba (SaBM) module for resolving spatial heterogeneity and capturing long-range dependencies.
- 3.
- We also introduce geometry-aware Gaussian Distance Decay (GDD) to dynamically extract spatial feature, which is a novel mechanism that adaptively reweights spatial neighbors based on Euclidean distances.
2. Related Work
2.1. Convolution Neural Network-Based Methods for HSI Classification
2.2. Transformer-Based Methods for HSI Classification
2.3. Mamba-Based Methods for HSI Classification
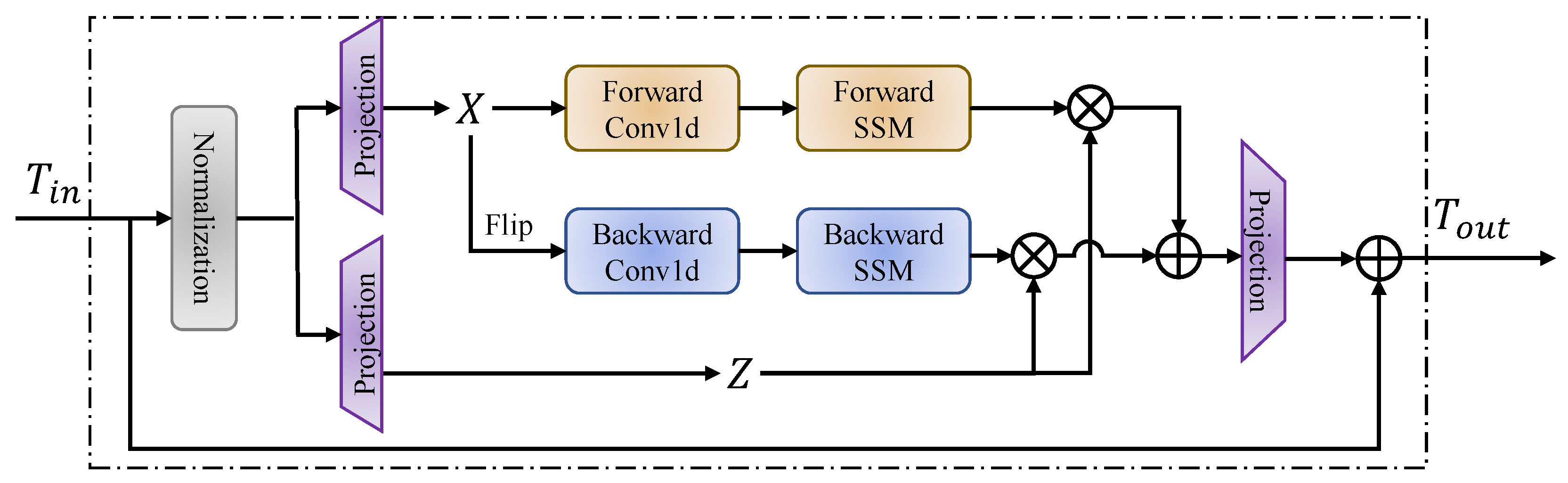
3. Preliminaries
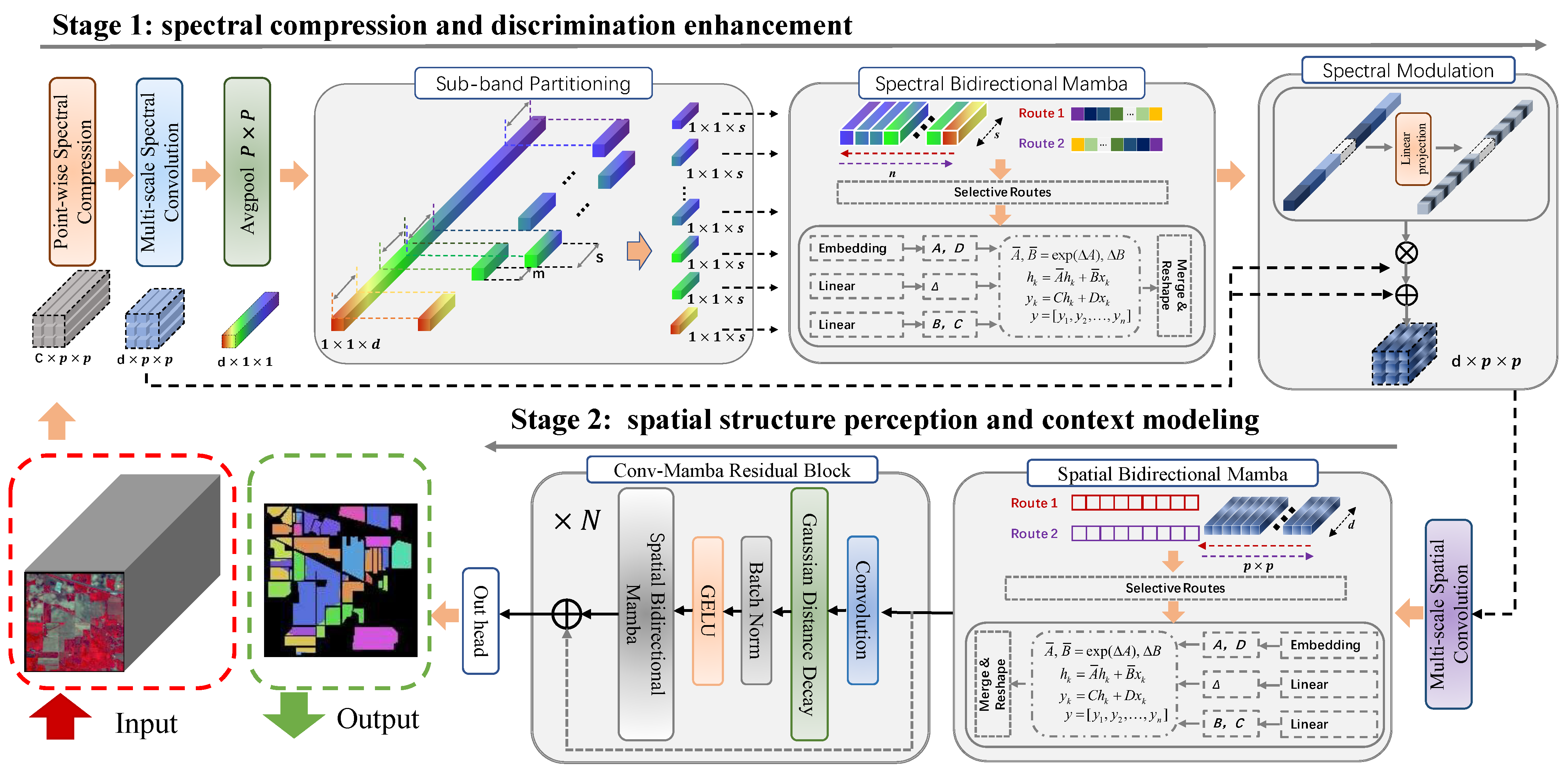
4. Proposed Approach
4.1. Overall Architecture
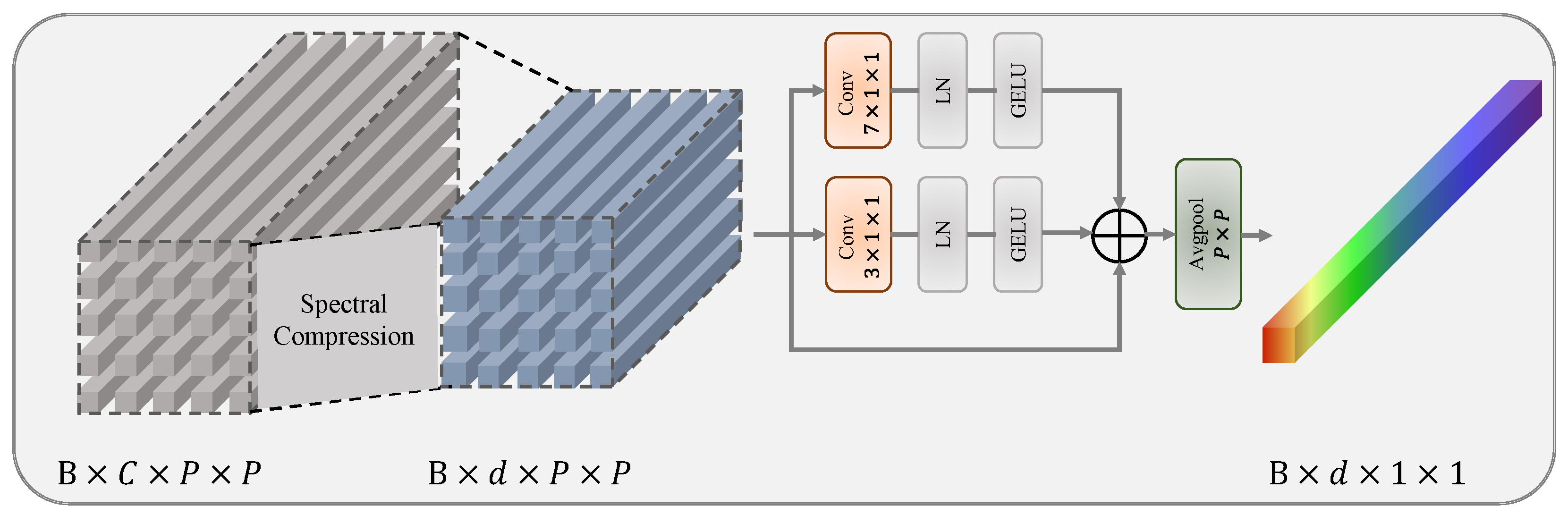
4.2. Spectral Compression and Discrimination Enhancement
4.3. Spatial Structure Perception and Context Modeling
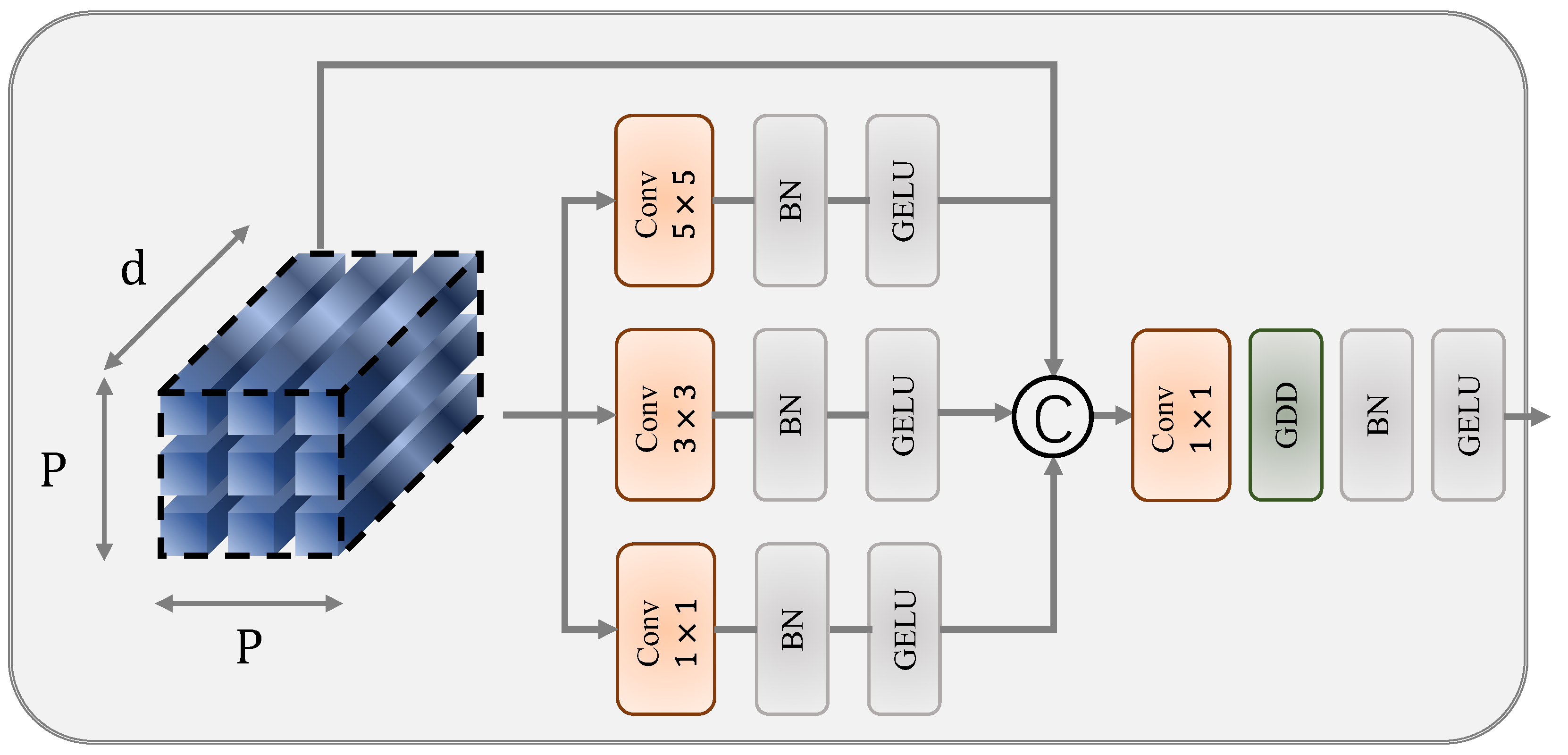
4.3.1. Multi-Scale Spatial Structure Extraction
4.3.2. Gaussian Distance Decay (GDD)
4.3.3. Hierarchical Refinement with Spatial Bidirectional Mamba
5. Experiments
5.1. Datasets and Setting
- Indian Pines Scene: This HSI dataset was acquired in 1992 by the Airborne Visible Imaging Spectrometer (AVIRIS) instrument over a mixed agricultural and forest area in Northwestern Indiana, USA. The original imagery comprised 220 spectral bands. After preprocessing that involved the removal of 20 noisy bands, 200 spectral bands were retained for analysis. The spatial dimensions of the image are 145 × 145 pixels. The scene includes 16 distinct land cover classes, encompassing a variety of agricultural and natural surface types. The complete set of classes is as follows: Alfalfa, Corn-notill, Corn-mintill, Corn, Grass-pasture, Grass-trees, Grass-pasture-mowed, Hay-windrowed, Oats, Soybean-notill, Soybean-mintill, Soybean-clean, Wheat, Woods, Buildings-Grass-Trees-Drives, and Stone-Steel-Towers.For the purpose of training and testing, a subset constituting 10% of the total labeled samples was allocated for model training, with the remaining 90% designated for performance evaluation.
- Houston2013 Dataset: This dataset captures an urban scene covering the University of Houston and its vicinities in Texas, USA. The data was collected using the ITRES CASI-1500 sensor. The imagery provides spatial dimensions of 349 × 1905 pixels and contains 144 spectral band. Provided as a cloud-free image by the Geo-science and Remote Sensing Society (GRSS), it serves as a standard benchmark. The dataset is composed of a total of 15 labeled land cover classes. The complete set of classes includes: Grass-healthy, Grass-stressed, Grass-synthetic, Tree, Soil, Water, Residential, Commercial, Road, Highway, Railway, Parking Lot 1, Parking Lot 2, Tennis Court, and Running Track.In our experimental setup, 10% of the available samples were selected to form the training set, while the remaining samples constituted the test set.
- WHU-Hi-LongKou (WHL) Dataset: Acquired on 17 July 2018, this dataset covers Longkou Town, Hubei province, China. Data collection was performed via a UAV platform (DJI Matrice 600 Pro) equipped with a Headwall Nano-Hyperspec imaging sensor featuring an 8 mm focal length. The UAV flew at an altitude of 500 m, resulting in imagery with a spatial resolution of 550 × 400 pixels. The spectral range of the sensor spans from 400 to 1000 nm, capturing data across 270 bands. The dataset comprises 204,542 labeled samples distributed among nine distinct land cover classes. The complete set of classes includes: Corn, Cotton, Sesame, Broad-leaf soybean, Narrow-leaf soybean, Rice, Water, Roads and houses, and Mixed weed.In this study, a small fraction, specifically 1%, of the labeled samples was utilized for training, with the predominant portion (99%) reserved for testing.
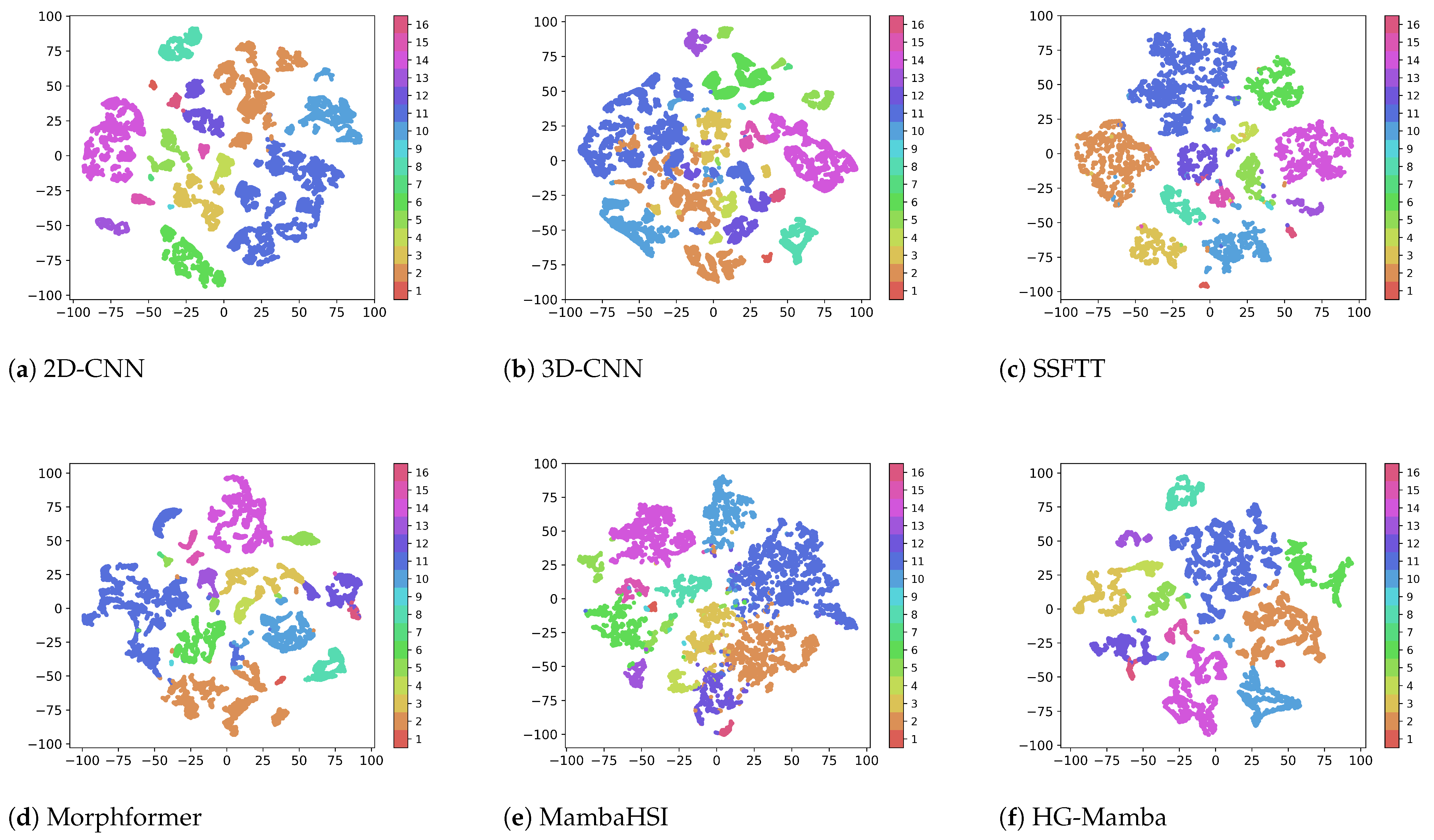
5.2. Results and Analysis
5.3. Comparison of Computational Complexity
6. Ablation Studies
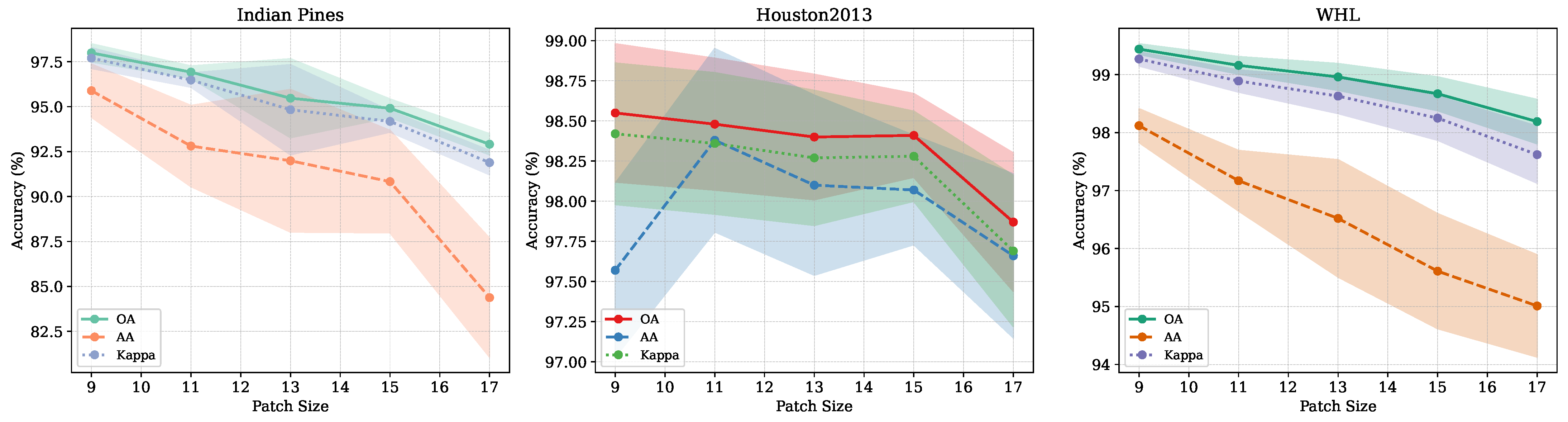
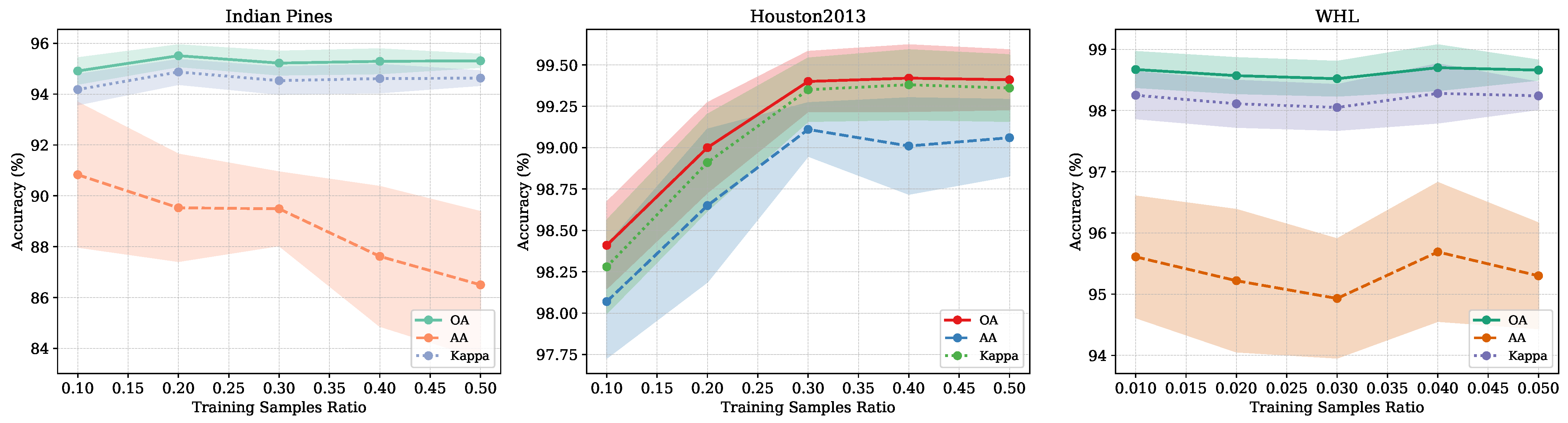
6.1. Patch Size Sensitivity Analysis
6.2. Training Sample Ratio Sensitivity Analysis
6.3. Ablation Study of Different Modules
6.4. Analysis of Network Depth
6.5. Limitations and Future Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhadra, S.; Sagan, V.; Sarkar, S.; Braud, M.; Mockler, T.C.; Eveland, A.L. PROSAIL-Net: A transfer learning-based dual stream neural network to estimate leaf chlorophyll and leaf angle of crops from UAV hyperspectral images. ISPRS J. Photogramm. Remote Sens. 2024, 210, 1–24. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Chanussot, J.; Zhu, X.X. An augmented linear mixing model to address spectral variability for hyperspectral unmixing. IEEE Trans. Image Process. 2018, 28, 1923–1938. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Hong, D.; Zhu, X.X. High-resolution satellite images reveal the prevalent positive indirect impact of urbanization on urban tree canopy coverage in South America. Landsc. Urban Plan. 2024, 247, 105076. [Google Scholar] [CrossRef]
- Ali, M.A.; Lyu, X.; Ersan, M.S.; Xiao, F. Critical evaluation of hyperspectral imaging technology for detection and quantification of microplastics in soil. J. Hazard. Mater. 2024, 476, 135041. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Chen, Y. Optimized input for CNN-based hyperspectral image classification using spatial transformer network. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1884–1888. [Google Scholar] [CrossRef]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.Y.; Zhang, X.; Huang, X. Hyperspectral image classification with deep learning models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, X.; Ye, Y.; Lau, R.Y.; Lu, S.; Li, X.; Huang, X. Synergistic 2D/3D convolutional neural network for hyperspectral image classification. Remote Sens. 2020, 12, 2033. [Google Scholar] [CrossRef]
- Mou, L.; Zhu, X.X. Learning to pay attention on spectral domain: A spectral attention module-based convolutional network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 110–122. [Google Scholar] [CrossRef]
- Sun, W.; Du, Q. Hyperspectral band selection: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Tu, C.; Liu, W.; Jiang, W.; Zhao, L. Hyperspectral image classification based on residual dense and dilated convolution. Infrared Phys. Technol. 2023, 131, 104706. [Google Scholar] [CrossRef]
- Ye, Z.; Wang, J.; Bai, L. Multi-Scale Spatial-Spectral Feature Extraction Based on Dilated Convolution for Hyperspectral Image Classification. In Proceedings of the 2023 6th International Conference on Image and Graphics Processing, Chongqing, China, 6–8 January 2023; pp. 97–103. [Google Scholar]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Shah, C.; Haut, J.M.; Du, Q.; Plaza, A. Spectral–spatial morphological attention transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Li, Y.; Luo, Y.; Zhang, L.; Wang, Z.; Du, B. MambaHSI: Spatial-spectral mamba for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5524216. [Google Scholar] [CrossRef]
- Yao, J.; Hong, D.; Li, C.; Chanussot, J. Spectralmamba: Efficient mamba for hyperspectral image classification. arXiv 2024, arXiv:2404.08489. [Google Scholar]
- Lee, H.; Kwon, H. Going deeper with contextual CNN for hyperspectral image classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef]
- Xu, Y.; Du, B.; Zhang, L. Self-attention context network: Addressing the threat of adversarial attacks for hyperspectral image classification. IEEE Trans. Image Process. 2021, 30, 8671–8685. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Lu, R.; Zhang, H.; Liu, H.; Varshney, P.K. FusionNet: An unsupervised convolutional variational network for hyperspectral and multispectral image fusion. IEEE Trans. Image Process. 2020, 29, 7565–7577. [Google Scholar] [CrossRef]
- Zhao, C.; Zhu, W.; Feng, S. Superpixel guided deformable convolution network for hyperspectral image classification. IEEE Trans. Image Process. 2022, 31, 3838–3851. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Diba, A.; Tuytelaars, T.; Van Gool, L. Hyperspectral CNN for Image Classification & Band Selection, with Application to Face Recognition; Technical Report KUL/ESAT/PSI/1604; KU Leuven; ESAT: Leuven, Belgium, 2016. [Google Scholar]
- Ahmad, M.; Khan, A.M.; Mazzara, M.; Distefano, S.; Ali, M.; Sarfraz, M.S. A fast and compact 3-D CNN for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Zhao, G.; Wang, X.; Kong, Y.; Cheng, Y. Spectral-spatial joint classification of hyperspectral image based on broad learning system. Remote Sens. 2021, 13, 583. [Google Scholar] [CrossRef]
- Wei, Y.; Zhou, Y. Spatial-aware network for hyperspectral image classification. Remote Sens. 2021, 13, 3232. [Google Scholar] [CrossRef]
- Ranjan, P.; Girdhar, A. Xcep-Dense: A novel lightweight extreme inception model for hyperspectral image classification. Int. J. Remote Sens. 2022, 43, 5204–5230. [Google Scholar] [CrossRef]
- Tu, B.; Liao, X.; Li, Q.; Peng, Y.; Plaza, A. Local semantic feature aggregation-based transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Yang, X.; Cao, W.; Tang, D.; Zhou, Y.; Lu, Y. ACTN: Adaptive Coupling Transformer Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5503115. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, X.; Yang, X.; Peng, J.; Ban, Y. DCTN: Dual-branch convolutional transformer network with efficient interactive self-attention for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Pan, Z.; Li, C.; Plaza, A.; Chanussot, J.; Hong, D. Hyperspectral Image Classification with Mamba. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–14. [Google Scholar] [CrossRef]
- Ahmad, M.; Butt, M.H.F.; Khan, A.M.; Mazzara, M.; Distefano, S.; Usama, M.; Roy, S.K.; Chanussot, J.; Hong, D. Spatial–spectral morphological mamba for hyperspectral image classification. Neurocomputing 2025, 636, 129995. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. Mar. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model. arXiv 2024, arXiv:2401.09417. [Google Scholar]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhou, D.; Kang, B.; Jin, X.; Yang, L.; Lian, X.; Jiang, Z.; Hou, Q.; Feng, J. Deepvit: Towards deeper vision transformer. arXiv 2021, arXiv:2103.11886. [Google Scholar]
- Wu, H.; Xiao, B.; Codella, N.; Liu, M.; Dai, X.; Yuan, L.; Zhang, L. Cvt: Introducing convolutions to vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 22–31. [Google Scholar]
- Yang, X.; Cao, W.; Lu, Y.; Zhou, Y. Hyperspectral image transformer classification networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Huang, X.; Zhou, Y.; Yang, X.; Zhu, X.; Wang, K. Ss-tmnet: Spatial–spectral transformer network with multi-scale convolution for hyperspectral image classification. Remote Sens. 2023, 15, 1206. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, X.; Peng, Z.; Zhang, T.; Jiao, L. S2mamba: A spatial-spectral state space model for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5511413. [Google Scholar] [CrossRef]
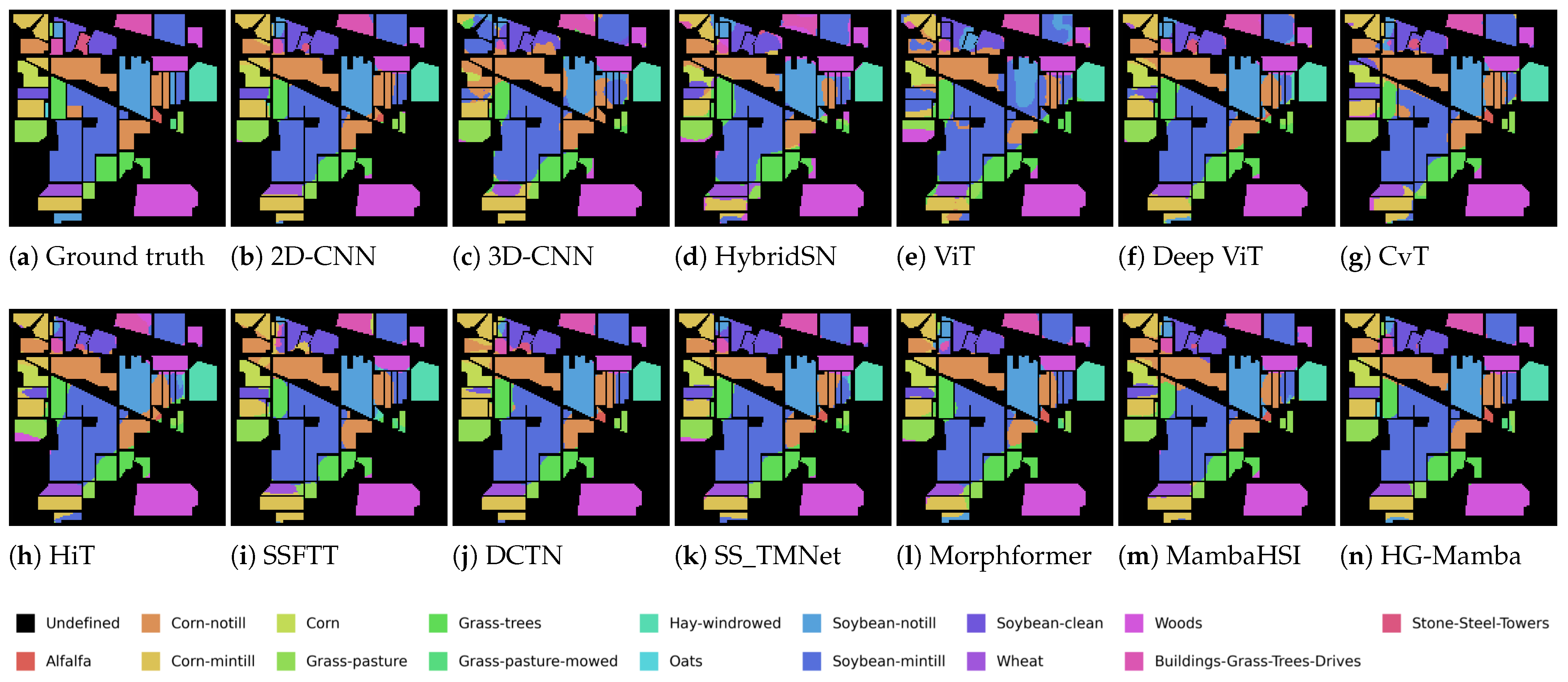

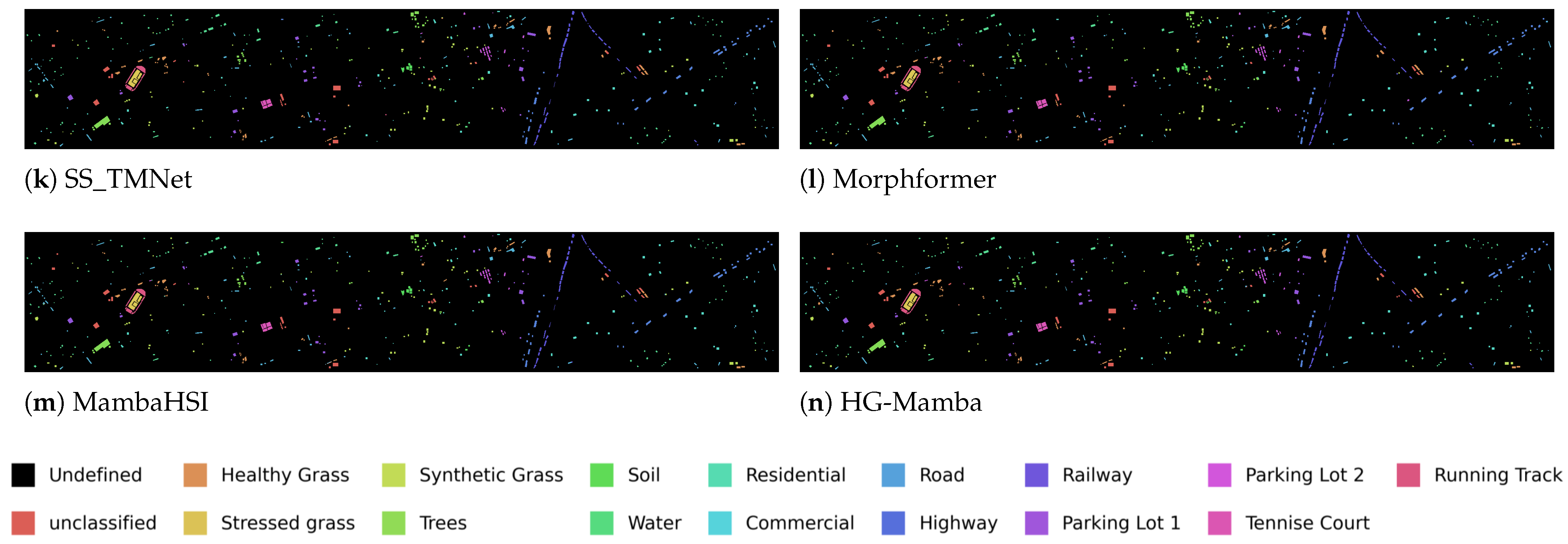
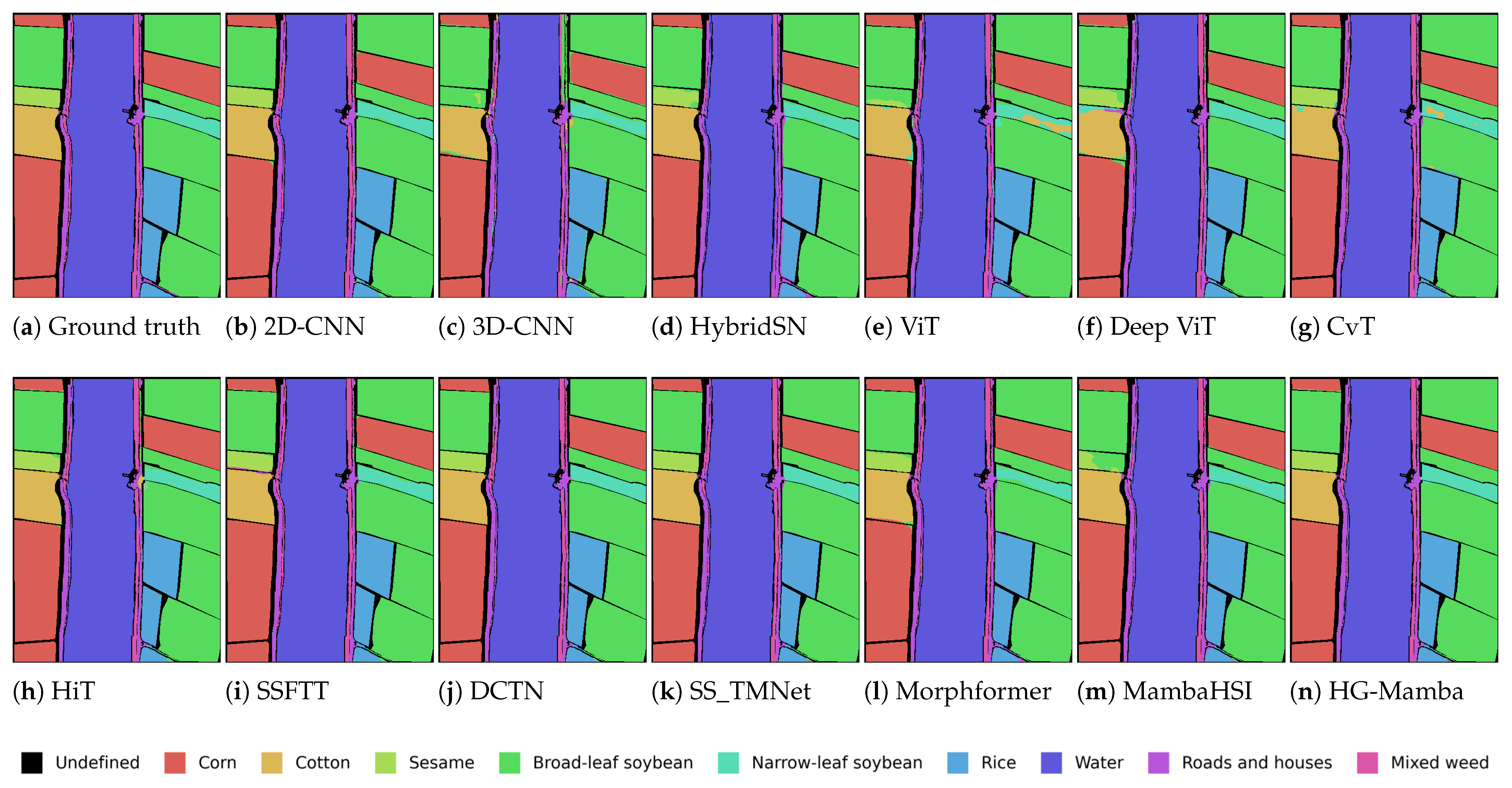

| Class | 2D-CNN | 3D-CNN | Hybridsn | ViT | Deep ViT | CvT | HiT | SSFTT | MorphFormer | SS_TMNet | DCTN | MambaHSI | S2Mamba | HG-Mamba |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alfalfa | 92.82 ± 4.80 | 69.95 ± 17.92 | 18.85 ± 29.79 | 80.76 ± 5.74 | 81.65 ± 10.84 | 48.74 ± 15.97 | 14.63 ± 19.68 | 89.65 ± 6.91 | 82.13 ± 22.40 | 87.48 ± 8.15 | 72.29 ± 11.04 | 54.15 ± 14.91 | 10.73 ± 11.91 | 94.15 ± 4.39 |
| Corn-notill | 93.81 ± 1.97 | 88.61 ± 1.17 | 84.84 ± 11.22 | 94.29 ± 0.77 | 94.14 ± 1.06 | 91.40 ± 2.24 | 90.74 ± 0.89 | 94.11 ± 1.08 | 93.38 ± 2.14 | 88.56 ± 2.34 | 95.70 ± 1.57 | 89.07 ± 2.22 | 84.01 ± 3.29 | 92.61 ± 3.28 |
| Corn-mintill | 92.19 ± 1.77 | 86.74 ± 1.90 | 75.93 ± 18.40 | 93.63 ± 0.58 | 92.86 ± 1.30 | 85.23 ± 4.89 | 86.88 ± 1.90 | 90.13 ± 2.66 | 91.28 ± 3.66 | 76.50 ± 3.23 | 88.93 ± 1.40 | 89.10 ± 6.23 | 90.19 ± 4.64 | 97.32 ± 1.85 |
| Corn | 97.94 ± 1.50 | 93.92 ± 2.44 | 80.93 ± 17.01 | 99.62 ± 0.28 | 99.22 ± 1.22 | 92.32 ± 4.40 | 79.81 ± 11.13 | 94.90 ± 3.46 | 95.26 ± 4.04 | 82.19 ± 3.92 | 92.77 ± 2.77 | 91.60 ± 5.31 | 93.43 ± 6.32 | 97.70 ± 2.94 |
| Grass-pasture | 93.09 ± 3.32 | 93.44 ± 0.70 | 73.56 ± 16.43 | 92.00 ± 1.11 | 89.45 ± 2.91 | 88.40 ± 2.40 | 83.91 ± 9.24 | 93.08 ± 2.52 | 94.72 ± 1.55 | 81.71 ± 3.49 | 92.04 ± 1.28 | 87.38 ± 7.67 | 75.82 ± 20.84 | 95.54 ± 2.30 |
| Grass-trees | 95.65 ± 2.97 | 94.82 ± 0.67 | 75.90 ± 15.75 | 90.79 ± 1.41 | 90.74 ± 2.85 | 93.92 ± 1.02 | 94.06 ± 0.63 | 95.98 ± 1.29 | 95.47 ± 1.38 | 97.76 ± 0.92 | 98.64 ± 0.68 | 93.21 ± 2.30 | 91.54 ± 2.36 | 95.95 ± 5.36 |
| Grass-pasture-mowed | 7.94 ± 18.29 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | 8.08 ± 22.04 | 0.00 ± 0.00 | 54.69 ± 35.84 | 71.56 ± 18.01 | 72.09 ± 16.30 | 73.76 ± 9.76 | 0.00 ± 0.00 | 0.00 ± 0.00 | 83.60 ± 28.65 |
| Hay-windrowed | 99.69 ± 0.55 | 98.87 ± 1.10 | 87.72 ± 13.09 | 99.77 ± 0.22 | 99.79 ± 0.17 | 99.31 ± 0.81 | 100.00 ± 0.00 | 98.77 ± 1.35 | 99.81 ± 0.39 | 94.39 ± 0.47 | 97.75 ± 0.95 | 99.79 ± 0.63 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| Oats | 73.30 ± 29.09 | 0.00 ± 0.00 | 2.45 ± 5.09 | 4.29 ± 10.09 | 25.28 ± 27.21 | 8.49 ± 15.63 | 0.00 ± 0.00 | 54.34 ± 32.04 | 21.28 ± 30.14 | 68.66 ± 17.26 | 76.70 ± 15.73 | 0.00 ± 0.00 | 0.00 ± 0.00 | 90.00 ± 13.56 |
| Soybean-notill | 87.78 ± 1.60 | 83.25 ± 1.22 | 78.05 ± 9.87 | 89.90 ± 0.36 | 88.77 ± 1.22 | 84.38 ± 1.41 | 84.11 ± 0.27 | 87.11 ± 1.77 | 88.80 ± 3.58 | 87.19 ± 1.98 | 93.57 ± 1.21 | 80.54 ± 3.20 | 81.28 ± 2.00 | 82.15 ± 3.53 |
| Soybean-mintill | 96.26 ± 1.24 | 94.38 ± 0.51 | 91.41 ± 4.16 | 96.55 ± 0.12 | 96.65 ± 0.55 | 94.64 ± 0.63 | 97.06 ± 0.06 | 96.78 ± 0.82 | 96.27 ± 0.59 | 90.70 ± 1.63 | 95.46 ± 0.53 | 97.61 ± 1.33 | 97.59 ± 1.22 | 99.03 ± 0.40 |
| Soybean-clean | 91.80 ± 2.21 | 89.11 ± 1.71 | 78.53 ± 12.76 | 92.96 ± 1.34 | 93.57 ± 1.30 | 86.16 ± 5.24 | 91.20 ± 0.42 | 89.52 ± 3.35 | 87.66 ± 5.08 | 81.85 ± 3.97 | 94.68 ± 1.39 | 93.03 ± 4.38 | 94.51 ± 2.01 | 94.91 ± 1.81 |
| Wheat | 98.12 ± 1.32 | 86.71 ± 7.81 | 54.68 ± 33.43 | 96.73 ± 1.43 | 97.08 ± 1.64 | 89.64 ± 4.40 | 100.00 ± 0.00 | 95.00 ± 3.62 | 94.35 ± 4.88 | 97.18 ± 3.02 | 99.89 ± 0.18 | 94.38 ± 7.55 | 86.11 ± 6.01 | 92.38 ± 6.74 |
| Woods | 98.28 ± 2.42 | 97.81 ± 0.58 | 94.10 ± 5.22 | 98.27 ± 0.38 | 97.75 ± 0.75 | 98.39 ± 0.52 | 99.56 ± 0.17 | 98.67 ± 0.66 | 98.87 ± 0.31 | 96.21 ± 0.89 | 98.49 ± 0.40 | 99.58 ± 0.44 | 99.52 ± 0.25 | 98.88 ± 1.28 |
| Buildings-Grass-Trees-Drives | 97.82 ± 1.46 | 93.48 ± 2.25 | 73.19 ± 17.09 | 98.00 ± 0.60 | 98.25 ± 1.12 | 91.41 ± 3.60 | 86.17 ± 1.47 | 96.08 ± 2.76 | 96.06 ± 1.48 | 63.92 ± 3.78 | 77.76 ± 1.60 | 86.48 ± 9.27 | 87.67 ± 5.33 | 95.19 ± 2.69 |
| Stone-Steel-Towers | 52.74 ± 21.39 | 46.87 ± 17.62 | 41.04 ± 32.91 | 53.30 ± 17.49 | 63.78 ± 21.77 | 67.35 ± 23.50 | 8.33 ± 22.82 | 39.20 ± 32.30 | 25.11 ± 33.47 | 87.73 ± 3.15 | 96.80 ± 1.98 | 29.05 ± 25.48 | 0.00 ± 0.00 | 43.93 ± 23.09 |
| OA (%) | 94.48 ± 1.41 | 91.48 ± 0.52 | 83.10 ± 10.19 | 94.50 ± 0.30 | 94.28 ± 0.43 | 91.41 ± 0.93 | 91.02 ± 0.95 | 94.09 ± 0.97 | 94.03 ± 0.90 | 84.67 ± 1.25 | 92.85 ± 0.41 | 91.50 ± 0.67 | 89.84 ± 1.26 | 94.91 ± 0.51 |
| AA (%) | 83.81 ± 3.38 | 73.92 ± 2.12 | 62.87 ± 12.02 | 78.40 ± 1.18 | 79.90 ± 2.11 | 77.31 ± 2.41 | 69.78 ± 4.52 | 84.54 ± 3.91 | 82.75 ± 2.85 | 85.56 ± 4.91 | 86.55 ± 3.55 | 74.06 ± 1.50 | 68.27 ± 1.83 | 90.83 ± 2.84 |
| (%) | 93.69 ± 1.61 | 90.25 ± 0.59 | 80.70 ± 11.52 | 93.71 ± 0.35 | 93.46 ± 0.49 | 90.20 ± 1.06 | 89.72 ± 1.07 | 93.25 ± 1.10 | 93.18 ± 1.03 | 82.66 ± 1.41 | 91.87 ± 0.47 | 90.28 ± 0.77 | 88.36 ± 1.45 | 94.18 ± 0.59 |
| Class | 2D-CNN | 3D-CNN | HybridSN | ViT | Deep ViT | CvT | HiT | SSFTT | Morphformer | SS_TMNet | DCTN | MambaHSI | S2Mamba | HG-Mamba |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Healthy Grass | 95.21 ± 1.66 | 91.06 ± 3.44 | 90.76 ± 1.88 | 87.43 ± 3.25 | 91.33 ± 2.17 | 87.30 ± 10.73 | 94.49 ± 0.52 | 96.42 ± 1.16 | 85.97 ± 8.75 | 97.60 ± 0.64 | 98.86 ± 0.50 | 94.08 ± 2.29 | 93.14 ± 1.48 | 96.47 ± 0.85 |
| Stressed grass | 95.51 ± 1.72 | 88.85 ± 6.46 | 86.26 ± 8.27 | 80.16 ± 5.76 | 83.59 ± 2.71 | 90.21 ± 4.40 | 91.22 ± 2.10 | 97.16 ± 1.42 | 88.97 ± 5.58 | 98.44 ± 0.56 | 99.33 ± 0.22 | 97.40 ± 1.29 | 97.50 ± 0.94 | 97.96 ± 1.47 |
| Synthetic GrassTrees | 99.24 ± 0.45 | 97.36 ± 3.06 | 95.85 ± 3.67 | 97.95 ± 0.85 | 98.64 ± 0.56 | 97.70 ± 2.80 | 98.97 ± 0.29 | 99.30 ± 0.58 | 91.37 ± 13.84 | 99.50 ± 0.23 | 99.74 ± 0.29 | 94.95 ± 2.05 | 95.27 ± 2.07 | 98.24 ± 1.13 |
| Trees | 94.72 ± 2.18 | 88.28 ± 4.52 | 79.71 ± 7.46 | 81.31 ± 6.65 | 83.87 ± 4.62 | 89.45 ± 3.27 | 89.26 ± 1.20 | 97.68 ± 0.90 | 90.96 ± 4.95 | 97.26 ± 0.96 | 99.21 ± 0.41 | 97.17 ± 0.87 | 92.68 ± 3.47 | 99.10 ± 0.87 |
| Soil | 99.81 ± 0.17 | 95.72 ± 3.71 | 96.41 ± 3.83 | 97.80 ± 1.25 | 98.62 ± 1.51 | 99.17 ± 0.67 | 99.53 ± 0.24 | 99.43 ± 0.63 | 97.96 ± 2.17 | 98.19 ± 0.33 | 98.65 ± 0.12 | 99.50 ± 0.56 | 99.87 ± 0.13 | 99.86 ± 0.43 |
| Water | 94.05 ± 0.97 | 86.16 ± 1.92 | 91.69 ± 3.12 | 86.50 ± 1.79 | 87.48 ± 2.36 | 93.58 ± 2.23 | 86.87 ± 0.82 | 93.61 ± 3.07 | 90.85 ± 4.25 | 93.67 ± 2.33 | 98.75 ± 1.07 | 84.38 ± 4.04 | 80.75 ± 4.77 | 89.04 ± 5.59 |
| Residential | 96.82 ± 1.02 | 83.00 ± 6.98 | 78.74 ± 17.12 | 87.38 ± 1.99 | 87.28 ± 2.68 | 92.51 ± 3.82 | 91.87 ± 0.83 | 97.52 ± 0.80 | 85.78 ± 24.73 | 94.54 ± 1.03 | 98.20 ± 0.45 | 97.00 ± 1.69 | 88.33 ± 5.12 | 98.35 ± 0.76 |
| Commercial | 97.62 ± 1.51 | 89.55 ± 1.61 | 93.01 ± 2.65 | 90.55 ± 3.34 | 94.05 ± 1.95 | 94.16 ± 3.55 | 96.41 ± 0.64 | 97.88 ± 1.24 | 90.76 ± 9.56 | 95.74 ± 1.35 | 98.22 ± 0.69 | 93.78 ± 1.64 | 95.32 ± 1.98 | 97.69 ± 1.29 |
| Road | 95.42 ± 1.51 | 85.03 ± 3.38 | 73.95 ± 14.36 | 86.62 ± 1.57 | 87.98 ± 1.78 | 87.78 ± 2.93 | 89.78 ± 0.99 | 96.70 ± 1.56 | 87.54 ± 7.99 | 94.29 ± 1.32 | 97.66 ± 0.56 | 92.94 ± 1.74 | 88.00 ± 3.06 | 98.97 ± 0.81 |
| Highway | 99.09 ± 1.57 | 91.67 ± 6.54 | 91.92 ± 7.92 | 96.43 ± 3.22 | 95.01 ± 3.44 | 97.50 ± 1.56 | 97.93 ± 0.51 | 99.78 ± 0.38 | 93.89 ± 9.76 | 96.91 ± 0.81 | 98.89 ± 0.49 | 99.27 ± 1.03 | 99.97 ± 0.08 | 99.98 ± 0.05 |
| Railway | 99.58 ± 0.46 | 81.57 ± 5.87 | 85.29 ± 7.92 | 93.86 ± 2.51 | 93.32 ± 4.12 | 94.73 ± 3.22 | 99.37 ± 0.45 | 99.76 ± 0.44 | 91.69 ± 16.26 | 94.94 ± 0.72 | 98.51 ± 0.33 | 98.79 ± 1.16 | 97.41 ± 1.50 | 99.39 ± 1.05 |
| Parking Lot 1 | 97.88 ± 1.83 | 94.30 ± 1.81 | 95.79 ± 2.71 | 91.42 ± 4.91 | 93.49 ± 3.96 | 95.83 ± 3.47 | 98.68 ± 0.21 | 98.70 ± 1.24 | 88.63 ± 13.89 | 96.50 ± 1.00 | 98.96 ± 0.22 | 95.81 ± 1.75 | 97.49 ± 0.92 | 97.32 ± 1.59 |
| Parking Lot 2 | 97.55 ± 2.44 | 81.89 ± 6.24 | 86.51 ± 8.08 | 91.84 ± 1.55 | 89.01 ± 4.03 | 95.80 ± 2.87 | 95.93 ± 1.53 | 98.54 ± 1.23 | 92.25 ± 6.66 | 93.42 ± 1.61 | 97.68 ± 1.01 | 95.85 ± 2.44 | 96.23 ± 2.16 | 98.86 ± 1.41 |
| Tennise Court | 99.98 ± 0.07 | 98.60 ± 0.97 | 92.98 ± 6.16 | 99.20 ± 0.85 | 98.43 ± 2.66 | 97.96 ± 3.28 | 99.99 ± 0.04 | 99.67 ± 0.47 | 99.04 ± 1.46 | 99.88 ± 0.19 | 100.00 ± 0.00 | 99.97 ± 0.08 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| Running Track | 97.87 ± 1.71 | 94.77 ± 5.41 | 91.48 ± 5.60 | 96.93 ± 1.89 | 98.14 ± 0.72 | 96.65 ± 3.12 | 98.39 ± 0.33 | 98.95 ± 0.71 | 93.32 ± 7.49 | 98.98 ± 0.58 | 99.24 ± 0.88 | 99.21 ± 1.04 | 100.00 ± 0.00 | 99.83 ± 0.40 |
| OA (%) | 97.32 ± 0.48 | 89.54 ± 3.21 | 88.19 ± 4.75 | 90.27 ± 1.69 | 91.58 ± 1.50 | 93.52 ± 1.88 | 95.20 ± 0.33 | 98.15 ± 0.53 | 90.98 ± 7.71 | 96.22 ± 0.35 | 98.31 ± 0.16 | 96.33 ± 0.38 | 94.98 ± 0.55 | 98.41 ± 0.26 |
| AA (%) | 97.03 ± 0.37 | 89.74 ± 2.87 | 88.97 ± 4.09 | 90.45 ± 1.42 | 91.38 ± 1.43 | 93.74 ± 1.95 | 94.80 ± 0.32 | 97.81 ± 0.59 | 90.99 ± 7.46 | 95.15 ± 0.45 | 97.32 ± 0.36 | 96.01 ± 0.44 | 94.80 ± 0.59 | 98.07 ± 0.34 |
| (%) | 97.10 ± 0.51 | 88.70 ± 3.47 | 87.24 ± 5.13 | 89.48 ± 1.83 | 90.89 ± 1.62 | 92.99 ± 2.04 | 94.81 ± 0.35 | 98.00 ± 0.58 | 90.24 ± 8.36 | 95.92 ± 0.38 | 98.17 ± 0.17 | 96.03 ± 0.41 | 94.57 ± 0.60 | 98.28 ± 0.28 |
| Class | 2D-CNN | 3D-CNN | HybridSN | ViT | Deep ViT | CvT | HiT | SSFTT | Morphformer | SS_TMNet | DCTN | MambaHSI | S2Mamba | HG-Mamba |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corn | 99.87 ± 0.03 | 99.34 ± 0.40 | 99.34 ± 0.58 | 99.33 ± 0.13 | 99.66 ± 0.08 | 99.83 ± 0.07 | 99.77 ± 0.04 | 99.71 ± 0.23 | 99.70 ± 0.28 | 99.86 ± 0.11 | 99.99 ± 0.01 | 99.43 ± 0.25 | 99.73 ± 0.19 | 99.87 ± 0.12 |
| Cotton | 99.72 ± 0.09 | 96.30 ± 1.24 | 97.55 ± 3.18 | 83.45 ± 0.89 | 96.41 ± 1.60 | 99.39 ± 0.23 | 97.74 ± 0.69 | 99.69 ± 0.25 | 98.18 ± 1.74 | 98.55 ± 1.50 | 99.98 ± 0.01 | 98.12 ± 1.90 | 99.56 ± 0.39 | 98.86 ± 0.91 |
| Sesame | 94.97 ± 1.27 | 55.88 ± 29.79 | 81.52 ± 14.54 | 51.31 ± 21.70 | 88.79 ± 4.29 | 97.91 ± 0.71 | 91.44 ± 1.50 | 92.35 ± 5.03 | 94.05 ± 5.56 | 95.42 ± 4.00 | 98.80 ± 0.68 | 69.48 ± 24.88 | 97.66 ± 1.66 | 98.90 ± 1.34 |
| Broad-leaf soybean | 99.12 ± 0.08 | 96.24 ± 0.89 | 98.22 ± 0.64 | 96.51 ± 0.67 | 98.52 ± 0.22 | 99.49 ± 0.09 | 98.71 ± 0.21 | 99.69 ± 0.16 | 99.51 ± 0.41 | 99.79 ± 0.10 | 99.95 ± 0.02 | 99.73 ± 0.09 | 99.89 ± 0.09 | 99.86 ± 0.09 |
| Narrow-leaf soybean | 95.42 ± 0.71 | 87.80 ± 2.44 | 81.06 ± 10.19 | 42.38 ± 7.08 | 89.80 ± 2.31 | 97.10 ± 1.00 | 95.35 ± 1.41 | 91.00 ± 4.09 | 88.15 ± 8.32 | 91.07 ± 4.08 | 94.13 ± 1.47 | 89.56 ± 3.82 | 94.16 ± 1.46 | 96.56 ± 1.61 |
| Rice | 98.57 ± 0.19 | 98.11 ± 0.66 | 97.28 ± 0.91 | 98.54 ± 0.40 | 98.87 ± 0.16 | 98.80 ± 0.11 | 99.26 ± 0.05 | 99.06 ± 0.66 | 98.77 ± 1.59 | 99.23 ± 0.25 | 99.18 ± 0.18 | 98.13 ± 0.52 | 99.24 ± 0.31 | 99.09 ± 0.42 |
| Water | 99.74 ± 0.04 | 99.51 ± 0.22 | 97.11 ± 0.53 | 99.28 ± 0.11 | 99.39 ± 0.18 | 99.70 ± 0.12 | 99.45 ± 0.04 | 99.95 ± 0.05 | 99.97 ± 0.01 | 99.98 ± 0.01 | 100.00 ± 0.00 | 99.99 ± 0.01 | 99.99 ± 0.00 | 99.81 ± 0.38 |
| Roads and houses | 85.56 ± 0.78 | 82.84 ± 2.22 | 78.60 ± 7.09 | 80.96 ± 2.04 | 83.05 ± 1.42 | 84.75 ± 0.96 | 87.96 ± 0.74 | 85.45 ± 5.91 | 89.66 ± 4.22 | 88.66 ± 3.04 | 80.26 ± 4.53 | 89.38 ± 3.52 | 85.76 ± 5.08 | 80.02 ± 6.18 |
| Mixed weed | 78.58 ± 2.04 | 79.05 ± 2.99 | 37.10 ± 12.86 | 77.37 ± 2.01 | 74.30 ± 2.89 | 79.17 ± 2.84 | 80.65 ± 1.01 | 84.71 ± 9.52 | 77.91 ± 7.96 | 78.67 ± 8.08 | 77.96 ± 4.87 | 74.92 ± 5.50 | 76.94 ± 3.02 | 87.52 ± 6.65 |
| OA (%) | 98.35 ± 0.09 | 96.60 ± 0.63 | 95.77 ± 0.80 | 95.28 ± 0.48 | 97.55 ± 0.17 | 98.50 ± 0.12 | 98.18 ± 0.11 | 98.58 ± 0.37 | 98.39 ± 0.38 | 98.61 ± 0.26 | 98.54 ± 0.14 | 97.96 ± 0.44 | 98.61 ± 0.15 | 98.67 ± 0.29 |
| AA (%) | 93.24 ± 0.46 | 84.58 ± 3.95 | 82.29 ± 3.59 | 77.94 ± 3.08 | 90.01 ± 1.04 | 94.34 ± 0.58 | 92.43 ± 0.53 | 94.62 ± 1.24 | 93.99 ± 1.76 | 94.58 ± 1.04 | 94.47 ± 0.57 | 90.97 ± 3.22 | 94.77 ± 0.51 | 95.61 ± 0.99 |
| (%) | 97.82 ± 0.13 | 95.49 ± 0.85 | 94.38 ± 1.07 | 93.74 ± 0.65 | 96.76 ± 0.23 | 98.03 ± 0.16 | 97.60 ± 0.15 | 98.13 ± 0.49 | 97.88 ± 0.50 | 98.17 ± 0.35 | 98.08 ± 0.18 | 97.30 ± 0.59 | 98.17 ± 0.19 | 98.25 ± 0.38 |
| Method | FLOPs (G) | Param (MB) | Training Time (s) | Testing Time (s) | OA (%) | AA (%) | (%) |
|---|---|---|---|---|---|---|---|
| 2D-CNN | 0.77 | 1.71 | 30.13 | 1.28 | 94.48 ± 1.41 | 93.81 ± 3.38 | 93.69 ± 1.61 |
| 3D-CNN | 1.35 | 1.45 | 81.48 | 2.56 | 91.48 ± 0.52 | 73.92 ± 2.12 | 90.25 ± 0.50 |
| Deep ViT | 13.69 | 52.75 | 142.50 | 3.69 | 94.28 ± 0.43 | 79.90 ± 2.11 | 93.46 ± 0.49 |
| HiT | 2.20 | 27.22 | 534.29 | 8.06 | 91.02 ± 0.95 | 69.78 ± 4.52 | 89.72 ± 1.07 |
| MambaHSI | 0.006 | 0.02 | 174.55 | 6.98 | 91.50 ± 0.67 | 74.06 ± 1.50 | 90.28 ± 0.77 |
| HG-Mamba | 0.57 | 1.30 | 248.20 | 8.88 | 94.91 ± 0.51 | 90.83 ± 2.84 | 94.18 ± 0.59 |
| Module Removed | OA (%) | AA (%) | (%) | |||
|---|---|---|---|---|---|---|
| Val ± Std | Val ± Std | Val ± Std | ||||
| Stage 1 | 93.92 ± 0.48 | (0.99↓) | 85.87 ± 3.42 | (4.96↓) | 93.05 ± 0.55 | (1.13↓) |
| Stage 2 | 92.98 ± 0.54 | (1.93↓) | 81.46 ± 2.83 | (9.37↓) | 91.98 ± 0.63 | (2.20↓) |
| Spectral Bidirectional Mamba | 94.53 ± 0.43 | (0.38↓) | 87.25 ± 2.38 | (3.58↓) | 93.75 ± 0.49 | (0.43↓) |
| Spatial Bidirectional Mamba | 94.84 ± 0.61 | (0.07↓) | 87.89 ± 2.85 | (2.94↓) | 94.10 ± 0.69 | (0.08↓) |
| Only Unidirectional Mamba | 94.19 ± 0.80 | (0.72↓) | 86.46 ± 2.68 | (4.37↓) | 93.36 ± 0.91 | (0.82↓) |
| Spectral Compression | 94.01 ± 0.47 | (0.90↓) | 86.18 ± 3.98 | (4.65↓) | 93.16 ± 0.54 | (1.02↓) |
| GDD | 94.45 ± 0.73 | (0.46↓) | 88.90 ± 2.48 | (1.93↓) | 93.66 ± 0.84 | (0.52↓) |
| Full Model (None Removed) | 94.91 ± 0.51 | – | 90.83 ± 2.84 | – | 94.18 ± 0.59 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Yang, J.; Li, L.; Xue, S.; Shi, H.; Tang, H.; Huang, X. HG-Mamba: A Hybrid Geometry-Aware Bidirectional Mamba Network for Hyperspectral Image Classification. Remote Sens. 2025, 17, 2234. https://doi.org/10.3390/rs17132234
Yang X, Yang J, Li L, Xue S, Shi H, Tang H, Huang X. HG-Mamba: A Hybrid Geometry-Aware Bidirectional Mamba Network for Hyperspectral Image Classification. Remote Sensing. 2025; 17(13):2234. https://doi.org/10.3390/rs17132234
Chicago/Turabian StyleYang, Xiaofei, Jiafeng Yang, Lin Li, Suihua Xue, Haotian Shi, Haojin Tang, and Xiaohui Huang. 2025. "HG-Mamba: A Hybrid Geometry-Aware Bidirectional Mamba Network for Hyperspectral Image Classification" Remote Sensing 17, no. 13: 2234. https://doi.org/10.3390/rs17132234
APA StyleYang, X., Yang, J., Li, L., Xue, S., Shi, H., Tang, H., & Huang, X. (2025). HG-Mamba: A Hybrid Geometry-Aware Bidirectional Mamba Network for Hyperspectral Image Classification. Remote Sensing, 17(13), 2234. https://doi.org/10.3390/rs17132234







