Quantifying the Added Values of a Merged Precipitation Product in Streamflow Prediction over the Central Himalayas
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Gridded Precipitation Datasets (GPDs)
2.2.2. Gauge Observation
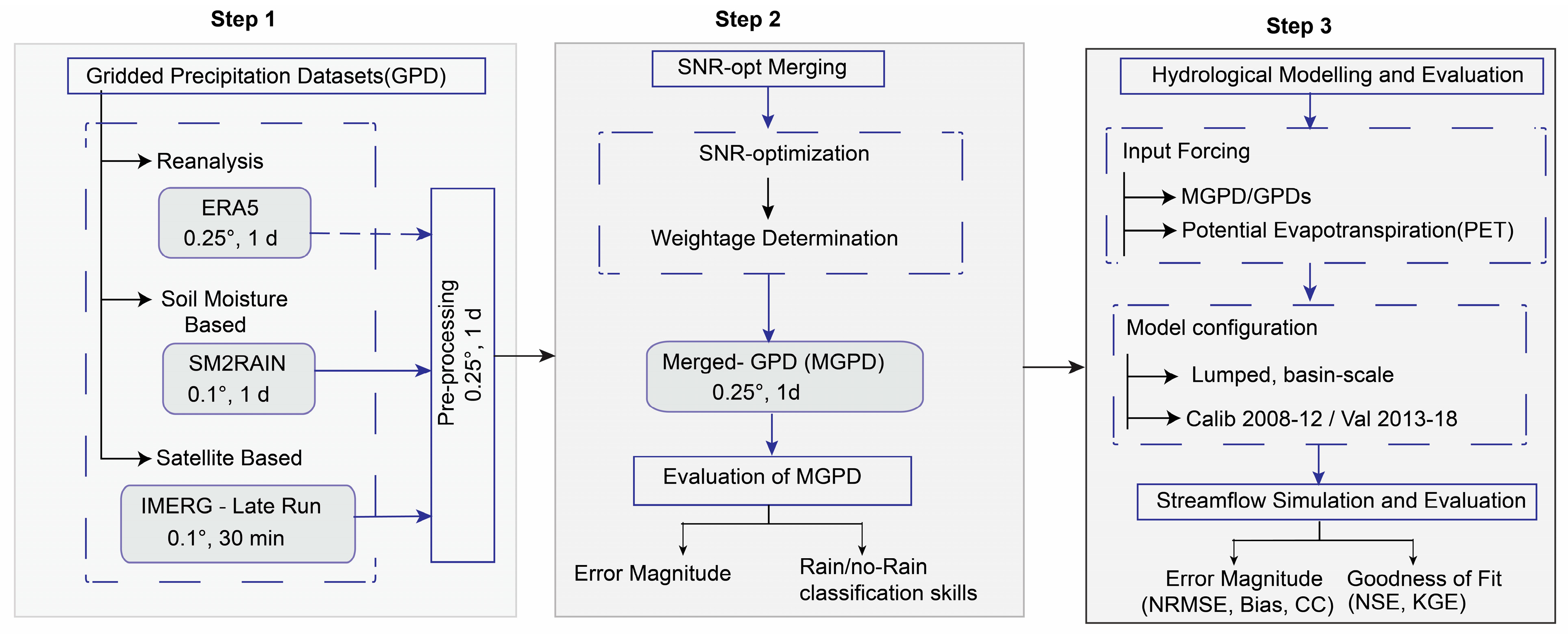
2.3. Methodological Framework
2.3.1. Merging Method
SNR Optimization (SNR-Opt)
SNR Estimation
2.3.2. Hydrological Model
2.4. Parameters for Assessment of Merged Product
2.4.1. Error Magnitude
2.4.2. Rainfall Classification
2.4.3. Streamflow Simulation
3. Results
3.1. Evaluation of the Merged Precipitation Product
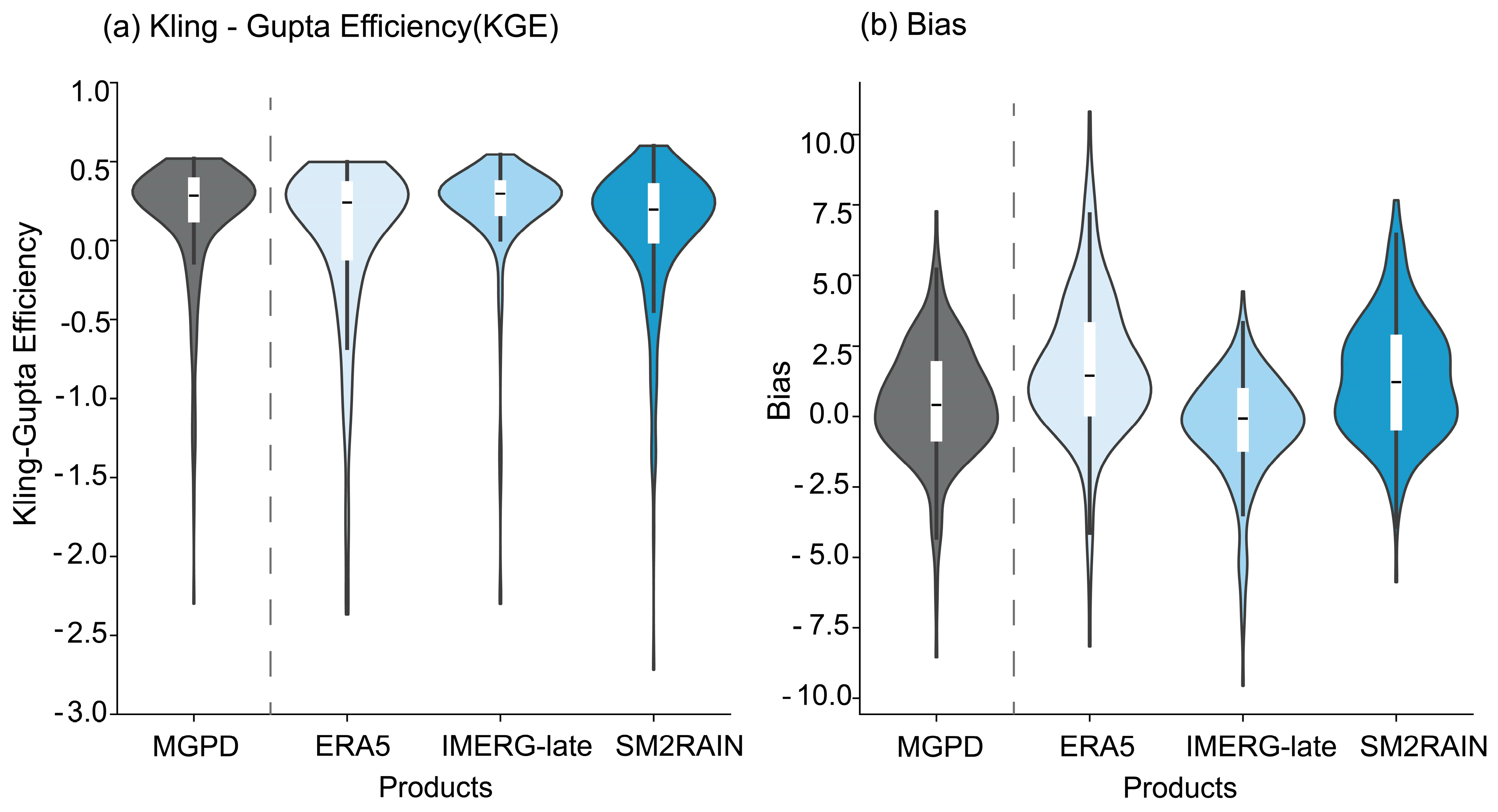
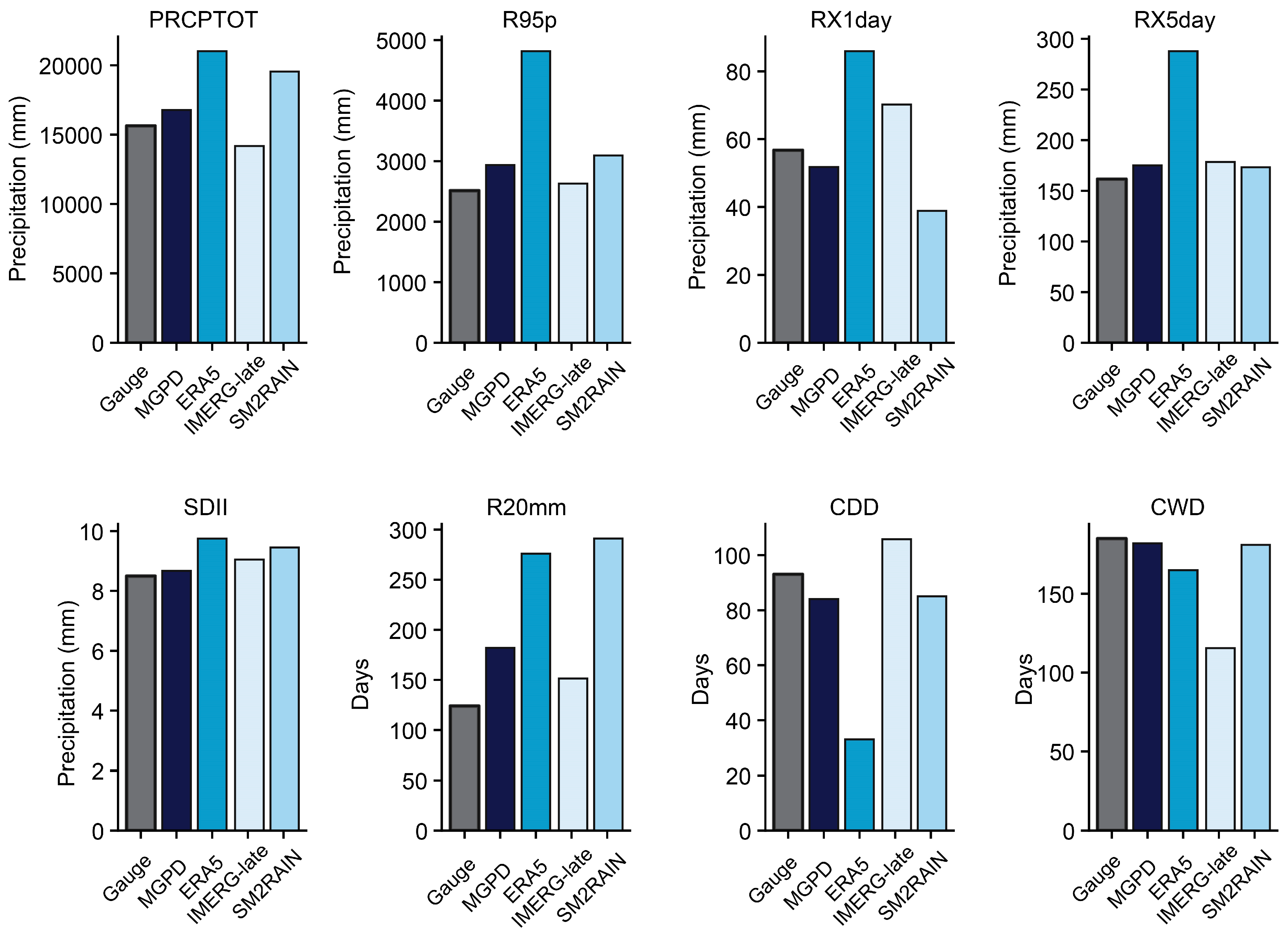
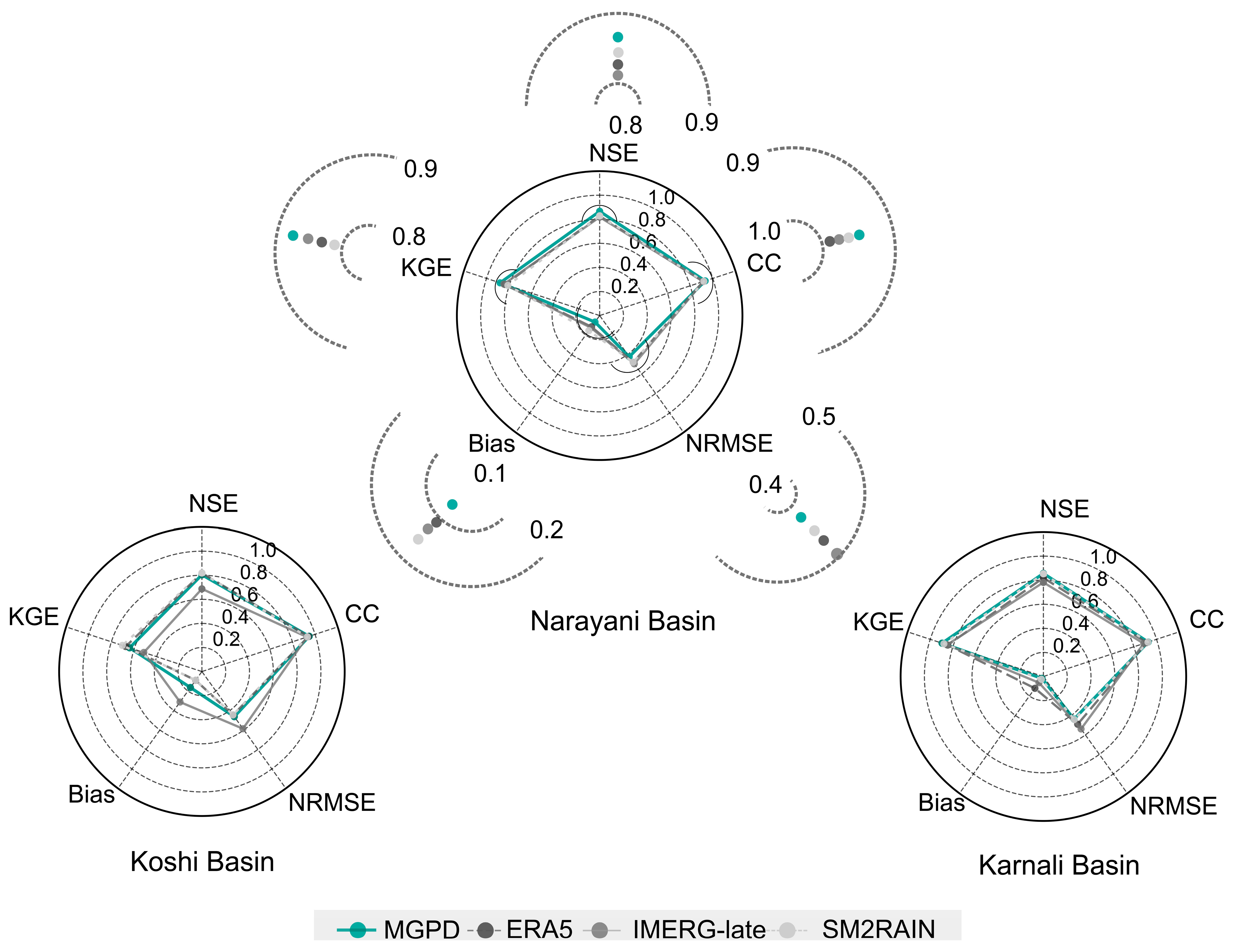
3.1.1. Error Magnitude Assessment
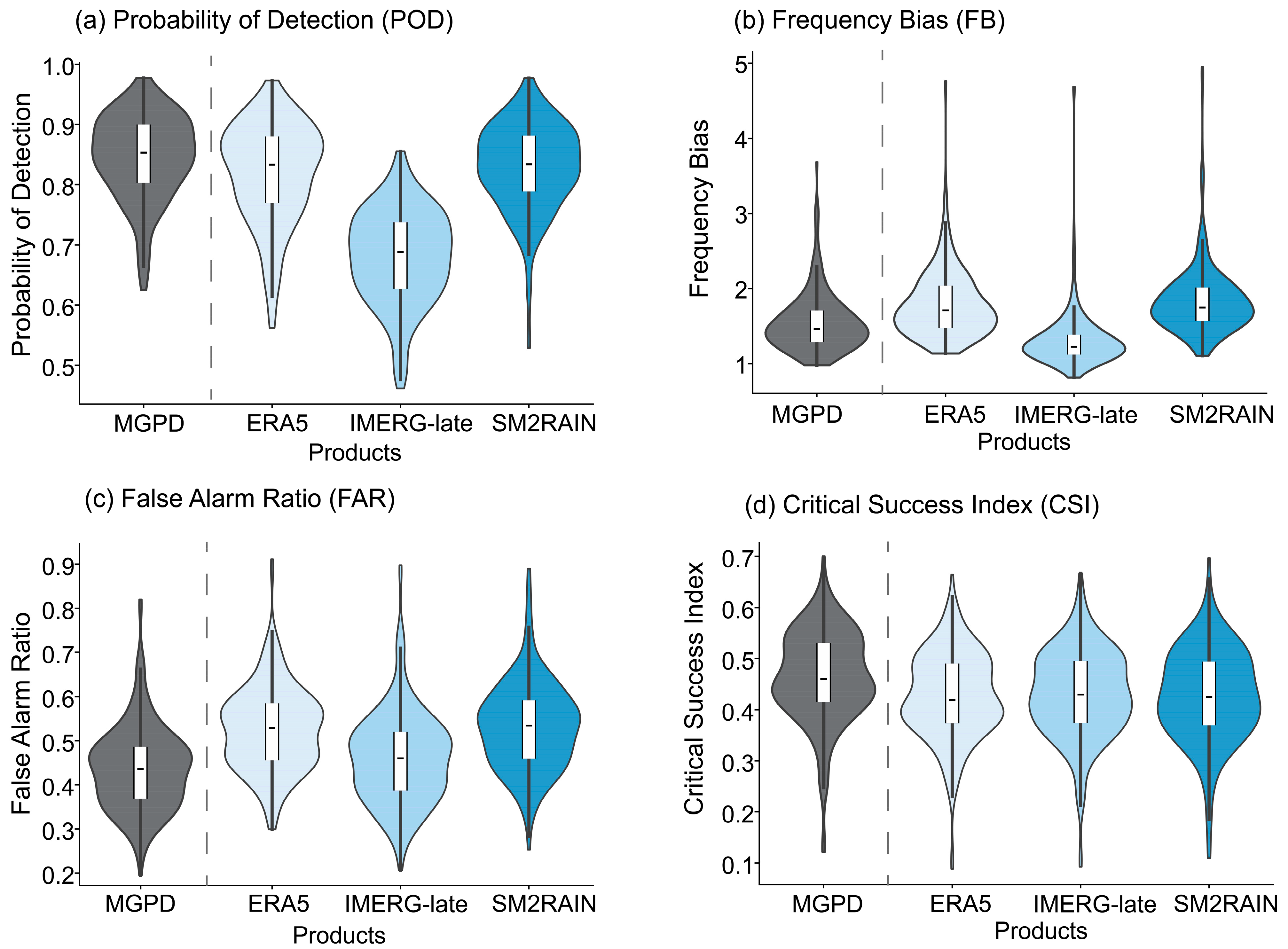
3.1.2. Rainfall Classification Performance
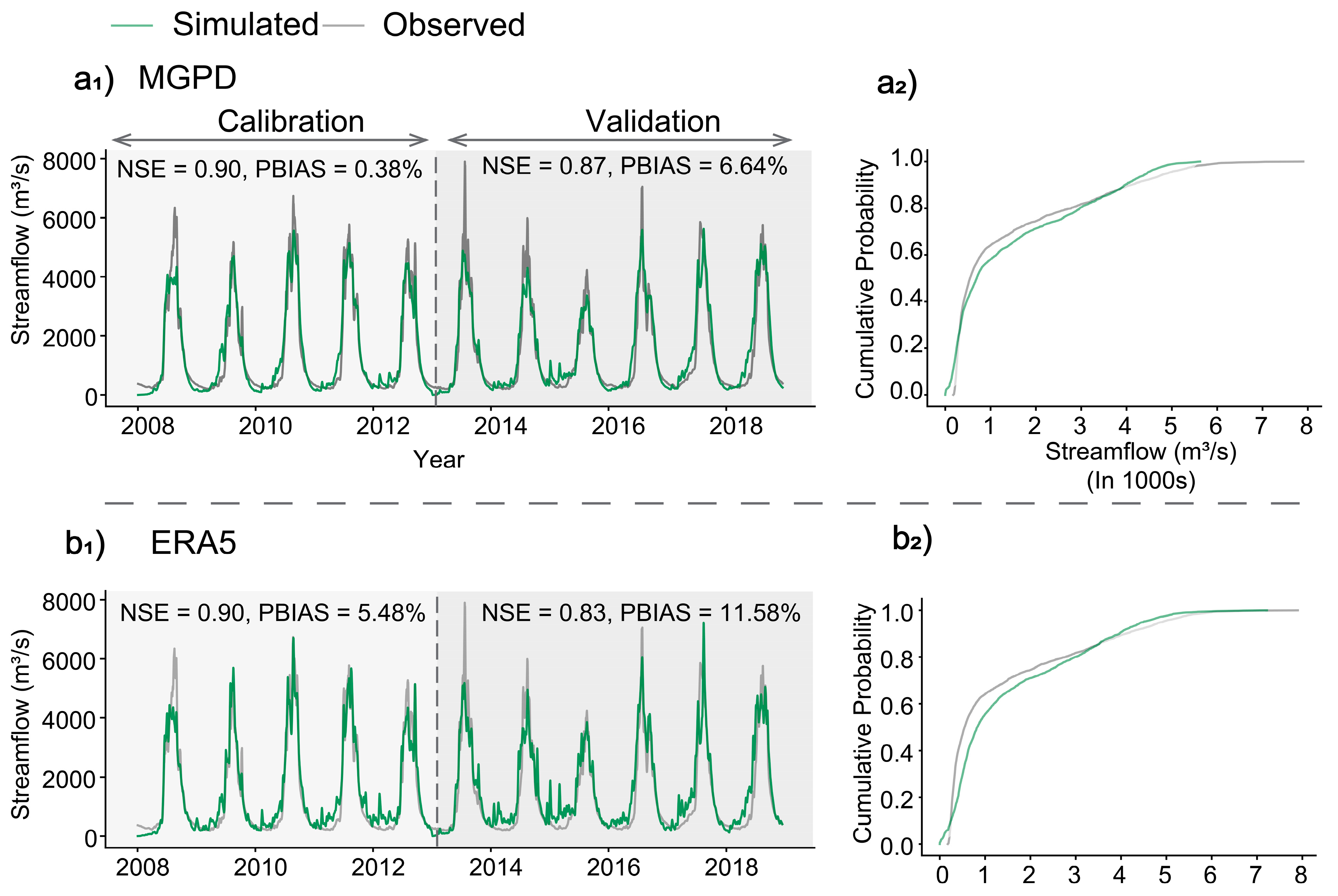
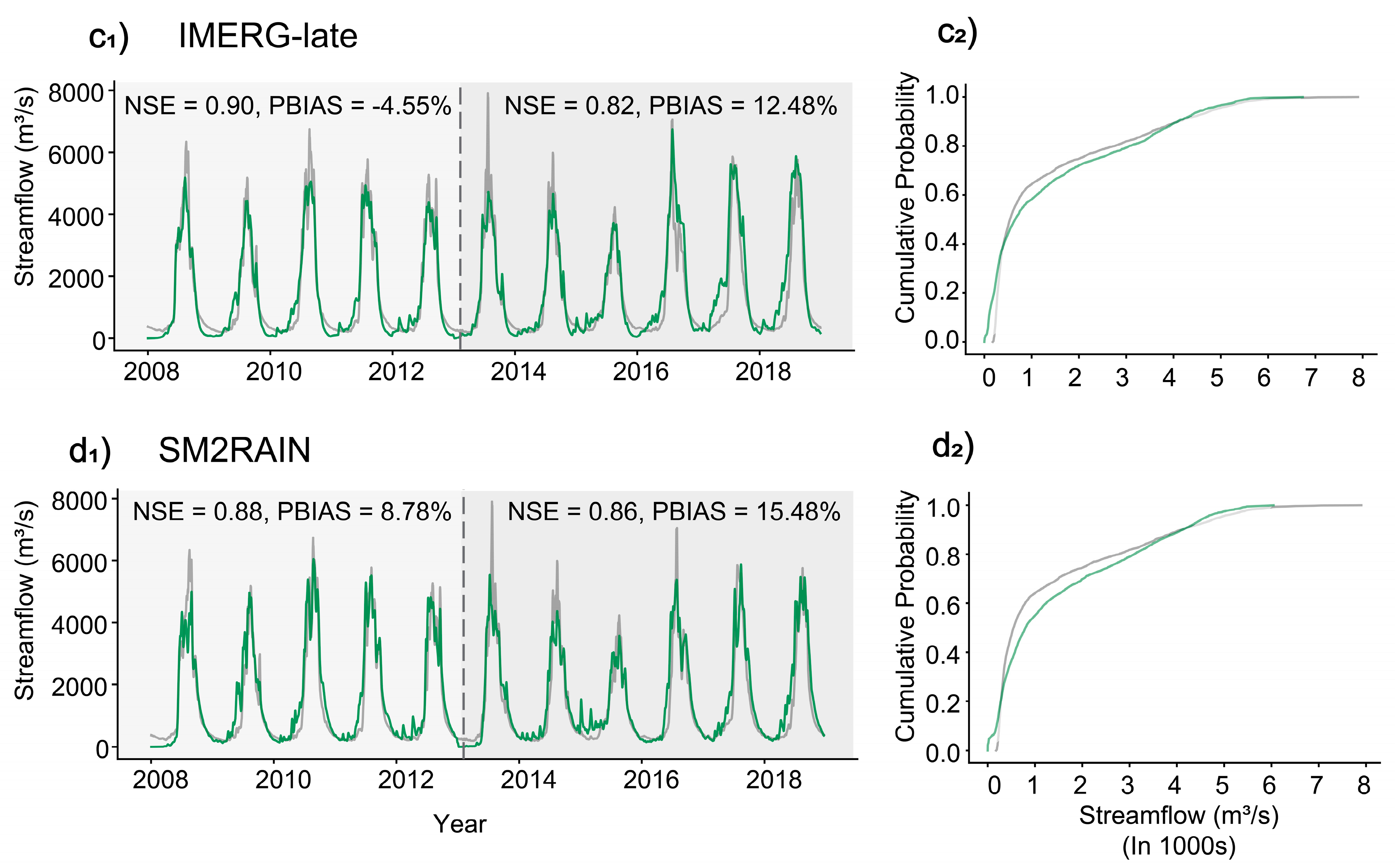
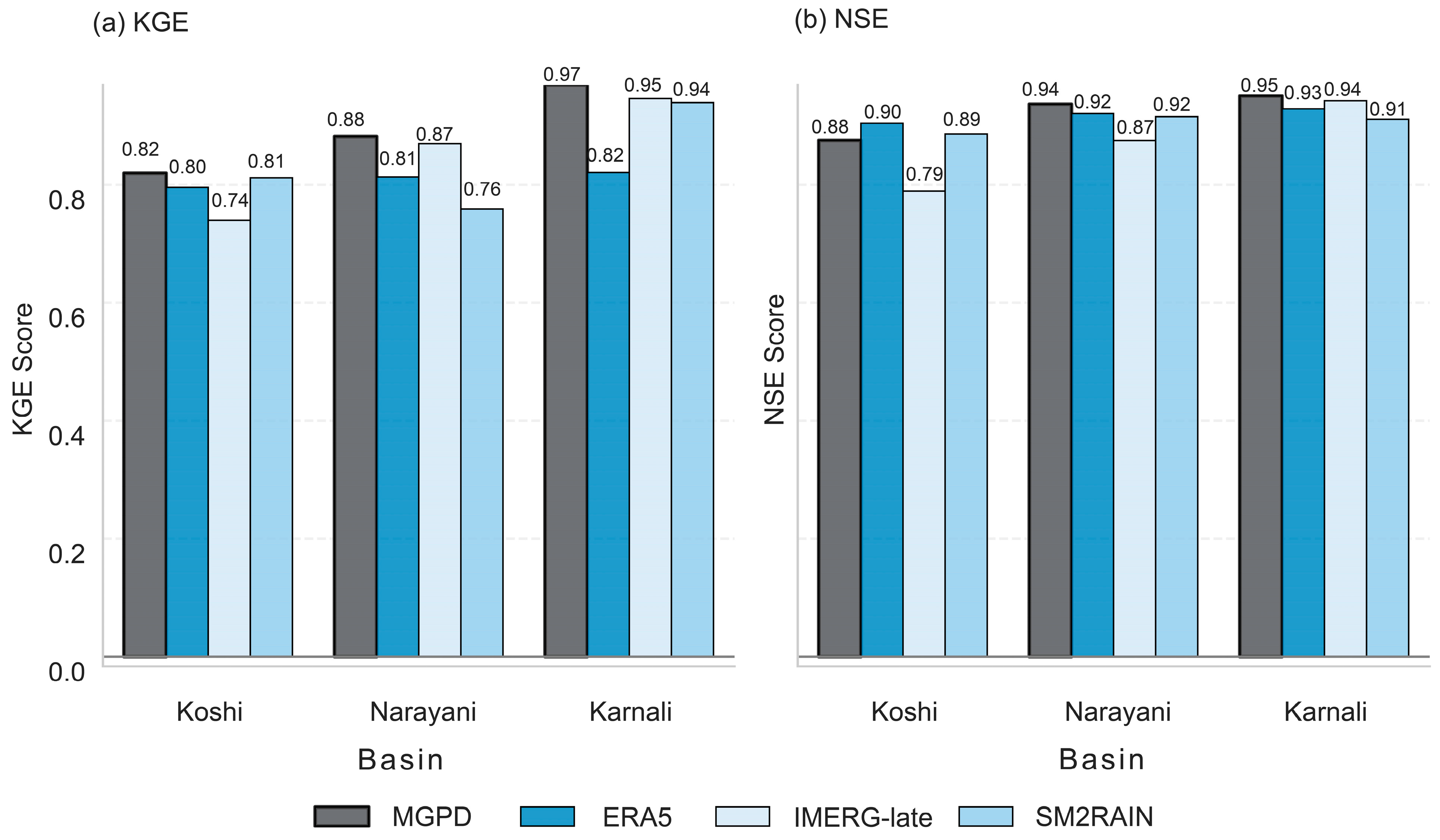
3.1.3. Streamflow Simulation Results
4. Discussion
4.1. Performance of the Merged Precipitation Product
4.1.1. Analysis of Error Magnitude and Rainfall Classification
4.1.2. Analysis of Streamflow Simulation
4.2. Limitations and Future Directions
5. Conclusions
- (i)
- MGPD outperformed individual GPDs in terms of both magnitude errors and rainfall classification, effectively integrating diverse sources to reduce bias and random errors;
- (ii)
- Streamflow simulations using MGPD further demonstrated its superiority, benefitting from error compensation and bias minimization, leading to improved hydrological performance.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J. Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement: Volume 1; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 343–353. [Google Scholar] [CrossRef]
- Ghomlaghi, A.; Nasseri, M.; Bayat, B. Comparing and Contrasting the Performance of High-Resolution Precipitation Products via Error Decomposition and Triple Collocation: An Application to Different Climate Classes of the Central Iran. J. Hydrol. 2022, 612, 128298. [Google Scholar] [CrossRef]
- Miri, M.; Masoudi, R.; Raziei, T. Performance Evaluation of Three Satellites-Based Precipitation Data Sets Over Iran. J. Indian Soc. Remote Sens. 2019, 47, 2073–2084. [Google Scholar] [CrossRef]
- Tudaji, M.; Nan, Y.; Tian, F. Assessing the value of high-resolution rainfall and streamflow data for hydrological modeling: An analysis based on 63 catchments in southeast China. Hydrol. Earth Syst. Sci. 2025, 29, 1919–1937. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have Satellite Precipitation Products Improved over Last Two Decades? A Comprehensive Comparison of GPM IMERG with Nine Satellite and Reanalysis Datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Livneh, B.; Deems, J.S.; Schneider, D.; Barsugli, J.J.; Molotch, N.P. Filling in the gaps: Inferring spatially distributed precipitation from gauge observations over complex terrain. Water Resour. Res. 2014, 50, 8589–8610. [Google Scholar] [CrossRef]
- Serreze, M.C.; Clark, M.P.; Bromwich, D.H. Monitoring Precipitation over the Arctic Terrestrial Drainage System: Data Requirements, Shortcomings, and Applications of Atmospheric Reanalysis. April 2003. Available online: https://journals.ametsoc.org/view/journals/hydr/4/2/1525-7541_2003_4_387_mpotat_2_0_co_2.xml (accessed on 8 March 2025).
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Li, R.; Guilloteau, C.; Kirstetter, P.-E.; Foufoula-Georgiou, E. A New Event-Based Error Decomposition Scheme for Satellite Precipitation Products. Geophys. Res. Lett. 2023, 50, e2023GL105343. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.; Lai, R.; Zhu, Z. Performance of satellite-based and reanalysis precipitation products under multi-temporal scales and extreme weather in mainland China. J. Hydrol. 2022, 605, 127389. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, L.; Yang, K.; Song, L.; Ni, X.; Han, X.; Ma, M.; Fan, L. Uncertainty Quantification of Satellite Soil Moisture Retrieved Precipitation in the Central Tibetan Plateau. Remote Sens. 2023, 15, 2600. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhao, Q.; Luo, Y.-T.; Ma, S.-G.; Kang, Y.; Li, Y.-Q.; Chen, H.; Xu, C.-Y. Uncertainty estimation of hydrological modelling using gridded precipitation as model inputs in the Gandaki River Basin. J. Hydrol. Reg. Stud. 2024, 53, 101825. [Google Scholar] [CrossRef]
- Dong, J.; Crow, W.T.; Duan, Z.; Wei, L.; Lu, Y. A double instrumental variable method for geophysical product error estimation. Remote Sens. Environ. 2019, 225, 217–228. [Google Scholar] [CrossRef]
- Maggioni, V.; Vergara, H.J.; Anagnostou, E.N.; Gourley, J.J.; Hong, Y.; Stampoulis, D. Investigating the Applicability of Error Correction Ensembles of Satellite Rainfall Products in River Flow Simulations. J. Hydrometeorol. 2013, 14, 1194–1211. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Using High-Resolution Satellite Rainfall Products to Simulate a Major Flash Flood Event in Northern Italy. J. Hydrometeorol. 2013, 14, 171–185. [Google Scholar] [CrossRef]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L.R. Propagation of satellite precipitation uncertainties through a distributed hydrologic model: A case study in the Tocantins–Araguaia basin in Brazil. J. Hydrol. 2015, 527, 943–957. [Google Scholar] [CrossRef]
- Lorenz, C.; Kunstmann, H. The Hydrological Cycle in Three State-of-the-Art Reanalyses: Intercomparison and Performance Analysis. J. Hydrometeorol. 2012, 13, 1397–1420. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Thinh, N.X. RF-MEP: A novel Random Forest method for merging gridded precipitation products and ground-based measurements. Remote Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Zheng, D.; Zhang, K.; Ma, Q.; Zhao, Y.; Ge, Y. Merging multiple satellite-based precipitation products and gauge observations using a novel double machine learning approach. J. Hydrol. 2021, 594, 125969. [Google Scholar] [CrossRef]
- Kim, S.; Sharma, A.; Liu, Y.Y.; Young, S.I. Rethinking Satellite Data Merging: From Averaging to SNR Optimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4405215. [Google Scholar] [CrossRef]
- Chen, S.; Xiong, L.; Ma, Q.; Kim, J.-S.; Chen, J.; Xu, C.-Y. Improving daily spatial precipitation estimates by merging gauge observation with multiple satellite-based precipitation products based on the geographically weighted ridge regression method. J. Hydrol. 2020, 589, 125156. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, Y.; Han, Z.; Tang, G.; Maguire, L.; Chu, Z.; Hong, Y. Comprehensive evaluation of Ensemble Multi-Satellite Precipitation Dataset using the Dynamic Bayesian Model Averaging scheme over the Tibetan Plateau. J. Hydrol. 2017, 556, 634–644. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Tian, F.; Hou, S.; Yang, L.; Hu, H.; Hou, A. How Does the Evaluation of the GPM IMERG Rainfall Product Depend on Gauge Density and Rainfall Intensity? J. Hydrometeorol. 2018, 19, 339–349. [Google Scholar] [CrossRef]
- Dong, J.; Crow, W.T.; Chen, X.; Tangdamrongsub, N.; Gao, M.; Sun, S.; Qiu, J.; Wei, L.; Gao, H.; Duan, Z. Statistical uncertainty analysis-based precipitation merging (SUPER): A new framework for improved global precipitation estimation. Remote Sens. Environ. 2023, 283, 113299. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Oceans 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Sjoberg, J.P.; Anthes, R.A.; Rieckh, T. The Three-Cornered Hat Method for Estimating Error Variances of Three or More Atmospheric Datasets. Part I: Overview and Evaluation. J. Atmos. Ocean. Technol. 2021, 38, 555–572. [Google Scholar] [CrossRef]
- Gruber, A.; Su, C.-H.; Crow, W.T.; Zwieback, S.; Dorigo, W.A.; Wagner, W. Estimating error cross-correlations in soil moisture data sets using extended collocation analysis. J. Geophys. Res. Atmos. 2016, 121, 1208–1219. [Google Scholar] [CrossRef]
- Duan, Z.; Duggan, E.; Chen, C.; Gao, H.; Dong, J.; Liu, J. Comparison of Traditional Method and Triple Collocation Analysis for Evaluation of Multiple Gridded Precipitation Products across Germany. J. Hydrometeorol. 2021, 1, 2983–2999. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Hong, Y. Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: Applicability of the Triple Collocation method across Mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Dong, J.; Lei, F.; Wei, L. Triple Collocation Based Multi-Source Precipitation Merging. Front. Water 2020, 2, 1. [Google Scholar] [CrossRef]
- Lyu, F.; Tang, G.; Behrangi, A.; Wang, T.; Tan, X.; Ma, Z.; Xiong, W. Precipitation Merging Based on the Triple Collocation Method across Mainland China. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3161–3176. [Google Scholar] [CrossRef]
- Shah, S.; Liu, Y.; Kim, S.; Sharma, A. Advancing High-Mountain Precipitation Reconstruction Through Merging of Multiple Data Sources: Triple Collocation Versus Signal-to-Noise Ratio Optimization. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4212315. [Google Scholar] [CrossRef]
- Gu, J.; Ye, Y.; Jiang, Y.; Guan, H.; Huang, J.; Cao, Y. Improving daily precipitation estimation using a double triple collocation-based (DTC) merging framework. J. Hydrol. 2025, 648, 132422. [Google Scholar] [CrossRef]
- Pan, M.; Fisher, C.K.; Chaney, N.W.; Zhan, W.; Crow, W.T.; Aires, F.; Entekhabi, D.; Wood, E.F. Triple collocation: Beyond three estimates and separation of structural/non-structural errors. Remote Sens. Environ. 2015, 171, 299–310. [Google Scholar] [CrossRef]
- Kim, S.; Shah, S.; Liu, Y.; Sharma, A. Improving Precipitation Merging: A Generalized Two-Stage Framework Using the Signal-to-Noise Ratio Optimization (SNR-opt). In Proceedings of the Copernicus Meetings, General Assembly 2025, Vienna, Austria, 27 April–2 May 2025; Copernicus Publications: Göttingen, Germany, 2025. EGU25-530. [Google Scholar] [CrossRef]
- Belay, H.; Melesse, A.M.; Tegegne, G. Merging Satellite Products and Rain-Gauge Observations to Improve Hydrological Simulation: A Review. Earth 2022, 3, 72. [Google Scholar] [CrossRef]
- Cao, D.; Li, H.; Hou, E.; Song, S.; Lai, C. Assessment and Hydrological Validation of Merged Near-Real-Time Satellite Precipitation Estimates Based on the Gauge-Free Triple Collocation Approach. Remote Sens. 2022, 14, 3835. [Google Scholar] [CrossRef]
- Uddin, K.; Shrestha, H.L.; Murthy, M.; Bajracharya, B.; Shrestha, B.; Gilani, H.; Pradhan, S.; Dangol, B. Development of 2010 national land cover database for the Nepal. J. Environ. Manag. 2015, 148, 82–90. [Google Scholar] [CrossRef]
- Paudel, B.; Panday, D.; Dhakal, K. Climate. In The Soils of Nepal; Ojha, R.B., Panday, D., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 15–27. [Google Scholar] [CrossRef]
- Hersbach, H.; Comyn-Platt, E.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Peubey, C.; Radu, R.; et al. ERA5 Post-Processed Daily Statistics on Pressure Levels from 1940 to Present. In Copernicus Climate Change Service (C3S) Climate Data Store (CDS); 2023. Available online: https://cds.climate.copernicus.eu/datasets/derived-era5-pressure-levels-daily-statistics?tab=overview (accessed on 5 February 2025).
- Huffman, G.J.; Bolvin, D.T.; Joyce, R.; Nelkin, E.J.; Tan, J.; Braithwaite, D.; Hsu, K.; Kelley, O.A.; Nguyen, P.; Sorooshian, S.; et al. Algorithm Theoretical Basis Document (ATBD) for Integrated Multi-Satellite Retrievals for GPM (IMERG) Version 07; Technical Report; National Aeronautics and Space Administration (NASA), NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2023. Available online: https://gpm.nasa.gov (accessed on 15 January 2025).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Brocca, L.; Filippucci, P.; Hahn, S.; Ciabatta, L.; Massari, C.; Camici, S.; Schüller, L.; Bojkov, B.; Wagner, W. SM2RAIN-ASCAT (2007-2018): Global daily satellite rainfall data from ASCAT soil moisture observations. Earth Syst. Sci. Data 2019, 11, 1583–1601. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S. Multicriteria calibration of hydrologic models. Calibration Watershed Models 2011, 6, 185–196. [Google Scholar] [CrossRef]
- Sun, W.; Ishidaira, H.; Bastola, S. Towards improving river discharge estimation in ungauged basins: Calibration of rainfall-runoff models based on satellite observations of river flow width at basin outlet. Hydrol. Earth Syst. Sci. 2010, 14, 2011–2022. [Google Scholar] [CrossRef]
- Quan, Z.; Teng, J.; Sun, W.; Cheng, T.; Zhang, J. Evaluation of the HYMOD model for rainfall-runoff simulation using the GLUE method. In Remote Sensing and GIS for Hydrology and Water Resources (Proceedings RSHS14 and ICGRHWE14, Guangzhou, China, August 2014); IAHS Publ. 368; Copernicus GmbH: Wallingford, UK, 2015; pp. 180–185. [Google Scholar] [CrossRef]
- Bastola, S. The regionalization of a parameter of HYMOD, a conceptual hydrological model, using data from across the globe. HydroResearch 2022, 5, 13–21. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall-runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale Comparative Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products from 2015 to 2017 over a Climate Transition Area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. WIREs Clim. Change 2011, 2, 851–870. [Google Scholar] [CrossRef]
- de Medeiros, F.J.; de Oliveira, C.P.; Avila-Diaz, A. Evaluation of extreme precipitation climate indices and their projected changes for Brazil: From CMIP3 to CMIP6. Weather Clim. Extrem. 2022, 38, 100511. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Bogerd, L.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. A Comprehensive Five-Year Evaluation of IMERG Late Run Precipitation Estimates over the Netherlands. J. Hydrometeorol. 2021, 1, 1855–1868. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Xin, Y.; Lu, N.; Jiang, H.; Liu, Y.; Yao, L. Performance of ERA5 reanalysis precipitation products in the Guangdong-Hong Kong-Macao greater Bay Area, China. J. Hydrol. 2021, 602, 126791. [Google Scholar] [CrossRef]
- Biswas, S.; Singh, C.; Bharti, V. An assessment of GPM IMERG Version 7 rainfall estimates over the North West Himalayan region. Atmos. Res. 2025, 315, 107910. [Google Scholar] [CrossRef]
- Li, Z.; Wang, H.; Zhang, T.; Zeng, Q.; Xiang, J.; Liu, Z.; Yang, R. Multi-Source Precipitation Data Merging for High-Resolution Daily Rainfall in Complex Terrain. Remote Sens. 2023, 15, 4345. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Lei, H.; Zhao, H.; Ao, T. A two-step merging strategy for incorporating multi-source precipitation products and gauge observations using machine learning classification and regression over China. Hydrol. Earth Syst. Sci. 2022, 26, 2969–2995. [Google Scholar] [CrossRef]
- Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. IMERG V06: Changes to the Morphing Algorithm. J. Atmos. Ocean. Technol. 2019, 36, 2471–2482. [Google Scholar] [CrossRef]
- Ouyang, L.; Lu, H.; Yang, K.; Leung, L.R.; Wang, Y.; Zhao, L.; Zhou, X.; Zhu, L.; Chen, Y.; Jiang, Y.; et al. Characterizing Uncertainties in Ground ‘Truth’ of Precipitation Over Complex Terrain Through High-Resolution Numerical Modeling. Geophys. Res. Lett. 2021, 48, e2020GL091950. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A Review of Merged High-Resolution Satellite Precipitation Product Accuracy during the Tropical Rainfall Measuring Mission (TRMM) Era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Gao, Z.; Tang, G.; Jing, W.; Hou, Z.; Yang, J.; Sun, J. Evaluation of Multiple Satellite, Reanalysis, and Merged Precipitation Products for Hydrological Modeling in the Data-Scarce Tributaries of the Pearl River Basin, China. Remote Sens. 2023, 15, 5349. [Google Scholar] [CrossRef]
- Rahman, K.U.; Shang, S.; Shahid, M.; Wen, Y. Hydrological evaluation of merged satellite precipitation datasets for streamflow simulation using SWAT: A case study of Potohar Plateau, Pakistan. J. Hydrol. 2020, 587, 125040. [Google Scholar] [CrossRef]
- Chiaravalloti, F.; Brocca, L.; Procopio, A.; Massari, C.; Gabriele, S. Assessment of GPM and SM2RAIN-ASCAT rainfall products over complex terrain in southern Italy. Atmos. Res. 2018, 206, 64–74. [Google Scholar] [CrossRef]
- Duan, Z.; Tuo, Y.; Liu, J.; Gao, H.; Song, X.; Zhang, Z.; Yang, L.; Mekonnen, D.F. Hydrological evaluation of open-access precipitation and air temperature datasets using SWAT in a poorly gauged basin in Ethiopia. J. Hydrol. 2019, 569, 612–626. [Google Scholar] [CrossRef]
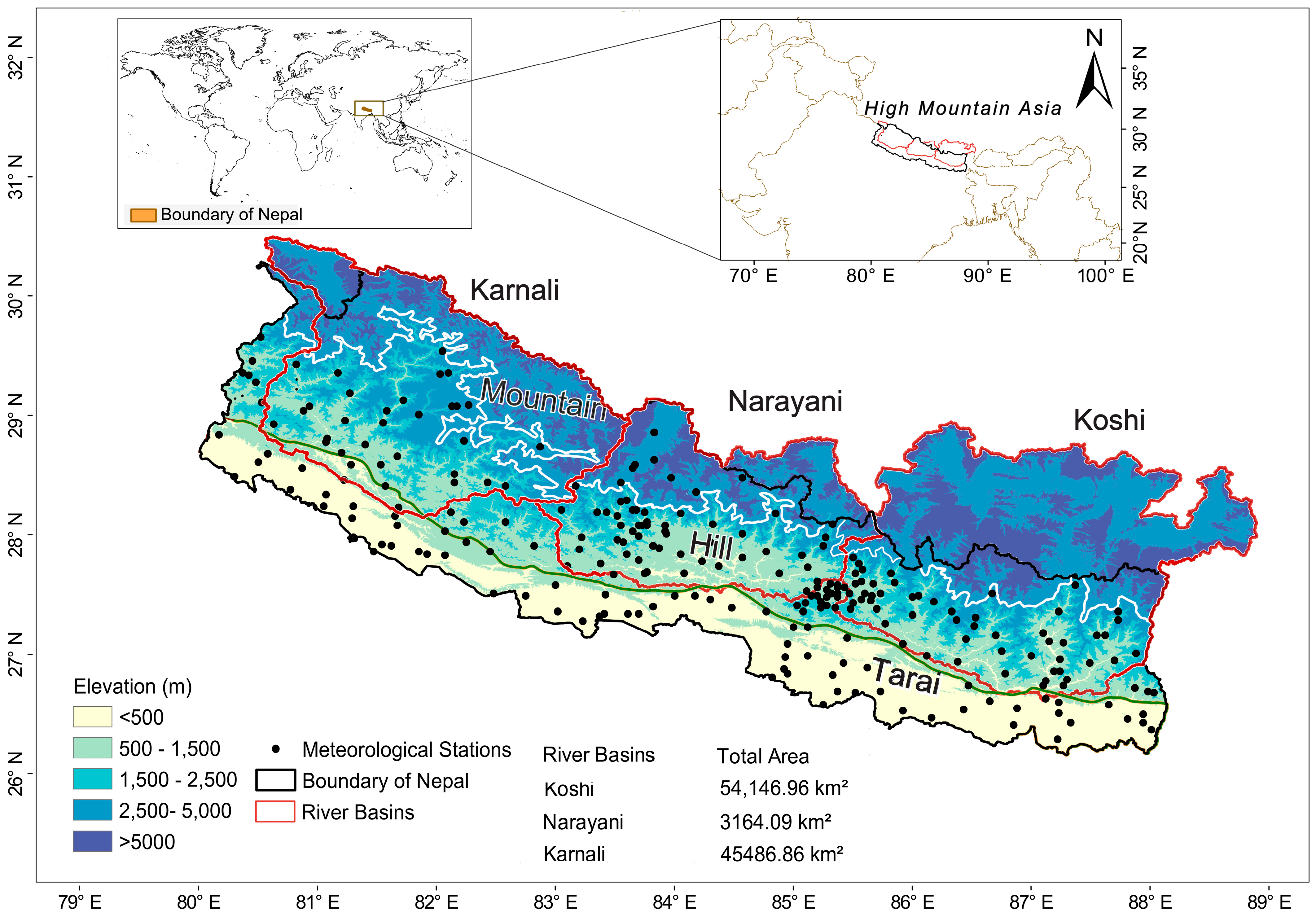

| Type | Data Set | Spatial Resolution | Temporal Resolution | Spatio-Temporal Coverage | Algorithm | Key Ref. |
|---|---|---|---|---|---|---|
| Satellite | IMERG-Late Run | 0.1° | 0.5 h | Global (2000–present) | Integrated Multi-satellite Retrievals for GPM | [43] |
| Re-analysis | ERA-5 | 0.25° | 1 d | Global (1950–present) | ECMWF Integrated Forecasting System (IFS), cycle 31r2 | [44] |
| Soil moisture | SM2RAIN-ASCAT | 0.1° | 1 d | Global (2007–2020.6) | SM2RAIN | [45] |
| Parameter | Description | Range |
|---|---|---|
| Cmax | Maximum storage capacity | 1–500 |
| Bexp | Degree of spatial variability of the soil moisture capacity | 0–2 |
| α | Factor distributing the flow between slow and quick release reservoirs | 0–1 |
| Ks | Residence time of the slow-release reservoir | 0.001–0.5 |
| Kq | Residence time of the quick release reservoirs | 0.5–12 |
| Criteria | Metrics | Formula/Index | Purpose |
|---|---|---|---|
| (a) Error magnitude | Root Mean Squared Error | Compares MGPD and GPDs with daily gauge data; measures average error magnitude. | |
| Bias | Measures whether the (M)GPDs overpredicts or underpredicts relative to observed data. | ||
| KGE | Combines correlation, bias ratio and variability ratio into a single efficiency score. | ||
| Extreme precipitation climate index | PRCPTOT, R95p, RX1day, RX5day, SDII, R20mm, CDD, CWD | Assessment of intensity and duration of extreme precipitation | |
| (b) Rainfall Classification | Probability of Detection | Measures the fraction of observed rainfall events correctly detected. | |
| Frequency Bias | Determines if rainfall events are overestimated or underestimated. | ||
| False Alarm Ratio | Indicates false rainfall events predicted. | ||
| Critical Success Index | Assess the overall accuracy in detecting rainfall events. | ||
| (c) Streamflow Simulation | Nash–Sutcliffe Efficiency | Evaluates how well simulated streamflow matches observations. | |
| Coefficient of Correlation | = | Quantifies the linear relationship between simulated and observed flows. | |
| Normalized RMSE | Normalizes RMSE by the mean of observed streamflow. | ||
| Bias | Indicates whether estimates are biased high or low. | ||
| Kling Gupta Efficiency | Integrates correlation (r), variability ratio (α), and bias ratio (β) into one efficiency measure. |
| Abbreviation | Index Name | Unit |
|---|---|---|
| PRCPTOT | Total annual wet-day rainfall | mm |
| R95p | Very-wet-day rainfall | mm |
| RX1day | Max 1-day rainfall | mm |
| RX5day | Max 5-day rainfall | mm |
| SDII | Mean wet-day intensity | mm day−1 |
| R20mm | Very-heavy-rain days | days |
| CDD | Longest dry spell | days |
| CWD | Longest wet spell | days |
| Basin | Products | Weight |
|---|---|---|
| Koshi | ERA5 | 0.18 |
| IMERG-late | 0.21 | |
| SM2RAIN | 0.48 | |
| Narayani | ERA5 | 0.19 |
| IMERG-late | 0.20 | |
| SM2RAIN | 0.49 | |
| Karnali | ERA5 | 0.27 |
| IMERG-late | 0.23 | |
| SM2RAIN | 0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guragain, S.; Shah, S.; Albano, R.; Kim, S.; Hammad, M.; Asif, M. Quantifying the Added Values of a Merged Precipitation Product in Streamflow Prediction over the Central Himalayas. Remote Sens. 2025, 17, 2170. https://doi.org/10.3390/rs17132170
Guragain S, Shah S, Albano R, Kim S, Hammad M, Asif M. Quantifying the Added Values of a Merged Precipitation Product in Streamflow Prediction over the Central Himalayas. Remote Sensing. 2025; 17(13):2170. https://doi.org/10.3390/rs17132170
Chicago/Turabian StyleGuragain, Shrija, Suraj Shah, Raffaele Albano, Seokhyeon Kim, Muhammad Hammad, and Muhammad Asif. 2025. "Quantifying the Added Values of a Merged Precipitation Product in Streamflow Prediction over the Central Himalayas" Remote Sensing 17, no. 13: 2170. https://doi.org/10.3390/rs17132170
APA StyleGuragain, S., Shah, S., Albano, R., Kim, S., Hammad, M., & Asif, M. (2025). Quantifying the Added Values of a Merged Precipitation Product in Streamflow Prediction over the Central Himalayas. Remote Sensing, 17(13), 2170. https://doi.org/10.3390/rs17132170









