Constant Modulus Wideband MIMO Radar Waveform Design for Transmit Beampattern and Angular Waveform Synthesis
Abstract
1. Introduction
- Different from the existing works where only the space–frequency pattern is considered, in this paper, the transmit beampattern and AW expressions for wideband MIMO radar are recast as a more compact form.
- Based on the compact forms of the transmit beampattern and AW, we extend the design concept of the transmit beampattern and the similarity analysis of the AW in narrowband MIMO radar to the wideband MIMO radar model. Then, a transmit beampattern design problem under AM similarity and CM constraints is formulated.
- An algorithm based on the ADMM framework is proposed to address the aforementioned problem. Some improvements are proposed to reduce the computational complexity, and the final computational complexity analysis is given. Numerical simulations show that the optimized waveform can form the multi-beam beampattern and its AWs can realize the de-chirp operation.
2. Signal Model
3. Problem Formulation
3.1. Multi-Beam Beampattern Design
3.2. Proposed Model for Co-Optimization of Transmit Beampattern and AWs
4. Proposed Algorithm and Computational Complexity Analysis
4.1. Proposed Algorithm
- (1)
- The solution to subproblem (30)It can be noticed that subproblem (30) is a unconstrained problem with respect to . Therefore, the L-BFGS is adopted to solve (30), and the gradient with respect to is given:where . According to (7) and (8), we can calculate the gradient of the transmit beampattern and AW about as follows:and we have
- (2)
- The solution to subproblem (31)
- (3)
- UpdateAfter obtaining the updated and , we can calculate according to (32). Then, the ADMM iteration can be carried out by setting the initial point . Finally, the proposed algorithm is summarized in Algorithm 1.
4.2. Computational Complexity Analysis
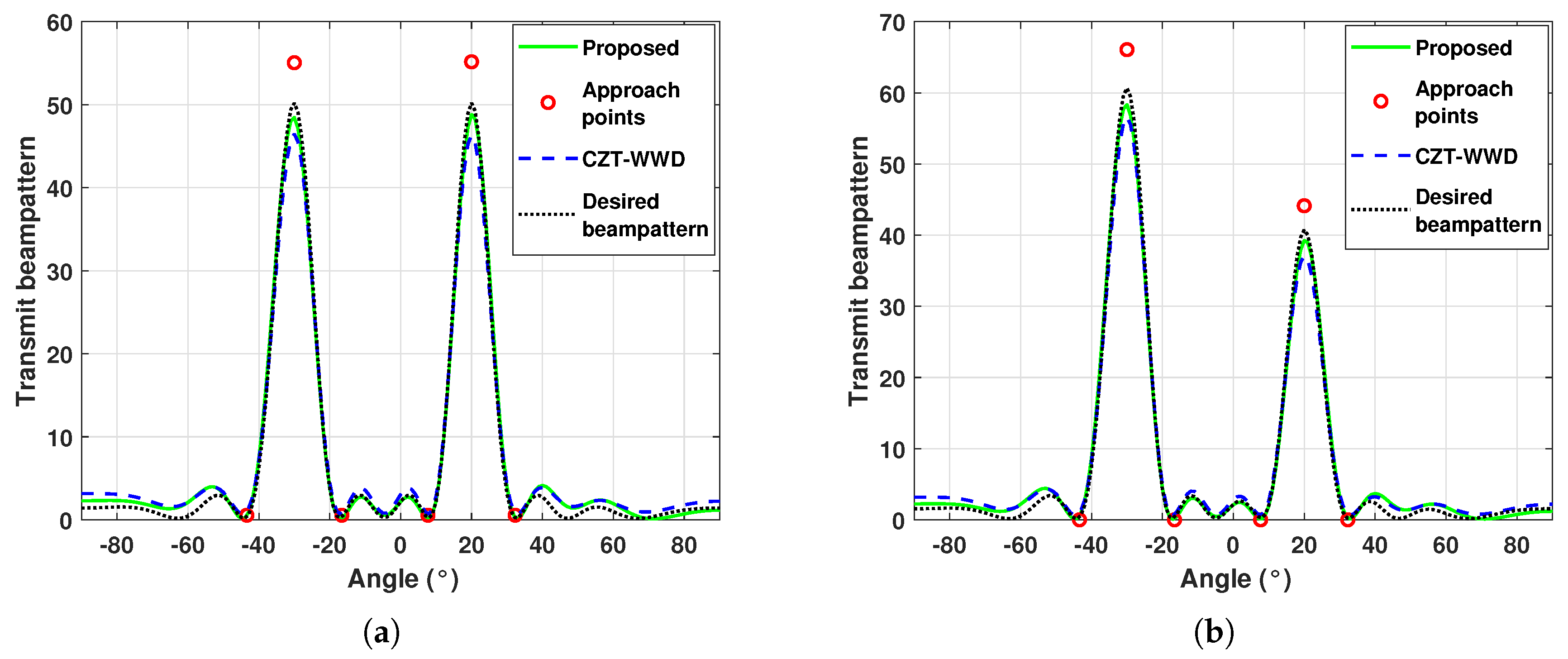
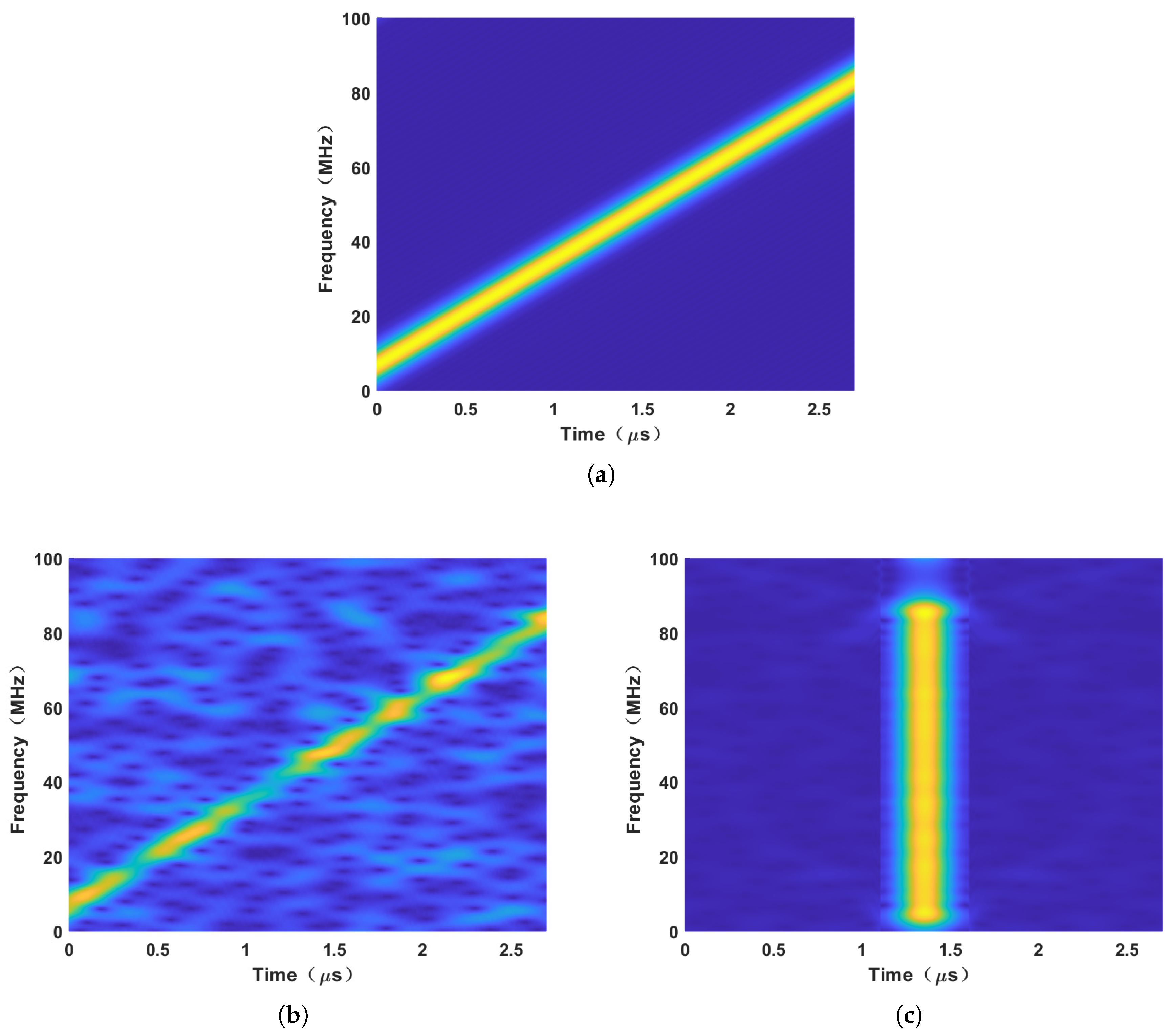
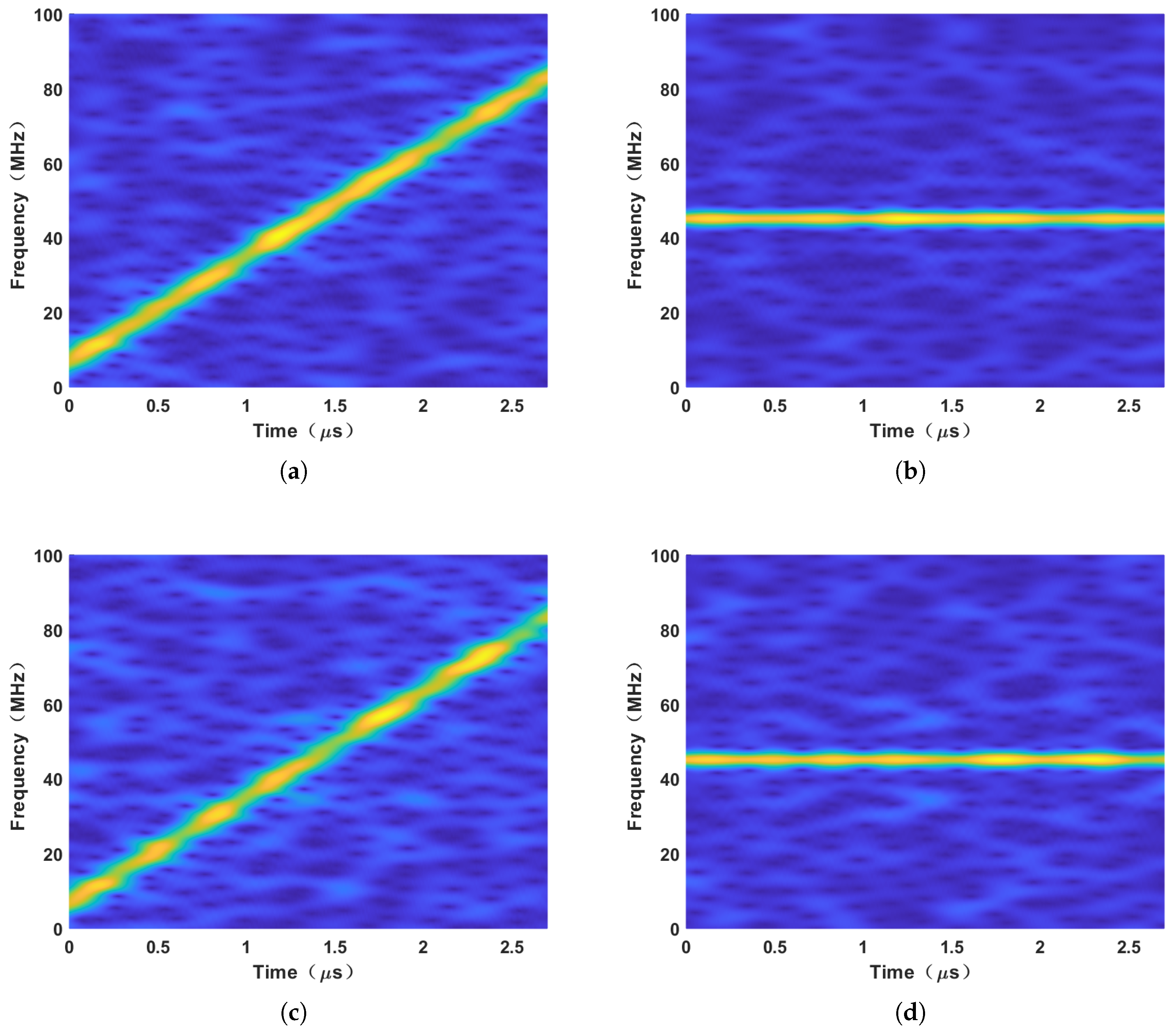
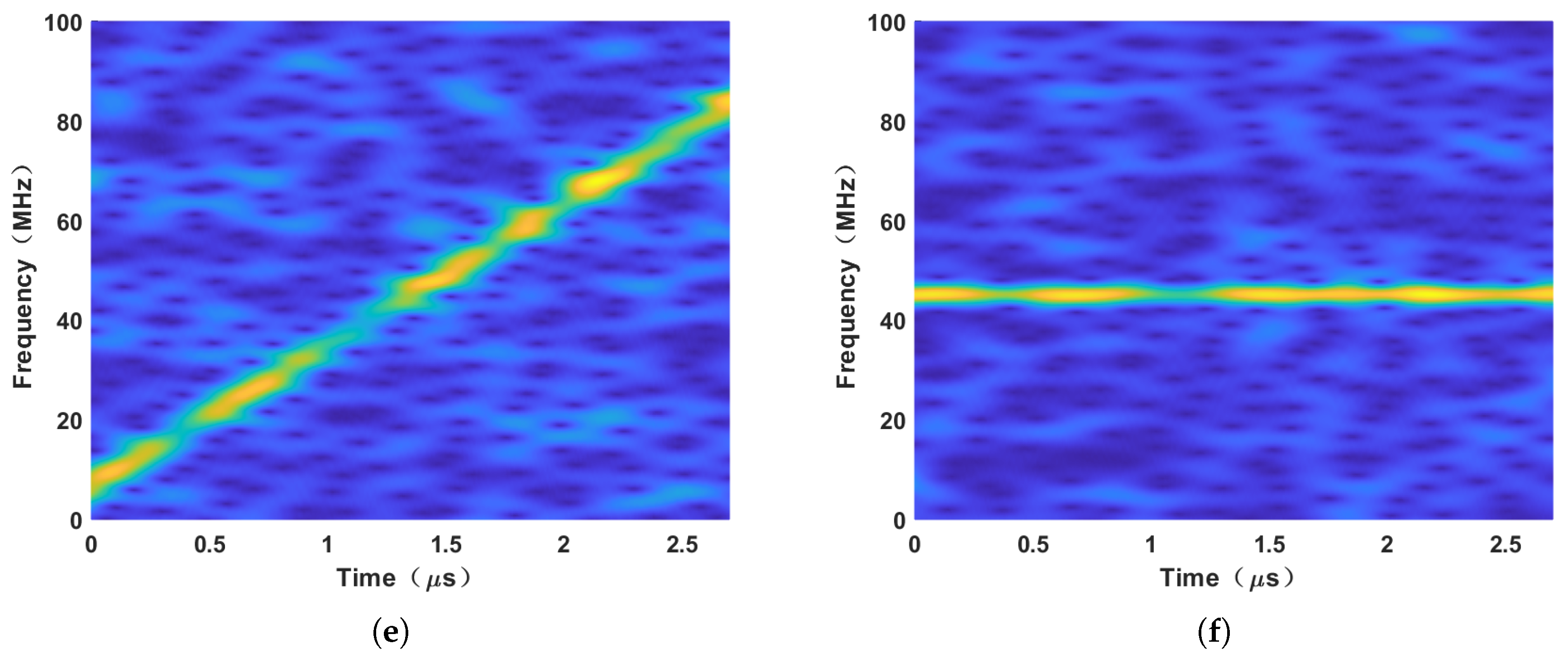
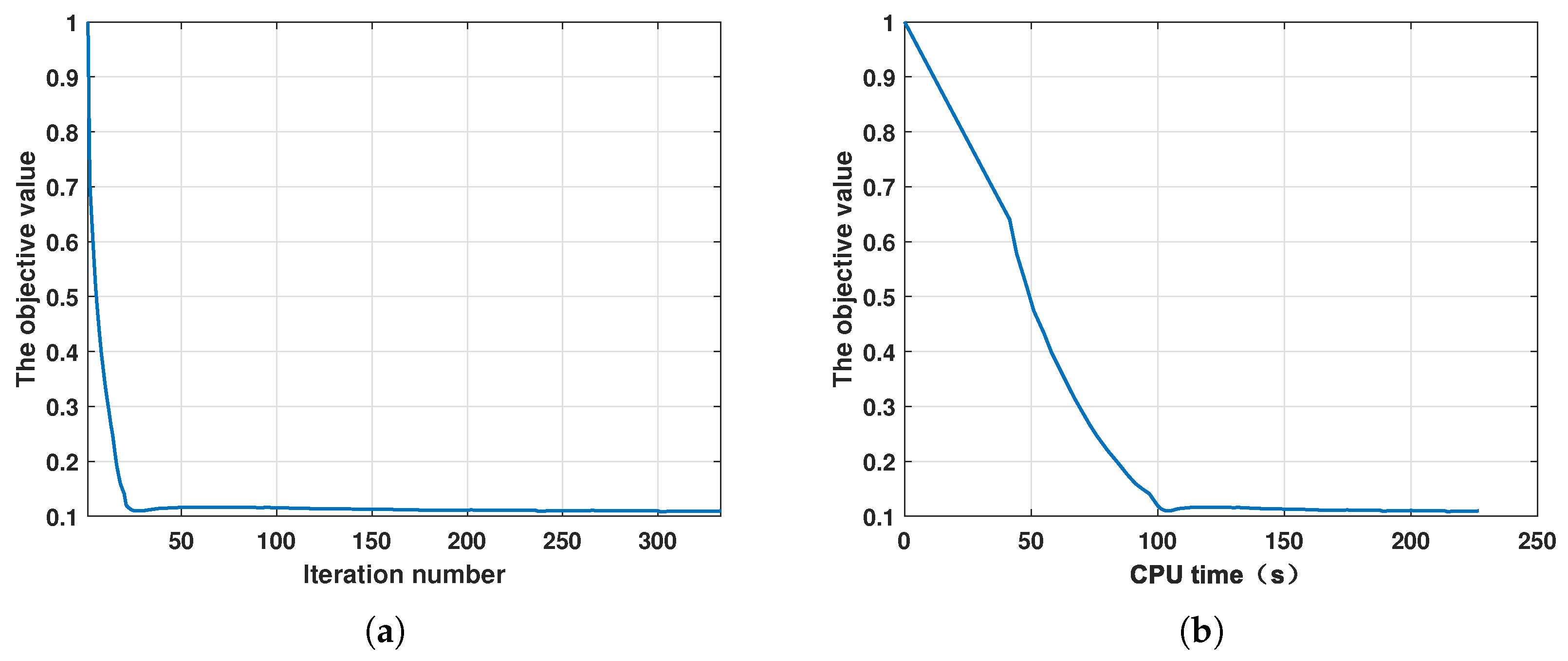
5. Simulation Results
6. Discussion
6.1. Quantitative Description of Waveform Performance
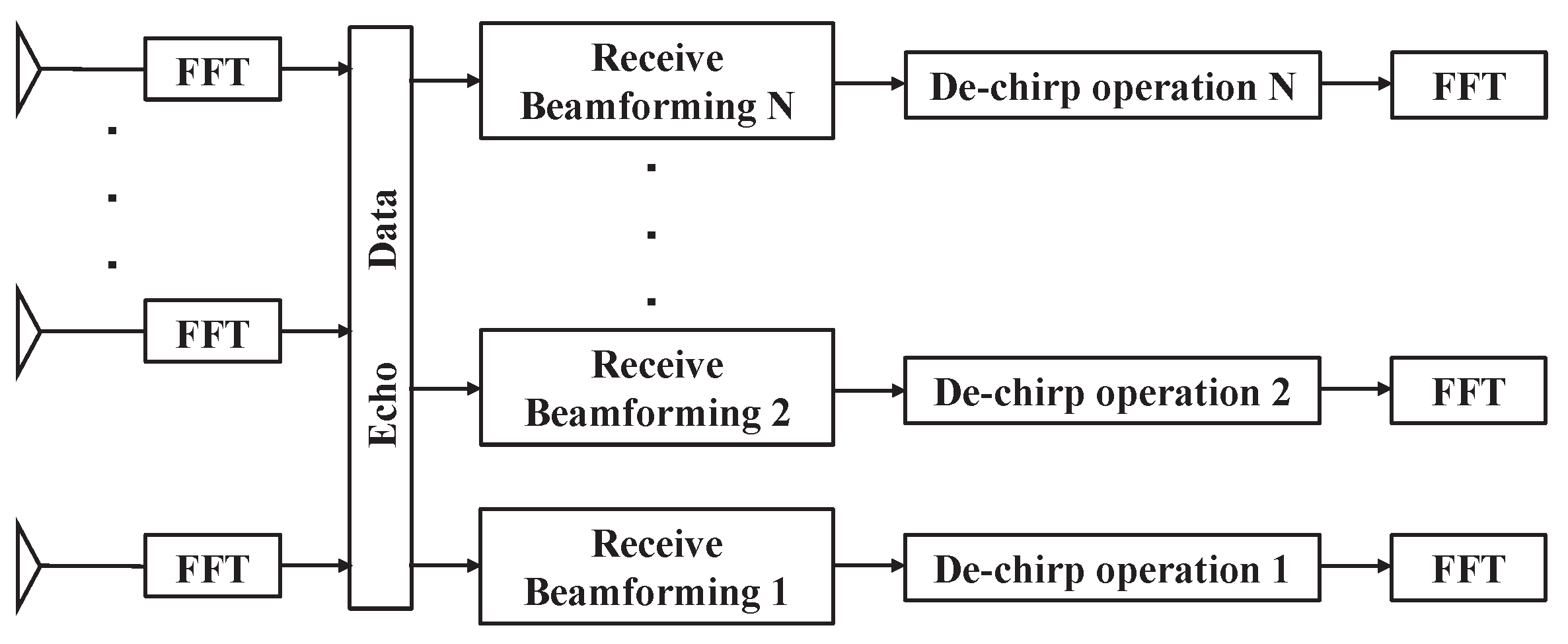
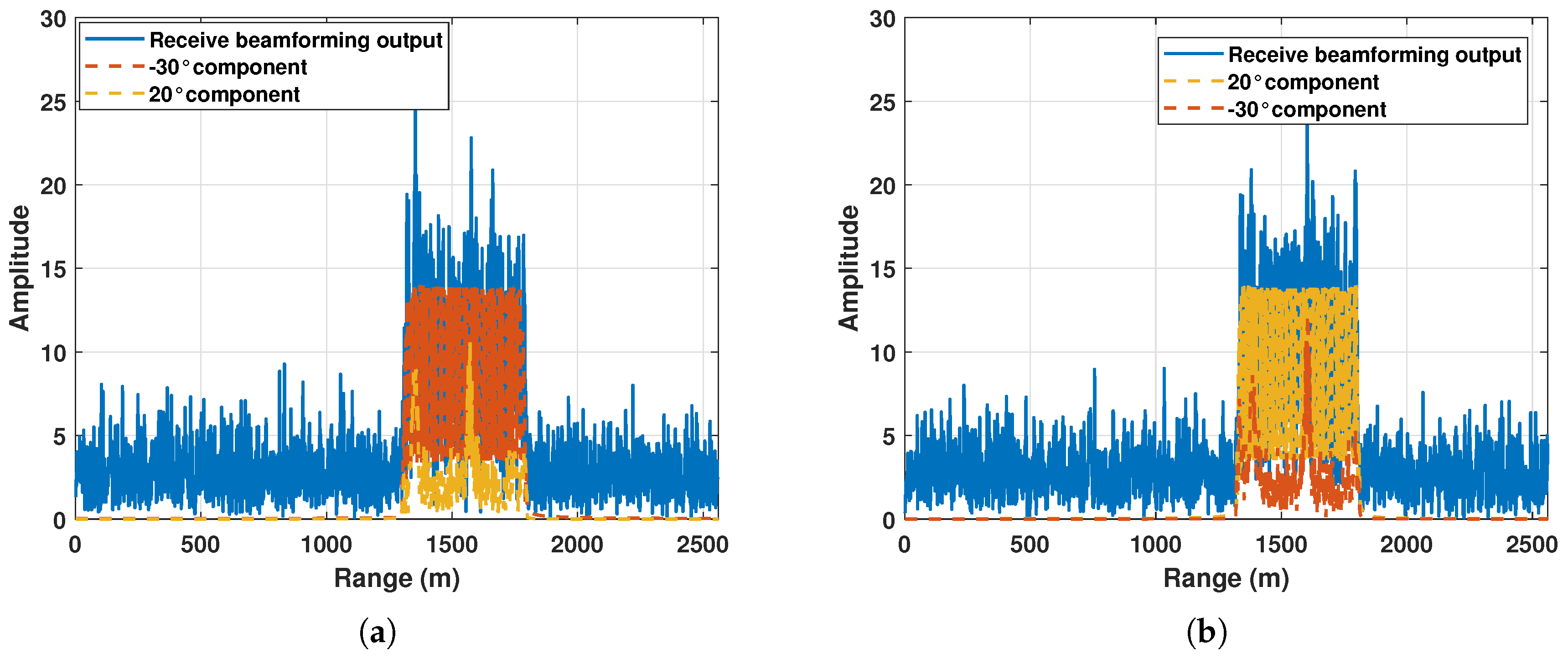
6.2. The Role of Receive Beamforming
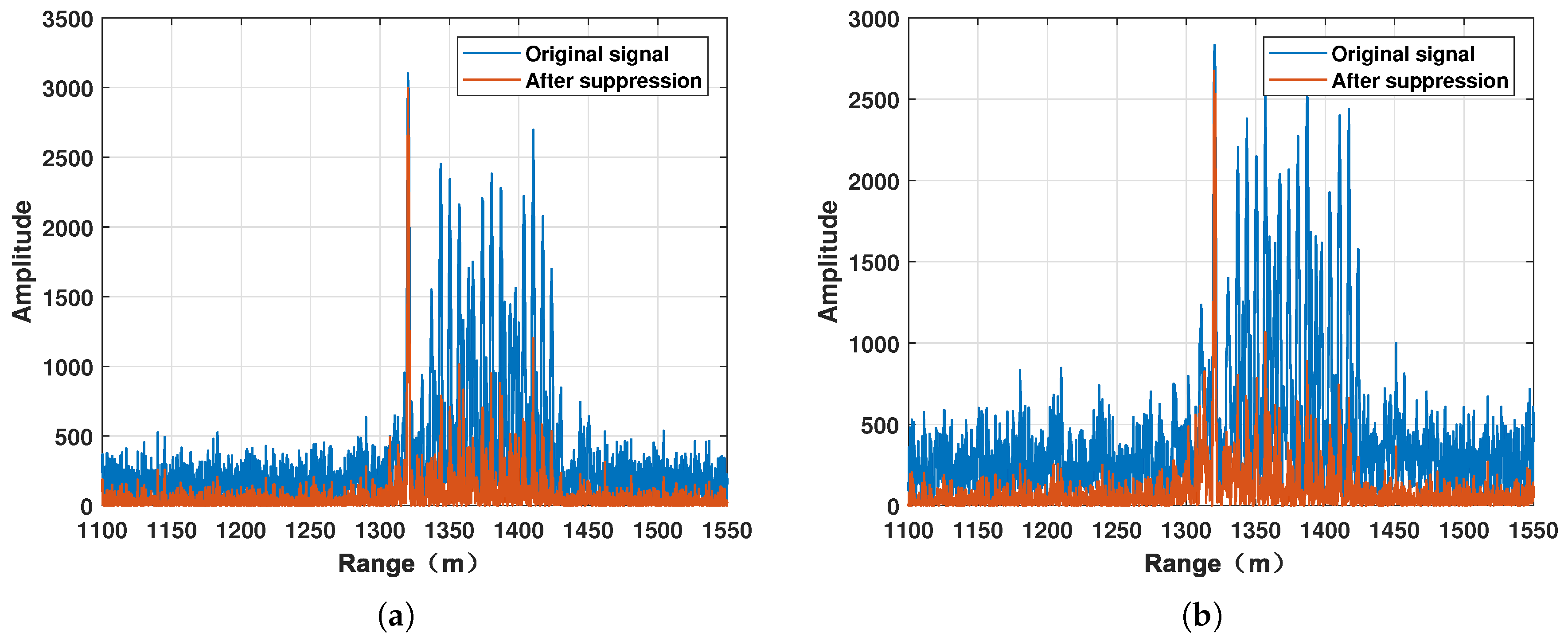
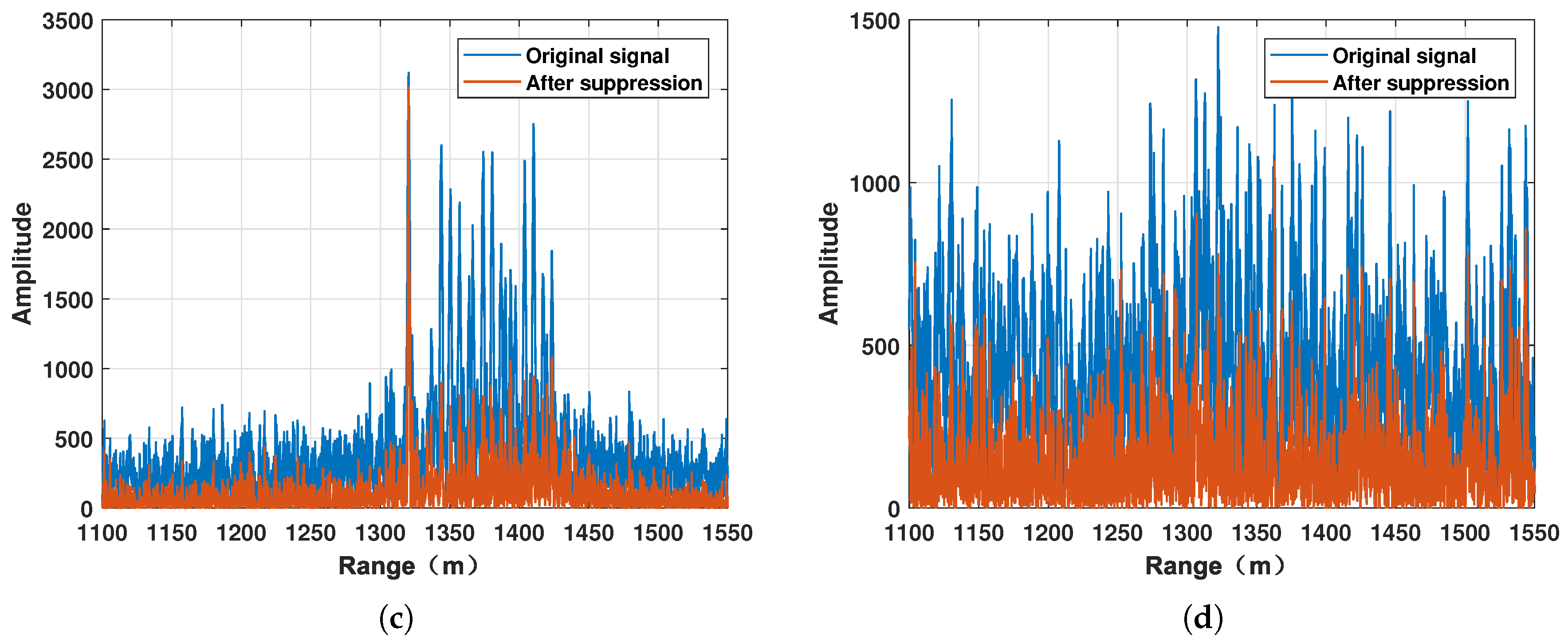
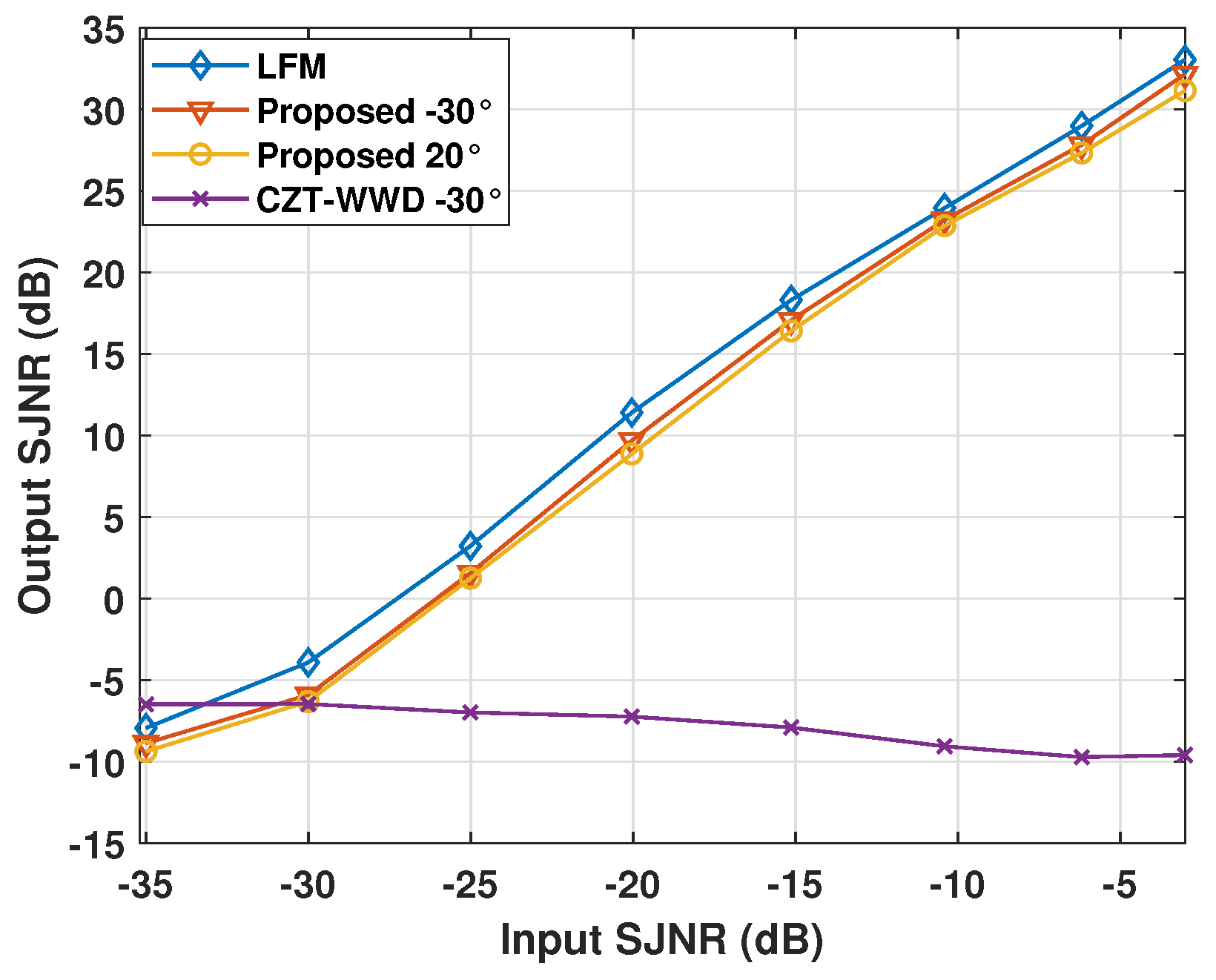
6.3. An Anti-ISRJ Example
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fuhrmann, D.; San Antonio, G. Transmit beamforming for MIMO radar systems using partial signal correlation. In Proceedings of the Conference Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2004; Volume 1, pp. 295–299. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.; Cimini, R.; Chizhik, D.; Valenzuela, R. Performance of MIMO radar systems: Advantages of angular diversity. In Proceedings of the Conference Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2004; Volume 1, pp. 305–309. [Google Scholar] [CrossRef]
- Robey, F.; Coutts, S.; Weikle, D.; McHarg, J.; Cuomo, K. MIMO radar theory and experimental results. In Proceedings of the Conference Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2004; Volume 1, pp. 300–304. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J.; Xie, Y. On Probing Signal Design for MIMO Radar. IEEE Trans. Signal Process. 2007, 55, 4151–4161. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J.; Zhu, X. Waveform Synthesis for Diversity-Based Transmit Beampattern Design. IEEE Trans. Signal Process. 2008, 56, 2593–2598. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Zhang, T.; Kong, L. Constrained transmit beampattern design for colocated MIMO radar. Signal Process. 2018, 144, 145–154. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Cheng, Z.; Feng, D. Correlated LFM Waveform Set Design for MIMO Radar Transmit Beampattern. IEEE Geosci. Remote Sens. Lett. 2017, 14, 329–333. [Google Scholar] [CrossRef]
- Zhou, S.; Lu, J.; Varshney, P.K.; Wang, J.; Liu, H. Colocated MIMO radar waveform optimization with receive beamforming. Digit. Signal Process. 2019, 98, 102635. [Google Scholar] [CrossRef]
- Wang, Y.C.; Xu, W.; Liu, H.; Luo, Z.Q. On the Design of Constant Modulus Probing Signals for MIMO Radar. IEEE Trans. Signal Process. 2012, 60, 4432–4438. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y. On the Design of Constant Modulus Probing Waveforms with Good Correlation Properties for MIMO Radar via Consensus-ADMM Approach. IEEE Trans. Signal Process. 2019, 67, 4317–4332. [Google Scholar] [CrossRef]
- Cheng, Z.; He, Z.; Zhang, S.; Jian, L. Constant Modulus Waveform Design for MIMO Radar Transmit Beampattern. IEEE Trans. Signal Process. 2017, 65, 4912–4923. [Google Scholar] [CrossRef]
- Aldayel, O.; Monga, V.; Rangaswamy, M. Tractable Transmit MIMO Beampattern Design Under a Constant Modulus Constraint. IEEE Trans. Signal Process. 2017, 65, 2588–2599. [Google Scholar] [CrossRef]
- Imani, S.; Nayebi, M.M.; Ghorashi, S. Transmit Signal Design in Co-located MIMO Radar Without Covariance Matrix Optimization. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2178–2186. [Google Scholar] [CrossRef]
- Mccormick, P.M.; Blunt, S.D.; Metcalf, J.G. Wideband MIMO Frequency Modulated Emission Design with Space-Frequency Nulling. IEEE J. Sel. Top. Signal Process. 2016, 11, 363–378. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Yang, J.; Kong, L.; Li, J. Wideband MIMO Radar Waveform Design. IEEE Trans. Signal Process. 2019, 67, 3487–3501. [Google Scholar] [CrossRef]
- He, H.; Stoica, P.; Li, J. Wideband MIMO Systems: Signal Design for Transmit Beampattern Synthesis. IEEE Trans. Signal Process. 2011, 59, 618–628. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Y.D.; Amin, M.G.; Sheng, W. Wideband Multiple-Input Multiple-Output Radar Waveform Design with Low Peak-to-Average Ratio Constraint; IET: Washington, DC, USA, 2016. [Google Scholar]
- Liu, H.; Wang, X.; Jiu, B.; Yan, J.; Wu, M.; Bao, Z. Wideband MIMO Radar Waveform Design for Multiple Target Imaging. IEEE Sens. J. 2016, 16, 8545–8556. [Google Scholar] [CrossRef]
- Friedlander, B. On Transmit Beamforming for MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3376–3388. [Google Scholar] [CrossRef]
- Shi, J.; Bo, J.; Liu, H.; Ming, F.; Yan, J. Transmit design for airborne MIMO radar based on prior information. Signal Process. 2016, 128, 521–530. [Google Scholar] [CrossRef]
- Yan, J.; Liu, H.; Jiu, B.; Chen, B.; Liu, Z.; Bao, Z. Simultaneous Multibeam Resource Allocation Scheme for Multiple Target Tracking. IEEE Trans. Signal Process. 2015, 63, 3110–3122. [Google Scholar] [CrossRef]
- Yan, J.; Jiu, B.; Liu, H.; Chen, B.; Bao, Z. Prior Knowledge-Based Simultaneous Multibeam Power Allocation Algorithm for Cognitive Multiple Targets Tracking in Clutter. IEEE Trans. Signal Process. 2015, 63, 512–527. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, H.; Hongtao Su, H.Z. Doppler sensitivity of MIMO radar waveforms. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2091–2110. [Google Scholar] [CrossRef]
- Zheng, H.; Jiu, B.; Li, K.; Liu, H. Joint Design of the Transmit Beampattern and Angular Waveform for Colocated MIMO Radar under a Constant Modulus Constraint. Remote Sens. 2021, 13, 3392. [Google Scholar] [CrossRef]
- Lazecky, M.; Hlavacova, I.; Bakon, M.; Sousa, J.J.; Perissin, D.; Patricio, G. Bridge Displacements Monitoring Using Space-Borne X-Band SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 205–210. [Google Scholar] [CrossRef]
- Zhou, X.; Chong, J.; Yang, X.; Li, W.; Guo, X. Ocean Surface Wind Retrieval Using SMAP L-Band SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 65–74. [Google Scholar] [CrossRef]
- Wang, X.S.; Liu, J.C.; Zhang, W.M.; Qixiang, F.U.; Liu, Z.; Xie, X.X. Mathematic principles of interrupted-sampling repeater jamming (ISRJ). Sci. China 2007, 50, 113–123. [Google Scholar] [CrossRef]
- Gong, S.; Wei, X.; Li, X. ECCM scheme against interrupted sampling repeater jammer based on time-frequency analysis. J. Syst. Eng. Electron. 2014, 25, 996–1003. [Google Scholar] [CrossRef]
- Chen, J.; Wu, W.; Xu, S.; Chen, P.; Zou, J.W. A Band Pass Filter Design against Interrupted-Sampling Repeater Jamming based on Time-Frequency Analysis. IET Radar Sonar Navig. 2019, 13. [Google Scholar] [CrossRef]
- Yuan, H.; Wang, C.; Li, X.; An, L. A Method against Interrupted-Sampling Repeater Jamming Based on Energy Function Detection and Band-Pass Filtering. Int. J. Antennas Propag. 2017, 2017, 6759169. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Yu, W.; Luo, Y.; Zhao, Y.; Yu, Z. Energy function-guided histogram analysis for interrupted sampling repeater jamming suppression. Electron. Lett. 2023, 59, e12778. [Google Scholar] [CrossRef]
- Meng, Y.; Yu, L.; Wei, Y. Interrupted Sampling Repeater Jamming Suppression Based on Time-frequency Segmentation Network and Target Signal Reconstruction. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, Australia, 6–10 November 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Duan, L.; Du, S.; Quan, Y.; Lv, Q.; Li, S.; Xing, M. Interference Countermeasure System Based on Time–Frequency Domain Characteristics. IEEE J. Miniat. Air Space Syst. 2023, 4, 76–84. [Google Scholar] [CrossRef]
- Trees, H.L.V. Optimum Array Processing; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; Chapter 7; pp. 710–916. [Google Scholar] [CrossRef]




| M | 10 |
| 2 GHz | |
| B | 100 MHz |
| 3.2 s | |
| L | 320 |
| d | |
| Beam Directions | [, ] | [, 0, ] | [, 0, , ] | [, , 0, , ] | |
|---|---|---|---|---|---|
| Proposed | Similarity | 0.33 | 0.47 | 0.64 | 0.88 |
| Beam gain | 48.74 | 31.6 | 23.08 | 17.16 | |
| CZT-WWD | Similarity | 1.94 | 1.93 | 1.94 | 1.93 |
| Beam gain | 47.6 | 29.6 | 25.22 | 20.5 |
| Beam Directions | [, ] | [, 0, ] | [, 0, , ] | [, , 0, , ] | |
|---|---|---|---|---|---|
| Proposed | Similarity | 0.29 | 0.34 | 0.23 | 0.52 |
| Beam gain | 93.87 | 61.57 | 50.04 | 33.59 | |
| CZT-WWD | Similarity | 1.94 | 1.94 | 1.94 | 1.94 |
| Beam gain | 90.46 | 60.86 | 46.27 | 38.25 |
| Beam Directions | [, ] | [, 0, ] | [, 0, , ] | [, , 0, , ] | |
|---|---|---|---|---|---|
| Proposed | Similarity | 0.33 | 0.36 | 0.32 | 0.36 |
| Beam gain | 134.54 | 90.25 | 69.7 | 53.99 | |
| CZT-WWD | Similarity | 1.94 | 1.94 | 1.94 | 1.94 |
| Beam gain | 129.74 | 86.33 | 65.82 | 51.44 |
| Parameter | Value |
|---|---|
| The interception width | 0.2 s |
| Forwarded times | 3 |
| Location of targets | (1320 m, , (1320 m, |
| Location of jammers | (1320 m, , (1320 m, |
| Noise power | 1 |
| Input SNR of each receive element | 0 dB |
| Input jamming to noise ratio of each receive element | 10 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Zhang, X.; Wang, S.; Yan, J. Constant Modulus Wideband MIMO Radar Waveform Design for Transmit Beampattern and Angular Waveform Synthesis. Remote Sens. 2025, 17, 2124. https://doi.org/10.3390/rs17132124
Zheng H, Zhang X, Wang S, Yan J. Constant Modulus Wideband MIMO Radar Waveform Design for Transmit Beampattern and Angular Waveform Synthesis. Remote Sensing. 2025; 17(13):2124. https://doi.org/10.3390/rs17132124
Chicago/Turabian StyleZheng, Hao, Xiaoxia Zhang, Shubin Wang, and Junkun Yan. 2025. "Constant Modulus Wideband MIMO Radar Waveform Design for Transmit Beampattern and Angular Waveform Synthesis" Remote Sensing 17, no. 13: 2124. https://doi.org/10.3390/rs17132124
APA StyleZheng, H., Zhang, X., Wang, S., & Yan, J. (2025). Constant Modulus Wideband MIMO Radar Waveform Design for Transmit Beampattern and Angular Waveform Synthesis. Remote Sensing, 17(13), 2124. https://doi.org/10.3390/rs17132124






