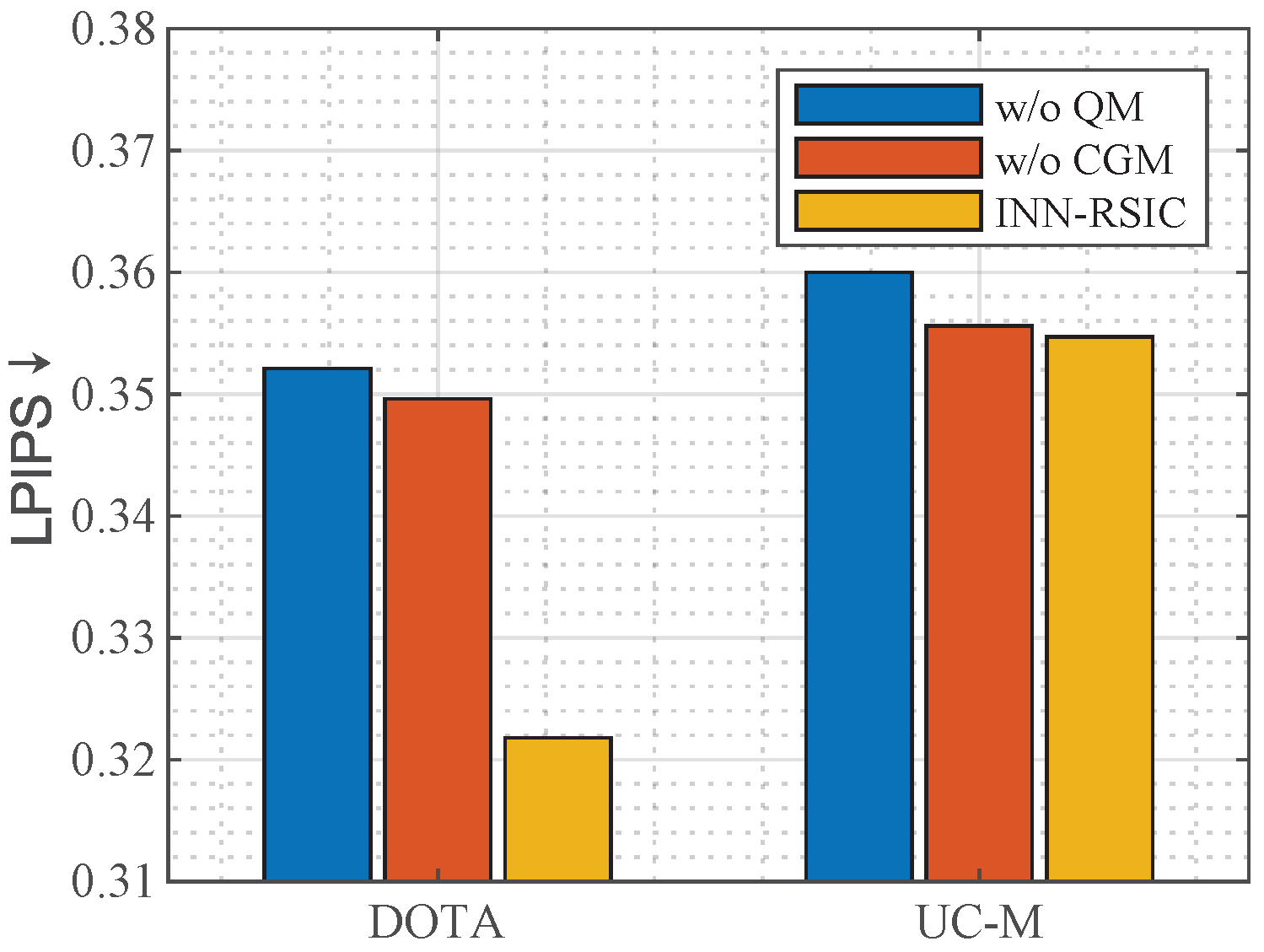Enhancing Perception Quality in Remote Sensing Image Compression via Invertible Neural Network

Abstract

Despite the impressive performance of existing image compression algorithms, they struggle to balance perceptual quality and high image fidelity. To address this issue, we propose a novel invertible neural network-based remote sensing image compression (INN-RSIC) method. Our approach captures the compression distortion from an existing image compression algorithm and encodes it as Gaussian-distributed latent variables using an INN, ensuring that the distortion in the decoded image remains independent of the ground truth. By using the inverse mapping of the INN, we input the decoded image with randomly resampled Gaussian variables, generating enhanced images with improved perceptual quality. We incorporate channel expansion, Haar transformation, and invertible blocks into the INN to accurately represent compression distortion. Additionally, a quantization module (QM) is introduced to mitigate format conversion impact, enhancing generalization and perceptual quality. Extensive experiments show that INN-RSIC achieves superior perceptual quality and fidelity compared to existing algorithms. As a lightweight plug-and-play (PnP) method, the proposed INN-based enhancer can be easily integrated into existing high-fidelity compression algorithms, enabling flexible and simultaneous decoding of images with enhanced perceptual quality.

1. Introduction

Remote sensing (RS) images have been widely applied in various fields, including urban planning [1], resource management [2], and disaster monitoring [3]. However, RS images are typically characterized by high content, high resolution, and a large size [4]. Furthermore, with the advancement of sensor technology and the enhancement of the image acquisition capability of satellite and airborne equipment, the necessity for storing or transmitting RS images is also growing in importance. To cope with these challenges, high-resolution RS images are usually compressed before they are stored and transmitted to the ground. In this case, it is critical to achieve low-bitrate compression while obtaining decoded images with high perceptual quality.

Traditional image compression algorithms, including JPEG2000 [5], BPG [6], and VVC [7], have been instrumental in facilitating the storage and transmission of image data. However, image compression with these algorithms inevitably suffers from undesired blocking, ringing artifacts, and blurring [8,9], which may highly influence the perception quality.

With the development of deep learning techniques, learning-based image compression methods have made significant progress in obtaining high rate-distortion (RD) performance [10,11,12,13,14,15]. Notably, in natural image compression, Ballé et al. [16] proposed to view additional side information as a hyper-prior entropy model to estimate a zero-mean Gaussian distribution, laying the foundation for subsequent improvements in entropy modeling. Cheng et al. [9] further introduced discretized Gaussian mixture likelihoods to realize the distribution estimation of the entropy model, resulting in impressive decoding performance. Meanwhile, He et al. [17] developed a spatial-channel contextual adaptive model, enhancing compression performance without sacrificing computational speed. Liu et al. [13] leveraged the local modeling ability of convolutional neural networks (CNNs) and the non-local modeling strengths of Transformers to develop the encoder and decoder networks. A channel-squeezing-based entropy model was further proposed to enhance RD performance. Jiang et al. [15] proposed capturing the channel-wise, local spatial, and global spatial correlations present in latent representations to develop a comprehensive entropy model, which was then employed to design the competitive image compression method MLIC++. Despite the success of learning-based compression algorithms in natural scenes, RS images present unique challenges due to their rich texture, weak correlation, and low redundancy compared to natural images [18,19]. Traditional metrics, such as PSNR and SSIM, though widely used to evaluate the fidelity of compressed images, often fail to align with human visual perception, particularly in low-bitrate scenarios. These metrics emphasize pixel-wise similarity but overlook global structural consistency and fine details that are crucial for visually appealing images. This limitation has been extensively discussed in recent studies on deep learning-based image compression, where perceptual quality, rather than purely objective fidelity, has proven to better match human visual preferences. Enhanced perceptual quality allows for more reliable real-time monitoring and decision making in fields such as environmental monitoring and disaster management.

To achieve high perceptual quality, Zhang et al. [10] introduced a multi-scale attention module to enhance the network’s feature extraction capability, and they developed an improved entropy model using global priors and anchored-stripe attention. Pan et al. [20] resorted to generative adversarial networks (GANs) to independently reconstruct the image content and detailed textures, subsequently fusing these features to achieve low-bitrate RS image compression. Additionally, Xiang et al. [21] utilized discrete wavelet transform to separate image features into high- and low-frequency components, and they also designed compression networks to enhance the model’s representation ability of both of the types of features.

In summary, the abovementioned deep learning-based image compression methods typically achieve image compression through CNN blocks [9,10,11,16,17,21] or Transformer blocks [22,23,24,25,26], followed by optimization using distance measurements like ${\mathrm{L}}_1$, ${\mathrm{L}}_2$, or adversarial loss [27]. Despite their impressive performance, these methods usually struggle to generate satisfactory perception quality while maintaining high image fidelity. Recently, invertible neural network (INN) has emerged as a new paradigm for image generation, demonstrating remarkable performance across various applications [28,29,30,31,32]. For instance, Zhao et al. [28] leveraged INN to allow the color information lost during grayscale image generation to remain independent of the input image. Similarly, Xiao et al. [32] employed an INN-based framework to address the information loss during downscaling mapping by modeling the bidirectional degradation and restoration from a new perspective. Building on the success, several approaches have integrated INN into image compression to capture richer texture details [25,29].

For instance, in [25], an enhanced INN-based encoding network was devised to improve the decoding performance of natural image compression. In [29], the authors utilized INN to develop an invertible image generation module, aiming to prevent information loss and propose a competitive low-bit-rate compression algorithm. Unlike these methods, the proposed approach focuses on leveraging the invertible capabilities of INN to recover more texture information of the images that are decoded by an existing compression algorithm without requiring additional bitstreams and model retraining. Particularly, it aims to transform the complex compression distortion distribution of the compression algorithm into a simpler, well-defined Gaussian distribution through forward processing. During inverse processing, it samples additional texture details from the Gaussian-distributed variables conditioned on the decoded image, thereby enriching the reconstructed output with finer details. Figure 1 illustrates the perception comparison between the decoded images and the enhanced images. Here, bits per pixel (bpp) is used as a key metric to quantify the compression efficiency, representing the average number of bits required to encode each pixel in the image. A lower bpp value indicates higher compression efficiency, while a higher bpp value typically corresponds to better image quality. One can see that the proposed INN-RSIC exhibits a high capability in recovering texture-rich details without additional bitrates, demonstrating its effectiveness in balancing compression efficiency and perceptual quality.

In this paper, we propose the invertible neural network-based remote sensing image compression (INN-RSIC) method. Specifically, we utilize an invertible forward network with a conditional generation module (CGM) to encode the compression loss information of an existing image compression algorithm into Gaussian-distributed latent variables. As a result, it is expected to sample some of the lost prior information from Gaussian distribution, thereby facilitating the recovery of visually enhanced images during inverse mapping. Additionally, to effectively learn compression distortion, we adopted channel expansion and Haar transformation [33] to separate the high and low frequencies and introduced a quantization module (QM) to reduce the impact of the reconstruction quality due to data type conversion in the inference stage.

The primary contributions of this paper can be summarized as follows.

• The proposed INN-RSIC is the first attempt to model the image compression distortion of an image compression method using invertible transforms. It serves as a PnP method to obtain highly perceptible decoded images while preserving the performance of the baseline algorithm.
• We develop a novel, effective yet simple architecture with channel expansion, Haar transformation, and invertible blocks. This architecture enables projecting compression distortion into a case-agnostic distribution so that the compression distortion information can be obtained based on samples from a Gaussian distribution.
• CGM is introduced to split and encode the compression distortion information from the ground truth into the latent variables conditioned on the synthetic image. This process generates pattern-free synthetic images and enhances the texture details of the reconstructed images during inverse mapping.
• Extensive experiments indicate that the proposed INN-RSIC achieves a superior balance of perceptual quality and high image fidelity compared to existing state-of-the-art image compression algorithms. Our method offers a novel perspective for image compression algorithms to improve their perception quality.

2. Related Work

2.1. End-to-End RS Image Compression

In RS image compression, many researchers have directed their attention toward network structure and image transformation techniques [20,21,34,35]. For instance, Pan et al. [20] adopted GANs to independently decode the image content and detailed textures, later combining these features to achieve a low-bitrate compression of RS images. More recently, Xiang et al. [21] leveraged the discrete wavelet transform to separate image features into high- and low-frequency components. They then designed compression networks to bolster the model’s ability to present these features at different frequencies to recover texture-rich details.

Moreover, in the pursuit of advancing network modules for decoding more texture-rich details of RS image compression, some studies have aimed to improve the estimated accuracy of the entropy model. Pan et al. [8] proposed a hybrid attention network to improve the prediction accuracy of the entropy model and enhance the representation capabilities of both the encoder and decoder. In [36], a long-range convolutional network was developed as a network model to improve the decoding performance of RS image compression. Fu et al. [37] considered the local and non-local redundancies presented in RS images and developed a mixed hyperprior network to explore both, thus improving the accuracy of entropy estimation.

In summary, the above RS image compression algorithms mainly focus on designing complex networks for compact latent variable representation and more accurate entropy estimation to achieve texture-rich decoding results. Different from the above methods, we innovatively project the compression distortion loss of decoded images from an image compression method into Gaussian-distributed latent variables in the forward network, while combining the Gaussian distribution with the decoded images in the inverse network to obtain texture-rich enhanced images.

2.2. Invertible Neural Network (INN)

INN offers several advantages, including bijective mapping, efficient mapping access, and computable Jacobi matrices, making it promising for various machine learning tasks [38,39,40,41,42]. For instance, Zhao et al. [28] employed INN to generate invertible grayscale images by separating color information from color images and encoding it into Gaussian-distributed latent variables. This approach ensures that the color information lost during grayscale generation remains independent of the input image. Similarly, Xiao et al. [32] developed invertible models to generate valid degraded images while transforming the distribution of lost contents to a fixed distribution of a latent variable during forward degradation. The restoration was then made tractable by applying the inverse transformation on the generated degraded image along with a randomly drawn latent variable. Liu et al. [41] considered image degradation and super-resolution as a pair of inverse tasks and replaced the generators in GAN with INN for unpaired image super-resolution. In addition, INN technology has been leveraged to improve the transformation between the image space and the latent feature space, thereby mitigating information loss [25]. For instance, Xie et al. [25] proposed an enhanced INN-based encoding network for better image compression. Gao et al. [29] integrated INN into the development of an invertible image generation module to prevent information loss and developed a competitive low-bitrate image compression algorithm.

3. Materials and Methods

Compared to natural images, RS images usually contain richer textures, which makes acquiring RS images at low bit rates more challenging [19]. Therefore, the proposed INN-RSIC aims to utilize INN to encode the residual distortion after compression of an existing image compression algorithm into a set of latent variables $\mathbf{z}$, following a pre-defined distribution, such as a Gaussian distribution. As a result, the distribution of latent variables becomes independent of the distribution of the input image. In the enhanced reconstruction stage of our framework (i.e., the inverse mapping of the proposed INN-RSIC), a new set of randomly sampled latent variables $\overrightarrow{\mathbf{z}}$ can effectively represent the residual distortion after compression information to some extent. Thus, we can simply feed the re-sampled $\overrightarrow{\mathbf{z}}$, along with the decoded images, to the INN-RSIC of the inverse network for enhanced images.

Generally, the distribution of compression distortion information varies among different learning-based methods, as each exhibits distinct preferences in learning data distribution. For instance, some algorithms excel in achieving high performance on texture-rich images, while others deliver on the opposite. Therefore, we focus here on the compression distortion distribution of the impressive image compression algorithm ELIC at different bitrates. Unfortunately, pinpointing the distortion distribution directly is challenging. Therefore, we chose to capture the distortion by investigating the relationship between the input image and the decoded image of ELIC. In this way, we can indirectly explore the distortion distribution inherent in the compression algorithm.

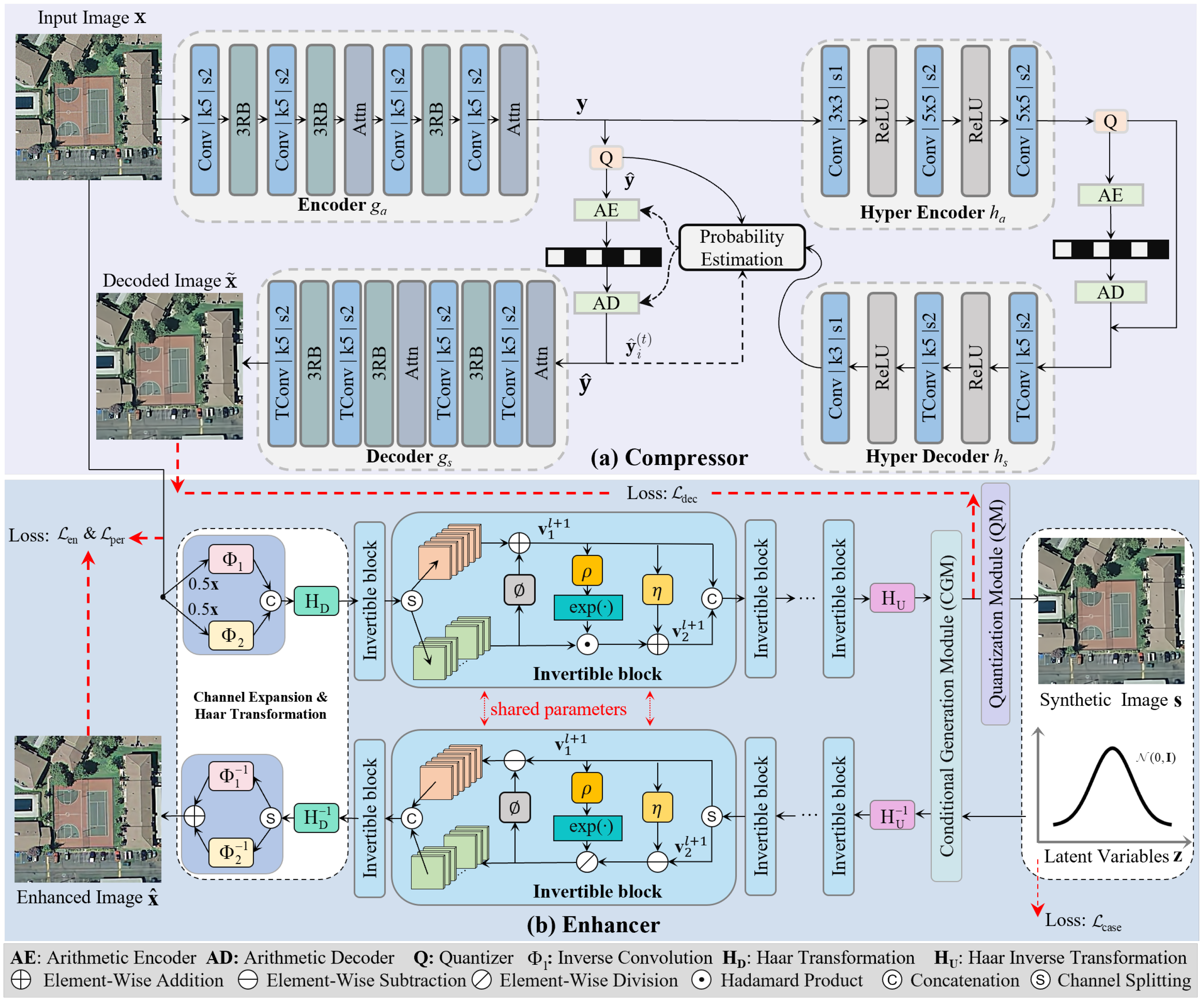
The architecture of the proposed INN-RSIC, consisting of a compressor and an enhancer, is depicted in Figure 2. For the compressor, given an input image $\mathbf{x}\in {\mathbb{R}}^{W\times H\times 3}$, the encoder $g_a(·)$ first extracts the latent representation $\mathbf{y}$, which is then quantized through the operation $Q(·)$ to obtain $\widehat{\mathbf{y}}$. Subsequently, $\widehat{\mathbf{y}}$ is encoded into a bitstream using the estimated probability distribution. On the decoding side, the decoded image $\tilde{\mathbf{x}}$ is reconstructed by feeding $\widehat{\mathbf{y}}$ into the decoder $g_s(·)$. This process can be formally described as follows:

$$\begin{array}{cc}\hfill \mathbf{y}& =g_a\left(\mathbf{x}\right),\hfill \\ \hfill \widehat{\mathbf{y}}& =Q\left(\mathbf{y}\right),\hfill \\ \hfill \tilde{\mathbf{x}}& =g_s\left(\widehat{\mathbf{y}}\right).\hfill \end{array}$$

(1)

To enable efficient arithmetic coding of $\widehat{\mathbf{y}}$, the hyper networks $h_a(·)$ and $h_s(·)$ are typically employed to estimate the probability model. For the enhancer, it mainly comprises two streams: the forward and inverse networks, denoted as $f_{\mathsf{\Theta }}(·)$ and $f_{\mathsf{\Theta }}^{-1}(·)$, respectively, where $\mathsf{\Theta }$ represents the network parameters.

3.1. INN Architecture

3.1.1. Invertible Block

The invertible block layer is a crucial component in invertible architectures, acting as a bridge to adapt between two different distributions via its trainable parameters. Figure 2b depicts the structure of an invertible block. An inverse block operates on an input feature map $\mathbf{v}\in {\mathbb{R}}^{H\times W\times C}$, where H, W, and C denote the height, width, and the number of channels, respectively. In each invertible block, $\mathbf{v}$ is split along the channel dimension into two parts $[{\mathbf{v}}_1,{\mathbf{v}}_2]$, where ${\mathbf{v}}_1\in {\mathbb{R}}^{H\times W\times C_1}$, ${\mathbf{v}}_2\in {\mathbb{R}}^{H\times W\times C_2}$, and $C_1+C_2=C$. To obtain the input features of the $(l+1)$-th invertible block, inverse transformations are applied to both segments using learnable scale and shift parameters by

$$\begin{array}{cc}\hfill {\mathbf{v}}_1^{l+1}& ={\mathbf{v}}_1^l+\varphi \left({\mathbf{v}}_2^l\right),\hfill \\ \hfill {\mathbf{v}}_2^{l+1}& ={\mathbf{v}}_2^l\odot \exp \left(\rho \left({\mathbf{v}}_1^{l+1}\right)\right)+\eta \left({\mathbf{v}}_1^{l+1}\right),\hfill \end{array}$$

(2)

where ⊙ refers to the Hadamard product. The $\phi (·)$, $\rho (·)$, and $\eta (·)$ are achieved by the dense blocks [43]. Therefore, the inverse transformation can be derived from Equation (2) by 

$$\begin{array}{cc}\hfill {\mathbf{v}}_1^l& ={\mathbf{v}}_1^{l+1}-\varphi \left({\mathbf{v}}_2^l\right),\hfill \\ \hfill {\mathbf{v}}_2^l& =({\mathbf{v}}_2^{l+1}-\eta \left({\mathbf{v}}_1^{l+1}\right))\oslash \exp \left(\rho \left({\mathbf{v}}_1^{l+1}\right)\right),\hfill \end{array}$$

(3)

where ⊘ denotes element-wise division.

In addition, as illustrated in Figure 2b, the forward network outputs the synthetic image $\mathbf{s}$ and the latent variable $\mathbf{z}$. Following the studies [25,29], we assume that $\mathbf{z}$ follows a Gaussian distribution, which can be randomly sampled from the same distribution for the inverse mapping. Consequently, in the training stage, the synthetic image $\mathbf{s}$ and $\mathbf{z}$ can be merged and fed into the inverse network for model optimization. In the inference stage, the decoded image $\tilde{\mathbf{x}}$ and resampled $\overrightarrow{\mathbf{z}}\sim \mathcal{N}(0,\mathbf{I})$ can be combined and fed into the inverse network for image enhancement.

3.1.2. Channel Expansion and Haar Transformation

Within each invertible block, the channels of both its input and output signals have the same number. However, in addition to generating the synthetic image, we also need to produce an expanded output to derive the Gaussian latent variable $\mathbf{z}$. To achieve this, as shown in Figure 2b, we double the number of channels of the input image using $1\times 1$ convolutional layers. In addition, Haar transformation [33] is used here to separate the compression distortion information by splitting the high and low frequencies, which are then fed into the invertible blocks.

Specifically, in the forward network, given the ground truth $\mathbf{x}$, the feature $\mathbf{F}$ fed into the first invertible block can be expressed as

$$\mathbf{F}=H_D\left(\mathrm{Concat}({\mathsf{\Phi }}_1(\mathbf{x}/2.0),{\mathsf{\Phi }}_2(\mathbf{x}/2.0))\right),$$

(4)

where $H_D(·)$ denotes the Haar function, $\mathrm{Concat}(·)$ refers to a concatenation operation, and ${\mathsf{\Phi }}_1(·)$ and ${\mathsf{\Phi }}_2(·)$ refer to two $1\times 1$ convolution layers. After the last invertible block, the inverse Haar function $H_U(·)$ is adopted to transform the features from the frequency domain to the spatial domain.

As a result, at the end of the forward network, we can thus obtain six-channel signals with the same size as the input image, and, with CGM, we derive both the synthetic image $\mathbf{s}$ and Gaussian latent variables $\mathbf{z}$, which are then combined and fed into the inverse network for image recovery.

In the inverse network, the inverse processing of Equation (4) can be formulated as

$$\begin{array}{cc}\hfill {\mathbf{p}}_i& =\mathrm{Split}\left(H_D^{-1}\left(\mathbf{F}\right)\right), i\in \{1,2\},\hfill \\ \hfill \mathbf{x}& ={\mathsf{\Phi }}_1^{-1}\left({\mathbf{p}}_1\right)+{\mathsf{\Phi }}_2^{-1}\left({\mathbf{p}}_2\right),\hfill \end{array}$$

(5)

where ${\mathsf{\Phi }}_1^{-1}(·)$, ${\mathsf{\Phi }}_2^{-1}(·)$, and $H_D^{-1}(·)$ refer to the inverse functions of ${\mathsf{\Phi }}_1(·)$, ${\mathsf{\Phi }}_2(·)$, and $H_D(·)$, respectively. Next, we will illustrate CGM in detail.

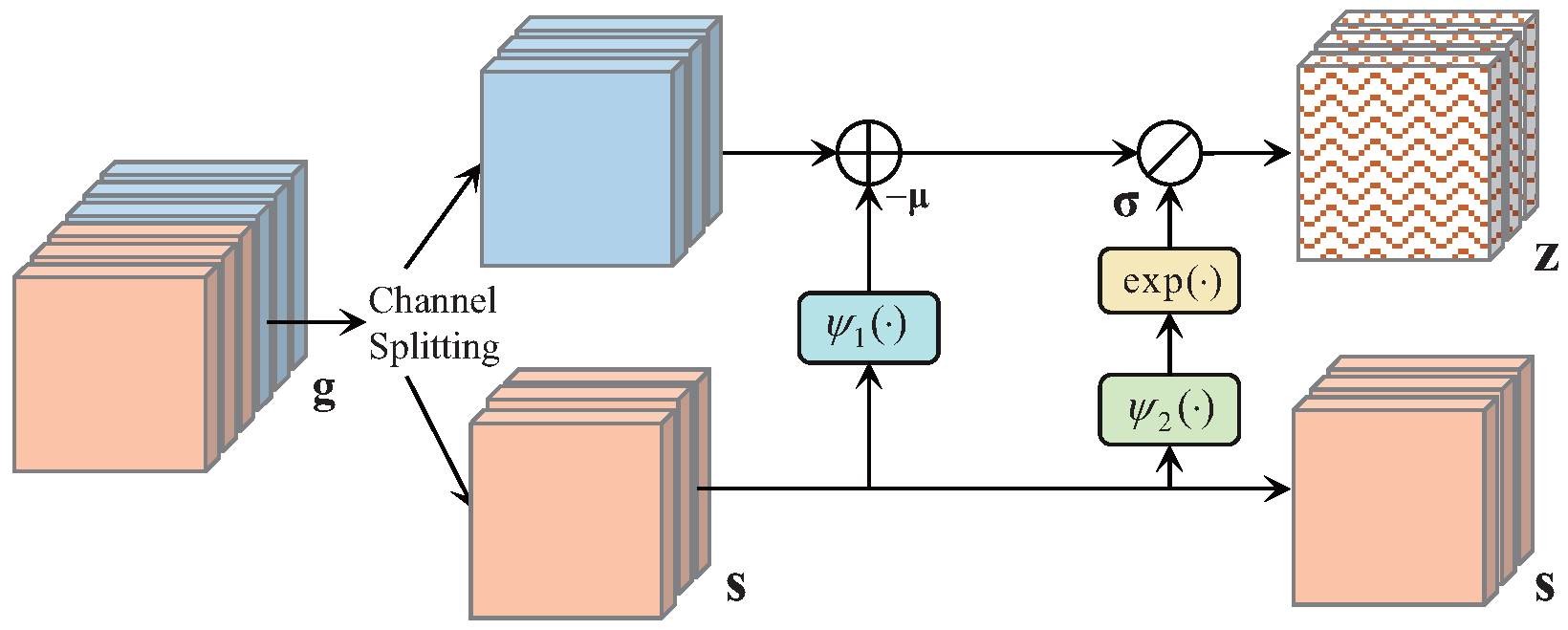
3.1.3. Conditional Generation Module (CGM)

As illustrated above, we aim to encode the compression distortion information of decoded RS images into a set of Gaussian-distributed latent variables, where the mean and variance are conditioned on the synthetic image. This conditioning enables the reconstruction process to be image-adaptive. To achieve this, as illustrated in Figure 2b, we introduce CGM at the end of the forward network. Specifically, to establish the dependency between $\mathbf{s}$ and $\mathbf{z}$, as depicted in Figure 3, the output six-channel tensor $\mathbf{g}$ from the last invertible block is further divided by CGM into two parts: a three-channel synthetic image $\mathbf{s}$, and a three-channel latent variable $\tilde{\mathbf{z}}$ (representing the compression distortion information).

In the forward mapping, inspired by [28], we normalize $\tilde{\mathbf{z}}$ into standard Gaussian-distributed variables $\mathbf{z}$ by $\mathbf{z}=(\tilde{\mathbf{z}}-\mathit{\mu })\oslash \mathit{\sigma }$, where $\mathbf{z}\sim \mathcal{N}(0,\mathbf{I})$, and the mean and scale of $\mathbf{s}$ can be calculated by

$$\begin{array}{cc}\hfill \mathit{\mu }& ={\psi }_1\left(\mathbf{s}\right),\hfill \\ \hfill \mathit{\sigma }& =\exp \left({\psi }_2\left(\mathbf{s}\right)\right),\hfill \end{array}$$

(6)

where ${\psi }_1(·)$ and ${\psi }_2(·)$ are achieved by the dense block [43]. Hence, its reverse mapping can be formulated as $\tilde{\mathbf{z}}=\mathbf{z}\odot \mathit{\sigma }+\mathit{\mu }$, where $\tilde{\mathbf{z}}\sim \mathcal{N}(\mathit{\mu },\mathit{\sigma })$. In this way, we encode the compression distortion information into the latent variables, whose distribution is conditioned on the synthetic image. The inverse network is similar to [28,32], where we sample a set of random variables from the Gaussian distribution conditioned on the synthetic images to reconstruct the enhanced images.

3.1.4. Quantization Module (QM)

To ensure compatibility with common decoded image storage formats, such as RGB (8 bits for each R, G, and B color channels), as shown in Figure 2b, we integrated QM after CGM. This module converts the floating-point values of the produced synthetic images into 8-bit unsigned integers by a rounding operation for quantization. However, it is essential to acknowledge a significant obstacle: the quantization module is inherently non-differentiable. To cope with the challenge, we employed the pass-through estimator technique used in [17] to ensure that INN-RSIC is efficiently optimized during the training process. Subsequently, in the inference stage, the decoded image can be reasonably fed into the inverse network for image enhancement.

3.2. Optimization Strategy

3.2.1. Compression Optimization Loss

As we aim to capture the compression distortion of ELIC [17], we provide here a brief overview of its loss function. Specifically, to balance the compression ratio and the image quality of the decoded image of ELIC, the loss function can be formulated as 

$${\mathcal{L}}_1=R+\lambda D(\mathbf{x},\tilde{\mathbf{x}}),$$

(7)

where the rate R refers to the entropy of the quantized latent variables of ELIC. Meanwhile, $D(·,·)$ denotes the similarity between the input image and the decoded image, which is typically measured using the mean squared error (MSE). Different compression rates can be achieved by adjusting the hyperparameter $\lambda$, where the higher the value of $\lambda$, the higher the bpp and the better the image quality.

3.2.2. Forward Presentation Loss

The forward network is primarily focused on enabling the proposed model to capture the compression distortion distribution of the decoded image. This is achieved by establishing a correspondence between the input image $\mathbf{x}$ and the decoded image $\tilde{\mathbf{x}}$, as well as a case-agnostic distribution $p\left(\mathbf{z}\right)$ of $\mathbf{z}$. It can be realized by developing two loss functions: decoded image loss and case-agnostic distribution loss.

Decoded Image Loss

To generate the guidance images for training the forward network, ELIC is adopted to generate the labeled image $\tilde{\mathbf{x}}$, which can be formulated as

$$\tilde{\mathbf{x}}=\mathrm{ELIC}(\mathbf{x},\lambda ).$$

(8)

Thereafter, to make our model follow the guidance, we drive the synthetic image $\mathbf{s}=f_{\mathsf{\Theta }}\left(\mathbf{x}\right)$ to resemble $\tilde{\mathbf{x}}$, which can be derived by

$${\mathcal{L}}_{\mathrm{dec}}=\left|\right|f_{\mathsf{\Theta }}\left(\mathbf{x}\right)-\tilde{\mathbf{x}}{\left|\right|}^2.$$

(9)

Case-Agnostic Distribution Loss

To regularize the distribution of $\mathbf{z}$, we maximize, inspired by [28], the log-likelihood of $p\left(\mathbf{z}\right)$. Thus, the loss function to constrain the latent variables $\mathbf{z}$ can be formulated as

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{case}}& =-\log \left(p\right(\mathbf{z}\left)\right)\hfill \\ & =-\log \left({\displaystyle \frac{1}{{\left(2\pi \right)}^{M/2}}}\exp \left(-{\displaystyle \frac{1}{2}}{\left|\right|\mathbf{z}\left|\right|}^2\right)\right),\hfill \end{array}$$

(10)

where M is the dimensionality of $\mathbf{z}$. This loss function penalizes the normalized latent variables $\mathbf{z}$ to follow standard Gaussian distribution. Consequently, in the inverse processing, we can randomly sample a set of Gaussian-distributed variables along with the synthetic image to derive the enhanced image.

3.2.3. Reverse Reconstruction Loss

The inverse network aims to guide the model in recovering visually appealing images using randomly sampled latent variables and synthetic images. This is achieved by developing two loss functions: enhancement reconstruction loss and quality perception loss.

Enhancing Reconstruction Loss

In theory, the synthetic image can be perfectly restored to the corresponding ground truth version through the inverse network of INN because there is no information omission. However, in practice, the decoded image is not generated by the forward network of the proposed INN-RSIC but with an image compression method, that is, the synthetic image should be stored in 8-bit unsigned integer format so that the decoded image can be used directly here instead of the synthetic image for image detail enhancement during the inference stage. To address this, we adopt QM at the end of the forward network during training. Consequently, by penalizing the discrepancy between the reconstructed image and the ground truth, we can derive the enhancing reconstruction loss given as

$${\mathcal{L}}_{\mathrm{en}}=\left|\right|f_{\mathsf{\Theta }}^{-1}(\mathbf{s},\overrightarrow{\mathbf{z}})-\mathbf{x}{\left|\right|}^2,$$

(11)

where $\overrightarrow{\mathbf{z}}$ denotes the re-sampled latent variables from standard Gaussian distribution, and the synthetic image can be derived by $\mathbf{s}=\mathrm{QM}\left(f_{\mathsf{\Theta }}\left(\mathbf{x}\right)\right)$.

Quality Perception Loss

To improve the perceptual performance of the network by estimating the distances in predefined feature space rather than image space, a perceptual loss function called ${\mathcal{L}}_{\mathrm{per}}$ is used here. In other words, the feature space distance is represented by an optimization function, which serves as a driver for the network to perform image reconstruction while retaining a feature representation similar to the ground truth. Concretely, the learning perceptual image patch similarity (LPIPS) [44] is utilized to indicate the perceptual loss, which is defined as

$${\mathcal{L}}_{\mathrm{per}}=\left|\right|\mathrm{Vgg}\left(\widehat{\mathbf{x}}\right)-\mathrm{Vgg}\left(\mathbf{x}\right){\left|\right|}^2,$$

(12)

where $\mathrm{Vgg}(·)$ denotes a feature function that leverages the features extracted at the “Conv4-4” layer of VGG19 to penalize the contrast similarity between $\widehat{\mathbf{x}}$ and $\mathbf{x}$, as was adopted in [45].

Therefore, the total loss function can be given by

$${\mathcal{L}}_{\mathrm{total}}={\lambda }_1{\mathcal{L}}_{\mathrm{dec}}+{\lambda }_2{\mathcal{L}}_{\mathrm{case}}+{\lambda }_3{\mathcal{L}}_{\mathrm{en}}+{\lambda }_4{\mathcal{L}}_{\mathrm{per}},$$

(13)

where ${\lambda }_1,{\lambda }_2,{\lambda }_3$, and ${\lambda }_4$ are hyperparameters used to balance the different loss terms.

Thus, after obtaining the trained model, in the inference stage, given a decoded image $\tilde{\mathbf{x}}$ through using Equation (8), we can derive its enhanced image $\widehat{\mathbf{x}}$ by $\widehat{\mathbf{x}}=f_{\mathsf{\Theta }}^{-1}(\tilde{\mathbf{x}},\overrightarrow{\mathbf{z}})$, where $\overrightarrow{\mathbf{z}}$ refers to the latent variables sampled from Gaussian distribution $\overrightarrow{\mathbf{z}}\sim \mathcal{N}(0,\mathbf{I})$. It can be observed that there is no additional bitrate acquirement for the enhancement processing of the decoded image. The training and inference stages of the proposed INN-RSIC are summarized in Algorithm 1.

Algorithm 1: Processing of INN-RSIC

1 Training Stage:

2      Input: $\mathbf{x},\lambda$

3      Output: $\tilde{\mathbf{x}},\mathsf{\Theta }$

1: Procedure: Compressor $(\mathbf{x},\lambda )$  2:     $\tilde{\mathbf{x}}=\mathrm{ELIC}(\mathbf{x},\lambda ),$  3: Return: $\tilde{\mathbf{x}}$  4: Procedure: Enhancer $\left(\mathbf{x}\right)$  5:     Initialize parameters $\mathsf{\Theta }$ of INN-RSIC with Xavier.  6:     for epoch ← 1 to num_epochs do  7:         // Compute forward loss:         ${\mathcal{L}}_{\mathrm{dec}}=\left|\right|f_{\mathsf{\Theta }}\left(\mathbf{x}\right)-\tilde{\mathbf{x}}{\left|\right|}^2,$         ${\mathcal{L}}_{\mathrm{case}}=-\log \left({\displaystyle \frac{1}{{\left(2\pi \right)}^{M/2}}}\exp \left(-{\displaystyle \frac{1}{2}}{\left|\right|\mathbf{z}\left|\right|}^2\right)\right),$  8:         // Compute backward loss:         ${\mathcal{L}}_{\mathrm{en}}=\left|\right|f_{\mathsf{\Theta }}^{-1}(\mathrm{QM}\left(f_{\mathsf{\Theta }}\left(\mathbf{x}\right)\right),\overrightarrow{\mathbf{z}})-\mathbf{x}{\left|\right|}^2,$         ${\mathcal{L}}_{\mathrm{per}}=\left|\right|\mathrm{Vgg}\left(\widehat{\mathbf{x}}\right)-\mathrm{Vgg}\left(\mathbf{x}\right){\left|\right|}^2,$  9:         // Compute total loss:         ${\mathcal{L}}_{\mathrm{total}}={\lambda }_1{\mathcal{L}}_{\mathrm{dec}}+{\lambda }_2{\mathcal{L}}_{\mathrm{case}}+{\lambda }_3{\mathcal{L}}_{\mathrm{en}}+{\lambda }_4{\mathcal{L}}_{\mathrm{per}},$  10:        // Update $\mathsf{\Theta }$ using gradient descent:        $\mathsf{\Theta }\leftarrow \mathsf{\Theta }-\alpha \nabla {\mathcal{L}}_{\mathrm{total}}\left(\mathsf{\Theta }\right),$  11:      end for  12: Return: $\mathsf{\Theta }$

Inference Stage:     Input: $\mathbf{x},\lambda$     Output: $\tilde{\mathbf{x}},\widehat{\mathbf{x}}$  1: Procedure: Compressor $(\mathbf{x},\lambda )$  2:      $\tilde{\mathbf{x}}=\mathrm{ELIC}(\mathbf{x},\lambda ),$  3: Return: $\tilde{\mathbf{x}}$  4: Procedure: Enhancer $\left(\tilde{\mathbf{x}}\right)$  5:      Loading the trained $\mathsf{\Theta }$ for INN-RSIC.  6:      // Randomly sample $\overrightarrow{\mathbf{z}}$ and conduct inverse mapping:      $\overrightarrow{\mathbf{z}}\sim \mathcal{N}(0,\mathbf{I}),$      $\widehat{\mathbf{x}}=f_{\mathsf{\Theta }}^{-1}(\tilde{\mathbf{x}},\overrightarrow{\mathbf{z}}),$  7: Return: $\widehat{\mathbf{x}}$

4. Results

4.1. Experimental Settings

4.1.1. Datasets

In this experiment, two datasets, including DOTA [46] and UC-Merced (UC-M) [47], were used for performance evaluation. Concretely, we used the training dataset of DOTA and 80% of the UC-M training set for model training. Each image was randomly cropped into the resolution of $128\times 128$. Random horizontal flip, random vertical flip, and random crop were applied for data augmentation. We randomly chose 100 images and 10% images from the DOTA testing dataset and UC-M, respectively. Then, each image was centrally cropped into the resolution of $256\times 256$ as the testing set.

4.1.2. Implementation Details

In our experiment, we utilized ELIC [17] to compress the images of the training dataset. Concretely, the ELIC models with parameters $\lambda \in \{4,8,32,100,450\}\times {10}^{-4}$ were used to separately derive the decoded images, which were then utilized as labeled images to constrain the forward latent representation. As different compression rates result in different compression distortion distributions of ELIC, the labeled images under each $\lambda$ were used to train the INN-RSIC model. Additionally, to train the proposed model, the widely-used AdamW [48], with ${\beta }_1$ = 0.9 and ${\beta }_2$ = 0.999, was employed for parameter optimization. The hyperparameters ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, and ${\lambda }_4$ were experimentally set to $1.0$, $200.0$, $0.05$, and $0.01$, respectively. We set the initial learning rate $\alpha$ to 1 $\times {10}^{-4}$ and the total number of epochs to 300, with the learning rate halved every 60 epochs until it reached a value smaller than 1 $\times {10}^{-6}$. PSNR, MS-SSIM, and LPIPS [44] were adopted as the evaluation metrics. PSNR and MS-SSIM primarily concentrate on numerical comparisons and structural similarity in images, whereas LPIPS emphasizes perceptual evaluation by leveraging deep learning-based models to extract high-level perceptual features, thus aligning more closely with human visual perception. To maintain experimental rigor and fairness, all of the models were thoroughly trained for comparison and validation.

4.2. Performance Evaluation

In this section, we conduct a comprehensive comparison of the proposed INN-RSIC and several competitive image compression algorithms, using the testing set of DOTA and UC-M. The benchmark includes the state-of-the-art image compression algorithms, including traditional standards such as JPEG2000 [5], BPG [6], VVC (YUV 444) [7], as well as the competitive learning-based image compression algorithms like HiFiC [27], InvComp [25], STF [22], Entrorformer [23], ELIC [17], TCM [13], and MLIC++ [15]. 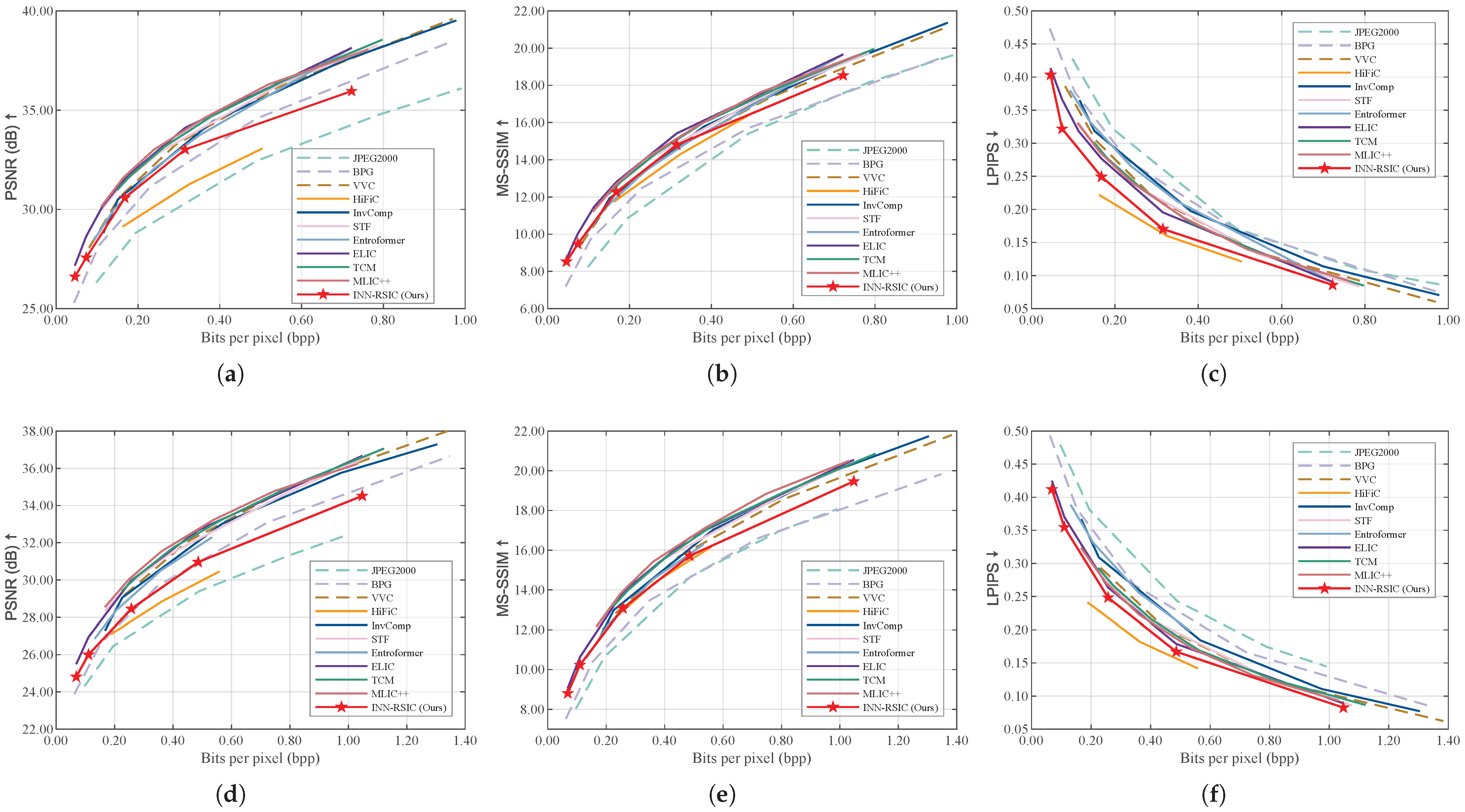The performance comparisons of the tested algorithms on the DOTA and UC-M datasets are presented in Figure 4. The results demonstrate that the proposed INN-RSIC achieves superior performance in terms of LPIPS, except when compared to HiFiC. While HiFiC achieves comparable perceptual quality, its performance suffers from poor image fidelity, as reflected by its low PSNR values.

Notably, at low bitrates (bpp), the gains in LPIPS are minimal for our method. This can be attributed to the high distortion in the decoded image, which limits the ability of the proposed INN-RSIC to effectively recover finer details from the Gaussian distribution conditioned on the decoded image. However, as the bitrate increases, the proposed INN-RSIC demonstrates significant improvements in LPIPS, highlighting its ability to balance perceptual quality and image fidelity more effectively at higher bitrates. Additionally, compared to GAN-based methods like HiFiC, which rely on adversarial training to generate fine-grained textures and global structural consistency, our lightweight INN-based method prioritizes simplicity and efficiency. As a result, while both methods achieved comparable LPIPS scores, HiFiC benefits from its generative capabilities of GAN. However, our method’s advantage lies in its reduced computational complexity and ability to seamlessly integrate with existing image compression frameworks as a lightweight PnP module.

Additionally, Figure 5 shows the decoding results of these algorithms on the testing images of DOTA and UC-M at low and high bitrates. As shown in Figure 5a, it is noticeable that the image “P0121” decoded by the state-of-the-art traditional compression algorithm VVC exhibited obvious distortion, even with an additional 23.66% increase in bpp compared to the proposed INN-RSIC. Moreover, the decoded image from the competitive learning-based compression algorithm STF still suffers from significant distortion, despite a 70.73% increase in bpp. At high bitrates, the decoded image “P0216” by VVC presents blurry texture details despite the higher bpp. Particularly, it is evident that the perception quality of the decoded images by STF remains inferior to that of the proposed INN-RSIC, even with a 65.63% increase in additional bpp. Similarly, as depicted in Figure 5b, the results further confirm that the proposed INN-RSIC demonstrates impressive perception quality compared to traditional and deep learning-based image compression algorithms at both low and high bitrates. Further, Figure 6 visualizes the decoded images from HiFiC and the proposed INN-RSIC. The results clearly demonstrate that, at comparable bpp values, the proposed method produces images with finer details and better image fidelity, achieving a closer resemblance to the ground truth.

In summary, we can safely demonstrate that the proposed INN-RSIC effectively and impressively contributes to the detailed recovery of decoded images without increasing additional bitrates.

4.3. Ablation Evaluation

4.3.1. Effectiveness of QM

QM considers the impact of the format mismatch on the reconstruction performance of the inverse mapping. Since the ground truth is not available at the decoding end, i.e., the synthetic image is not available, we therefore use the decoded image as the inverse input to the proposed INN-RSIC in the inference stage. Figure 7 shows the quality metrics of the proposed model with and without QM for enhancing the decoded images of ELIC on the testing set of DOTA and UC-M. From the results, it can be seen that the proposed model with QM presents better perception quality results on both datasets. The reason lies in the fact that the input images fed into the proposed INN-RSIC are 3-channel 8-bit RGB images during the inference stage, and QM can better contribute to the proposed model to match the data type of the input images.

4.3.2. Effectiveness of CGM

CGM aims to incorporate guidance from synthetic images into the latent variables during the reconstruction of texture-rich images. To demonstrate the effectiveness of this approach. Figure 7 presents the performance of the proposed INN-RSIC with and without CGM on the testing sets of DOTA and UC-M. It is evident that the INN-RSIC with CGM consistently outperforms the model without CGM in terms of LPIPS. This implies that encoding latent variables into Gaussian-distributed variables conditioned on synthetic images can enhance the reconstruction performance during inverse mapping. This observation is also consistent with earlier research [28].

To visualize the effectiveness of QM and CGM, Figure 8 shows the enhanced images of the proposed INN-RSIC with and without QM or CGM on the decoded images “P0088” and “P0097” by ELIC. The results indicate that, although the enhanced images have higher perceptual quality than the decoded images when either QM or CGM is not available, the proposed INN-RSIC provides the best perceptual quality when QM and CGM are used.

4.3.3. Effectiveness of Prior Distribution and Wavelet Transform

To evaluate the impact of the latent prior distribution and wavelet transform on the proposed INN-RSIC framework, we conducted comparative experiments using different prior types and wavelet bases. Specifically, we replaced the default Gaussian prior with a Laplacian distribution and also compared the commonly used Haar wavelet with the smoother Daubechies-4 (db4) wavelet. For consistency, the state-of-the-art compression model DCAE [49], with $\lambda =0.0018$, was used as the baseline. All comparative evaluations were conducted on the DOTA testing set.

As shown in

Table 1. Performance comparison using different prior distributions, showing that the Gaussian prior better supports residual mapping than the Laplacian prior.

Methods	PSNR (dB) ↑	MS-SSIM ↑	LPIPS ↓
Baseline (DCAE)	30.21	11.2960	0.3240
Laplacian + Haar	28.79	10.6048	0.3029
Gaussian + db4	29.39	10.9528	0.3047
Gaussian + Haar (Ours)	29.37	10.8302	0.3025

, replacing the Gaussian prior with a Laplacian one led to a drop in PSNR and MS-SSIM, and it introduced more visible artifacts in reconstructed images, as illustrated in Figure 9. This indicates that the Gaussian prior better models the residual distribution in the latent space, yielding more stable training and improved fidelity.

From a theoretical standpoint, the choice of a Gaussian prior is supported by the maximum entropy principle, which states that the Gaussian distribution maximizes entropy among all distributions with a given mean and variance. This makes it the least biased and most information-preserving assumption under limited prior knowledge. Furthermore, the smoothness and differentiability of the Gaussian log-likelihood facilitate more stable and efficient optimization in INN-based models. This is consistent with the fact that the default optimization objective in most INN-based architectures [28,29,32,45] assumes a standard Gaussian prior in the latent space.

Regarding the choice of wavelet, as also reported in Table 1, the comparison between Haar and db4 revealed only marginal differences in performance. This indicates that both wavelet bases are comparably effective for capturing the structural information during invertible mapping. Nonetheless, Haar remains slightly preferable in our setting due to its computational simplicity and marginally better perceptual metrics.

In summary, the experimental results support the rationale behind our design: the Gaussian prior, grounded in the maximum entropy principle, outperforms the Laplacian prior in both stability and reconstruction quality. While db4 yields comparable results, the Haar wavelet offers a better trade-off between perceptual performance and computational simplicity. Therefore, we adopted the Gaussian prior and Haar wavelet as the default configuration in INN-RSIC.

4.4. Robustness Evaluation

4.4.1. Adaptability to Different Compression Rates

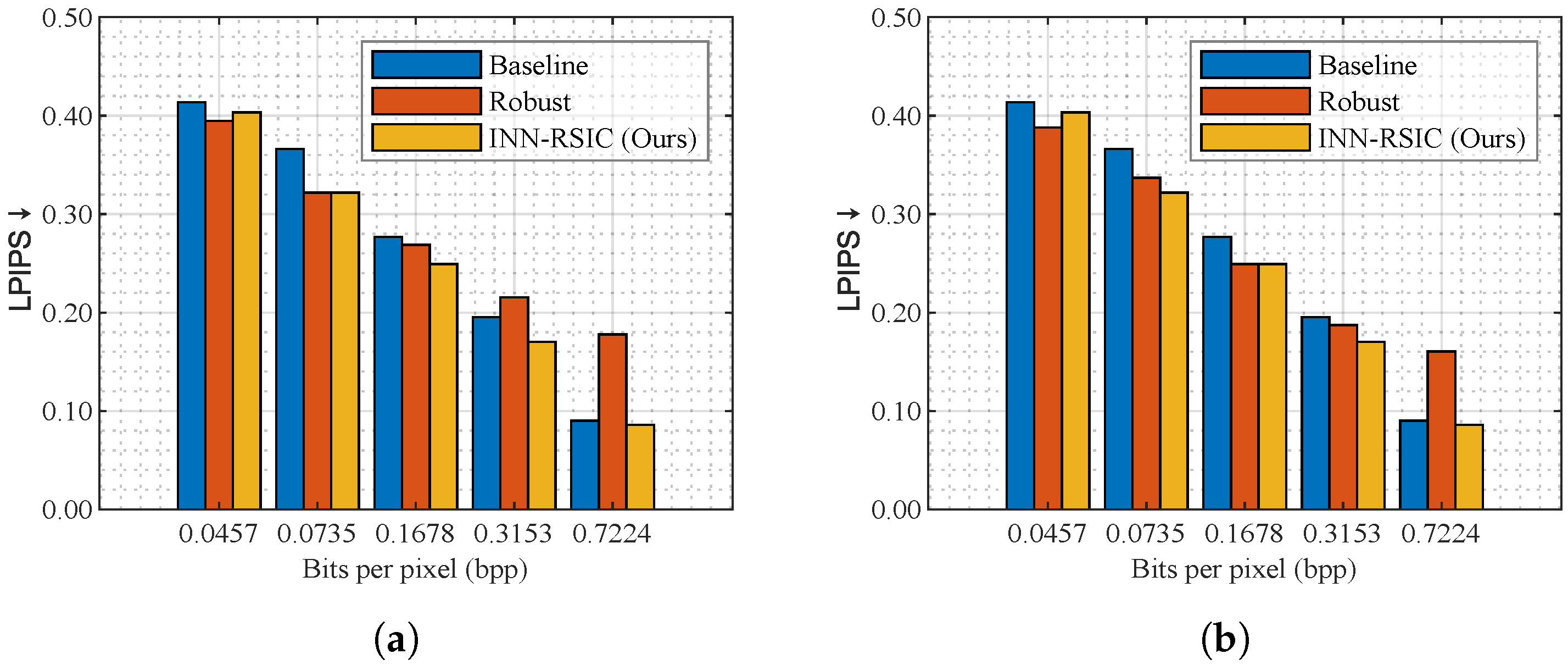
The robustness of a model is crucial for its practical deployment. We investigated the performance of INN-RSIC when trained at a specific compression rate but evaluated at different rates, aiming to examine its adaptability to varying compression conditions. Here, we employed two INN-RSIC models trained at two values of $\lambda$ to enhance the decoded images of ELIC across various compression ratios. The proposed INN-RSIC trained at $\lambda =8\times {10}^{-4}$ was used to enhance the images compressed and was decoded using ELIC at different $\lambda$ for the images in the testing set of DOTA, where $\lambda \in \{4,8,32,100,450\}\times {10}^{-4}$.

Figure 10a depicts the LPIPS comparison results, from which one can see that the proposed INN-RSIC trained with the corresponding $\lambda$ demonstrated the most significant improvement in perception quality in terms of LPIPS, except when $\mathrm{bpp}=0.0457$. The poorer performance of the proposed INN-RSIC at low bpp (i.e., $\lambda =4\times {10}^{-4}$) may be because the quality of the corresponding decoded image is poor at very low bpp, whereas the Gaussian-distributed variables are conditioned on the decoded image, that is, the decoded image has limited guidance to enable INN-RSIC to recover stable results.

Furthermore, we investigated the robustness of the proposed INN-RSIC model trained at high bitrate conditions in improving decoded images across different bitrate levels. The proposed INN-RSIC trained at $\lambda =32\times {10}^{-4}$ was used to enhance the images compressed and decoded using ELIC at different $\lambda$ for the images in the testing set of DOTA, where $\lambda \in \{4,8,32,100,450\}\times {10}^{-4}$. LPIPS comparison results are illustrated in Figure 10b. Comparing the LPIPS values between the baseline and robust cases, it was observed that, except for $\mathrm{bpp}=0.7224$, the proposed model trained at $\lambda =32\times {10}^{-4}$ can still improve perception quality across different bitrate levels, except for $\lambda =4\times {10}^{-4}$.

To visualize the robust performance of the model, the robust case in Figure 11a,b show the enhanced images obtained by augmenting the decoded images of ELIC at high and low bitrates using the INN-RSIC model trained at low and high bitrates, respectively. The baseline denotes the image decoded by ELIC. From the results, it can be observed that, although the decoded image of the robust case presents more artifacts and burrs compared to the ground truth and the proposed INN-RSIC, it presents better visual characteristics and recovers more texture information compared to the baseline on the global vision.

In summary, the results indicate that both the proposed models trained at low and high bitrates exhibit effective enhancement of perception quality for decoded images across a wide range of bpp levels, highlighting the impressive robustness of the proposed INN-RSIC in enhancing decoded images.

4.4.2. Generalizability with Other Image Compression Algorithms

We further evaluate the generalizability of INN-RSIC by replacing the baseline with both classical traditional and state-of-the-art learning-based image compression algorithms, namely JPEG2000 and DCAE [49]. Figure 12 illustrates the improved results on two testing images, “P0017” and “P0080”, from the DOTA dataset.

When combined with JPEG2000, it is evident that, while color distortion is significantly corrected and edge details are improved, the enhanced images still suffer from severe artifacts. This issue may arise because JPEG2000 tends to introduce “ringing” artifacts near edges or high-contrast areas due to the truncation effect of the wavelet transform. The complex and variable nature of these artifacts makes it challenging for the INN to suppress them effectively. In contrast, when combined with DCAE, the enhanced images exhibit improved perceptual quality. It is worth noting that, in these experiments, the quantization parameter (QP) for JPEG2000 was set to 0.2, and a rate of $\lambda =0.0018$ was adopted in DCAE to generate the baseline images.

To sum up, these results demonstrate the effectiveness of the proposed method in integrating with both traditional and learning-based algorithms, further highlighting the generalizability and versatility of the developed framework.

4.4.3. Robustness Across Various Resolutions

We assessed the effectiveness of INN-RSIC on input images of varying resolutions, validating its robustness across different scales. Specifically, we evaluated the performance of the developed INN-RSIC on input images with resolutions of $128\times 128$ and $512\times 512$. The $128\times 128$ images were obtained by center-cropping two images from the DOTA testing set, while the $512\times 512$ images were randomly cropped from the DOTA testing dataset. As shown in Figure 13, INN-RSIC consistently improved performance compared to the baseline, demonstrating its effectiveness across different resolutions. These results highlight the robustness of the proposed method when handling images of varying scales.

4.5. Model Complexity

To assess the computational complexity of the proposed method, we conducted the experiments on the DOTA testing set with an Intel Silver 4214R CPU running at 2.40 GHz and one NVIDIA GeForce RTX 3090 Ti GPU. The average results are given in

Table 2. Comparison of the parameters and computational cost of the various image compression algorithms.

Methods	Parameters (M)	FLOPs (G)	CPU		GPU
			Enc. Time (s)	Dec. Time (s)	Enc. Time (s)	Dec. Time (s)
STF	33.35	99.83	1.1582	1.3173	0.0768	0.1022
HiFiC	55.42	148.24	0.1959	0.5344	0.1253	0.2844
ELIC	54.46	31.66	0.9205	0.9245	0.1746	0.0988
TCM	44.97	35.23	0.3951	0.4171	0.1269	0.1238
MLIC++	82.36	116.48	0.5320	0.6453	0.1254	0.1761
INN-RSIC (Ours)	55.71	63.57	0.9205	0.9554	0.1746	0.1143

.

From the results, it is clear that MLIC++ has 82.36 M parameters, whereas the proposed INN-RSIC comprises only 67.64% of that count. Notably, the INN-based enhancer we introduced adds only 1.25 M parameters, representing a mere 2.30% increase over the baseline ELIC, which underscores its remarkable memory efficiency and lightweight design. In terms of floating point operations per second (FLOPs), HiFiC and MLIC++ bear a heavy computational load, with FLOPs values of 148.24 G and 116.48 G, respectively. In contrast, the proposed INN-RSIC requires only 42.88% and 54.58% of the FLOPs of HiFiC and MLIC++, respectively. This significant reduction in computational complexity is achieved, while maintaining competitive performance, thanks to the efficient design of the INN-based enhancer. As for the decoding times, it can be observed that the proposed INN-RSIC adds only 0.0155 s to the GPU decoding time compared to its baseline, ELIC. This minimal increase highlights the efficiency of the INN-based enhancement module, ensuring that the proposed method maintains fast decoding speeds while improving perceptual quality.

To sum up, the proposed INN-RSIC requires less memory space, has lower computational complexity, and enjoys outstanding decoding speed on both CPU and GPU. The lightweight and efficient design of the INN-based enhancer ensures that the overall system remains highly practical for real-world applications.

5. Discussion

During training, we utilized decoded images as labels to guide the forward training of INN-RSIC in generating synthetic images, which were then fed into the inverse network along with Gaussian-distributed latent variables for image reconstruction. However, in the inference stage, as the ground truth cannot be obtained to feed into the forward network at the decoding end, i.e., the synthetic image cannot be derived, we resorted to using labeled images instead of synthetic ones. In other words, the decoded images were fed into the inverse network along with Gaussian-distributed latent variables for enhancing the texture of the decoded images. While the texture information of the enhanced images is enriched with the assistance of Gaussian-distributed latent variables, the strictly invertible characteristic of INN inevitably affects the reconstruction quality of the enhanced image when using decoded images instead of synthetic ones.

This investigation primarily focused on exploring the input sensitivity of the proposed INN-RSIC model. Figure 14 showcases the images restored by INN-RSIC with synthetic images and the decoded images as inputs during the inference stage. The results reveal that, when synthetic images are used as input, the reconstructed image effectively recovers texture-rich details. However, when decoded images are employed as input, although some details are still recovered in the enhanced image, noticeable detail distortions emerge, particularly in texture-rich regions. To explore this issue further, we analyzed the residual image between the synthetic image and the decoded image. It became evident that the differences contradicted the invertible characteristic of INN, thereby inevitably limiting the performance of the final texture recovery.

In summary, the similarity between the decoded and synthetic images significantly influenced the recovery of texture-rich image details. Optimizing the algorithm design to ensure that the resulting synthetic and decoded images were as similar as possible will greatly enhance the decoding of detailed texture-rich RS images without requiring additional bitrates. This optimization holds the potential to improve the overall performance and fidelity of the INN-RSIC model, allowing for a more accurate reconstruction of RS images.

6. Conclusions

In this paper, we present INN-RSIC, a novel method designed to enhance the perceptual quality of decoded RS images. This approach encodes the compression distortion of an image compression algorithm into Gaussian-distributed latent variables and leverages invertible transformations to substantially restore texture details. Additionally, we introduced the CCGM to separate and encode the compression distortion from the ground truth into latent variables conditioned on the synthetic image, thereby improving the reconstruction of the enhanced image. Moreover, we incorporated QM to mitigate the impact of data type conversions on reconstruction quality during inference. Extensive experiments on two widely used RS image datasets demonstrate that INN-RSIC achieves a superior balance between perceptual quality and high image fidelity compared to state-of-the-art image compression algorithms with low model complexity. Furthermore, our approach offers a new research perspective for enhancing the texture reconstruction capability of RS image compression algorithms by minimizing the gap between synthetic and decoded images.