Abstract
The transponder-style deception jamming implemented by Digital Radio Frequency Memory (DRFM) exhibits high similarity to real target radar echoes, while traditional detection methods suffer severe performance degradation under low signal-to-noise ratio (SNR) conditions. To address this issue, this paper proposes a DRFM active deception jamming detection method based on diagonal integral bispectrum, aiming to overcome the bottleneck of jamming detection under low-SNR conditions. By establishing a harmonic effect signal model for DRFM deception jamming, the cross-term generation mechanism in the bispectrum domain is revealed: the jamming signal generates dense cross-terms due to harmonic distortion, whereas the real target energy exhibits single-peak aggregation. To quantify this difference, the Diagonal Integral Bispectrum Relative Peak Height (DIBRP) is proposed to characterize the energy aggregation of true and false targets in the diagonal integral bispectrum, and the Diagonal Integral Bispectrum Approximate Entropy (DIBAE) is introduced to describe their complexity. A joint detection framework combining the DIBRP-DIBAE dual-feature space and a polynomial kernel support vector machine (SVM) is constructed to achieve active deception jamming detection. The proposed method demonstrates excellent performance under low-SNR conditions. Simulations and experimental results show that the correct detection rate reaches 92% at a jamming-to-signal ratio (JSR) and SNR of 0 dB, validating the effectiveness of the algorithm.
1. Introduction
Over recent decades, the emergence and advancement of Digital Radio Frequency Memory (DRFM) technology have enabled jammers to generate active deceptive signals highly coherent with radar-transmitted waveforms, posing significant challenges to accurate target identification [1,2,3]. By leveraging diverse modulation schemes and flexible parameter configurations, jammers further exacerbate the difficulty of radar recognition. To counter such threats, researchers have explored anti-jamming strategies from multiple dimensions. However, whether focusing on signal-level countermeasures [4] or radar network-layer defenses [5], the core objective remains focused on improving target identification accuracy. In real-world electronic warfare scenarios, rapidly and effectively distinguishing jamming signals is critical to maintaining operational superiority.
In studies on DRFM repeater jamming, Hill identified that DRFM jammers introduce harmonic components during signal interception and storage due to sampling and quantization processes [6]. He pioneered the use of harmonic effects from sampling quantization as a means for jamming detection. Lu further developed a theoretical harmonic model for DRFM deception signals and validated the regularity of harmonic components using the fractional Fourier transform (FRFT) [7], clarifying their correlation with jammer parameters. Zhang theoretically confirmed the harmonic effects induced by DRFM sampling quantization and demonstrated the distinct differences between jamming signals and target echoes through time–frequency domain analysis [8]. Ding proposed a novel detection method by extracting singular values of jamming signals [9], normalizing them into histogram features (e.g., variance, skewness, entropy, and kurtosis), and training an SVM classifier using these feature vectors. Li employed singular spectrum analysis (SSA) and introduced a constant false alarm rate (CFAR) detection framework [10]. Conversely, the aforementioned studies predominantly focus on the harmonic effects of DRFM-based jammers. In addition to utilizing the harmonic effects of DRFM jammers to counteract active deception jamming, Hao proposed a dense false target jamming recognition method based on time–frequency atomic decomposition theory and an SVM. The extracted time–frequency parameters of Gabor atoms can effectively characterize the intrinsic features of both target jamming and dense false target jamming [11]. Dong introduced a blind source separation method based on tensor decomposition (TD-BSS) to suppress mainlobe DRFM jamming, enabling the separation of target echo signals and jamming signals [12]. However, both studies share similar limitations: Traditional time–frequency domain analysis struggles to extract frequency–phase coupling features of DRFM deception jamming signals. Since jammers cannot fully simulate the entire radar signal transmission process, nonlinear phase distortion during modulation cannot be accurately characterized, leading to differences in frequency–phase coupling between deceptive jamming signals and genuine target echoes. Moreover, in low signal-to-noise ratio (SNR) scenarios, the time–frequency feature resolution deteriorates sharply. Methods based on the short-time Fourier transform (STFT) or the Wigner–Ville distribution fail to distinguish time–frequency energy distribution differences between genuine target echoes and jamming signals, resulting in increased false alarms and reduced detection probability. With the continuous advancement of deep learning models, an increasing number of studies have applied such models to signal recognition tasks. Yang proposed a neural network architecture based on a hybrid attention module (HAM) and transformer to identify DRFM deception jamming, achieving a balance between accuracy and computational complexity [13]. Kong designed a deep convolutional separation network with a dilation mechanism that was inspired by the principle of blind source separation. This approach expands the receptive field of the convolution and enhances the network’s ability to capture the temporal dependencies of the input signals [14]. Although deep learning techniques have demonstrated their effectiveness in signal recognition, most existing methods still suffer from the following limitations: (1) low classification accuracy under low-JSR conditions and (2) a large number of network parameters, which hinder their deployment on resource-constrained mobile and embedded devices.
To address these issues, this study introduces bispectral analysis for distinguishing genuine target echoes and jamming signals. The bispectrum retains phase information, extracts phase coupling characteristics, and suppresses Gaussian noise, enabling the extraction of subtle features that traditional methods overlook. Among the existing research methods, Li compared the distinct characteristics of target echoes and deception jamming in terms of higher-order cumulants and the bispectrum. Simulation results revealed notable differences between target echoes and deception jamming in these higher-order statistical domains [15]. However, the study directly processed the bispectral data, which resulted in relatively high computational complexity. To reduce the computational complexity of the algorithm, it is advisable to consider applying dimensionality reduction to the bispectrum. Existing research shows that a dimensionality-reduced bispectrum performs well under harmonic conditions [16]. To address these limitations, this paper proposes an innovative solution by pioneering the application of higher-order statistical analysis (HOSA) to deception jamming detection, particularly HOSA. HOSA excels in capturing phase information, phase coupling, and non-Gaussian characteristics while maintaining phase preservation and scale invariance, significantly enhancing signal processing robustness.
As a powerful tool in signal processing, a higher-order spectrum (HOS) can intuitively reveal the frequency and phase coupling relationships between harmonic components in signals. In recent years, it has demonstrated broad application potential in fields such as image processing and object recognition. Particularly, the bispectrum—the lowest-order HOS—offers minimal computational complexity while retaining all the advantageous properties of HOS, including complete suppression of Gaussian noise interference. This makes bispectral analysis the preferred choice in HOS applications. However, despite being the lowest-order HOS, the bispectrum is inherently a two-dimensional function due to its computational formulation. Direct computation imposes a significant computational burden, making it impractical for real-time monitoring requirements. To address computational complexity, Li [17] proposed an innovative approach by extracting only the diagonal slices of the bispectrum for analysis, thereby reducing the computational load. Meng [18] adopted another method, leveraging diagonal integration to compress the originally high-dimensional bispectral data into two dimensions. Both strategies enhance efficiency and lower algorithmic complexity for specific applications, demonstrating practical utility. A critical consideration lies in preserving the intrinsic discriminative features between genuine and deceptive targets within the bispectral space during dimensionality reduction, thereby avoiding information obscuration caused by compression. The core challenge resides in designing dimensionality reduction mapping functions that maintain the nonlinear separability of target categories—originally embedded in the full-dimensional bispectrum—within the compressed feature space.
To address the above challenges, this study proposes a difference-guided dimensionality reduction mechanism—bispectral projection based on diagonal integration paths. By constraining the alignment between the integration path and the principal components of signal nonlinear coupling, this method ensures that dimensionality reduction not only compresses data dimensions but also directionally enhances discriminative features between genuine and deceptive targets. Specifically, DRFM deception jamming manifests in the bispectral domain as phase coupling distortion at specific frequency points. The diagonal integration path accumulates these distortion features through integration along interference-sensitive directions, thereby amplifying inter-class separability in the low-dimensional space.
This study proposes a diagonal integrated bispectrum (DIB)-based DRFM deception jamming detection method, leveraging the unique advantages of bispectral analysis in extracting nonlinear phase coupling through third-order cumulants while inherently suppressing Gaussian noise due to the vanishing third-order cumulants of Gaussian processes. By computing the bispectrum of the received signal, the method captures essential discriminative features between jamming and genuine targets, particularly under low-SNR conditions. To address the computational complexity of high-dimensional bispectral data, a dimensionality reduction strategy is implemented via diagonal integration along the bispectral sub-diagonal, which not only compresses the feature space but also concentrates the nonlinear distortion patterns induced by DRFM artifacts. Two discriminative metrics—Diagonal Integrated Bispectrum Relative Peak Height (DIBRP) and Diagonal Integrated Bispectrum Approximate Entropy (DIBAE)—are subsequently extracted to quantify energy concentration and dynamic complexity, respectively. These features are fed into a polynomial kernel support vector machine (SVM) to resolve nonlinear separability challenges in the compressed feature space. The framework achieves robust detection performance by directionally amplifying DRFM-specific phase coupling signatures, enabling reliable discrimination even in noise-dominated environments, as validated through simulations and field-measured data experiments.
The structure of this paper is organized as follows: Section 2 constructs a signal model of DRFM deceptive jamming, serving as the theoretical foundation of this study. Section 3 provides a systematic explanation of bispectral analysis, introduces the symmetry properties of the bispectrum, and demonstrates the rationality and superiority of the bispectral dimensionality reduction method employed in this work. Section 4 investigates the differences between DRFM deceptive jamming and genuine target echoes in the diagonal integrated bispectrum and further analyzes the theoretical basis and discriminative effectiveness of the proposed features. Section 5 validates the proposed method through a series of simulation experiments, covering performance evaluations under various jamming scenarios. A comparative analysis with existing methods is conducted to verify the superiority and robustness of the proposed approach. Moreover, experiments based on measured data are designed across multiple datasets with different types of jamming to further demonstrate the practical applicability of the algorithm. Finally, Section 6 summarizes the main conclusions of this work.
2. DRFM-Based Deception Jamming Signal Model
In this section, a signal model for deception jamming based on DRFM is constructed. The variations in the central frequency and chirp rate of the jamming signal are analyzed, providing a foundation for subsequent research. This facilitates the use of bispectral analysis to characterize the differences between deception jamming signals and real target echoes.
Given that pulse compression technology effectively addresses the trade-off between detection range and range resolution in conventional pulse radar systems, this study will consistently adopt the commonly used linear frequency modulation (LFM) signal for subsequent analyses. Let the transmitted radar signal have a bandwidth of , a pulse width of , a chirp rate of , and a pulse repetition period of , with a central frequency of . The transmitted radar signal can be expressed in terms of these parameters as follows [8]:
Once the DRFM receiver successfully intercepts the radar signal, it first performs frequency conversion, modulating the signal to the receiver’s intermediate frequency (IF). Subsequent modulation is then carried out in the IF domain. Let the intermediate frequency of the DRFM receiver be . After down-conversion, the received signal at the DRFM receiver can be expressed as follows:
Assuming that the quantization bit number of the jammer receiver during sampling quantization is and it undergoes bit quantization, according to reference [19], the signal after bit quantization can be expressed as
A DRFM jammer modulates signals that have undergone phase quantization by introducing false Doppler shifts and time delays. The signal is then upconverted to restore carrier information before being transmitted. The emitted signal can be expressed as
In the above equation, represents the false Doppler shift, while is a time delay function. It is typically assumed that follows a linear function; however, in practical DRFM jammers, it is often approximated using a staircase function. Consequently, is quantized into a piecewise continuous time function denoted as . Based on this, a mathematical model for the deceptive jamming signal generated by a DRFM jammer can be established.
Thus, after down-conversion, the radar receiver detects the deceptive jamming LFM signal retransmitted by the DRFM jammer, which can be expressed as follows:
After receiving the deception signal retransmitted by the DRFM jammer at the radar receiver, it is necessary to further analyze the spectral characteristics of the signal. Therefore, for ease of representation, the above equation can be rewritten as
Let the primary term be denoted as , and the secondary term is denoted as . Performing a Fourier transform on the secondary term yields . Given the complexity of the primary term, a fractional Fourier transform is considered for its analysis [20].
According to the principles of the Fourier transform, the spectrum of the product of and in the time domain corresponds to the convolution of their respective spectra, and , in the frequency domain. Considering the frequency-domain representation of , this operation results in an -to- spectral shift. Under the condition of , we obtain
where represents the spectrum of . The spectrum of the interference signal , as can be seen from the above equation, is composed of multiple distinct components.
The component of when lies within the same frequency band as the genuine target echo is important. Therefore, the component of when can play a deceptive role. Thus, the component of when is referred to as the main term. Aside from the main term, the interference spectrum still contains components for , which are referred to as harmonic components or interference spurious terms. As observed from the frequency spectrum analysis of in Equation (9), the amplitude term decreases with increasing m, while the bandwidth of the spurious terms increases accordingly. The intensity of the spurious terms is primarily determined by , and it undergoes attenuation by a factor of . These harmonic components, exhibiting a certain regularity, provide the potential for distinguishing between true and false targets.
Based on the above analysis, the following conclusion can be drawn: the frequency information of both the main and spurious components in the deceptive jamming signal can be calculated. For clarity, let denote the modulation frequency of the harmonic components under a quantization bit depth of and , and let represent the center frequency of the harmonic components under the same quantization condition. In practical applications, since the towing rate is generally on the order of [7], is approximately equal to 1. Thus, the following equation holds [7]:
In the above equation, . Based on this equation, the center frequency and modulation frequency of both the main component and harmonic components in the jamming signal can be uniquely determined. Specifically, the center frequency depends on two variables, and , indicating that the center frequency of the interference harmonics is related to the quantization bit depth of the jammer. Here, is given by ,where represents the down-conversion frequency of the jammer and corresponds to the Doppler frequency of the target. Similarly, the modulation frequency also depends on two variables, and , meaning that the modulation frequency of the interference harmonics is determined by both the quantization bit depth of the jammer and the modulation frequency of the radar-transmitted signal.
Next, simulations will be conducted to validate the aforementioned theoretical analysis. The experiment simulates two types of signals: the genuine target echo and the deceptive jamming signal generated by a DRFM jammer. A time–frequency domain comparison of these two signal types is performed.
Figure 1 presents a time–frequency domain comparison between the true genuine echo and the deceptive jamming signal generated by the DRFM jammer, as received by the radar receiver in a noise-free environment. The interference signal is an LMF signal with a bandwidth of 10 MHz, a sampling frequency of 1.024/2 GHz, and a pulse width of 1 µs. From the figure, the modulation characteristics of the spurious components can be clearly observed. In the left panel, only a single linear modulation component is present. However, in the right panel, in addition to the frequency modulation characteristic similar to that in the left panel, two additional modulation components with steeper slopes can be observed. Since the slope corresponds to the modulation frequency, a steeper slope indicates a higher modulation frequency. These steeper modulation components represent the modulation characteristics of the spurious terms.
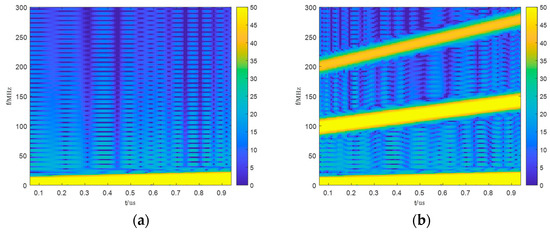
Figure 1.
Comparison of the genuine target echo with the DRFM jamming signal in the time–frequency domain: (a) time–frequency diagram of the genuine target echo; (b) time–frequency of the DRFM jamming signal.
In conclusion, when the radar echo contains only the genuine target echo, it appears as a single independent LFM signal. However, once the radar receives a deceptive jamming signal modulated and generated by the DRFM jammer, the harmonic effect causes multiple LFM signals with specific frequency characteristics to appear simultaneously in the received echo [7]. The theoretical analysis aligns well with the experimental results.
3. Bispectral Analysis and Dimensionality-Reduced Bispectrum via Diagonal Integration
Through the analysis in the previous section, it is established that when radar receives deceptive jamming signals forwarded by DRFM jammers, multiple LFM signals will simultaneously appear in radar echoes. Within this research framework, this section introduces higher-order cumulants and the bispectrum based on the definition of higher-order statistics. Theoretical validation was conducted to demonstrate the feasibility of bispectral analysis in addressing this specific problem. Furthermore, we propose the implementation of diagonal integration as a dimensionality reduction technique for bispectral features. This approach enables directional focusing of nonlinear phase coupling characteristics in DRFM jamming signals through bispectral feature concentration and extraction.
To achieve accurate radar signal identification and detection, it is essential to extract discriminative key parameters from signal characteristics. Compared with traditional time–frequency analysis methods, higher-order cumulants exhibit significant theoretical advantages in feature extraction. Notably, their inherent blindness to Gaussian noise stems from the theoretical property that third-order and higher cumulants vanish for Gaussian processes, thereby effectively suppressing interference from additive Gaussian noise. Moreover, compared to second-order statistical methods, higher-order cumulants not only preserve the phase information, non-Gaussian characteristics, and discriminative classification properties of signals but also enable the extraction of higher-order spectral domain features through multidimensional Fourier transforms, thereby transcending the inherent limitations of second-order statistics in feature representation dimensionality. Consequently, this study adopts bispectral features derived from higher-order cumulants as the core analytical framework.
Let be defined as a random variable, where , and let denote the probability density function of random variable . The first and second characteristic functions are defined as follows [21]:
The kth-order cumulant, , of random variable is defined as
For a stationary random signal , the third-order cumulant with time delays is defined as [18]
The bispectrum is defined as the two-dimensional Fourier transform of the third-order cumulant, expressed mathematically as [18]
Based on the analysis in the preceding section, when radar systems are subjected to DRFM-based deception jamming, the received echoes will contain multiple LFM signal components. Conversely, in the absence of DRFM jamming, only a single LFM component corresponding to the genuine target echo exists. This section conducts bispectral analysis on both signal models and theoretically investigates whether discriminative bispectral features exist between genuine target echoes and DRFM-generated deceptive jamming signals.
Let the DRFM jamming signal be represented as , where . Here, denotes the amplitude envelope (typically a constant). , where represents the initial frequency and corresponds to the chirp rate. Similarly, for the genuine target echo , an analogous parameterization can be expressed as .
To simplify computation, the bispectrum is defined as the expectation of the triple product of the signal’s Fourier transform [19]:
where denotes the Fourier transform of signal , represents the expectation operator, and indicates complex conjugation.
In the frequency domain, the Fourier transform of the DRFM jamming signal is expressed as
Substituting this representation into the bispectrum formula yields
A detailed expansion of the aforementioned equation reveals that the bispectrum of the DRFM jamming signal comprises 27 combinatorial terms, categorized into self-product terms and cross-product terms. The self-product terms, such as , account for 3 terms, which are analogous to the bispectrum of a single LFM signal. The remaining 24 cross-product terms arise from nonlinear interactions between distinct signal components; here, it refers to the phase coupling phenomena induced by DRFM modulation mechanisms.
The bispectrum of the genuine target echo, which corresponds to a single LFM signal, is expressed as
Since no multiple signal components are present in this scenario, cross-product terms are inherently absent, leaving only self-product terms in the bispectral representation.
By comparing Equation (18) and Equation (19), the following conclusions can be drawn: The bispectrum of DRFM jamming signals contains three self-product terms and multiple cross terms, resulting in a higher number of coupling frequencies and bispectral peaks compared to genuine target echoes. Consequently, bispectral analysis serves as an effective tool for discriminating between genuine target returns and DRFM deception jamming in this context.
Prior to bispectral dimensionality reduction, the symmetry properties of the bispectrum must be thoroughly investigated to ensure that the selected reduction approach effectively extracts discriminative bispectral features between the two genuine and DRFM-jammed signals.
The third-order cumulant, , of a real-valued stationary random sequence satisfies the following six fundamental symmetry relations in the two-dimensional temporal domain [19]:
In radar systems, complex-valued signals are conventionally employed due to their inherent capability to simultaneously preserve both amplitude and phase information. This necessity underscores the critical importance of bispectral analysis for complex signals in such applications.
For a complex-valued stationary signal , the conjugation operator in the third-order cumulant definition (Equation (14)) may be applied to any one term or two terms within the product. However, for each distinct conjugation configuration, only one of the six symmetry relations in Equation (18) remains valid. The bispectrum of a complex signal typically exhibits symmetry about a specific axis in the frequency plane, where . Table 1 enumerates the six conjugation configurations and their corresponding bispectral symmetry relations [19], where denotes the Fourier transform of the complex signal .

Table 1.
Corresponding symmetry relations.
The analysis in this study adopts the first definition, as enumerated in Table 1.
Third-order cumulant: .
Bispectrum: .
Symmetry axis: ; this implies symmetry about the principal diagonal.
To address the high computational complexity inherent in bispectral analysis due to the massive data volume of two-dimensional bispectral representations, dimensionality reduction techniques are conventionally employed in higher-order spectral analysis.
In this study, the bispectral data is processed as follows: it is integrated along the sub-diagonal direction, and the resulting output is termed the DIB [18]. Due to the inherent symmetry of the bispectrum about the main diagonal, sub-diagonal integration superimposes symmetrical discriminative features with respect to the main diagonal, thereby amplifying their distinctiveness. The mathematical representation is given by [22]:
The coordinate system, , is derived by rotating the original coordinate system 45° counterclockwise about the origin [22].
Subsequent experimental validation of the theoretical analysis was conducted using both simulated and field-measured datasets [23,24,25,26,27]. The bispectral characteristics and diagonally integrated bispectral profiles of genuine and DRFM-jammed signals were systematically analyzed. Experimental results are summarized as follows:
Figure 2 shows the bispectra of DRFM-jammed signals and genuine target echoes obtained through simulations. The simulation parameters were set as follows: a sampling frequency of 150 MHz, a bandwidth of 10 MHz, a pulse width of 1 μs, and an SNR of 0 dB. The Fourier transform length is set to 1024; the window length is 128; the sliding step is 64, and the direct method is used to estimate the bispectrum. As can be seen from the figure, the bispectrum of the authentic target echoes exhibits more concentrated energy, while the bispectrum of the deceptive jamming signals displays numerous glitches and distinct peaks at specific frequency positions, corresponding to the cross-product terms and self-product terms mentioned in the theoretical analysis above.
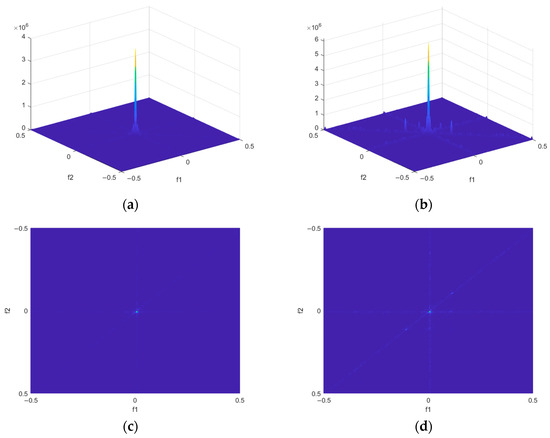
Figure 2.
Bispectrum of the genuine target echo signal and the DRFM deception jamming signal: (a) bispectrum of the genuine target; (b) bispectrum of the DRFM deception jamming signal. Figure (c) is the top view of Figure (a). Figure (d) is the top view of Figure (b).
Figure 3 and Figure 4 present the bispectrum and DIB of genuine target echoes and DRFM deceptive jamming signals derived from field-measured datasets [23,24,25,26,27].
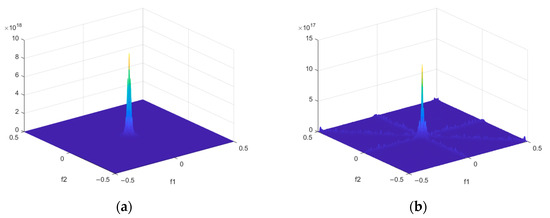
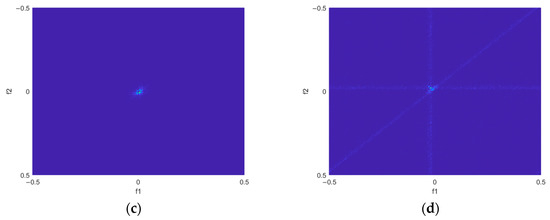
Figure 3.
Bispectrum of the genuine target echo signal and the DRFM deception jamming signal: (a) bispectrum of the genuine target; (b) bispectrum of the DRFM deception jamming signal. Figure (c) is the top view of Figure (a). Figure (d) is the top view of Figure (b).
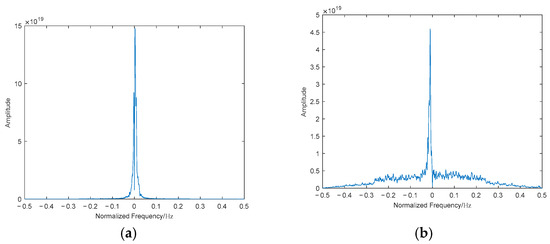
Figure 4.
Diagonal integral bispectral of the genuine target echo and the DRFM deception jamming signal: (a) DIB of the genuine target echo signal; (b) DIB of the DRFM deception jamming signal.
A comparative analysis of bispectral plots between simulated genuine target echoes and DRFM deception jamming signals demonstrates that the simulated signals exhibit high fidelity in replicating measured data, thereby corroborating the theoretical feasibility of the proposed framework.
A comparative analysis of the dimensionally reduced bispectral plots between the two signal classes reveals significant discrepancies in their diagonally integrated bispectral profiles. As illustrated in the plots (generated from field-measured datasets), the diagonally integrated bispectrum of the genuine target exhibits a localized energy peak with minimal surrounding fluctuations (left panel). In stark contrast, the diagonally integrated bispectrum of the DRFM-jammed signal demonstrates extensive undulations around the primary energy concentration, particularly along the frequency axis and principal diagonal (right panel). These distinctive fluctuations originate from spurious modulation artifacts introduced by DRFM-generated false components during frequency-agile deception.
Figure 5 presents the feature extraction results for DRFM deception jamming signals under 0 dB SNR conditions, obtained through spectral analysis and DIB analysis. This study demonstrates that both methodologies effectively detect spurious modulation features inherent in the jamming signals. To validate the robustness of bispectral analysis in low-SNR environments, comparative experiments were conducted at a reduced SNR of −5 dB, with results illustrated in Figure 6.
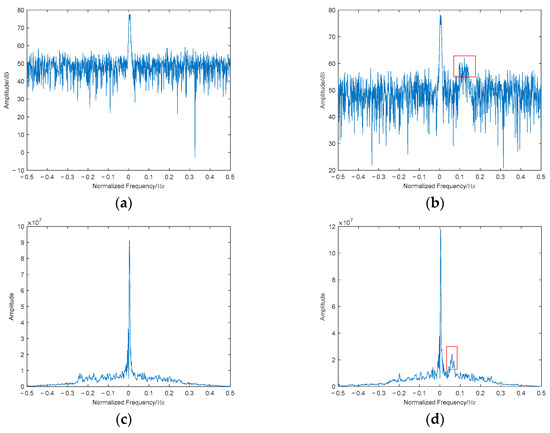
Figure 5.
Spectrograms and DIB plots of genuine and deceptive targets at 0 dB: (a) spectrogram of the genuine target at 0 dB; (b) spectrogram of the deceptive target at 0 dB; (c) DIB of the genuine target at 0 dB; (d) DIB of the deceptive target at 0 dB.
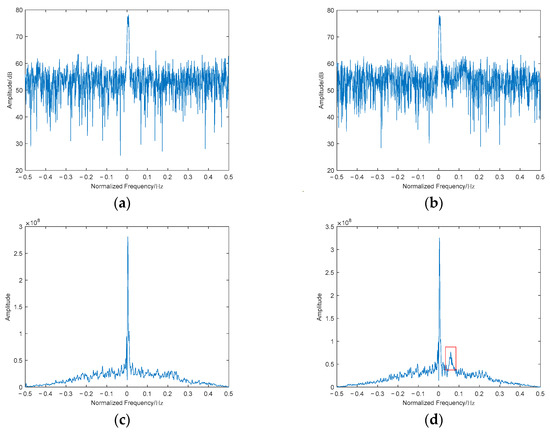
Figure 6.
Spectrograms and DIB plots of genuine and deceptive targets at −5 dB: (a) spectrogram of the genuine target at −5 dB; (b) spectrogram of the deceptive target at −5 dB; (c) DIB of the genuine target at −5 dB; (d) DIB of the deceptive target at −5 dB.
As shown in Figure 6, conventional spectral analysis exhibits significant degradation in spurious component detection under low-SNR conditions, while the diagonal integrated bispectrum maintains high feature discriminability. This observation aligns with the theoretical analysis of bispectral noise suppression: The third-order cumulant calculation in bispectral analysis inherently suppresses Gaussian noise while retaining critical phase information neglected by conventional power spectrum methods.
4. Discriminative Feature Extraction from Diagonally Integrated Bispectral Differences
As demonstrated in the preceding analysis, significant discriminative disparities exist between genuine radar targets and DRFM deception jamming signals within the bispectral domain. The diagonal integration method not only reduces bispectral dimensionality but also accentuates and extracts these discriminative features, thereby amplifying the observable differences between the two signal classes in the DIB domain. To establish an effective detection model, this approach requires the transformation of morphological differences in diagonal integrated bispectra into quantifiable statistical features, providing a foundation for subsequent classifier design based on third-order statistical properties.
4.1. Diagonal Integral Bispectrum Relative Peak Height Feature
To enable quantitative detection, a systematic analysis was conducted. As illustrated in Figure 4, the DIB of genuine target echoes demonstrates a compact energy concentration profile, whereas the DIB of DRFM deception jamming exhibits significant spurious fluctuations characterized by pronounced glitches. This disparity motivates the extraction of relative peak height discrepancies in their diagonal integrated bispectral representations. Accordingly, we propose the DIBRP metric to quantify the energy concentration disparity between the two signal types through third-order statistical analysis. The DIBRP parameter effectively captures the fundamental difference in energy aggregation patterns caused by nonlinear phase coupling characteristics inherent to genuine radar returns.
The DIBRP is mathematically defined as the ratio of the DIB peak amplitude in the test unit to the average DIB peak amplitude of reference units. This metric reflects the energy magnitudes contained in different signal components.
The calculation formula of DIBRP is as follows:
In Equation (22), denotes the normalized frequency of the DIB, while represents the magnitude spectrum obtained through bispectral diagonal integration.
The offset of the DIB is
The DIBRP is defined as
In Equation (24), where , δ1 denotes the interval width of reference units for the DIB; δ2 represents the maximum possible bandwidth of the target; Δ is the set composed of reference units; and #Δ indicates the number of elements in the set Δ.
Building upon the theoretical analysis of the DIBRP, the following conclusion is derived: the concentrated energy distribution in the DIB of genuine target echoes results in significantly higher DIBRP values compared to DRFM deception jamming signals, whose dispersed bispectral energy profiles yield attenuated DIBRP magnitudes. To validate this hypothesis, a comparative simulation study was conducted using 300 samples of radar returns from both genuine targets and DRFM-generated deception jamming signals under an SNR of 5 dB. The DIBRP features extracted from these datasets were statistically analyzed, with the resultant feature histogram presented in the figure below:
As evidenced in the Figure 7, the DIBRP exhibits substantial discriminative capability between genuine radar target echoes and DRFM-generated deception signals. The experimental results align rigorously with theoretical predictions, thereby validating DIBRP as an effective discriminative feature for integration into the proposed detection algorithm.
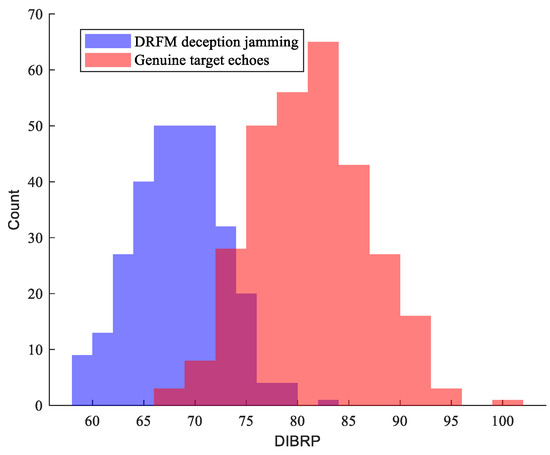
Figure 7.
Discrimination capability of DIBRP features.
4.2. Diagonally Integrated Bispectrum Approximate Entropy Feature
As illustrated in Figure 4, the energy concentration characteristics of genuine target echoes and DRFM deception jamming signals exhibit significant divergence, which can be conceptualized as restructured signal ensembles. These restructured ensembles exhibit distinct complexity profiles, a disparity that can be quantified using entropy features—a well-established metric for evaluating signal sequence complexity—as demonstrated in prior studies [28,29].
Considering that approximate entropy (ApEn) serves as a robust method for detecting sequence randomness and unpredictability, it effectively quantifies the complexity of signal sequences and the likelihood of novel information generation. By incorporating permutation concepts, this metric combines inherent noise resistance with computational efficiency. This paper proposes the Diagonal Integral Bispectrum Approximate Entropy (DIBAE) to measure the structural complexity of diagonal integrated bispectral sequences and quantify their discriminative characteristics. The DIBAE is formally defined as
For an n-point sequence, the sequence is sequentially partitioned into m-dimensional pattern vectors , where . The distance between two pattern vectors, and , is defined as the Chebyshev distance (maximum absolute difference):
Given a threshold tolerance r, count the number of pattern vectors u(j) whose Chebyshev distance from u(i) is less than r. For , compute the ratio of to :
For all pattern vectors u, take the natural logarithm of their corresponding values and compute the average:
Repeating the aforementioned procedure in the m + 1 dimensional space yields . The approximate entropy of the DIB sequence, termed DIBAE, is then computed as
Building upon the theoretical analysis of the DIBAE, the following conclusion is derived: due to the inherently higher complexity of DRFM deception signals in the DIB domain compared to the relatively stable and low-complexity DIB profiles of genuine target radar echoes, the DIBAE values extracted from genuine target returns are expected to be significantly lower than those of DRFM-jammed signals. To validate this hypothesis and empirically assess the discriminative capability of DIBAE, a simulation study was conducted using 300 independent samples of radar returns—150 from genuine targets and 150 from DRFM-based deception jammers—under an SNR of 5 dB. The computed DIBAE distributions for both signal classes are statistically summarized in Figure 6.
As can be seen from the Figure 8, the DIBAE feature can completely distinguish between genuine radar target echoes and DRFM interference signal echoes, without any aliasing. This indicates that DIBAE exhibits strong discriminative capability in feature separation. The experimental results are consistent with the theoretical analysis. Therefore, DIBAE can be used as an effective feature for algorithm detection in this paper.
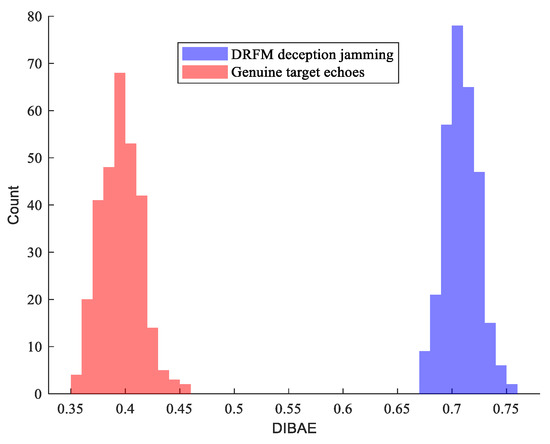
Figure 8.
Discrimination capability of DIBAE features.
4.3. Nonlinear Decision Modeling Based on Polynomial Kernel SVM
To address the nonlinear separability characteristics inherent in the authentic/deceptive target classification task, this study employs a polynomial kernel-based support vector machine (SVM) to construct nonlinear decision boundaries, significantly enhancing classification robustness under low-SNR conditions. Unlike conventional linear SVM that only generates linear hyperplanes, the polynomial kernel effectively captures interaction effects between DIBAE and DIBRP feature spaces through kernel-induced mapping into the higher-dimensional Hilbert space [30].
The polynomial kernel function is defined as , where d denotes the polynomial degree, γ represents the kernel coefficient, and r indicates the bias term. This kernel mapping projects the original 2D feature space into a d-th-order polynomial-combined space, thereby transforming the originally nonlinearly inseparable deceptive jamming signals and genuine target echoes into linearly separable representations within the transformed space. By adjusting the polynomial degree d, the complexity of the decision boundary can be dynamically controlled: Lower degrees (e.g., d = 2) construct smooth nonlinear boundaries to mitigate overfitting, while higher degrees (e.g., d = 3) precisely capture localized nonlinear structures in the feature distribution.
After obtaining the two types of discriminative features mentioned above, the true and false targets are separately subjected to feature extraction of these differences. These two categories of discriminative features are then input into a polynomial kernel SVM classifier, resulting in a well-defined decision boundary.
Using simulated data, radar target echo signals and DRFM deceptive jamming signals were generated under a JSR of 0 dB, with SNRs of 10 dB, 8 dB, 6 dB, and −2 dB, respectively. For each SNR level, 500 samples of genuine radar echoes and 500 samples of DRFM deception jamming signals were selected. Discriminative features were extracted from each dataset and subsequently fed into the polynomial kernel SVM classifier. The corresponding decision boundaries were numerically reconstructed based on spatial feature distributions, with visualization results presented in Figure 9.
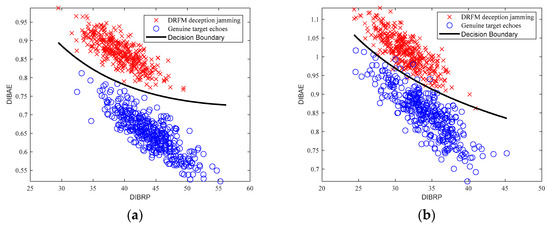
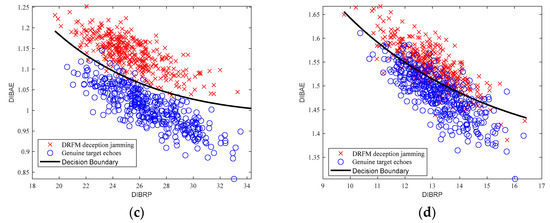
Figure 9.
SVM decision boundaries of genuine radar echoes and DRFM jamming signals: (a) 10 dB; (b) 8 dB; (c) 6 dB; (d) −2 dB.
From Figure 7, it can be observed that genuine radar echo signals exhibit smaller DIBAE values and larger DIBRP values, indicating superior energy concentration (i.e., better energy aggregation) and lower complexity. In contrast, DRFM deception jamming signals, due to the presence of coupling phenomena, display larger DIBAE values and smaller DIBRP values, reflecting poorer energy concentration (i.e., energy dispersion) and higher complexity.
4.4. Implementation Steps of the Algorithm
In summary, the flowchart of the DRFM deception jamming detection method based on the DIB is illustrated in Figure 10, and the procedure can be summarized as follows:
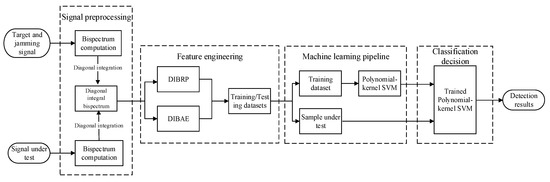
Figure 10.
Flow chart of the DRFM jamming signal detection method.
- Signal Preprocessing: The raw signal is subjected to third-order cumulant computation, generating a two-dimensional bispectrum matrix that preserves phase information while exhibiting enhanced noise robustness. Leveraging the higher-order statistical properties of the bispectrum enables the effective characterization of nonlinear coupling phenomena, demonstrating superior discriminative capability over conventional power spectrum-based approaches.
- Dimensionality Reduction via Diagonal Integration: An integration operation is performed along the bispectrum’s sub-diagonal direction, compressing the 2D bispectral representation into a 1D DIB. This methodology circumvents interpolation artifacts inherent in axial or radial integration strategies while preserving the concentrated expression of bispectral differences between genuine and deceptive targets.
- Multi-Dimensional Feature Extraction: From the dimensionality-reduced diagonal integrated bispectrum, two complementary discriminative features are derived: the DIBRP, which quantifies the energy concentration by measuring the relative amplitude of the dominant spectral peak, and the DIBAE, which evaluates nonlinear dynamical complexity through approximate entropy analysis. These features synergistically enhance separability by exploiting distinct signal characteristics: DIBRP captures amplitude-domain energy aggregation differences, while DIBAE isolates nonlinearity-driven irregularities induced by DRFM modulation artifacts.
- Kernel SVM-Based Classification: A polynomial kernel support vector machine (SVM) is employed to address nonlinear separability challenges in the feature space. The kernel function parameters are optimized through cross-validation to balance model complexity and generalization performance, effectively mitigating overfitting risks associated with conventional linear classifiers.
5. Experiments and Results
5.1. Simulation Experiment Validation
To validate the effectiveness of the proposed method, simulation experiments were conducted using MATLAB R2020a and the HOSA toolbox, with the following experimental parameters. The simulation conditions were set according to the configurations described in reference [8], as detailed in Table 2 below:

Table 2.
Simulation parameters.
Referencing the architecture of typical DRFM jammers, the DRFM quantization bit number was set to (a low value reflecting the prevalence of miniaturized jammers in practical airborne systems [8]). The noise was modeled as zero-mean additive white Gaussian noise (AWGN) following a Gaussian distribution. The SNR is defined as , where and denote the signal and noise, respectively. The jamming-to-signal ratio (JSR) is defined as , where represents the jamming signal. Since jamming signals typically exhibit higher energy than target signals, three JSR conditions (0 dB, 3 dB, and 5 dB) were specifically designed for experimental validation.
Figure 11, Figure 12 and Figure 13 present the jamming detection performance curves derived from 1000 Monte Carlo simulations under varying SNRs (from −10 dB to 10 dB) with a quantization bit number of . For each SNR, 750 samples were used for training, and 250 samples were reserved for testing. Figure 11 illustrates the overall correct detection rate of the test dataset, reflecting the algorithm’s comprehensive detection accuracy. Figure 12 demonstrates the target misclassification rate (TMR), defined as the probability of genuine targets being erroneously classified as jamming signals. Figure 13 quantifies the jamming misclassification rate (JMR), characterizing the probability distribution of jamming signals being misidentified as target echoes.
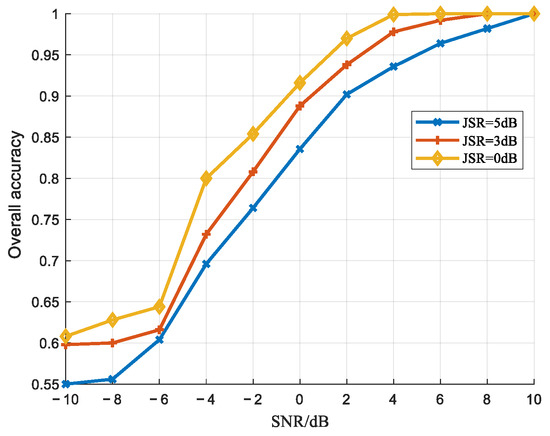
Figure 11.
Overall accuracy recognition rate curves.
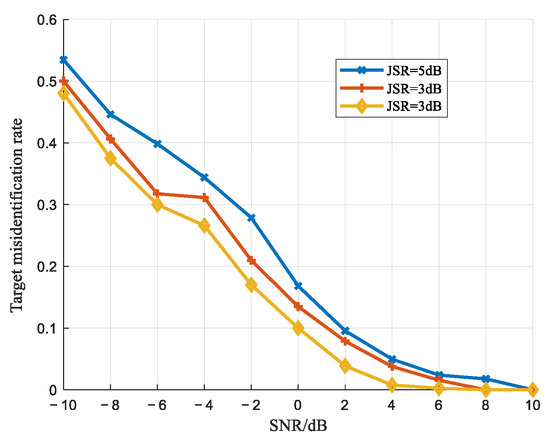
Figure 12.
Target misidentification rate curves.
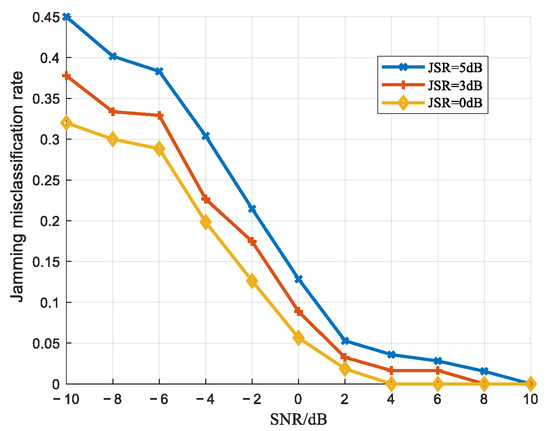
Figure 13.
Jamming misclassification rate curves.
As illustrated in Figure 11, under identical SNR conditions, the overall detection rate exhibits an upward trend as the JSR decreases, indicating improved classification accuracy. Conversely, for a fixed JSR, increasing the SNR progressively reduces the impact of environmental noise on jamming harmonic features, thereby enhancing the quality of discriminative features that can be effectively extracted. This results in a monotonic increase in detection probability, which ultimately converges to a stable level.
As shown in Figure 12 and Figure 13, under identical SNR conditions, both the TMR and JMR decrease as the JSR decreases. Furthermore, for a fixed JSR, elevating the SNR progressively reduces misclassification rates for both the target and jamming signals until they ultimately approach zero.
In [10], a phase-quantized representation model for jamming signals was constructed, and the spectral characteristics of quantized jamming were analyzed. The analysis revealed that quantized jamming contains multiple spurious components distinct from genuine target echoes. Subsequently, the study extracted singular-value energy distribution characteristics induced by these spurious components from the discrepancies between jamming and target echoes by utilizing the SSA algorithm for jamming detection.
Figure 14, Figure 15 and Figure 16 present a comparison between the algorithm proposed in this paper and the method from reference [10]. The jamming detection performance curves were derived under the following conditions: a quantization bit number of , , an ranging from −10 dB to 10 dB, and 300 Monte Carlo simulations conducted at each SNR level.
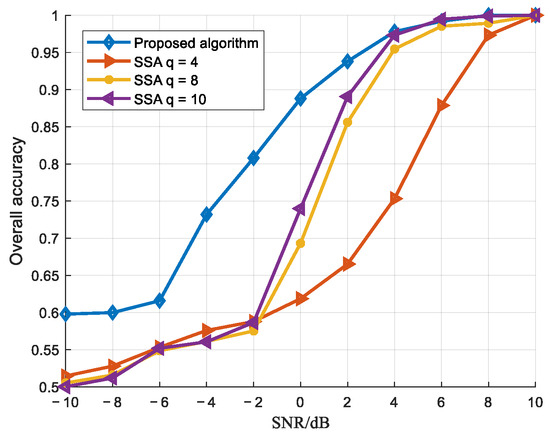
Figure 14.
Comparison curve of overall recognition accuracy.
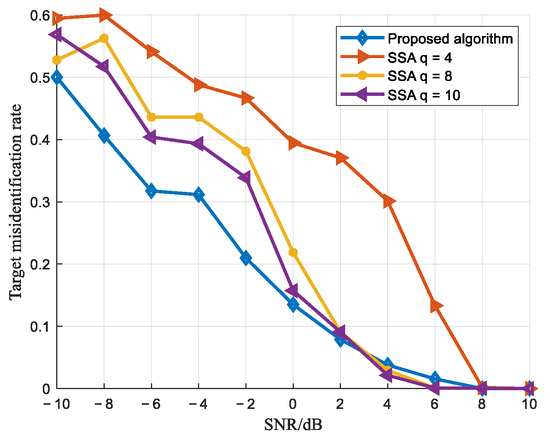
Figure 15.
Target misidentification rate comparison curve.
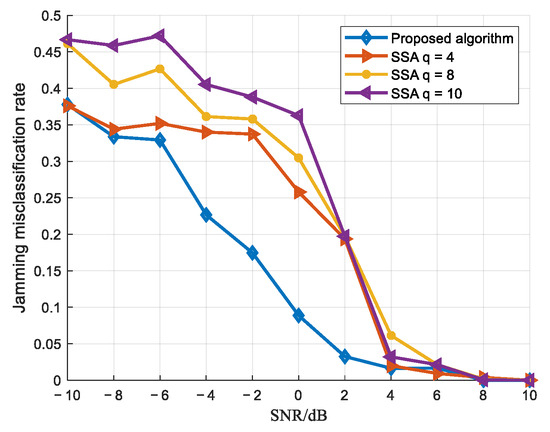
Figure 16.
Jamming misidentification rate comparison curve.
As shown in the figures, the proposed algorithm achieves superior correct detection rates under low-SNR conditions compared to the reference algorithm, enabling reliable jamming detection even in low signal-to-noise ratio scenarios. To provide a more intuitive comparison of the performance between the proposed algorithm and the reference algorithm, a table has been created. In the table, the overall detection performance is compared under a JSR of 3 dB and SNR values of 0 dB and 4 dB, where the reference algorithm is evaluated with parameter q set to 4, 8, and 10.
As clearly shown in Table 3, the proposed algorithm achieves a 14.8% improvement in recognition accuracy under a low SNR of 0 dB. Even when the SNR increases to 4 dB, it still maintains a 0.5% improvement over the reference algorithm. These results clearly demonstrate the superior performance of the proposed method in low-SNR scenarios.

Table 3.
Comparison of overall recognition accuracy at SNRs of 0 dB and –4 dB.
In [7], a chirp rate matching method based on harmonic components was proposed to address the detection of retransmitted LFM active deception jamming. This approach analyzes the spectral characteristics of jamming signals and constructs a database of chirp rates for harmonic components. The chirp rate of echoes is estimated using FRFT techniques, followed by matching the estimated chirp rates against the database to detect jamming signals.
Figure 17 presents a comparative analysis between the proposed algorithm and the method in [7]. Due to differences in the training sample size and parameter settings used in the aforementioned simulations, a separate comparative experiment was conducted. The simulation settings were adjusted to align with [7], including the intermediate frequency, sampling frequency, and target Doppler frequency. The jamming-to-noise ratio (JNR) is defined as , where and denote the power of jamming and noise, respectively. Following the experimental conditions in [7], where jamming signals are typically times stronger than genuine signals, the JNR was set as . The SNR range spanned from −15 dB to 15 dB, with 1000 Monte Carlo simulations performed at each SNR level. The test results are illustrated in Figure 17.
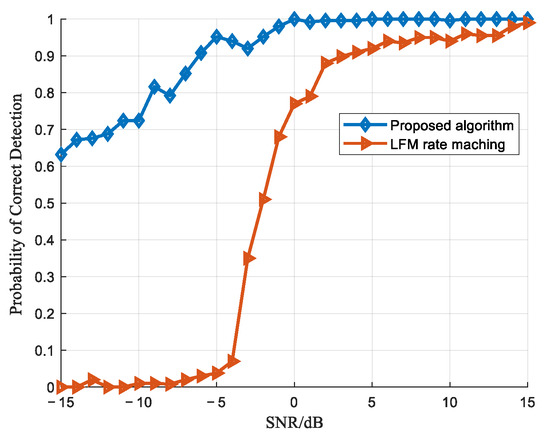
Figure 17.
Comparison of interference detection performance with Reference [7].
In reference [9], a classification and detection method based on SSA feature extraction and the SVM was proposed, which is used for comparison with the algorithm presented in this paper. According to the experimental setup in [9], with M = 2, a JSR of 3 dB, and an SSA decomposition window length of 100, 1000 training samples and 500 testing samples were generated for each SNR level. Figure 18 illustrates the detection performance comparison between the proposed algorithm and the method from ref. [9].
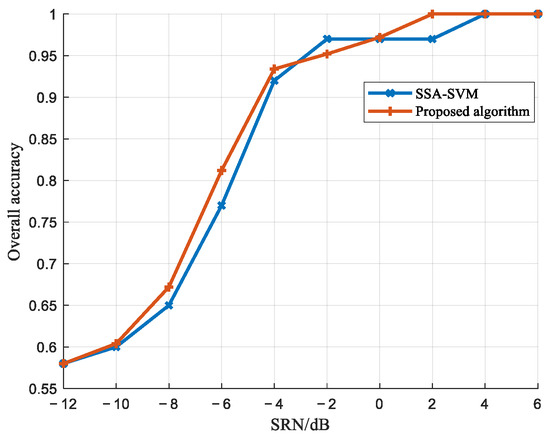
Figure 18.
Comparison of interference detection performance with Reference [9].
As evident from the figures, compared to other algorithms, the proposed method maintains robust detection performance even when the SNR is below 0 dB. At an SNR of −4 dB, the correct detection rate reaches 90%, enabling the effective identification of DRFM jamming. This robustness stems from the algorithm’s utilization of higher-order spectral analysis (bispectrum), as discussed earlier. Specifically, higher-order cumulants exhibit inherent blindness to Gaussian noise, thereby effectively suppressing the impact of Gaussian noise during signal feature extraction.
Figure 19 compares the detection performance of different dimensionality reduction methods. Since the bispectrum is symmetric with respect to the main diagonal, integrating along the anti-diagonal can superimpose the symmetric differences relative to the main diagonal, thereby enhancing the distinguishability. As shown in the figure, anti-diagonal integration outperforms both main diagonal slicing and main diagonal integration.
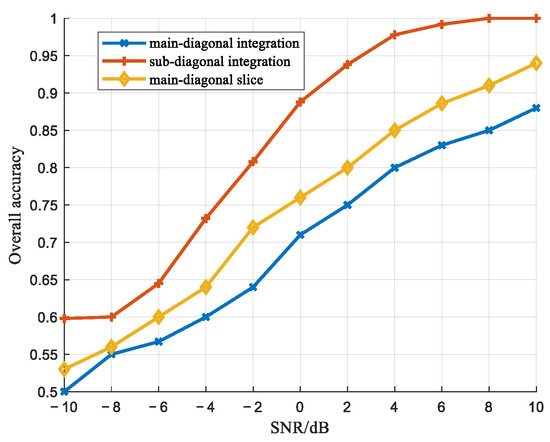
Figure 19.
Comparison of detection performance of different dimensionality reduction methods.
Figure 20 presents a comparison of detection performance under different quantization bit numbers M. According to Equation (10), as the quantization bit number increases, the bandwidth of the spurious components increases, but their corresponding power decreases, making it more difficult to extract spurious features and thereby degrading detection performance. As shown in Figure 20, the detection performance decreases with increasing quantization bit numbers, which is consistent with the theoretical analysis.
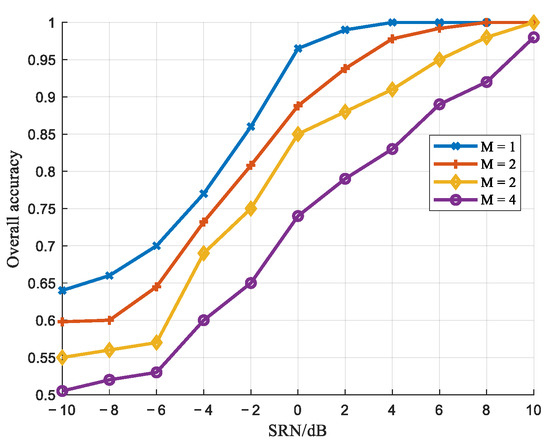
Figure 20.
Comparison of detection performance under different M values.
5.2. Validation Experiment with Field-Measured Data
The experimental data selected in this study were obtained from maritime target detection trials conducted by the Maritime Target Detection Research Group of the Naval Aviation University [23,24,25,26,27]. The data were acquired using the X-band solid-state fully coherent radar illustrated in Figure 21 and Figure 22, with key radar parameters summarized in Table 4. The radar was deployed at a test site in Yantai, it operated in scanning mode at an elevation of approximately 80 m.

Figure 21.
Radar antenna.
Figure 22.
Display and control terminal interface.

Table 4.
Radar parameter list.
The trial involved cooperative targets including Vessel A, Vessel B, Vessel C, and Vessel D, with off-board active jamming deployed by Vessel C. All subsequent analyses reference Vessel C as the target. The estimated SNR and JNR of the collected echoes and deception jamming signals ranged from −12.6 dB to 10.5 dB, where the jamming signals were typically times stronger than genuine signals. The dataset encompasses multiple active jamming types, such as dense false target jamming, smart noise jamming, range gate pull-off jamming, and range–velocity synchronized pull-off jamming. The data are categorized by jamming type, with each type further divided into multiple frames based on radar scan start/stop times. Each frame corresponds to a 1 s scan, with a 2.5 s interval between consecutive frames.
The proposed algorithm was applied to detect field-measured data, selecting multiple jamming types including range gate pull-off jamming, range–velocity synchronized pull-off jamming, and dense false target jamming. For each jamming type, one or two frames of data were extracted, with each frame consisting of 8900 pulses and 8100 range cells. Approximately 300 samples, including both real targets and DRFM-based deceptive jamming targets, were selected from each frame to form a dataset. Furthermore, the environmental conditions in the dataset corresponded to a sea state of Level 2, with a wave height of 0.2 m, a wave direction of 63°, a wind speed of 2.7 m/s, a wind direction of 246°, and a Beaufort wind force of Level 2 [23,24,25,26,27]. A total of nine datasets were selected for experimental validation using field-measured data. The experimental results are summarized as follows:
The proposed algorithm and the method in [10] were applied to different datasets, and the overall correct detection rate bar chart shown in Figure 23 reveals that the proposed algorithm outperforms the comparative method across all test scenarios. Specifically, the proposed algorithm achieves a minimum correct detection rate exceeding 91.3% and an average correct detection rate of 94.20%. This superior performance is attributed to the fact that, in field-measured data, jamming signals typically exhibit higher intensity than genuine target signals, thereby enhancing detection robustness compared to simulated experiments.
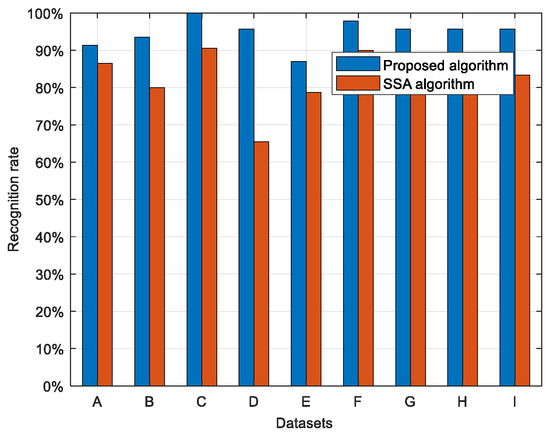
Figure 23.
The overall recognition accuracy of different datasets.
6. Conclusions and Discussion
This study establishes a transceiver model for genuine target echoes and DRFM deception jamming signals by analyzing the harmonic distortion mechanism inherent to DRFM-based spoofing. Leveraging higher-order statistical signal processing, the bispectrum is utilized to preserve phase information while suppressing Gaussian noise. We innovatively apply the diagonal integral bispectrum to active deception jamming detection. At the feature engineering level, a joint discriminative framework combining the DIBRP, which quantifies energy concentration via dominant spectral peak analysis, and the DIBAE, which characterizes modulation discrepancies through nonlinear complexity metrics, is proposed. A polynomial kernel SVM is subsequently designed to address nonlinear separability challenges in the high-dimensional feature space via kernel mapping.
Experimental validation indicates that under simultaneous SJR and SNR conditions of 0 dB, the proposed system achieves a detection accuracy of 92%. In practical measured-data validation, the algorithm attains a minimum detection accuracy of 91.3%, with its average accuracy further increasing to 94.2%. Furthermore, cross-comparative experiments reveal that the system maintains a detection accuracy of 90% even when the SNR deteriorates to −5 dB, highlighting the robustness and advantages of the proposed algorithm in low-SNR environments.
The core assumption of this study—that DRFM jammers consistently produce detectable harmonic distortion when generating deceptive interference—is based on the hardware characteristics of current-generation DRFM systems and is applicable to most existing DRFM jammers. However, as future DRFM systems incorporate advanced quantization, sampling, and digital compensation techniques, such harmonic effects may be significantly suppressed. Therefore, future research will focus on extending the proposed framework to scenarios involving low or negligible harmonic distortion.
Author Contributions
Conceptualization, A.L. and H.D.; Methodology, H.D.; Software, H.D.; Validation, A.L. and J.W.; Formal analysis, A.L.; Investigation, A.L. and J.W.; Resources, D.S.; Data curation, A.L. and J.W.; Writing—original draft, A.L.; Writing—review & editing, A.L., H.D. and J.W.; Supervision, H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Defense Science and Technology Key Laboratory Fund Project (Grant No. 2023-JCJQ-LB-016).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DRFM | Digital Radio Frequency Memory |
| SNR | signal-to-noise ratio |
| DIBRP | Diagonal Integral Bispectrum Relative Peak Height |
| DIBAE | Diagonal Integral Bispectrum Approximate Entropy |
| SVM | support vector machine |
| JSR | jamming-to-signal ratio |
| FrFT | fractional Fourier transform |
| SSA | singular spectrum analysis |
| CFAR | constant false alarm rate |
| STFT | short-time Fourier transform |
| HOSA | higher-order statistical analysis |
| HOS | higher-order spectrum |
| DIB | diagonal integrated bispectrum |
| IF | intermediate frequency |
| LFM | linear frequency modulation |
| ApEn | approximate entropy |
| AWGN | additive white Gaussian noise |
| TMR | target misclassification rate |
| JMR | jamming misclassification rate |
References
- Greco, M.; Gini, F.; Farina, A. Radar Detection and Classification of Jamming Signals Belonging to a Cone Class. IEEE Trans. Signal Process. 2008, 56, 1984–1993. [Google Scholar] [CrossRef]
- Berger, S.D. The spectrum of a digital radio frequency memory linear range gate stealer electronic attack signal. In Proceedings of the 2001 IEEE Radar Conference (Cat. No.01CH37200), Atlanta, GA, USA, 3 May 2001; pp. 27–30. [Google Scholar] [CrossRef]
- Berger, S.D. Digital radio frequency memory linear range gate stealer spectrum. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 725–735. [Google Scholar] [CrossRef]
- Peng, R.; Wei, W.; Sun, D.; Tan, S.; Wang, G. Dense False Target Jamming Recognition Based on Fast–Slow Time Domain Joint Frequency Response Features. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9142–9159. [Google Scholar] [CrossRef]
- Han, X.; He, H.; He, Y.; Zhou, T.; Zhang, Q.; Zhang, X. A Method Against False-target Jamming Based on Active/Passive Isomerism Missile-borne Radar Network. Acta Armamentarii 2022, 43, 3142–3150. [Google Scholar]
- Hill, P.C.J.; Truffert, V. Statistical processing techniques for detecting DRFM repeat-jam radar signals. In IEE Colloquium on Signal Processing Techniques for Electronic Warfare; IET: London, UK, 1992; pp. 1/1–1/6. [Google Scholar]
- Lu, Y.; Li, M.; Yan, Y. Method for detecting DRFM deception jamming based on LFM rate matching. J. Xidian Univ. 2014, 41, 67–73. [Google Scholar]
- Zhang, S.; Chen, S.; Wang, W. Radar deception jamming detection method with digital radio frequency memory. J. Natl. Univ. Def. Technol. 2024, 46, 174–181. [Google Scholar]
- Ding, S.; Tang, J. DRFM Velocity Deception Jamming Recognition Based on Singular Spectrum Analysis. Radar Sci. Technol. 2020, 18, 44–50. [Google Scholar]
- Lu, Y.; Li, S. CFAR detection of DRFM deception jamming based on singular spectrum analysis. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Hao, Z.; Yu, W.; Chen, W. Recognition method of dense false targets jamming based on time-frequency atomic decomposition. J. Eng. 2019, 2019, 6354–6358. [Google Scholar] [CrossRef]
- Dong, L.; Wang, B.; Pan, B.; Kong, Y.; Yu, X.; Cui, G. Mainlobe DRFM Jamming Suppression via Blind Source Separation Using Tensor Decomposition. In Proceedings of the 2023 8th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 8–10 July 2023; pp. 732–736. [Google Scholar]
- Yang, J.; Bai, Z.; Xian, Z.; Xiang, H.; Li, J.; Hu, H.; Hao, X. Hybrid Attention Module and Transformer based Fuze DRFM Jamming Signal Recognition. IEEE Commun. Lett. 2024, 28, 9. [Google Scholar] [CrossRef]
- Kong, Y.; Yu, X.; Li, J.; Cui, G. DRFM-Based Jamming Suppression via Convolutional Neural Network with Dilated Mechanism. In Proceedings of the 2024 6th International Conference on Data-driven Optimization of Complex Systems (DOCS), Hangzhou, China, 16–18 August 2024; pp. 903–908. [Google Scholar]
- Jian-xun, L.; Qi, S.; Hai, Y. Signal feature analysis and experimental verification of radar deception jamming. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011; Volume 1, pp. 230–233. [Google Scholar]
- Hu, J.B.; Zhu, R.W.; Sun, F.L.; Liu, Y.T. False Target Jamming Feature Extraction and Recognition Method Based on Axial Integral Bispectrum. Guid. Fuze 2024, 45, 15–20. [Google Scholar]
- Li, T.; Ting, J. Target identification based on diagonal slice of the complex bispectrum. In Proceedings of the 2014 IEEE International Conference on Communiction Problem-solving, Beijing, China, 5–7 December 2014; pp. 303–306. [Google Scholar] [CrossRef]
- Meng, X.; Zhao, H.; Liang, Y. A composite modulated LPI radar signal recognition method based on diagonal integral bispectra. Aerosp. Electron. Countermeas. 2021, 37, 13–18. [Google Scholar]
- Ji, H. Research on Target Recognition and Classification Methods of Conventional Radar. Ph.D. Thesis, Shaanxi: Xidian University, Xi’an, China, 1999. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Chen, H. Anti-ISRJ method based on intrapulse frequency-coded joint frequency modulation slope agile radar waveform. J. Radars 2024, 13, 1019–1036. [Google Scholar]
- Wen, Y.; Bai, L.; Shang, S.; Song, D. Blind detection method of weak target echo in GNSS-R passive radar. J. Natl. Univ. Def. Technol. 2024, 46, 121–130. [Google Scholar]
- Guan, J.; Wu, X.; Ding, H.; Liu, N.; Dong, Y.; Zhang, P. A Method for Detecting Small Slow Targets in Sea Surface Based on Diagonal Integrated Bispectrum. J. Electron. Inf. Technol. 2022, 44, 2449–2460. [Google Scholar]
- Liu, N.; Dong, Y.; Wang, G.; Ding, H.; Huang, Y.; Guan, J.; Chen, X.; He, Y. Sea-detecting X-band radar and data acquisition program. J. Radars 2019, 8, 656–667. [Google Scholar]
- Guan, J.; Liu, N.; Wang, G.; Ding, H.; Dong, Y.; Huang, Y.; Tian, K.; Zhang, M. Sea-detecting radar experiment and target feature data acquisition for dual polarization multistate scattering dataset of marine targets. J. Radars 2023, 12, 456–469. [Google Scholar]
- Liu, N.; Ding, H.; Huang, Y.; Dong, Y.; Wang, G.; Dong, K. Annual progress of the sea-detecting X-band radar and data acquisition program. J. Radars 2021, 10, 173–182. [Google Scholar]
- Ding, H.; Liu, N.; Dong, Y.; Chen, X.; Guan, J. Overview and prospects of radar sea clutter measurement experiments. J. Radars 2019, 8, 281–302. [Google Scholar]
- Ding, H.; Dong, Y.; Liu, N.; Wang, G.; Guan, J. Overview and Prospects of Research on Sea Clutter Property Cognition. J. Radars 2016, 5, 499–516. [Google Scholar]
- Espinosa, R.A.; Calderón, R. Choice of tau in the estimation of ApEn and SampEn entropy of EMG, ECG and EEG signals. In Proceedings of the 2019 XXII Symposium on Image, Signal Processing and Artificial Vision (STSIVA), Bucaramanga, Colombia, 24–26 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Li, H.; Feng, X.; Cao, L.; Li, E.; Liang, H.; Chen, X. A New ECG Signal Classification Based on WPD and ApEn Feature Extraction. Circuits Syst. Signal Process. 2016, 35, 339–352. [Google Scholar] [CrossRef]
- Mathur, A.; Foody, G.M. Multiclass and Binary SVM Classification Implications for Training and Classification Users. IEEE Geosci. Remote Sens. Lett. 2008, 5, 241–245. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).