Remote Sensing in the 15 µm CO2 Band: Key Concepts and Implications for the Heat Balance of Mesosphere and Thermosphere
Abstract
1. Introduction
2. The Limb Observations of the CO2 15 µm Emission of MLT
2.1. The 15 µm Radiative Flux Divergence
2.2. Radiative Flux Divergence and the 15 µm Limb Emission
2.3. The Radiative Flux Divergence and the 15 µm Cooling
2.4. The 15 µm “Cooling” Derived from Observations and the CO2 Cooling in the GCMs
3. New Model for Calculating the 15 µm Cooling of MLT
3.1. Constrained CO2 Vibrational Level Populations
3.2. Low Laboratory-Measured for Calculating the CO2 Cooling
3.3. The Model Performance
3.4. Modification of the ALI-ARMS Code
4. Calculation Results and Discussion
4.1. True Cooling for the Lower Limit of the Laboratory-Confirmed Value
4.2. New Heating Source of MLT
4.3. The Excess Cooling
4.4. True Cooling for the Upper Limit of the Laboratory-Confirmed Value
4.5. The Accounting for the Absorption of the Solar Radiation
5. Practical Application of the New the 15 µm Cooling Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALI-ARMS | Accelerated lambda iteration for atmospheric radiation and molecular spectra research code |
| CMAT2 | Coupled middle-atmosphere-thermosphere-2 GCM |
| CO2 | Carbon dioxide |
| GSFC | Goddard Space Flight Center |
| GCM | General circulation model |
| K | Kelvin degrees |
| MLS | Mid-latitude summer atmosphere |
| MLT | Mesosphere and lower thermosphere |
| MLW | Mid-latitude winter atmosphere |
| NASA | National Atmospheric and Space Administration |
| Non-LTE | Non-local thermodynamic equilibrium |
| [NN] | Density of the molecular or atomic atmospheric component NN |
| N2 | Molecular nitrogen |
| O2 | Molecular oxygen |
| O(3P) | Atom of oxygen in the ground state 3P |
| RT | Rotational–translational energy transfer |
| RTE | Radiative transfer equation |
| SABER | Sounding of the atmosphere using broadband emission radiometry instrument on board of TIMED |
| SAS | Subarctic summer atmosphere |
| SAW | Subarctic winter atmosphere |
| TIMED | NASA’s Thermosphere Ionosphere Mesosphere Energetics Dynamics satellite |
| TROP | tropical atmosphere |
| VT | Vibrational–translational energy transfer |
| VV | Vibrational–vibrational energy transfer |
| 83°N | Latitude 83 degrees north of the Equator |
References
- Crutzen, P.J. Discussion of paper “Absorption and emission by carbon dioxide in the atmosphere” by J. T. Houghton. Q. J. R. Meteorol. Soc. 1970, 96, 767–770. [Google Scholar] [CrossRef]
- Offermann, D.; Grossmann, K.U.; Barthol, P.; Knieling, P.; Riese, M.; Trant, R. Cryogenic Infrared Spectrometers and Telescopes for the Atmosphere (CRISTA) experiment and middle atmosphere variability. J. Geophys. Res. 1999, 104, 16311–16326. [Google Scholar] [CrossRef]
- Russell, J.M.; Mlynczak, M.G.; Gordley, L.L.; Tansock, J.J.; Esplin, R.W. Overview of the SABER experiment and preliminary calibration results. In Proceedings of the Optical Spectroscopic Techniques and Instrumentation for Atmospheric and Space Research III; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; Larar, A.M., Ed.; SPIE: Bellingham, WA, USA, 1999; Volume 3756, pp. 277–288. [Google Scholar] [CrossRef]
- Fischer, H.; Birk, M.; Blom, C.; Carli, B.; Carlotti, M.; von Clarmann, T.; Delbouille, L.; Dudhia, A.; Ehhalt, D.; Endemann, M.; et al. MIPAS: An instrument for atmospheric and climate research. Atmos. Chem. Phys. 2008, 8, 2151–2188. [Google Scholar] [CrossRef]
- Goody, R.M.; Yung, Y.L. Atmospheric Radiation: Theoretical Basis, 2nd ed.; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Sharma, R.D.; Wintersteiner, P.P. Role of carbon dioxide in cooling planetary thermospheres. Geophys. Res. Lett. 1990, 17, 2201–2204. [Google Scholar] [CrossRef]
- Pollock, D.S.; Scott, G.B.I.; Phillips, L.F. Rate constant for quenching of CO2(010) by atomic oxygen. Geophys. Res. Lett. 1993, 20, 727–729. [Google Scholar] [CrossRef]
- Bougher, S.W.; Hunten, D.M.; Roble, R.G. CO2 cooling in terrestrial planet thermospheres. J. Geophys. Res. 1994, 99, 14609–14622. [Google Scholar] [CrossRef]
- Lopez-Puertas, M.; Taylor, F.W. Non–LTE Radiative Transfer in the Atmosphere; World Scientific: Singapore, 2001; ISBN 9810245661. [Google Scholar] [CrossRef]
- Feofilov, A.G.; Kutepov, A.A. Infrared Radiation in the Mesosphere and Lower Thermosphere: Energetic Effects and Remote Sensing. Surv. Geophys. 2012, 33, 1231–1280. [Google Scholar] [CrossRef]
- Kutepov, A.A. Parametrization of the radiant energy influx in the CO2 15 microns band for Earth’s atmosphere in the spoilage layer of local thermodynamic equilibrium. Akad. Nauk SSSR Fiz. Atmos. I Okeana 1978, 14, 216–218. [Google Scholar]
- Zhu, X. Carbon dioxide 15-micron band cooling rates in the upper middle atmosphere calculated by Curtis matrix interpolation. J. Atmos. Sci. 1990, 47, 755–774. [Google Scholar] [CrossRef]
- Kutepov, A.A.; Fomichev, V.I. Application of the second-order escape probability approximation to the solution of the NLTE vibration-rotational band radiative transfer problem. J. Atmos. Terr. Phys. 1993, 55, 1–6. [Google Scholar] [CrossRef]
- Fomichev, V.I.; Kutepov, A.A.; Akmaev, R.A.; Shved, G.M. Parameterization of the 15-micron CO2 band cooling in the middle atmosphere (15–115 km). J. Atmos. Terr. Phys. 1993, 55, 7–18. [Google Scholar] [CrossRef]
- Fomichev, V.I.; Blanchet, J.P.; Turner, D.S. Matrix parameterization of the 15 µm CO2 band cooling in the middle and upper atmosphere for variable CO2 concentration. J. Geophys. Res. Atmos. 1998, 103, 11505–11528. [Google Scholar] [CrossRef]
- Hartogh, P.; Medvedev, A.S.; Kuroda, T.; Saito, R.; Villanueva, G.; Feofilov, A.G.; Kutepov, A.A.; Berger, U. Description and climatology of a new general circulation model of the Martian atmosphere. J. Geophys. Res. (Planets) 2005, 110, E11008. [Google Scholar] [CrossRef]
- López-Puertas, M.; Fabiano, F.; Fomichev, V.; Funke, B.; Marsh, D.R. An improved and extended parameterization of the CO2 15 µm cooling in the middle/upper atmosphere (CO2_cool_fort-1.0). Goesci. Model Dev. 2024, 17, 4401–4432. [Google Scholar] [CrossRef]
- Kutepov, A.; Feofilov, A. New Routine NLTE15µmcool-E V1.0 For Calculating The Non-Local Thermodynamic Equilibrium (Non-LTE) CO2 15 µm Cooling in General Circulation Models (GCMs) of Earth’s Atmosphere. Geosci. Model Dev. 2024, 17, 5331–5347. [Google Scholar] [CrossRef]
- Feofilov, A.G.; Kutepov, A.A.; She, C.Y.; Smith, A.K.; Pesnell, W.D.; Goldberg, R.A. CO2(ν2)-O quenching rate coefficient derived from coincidental SABER/TIMED and Fort Collins lidar observations of the mesosphere and lower thermosphere. Atmos. Chem. Phys. 2012, 12, 9013–9023. [Google Scholar] [CrossRef]
- Mlynczak, M.G.; Hunt, L.A.; Thomas Marshall, B.; Martin-Torres, F.J.; Mertens, C.J.; Russell, J.M.; Remsberg, E.E.; López-Puertas, M.; Picard, R.; Winick, J.; et al. Observations of infrared radiative cooling in the thermosphere on daily to multiyear timescales from the TIMED/SABER instrument. J. Geophys. Res. (Space Phys.) 2010, 115, A03309. [Google Scholar] [CrossRef]
- Gusev, O.; Kaufmann, M.; Grossmann, K.U.; Schmidlin, F.J.; Shepherd, M.G. Atmospheric neutral temperature distribution at the mesopause altitude. J. Atmos. Sol.-Terr. Phys. 2006, 68, 1684–1697. [Google Scholar] [CrossRef]
- García-Comas, M.; López-Puertas, M.; Marshall, B.T.; Wintersteiner, P.P.; Funke, B.; Bermejo-Pantaleón, D.; Mertens, C.J.; Remsberg, E.E.; Gordley, L.L.; Mlynczak, M.G.; et al. Errors in Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) kinetic temperature caused by non-local-thermodynamic-equilibrium model parameters. J. Geophys. Res. (Atmos.) 2008, 113, D24106. [Google Scholar] [CrossRef]
- García-Comas, M.; Funke, B.; López-Puertas, M.; Bermejo-Pantaleón, D.; Glatthor, N.; von Clarmann, T.; Stiller, G.; Grabowski, U.; Boone, C.D.; French, W.J.R.; et al. On the quality of MIPAS kinetic temperature in the middle atmosphere. Atmos. Chem. Phys. 2012, 12, 6009–6039. [Google Scholar] [CrossRef]
- Rezac, L.; Kutepov, A.; Russell, J.M.; Feofilov, A.G.; Yue, J.; Goldberg, R.A. Simultaneous retrieval of T(p) and CO2 VMR from two-channel non-LTE limb radiances and application to daytime SABER/TIMED measurements. J. Atmos. Sol.-Terr. Phys. 2015, 130, 23–42. [Google Scholar] [CrossRef]
- Akmaev, R.A.; Fomichev, V.I. Cooling of the mesosphere and lower thermosphere due to doubling of CO2. Ann. Geophys. 1998, 16, 1501–1512. [Google Scholar] [CrossRef]
- Laštovička, J.; Akmaev, R.A.; Beig, G.; Bremer, J.; Emmert, J.T.; Jacobi, C.; Jarvis, M.J.; Nedoluha, G.; Portnyagin, Y.I.; Ulich, T. Emerging pattern of global change in the upper atmosphere and ionosphere. Ann. Geophys. 2008, 26, 1255–1268. [Google Scholar] [CrossRef]
- Jackson, D.R.; Fuller-Rowell, T.J.; Griffin, D.J.; Griffith, M.J.; Kelly, C.W.; Marsh, D.R.; Walach, M.T. Future Directions for Whole Atmosphere Modeling: Developments in the Context of Space Weather. Space Weather 2019, 17, 1342–1350. [Google Scholar] [CrossRef]
- Garcia, R.R.; Yue, J.; Russell, J.M. Middle Atmosphere Temperature Trends in the Twentieth and Twenty-First Centuries Simulated With the Whole Atmosphere Community Climate Model (WACCM). J. Geophys. Res. (Space Phys.) 2019, 124, 7984–7993. [Google Scholar] [CrossRef]
- Jackson, D.R.; Bruinsma, S.; Negrin, S.; Stolle, C.; Budd, C.J.; Dominguez Gonzalez, R.; Down, E.; Griffin, D.J.; Griffith, M.J.; Kervalishvili, G.; et al. The Space Weather Atmosphere Models and Indices (SWAMI) project: Overview and first results. J. Space Weather Space Clim. 2020, 10, 18. [Google Scholar] [CrossRef]
- Wallis, S.; Schmidt, H.; von Savigny, C. Impact of a strong volcanic eruption on the summer middle atmosphere in UA-ICON simulations. Atmos. Chem. Phys. 2023, 23, 7001–7014. [Google Scholar] [CrossRef]
- McInerney, J.M.; Qian, L.; Liu, H.L.; Solomon, S.C.; Nossal, S.M. Climate Change in the Thermosphere and Ionosphere From the Early Twentieth Century to Early Twenty-First Century Simulated by the Whole Atmosphere Community Climate Model—eXtended. J. Geophys. Res. (Atmos.) 2024, 129, e2023JD039397. [Google Scholar] [CrossRef]
- Laštovička, J. Progress in investigating long-term trends in the mesosphere, thermosphere, and ionosphere. Atmos. Chem. Phys. 2023, 23, 5783–5800. [Google Scholar] [CrossRef]
- Lübken, F.J. Physics in the mesosphere/lower thermosphere: A personal perspective. Front. Astron. Space Sci. 2022, 9, 1000766. [Google Scholar] [CrossRef]
- Mlynczak, M.G.; Hunt, L.A.; Garcia, R.; Lopez-Puertas, M.; Mertens, C.J.; Nowak, N.; Marshall, B.T. Energy Conservation in the Cooling and Contracting Upper Mesosphere and Lower Thermosphere. Geophys. Res. Lett. 2024, 51, e2024GL109757. [Google Scholar] [CrossRef]
- Mlynczak, M.G.; Hunt, L.; Nowak, N.; Marshall, B.T.; Mertens, C.J. Infrared Radiation in the Thermosphere From 2002 to 2023. Geophys. Res. Lett. 2024, 51, e2024GL109470. [Google Scholar] [CrossRef]
- Ogibalov, V.P.; Kutepov, A.A.; Shved, G.M. Non-local thermodynamic equilibrium in CO2 in the middle atmosphere. II. Populations in the ν1ν2 mode manifold states. J. Atmos. Sol.-Terr. Phys. 1998, 60, 315–329. [Google Scholar] [CrossRef]
- Kutepov, A.A.; Gusev, O.A.; Ogibalov, V.P. Solution of the non-LTE problem for molecular gas in planetary atmospheres: Superiority of accelerated lambda iteration. J. Quant. Spectrosc. Radiat. Transf. 1998, 60, 199–220. [Google Scholar] [CrossRef]
- Funke, B.; López-Puertas, M.; García-Comas, M.; Kaufmann, M.; Höpfner, M.; Stiller, G.P. GRANADA: A Generic RAdiative traNsfer AnD non-LTE population algorithm. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1771–1817. [Google Scholar] [CrossRef]
- Goody, R.M. Atmospheric Radiation. I. Theoretical Basis (Oxford Monographs on Meteorology); Clarendon Press, Oxford University Press: Oxford, UK, 1964. [Google Scholar]
- Ivanov, V.V. Transfer of Radiation in Spectral Lines; National Bureo of Standarts: Gaithersburg, MD, USA, 1973; Volume 385. [Google Scholar]
- Mihalas, D. Stellar Atmospheres; Freeman: San Francisco, CA, USA, 1978. [Google Scholar]
- Hubeny, I.; Mihalas, D. Theory of Stellar Atmospheres; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Abbas, M.M.; Guo, J.; Conrath, B.J.; Kunde, V.G.; Maguire, W.C. Finite field of view effects on inversion of limb thermal emission observations. J. Geophys. Res. Atmos. 1985, 90, 3903–3909. [Google Scholar] [CrossRef]
- Bullitt, M.K.; Bakshi, P.M.; Picard, R.H.; Sharma, R.D. Numerical and analytical study of high-resolution limb spectral radiance from nonequilibrium atmospheres. J. Quant. Spectrosc. Radiat. Transf. 1985, 34, 33–53. [Google Scholar] [CrossRef]
- López-Puertas, M.; Rodrigo, R.; Molina, A.; Taylor, F.W. A non-LTE radiative transfer model for infrared bands in the middle atmosphere. I. Theoretical basis and application to CO2 15 µm bands. J. Atmos. Terr. Phys. 1986, 48, 729–748. [Google Scholar] [CrossRef]
- Lopez-Puertas, M.; Rodrigo, R.; Lopez-Moreno, J.J.; Taylor, F.W. A non-LTE radiative transfer model for infrared bands in the middle atmosphere. II. CO2 (2.7 and 4.3 µm) and water vapour (6.3 µm) bands and N2(1) and O2(1) vibrational levels. J. Atmos. Terr. Phys. 1986, 48, 749–764. [Google Scholar] [CrossRef]
- Gordley, L.L.; Marshall, B.T.; Jacobson, S.B.; Mlynczak, M.G.; Russell, J.M., III. Rapid non-LTE analysis of CO2 limb emission from the upper mesosphere to obtain kinetic temperature and pressure. In Proceedings of the Remote Sensing of Clouds and the Atmosphere VIII; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; Schaefer, K.P., Comeron, A., Carleer, M.R., Picard, R.H., Eds.; SPIE: Bellingham, WA, USA, 2004; Volume 5235, pp. 240–249. [Google Scholar] [CrossRef]
- Shved, G.M.; Kutepov, A.A.; Ogibalov, V.P. Non-local thermodynamic equilibrium in CO2 in the middle atmosphere. I. Input data and populations of the ν3 mode manifold states. J. Atmos. Sol.-Terr. Phys. 1998, 60, 289–314. [Google Scholar] [CrossRef]
- Kutepov, A.A.; Shved, G.M. Radiative transfer in the 15-micron CO2 band with the breakdown of local thermodynamic equilibrium in the earth’s atmosphere. Acad. Sci. USSR Izv. Atmos. Ocean. Phys. Transl. 1978, 14, 18–30. [Google Scholar]
- Shved, G.M. Non-LTE radiative transfer in the vibration-rotation bands of linear molecules. Astron. Zhurnal 1974, 51, 841. [Google Scholar]
- She, C.Y.; Sherman, J.; Yuan, T.; Williams, B.P.; Arnold, K.; Kawahara, T.D.; Li, T.; Xu, L.F.; Vance, J.D.; Acott, P.; et al. The first 80-hour continuous lidar campaign for simultaneous observation of mesopause region temperature and wind. Geophys. Res. Lett. 2003, 30, 1319. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kharchenko, V.; Dalgarno, A. Slowing of energetic O(3P) atoms in collisions with N2. J. Geophys. Res. 1998, 103, 23393–23398. [Google Scholar] [CrossRef]
- Kharchenko, V.; Dalgarno, A.; Fox, J.L. Thermospheric distribution of fast O(1D) atoms. J. Geophys. Res. (Space Phys.) 2005, 110, A12305. [Google Scholar] [CrossRef]
- Sharma, R.D.; Wintersteiner, P.P.; Kalogerakis, K.S. A new mechanism for OH vibrational relaxation leading to enhanced CO2 emissions in the nocturnal mesosphere. J. Geophys. Res. Atmos. 2015, 42, 4639–4647. [Google Scholar] [CrossRef]
- Dawkins, E.C.M.; Feofilov, A.; Rezac, L.; Kutepov, A.A.; Janches, D.; Höffner, J.; Chu, X.; Lu, X.; Mlynczak, M.G.; Russell, J. Validation of SABER v2.0 Operational Temperature Data with Ground-Based Lidars in the Mesosphere-Lower Thermosphere Region (75–105 km). J. Geophys. Res. (Atmos.) 2018, 123, 9916–9934. [Google Scholar] [CrossRef]
- Shved, G.M.; Khvorostovskaya, L.E.; Potekhin, I.Y.; Ogibalov, V.P.; Uzyukova, T.V. Measurement of rate constant for quenching CO2(0110) by atomic oxygen at low temperatures: Reassessment of the population of CO2(0110) and the CO2 15-µm emission cooling in the lower thermosphere. In Proceedings of the Remote Sensing of Clouds and the Atmosphere VII; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; Schaefer, K.P., Lado-Bordowsky, O., Comeron, A., Picard, R.H., Eds.; SPIE: Bellingham, WA, USA, 2003; Volume 4882, pp. 106–116. [Google Scholar] [CrossRef]
- Shved, G.M.; Khvorostovskaia, L.E.; Potekhin, I.I.; Dem’ianikov, A.I.; Kutepov, A.A. The measurement of the rate constant of CO2/01 super-1 0/ quenching by atomic oxygen and the importance of the rate constant magnitude for the thermal regime and radiation of the lower thermosphere. Akad. Nauk SSSR Fiz. Atmos. I Okeana 1991, 27, 431–437. [Google Scholar]
- Castle, K.J.; Black, L.A.; Simione, M.W.; Dodd, J.A. Vibrational relaxation of CO2(ν2) by O(3P) in the 142–490 K temperature range. J. Geophys. Res. (Space Phys.) 2012, 117, A04310. [Google Scholar] [CrossRef]
- Kutepov, A.A.; Feofilov, A.G.; Medvedev, A.S.; Berger, U.; Kaufmann, M.; Pauldrach, A.W.A. Infra-red Radiative Cooling/Heating of the Mesosphere and Lower Thermosphere Due to the Small-Scale Temperature Fluctuations Associated with Gravity Waves. In Climate and Weather of the Sun-Earth System (CAWSES): Highlights from a Priority Program; Lübken, F.J., Ed.; Springer: Dordrecht, The Netherlands, 2013; pp. 429–442. [Google Scholar] [CrossRef]
- Ogibalov, V.P.; Fomichev, V.I. Parameterization of solar heating by the near IR CO2 bands in the mesosphere. Adv. Space Res. 2003, 32, 759–764. [Google Scholar] [CrossRef]
- Walterscheid, R.L. Dynamical cooling induced by dissipating internal gravity waves. Geophys. Res. Lett. 1981, 8, 1235–1238. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Klaassen, G.P. Thermal effects of saturating gravity waves in the atmosphere. J. Geophys. Res. (Atmos.) 2003, 108, 4040. [Google Scholar] [CrossRef]
- Yiǧit, E.; Medvedev, A.S. Heating and cooling of the thermosphere by internal gravity waves. Geophys. Res. Lett. 2009, 36, L14807. [Google Scholar] [CrossRef]
- Jonsson, A.I.; de Grandpré, J.; Fomichev, V.I.; McConnell, J.C.; Beagley, S.R. Doubled CO2-induced cooling in the middle atmosphere: Photochemical analysis of the ozone radiative feedback. J. Geophys. Res. (Atmos.) 2004, 109, D24103. [Google Scholar] [CrossRef]
- Chen, H.; Wolf, E.T.; Zhan, Z.; Horton, D.E. Habitability and Spectroscopic Observability of Warm M-dwarf Exoplanets Evaluated with a 3D Chemistry-Climate Model. Astrophys. J. 2019, 886, 16. [Google Scholar] [CrossRef]


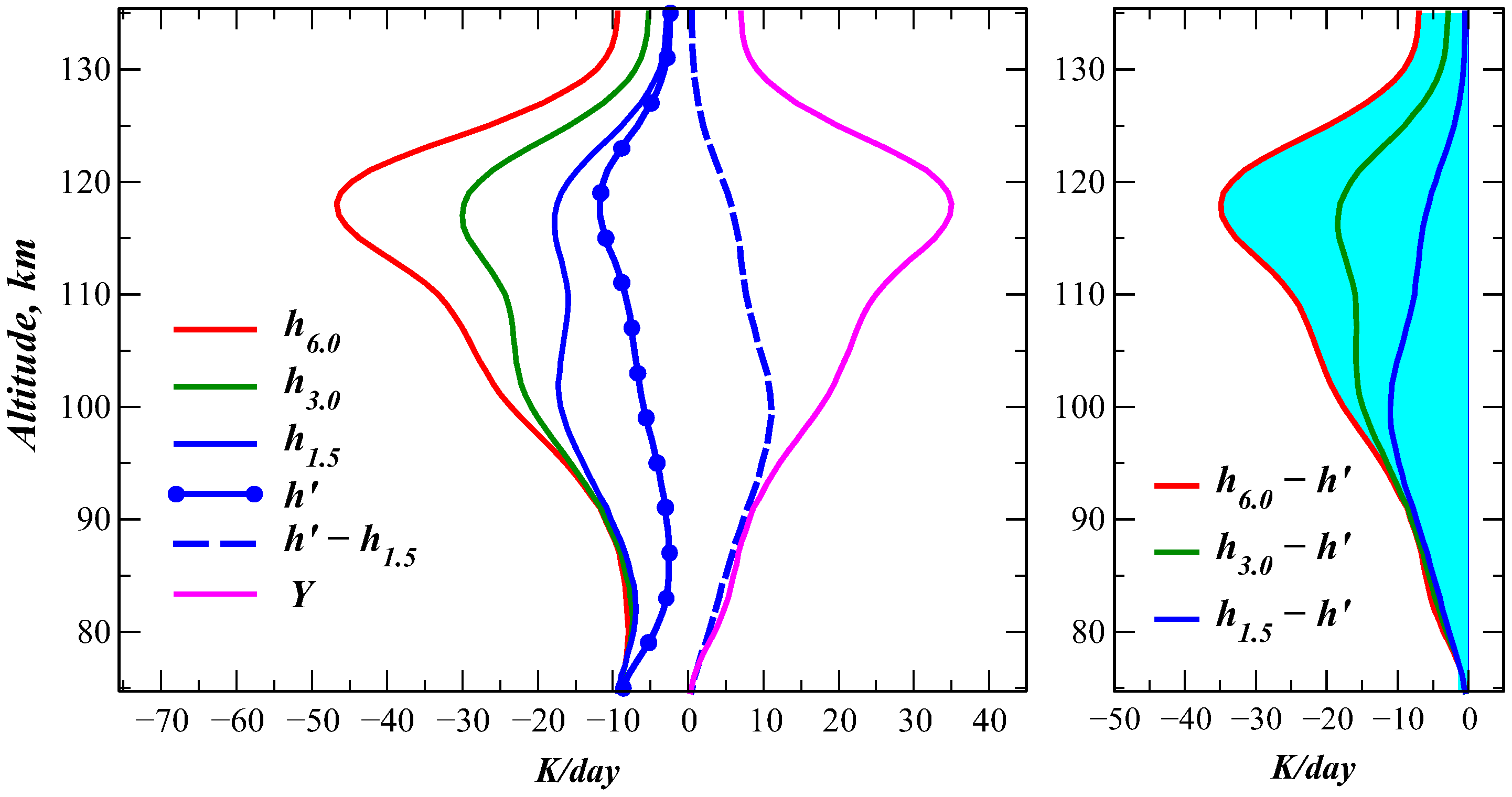


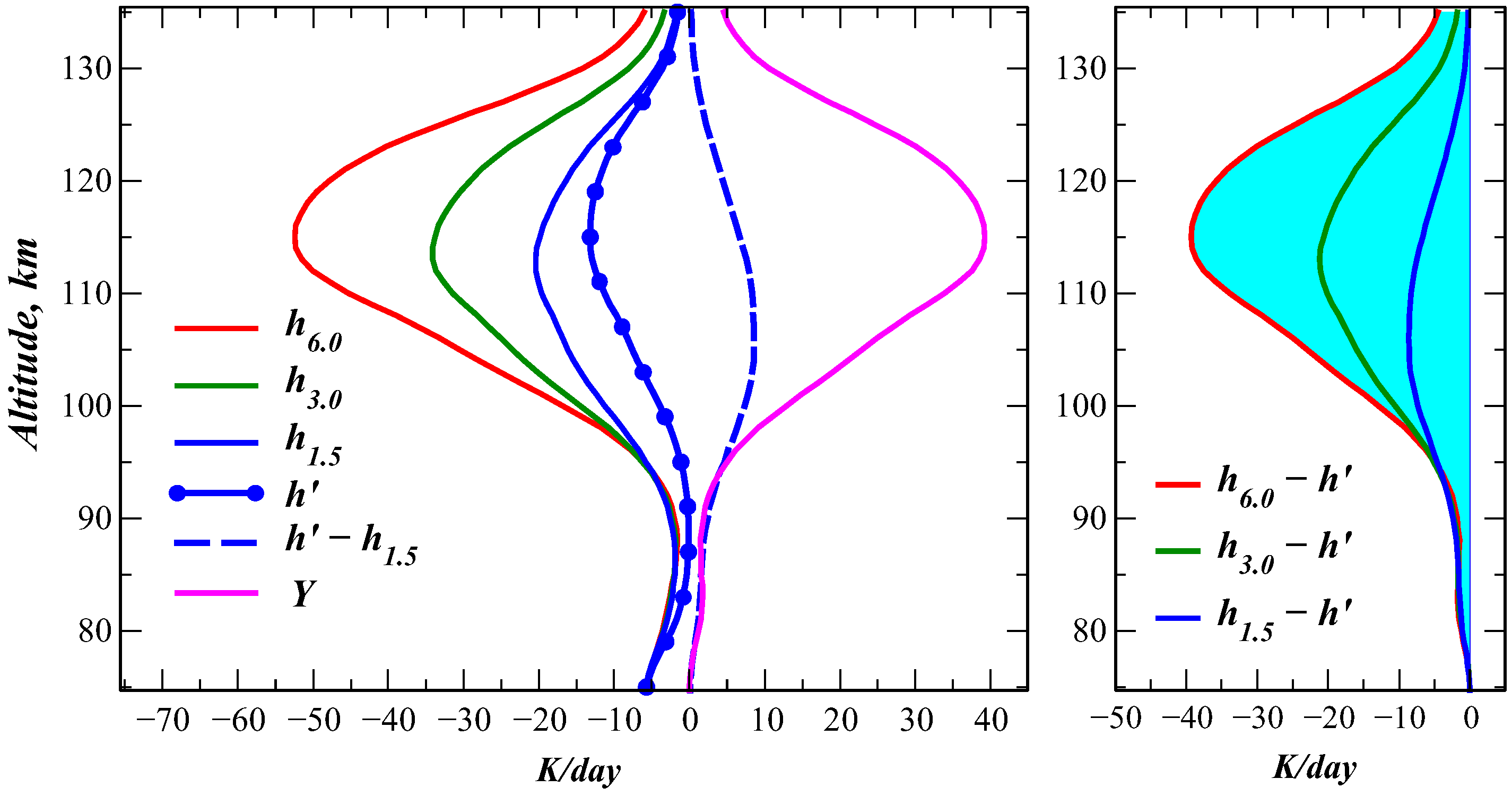

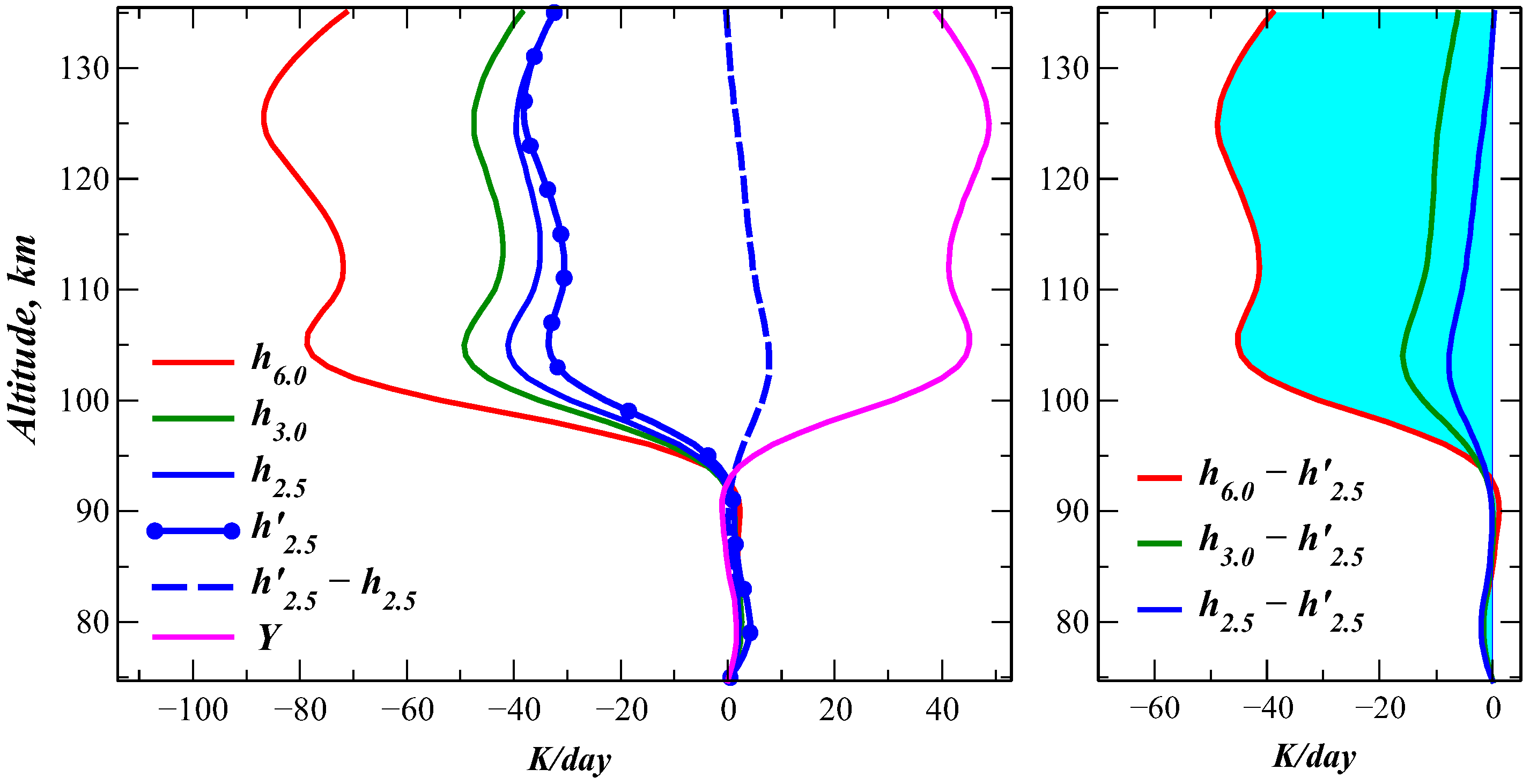

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kutepov, A.; Feofilov, A.; Rezac, L.; Kalogerakis, K.S. Remote Sensing in the 15 µm CO2 Band: Key Concepts and Implications for the Heat Balance of Mesosphere and Thermosphere. Remote Sens. 2025, 17, 1896. https://doi.org/10.3390/rs17111896
Kutepov A, Feofilov A, Rezac L, Kalogerakis KS. Remote Sensing in the 15 µm CO2 Band: Key Concepts and Implications for the Heat Balance of Mesosphere and Thermosphere. Remote Sensing. 2025; 17(11):1896. https://doi.org/10.3390/rs17111896
Chicago/Turabian StyleKutepov, Alexander, Artem Feofilov, Ladislav Rezac, and Konstantinos S. Kalogerakis. 2025. "Remote Sensing in the 15 µm CO2 Band: Key Concepts and Implications for the Heat Balance of Mesosphere and Thermosphere" Remote Sensing 17, no. 11: 1896. https://doi.org/10.3390/rs17111896
APA StyleKutepov, A., Feofilov, A., Rezac, L., & Kalogerakis, K. S. (2025). Remote Sensing in the 15 µm CO2 Band: Key Concepts and Implications for the Heat Balance of Mesosphere and Thermosphere. Remote Sensing, 17(11), 1896. https://doi.org/10.3390/rs17111896






