Fine-Resolution Satellite Remote Sensing Improves Spatially Distributed Snow Modeling to Near Real Time
Abstract
1. Introduction
2. Materials and Methods
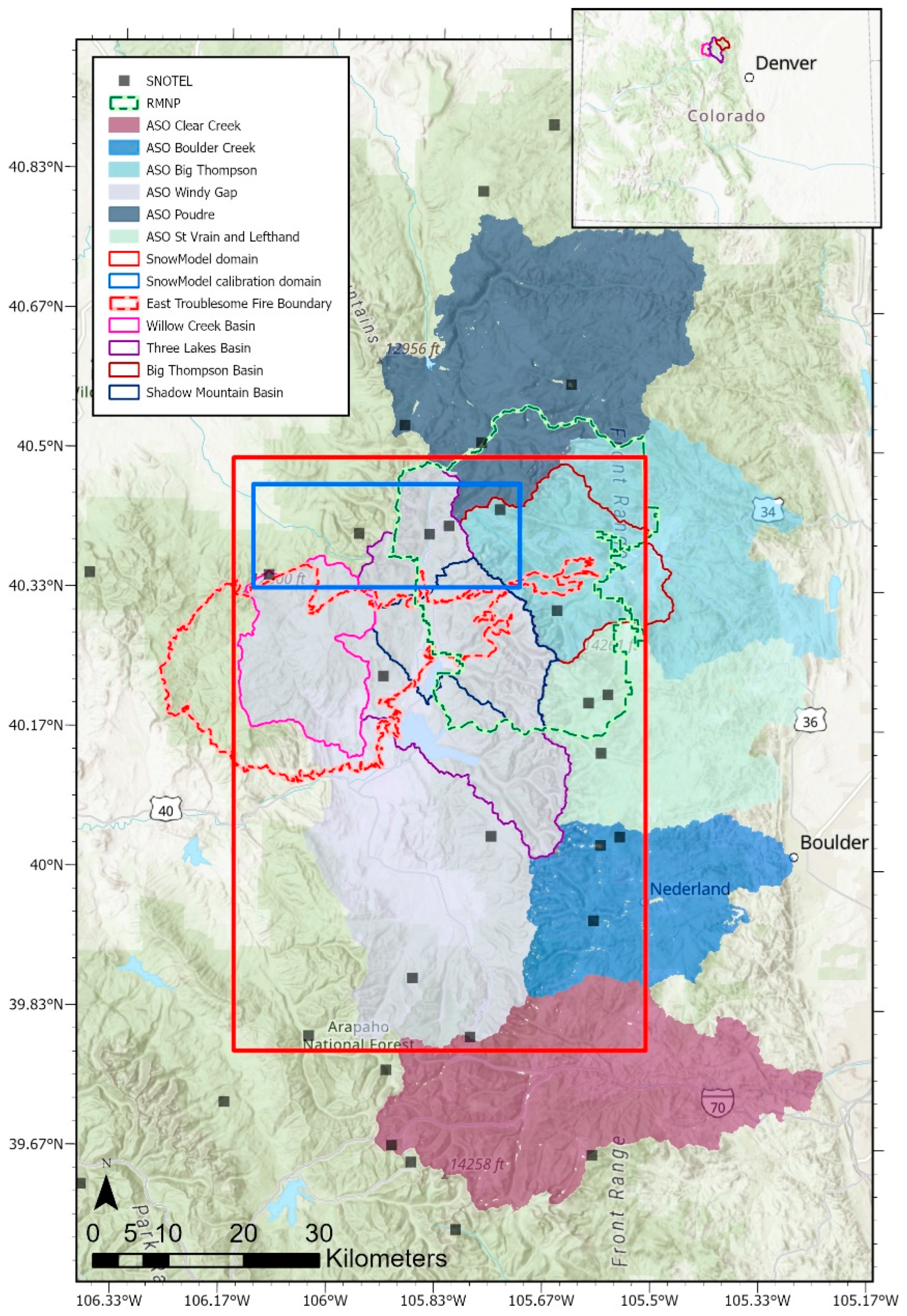
2.1. Study Area
2.2. Model Description and Simulations
2.3. Model Calibration
2.4. SnowModel Output Grid Updates Using Remotely Sensed SCA
2.5. Model Evaluation
| Parameter Description (Parameter Name) | Calibration Step and Process | Default Value | Calibrated Value [Calibration Range] |
|---|---|---|---|
| Rain–snow threshold (snowfall_frac) | not calibrated | [72] | [72] |
| Snow density rate adjustment factor (ro_adjust) | step 1: snow density evolution | 5.0 | 0.4 [0.1–5.0] |
| Curvature length scale (curve_len_scale) | step 2: wind redistribution of snow | 500 | 575 [30–600] |
| Slope weight factor (slopewt) | step 2: wind redistribution of snow | 0.58 | 0.18 [0, 1] |
| Curvature weight factor (curvewt) | step 2: wind redistribution of snow | 0.42 | 0.82 [0, 1] |
| Wind increase/decrease with elevation (wind_lapse_rate) | step 2: wind redistribution of snow | 0.0 | 1.81 [1, 2] |
| Forest snow albedo minimum (for_al_min) | step 3: snow albedo | 0.40 | 0.22 [0.10–0.55] |
| Open area snow albedo minimum (open_al_min) | step 3: snow albedo | 0.50 | 0.42 [0.10–0.55] |
| Forest snow albedo maximum (for_al_max) | step 3: snow albedo | 0.68 | 0.56 [0.55–0.90] |
| Open area snow albedo maximum (open_al_max) | step 3: snow albedo | 0.80 | 0.71 [0.55–0.90] |
| Forest snow albedo decay cold snow (for_al_gr_cold) | step 3: snow albedo | 0.03 | 0.02 [0.010–0.035] |
| Open area snow albedo decay cold snow (open_al_gr_cold) | step 3: snow albedo | 0.02 | 0.02 [0.010–0.035] |
| Forest snow albedo decay melting snow (for_al_gr_melt) | step 3: snow albedo | 0.06 | 0.06 [0.045–0.095] |
3. Results
3.1. Model Calibration
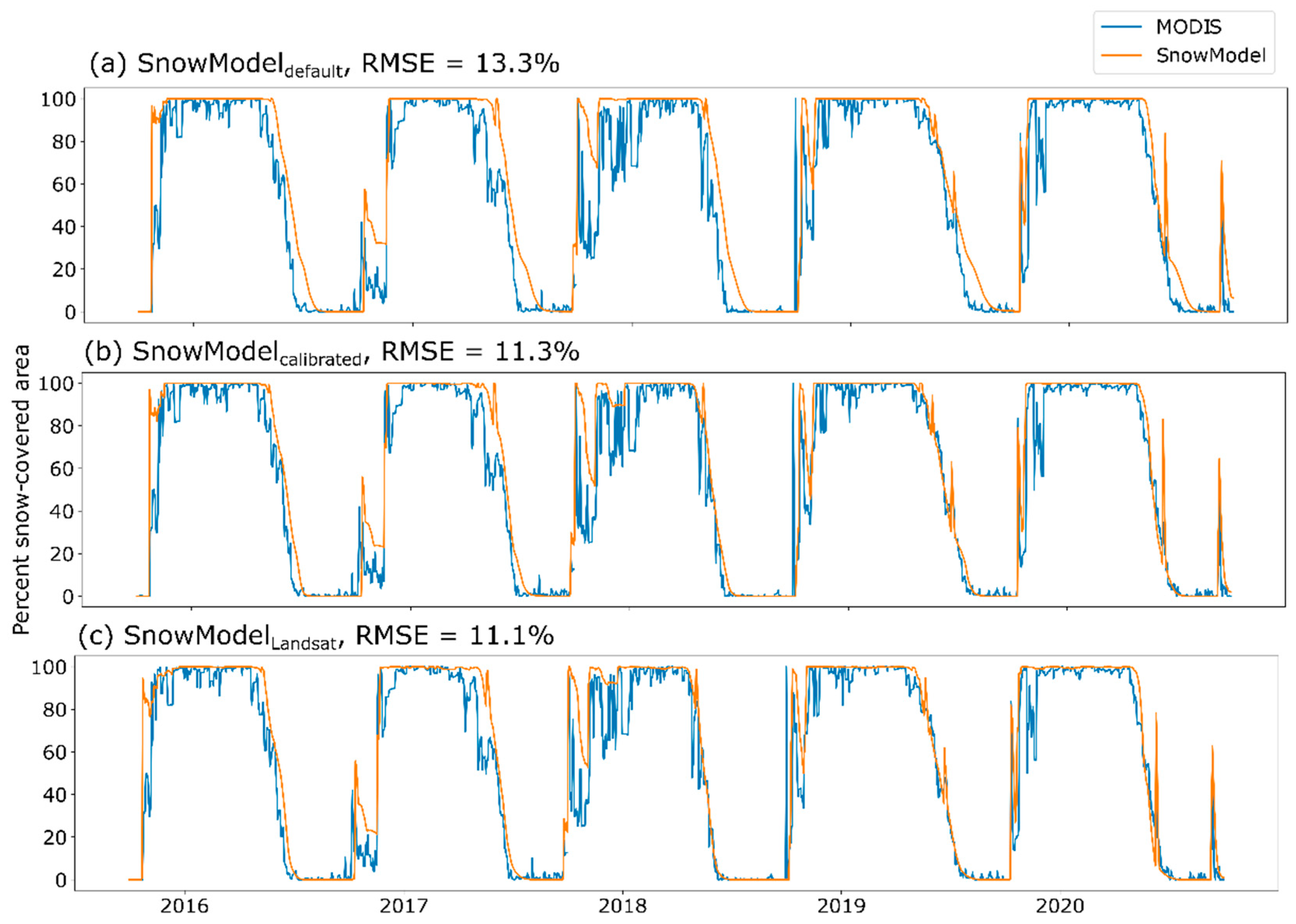
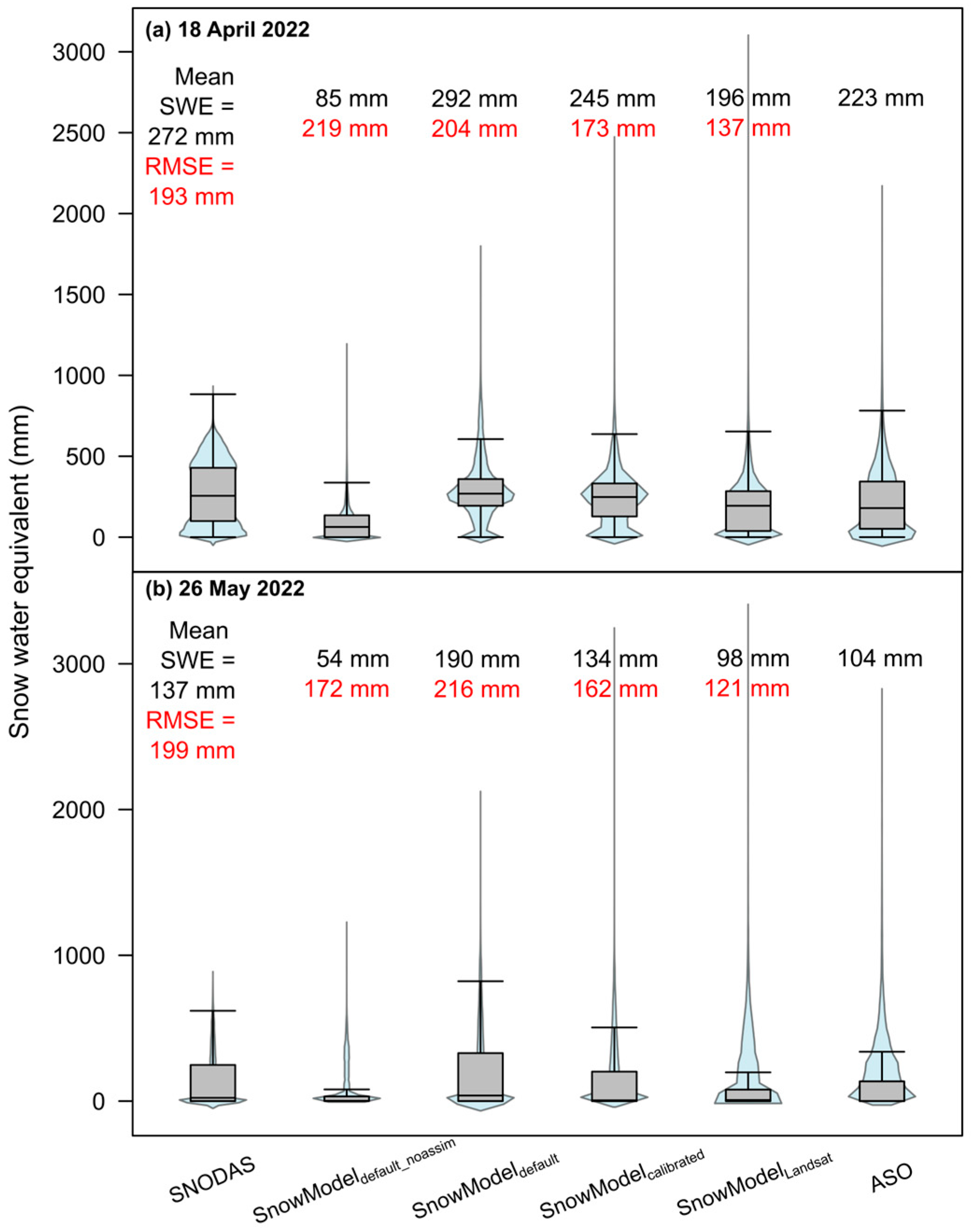
3.2. Model Comparisons with Historical Model
3.3. Model Evaluations Compared to ASO
3.4. Value Added Using Additional Real-Time Remote Sensing Datasets
4. Discussion
4.1. Advantages of Near-Real-Time Spatially Distributed Snow Modeling Approach
4.2. Comparisons to Previous Investigations
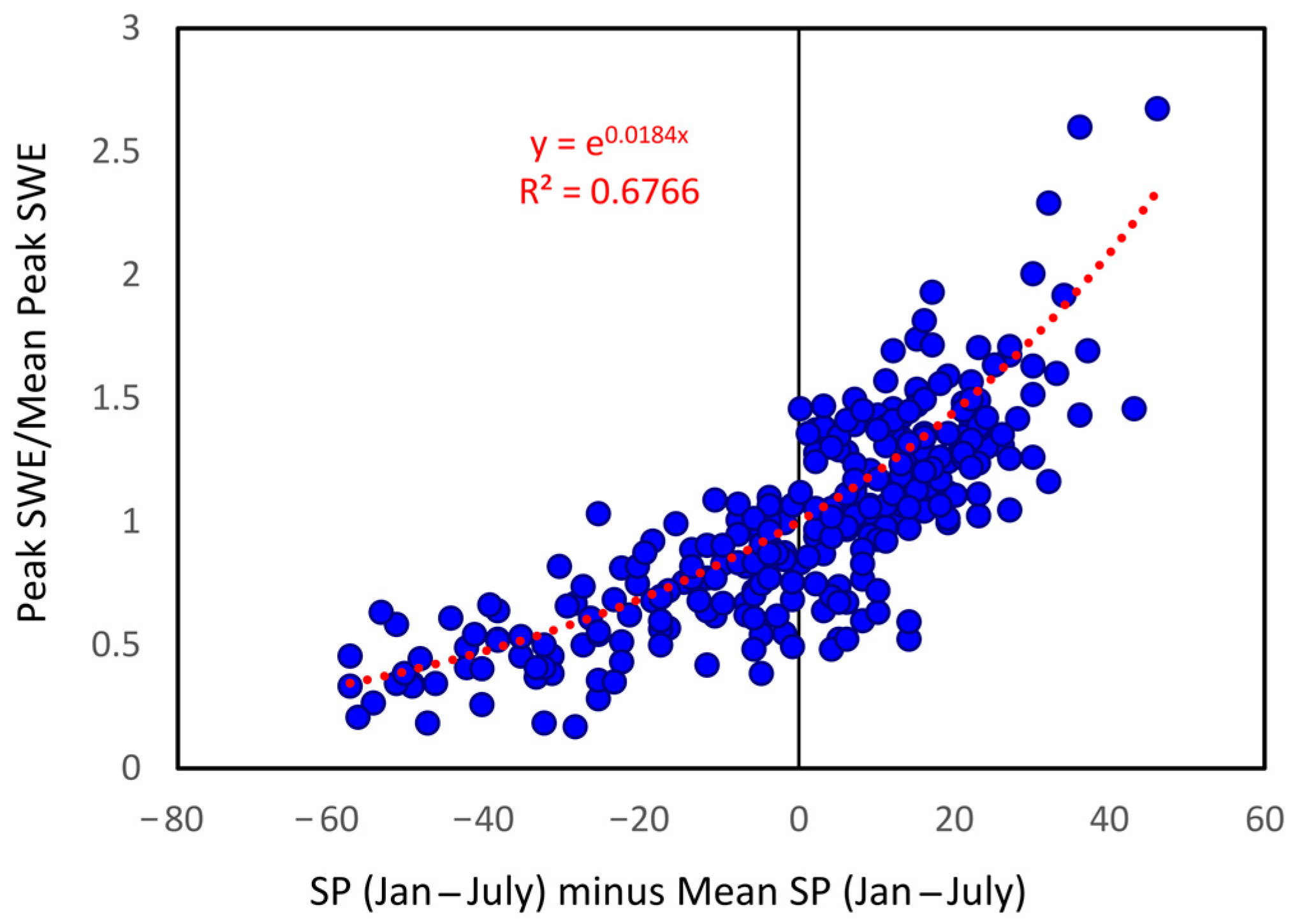
4.3. Temporal Consistency of Snow Patterns
4.4. Uncertainties and Future Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, D.; Wrzesien, M.L.; Durand, M.; Adam, J.; Lettenmaier, D.P. How much runoff originates as snow in the western United States, and how will that change in the future? Geophys. Res. Lett. 2017, 44, 6163–6172. [Google Scholar] [CrossRef]
- Lukas, J.; Payton, E. Colorado River Basin Climate and Hydrology: State of the Science, Western Water Assessment; University of Colorado Boulder: Boulder, CO, USA, 2020. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Pagano, T.; Garen, D.; Sorooshian, S. Evaluation of Official Western U.S. Seasonal Water Supply Outlooks, 1922–2002. J. Hydrometeorol. 2004, 5, 896–909. [Google Scholar] [CrossRef]
- Wheeler, K.G.; Udall, B.; Wang, J.; Kuhn, E.; Salehabadi, H.; Schmidt, J.C. What will it take to stabilize the Colorado River? Science 2022, 377, 373–375. [Google Scholar] [CrossRef] [PubMed]
- Richter, B.D.; Lamsal, G.; Marston, L.; Dhakal, S.; Sangha, L.S.; Rushforth, R.R.; Wei, D.Y.; Ruddell, B.L.; Davis, K.F.; Hernandez-Cruz, A.; et al. New water accounting reveals why the Colorado River no longer reaches the sea. Commun. Earth Environ. 2024, 5, 134. [Google Scholar] [CrossRef]
- Bales, R.C.; Molotch, N.P.; Painter, T.H.; Dettinger, M.D.; Rice, R.; Dozier, J. Mountain hydrology of the western United States. Water Resour. Res. 2006, 42, W08432. [Google Scholar] [CrossRef]
- Hammond, J.C.; Sexstone, G.A.; Putman, A.L.; Barnhart, T.B.; Rey, D.M.; Driscoll, J.M.; Liston, G.E.; Rasmussen, K.L.; McGrath, D.; Fassnacht, S.R.; et al. High Resolution SnowModel Simulations Reveal Future Elevation-Dependent Snow Loss and Earlier, Flashier Surface Water Input for the Upper Colorado River Basin. Earth’s Future 2023, 11, e2022EF003092. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Venable, N.B.H.; McGrath, D.; Patterson, G.G. Sub-Seasonal Snowpack Trends in the Rocky Mountain National Park Area, Colorado, USA. Water 2018, 10, 562. [Google Scholar] [CrossRef]
- Mote, P.W.; Li, S.H.; Lettenmaier, D.P.; Xiao, M.; Engel, R. Dramatic declines in snowpack in the western US. Npj Clim. Atmos. Sci. 2018, 1, 2. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Revuelto, J.; Fassnacht, S.R.; Azorín-Molina, C.; Vicente-Serrano, S.M.; Morán-Tejeda, E.; Sexstone, G.A. Snowpack variability across various spatio-temporal resolutions. Hydrol. Process. 2015, 29, 1213–1224. [Google Scholar] [CrossRef]
- Sexstone, G.A.; Fassnacht, S.R.; López-Moreno, J.I.; Hiemstra, C.A. Subgrid snow depth coefficient of variation spanning alpine to sub-alpine mountainous terrain. Cuad. Investig. Geográfica (Geogr. Res. Lett.) 2022, 48, 79–96. [Google Scholar] [CrossRef]
- Elder, K.; Dozier, J.; Michaelsen, J. Snow Accumulation and Distribution in an Alpine Watershed. Water Resour. Res. 1991, 27, 1541–1552. [Google Scholar] [CrossRef]
- Egli, L.; Jonas, T. Hysteretic dynamics of seasonal snow depth distribution in the Swiss Alps. Geophys. Res. Lett. 2009, 36, L02501. [Google Scholar] [CrossRef]
- Sexstone, G.A.; Clow, D.W.; Fassnacht, S.R.; Liston, G.E.; Hiemstra, C.A.; Knowles, J.F.; Penn, C.A. Snow Sublimation in Mountain Environments and Its Sensitivity to Forest Disturbance and Climate Warming. Water Resour. Res. 2018, 54, 1191–1211. [Google Scholar] [CrossRef]
- Fleming, S.W.; Zukiewicz, L.; Strobel, M.L.; Hofman, H.; Goodbody, A.G. SNOTEL, the Soil Climate Analysis Network, and water supply forecasting at the Natural Resources Conservation Service: Past, present, and future. JAWRA J. Am. Water Resour. Assoc. 2023, 59, 585–599. [Google Scholar] [CrossRef]
- Sexstone, G.A.; Fassnacht, S.R. What drives basin scale spatial variability of snowpack properties in northern Colorado? Cryosphere 2014, 8, 329–344. [Google Scholar] [CrossRef]
- Gleason, K.E.; Nolin, A.W.; Roth, T.R. Developing a representative snow-monitoring network in a forested mountain watershed. Hydrol. Earth Syst. Sci. 2017, 21, 1137–1147. [Google Scholar] [CrossRef]
- Meromy, L.; Molotch, N.P.; Link, T.E.; Fassnacht, S.R.; Rice, R. Subgrid variability of snow water equivalent at operational snow stations in the western USA. Hydrol. Process. 2013, 27, 2383–2400. [Google Scholar] [CrossRef]
- Molotch, N.P.; Bales, R.C. Scaling snow observations from the point to the grid element: Implications for observation network design. Water Resour. Res. 2005, 41, W11421. [Google Scholar] [CrossRef]
- Fang, Y.; Liu, Y.; Margulis, S.A. A western United States snow reanalysis dataset over the Landsat era from water years 1985 to 2021. Sci. Data 2022, 9, 677. [Google Scholar] [CrossRef]
- Margulis, S.A.; Cortés, G.; Girotto, M.; Durand, M. A Landsat-Era Sierra Nevada Snow Reanalysis (1985–2015). J. Hydrometeorol. 2016, 17, 1203–1221. [Google Scholar] [CrossRef]
- Smyth, E.J.; Raleigh, M.S.; Small, E.E. Improving SWE Estimation with Data Assimilation: The Influence of Snow Depth Observation Timing and Uncertainty. Water Resour. Res. 2020, 56, e2019WR026853. [Google Scholar] [CrossRef]
- Yang, K.H.; Musselman, K.N.; Rittger, K.; Margulis, S.A.; Painter, T.H.; Molotch, N.P. Combining ground-based and remotely sensed snow data in a linear regression model for real-time estimation of snow water equivalent. Adv. Water Resour. 2022, 160, 104075. [Google Scholar] [CrossRef]
- Bair, E.H.; Calfa, A.A.; Rittger, K.; Dozier, J. Using machine learning for real-time estimates of snow water equivalent in the watersheds of Afghanistan. Cryosphere 2018, 12, 1579–1594. [Google Scholar] [CrossRef]
- Schneider, D.; Molotch, N.P. Real-time estimation of snow water equivalent in the Upper Colorado River Basin using MODIS-based SWE Reconstructions and SNOTEL data. Water Resour. Res. 2016, 52, 7892–7910. [Google Scholar] [CrossRef]
- Carroll, T.; Cline, D.; Olheiser, C.; Rost, A.; Nilsson, A.; Fall, G.; Bovitz, C.; Li, L. NOAA’s national snow analyses. In Proceedings of the 74th Annual Meeting of The Western Snow Conference, Las Cruces, NM, USA, 17–20 April 2006; p. 13. [Google Scholar]
- Clow, D.W.; Nanus, L.; Verdin, K.L.; Schmidt, J. Evaluation of SNODAS snow depth and snow water equivalent estimates for the Colorado Rocky Mountains, USA. Hydrol. Process. 2012, 26, 2583–2591. [Google Scholar] [CrossRef]
- Hedrick, A.; Marshall, H.P.; Winstral, A.; Elder, K.; Yueh, S.; Cline, D. Independent evaluation of the SNODAS snow depth product using regional-scale lidar-derived measurements. Cryosphere 2015, 9, 13–23. [Google Scholar] [CrossRef]
- Barnhart, T.B.; Putman, A.L.; Heldmyer, A.J.; Rey, D.M.; Hammond, J.C.; Driscoll, J.M.; Sexstone, G.A. Evaluating Distributed Snow Model Resolution and Meteorology Parameterizations Against Streamflow Observations: Finer Is Not Always Better. Water Resour. Res. 2024, 60, e2023WR035982. [Google Scholar] [CrossRef]
- Largeron, C.; Dumont, M.; Morin, S.; Boone, A.; Lafaysse, M.; Metref, S.; Cosme, E.; Jonas, T.; Winstral, A.; Margulis, S.A. Toward Snow Cover Estimation in Mountainous Areas Using Modern Data Assimilation Methods: A Review. Front. Earth Sci. 2020, 8, 325. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Lettenmaier, D.P. Assimilating remotely sensed snow observations into a macroscale hydrology model. Adv. Water Resour. 2006, 29, 872–886. [Google Scholar] [CrossRef]
- Fletcher, S.J.; Liston, G.E.; Hiemstra, C.A.; Miller, S.D. Assimilating MODIS and AMSR-E Snow Observations in a Snow Evolution Model. J. Hydrometeorol. 2012, 13, 1475–1492. [Google Scholar] [CrossRef]
- Stigter, E.E.; Wanders, N.; Saloranta, T.M.; Shea, J.M.; Bierkens, M.F.P.; Immerzeel, W.W. Assimilation of snow cover and snow depth into a snow model to estimate snow water equivalent and snowmelt runoff in a Himalayan catchment. Cryosphere 2017, 11, 1647–1664. [Google Scholar] [CrossRef]
- Thirel, G.; Salamon, P.; Burek, P.; Kalas, M. Assimilation of MODIS Snow Cover Area Data in a Distributed Hydrological Model Using the Particle Filter. Remote Sens. 2013, 5, 5825–5850. [Google Scholar] [CrossRef]
- Baba, M.W.; Gascoin, S.; Hanich, L. Assimilation of Sentinel-2 Data into a Snowpack Model in the High Atlas of Morocco. Remote Sens. 2018, 10, 1982. [Google Scholar] [CrossRef]
- Raleigh, M.S.; Deems, J.S. Filling the Holes in the Space-Time Cube of Snowpack Evolution with Lasers, Cameras, Computers, and Snow Shovels. In Proceedings of the 86th Annual Western Snow Conference, Albuquerque, NM, USA, 15–18 April 2018. [Google Scholar]
- Raleigh, M.S.; Lundquist, J.D.; Clark, M.P. Exploring the impact of forcing error characteristics on physically based snow simulations within a global sensitivity analysis framework. Hydrol. Earth Syst. Sci. 2015, 19, 3153–3179. [Google Scholar] [CrossRef]
- Deems, J.S.; Painter, T.H.; Finnegan, D.C. Lidar measurement of snow depth: A review. J. Glaciol. 2017, 59, 467–479. [Google Scholar] [CrossRef]
- Hedrick, A.R.; Marks, D.; Havens, S.; Robertson, M.; Johnson, M.; Sandusky, M.; Marshall, H.P.; Kormos, P.R.; Bormann, K.J.; Painter, T.H. Direct Insertion of NASA Airborne Snow Observatory-Derived Snow Depth Time Series Into the iSnobal Energy Balance Snow Model. Water Resour. Res. 2018, 54, 8045–8063. [Google Scholar] [CrossRef]
- Painter, T.H.; Berisford, D.F.; Boardman, J.W.; Bormann, K.J.; Deems, J.S.; Gehrke, F.; Hedrick, A.; Joyce, M.; Laidlaw, R.; Marks, D. The Airborne Snow Observatory: Fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo. Remote Sens. Environ. 2016, 184, 139–152. [Google Scholar] [CrossRef]
- Yang, K.; Rittger, K.; Musselman, K.N.; Bair, E.H.; Dozier, J.; Margulis, S.A.; Painter, T.H.; Molotch, N.P. Intercomparison of snow water equivalent products in the Sierra Nevada California using airborne snow observatory data and ground observations. Front. Earth Sci. 2023, 11, 1106621. [Google Scholar] [CrossRef]
- Akie, G.A.; Barnhart, T.B.; Selkowitz, D.; Sexstone, G.A. Historical simulated snowpack for the Willow Creek and Big Thompson, CO watersheds and vicinity, water years 1994–2023. In U.S. Geological Survey Data Release; United States Geological Survey: St. Petersburg, FL, USA, 2025. [Google Scholar] [CrossRef]
- MTBS. Monitoring Trends in Burn Severity (MTBS). 2024. Available online: https://mtbs.gov/ (accessed on 3 January 2024).
- NRCS. Natural Resources Conservation Service (NRCS) Snow and Water Interactive Map. 2024. Available online: https://www.nrcs.usda.gov/resources/data-and-reports/snow-and-water-interactive-map (accessed on 3 January 2024).
- ASO. Airborne Snow Observatories (ASO). 2024. Available online: https://data.airbornesnowobservatories.com/ (accessed on 3 January 2024).
- Liston, G.E.; Elder, K. A distributed snow-evolution modeling system (SnowModel). J. Hydrometeorol. 2006, 7, 1259–1276. [Google Scholar] [CrossRef]
- Liston, G.E.; Itkin, P.; Stroeve, J.; Tschudi, M.; Stewart, J.S.; Pedersen, S.H.; Reinking, A.K.; Elder, K. A Lagrangian Snow-Evolution System for Sea-Ice Applications (SnowModel-LG): Part I-Model Description. J. Geophys. Res. Ocean. 2020, 125, e2019JC015913. [Google Scholar] [CrossRef] [PubMed]
- Liston, G.E. SnowModel (Version 2020_10_02). 2020. Available online: ftp://gliston.cira.colostate.edu/SnowModel/code/ (accessed on 3 January 2024).
- Liston, G.E.; Elder, K. A meteorological distribution system for high-resolution terrestrial modeling (MicroMet). J. Hydrometeorol. 2006, 7, 217–234. [Google Scholar] [CrossRef]
- Liston, G.E. Local Advection of Momentum, Heat, and Moisture during the Melt of Patchy Snow Covers. J. Appl. Meteorol. 1995, 34, 1705–1715. [Google Scholar] [CrossRef]
- Liston, G.E.; Hall, D.K. An Energy-Balance Model of Lake-Ice Evolution. J. Glaciol. 1995, 41, 373–382. [Google Scholar] [CrossRef]
- Liston, G.E.; Haehnel, R.B.; Sturm, M.; Hiemstra, C.A.; Berezovskaya, S.; Tabler, R.D. Instruments and methods simulating complex snow distributions in windy environments using SnowTran-3D. J. Glaciol. 2007, 53, 241–256. [Google Scholar] [CrossRef]
- Liston, G.E.; Sturm, M. A snow-transport model for complex terrain. J. Glaciol. 1998, 44, 498–516. [Google Scholar] [CrossRef]
- Liston, G.E.; Hiemstra, C.A. A Simple Data Assimilation System for Complex Snow Distributions (SnowAssim). J. Hydrometeorol. 2008, 9, 989–1004. [Google Scholar] [CrossRef]
- Greene, E.M.; Liston, G.E.; Pielke, R.A. Simulation of above treeline snowdrift formation using a numerical snow-transport model. Cold Reg. Sci. Technol. 1999, 30, 135–144. [Google Scholar] [CrossRef]
- Hiemstra, C.A.; Liston, G.E.; Reiners, W.A. Observing, modelling, and validating snow redistribution by wind in a Wyoming upper treeline landscape. Ecol. Model. 2006, 197, 35–51. [Google Scholar] [CrossRef]
- Sexstone, G.A.; Penn, C.A.; Liston, G.E.; Gleason, K.E.; Moeser, C.D.; Clow, D.W. Spatial Variability in Seasonal Snowpack Trends across the Rio Grande Headwaters (1984–2017). J. Hydrometeorol. 2020, 21, 2713–2733. [Google Scholar] [CrossRef]
- Liston, G.E.; Polashenski, C.; Rösel, A.; Itkin, P.; King, J.; Merkouriadi, I.; Haapala, J. A Distributed Snow-Evolution Model for Sea-Ice Applications (SnowModel). J. Geophys. Res. Ocean. 2018, 123, 3786–3810. [Google Scholar] [CrossRef]
- Gesch, D.; Evans, G.; Oimoen, M.; Arundel, S. The National Elevation Dataset; American Society for Photogrammetry and Remote Sensing: Baton Rouge, LA, USA, 2018; pp. 83–110. Available online: https://pubs.usgs.gov/publication/70201572 (accessed on 3 January 2024).
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States–representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Salas, D.; Stevens, J.; Schulz, K. Rocky Mountain National Park, Colorado 2001–2005 Vegetation Classification and Mapping Project Report; Remote Sensing and GIS Group Technical Service Center Bureau of Reclamation: Denver, CO, USA, 2005. Available online: https://irma.nps.gov/DataStore/DownloadFile/425168 (accessed on 3 January 2024).
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. Atmos. 2012, 117, D03110. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; DiGirolamo, N.E.; Román, M.O. Evaluation of MODIS and VIIRS cloud-gap-filled snow-cover products for production of an Earth science data record. Hydrol. Earth Syst. Sci. 2019, 23, 5227–5241. [Google Scholar] [CrossRef]
- Koch, J.; Demirel, M.C.; Stisen, S. The SPAtial EFficiency metric (SPAEF): Multiple-component evaluation of spatial patterns for optimization of hydrological models. Geosci. Model Dev. 2018, 11, 1873–1886. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Falgout, J.T.; Gordon, J.; Williams, B.; Davis, M.J. USGS Advanced Research Computing, USGS Denali Supercomputer: U.S. Geological Survey, 2024. Available online: https://www.usgs.gov/advanced-research-computing/usgs-mckinley-supercomputer (accessed on 3 January 2024).
- Gascoin, S.; Lhermitte, S.; Kinnard, C.; Bortels, K.; Liston, G.E. Wind effects on snow cover in Pascua-Lama, Dry Andes of Chile. Adv. Water Resour. 2013, 55, 25–39. [Google Scholar] [CrossRef]
- Heldmyer, A.; Livneh, B.; Molotch, N.; Rajagopalan, B. Investigating the Relationship Between Peak Snow-Water Equivalent and Snow Timing Indices in the Western United States and Alaska. Water Resour. Res. 2021, 57, e2020WR029395. [Google Scholar] [CrossRef]
- Selkowitz, D.J.; Forster, R.R. Automated mapping of persistent ice and snow cover across the western US with Landsat. ISPRS J. Photogramm. Remote Sens. 2016, 117, 126–140. [Google Scholar] [CrossRef]
- U.S. Geological Survey (USGS) Earth Resources Observation and Science (EROS) Center. USGS EROS Archive-Landsat Collection 2 Level-3 Fractional Snow Covered Area (fSCA) Science Product; U.S. Geological Survey: Reston, VA, USA, 2022. [CrossRef]
- Dai, A. Temperature and pressure dependence of the rain-snow phase transition over land and ocean. Geophys. Res. Lett. 2008, 35, L12802. [Google Scholar] [CrossRef]
- Wayand, N.E.; Marsh, C.B.; Shea, J.M.; Pomeroy, J.W. Globally scalable alpine snow metrics. Remote Sens. Environ. 2018, 213, 61–72. [Google Scholar] [CrossRef]
- Hammond, J.C.; Saavedra, F.A.; Kampf, S.K. How Does Snow Persistence Relate to Annual Streamflow in Mountain Watersheds of the Western U.S. with Wet Maritime and Dry Continental Climates? Water Resour. Res. 2018, 54, 2605–2623. [Google Scholar] [CrossRef]
- Trujillo, E.; Molotch, N.P. Snowpack regimes of the Western United States. Water Resour. Res. 2014, 50, 5611–5623. [Google Scholar] [CrossRef]
- Sturm, M.; Wagner, A.M. Using repeated patterns in snow distribution modeling: An Arctic example. Water Resour. Res. 2010, 46, W12549. [Google Scholar] [CrossRef]
- Vögeli, C.; Lehning, M.; Wever, N.; Bavay, M. Scaling Precipitation Input to Spatially Distributed Hydrological Models by Measured Snow Distribution. Front. Earth Sci. 2016, 4, 108. [Google Scholar] [CrossRef]
- Pflug, J.M.; Lundquist, J.D. Inferring Distributed Snow Depth by Leveraging Snow Pattern Repeatability: Investigation Using 47 Lidar Observations in the Tuolumne Watershed, Sierra Nevada, California. Water Resour. Res. 2020, 56, e2020WR027243. [Google Scholar] [CrossRef]
- Deems, J.S.; Fassnacht, S.R.; Elder, K.J. Interannual Consistency in Fractal Snow Depth Patterns at Two Colorado Mountain Sites. J. Hydrometeorol. 2008, 9, 977–988. [Google Scholar] [CrossRef]
- McGrath, D.; Sass, L.; O’Neel, S.; McNeil, C.; Candela, S.G.; Baker, E.H.; Marshall, H.-P. Interannual snow accumulation variability on glaciers derived from repeat, spatially extensive ground-penetrating radar surveys. Cryosphere 2018, 12, 3617–3633. [Google Scholar] [CrossRef]
- Arsenault, K.R.; Houser, P.R.; De Lannoy, G.J.M.; Dirmeyer, P.A. Impacts of snow cover fraction data assimilation on modeled energy and moisture budgets. J. Geophys. Res. Atmos. 2013, 118, 7489–7504. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Gascoin, S.; Herrero, J.; Sproles, E.A.; Pons, M.; Alonso-González, E.; Hanich, L.; Boudhar, A.; Musselman, K.N.; Molotch, N.P.; et al. Different sensitivities of snowpacks to warming in Mediterranean climate mountain areas. Environ. Res. Lett. 2017, 12, 074006. [Google Scholar] [CrossRef]
- Marshall, A.M.; Abatzoglou, J.T.; Link, T.E.; Tennant, C.J. Projected Changes in Interannual Variability of Peak Snowpack Amount and Timing in the Western United States. Geophys. Res. Lett. 2019, 46, 8882–8892. [Google Scholar] [CrossRef]
- Musselman, K.N.; Lehner, F.; Ikeda, K.; Clark, M.P.; Prein, A.F.; Liu, C.; Barlage, M.; Rasmussen, R. Projected increases and shifts in rain-on-snow flood risk over western North America. Nat. Clim. Chang. 2018, 8, 808–812. [Google Scholar] [CrossRef]
- Liston, G.E. Representing Subgrid Snow Cover Heterogeneities in Regional and Global Models. J. Clim. 2004, 17, 1381–1397. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Fassnacht, S.R.; Heath, J.T.; Musselman, K.N.; Revuelto, J.; Latron, J.; Morán-Tejeda, E.; Jonas, T. Small scale spatial variability of snow density and depth over complex alpine terrain: Implications for estimating snow water equivalent. Adv. Water Resour. 2013, 55, 40–52. [Google Scholar] [CrossRef]
- Rittger, K.; Krock, M.; Kleiber, W.; Bair, E.H.; Brodzik, M.J.; Stephenson, T.R.; Rajagopalan, B.; Bormann, K.J.; Painter, T.H. Multi-sensor fusion using random forests for daily fractional snow cover at 30 m. Remote Sens. Environ. 2021, 264, 112608. [Google Scholar] [CrossRef]
- Gascoin, S.; Barrou Dumont, Z.; Deschamps-Berger, C.; Marti, F.; Salgues, G.; López-Moreno, J.I.; Revuelto, J.; Michon, T.; Schattan, P.; Hagolle, O. Estimating Fractional Snow Cover in Open Terrain from Sentinel-2 Using the Normalized Difference Snow Index. Remote Sens. 2020, 12, 2904. [Google Scholar] [CrossRef]
- Meyer, J.; Horel, J.; Kormos, P.; Hedrick, A.; Trujillo, E.; Skiles, S.M. Operational water forecast ability of the HRRR-iSnobal combination: An evaluation to adapt into production environments. Geosci. Model Dev. 2023, 16, 233–250. [Google Scholar] [CrossRef]
- Bair, E.H.; Rittger, K.; Davis, R.E.; Painter, T.H.; Dozier, J. Validating reconstruction of snow water equivalent in California’s Sierra Nevada using measurements from the NASA Airborne Snow Observatory. Water Resour. Res. 2016, 52, 8437–8460. [Google Scholar] [CrossRef]
- Dawson, N.; Broxton, P.; Zeng, X. Evaluation of Remotely Sensed Snow Water Equivalent and Snow Cover Extent over the Contiguous United States. J. Hydrometeorol. 2018, 19, 1777–1791. [Google Scholar] [CrossRef]
- Broxton, P.D.; Dawson, N.; Zeng, X. Linking snowfall and snow accumulation to generate spatial maps of SWE and snow depth. Earth Space Sci. 2016, 3, 246–256. [Google Scholar] [CrossRef]
- Lehning, M.; Völksch, I.; Gustafsson, D.; Nguyen, T.A.; Stähli, M.; Zappa, M. ALPINE3D: A detailed model of mountain surface processes and its application to snow hydrology. Hydrol. Process. 2006, 20, 2111–2128. [Google Scholar] [CrossRef]
- Pflug, J.M.; Hughes, M.; Lundquist, J.D. Downscaling Snow Deposition Using Historic Snow Depth Patterns: Diagnosing Limitations From Snowfall Biases, Winter Snow Losses, and Interannual Snow Pattern Repeatability. Water Resour. Res. 2021, 57, e2021WR029999. [Google Scholar] [CrossRef]
- Reynolds, D.S.; Pflug, J.M.; Lundquist, J.D. Evaluating Wind Fields for Use in Basin-Scale Distributed Snow Models. Water Resour. Res. 2021, 57, e2020WR028536. [Google Scholar] [CrossRef]
- Henn, B.; Newman, A.J.; Livneh, B.; Daly, C.; Lundquist, J.D. An assessment of differences in gridded precipitation datasets in complex terrain. J. Hydrol. 2018, 556, 1205–1219. [Google Scholar] [CrossRef]
- Raleigh, M.S.; Small, E.E. Snowpack density modeling is the primary source of uncertainty when mapping basin-wide SWE with lidar. Geophys. Res. Lett. 2017, 44, 3700–3709. [Google Scholar] [CrossRef]
- PlanetTeam. Planet Application Program Interface: In Space for Life on Earth. San Francisco, CA, 2024. Available online: https://api.planet.com/ (accessed on 3 January 2024).



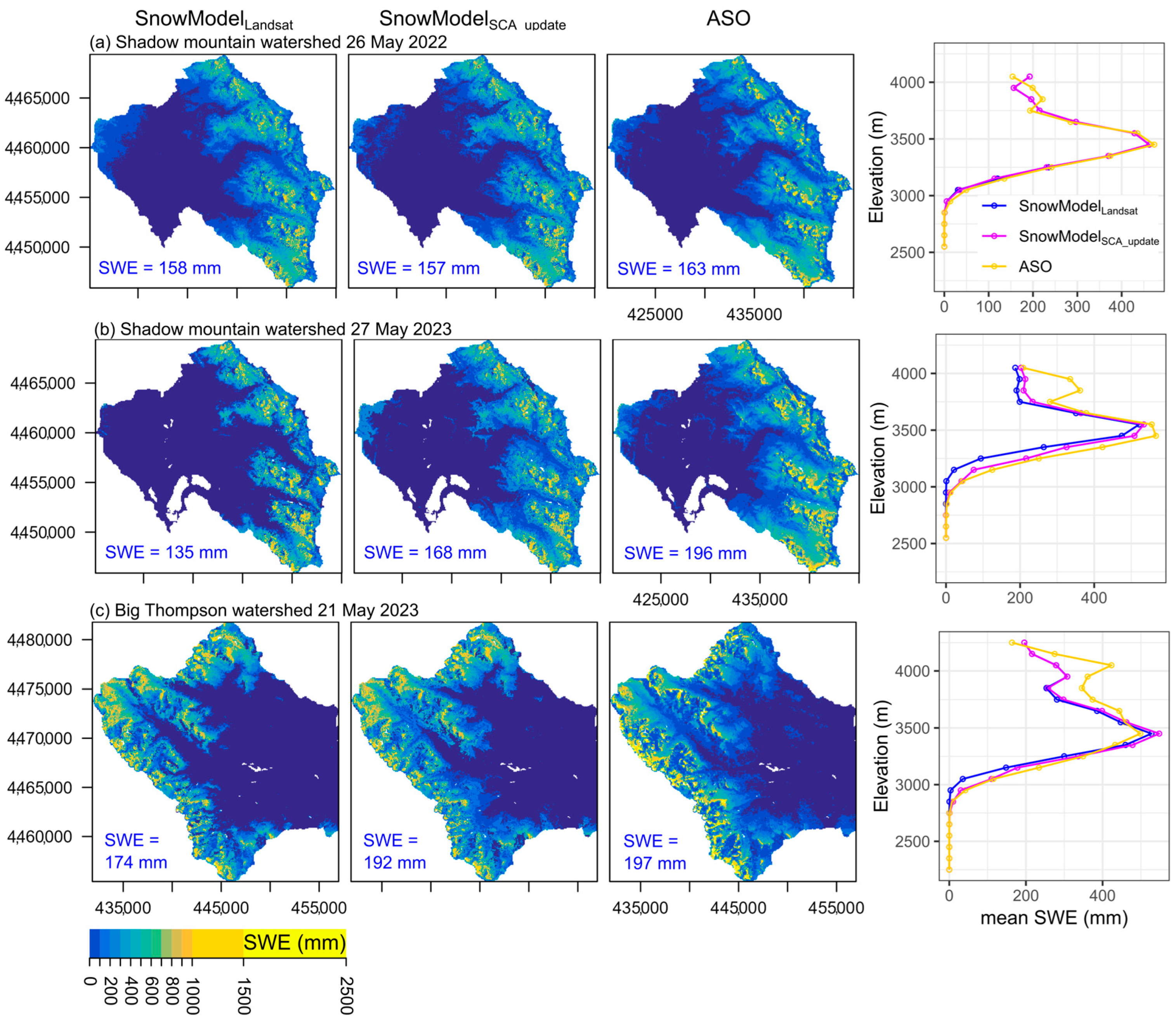
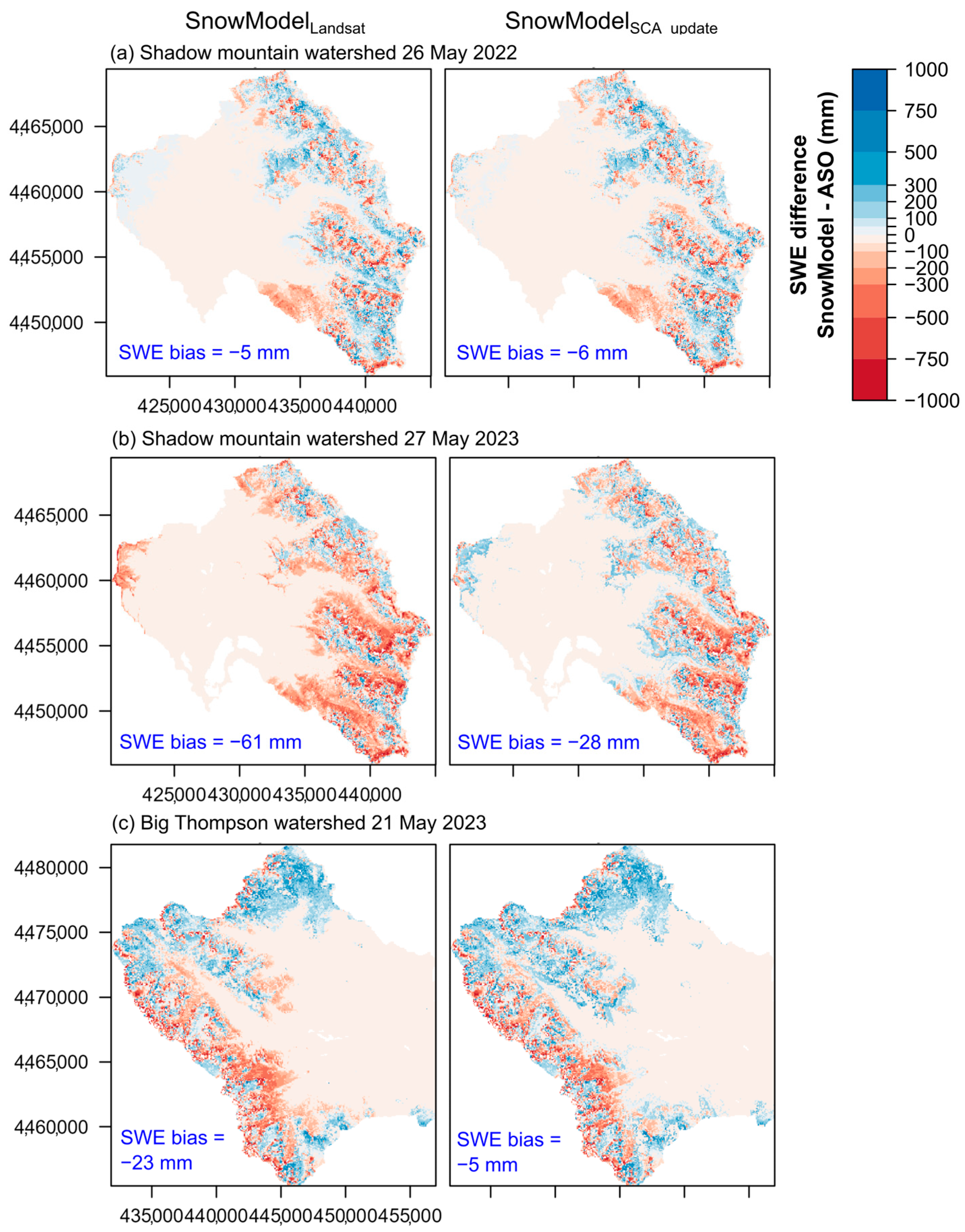

| SnowModel Configuration Name | SnowModel Configuration Description |
|---|---|
| SnowModeldefault_noassim | Default SnowModel parameters without data assimilation. |
| SnowModeldefault | Default SnowModel parameters with data assimilation of SNOwpack TELemetry Network (SNOTEL) snow water equivalent (SWE). |
| SnowModelcalibrated | Calibrated SnowModel parameters with data assimilation of SNOTEL SWE. |
| SnowModelLandsat | Calibrated SnowModel parameters with data assimilation of SNOTEL SWE and Landsat snow persistence (SP) precipitation correction field. |
| SnowModelSCA_update | SnowModelLandsat gridded outputs post-processed and updated for dates corresponding with remotely sensed snow-covered area (SCA) images. |
| 18 April 2022 | 26 May 2022 | ||||
|---|---|---|---|---|---|
| Model Version | SNODAS | SnowModelLandsat | SNODAS | SnowModelLandsat | |
| All Elevations | Model mean SWE (mm) | 272 | 196 | 138 | 98 |
| ASO mean SWE (mm) | 223 | 223 | 104 | 104 | |
| RMSE (mm) | 193 | 137 | 199 | 121 | |
| NSE | 0.13 | 0.56 | 0.00 | 0.63 | |
| High Elevations | Model mean SWE (mm) | 405 | 320 | 309 | 273 |
| ASO mean SWE (mm) | 406 | 406 | 284 | 284 | |
| RMSE (mm) | 260 | 200 | 307 | 203 | |
| NSE | −0.38 | 0.18 | −0.42 | 0.38 | |
| Middle Elevations | Model mean SWE (mm) | 209 | 136 | 54 | 11 |
| ASO mean SWE (mm) | 135 | 135 | 14 | 14 | |
| RMSE (mm) | 150 | 91 | 114 | 38 | |
| NSE | −0.56 | 0.44 | −4.65 | 0.38 | |
| Low Elevations | Model mean SWE (mm) | 18 | 1 | 0 | 0 |
| ASO mean SWE (mm) | 10 | 10 | 0 | 0 | |
| RMSE (mm) | 20 | 23 | --- | --- | |
| NSE | −0.07 | −0.36 | --- | --- | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sexstone, G.A.; Akie, G.A.; Selkowitz, D.J.; Barnhart, T.B.; Rey, D.M.; León-Salazar, C.; Carbone, E.; Bearup, L.A. Fine-Resolution Satellite Remote Sensing Improves Spatially Distributed Snow Modeling to Near Real Time. Remote Sens. 2025, 17, 1704. https://doi.org/10.3390/rs17101704
Sexstone GA, Akie GA, Selkowitz DJ, Barnhart TB, Rey DM, León-Salazar C, Carbone E, Bearup LA. Fine-Resolution Satellite Remote Sensing Improves Spatially Distributed Snow Modeling to Near Real Time. Remote Sensing. 2025; 17(10):1704. https://doi.org/10.3390/rs17101704
Chicago/Turabian StyleSexstone, Graham A., Garrett A. Akie, David J. Selkowitz, Theodore B. Barnhart, David M. Rey, Claudia León-Salazar, Emily Carbone, and Lindsay A. Bearup. 2025. "Fine-Resolution Satellite Remote Sensing Improves Spatially Distributed Snow Modeling to Near Real Time" Remote Sensing 17, no. 10: 1704. https://doi.org/10.3390/rs17101704
APA StyleSexstone, G. A., Akie, G. A., Selkowitz, D. J., Barnhart, T. B., Rey, D. M., León-Salazar, C., Carbone, E., & Bearup, L. A. (2025). Fine-Resolution Satellite Remote Sensing Improves Spatially Distributed Snow Modeling to Near Real Time. Remote Sensing, 17(10), 1704. https://doi.org/10.3390/rs17101704








