Precipitation Retrieval from Geostationary Satellite Data Based on a New QPE Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. H9 Data
2.1.2. FY4B Data
2.1.3. IMERG Precipitation Data
2.1.4. GSMaP Precipitation Data
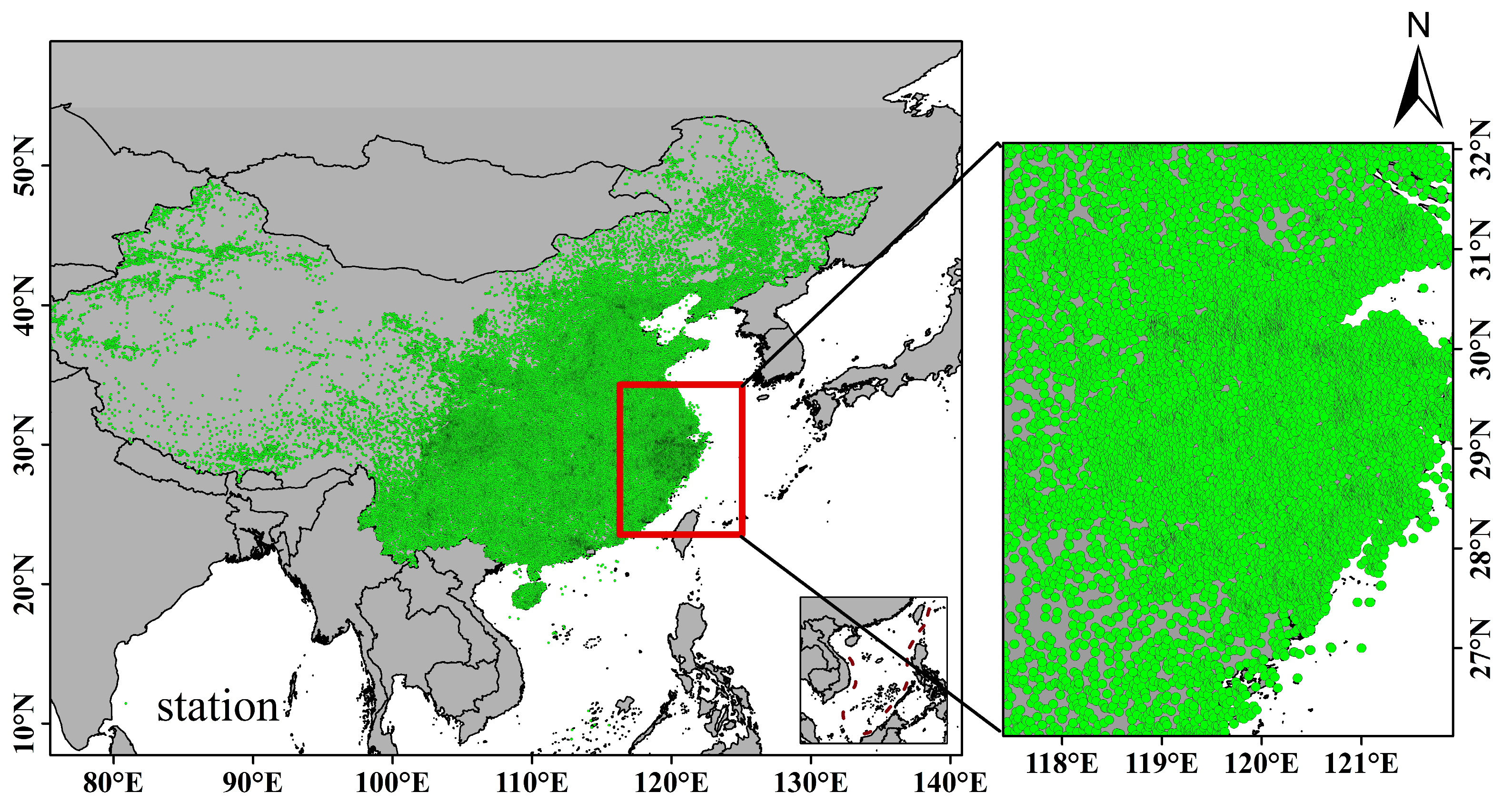
2.1.5. Gauge Rain Data
2.2. Methods
2.2.1. QPE Method
2.2.2. Correction Method
2.2.3. Verification Method
3. Results
3.1. Evaluation of Precipitation Results Across All Gauge Stations
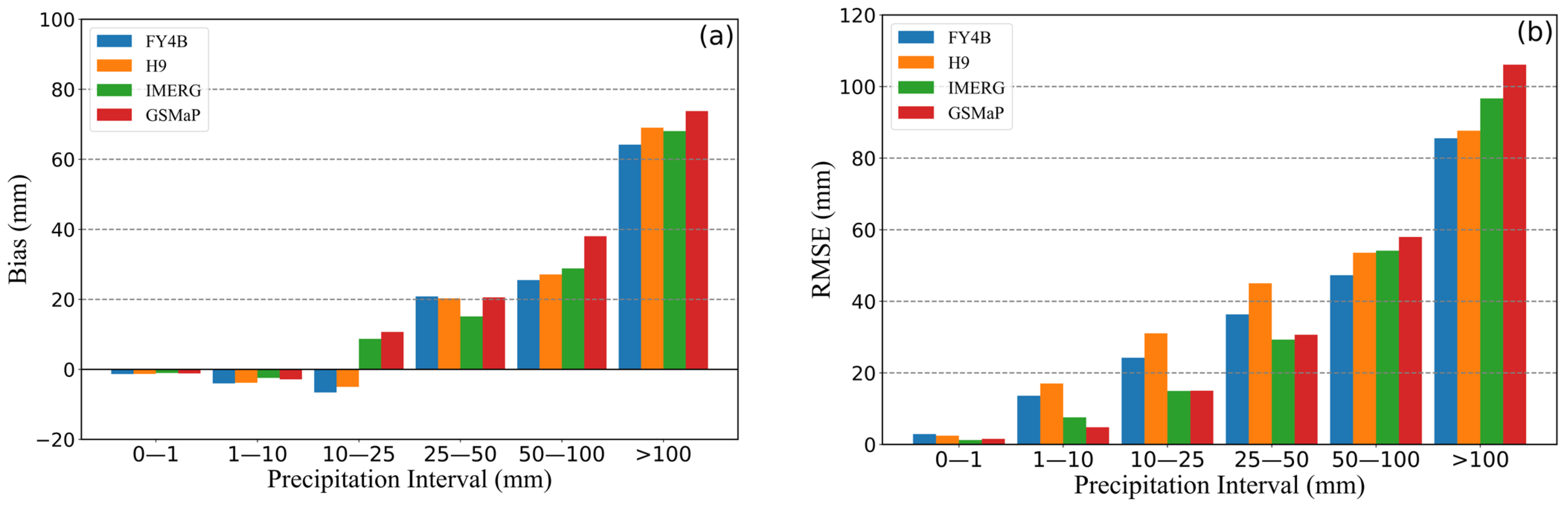
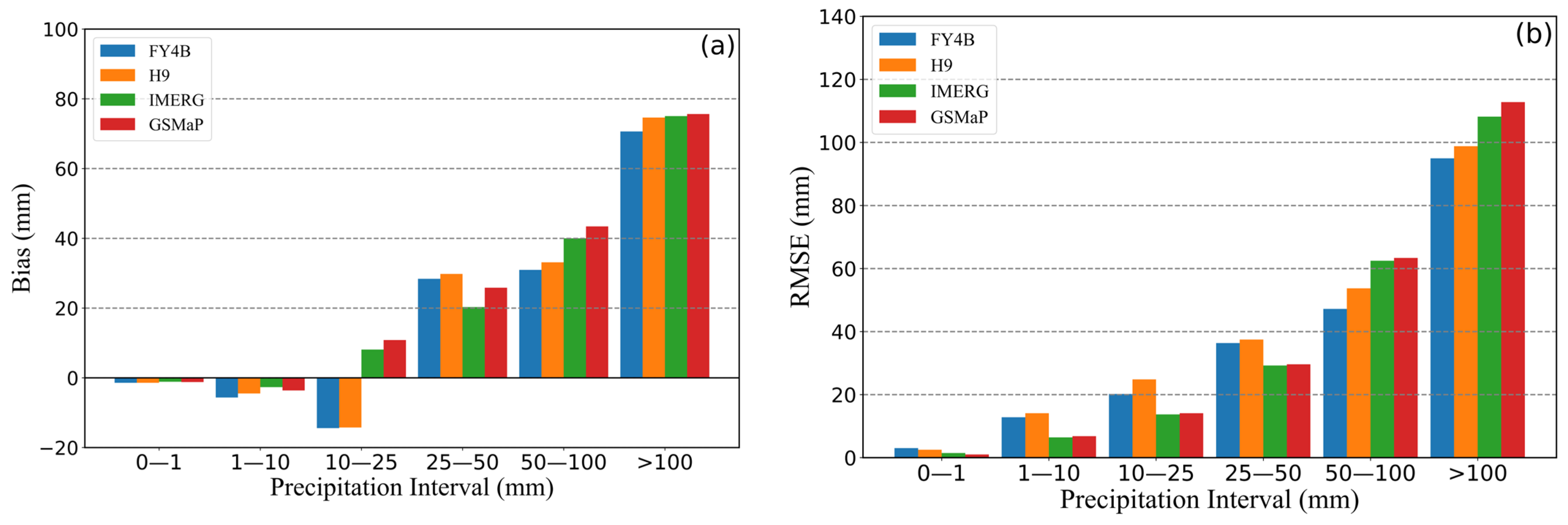
3.1.1. Results for 24-Hour Precipitation
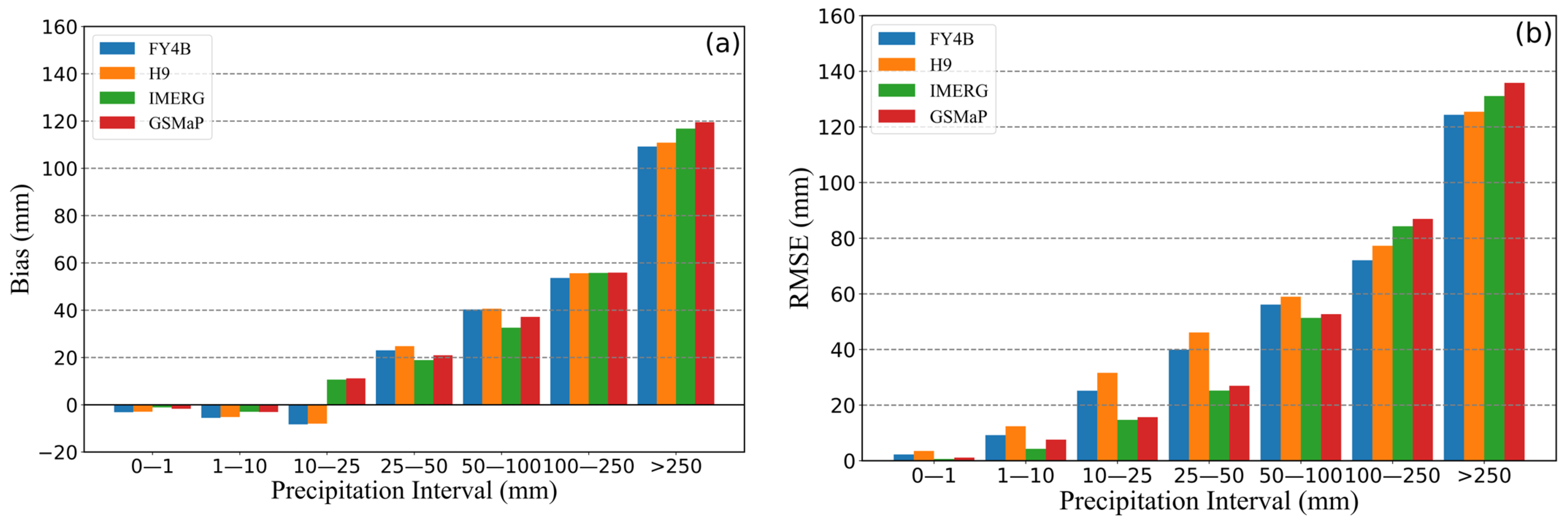
3.1.2. Results for 6-Hour Precipitation
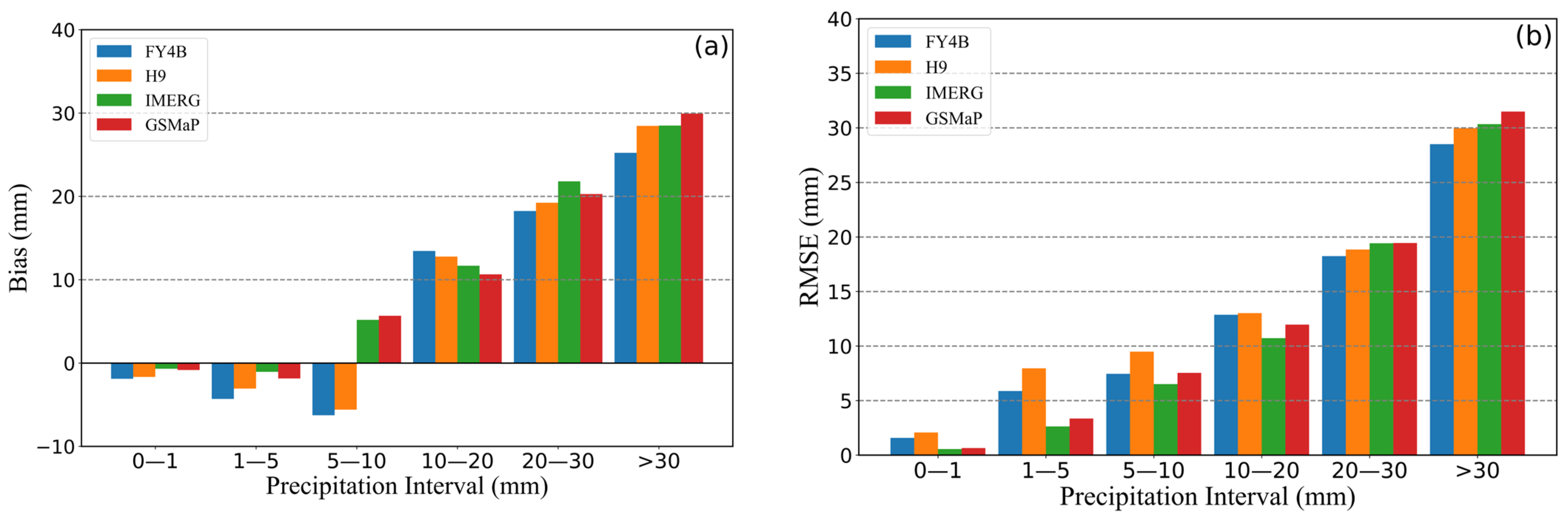
3.1.3. Results for Hourly Precipitation
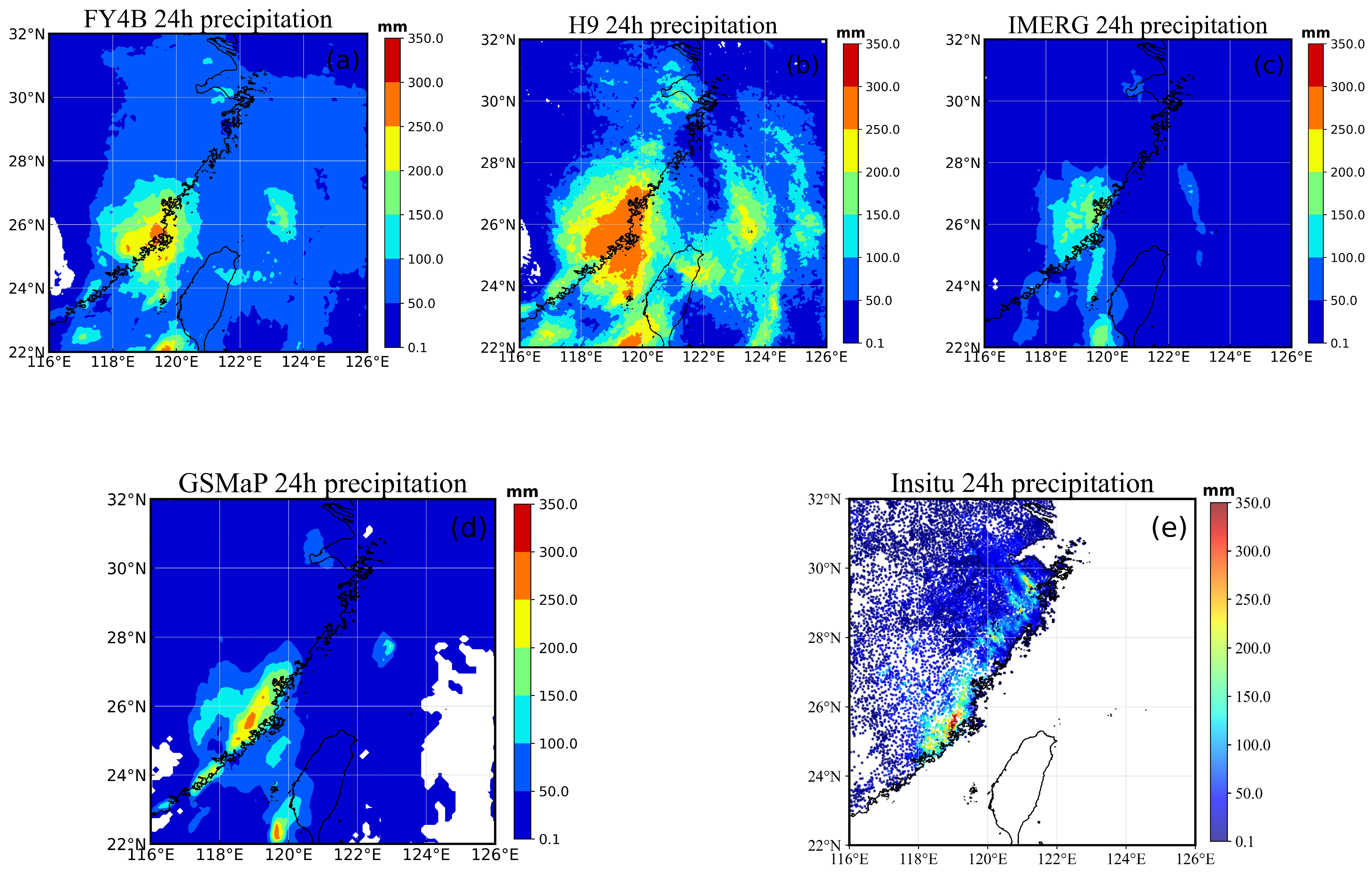
3.2. A Case Study
3.2.1. 24-Hour Precipitation Results
3.2.2. 6-Hour Precipitation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Markonis, Y.; Papalexiou, S.M.; Martinkova, M.; Hanel, M. Assessment of Water Cycle Intensification Over Land using a Multisource Global Gridded Precipitation DataSet. J. Geophys. Res. Atmos. 2019, 124, 11175–11187. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, B.; Xing, W.; Zhou, J.; Xu, F.; Xu, Y. Comprehensive evaluation of latest GPM era IMERG and GSMaP precipitation products over mainland China. Atmos. Res. 2020, 246, 105132. [Google Scholar] [CrossRef]
- Braithwaite, D.K.; Sorooshian, S.; Hsu, K.-L.; Ashouri, H.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G. Improving the global precipitation record: GPCP Version 2.1. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling Satellite Precipitation Estimates With Multiple Linear Regression, Artificial Neural Networks, and Spline Interpolation Techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Hong, Y.; Yu, J.; Pan, Y.; Chen, Z.; Saharia, M. Uncertainty analysis of five satellite-based precipitation products and evaluation of three optimally merged multi-algorithm products over the Tibetan Plateau. Int. J. Remote Sens. 2014, 35, 6843–6858. [Google Scholar] [CrossRef]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN family of global satellite precipitation data: A review and evaluation of products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef]
- Yang, Z.; Hsu, K.; Sorooshian, S.; Xu, X.; Braithwaite, D.; Zhang, Y.; Verbist, K.M.J. Merging high-resolution satellite-based precipitation fields and point-scale rain gauge measurements—A case study in Chile. J. Geophys. Res. Atmos. 2017, 122, 5267–5284. [Google Scholar] [CrossRef]
- Zhang, M.; Luo, C.; Zou, Y. A Model for Quantitatively Estimating Short-Range Precipitation Based on GMS Digitalized Cloud Maps-Part I: Analysis of Quantitative Cloud-Precipitation Relations and Model Design. ACTA Meteorol. Sin.-Engl. Ed. 2003, 17, 230–244. [Google Scholar]
- Jiang, S.; Wei, L.; Ren, L.; Xu, C.-Y.; Zhong, F.; Wang, M.; Zhang, L.; Yuan, F.; Liu, Y. Utility of integrated IMERG precipitation and GLEAM potential evapotranspiration products for drought monitoring over mainland China. Atmos. Res. 2021, 247, 105141. [Google Scholar] [CrossRef]
- Wei, L.; Jiang, S.; Ren, L.; Zhang, L.; Wang, M.; Duan, Z. Preliminary utility of the retrospective IMERG precipitation product for large-scale drought monitoring over Mainland China. Remote Sens. 2020, 12, 2993. [Google Scholar] [CrossRef]
- Hsu, K.-l.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. Climatol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- Yue, C.-j.; Chen, P.; Lei, X.-t.; Yang, Y. A preliminary study on method of Quantitative Precipitation Estimation (QPE) for landfall typhoon. Sci. Meteor. Sin 2006, 26, 17–23. [Google Scholar]
- Ma, Z.; Zhu, S.; Yang, J. FY4QPE-MSA: An all-day near-real-time quantitative precipitation estimation framework based on multispectral analysis from AGRI onboard Chinese FY-4 series satellites. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Min, M.; Bai, C.; Guo, J.; Sun, F.; Liu, C.; Wang, F.; Xu, H.; Tang, S.; Li, B.; Di, D. Estimating summertime precipitation from Himawari-8 and global forecast system based on machine learning. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2557–2570. [Google Scholar] [CrossRef]
- Sehad, M.; Lazri, M.; Ameur, S. Novel SVM-based technique to improve rainfall estimation over the Mediterranean region (north of Algeria) using the multispectral MSG SEVIRI imagery. Adv. Space Res. 2017, 59, 1381–1394. [Google Scholar] [CrossRef]
- Wang, C.; Tang, G.; Xiong, W.; Ma, Z.; Zhu, S. Infrared Precipitation Estimation using Convolutional neural network for FengYun satellites. J. Hydrol. 2021, 603, 127113. [Google Scholar] [CrossRef]
- Wang, X.; Ding, Y.; Zhao, C.; Wang, J. Similarities and improvements of GPM IMERG upon TRMM 3B42 precipitation product under complex topographic and climatic conditions over Hexi region, Northeastern Tibetan Plateau. Atmos. Res. 2019, 218, 347–363. [Google Scholar] [CrossRef]
- Wang, W.; Lu, H.; Zhao, T.; Jiang, L.; Shi, J. Evaluation and Comparison of Daily Rainfall From Latest GPM and TRMM Products Over the Mekong River Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2540–2549. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X.; Shao, H.; Chen, S.; Liu, T.; Chen, C.; Ding, Q.; Du, H. Evaluation and Intercomparison of High-Resolution Satellite Precipitation Estimates—GPM, TRMM, and CMORPH in the Tianshan Mountain Area. Remote Sens. 2018, 10, 1543. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, H.; Chen, P.; Qian, C.; Yue, C. Verification of tropical cyclone–related satellite precipitation estimates in mainland China. J. Appl. Meteorol. Climatol. 2009, 48, 2227–2241. [Google Scholar] [CrossRef]
- Adler, R.F.; Negri, A.J. A satellite infrared technique to estimate tropical convective and stratiform rainfall. J. Appl. Meteorol. Climatol. 1988, 27, 30–51. [Google Scholar] [CrossRef]
- Goldenbergl, S.B.; Houze, R.A., Jr.; Churchill, D.D. Convective and stratiform components of a winter monsoon cloud cluster determined from geosynchronous infrared satellite data. J. Meteorol. Soc. Jpn. Ser. II 1990, 68, 37–63. [Google Scholar] [CrossRef]
- Beattie, C.; Leibo, J.Z.; Teplyashin, D.; Ward, T.; Wainwright, M.; Küttler, H.; Lefrancq, A.; Green, S.; Valdés, V.; Sadik, A. Deepmind lab. arXiv 2016, arXiv:1612.03801. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. (ATBD) Vers. 2015, 4, 30. [Google Scholar]
- Wang, Y.; Li, Z.; Gao, L.; Zhong, Y.; Peng, X. Comparison of GPM IMERG version 06 final run products and its latest version 07 precipitation products across scales: Similarities, differences and improvements. Remote Sens. 2023, 15, 5622. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Adler, R.F.; Kubota, T.; Ushio, T. Evaluation of GSMaP precipitation estimates over the contiguous United States. J. Hydrometeorol. 2010, 11, 566–574. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Rajagopal, E.; Pai, D. Assessment of TRMM-based TMPA-3B42 and GSMaP precipitation products over India for the peak southwest monsoon season. Int. J. Climatol. 2016, 36, 1614–1631. [Google Scholar] [CrossRef]
- Li, J.; Wang, L.; Zhou, F. Convective and stratiform cloud rainfall estimation from geostationary satellite data. Adv. Atmos. Sci. 1993, 10, 475–480. [Google Scholar] [CrossRef]
- Yin, G.; Baik, J.; Park, J. Comprehensive analysis of GEO-KOMPSAT-2A and FengYun satellite-based precipitation estimates across Northeast Asia. GIScience Remote Sens. 2022, 59, 782–800. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Scofield, R.A.; Kuligowski, R.J. Status and outlook of operational satellite precipitation algorithms for extreme-precipitation events. Weather Forecast. 2003, 18, 1037–1051. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, B.; Ma, Z.; Chen, X.; Qiu, J.; Liu, D. Comprehensive comparisons of state-of-the-art gridded precipitation estimates for hydrological applications over southern China. Remote Sens. 2020, 12, 3997. [Google Scholar] [CrossRef]
- Basist, A.; Bell, G.D.; Meentemeyer, V. Statistical relationships between topography and precipitation patterns. J. Clim. 1994, 7, 1305–1315. [Google Scholar] [CrossRef]
- Upadhyaya, S.A.; Kirstetter, P.-E.; Gourley, J.J.; Kuligowski, R.J. On the propagation of satellite precipitation estimation errors: From passive microwave to infrared estimates. J. Hydrometeorol. 2020, 21, 1367–1381. [Google Scholar] [CrossRef]
- Vicente, G.A.; Scofield, R.A.; Menzel, W.P. The operational GOES infrared rainfall estimation technique. Bull. Am. Meteorol. Soc. 1998, 79, 1883–1898. [Google Scholar] [CrossRef]



| 1 | 10 | 25 | 50 | 100 | 250 | ||
|---|---|---|---|---|---|---|---|
| TS | FY4B | 0.42 | 0.39 | 0.36 | 0.33 | 0.30 | 0.15 |
| H9 | 0.45 | 0.42 | 0.35 | 0.31 | 0.28 | 0.11 | |
| IMERG | 0.54 | 0.51 | 0.47 | 0.36 | 0.27 | 0.13 | |
| GSMaP | 0.52 | 0.47 | 0.46 | 0.35 | 0.25 | 0.13 | |
| ETS | FY4B | 0.38 | 0.34 | 0.33 | 0.29 | 0.27 | 0.15 |
| H9 | 0.34 | 0.34 | 0.31 | 0.26 | 0.23 | 0.11 | |
| IMERG | 0.48 | 0.41 | 0.40 | 0.34 | 0.21 | 0.11 | |
| GSMaP | 0.42 | 0.39 | 0.38 | 0.33 | 0.16 | 0.11 | |
| CC | FY4B | 0.66 | 0.62 | 0.57 | 0.52 | 0.36 | 0.25 |
| H9 | 0.67 | 0.65 | 0.61 | 0.49 | 0.34 | 0.22 | |
| IMERG | 0.73 | 0.69 | 0.62 | 0.58 | 0.40 | 0.18 | |
| GSMaP | 0.72 | 0.67 | 0.60 | 0.50 | 0.36 | 0.12 | |
| HSS | FY4B | 0.44 | 0.39 | 0.38 | 0.43 | 0.31 | 0.28 |
| H9 | 0.51 | 0.51 | 0.48 | 0.42 | 0.32 | 0.19 | |
| IMERG | 0.67 | 0.63 | 0.60 | 0.55 | 0.36 | 0.18 | |
| GSMaP | 0.59 | 0.56 | 0.55 | 0.55 | 0.28 | 0.17 | |
| POD | FY4B | 0.80 | 0.74 | 0.65 | 0.54 | 0.44 | 0.19 |
| H9 | 0.80 | 0.68 | 0.61 | 0.49 | 0.31 | 0.11 | |
| IMERG | 0.85 | 0.82 | 0.78 | 0.56 | 0.42 | 0.16 | |
| GSMaP | 0.82 | 0.79 | 0.76 | 0.53 | 0.36 | 0.14 | |
| FAR | FY4B | 0.36 | 0.36 | 0.49 | 0.50 | 0.52 | 0.62 |
| H9 | 0.26 | 0.39 | 0.44 | 0.52 | 0.54 | 0.65 | |
| IMERG | 0.20 | 0.36 | 0.41 | 0.45 | 0.54 | 0.63 | |
| GSMaP | 0.22 | 0.38 | 0.41 | 0.44 | 0.58 | 0.66 |
| 1 | 10 | 25 | 50 | 100 | ||
|---|---|---|---|---|---|---|
| TS | FY4B | 0.40 | 0.26 | 0.22 | 0.20 | 0.14 |
| H9 | 0.42 | 0.31 | 0.21 | 0.17 | 0.08 | |
| IMERG | 0.48 | 0.39 | 0.33 | 0.17 | 0.08 | |
| GSMaP | 0.48 | 0.35 | 0.28 | 0.14 | 0.06 | |
| ETS | FY4B | 0.33 | 0.27 | 0.22 | 0.20 | 0.14 |
| H9 | 0.37 | 0.30 | 0.22 | 0.16 | 0.08 | |
| IMERG | 0.39 | 0.33 | 0.32 | 0.17 | 0.08 | |
| GSMaP | 0.39 | 0.32 | 0.27 | 0.14 | 0.06 | |
| CC | FY4B | 0.38 | 0.31 | 0.25 | 0.13 | 0.11 |
| H9 | 0.38 | 0.33 | 0.25 | 0.12 | 0.06 | |
| IMERG | 0.51 | 0.42 | 0.33 | 0.12 | 0.06 | |
| GSMaP | 0.48 | 0.37 | 0.28 | 0.11 | 0.04 | |
| HSS | FY4B | 0.46 | 0.36 | 0.34 | 0.33 | 0.16 |
| H9 | 0.52 | 0.42 | 0.32 | 0.28 | 0.11 | |
| IMERG | 0.56 | 0.48 | 0.43 | 0.26 | 0.11 | |
| GSMaP | 0.56 | 0.48 | 0.42 | 0.24 | 0.11 | |
| POD | FY4B | 0.82 | 0.49 | 0.38 | 0.28 | 0.16 |
| H9 | 0.82 | 0.49 | 0.36 | 0.24 | 0.11 | |
| IMERG | 0.88 | 0.62 | 0.54 | 0.26 | 0.11 | |
| GSMaP | 0.84 | 0.56 | 0.40 | 0.23 | 0.11 | |
| FAR | FY4B | 0.43 | 0.53 | 0.60 | 0.63 | 0.71 |
| H9 | 0.42 | 0.52 | 0.60 | 0.62 | 0.74 | |
| IMERG | 0.30 | 0.38 | 0.41 | 0.62 | 0.76 | |
| GSMaP | 0.33 | 0.43 | 0.48 | 0.67 | 0.79 |
| 1 | 5 | 10 | 20 | 30 | ||
|---|---|---|---|---|---|---|
| TS | FY4B | 0.30 | 0.16 | 0.10 | 0.08 | 0.05 |
| H9 | 0.34 | 0.17 | 0.11 | 0.06 | 0.04 | |
| IMERG | 0.40 | 0.22 | 0.17 | 0.06 | 0.04 | |
| GSMaP | 0.38 | 0.19 | 0.14 | 0.05 | 0.04 | |
| ETS | FY4B | 0.27 | 0.15 | 0.09 | 0.08 | 0.05 |
| H9 | 0.27 | 0.17 | 0.10 | 0.06 | 0.04 | |
| IMERG | 0.36 | 0.21 | 0.14 | 0.04 | 0.04 | |
| GSMaP | 0.34 | 0.18 | 0.11 | 0.04 | 0.03 | |
| CC | FY4B | 0.26 | 0.21 | 0.18 | 0.11 | 0.09 |
| H9 | 0.27 | 0.23 | 0.18 | 0.10 | 0.08 | |
| IMERG | 0.33 | 0.27 | 0.24 | 0.10 | 0.08 | |
| GSMaP | 0.28 | 0.24 | 0.19 | 0.09 | 0.07 | |
| HSS | FY4B | 0.39 | 0.30 | 0.17 | 0.11 | 0.09 |
| H9 | 0.42 | 0.30 | 0.19 | 0.08 | 0.08 | |
| IMERG | 0.52 | 0.41 | 0.28 | 0.10 | 0.07 | |
| GSMaP | 0.51 | 0.32 | 0.20 | 0.08 | 0.07 | |
| POD | FY4B | 0.37 | 0.24 | 0.20 | 0.09 | 0.07 |
| H9 | 0.36 | 0.25 | 0.21 | 0.05 | 0.05 | |
| IMERG | 0.41 | 0.34 | 0.27 | 0.05 | 0.04 | |
| GSMaP | 0.40 | 0.31 | 0.27 | 0.05 | 0.02 | |
| FAR | FY4B | 0.65 | 0.73 | 0.83 | 0.85 | 0.87 |
| H9 | 0.63 | 0.69 | 0.81 | 0.88 | 0.90 | |
| IMERG | 0.48 | 0.59 | 0.74 | 0.89 | 0.90 | |
| GSMaP | 0.50 | 0.63 | 0.80 | 0.91 | 0.95 |
| 1 | 10 | 25 | 50 | 100 | 250 | ||
|---|---|---|---|---|---|---|---|
| TS | FY4B | 0.46 | 0.39 | 0.33 | 0.26 | 0.20 | 0.18 |
| H9 | 0.46 | 0.34 | 0.32 | 0.23 | 0.19 | 0.18 | |
| IMERG | 0.53 | 0.47 | 0.44 | 0.34 | 0.18 | 0.14 | |
| GSMaP | 0.51 | 0.46 | 0.44 | 0.33 | 0.16 | 0.09 | |
| ETS | FY4B | 0.37 | 0.33 | 0.27 | 0.22 | 0.20 | 0.18 |
| H9 | 0.38 | 0.35 | 0.24 | 0.22 | 0.18 | 0.17 | |
| IMERG | 0.44 | 0.41 | 0.35 | 0.29 | 0.15 | 0.12 | |
| GSMaP | 0.40 | 0.38 | 0.30 | 0.29 | 0.13 | 0.07 | |
| CC | FY4B | 0.67 | 0.50 | 0.44 | 0.41 | 0.38 | 0.26 |
| H9 | 0.56 | 0.47 | 0.39 | 0.37 | 0.33 | 0.20 | |
| IMERG | 0.64 | 0.62 | 0.61 | 0.56 | 0.33 | 0.19 | |
| GSMaP | 0.61 | 0.60 | 0.58 | 0.53 | 0.32 | 0.15 | |
| HSS | FY4B | 0.48 | 0.40 | 0.34 | 0.32 | 0.22 | 0.20 |
| H9 | 0.47 | 0.37 | 0.32 | 0.28 | 0.21 | 0.20 | |
| IMERG | 0.66 | 0.63 | 0.52 | 0.48 | 0.22 | 0.14 | |
| GSMaP | 0.57 | 0.55 | 0.50 | 0.45 | 0.22 | 0.13 | |
| POD | FY4B | 0.86 | 0.76 | 0.61 | 0.40 | 0.38 | 0.21 |
| H9 | 0.87 | 0.65 | 0.57 | 0.48 | 0.36 | 0.19 | |
| IMERG | 0.93 | 0.90 | 0.81 | 0.58 | 0.36 | 0.18 | |
| GSMaP | 0.90 | 0.82 | 0.70 | 0.49 | 0.34 | 0.17 | |
| FAR | FY4B | 0.34 | 0.36 | 0.39 | 0.68 | 0.70 | 0.78 |
| H9 | 0.30 | 0.32 | 0.43 | 0.67 | 0.71 | 0.80 | |
| IMERG | 0.22 | 0.26 | 0.32 | 0.60 | 0.74 | 0.82 | |
| GSMaP | 0.26 | 0.28 | 0.41 | 0.63 | 0.82 | 0.86 |
| 1 | 10 | 25 | 50 | 100 | ||
|---|---|---|---|---|---|---|
| TS | FY4B | 0.44 | 0.33 | 0.24 | 0.18 | 0.15 |
| H9 | 0.45 | 0.32 | 0.20 | 0.12 | 0.10 | |
| IMERG | 0.52 | 0.48 | 0.27 | 0.22 | 0.09 | |
| GSMaP | 0.51 | 0.46 | 0.26 | 0.22 | 0.06 | |
| ETS | FY4B | 0.36 | 0.26 | 0.22 | 0.18 | 0.15 |
| H9 | 0.36 | 0.24 | 0.19 | 0.12 | 0.10 | |
| IMERG | 0.41 | 0.32 | 0.27 | 0.22 | 0.09 | |
| GSMaP | 0.39 | 0.29 | 0.26 | 0.22 | 0.06 | |
| CC | FY4B | 0.35 | 0.29 | 0.21 | 0.16 | 0.12 |
| H9 | 0.40 | 0.27 | 0.19 | 0.16 | 0.13 | |
| IMERG | 0.53 | 0.37 | 0.31 | 0.18 | 0.12 | |
| GSMaP | 0.48 | 0.32 | 0.29 | 0.14 | 0.09 | |
| HSS | FY4B | 0.51 | 0.37 | 0.36 | 0.28 | 0.20 |
| H9 | 0.53 | 0.33 | 0.31 | 0.26 | 0.18 | |
| IMERG | 0.56 | 0.51 | 0.48 | 0.33 | 0.12 | |
| GSMaP | 0.56 | 0.53 | 0.46 | 0.36 | 0.08 | |
| POD | FY4B | 0.80 | 0.44 | 0.30 | 0.19 | 0.17 |
| H9 | 0.83 | 0.39 | 0.26 | 0.15 | 0.16 | |
| IMERG | 0.89 | 0.51 | 0.44 | 0.14 | 0.11 | |
| GSMaP | 0.87 | 0.48 | 0.36 | 0.14 | 0.06 | |
| FAR | FY4B | 0.42 | 0.58 | 0.64 | 0.72 | 0.81 |
| H9 | 0.44 | 0.57 | 0.68 | 0.75 | 0.85 | |
| IMERG | 0.23 | 0.45 | 0.59 | 0.76 | 0.86 | |
| GSMaP | 0.25 | 0.54 | 0.61 | 0.79 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Yu, Z.; Rogers, R.; Yang, Y. Precipitation Retrieval from Geostationary Satellite Data Based on a New QPE Algorithm. Remote Sens. 2025, 17, 1703. https://doi.org/10.3390/rs17101703
Chen H, Yu Z, Rogers R, Yang Y. Precipitation Retrieval from Geostationary Satellite Data Based on a New QPE Algorithm. Remote Sensing. 2025; 17(10):1703. https://doi.org/10.3390/rs17101703
Chicago/Turabian StyleChen, Hao, Zifeng Yu, Robert Rogers, and Yilin Yang. 2025. "Precipitation Retrieval from Geostationary Satellite Data Based on a New QPE Algorithm" Remote Sensing 17, no. 10: 1703. https://doi.org/10.3390/rs17101703
APA StyleChen, H., Yu, Z., Rogers, R., & Yang, Y. (2025). Precipitation Retrieval from Geostationary Satellite Data Based on a New QPE Algorithm. Remote Sensing, 17(10), 1703. https://doi.org/10.3390/rs17101703




