We aim at producing a cloud-free version of a target image
given a stack of cloud-affected images
for a certain temporal horizon
T. Our method is based on the use of transformer networks [
17], which are powerful learning based estimators. Transformer networks are autoregressive models, i.e., each sequence element they produce, apart from the input, is also conditioned on all previously generated outputs.
3.1. Axial Transformers
Considering that both the number of parameters and their computational complexity depends quadratically on the number of sequence elements, for images where sequences of pixels are considered, transformer networks can have prohibitively large model sizes. To address this issue, several solutions have been proposed ([
30] provides a survey). In this work, we consider Axial Transformers whose basic building block is axial attention [
22]. An axial attention block performs self-attention over a single axis (here, columns and rows of an image), mixing information along that axis while keeping it independent along the other axes. This helps to reduce the model complexity to
, where
n is the total number of pixels, providing
savings. This is especially crucial for processing multi-temporal data that we consider here.
Models employing axial attention achieve a global receptive field by combining multiple axis attention blocks spanning different axes. The resulting autoregressive network models a distribution over a pixel x at position by processing all the past context from and following the raster scan order. Each axial attention block is composed of a self-attention block passing through a feed-forward block consisting of a layer normalization and a two-layer network. During training, a masked axial attention block is employed to prevent the model from considering subsequent outputs.
A full axial transformer architecture is composed of an encoder, capturing context from individual channels and images, an outer decoder capturing context of entire rows, and an inner decoder considering context within a single row. Specifically, the encoder consists of unmasked row and column attention layers and makes each pixel
depend on all the previous channels and images. The output of the encoder is used as context to condition the decoder. In this work, we follow the conditioning approach proposed in [
31].
Regarding the decoder, its outer part consists of unmasked row and masked column attention layers and makes each pixel depend on all the previous rows . The output context is then shifted down by a single row in order to ensure that it contains information only from previous rows and not from its own. This context is then summed with the encoder context and used to condition the inner decoder. The inner decoder consists of masked row attention layers, capturing information from the previous pixels of the same row . The inner decoder embeddings are shifted right by one pixel, ensuring that the current pixel is excluded from the receptive field. The new output context is then passed through a final dense layer to produce logits of shape , where V corresponds to the range of pixel values at each location.
Outputs of autoregressive models are produced by sampling a single pixel at a time, which is a particularly computationally expensive process as the whole network needs to be re-evaluated each time. Axial transformers enable the significantly more efficient semi-parallel autoregressive sampling where the encoder runs once per image, the outer decoder once per-row, and the inner decoder once per-pixel. The context from the encoder and outer decoder conditions the inner decoder, which generates a row, pixel-by-pixel. After generating all pixels in a row, the outer decoder runs to recompute the context and condition the inner decoder, to generate the next row. After all the pixels of an image are generated, the encoder recomputes the context to generate the next image.
3.2. Proposed Architecture
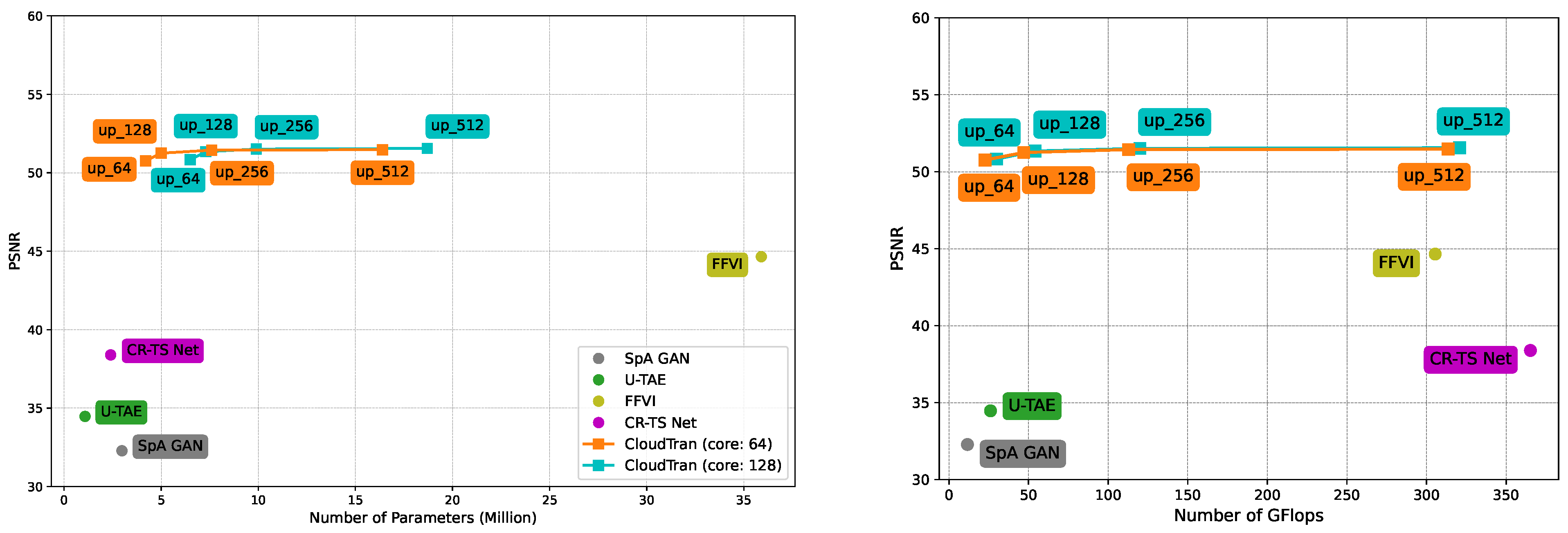
The complete architecture of the proposed CloudTran method is presented in
Figure 1. While the efficiency gains achieved by using axial attention blocks are substantial, it is still challenging to build encoder-decoder models for images of increased resolution (e.g.,
or higher) as, besides increased model size, sampling becomes excessively slow for generating images with higher resolutions. To address this issue, following similar ideas from [
31,
32], we split the cloud removal problem into two sub-problems, each addressed by a specialized network. The first network (core) is an encoder-decoder model that performs cloud removal to a downsampled version of the original inputs, while the second one (upsampler) brings the output of the core network to the original resolution.
Specifically, the core network takes as input a stack of downsampled
T image patches
, with
, and produces a cloud-free version of the downsampled target image
. The encoder, comprised of four layers of row and column attention, processes the input tensor
made of
T image patches corresponding to consecutive dates, with
the size of the downsampled images and
B the number of bands considered. In each patch
, cloudy regions are masked out using image masks
. Suitable embeddings are applied to the input, including positional encoding, which allows to explicitly model the non-uniform temporal differences between the images forming the tensor. Denoting
d the embedding dimension, the encoder produces separate contexts
for each date which are subsequently aggregated, producing a single context
for each band. The aggregated context
is then used for conditioning the layers of the decoder whose output captures the per-pixel distribution over the admissible values of the downsampled cloud-free target image, conditioned on the input tensor
, namely:
The context is considered independently for each band of the input tensor, and the model distinguishes between contexts corresponding to different bands via positional encoding.
Similarly to [
31], we also model the per-pixel distribution from the encoder output
to increase stability of the training process, by adding a dense and a softmax layer after the encoder’s aggregation layer. We denote this output of the model as CloudTran-Parallel (or in short, CloudTran-P), which due to its fully parallel nature is much more efficient for producing outputs in terms of time and computational cost, as in contrast to the full CloudTran++ model, it avoids autoregressive sampling (context recomputation for each pixel).
The upsampler network is a parallel model, i.e., all outputs are produced at once, given the input context. It is composed of three layers of row and column attention, and captures the per-pixel distribution of the cloud-free target image given the input tensor and the bilinearly upsampled cloud-free image, namely, .
Each network is trained independently by minimizing the negative log-likelihood of the data, considering the cloud-free version of the last image , which, in the case of the core network, is also given as input to the decoder during training. During inference, to generate the low-resolution cloud-free image , the context from the input data tensor is computed by the encoder given the input tensor . Based on the computed context, each pixel is sampled from the decoder in an autoregressive fashion, with previously sampled pixels being fed back to the decoder to condition generation of subsequent ones. We make use of the semi-parallel sampling property of axial transformers to speed up the sampling process, which avoids reevaluating the entire network for each pixel of the generated image. As the model considers the context corresponding to each band separately, sampling of each band is performed independently and the target image is obtained by stacking together the sampled bands. The image generated from the core network is then passed to the upsampler to produce the target cloud-free image .
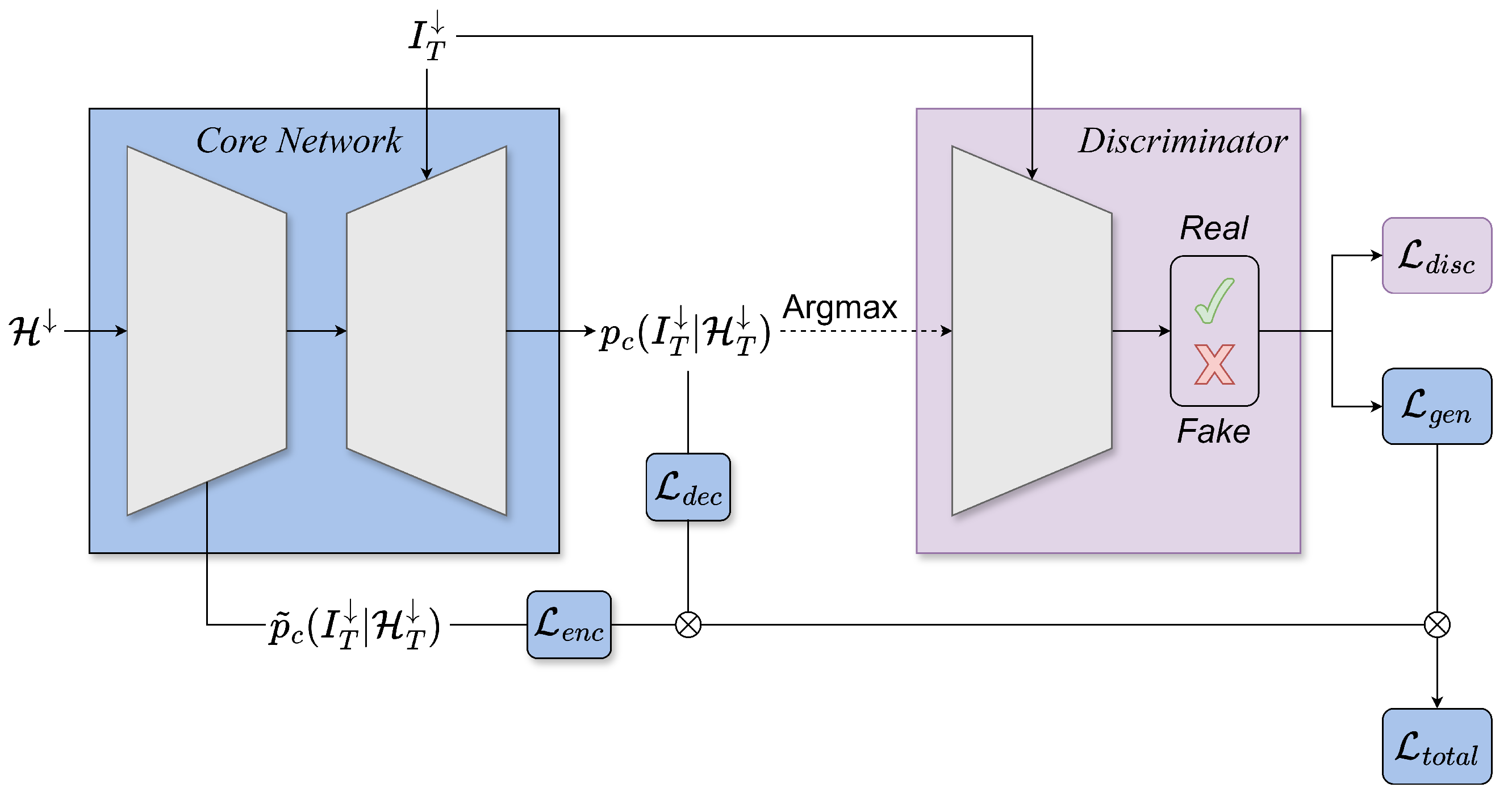
To limit the impact of the excessively bright values, we train a discriminator in parallel with our core network (
Figure 2). The discriminator is a convolutional PatchGAN classifier as described in [
33] and is responsible for the classification of an input image as real or fake. It has three inputs: the masked input image, the target (
) or the generated (
) cloud-free image, and finally, the channel index of the corresponding training step. The first two inputs are concatenated together, resulting in a final output of a single band
image patch. Inspired by WGAN [
34], we incorporated a clip constraint, restricting the discriminator weights within a defined range, for enhanced training stability. We employ Binary Cross Entropy as the loss function for both the discriminator and the generator losses with a relative loss factor of
. The latter derives from the transformer output logits compared to discriminator outputs. Each discriminator model is optimized via Adam with a learning rate of
and a momentum term
.
As a result, the total loss of our core network is given by Equation (
2):
where
,
are the decoder and encoder loss functions that are based on the Cross entropy following a Softmax activation function,
is the generator-like loss function for our transformer network, which serves as the generator in this context, based on the Binary Cross entropy, and
,
and
are the relative weighting factors for the encoder-decoder, encoder-only, and generator loss functions, respectively, with default values
,
and
. Finally, we incorporate the Binary Cross entropy loss
for the concurrent training of the discriminator network.