Abstract
This paper describes the creation of a fast, deterministic, 3D fractal cloud renderer for the AFIT Sensor and Scene Emulation Tool (ASSET). The renderer generates 3D clouds by ray marching through a volume and sampling the level-set of a fractal function. The fractal function is distorted by a displacement map, which is generated using horizontal wind data from a Global Forecast System (GFS) weather file. The vertical windspeed and relative humidity are used to mask the creation of clouds to match realistic large-scale weather patterns over the Earth. Small-scale detail is provided by the fractal functions which are tuned to match natural cloud shapes. This model is intended to run quickly, and it can run in about 700 ms per cloud type. This model generates clouds that appear to match large-scale satellite imagery, and it reproduces natural small-scale shapes. This should enable future versions of ASSET to generate scenarios where the same scene is consistently viewed from both GEO and LEO satellites from multiple perspectives.
1. Introduction
The Air Force Institute of Technology’s (AFIT’s) Sensor and Scene Emulation Tool (ASSET) is a whole-Earth, physics-based infrared scene emulation tool developed by the Air Force Institute of Technology (AFIT) capable of generating highly realistic synthetic electro-optical and infrared data [1]. When generating synthetic scenes for the development of novel tracking and discrimination algorithms or the training of machine learning models, the types of background clutter which exist in real-world satellite observations are of importance. Target detection in ASSET requires the ability to distinguish targets from the background. One important, highly complicated, and variable component of any background is the cloud cover over the Earth’s surface. This cover both obscures low-altitude targets and provides time-varying clutter, which complicates target detection algorithms.
Currently, ASSET uses satellite imagery of clouds to render individual cloud layers with several user-defined parameters, including cloud base, cloud height, drift speed, and direction, and radiometric properties such as albedo and extinction. These layers can come from any satellite imagery, but the most commonly used cloud file is the NASA Blue Marble: Clouds image [2], which is a full-Earth cloud image built from many different satellite observations. Using several cloud layers, it is possible to produce an approximation of three-dimensional clouds that produces highly realistic results and, for sensors with large ground sample distances (GSDs), covers any location on the Earth. However, for high-resolution sensors such as those in low Earth orbit (LEO), it is currently necessary to rescale the cloud mask in order to ensure enough structure is present and clouds are realistic. As a result, it is currently not possible to produce realistic simultaneous views from a high-resolution LEO satellite and a lower-resolution satellite with a very large field of view, as the cloud masks would not be consistent.
In order to develop a tool to create scenes for future scenarios of interest with multiple satellites and multiple viewing vantage points, a cloud model with the following properties is desired:
- The generated clouds must be three-dimensional.
- The generated clouds must be deterministic (the same clouds are generated from multiple viewing angles).
- The generated clouds must have both fine detail on the scale of tens of meters and a realistic distribution over the Earth on a scale of thousands of kilometers.
- ASSET, being an emulation tool and not a full climate simulation, must be capable of generating each frame of a scene quickly. In order to generate large quantities of synthetic data, runtime must be constrained to the order of seconds per frame at most.
- The generated cloud surfaces must supply realistic reflectance and thermal radiance across multiple visible, near, and far infrared wavelength bands.
A 3D deterministic global fractal cloud model, meeting these constraints, that generates projections of fractal clouds over the Earth has been developed for integration into future versions of ASSET. To run quickly, it takes advantage of multicore graphics card acceleration and compiled processing through the MATLAB mex interface. This model, its operation, results, and limitations are described in this paper.
2. Methods
Computer renderings of realistic-looking cloudscapes for movies and videogames have seen improvements over the past 10 years. Andrew Schneider describes the ray marching approach used to render the cloudscapes in the Horizon Zero Dawn videogame [3]. Ray marching involves stepping along a particular line of sight (the ray) and computing a function at each step. For rendering, a cloud density along each ray or accumulated radiance along the line of sight can be computed. In the Horizon Zero Dawn videogame, a series of Perlin, Worley, and Curl-Noise fractal textures were used to define the location and density of clouds within a volume. These textures, along with a 2D weather pattern, and some altitude boundaries were sampled during a ray march through a shell-shaped region over the viewpoint character.
Other authors, such as Wrennige et al., who developed the rendering process for the movie Oz, the Great and Powerful [4], and Häggström [5] describe similar ray marching approaches to render their scenes. In Wrennige’s work, a more complex means to render multiple scattering from hierarchies of objects was developed.
A ray marching cloud renderer was created for ASSET, inspired mainly by the Horizon Zero Dawn geometry. For each cloud type and layer, a cloud shell is defined over the surface of the Earth. A 3D function composed of fractal textures and boundary functions is defined within the cloud shell. The surfaces of the clouds are modeled as a level-set of this function, where the function takes on a threshold value. During the ray march, the first surface is found iteratively at the first threshold crossing, along with the first surface normal. The depth through the cloud is integrated during the remainder of the ray march. The radiance reaching the satellite sensor at each pixel is calculated from the depth, the sun position, and the first surface location and normal vector, as shown in Figure 1.
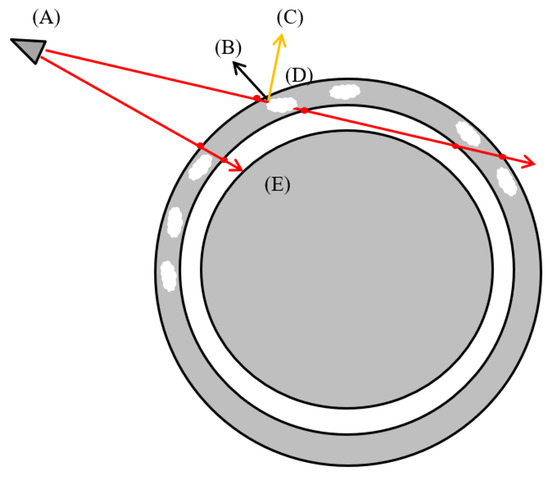
Figure 1.
Ray march geometry. (A) Sensor position, (B) first surface normal, (C) sun-pointing vector, (D) cloud shell, (E) Earth surface boundary. For each pixel in the field of view, a ray is generated, which intersects the cloud shell. Within the cloud shell, a fractal function is sampled to find a level-set boundary. If the ray crosses a cloud, radiance due to solar reflection and thermal emission is calculated for the pixel.
Existing algorithms within ASSET handle atmospheric path radiance and atmospheric attenuation. The algorithm in this paper renders only the unimpeded light from the cloudtops. While multiple scattering simulations can produce more realistic lighting effects in translucent clouds, a shortcut is taken in this algorithm to save runtime.
The majority of ASSET is written in MATLAB. However, in order to efficiently run the calculations needed for generating the fractals, interpolating weather data, ray marching, and rendering to the FPA, the MATLAB mex CUDA interface is used to pass the scenario parameters and GPU buffers to the compiled CUDA code (an extension of C++), in which the bulk of the processing is performed in parallel to the general-purpose GPU.
2.1. Fractal Functions and the Level-Set
A series of three-dimensional fractal textures are computed prior to rendering. The weighted sums of these scaled fractal textures, along with an exponential altitude barrier function and a function derived from the weather-mask, are interpolated to form a “cloud function”. The weather-mask, responsible for gating the large-scale appearance of cloud patterns over the Earth’s surface, is explained in the next section. This cloud function produces a scalar value for each point within the cloud shell. A threshold value is chosen to define a level-set, a two-dimensional fractal surface in the three-dimensional shell. Wherever the cloud function is greater than the threshold is considered within a cloud.
The cumulus and stratus clouds make use of a sum of three fractal textures: a coarse and fine Perlin fractal and a Worley fractal.
Perlin fractals, invented by Ken Perlin [6], are composed of a sum of values sampled on scaled grids. At each node on a grid, randomly oriented gradient vectors are computed. The value at a given point is a sum interpolated from the grid, weighted by the distance to each node and relative angle to the node’s vector in the containing cell. Each successive grid is scaled by 1/2, and the values are scaled by a factor called the persistence. The Perlin fractals are used to create the wrinkled fine details of the 3D cloud surfaces.
Worley fractals, also known as Voronoi noise, were invented by Steven Worley [7]. They are computed by randomly distributing “feature points” in a grid of cells and then computing the distance from the sampled point to the nearest feature point. Only the nearest neighbor cells (or wraparound nearest neighbors) and their feature points are needed to compute the distance to the nearest feature point. The function ends up being the distance to the nearest Voronoi cell boundary controlled by the nearest feature point. The role of the Worley fractals, inverted and added to the cloud function, is to break up clouds in a manner similar to the brokenness of cumulus forming in large-scale convection patterns.
The altitude barrier function suppresses the formation of cloud surfaces above and below the altitude limits of the cloud shell, simulating condensation levels. A simple exponential is used here.
In Equation (1), CF is the cloud function. are the fractal functions, with values scaled by and and length-scales scaled by . The exponential barrier functions for altitude take the bottom and top altitude of the cloud shell and adjustable length-scales and magnitudes as parameters. Parameters are adjusted to reproduce the appearance of clouds in satellite imagery on large and small scales.
Figure 2 shows the process by which scaled and added fractal shape functions and the exponential barrier function can produce realistic 3D cloud boundaries. The coarse- and fine-grained Perlin fractals provide surface structure, and the Worley fractal can be used to break up clouds into shapes similar to those seen in large-scale convection patterns. The altitude boundaries provide cutoffs by suppressing the clouds above and below certain altitudes, simulating condensation levels.
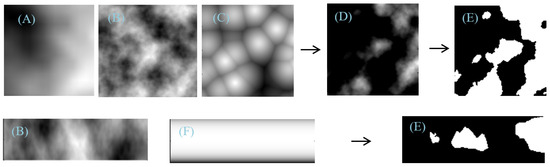
Figure 2.
Fractal functions and level-sets: (A) coarse Perlin fractal, (B) fine Perlin fractal, (C) Worley fractal, (D) weighted sum, (E) level-set for cloud surface, (F) altitude boundary shape function. The top row shows a top-down perspective, and the bottom row a horizontal perspective. Arrows are weighted sum and level set processing steps.
2.2. Large-Scale Weather Data and Wind Distortion of Fractal Shapes
In most videogames, the rendered clouds do not have to form part of, or mesh with, a realistic global weather system. The ASSET cloud renderer, however, must provide coverage that is consistent between multiple overhead sensors in both LEO and GEO and is realistic for viewpoints covering a full disc view and closer narrow fields of view.
Clouds do not appear uniformly over the Earth’s surface. Real cloud cover over the Earth depends on the distribution of atmospheric humidity, vertical air motion, and complicated wind patterns transporting and distorting the clouds.
ASSET is intended to run quickly, so the cloud renderer cannot be treated as a fluid dynamics or weather simulation, due to the computational complexity required for these simulations. However, weather analysis datafiles derived from the Global Forecast System (GFS) can be used as inputs providing a coarse (half- or quarter-degree longitude) global 3D source of relative humidity, temperature, and vertical and horizontal windspeeds. This is enough to predict where cloud cover should exist over the Earth.
An algorithm used in another AFIT tool, the Laser Environmental Effects Definition and Reference (LEEDR), was used as the starting point for a decision procedure used to derive cloud “weather-masks” [8] such as the one shown in Figure 3. LEEDR predicts the presence or absence of clouds for five cloud types determined by altitude, vertical windspeed, and temperature conditions. The decision procedure for this model is similar, but it is modified to reduce the number of cloud classes, in order to reduce runtime. Four cloud classes are chosen to reproduce the majority of cloud coverage seen with the GOES-16 satellite ABI instrument.

Figure 3.
A weather-mask for low-altitude cumulus cloud cover derived from a GFS grid-4 model file from the National Centers for Environmental Information (NCEI), processed by the ASSET cloud model decision procedure.
In the decision procedure used in the fractal cloud model, clouds are divided into classes: low-altitude and high-altitude clouds. The low-altitude clouds are divided into low-altitude stratus and low-altitude cumulus clouds. The high-altitude clouds are divided into altostratus and cirrus clouds. The GFS weather datafiles are sampled at particular altitudes for humidity, temperature, and vertical windspeed to derive weather-masks. The parameters used in the decision procedure are shown in Table 1.

Table 1.
Cloud weather-mask decision procedure.
Each cloud type has separate shape parameters defining the cloud function and requires a separate call to the renderer, so the types need to be broad enough to capture significant cloud coverage over the Earth but few enough in number to avoid excessive runtime.
Clouds are distorted and transported by the wind, which significantly alters the original isotropic cloud shapes. In order to represent the wind transport of the clouds in the model, a “displacement map” is created which maps points in the cloud shell to points which have been transported in the GFS-supplied wind field, as shown in Figure 4. A uniform equirectangular grid of points is initialized over the Earth at a target altitude. The points are then displaced backwards in the wind field for a length of time chosen to reproduce the apparent lengthening and shearing of cloud shapes seen in satellite imagery. Typical initial displacement times used range from 2 to 20 h. To provide greater flexibility, different displacement maps can be provided for the weather-mask and each of the fractal textures.

Figure 4.
Displacement map: equirectangular grid displaced in 2000 m wind field for 50 ks.
In addition, to provide cloud motion during a run, the displacement maps can continue to be propagated from frame to frame in about 500 ms.
When a point is sampled from the fractal shape function, an interpolation of the displacement map is made and a new upwind point at the same altitude is calculated. This upwind point is used to sample the fractal textures, providing the effect of the fractal propagating in the wind. Future applications of the cloud model can add motion to the clouds by propagating the displacement map further. Figure 5 demonstrates this.

Figure 5.
Clouds distorted by (A) no displacement, (B) 7 h displacement, and (C) 13 h displacement in the GFS-supplied wind field.
2.3. Light Transport Approximations in Clouds
The clouds rendered by this algorithm are usually thick relative to the extinction coefficients provided later in this section. In order to minimize runtime and avoid upsampling or staggered rendering, rather than attempting a multiple scattering model, a simplified model for reflection and emission from the cloud surfaces is used.
This model treats the illuminated surfaces of the cloud partially as a Lambertian reflector and partially as a Lambertian emitter (to simulate “indirectly scattered light” within the cloud). The non-illuminated portions of the cloud are treated as a Lambertian emitter. A proportion of sunlight incident on the cloud surface is treated as “indirectly scattered”, and it is set with a parameter.
The proportion of light that is reflected and emitted from illuminated and non-illuminated surfaces is approximated by a one-dimensional scattering model given in Equations (2a) and (2b). These equations simulate the transport of light within a one-dimensional cloud slab, where the coordinate is the depth through the cloud along the line of sight from the illuminated surface.
This effort has not made use of a scattering phase function. In future work, for more accurate simulation of optically thin clouds in the various infrared wavelengths of interest, a phase function will be incorporated. One possibility is a Henyey–Greenstein function with a wavelength-dependent asymmetry factor fit to Mie scattering, as described by Petty [9]. Other phase functions, as described by Cornette and Shanks [10], may fit Mie scattering more accurately.
Solving these equations for the case of pure scattering (single-scattering albedo of 1.0) gives the following simple relationships:
- Extinction coefficient [1/m]
- Mean free path for scattering [1/m]
- Mean free path for absorption [1/m]
- Single scattering albedo [ND] =
- Incident light [ or similar measure]
- Light transmitted through a cloud of thickness L [, or similar measure]
- Light scattered back from the cloud
- Light traveling forward from sunlit side to far side of cloud
- Light traveling backward to sunlit side of cloud
- L
- Cloud thickness [m]
In infrared wavelengths, above about 1.5 m [11], absorption becomes important in addition to scattering (the single-scattering albedo drops below 1). A rough effective fit to the numerical behavior of Equations (2a) and (2b) is made for different values of single-scattering albedo, which are given in Equations (4a) and (4b). The simulated behavior is depicted for a few single-scattering albedos in Figure 6.
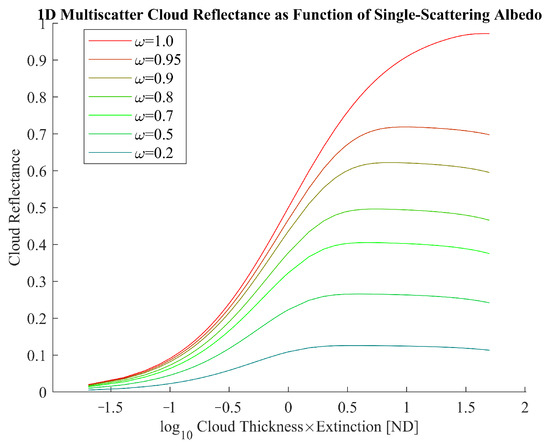
Figure 6.
Light scattered from the illuminated cloud surface in a simple 1D model given several values for the single-scattering albedo.
The observed relationship to single-scattering albedo is similar to other relationships derived, such as in Equation (4) of Shanks’ work [12].
In the model, the direct transmission of light through the clouds is modeled by Beer’s Law.
Information on liquid water content and droplet sizes for water and ice clouds is used to derive the single-scattering albedo and extinction coefficients for light transport.
Hu and Stamnes provide tables for the single-scattering albedo and extinction coefficient for water clouds as a function of wavelength and droplet diameter [11]. Hong et al. provide similar information for ice clouds, given particle effective diameter and wavelength or wavenumber [13].
Miles et al. provide some liquid water content and droplet size information for water clouds, given in Table 2 below [14]. Mitchell et al. provide a histogram of ice water content and droplet diameter for various kinds of cirrus clouds, ranging from 0.01 to 1 g/m3 and 60 to 120 µm [15].

Table 2.
Summary of selected cloud properties derived from Tables 1 and 2 of Miles et al.’s work [14].
Combining this information, one particular example is plotted in Figure 7 for stratus (10 µm, 0.35 g/m3) and cirrus clouds (90 µm, 0.01 g/m3). Note that for these two droplet sizes and mass densities, the number of droplets/volume for the stratus cloud is 3000 times higher than for an optically thin cirrus cloud. (8.4 × 107 #/m3 and 2.62 × 104 #/m3, respectively).
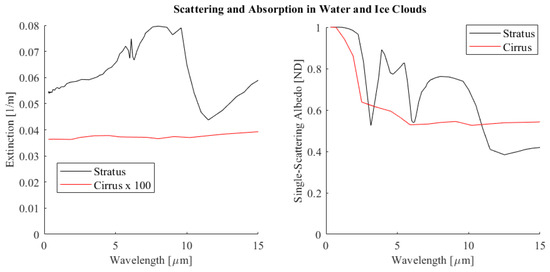
Figure 7.
Stratus and cumulus extinction coefficients and single-scattering albedo, derived from [11,14] for water clouds and [13,15] for cirrus clouds.
3. Results
High-resolution imagery from the Advanced Baseline Imager instrument (ABI) from the Geostationary Operational Environmental Satellite (GOES) was downloaded for comparison with the cloud cover produced by the fractal cloud generator. The imagery was used to check radiometry and to help tune the geometry of the clouds and ensure major features of cloud cover were reproduced by the model [16].
Both large- and small-scale cloud cover features have been realistically reproduced by the model. Multiple calls to the model overlaying differing cloud shape functions with independently adjustable parameters can create different cloud types. Figure 8 compares maritime cumulus over stratus clouds of comparable scale to similar features in the 23 April 2023 GOES-16 imagery.

Figure 8.
A comparison of fine features, maritime cumulus over stratus clouds. (A) GOES-16 Band-2 image, (B) fractal cloud simulation. The yellow line indicates an equivalent scale in the satellite and rendered image.
Cloudtop radiances from reflected and transmitted sunlight were compared with the radiances from lower-altitude, mid-latitude, and higher-altitude tropical cloudtops visible in the GOES images. Radiances are calculated in terms of reflected sunlight and thermally emitted light, with the temperature of the cloud taken to be the 1976 standard atmosphere temperature of the cloud surface altitude. ASSET’s current atmospheric model, while not the focus of the present work, models Rayleigh scattering and thermal path radiance and attenuation using interpolated data from MODTRAN-6. It is described more fully in [17].
The simulated and observed distributions of cloudtop spectral radiances are similar in the visible, near, and long-wave infrared. Using cloudtop altitude data inferred from GOES to select cloud pixels, histograms of cloudtop spectral radiance, compared to simulated cloudtop spectral radiance, are shown for three GOES bands in Figure 9.
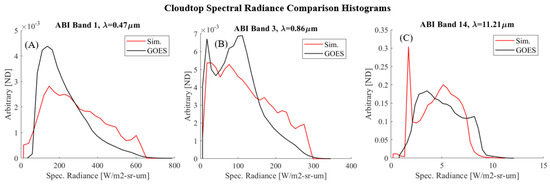
Figure 9.
Histograms of cloudtop spectral radiance derived from full disc GOES ABI and simulated images. (A) Visible, (B) NIR, (C) long-wave infrared.
In the infrared, cloudtop radiance is governed in the model by the standard atmosphere temperature of the cloudtop heights. Similar behavior is seen in the clearer infrared bands on GOES-16, with high-altitude cumulonimbus and altostratus clouds from the tropical Hadley cell appearing darker. The surface emission present in the GOES images indicates that the surface is warmer than the clouds. In addition, in the mid-infrared wavelengths, atmospheric opacity and path radiance play a large role in the visibility of cloudtops, with only the highest cloudtops visible. Figure 10, Figure 11 and Figure 12 illustrate this.

Figure 10.
GOES ABI Band-1 (visible band) compared with simulated fractal clouds showing plausible large-scale weather patterns. Also, comparable cloudtop radiances.

Figure 11.
Full disc comparison in NIR band (0.86 µm), 1200 EST.

Figure 12.
Long- wave infrared full disc comparison. High-altitude tropical altostratus clouds are cooler and dimmer in this band. Lower-altitude clouds are warmer and brighter but also attenuated by the atmospheric transmission.
Figure 13 demonstrates the ability of the model to overlay several 3D cloud shapes, distorted by complex wind, from multiple views. These shots are generated using the same projection routine as the global distributions.
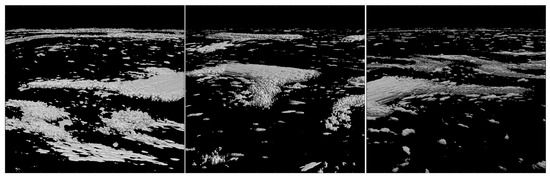
Figure 13.
Three views of a cloud-bank, 90 degrees apart, taken at 15 degrees of elevation with a 60-degree sun angle to the horizon.
On an NVIDIA GeForce GTX 1650X, for a 2000 × 2000 FPA, with a 256 × 256 × 256 fractal texture and 25 ray marching steps through the cloud shell, the clouds render in about 700 ms per cloud type. Overlaying the layers takes a negligible amount of time. Runtime is roughly proportional to FPA dimensions and can be reduced by a coarser fractal texture or fewer ray marching steps (which reduces the accuracy of the cloud depth along the line of sight information). Runtime is not strongly dependent on the specific field of view angle. Narrow or small-scale views render in about the same amount of time as whole-Earth views, as long as FPA dimensions are the same.
Some representative rendering times per cloud shell are given in Table 3 below for an NVIDIA GeForce GTX 1650X, 512 blocks × 256 threads, for a full-disc rendering of the Earth.

Table 3.
Average rendering times per cloud shell.
4. Discussion
Several aspects of previous cloud coverage emulation techniques were combined to create this 3D cloud model. Global weather data were used to reproduce realistic weather patterns over the Earth as in the LEEDR program. Techniques from the videogame industry were used to simulate fine three-dimensional details on clouds at higher resolution than weather data would provide. Volumetric sampling of fractal functions was used to create fine detail which could be viewed from multiple perspectives. Arbitrarily fine detail could be generated with appropriate pre-computed 3D fractal textures which could be scaled and added to create the cloud shapes.
A key innovation for this model is the use of the interpolated displacement map, which enables the distortion of the fractal textures along the pattern of the global wind field, enhancing the ability of the model to reproduce realistic-looking weather patterns on a global scale and to convect and distort the fractal clouds as a function of time. This method may be useful in other simulation domains where the distortion of a basic fractal shape in a convective field captures some essence of the problem.
This model will improve the AFIT Sensor and Scene Emulation tool’s ability to model multi-sensor, simultaneous scenarios, including both high-resolution LEO satellites as well as lower-resolution, wide-area-coverage satellites similar to GOES in geostationary orbit.
Author Contributions
A.M.S.—Conceptualization, software, original draft preparation. S.R.Y.—Rev-iew and editing, project administration. B.J.S.—Review and editing. M.D.—Supervision, project administration. A.K.—Review and editing. S.H.—Review and editing. R.D.—Review and editing, data curation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Space Systems Command/SNGT, 482 N Aviation Blvd, El Segundo, CA 90245. The authors would like to thank SSC for supporting the development of ASSET.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Young, S.R.; Steward, B.J.; Gross, K.C. Development and Validation of the AFIT Sensor Simulator for Evaluation and Testing (ASSET). Proc. SPIE 2017, 10178, 101780A. [Google Scholar]
- NASA. Blue Marble: Clouds. Available online: https://visibleearth.nasa.gov/ (accessed on 5 December 2023).
- Schneider, A. The Real-Time Volumetric Cloudscapes of Horizon: Zero Dawn. In Proceedings of the 42nd International Conference and Exhibition on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 9–13 August 2015. [Google Scholar]
- Wrenninge, M.; Kulla, C.; Lundqvist, V. Oz: The Great and Volumetric. In Proceedings of the ACM SIGGRAPH 2013 Talks on—SIGGRAPH’13, Anaheim, CA, USA, 21–25 July 2013. [Google Scholar] [CrossRef]
- Häggström, F. Real-Time Rendering of Volumetric Clouds. Master’s Thesis, Umeå University, Umeå, Sweden, 2018. [Google Scholar]
- Perlin, K. An image synthesizer. ACM SIGGRAPH Comput. Graph. 1985, 19, 287–296. [Google Scholar] [CrossRef]
- Worley, S. A cellular texture basis function. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, ACM, New York, NY, USA, 1 August 1996; pp. 291–294. [Google Scholar] [CrossRef]
- Burley, J.L.; Fiorino, S.T.; Elmore, B.J.; Schmidt, J.E. A Remote Sensing and Atmospheric Correction Method for Assessing Multispectral Radiative Transfer through Realistic Atmospheres and Clouds. J. Atmos. Ocean. Technol. 2019, 36, 203–216. [Google Scholar] [CrossRef]
- Petty, G.W. A First Course in Atmospheric Radiation, 2nd ed.; Sundog Publishing: Madison, WI, USA, 2006; pp. 331, 366. [Google Scholar]
- Cornette, W.M.; Shanks, J.G. Physically reasonable analytic expression for the single-scattering phase function. Appl. Opt. 1992, 31, 3152. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.X.; Stamnes, K. An Accurate Parameterization of the Radiative Properties of Water Clouds Suitable for Use in Climate Models. J. Clim. 1993, 6, 728. [Google Scholar] [CrossRef]
- Shanks, J.G.; Lynch, D.K. Specular scattering in cirrus clouds. In Proceedings of the Passive Infrared Remote Sensing of Clouds and the Atmosphere III, Paris, France, 25–28 September 1995; p. 227. [Google Scholar] [CrossRef]
- Hong, G.; Yang, P.; Baum, B.A.; Heymsfield, A.J.; Xu, K.M. Parameterization of Shortwave and Longwave Radiative Properties of Ice Clouds for Use in Climate Models. J. Clim. 2009, 22, 6287–6312. [Google Scholar] [CrossRef][Green Version]
- Miles, N.L.; Verlinde, J.; Clothiaux, E.E. Cloud Droplet Size Distributions in Low-Level Stratiform Clouds. J. Atmos. Sci. 2000, 57, 295–311. [Google Scholar] [CrossRef]
- Mitchell, D.L.; Mishra, S.; Lawson, R.P. Representing the Ice Fall Speed in Climate Models: Results from Tropical Composition, Cloud and Climate Coupling (TC4) and the Indirect and Semi-Direct Aerosol Campaign (ISDAC). J. Geophys. Res. 2011, 116, D00T03. [Google Scholar] [CrossRef]
- GOES-R Calibration Working Group and GOES-R Series Program. NOAA GOES-R Series Advanced Baseline Imager (ABI) Level 1b Radiances; [GOES-16 Full Disk 26 April 2023]; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2017. [CrossRef]
- Steward, B.J.; Wagner, B.; Hopkinson, K.; Young, S.R. Modeling EO/IR systems with ASSET: Applied machine learning for synthetic WFOV background signature generation. In Proceedings of the Electro-Optical and Infrared Systems: Technology and Applications XIX, SPIE, Berlin, Germany, 5–8 September 2022; p. 9. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).