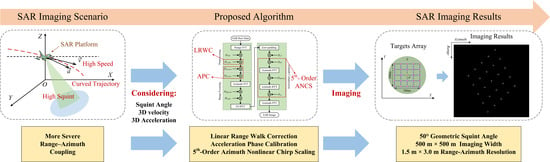
A Modified Frequency Nonlinear Chirp Scaling Algorithm for High-Speed High-Squint Synthetic Aperture Radar with Curved Trajectory
Abstract
1. Introduction
- A more accurate approximation of the range model is proposed, along with an MFNCS algorithm that utilizes a fifth-order CS function. Although several NCS algorithms exist for HSHS-SAR with curved trajectory, most of them utilize fourth-order CS functions to mitigate the azimuth spatial variability of Doppler parameters. However, these algorithms are not suitable when the squint angle, speed, and resolution are increasing. To address this problem, a more precise range model approximation is established, and an MFNCS algorithm with a fifth-order CS function is derived to accommodate the improved accuracy of the range model.
- The impacts of the LRWC, SIVAPC, and SVAPC are analyzed in the azimuth NCS processing. When SAR systems move with 3-D acceleration, it is necessary to eradicate its effects on the DB, i.e., the effects of the SIVAPC and SVAPC in this paper. However, most of the existing NCS algorithms only consider the range distortion introduced by the LRWC operation. Then, this will result in azimuth defocusing due to improved azimuth resolution. Hence, the effects of the SIVAPC and SVAPC are also discussed in the azimuth NCS processing to enhance the azimuth focusing capability.
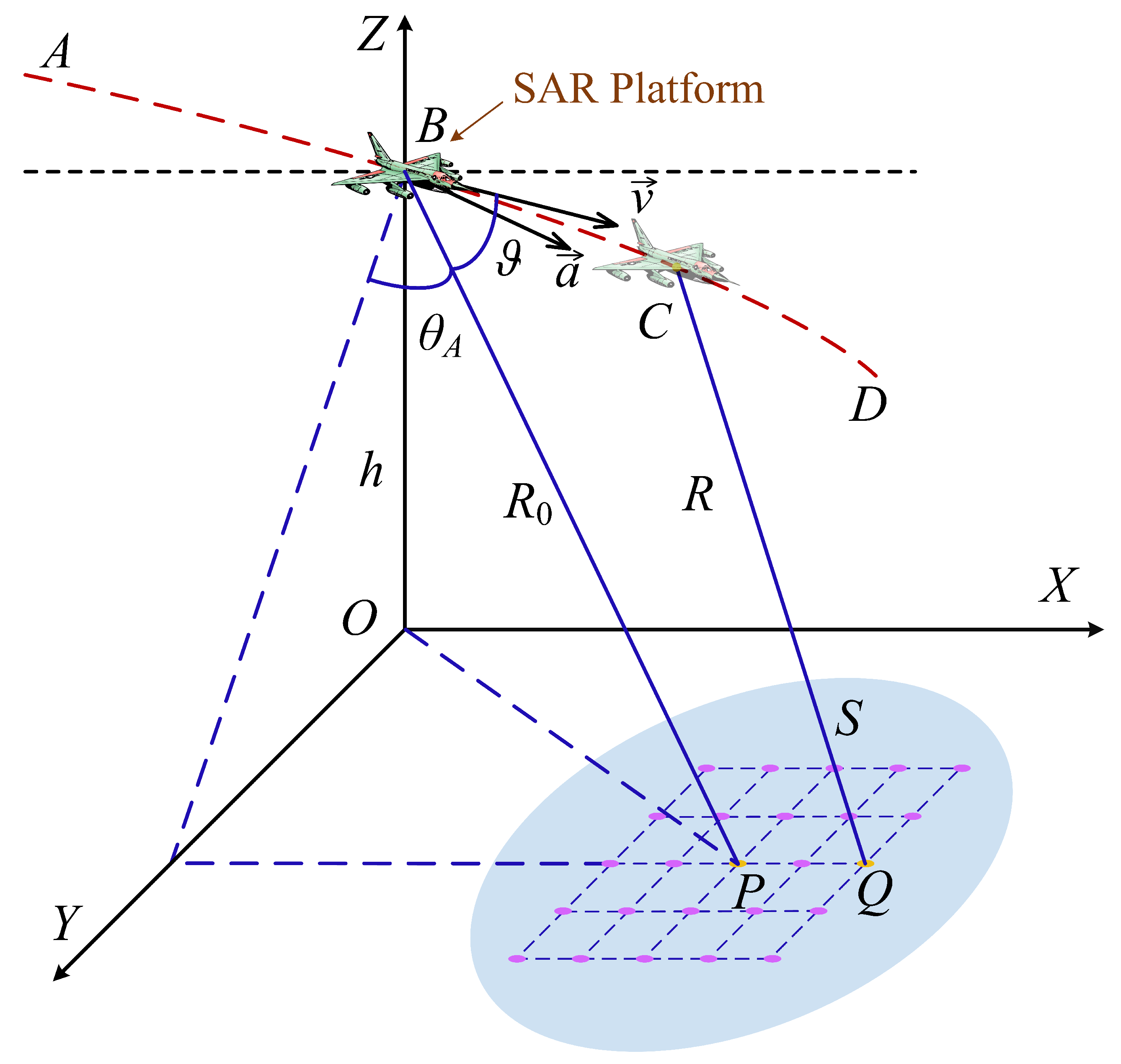
2. Signal Model
2.1. Range Model
2.2. Model Characteristics of the Range Model
2.3. Accuracy Analysis of Range Model
2.4. Echo Signal Model
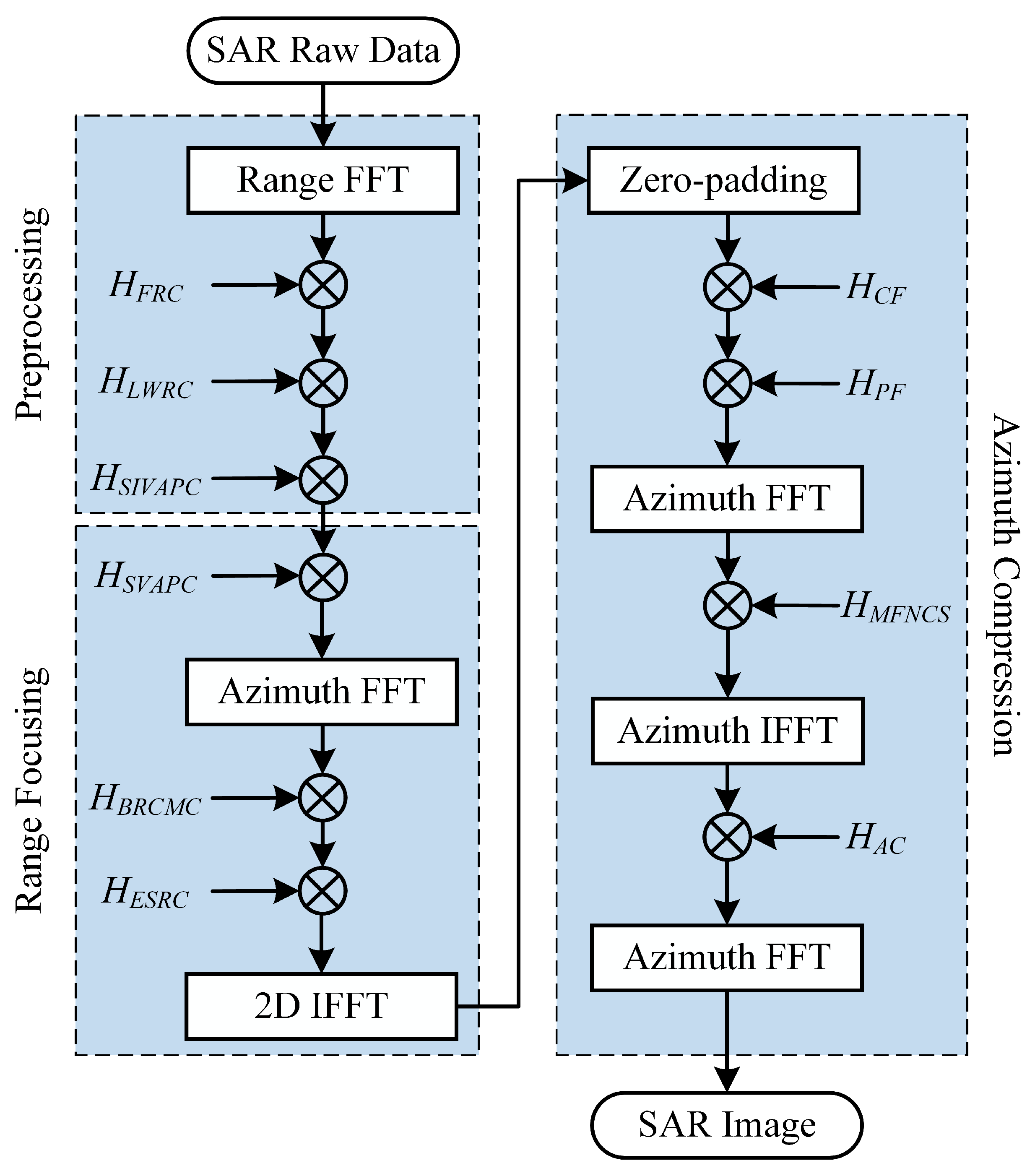
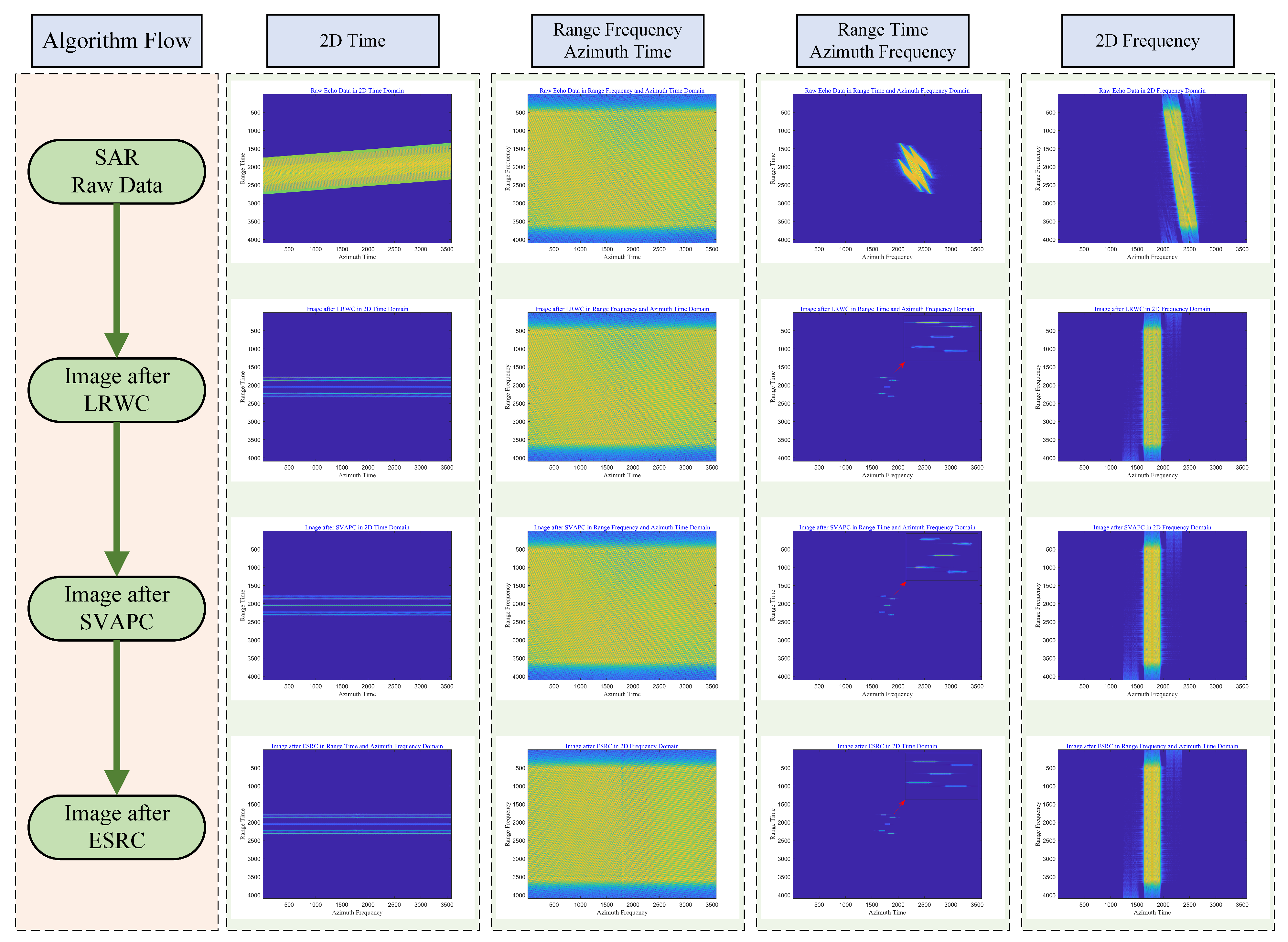
3. Preprocessing Based on FRC and LRWC
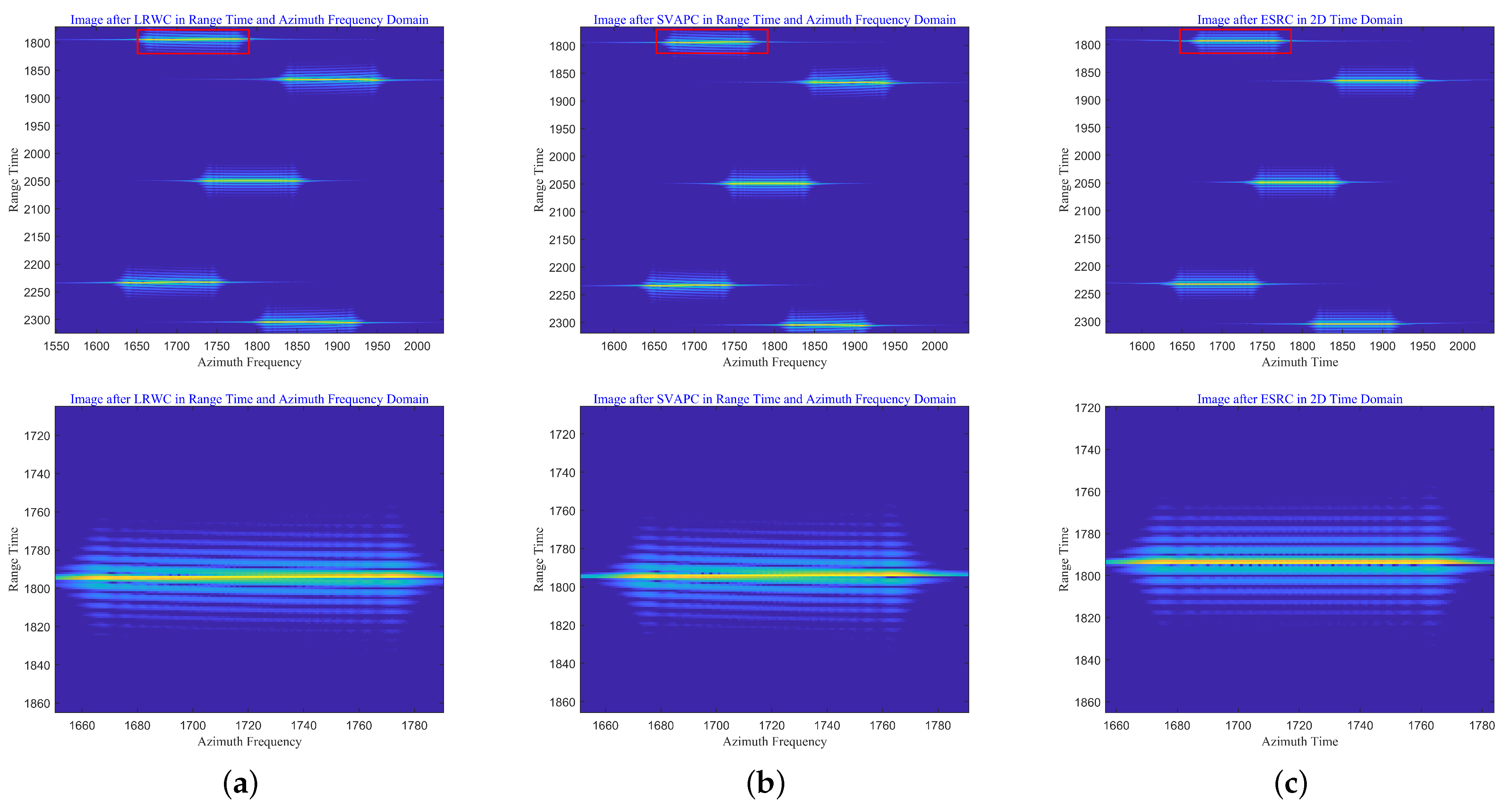
3.1. FRC and LRWC
3.2. Impacts of Acceleration and SIVAPC
4. Range Focusing via SVAPC
4.1. SVAPC
4.2. BRCMC and ESRC
4.3. Accuracy Analysis of BRCMC and ESRC
5. Azimuth Compression Based on the MFNCS Algorithm
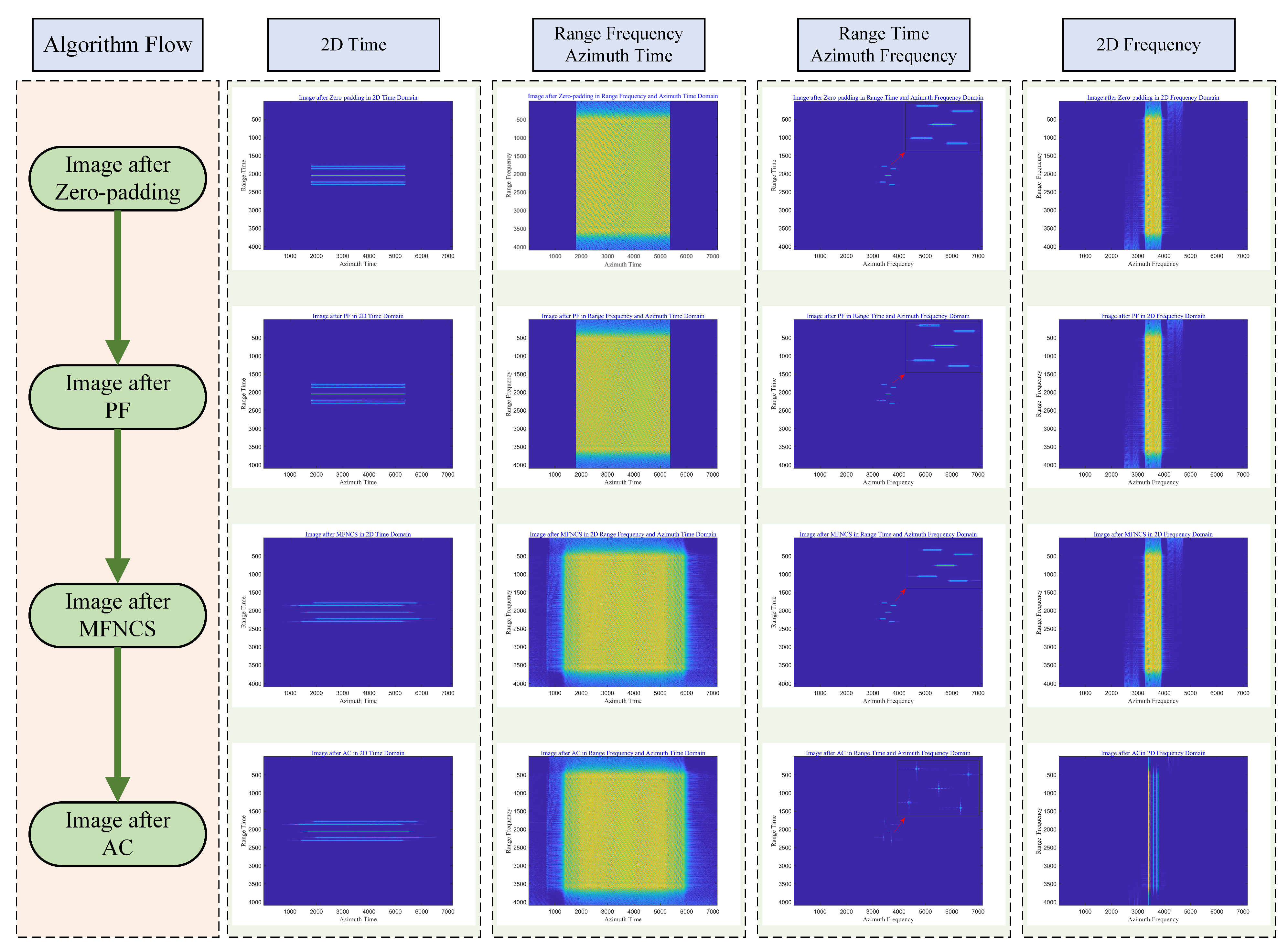
5.1. Zero-Padding and Cascade Processing
5.2. Azimuth-Dependent Characteristics Evaluation
5.3. Derivation of MFNCS Algorithm
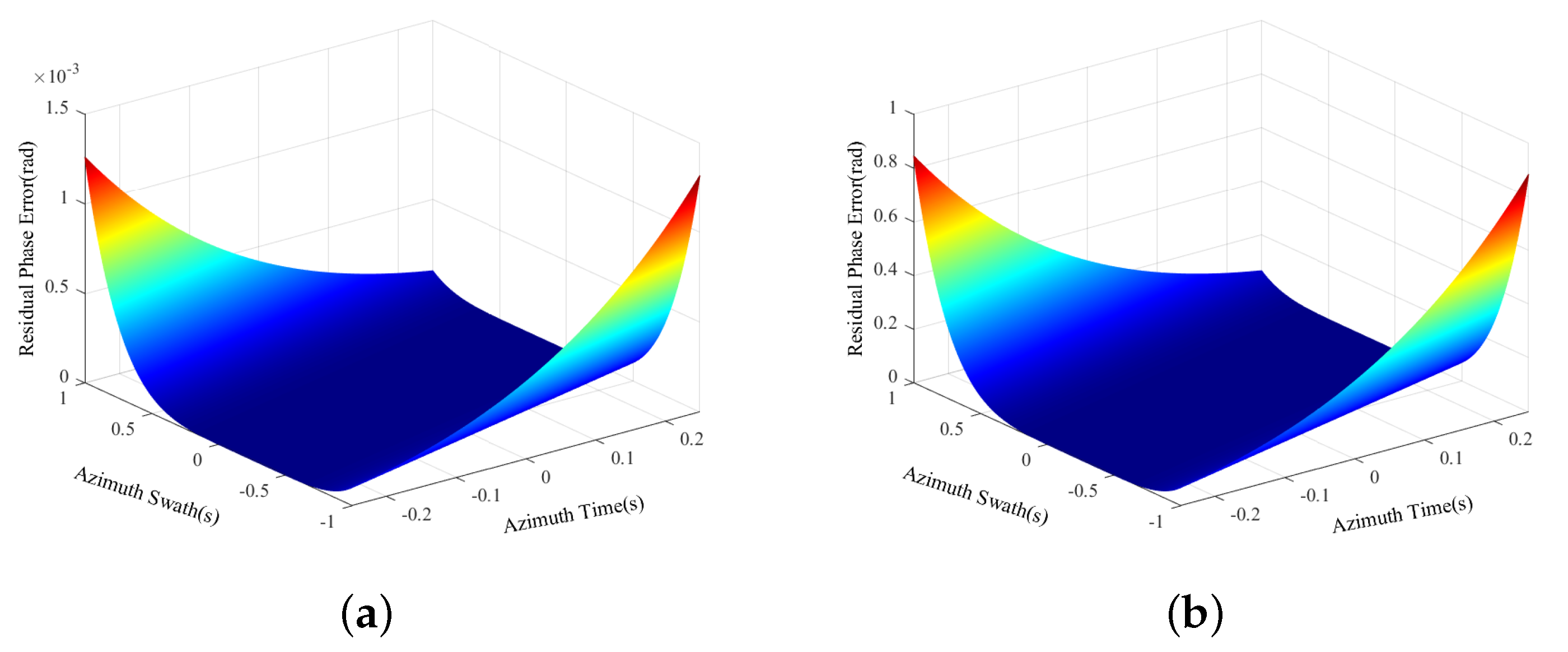
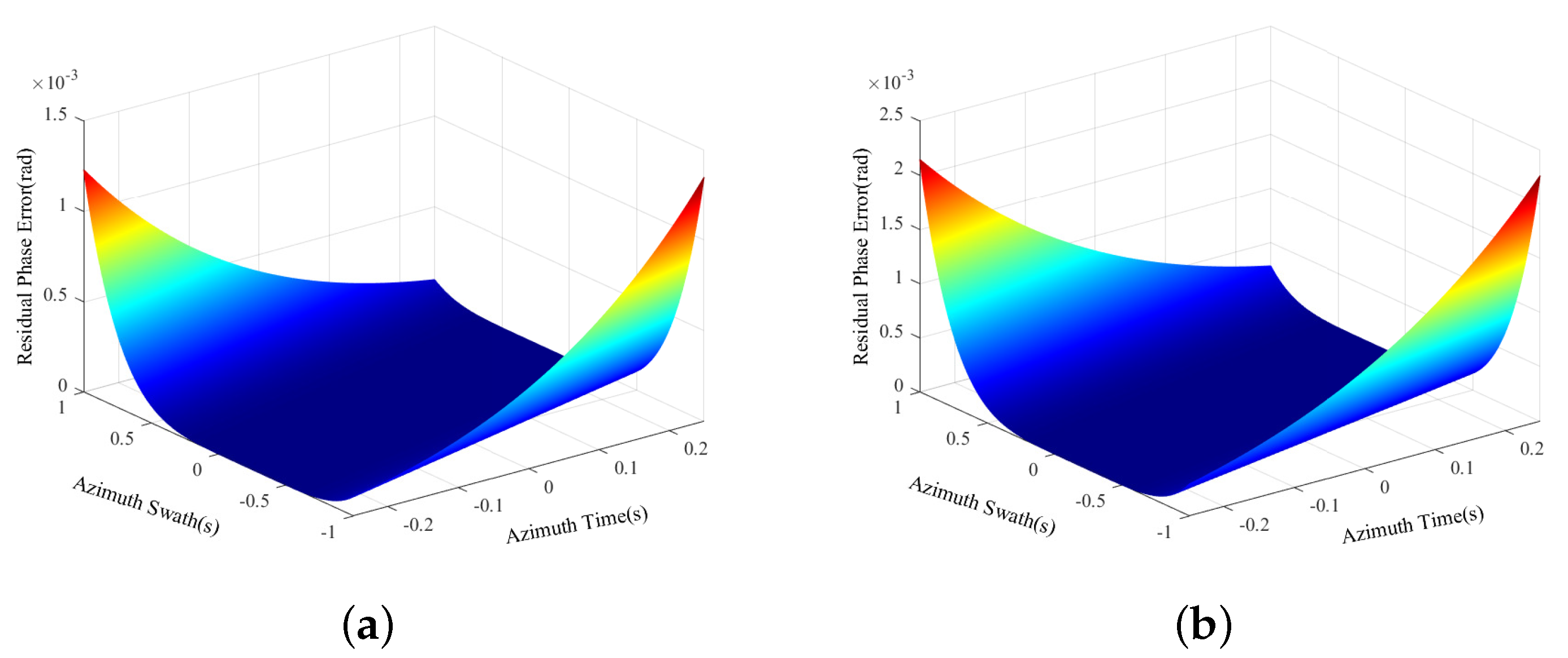
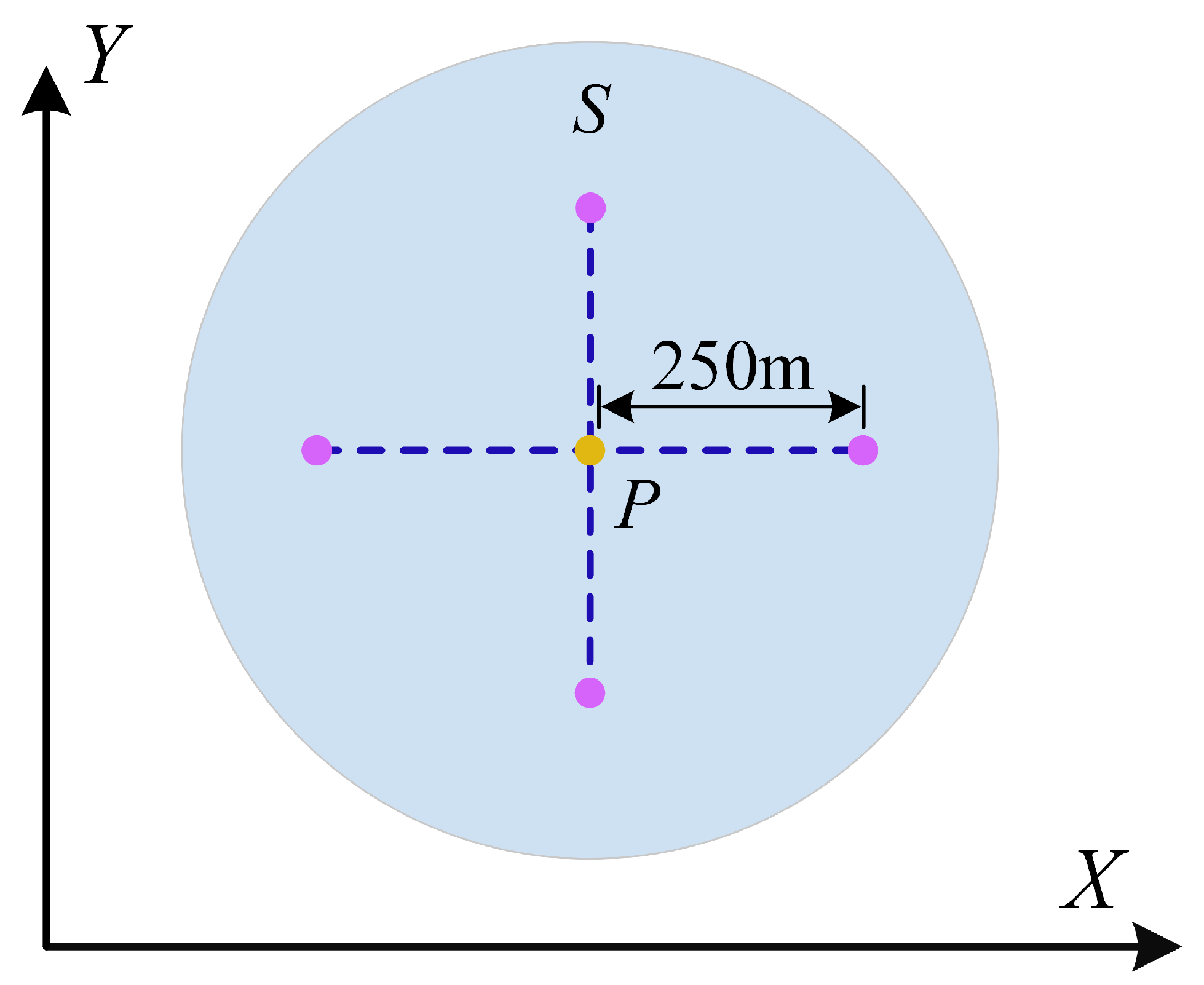
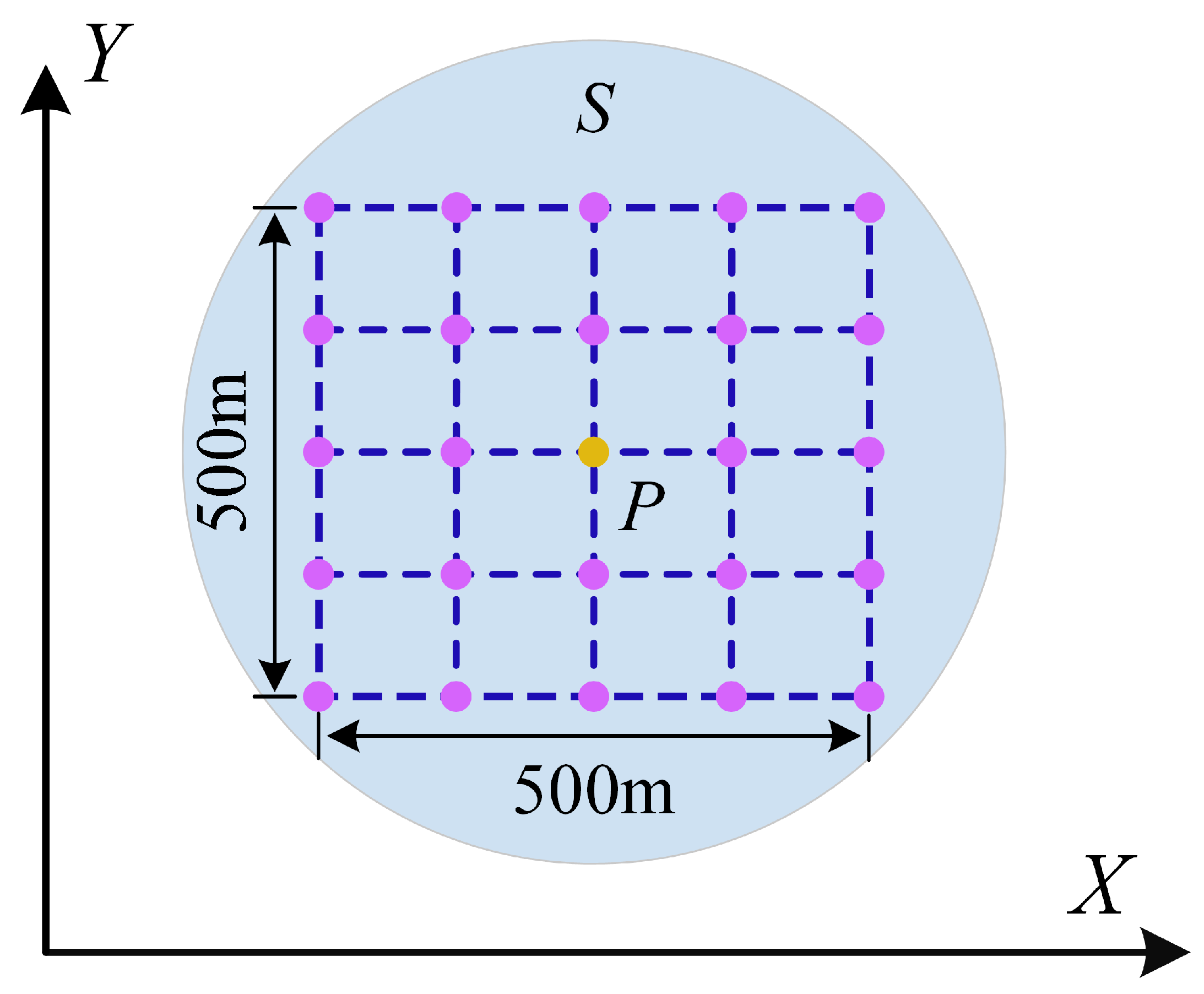
6. Simulation Results
6.1. Simulation Scenario 1
6.2. Simulation Scenario 2
7. Discussion and Analysis
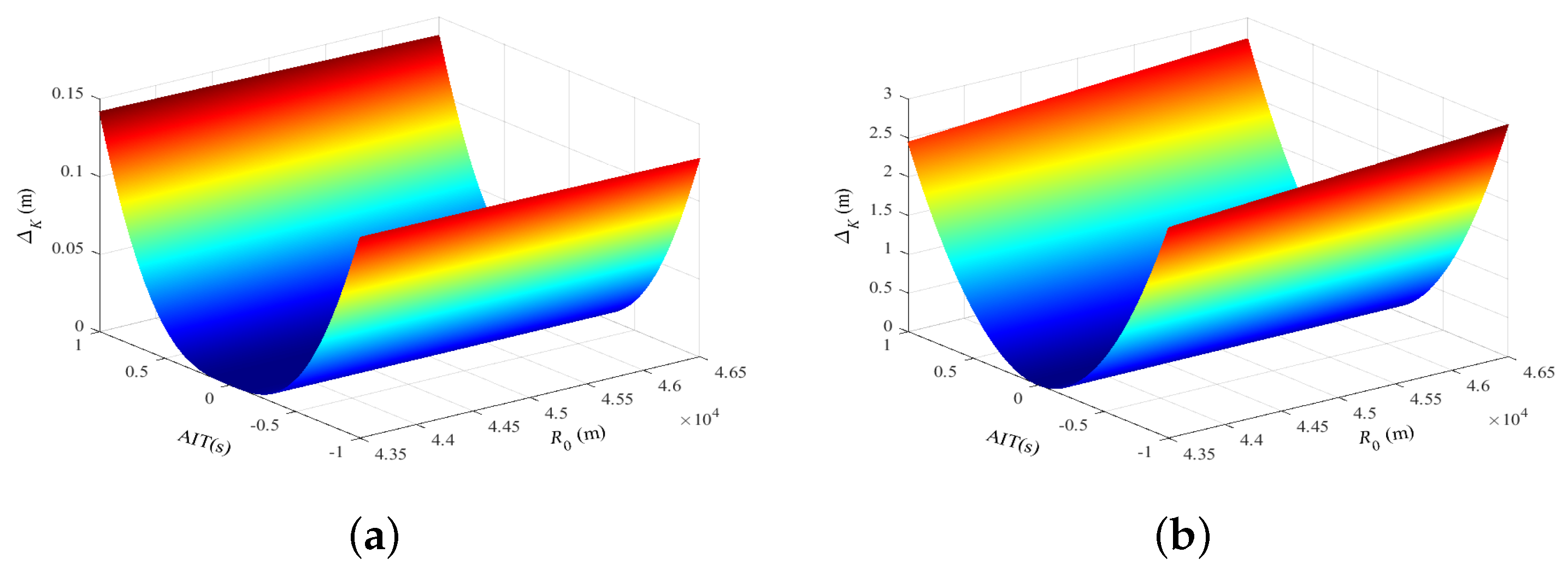
7.1. Fifth-Order CS Function Applicability Analysis
7.2. Geometric Distortion Analysis
7.3. Computational Complexity Analysis
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
References
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 108–110. [Google Scholar]
- Wu, Y.; Sun, G.C.; Xia, X.G.; Xing, M.; Yang, J.; Bao, Z. An Azimuth Frequency Non-Linear Chirp Scaling (FNCS) Algorithm for TOPS SAR Imaging with High Squint Angle. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 213–221. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Zeng, L.; Bao, Z. Focusing of Highly Squinted SAR Data with Frequency Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2016, 13, 23–27. [Google Scholar] [CrossRef]
- Zeng, T.; Li, Y.; Ding, Z.; Long, T.; Yao, D.; Sun, Y. Subaperture Approach Based on Azimuth-Dependent Range Cell Migration Correction and Azimuth Focusing Parameter Equalization for Maneuvering High-Squint-Mode SAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6718–6734. [Google Scholar] [CrossRef]
- Huo, W.; Li, M.; Wu, J.; Li, Z.; Yang, J.; Li, H. SAR Image Reconstruction and Autofocus Using Complex-Valued Feature Prior and Deep Network Implementation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Li, J.W. Theoretical Application of Overlapped Subaperture Algorithm for Quasi-Forward-Looking Parameter-Adjusting Spotlight SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 144–148. [Google Scholar] [CrossRef]
- Bao, M.; Zhou, S.; Xing, M. Processing Missile-Borne SAR Data by Using Cartesian Factorized Back Projection Algorithm Integrated with Data-Driven Motion Compensation. Remote Sens. 2021, 13, 1462. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Xing, W.; Liang, Y.; Gao, Y.; Dai, B.; Hu, L.; Bao, Z. A Modified Equivalent Range Model and Wavenumber-Domain Imaging Approach for High-Resolution-High-Squint SAR with Curved Trajectory. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3721–3734. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Yuan, M.; Guo, L.; Guo, j.; Lin, H.; Xing, M. Focusing Highly-Squinted FMCW SAR Data Using the Modified Wavenumber-Domain Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 17, 1999–2011. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, L.; Zhao, L.; Bi, G. Quasi-Polar-Based FFBP Algorithm for Miniature UAV SAR Imaging without Navigational Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7053–7065. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, F.; Chen, Z.; Li, J.; Hong, W. An Improved Map-Drift Algorithm for Unmanned Aerial Vehicle SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1–5. [Google Scholar] [CrossRef]
- Ren, H.; Sun, Z.; Yang, J.; Xiao, Y.; An, H.; Li, Z.; Wu, J. Swarm UAV SAR for 3-D Imaging: System Analysis and Sensing Matrix Design. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Luomei, Y.; Xu, F. Segmental Aperture Imaging Algorithm for Multirotor UAV-Borne MiniSAR. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Zhou, P.; Xing, M.; Xiong, T.; Wang, Y.; Zhang, L. A Variable-Decoupling- and MSR-Based Imaging Algorithm for a SAR of Curvilinear Orbit. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1145–1149. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Sun, G.C. Acceleration Model Analyses and Imaging Algorithm for Highly Squinted Airborne Spotlight-Mode SAR with Maneuvers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1120–1131. [Google Scholar] [CrossRef]
- Dong, Q.; Sun, G.C.; Yang, Z.; Guo, L.; Xing, M. Cartesian Factorized Backprojection Algorithm for High-Resolution Spotlight SAR Imaging. IEEE Sens. J. 2018, 18, 1160–1168. [Google Scholar] [CrossRef]
- Luo, Y.; Zhao, F.; Li, N.; Zhang, H. A Modified Cartesian Factorized Back-Projection Algorithm for Highly Squint Spotlight Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2019, 16, 902–906. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, W.; Sun, G.C.; Chen, X.; Han, L.; Xing, M. A Fast Cartesian Back-Projection Algorithm Based on Ground Surface Grid for GEO SAR Focusing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Li, Y.; Xu, G.; Zhou, S.; Xing, M.; Song, X. A Novel CFFBP Algorithm with Noninterpolation Image Merging for Bistatic Forward-Looking SAR Focusing. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Liu, Y.; Sun, L.; Bao, Z.; Wu, Y. Extended NCS Based on Method of Series Reversion for Imaging of Highly Squinted SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 446–450. [Google Scholar] [CrossRef]
- Xing, M.; Wu, Y.; Zhang, Y.D.; Sun, G.C.; Bao, Z. Azimuth Resampling Processing for Highly Squinted Synthetic Aperture Radar Imaging with Several Modes. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4339–4352. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Li, Z.; Huang, Y.; Yang, J. Highly Squint SAR Data Focusing Based on Keystone Transform and Azimuth Extended Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2015, 12, 145–149. [Google Scholar] [CrossRef]
- Ding, Z.; Zheng, P.; Li, H.; Zhang, T.; Li, Z. Spaceborne High-Squint High-Resolution SAR Imaging Based on Two-Dimensional Spatial-Variant Range Cell Migration Correction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Xiong, T.; Xing, M.; Xia, X.G.; Bao, Z. New Applications of Omega-K Algorithm for SAR Data Processing Using Effective Wavelength at High Squint. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3156–3169. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Gao, Y.; Zeng, L.; Bao, Z. An Improved Range Model and Omega-K-Based Imaging Algorithm for High-Squint SAR with Curved Trajectory and Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 656–660. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, T.; Mei, H.; Quan, Y.; Xing, M. Focusing Translational-Variant Bistatic Forward- Looking SAR Data Using the Modified Omega-K Algorithm. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Wang, J.; Xing, M.; Guo, L.; Zhang, P. A Modified Range Model and Extended Omega-K Algorithm for High-Speed-High-Squint SAR with Curved Trajectory. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Yegulalp, A. Fast backprojection algorithm for synthetic aperture radar. In Proceedings of the 1999 IEEE Radar Conference. Radar into the Next Millennium (Cat. No.99CH36249), Waltham, MA, USA, 20–22 April 1999; pp. 60–65. [Google Scholar] [CrossRef]
- Ulander, L.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Cafforio, C.; Prati, C.; Rocca, F. SAR data focusing using seismic migration techniques. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 194–207. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.; Nies, H.; Ender, J.H.G. Focusing Spaceborne/Airborne Hybrid Bistatic SAR Data Using Wavenumber-Domain Algorithm. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2275–2283. [Google Scholar] [CrossRef]
- de Wit, J.; Meta, A.; Hoogeboom, P. Modified range-Doppler processing for FM-CW synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2006, 3, 83–87. [Google Scholar] [CrossRef]
- Wong, F.; Yeo, T. New applications of nonlinear chirp scaling in SAR data processing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 946–953. [Google Scholar] [CrossRef]
- Qiu, X.; Hu, D.; Ding, C. An Improved NLCS Algorithm with Capability Analysis for One-Stationary BiSAR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3179–3186. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, P.; Zhou, X.; He, T.; Chen, J. A Decoupled Chirp Scaling Algorithm for High-Squint SAR Data Imaging. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Wang, R.; Deng, Y.K.; Loffeld, O.; Nies, H.; Walterscheid, I.; Espeter, T.; Klare, J.; Ender, J.H.G. Processing the Azimuth-Variant Bistatic SAR Data by Using Monostatic Imaging Algorithms Based on Two-Dimensional Principle of Stationary Phase. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3504–3520. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, Z.; Xing, M.d.; Yang, L.; Bao, Z. A Robust Motion Compensation Approach for UAV SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Moreira, A.; Huang, Y. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1029–1040. [Google Scholar] [CrossRef]
- Zhang, S.X.; Xing, M.D.; Xia, X.G.; Zhang, L.; Guo, R.; Bao, Z. Focus Improvement of High-Squint SAR Based on Azimuth Dependence of Quadratic Range Cell Migration Correction. IEEE Geosci. Remote Sens. Lett. 2013, 10, 150–154. [Google Scholar] [CrossRef]
- Sun, G.; Jiang, X.; Xing, M.; Qiao, Z.j.; Wu, Y.; Bao, Z. Focus Improvement of Highly Squinted Data Based on Azimuth Nonlinear Scaling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2308–2322. [Google Scholar] [CrossRef]
- Wang, W.; Liao, G.; Li, D.; Xu, Q. Focus Improvement of Squint Bistatic SAR Data Using Azimuth Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2014, 11, 229–233. [Google Scholar] [CrossRef]
- Liang, Y.; Li, Z.; Zeng, L.; Xing, M.; Bao, Z. A High-Order Phase Correction Approach for Focusing HS-SAR Small-Aperture Data of High-Speed Moving Platforms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4551–4561. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, S.; Zhao, H.; Chen, Y. A New Chirp Scaling Algorithm for Highly Squinted Missile-Borne SAR Based on FrFT. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3977–3987. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, T. Focusing highly squinted missile-borne SAR data using azimuth frequency nonlinear chirp scaling algorithm. J.-Real-Time Image Process. 2021, 18, 1301–1308. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Yu, H.; Xu, G.; Liang, B.; Yang, D.G.; Wang, H. Blind NCS-Based Autofocus for Airborne Wide-Beam SAR Imaging. IEEE Trans. Comput. Imaging 2022, 8, 626–638. [Google Scholar] [CrossRef]
- Liao, Y.; Luo, Z.; Wang, J.; Zheng, Z.; Zhang, S. Processing of Mosaic SAR Using Time Frequency Analysis and Azimuth NCS Algorithm. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4625–4639. [Google Scholar] [CrossRef]
- An, D.; Huang, X.; Jin, T.; Zhou, Z. Extended Nonlinear Chirp Scaling Algorithm for High-Resolution Highly Squint SAR Data Focusing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3595–3609. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Liang, Y.; Gao, Y.; Chen, J.; Huai, Y.; Zeng, L.; Sun, G.C.; Bao, Z. A Frequency-Domain Imaging Algorithm for Highly Squinted SAR Mounted on Maneuvering Platforms with Nonlinear Trajectory. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4023–4038. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, H.; Sun, H.; Ying, W. Multireceiver SAS Imagery Based on Monostatic Conversion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10835–10853. [Google Scholar] [CrossRef]
- Yang, P. An imaging algorithm for high-resolution imaging sonar system. Multimed. Tools Appl. 2023, 82, 1–17. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.; Cumming, I.G. A Two-Dimensional Spectrum for Bistatic SAR Processing Using Series Reversion. IEEE Geosci. Remote Sens. Lett. 2007, 4, 93–96. [Google Scholar] [CrossRef]
- Liang, Y.; Dang, Y.; Li, G.; Wu, J.; Xing, M. A Two-Step Processing Method for Diving-Mode Squint SAR Imaging with Subaperture Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 811–825. [Google Scholar] [CrossRef]
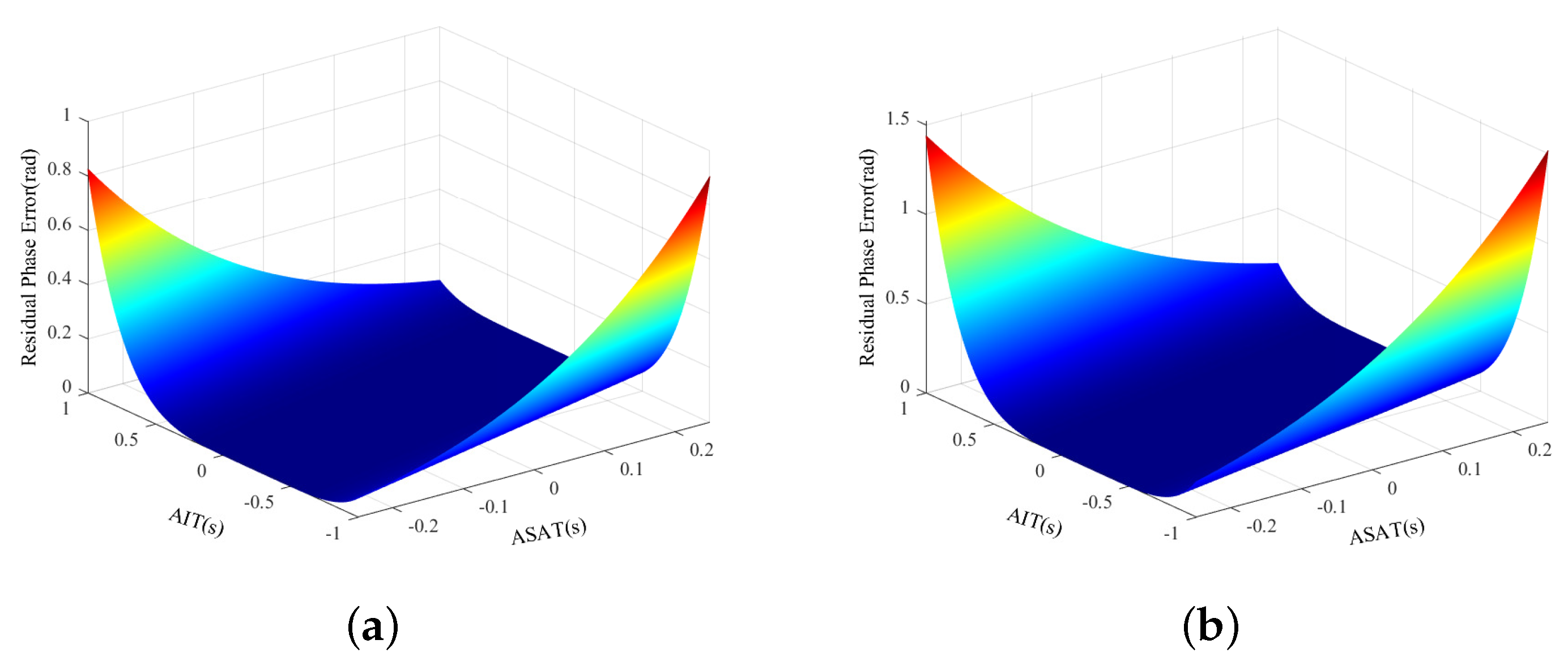

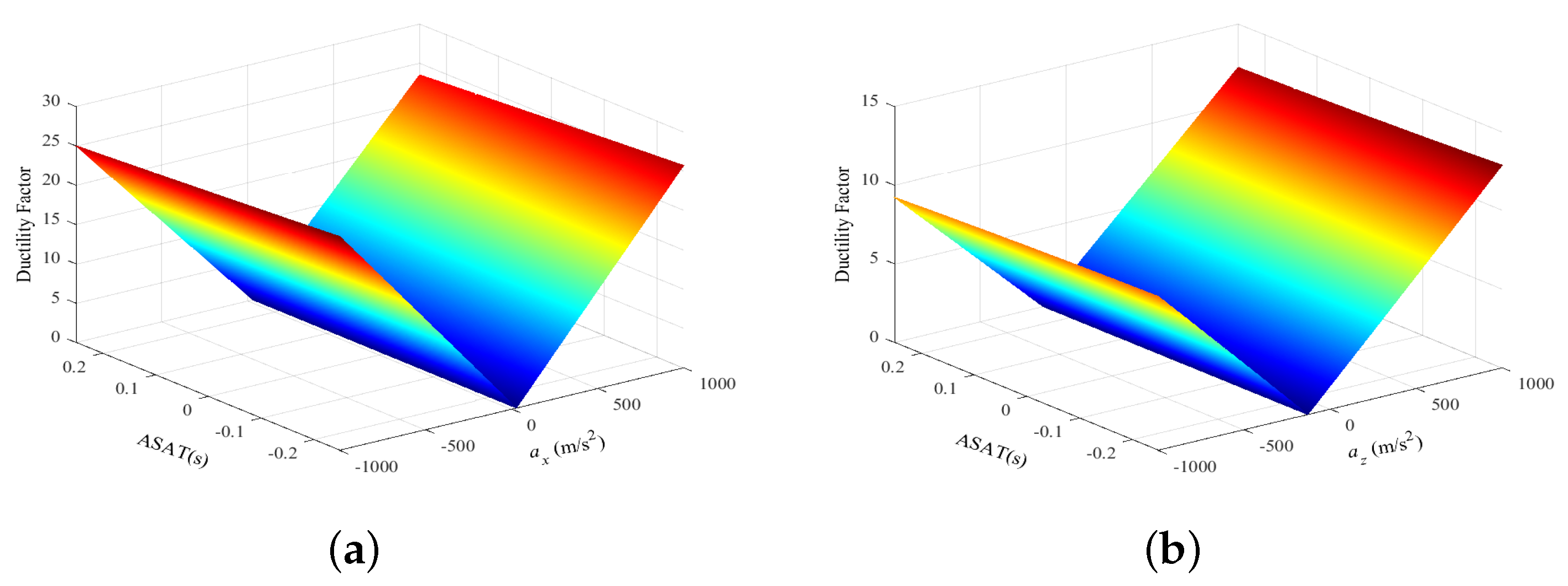
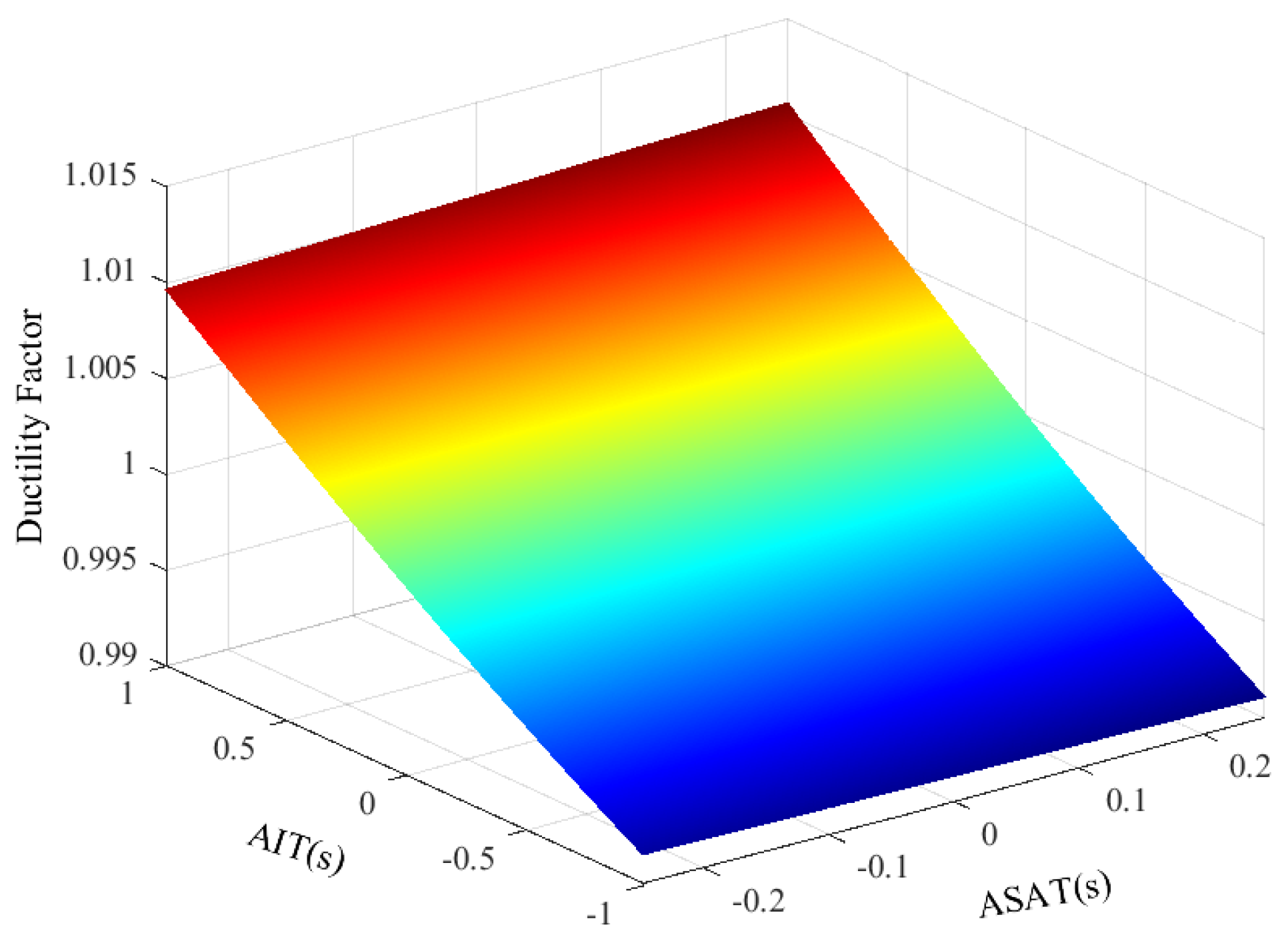
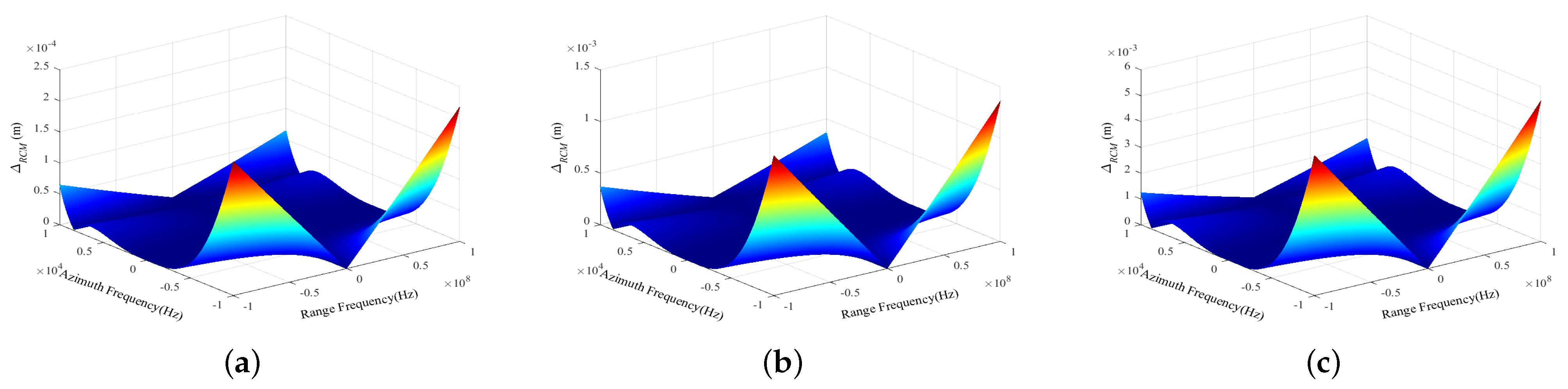

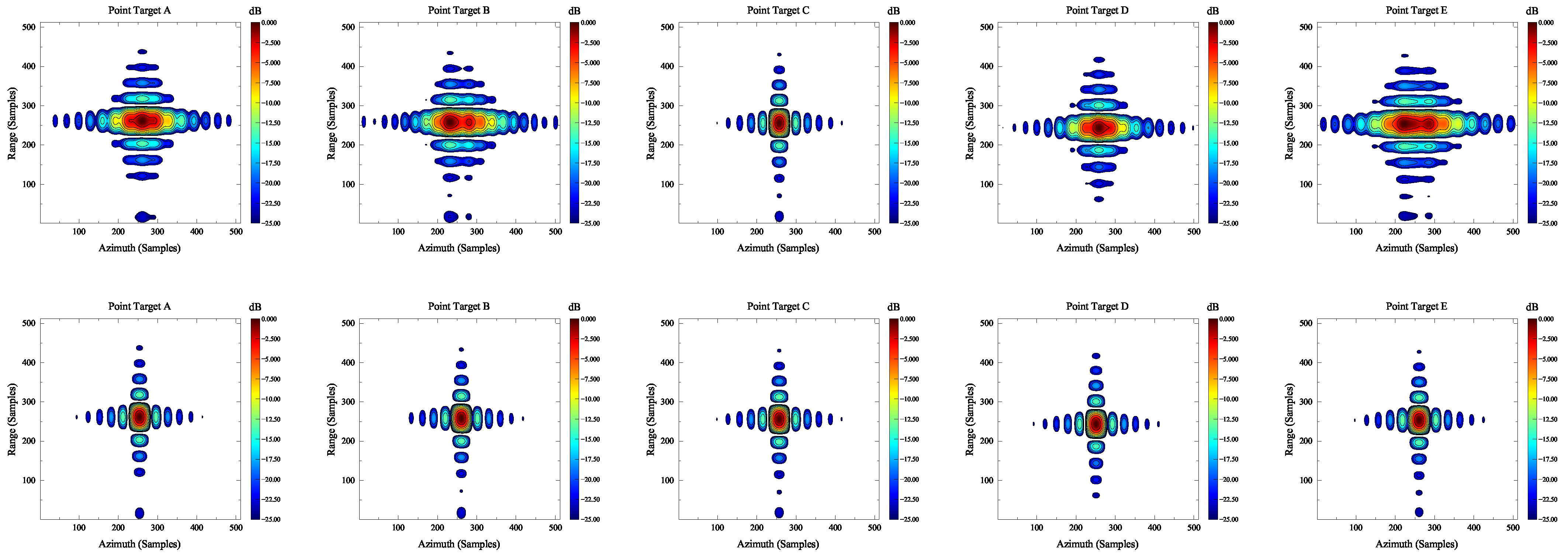
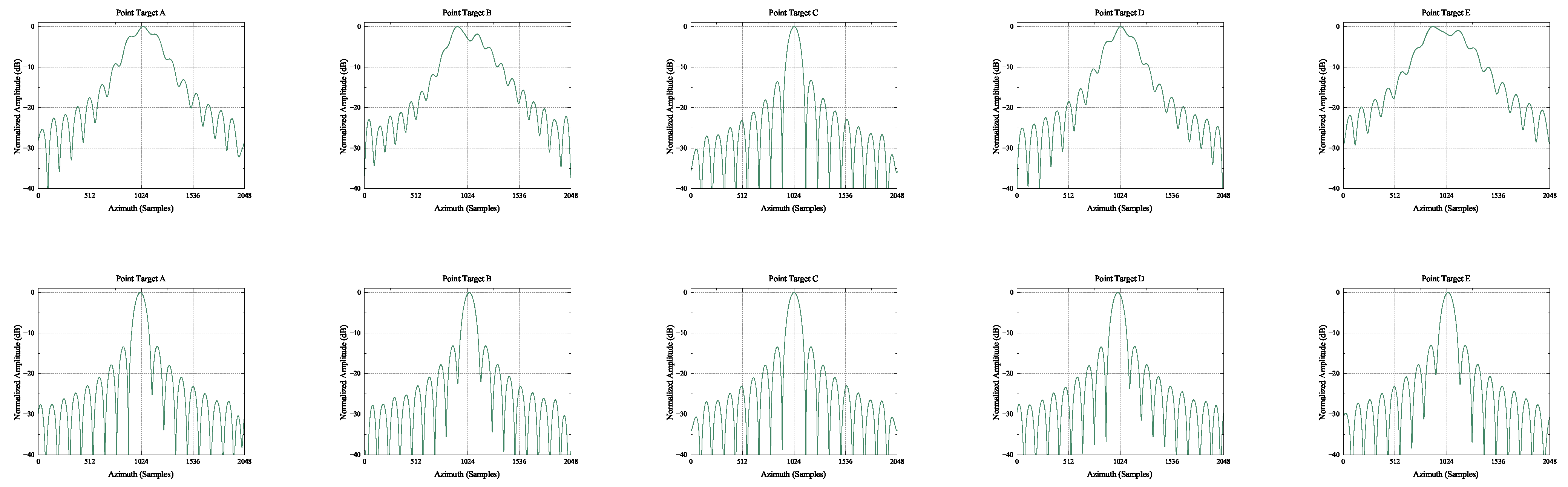
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Carrier Frequency | 16 GHz | Sampling Frequency | 200 MHz |
| PRF | 20 KHz | Geometric Squint Angle | |
| Range Bandwidth | 160 MHz | Beam Width | |
| Velocity | (2000, 0, −550) m/s | Acceleration | (−18, 0.01, −25) m/s2 |
| Reference Slant Range | 45 km | Height | 15 km |
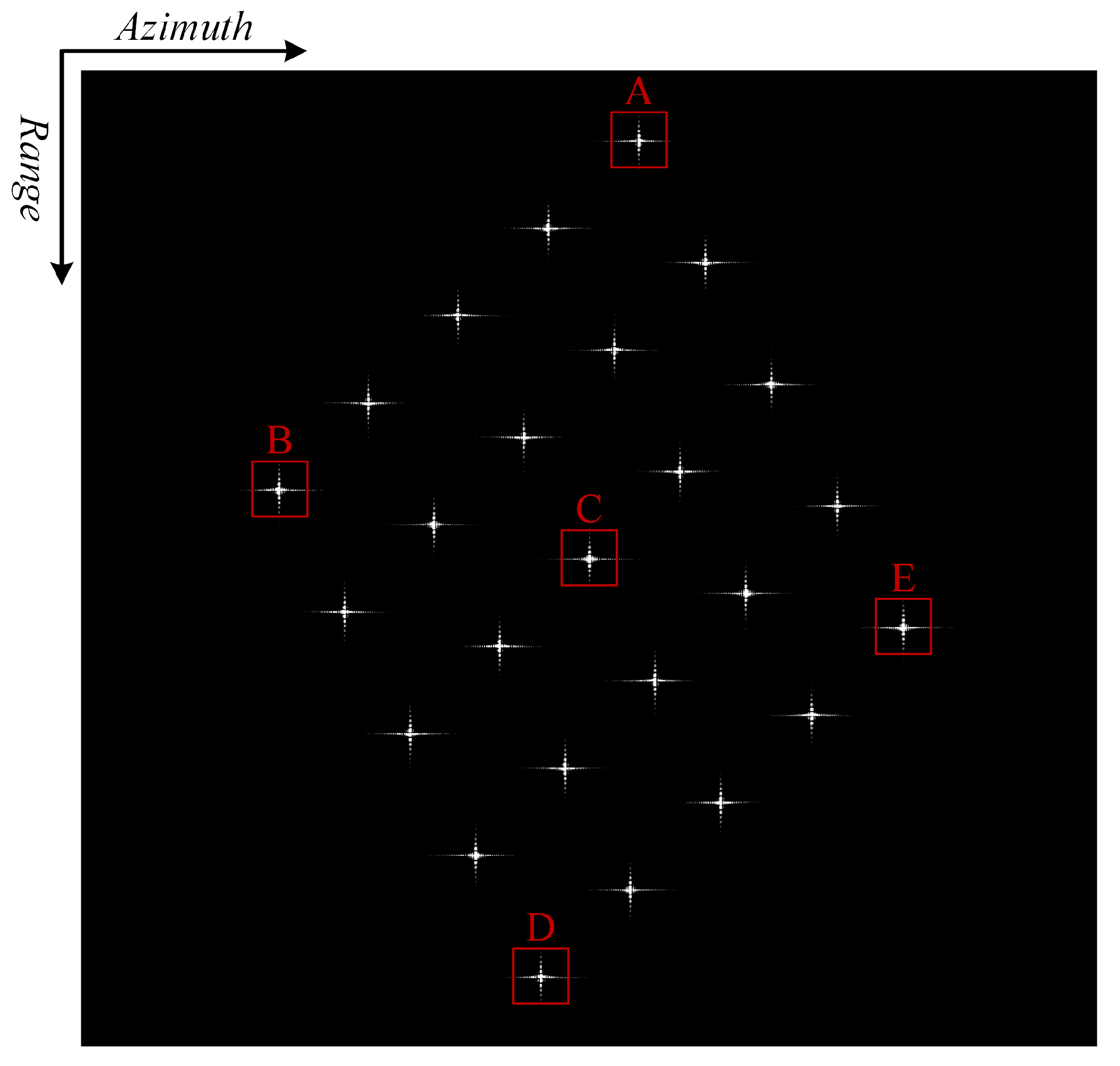
| Performance Metrics | Point Target | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| Azimuth Resolution/m | 3.09 | 3.04 | 3.06 | 3.06 | 3.17 |
| PSLR/dB | −13.27 | −13.13 | −13.39 | −13.26 | −13.03 |
| ISLR/dB | −10.28 | −10.07 | −10.39 | −10.25 | −10.02 |
| Performance Metrics | Point Target | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| Azimuth Resolution/m | / | / | 3.06 | / | / |
| PSLR/dB | −1.89 | −1.85 | −13.23 | −2.47 | −0.96 |
| ISLR/dB | 0.09 | −0.28 | −10.38 | −1.22 | −0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, K.; Huang, Y.; Chen, Z.; Fu, D.; Li, W.; Tian, X.; Hong, W. A Modified Frequency Nonlinear Chirp Scaling Algorithm for High-Speed High-Squint Synthetic Aperture Radar with Curved Trajectory. Remote Sens. 2024, 16, 1588. https://doi.org/10.3390/rs16091588
Deng K, Huang Y, Chen Z, Fu D, Li W, Tian X, Hong W. A Modified Frequency Nonlinear Chirp Scaling Algorithm for High-Speed High-Squint Synthetic Aperture Radar with Curved Trajectory. Remote Sensing. 2024; 16(9):1588. https://doi.org/10.3390/rs16091588
Chicago/Turabian StyleDeng, Kun, Yan Huang, Zhanye Chen, Dongning Fu, Weidong Li, Xinran Tian, and Wei Hong. 2024. "A Modified Frequency Nonlinear Chirp Scaling Algorithm for High-Speed High-Squint Synthetic Aperture Radar with Curved Trajectory" Remote Sensing 16, no. 9: 1588. https://doi.org/10.3390/rs16091588
APA StyleDeng, K., Huang, Y., Chen, Z., Fu, D., Li, W., Tian, X., & Hong, W. (2024). A Modified Frequency Nonlinear Chirp Scaling Algorithm for High-Speed High-Squint Synthetic Aperture Radar with Curved Trajectory. Remote Sensing, 16(9), 1588. https://doi.org/10.3390/rs16091588