Correcting the Location Error of Persistent Scatterers in an Urban Area Based on Adaptive Building Contours Matching: A Case Study of Changsha

Abstract

Persistent Scatterer InSAR (PS-InSAR) technology enables the monitoring of displacement in millimeters. However, without the use of external parameter correction, radar scatterers exhibit poor geopositioning precision in meters, limiting the correlation between observed deformation and the actual structure. The integration of PS-InSAR datasets and building databases is often overlooked in deformation research. This paper presents a novel strategy for matching between PS points and building contours based on spatial distribution characteristics. A convex hull is employed to simplify the building outline. Considering the influence of building height and incident angle on geometric distortion, an adaptive buffer zone is established. The PS points on a building are further identified through the nearest neighbor method. In this study, both ascending and descending TerraSAR-X orbit datasets acquired between 2016 and 2019 were utilized for PS-InSAR monitoring. The efficacy of the proposed method was evaluated by comparing the PS-InSAR results obtained from different orbits. Through a process of comparison and verification, it was demonstrated that the matching effect between PS points and building contours was significantly enhanced, resulting in an increase of 29.2% in the number of matching PS points. The results indicate that this novel strategy can be employed to associate PS points with building outlines without the need for complex calculations, thereby providing a robust foundation for subsequent building risk assessment.

1. Introduction

With the continuous development of Chinese cities, the construction of high-rise buildings is increasing while some buildings are aging [1,2]. Frequent construction changes the urban geological environment and seriously threatens the structural stability of buildings [3,4]. Interferometry synthetic aperture radar (InSAR) [5,6] has a large monitoring range, is all-weather, and has high precision; it is widely used in deformation monitoring [7,8,9]. Time-series InSAR technology represented by Persistent Scatterer InSAR (PS-InSAR) [10,11] can monitor the line-of-sight displacement of a radar with millimeter precision, which is especially suitable for the fine monitoring of urban structural health [12,13,14,15]. However, due to radar side-view imaging, the projection of urban surface objects, including buildings, roads, and bridges, will be geometrically distorted; thus, the position of the acquired PS points will also be biased relative to the actual surface objects. At the same time, without the use of external parameter correction, such as atmospheric delay correction, the geographical positioning accuracy of PS points is usually within the decimeter to meter level [16]. This level affects the accurate association of PS points with actual objects, meaning that the PS points between buildings and roads and between adjacent buildings are difficult to distinguish. The PS points representing features cannot be obtained comprehensively or correctly, which will cause incomplete deformation or errors, leading to unreliable deformation monitoring results and interpretation. Therefore, the accurate correlation between PS points and real targets is a key issue in detailed urban infrastructure health monitoring and risk assessment.

In recent years, many researchers have studied the precision of the PS geopositioning of high-resolution SAR data. This research can be roughly divided into the following categories. The first method uses high signal reflection intensity of corner reflectors (CRs) to improve the absolute precision. The authors of reference [16] interpreted the position of a PS point by establishing a 3D error ellipsoid to verify that the absolute positioning accuracy of the TerraSAR satellite in the geographical coordinate system is meter-level accurate by using corner reflectors. Subsequent studies have shown that corner reflectors can improve the geopositioning accuracy of PS points in the X-band (TerraSAR-X), reaching centimeter-level accuracy in 2D and decimeter-level accuracy in 3D [17,18,19,20]. However, these examples have a common limitation, that is, corner reflectors need to be installed on-site and are required to operate throughout the entire monitoring time series, which is difficult to achieve in practice [17].

The second method uses three-dimensional geometric fusion to correct the position of PS points. In [21], a single building is taken as the research object, and multiple TerraSAR-X PS point cloud data of ascending and descending orbit are fused. By finding PS point pairs representing the same object in multiple point cloud lists, the least squares method is adopted to correct the position deviation between PS point pairs. However, this method needs the establishment of error equations for each PS point pair, which requires a large number of calculations when expanding the study area [22]. The authors of reference [23] propose a method that fuses SAR image geodesy and TomoSAR. The opportunistic point scatterers of all stacks are identified, and their absolute 3D positions are calculated using stereo SAR. These scatterers serve as the reference point for TomoSAR estimation, resulting in an absolute positioning accuracy of approximately 20 cm, as confirmed via LiDAR data validation. The methods involved in three-dimensional geometric fusion typically require identifying the same scatterers in different orbits’ data [24,25]. Consequently, they heavily rely on such opportunistic targets, which can be challenging to achieve.

The third method is based on the use of external LiDAR data to assist PS point position correction. Airborne LiDAR technology can directly obtain 3D spatial information relating to ground objects, which is less affected by climate, high positioning accuracy, and short production cycles [26]. The authors of reference [27] propose the use of LiDAR data to fit PS points, and PS point position correction can be achieved through the intersection of error ellipses. Existing research indicates that LiDAR data can match PS points well and also serve as auxiliary data for radar scatterer classification [28,29,30]. However, due to the high cost of acquiring LiDAR data and limitations related to data sources, it is not suitable for widespread applications [26].

In addition to improving the absolute positioning accuracy of PS points, some scholars have also conducted research focused on matching a PS-InSAR dataset and building databases. The authors of reference [31] proposed a method for assigning PSs to the bounding surfaces of a 3D city model. The 3D city model obtained via LiDAR is matched with the obtained PS point cloud using the iterative closest point (ICP) algorithm. The matching results have a better effect on the building facade, which can effectively associate PS points with the building structure. However, this method needs to obtain PS point clouds that have good density, are continuous, and have obvious shape characteristics, which is difficult for densely built and cluttered areas. To obtain these PS points, the threshold value is relaxed in the point selection process, affecting the precision of the deformation solution.

Two-dimensional building contour vector data are easier to obtain and more widely used than three-dimensional building facade models. In research aimed at assessing building risks, building vector data are often used to segment and screen monitoring points [32,33,34]. This process is often oversimplified during implementation. The authors of reference [34] proposed a method of extracting the corresponding building’s PS point set based on the elevation of the PS points inside the building contour. By determining the spatial relationships between PS points located in the interior, exterior, and edge of the building contour, PS points inside are selected, and the height difference between PS points inside and outside the building is screened to extract the corresponding PS points set of the building. The idea of this method is simple and effective, but only nine buildings were selected in this research, and the margin for human interference is large; therefore, the effect of expanding the research scope is unknown.

In our study, a strategy that includes the matching of radar scatterers with actual building outlines is proposed. The complex building outlines are simplified into a convex hull. Considering the influence of incidence angle and building height on radar geometric distortion, an adaptive buffer zone is established. Then the nearest neighbor method and the spatial distribution characteristics of PS points are used to improve the matching accuracy.

This paper is structured as follows. Section 2 introduces the method of matching PS points with the building contour. In Section 3, the test area and datasets are specified. Section 4 addresses the results and analysis, followed by the discussion in Section 5. Section 6 presents the conclusions.

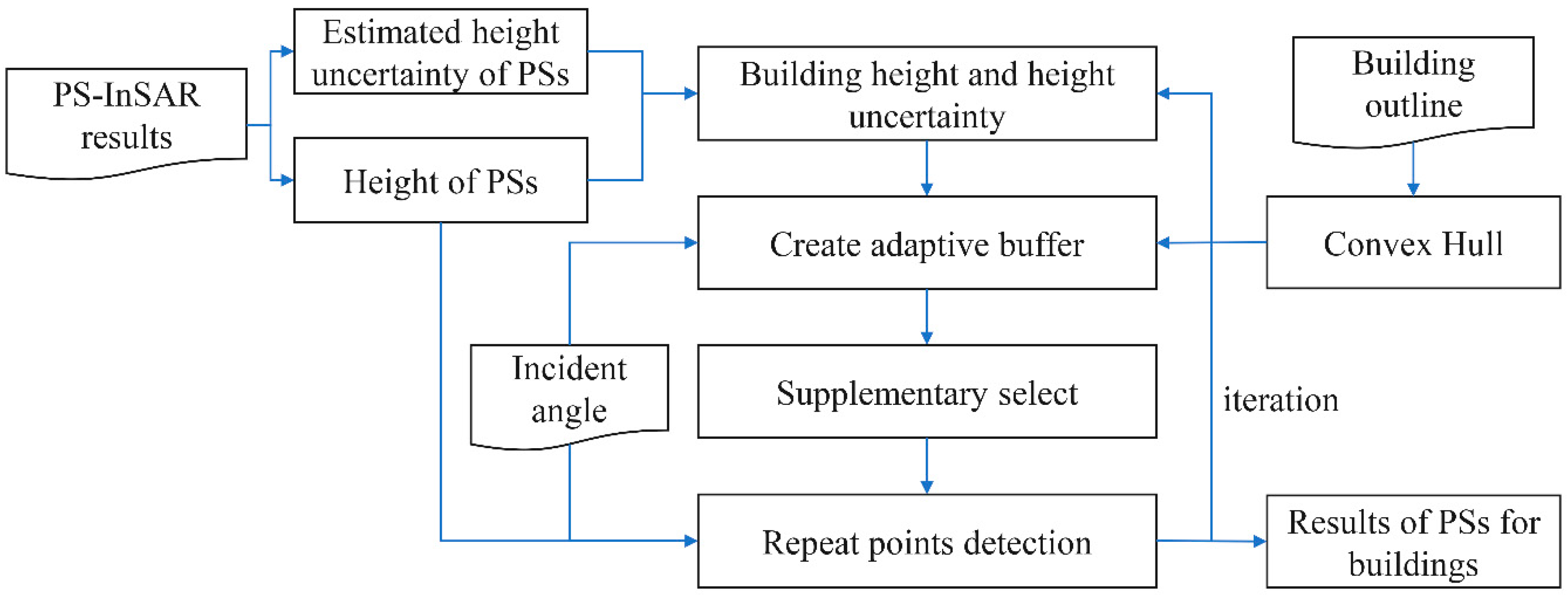
2. Methods Section

The proposed method is carried out based on building contour vector data [35,36] and PS-InSAR data processing results. Figure 1 presents a flow chart showing the strategy consisting of four major processing steps.

2.1. Rough Matching

Firstly, the PS points are roughly matched in terms of spatial position, which is mainly divided into two steps: generating the convex hull of building outlines and creating the adaptive buffer.

2.1.1. Generating the Convex Hull of Building Outlines

With the development of image processing algorithms, such as edge detection and image segmentation, and the improvement of artificial intelligence technology, building contours can be quickly and widely extracted from satellite images [37,38]. The building contours extracted from satellite images are usually pixel-level, and the non-orthophotograms are inherently deformed. There are rough edges and irregularities in building contour data (Figure 2a–c). When the outline of the building is a concave polygon or a ring, creating a buffer directly to the building will increase the computational burden and omit PS points matching. Therefore, it is necessary to use a convex hull to simplify the building outlines.

Given a set of points on a two-dimensional plane, a convex hull is a convex polygon formed by connecting the outermost points, which can contain all the points in the set, to simplify the original complex shapes for efficient calculation. The convex hull of a building contour point set can be obtained according to Melkman’s algorithm [39]. A convex hull can simplify the building contour while preserving the features of the original contour.

When the range of the convex hull far exceeds the original range of the building, the building can be split to reduce the overlapping of adjacent building convex hulls (Figure 3). In Figure 3a, the area of the irregular building contour in the middle is approximately 4295 m², while the generated convex hull area is 8205 m², which covers other surrounding buildings and affects the matching process. Through segmentation, this problem was effectively solved (Figure 3c).

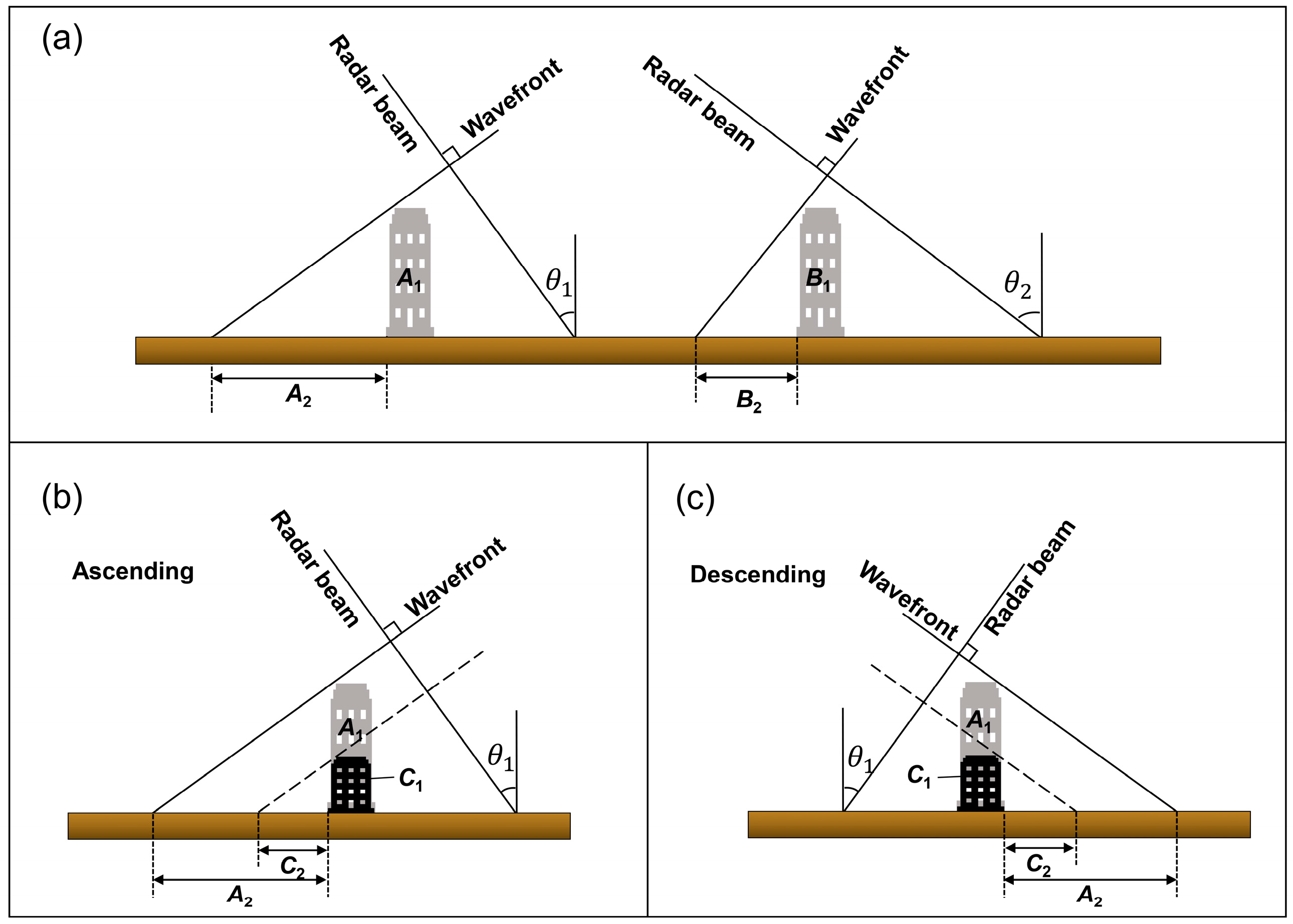
2.1.2. Creating the Adaptive Buffer

By creating a buffer for the convex hulls of building outlines, the PS point targets in the buffer can be screened out to complete the rough matching step. The method adopted in most studies is to establish a buffer for the building contour according to the SAR satellite spatial resolution, and then calculate the intersection with PS points [40,41]. This method will inevitably miss some PS points, which will subsequently lead to an inaccurate risk assessment.

Due to the working mode of radar side-view imaging, there will be geometric distortion in the building area, the degree of geometric distortion is related to the incidence angle and building height, and there will be different degrees of deviation between each building outline and the corresponding PS points. As shown in Figure 4a, a ground target of the same size has a larger range of distortion when the incidence angle is smaller. For buildings A₁ and B₁ that have the same size on the ground, the incidence angles are ${\theta }_1$ and ${\theta }_2$, respectively, and, obviously, ${\theta }_1<{\theta }_2$. After radar imaging, the ground range corresponds to A₂ and B₂, respectively, and in A₂ > B₂, there is the following relationship:

$$\begin{array}{l}{A}_2=A_1\cdot \cot {\theta }_1\\ B_2=B_1\cdot \cot {\theta }_2\end{array}$$

(1)

At the same time, in the small side view imaging range, the incidence angle is regarded as constant, and the building height is linear with the ground range (Figure 4b,c).

The precise heights of buildings cannot be directly obtained from remote sensing images. We can calculate the approximate heights of buildings based on the elevation estimation results of PS points. Firstly, calculate the elevation values of the PS points inside the building contour, and take the average of the maximum 10% of the data as the initial height $H_0$ of the building. Meanwhile, the uncertainty of the estimated height is used as the accuracy indicator for PS point height estimation. According to the law of error propagation, the accuracy calculation method for building height obtained from this is the average of the estimated height uncertainty of the PS points involved in the calculation.

Obviously, the conventional method of using the same buffer distance for all building outlines is not accurate. Taking this into account, an adaptive buffer zone is established in this paper. Assume that the spatial resolution of the radar satellite is $r$, the incidence angle at the center point is ${\theta }_0$, the incident angle of the $i$-th building is $\theta$, and the height uncertainty of the $i$-th building is ${\delta }_h$. Then, the buffer distance of the $i$-th building $D_i$ can be expressed as follows:

$$D_i=r+{\delta }_h\cdot \cot {\theta }_0+(\cot \theta -\cot {\theta }_0)$$

(2)

where ${\delta }_h\cdot \cot {\theta }_0$ reflects the uncertainty of building height in the horizontal position and $(\cot \theta -\cot {\theta }_0)$ represents the impact caused by changes in the incident angle. It can be considered that the above three parts are independent.

2.2. Supplementary Select and Repeat Point Detection

Through the processing of the above steps, the corresponding PS point target within a certain range of the building outline is initially matched, but there will inevitably be missing selection and repeated selection. For example, since the building outline data also have a certain deviation, there will be missing PS points outside the range of the buffer. When buildings are close to each other, buffer overlap occurs, and PS points match into multiple building lists at the same time. Therefore, it is necessary to further accurately match the PS points and the building contour.

2.2.1. Supplementary Selection

Every single building is taken as the research object, and the nearest neighbor method is used in supplementary selection (Figure 5). First, a point $p$ outside the buffer is taken, and the nearest neighbor search is carried out for this point. The search space is the list of PS points already matched by the current building. We obtain the minimum distance $D_{\min }$ and call the nearest point $q$. If $D_{\min }$ is less than the threshold $thd$ and the height difference between $p$ and $q$ is 5 m, point $p$ is considered to be the point on the building.

Obviously, PS points on buildings, especially the edges of buildings, have obvious line characteristics, and PS points rarely exist in isolation. Therefore, for urban areas, in the case of normal point density, the threshold $thd$ is related to the pixel size of the PS point, that is, to the spatial resolution of the SAR satellite.

In the above steps, the corresponding point list should be updated after each supplementary selection, and then the next point is calculated. In addition, the matching space of PS points should be narrowed to avoid carrying out the whole map, thus increasing unnecessary computation.

2.2.2. Repetitive Point Detection and Deleting

Rough matching and supplementary selection uses a larger buffer to match PS points than traditional methods, with the intention of minimizing incomplete deformation information caused by missing points. Therefore, matched PS points may exist in two or three building lists at the same time, and these repetitive points can be identified and reassigned through this step (Figure 6).

Considering the continuity of the elevation of PS points on the building and the influence of the incident angle, the repetitive points can be separated. On the one hand, the elevation of PS points on buildings of different heights is different. In general, the elevation of PS points on the building facade increases continuously from low to high, so there will be a jump in the elevation of PS points between two buildings. On the other hand, it can be seen from Section 2.1.2 that the deviation between PS points is directional, that is, it is related to the incidence angle. We can judge the separation of repetitive points according to this spatial feature.

After completing all of the matching steps mentioned above, the result after the first matching can be obtained. Calculate the height and height uncertainty of the building using the new matching PS point set, which is denoted as $H_i$ and ${\delta }_{h_i}$ ($i=1$), respectively. When $\left|H_i-H_{i-1}\right|$ is greater than the experience threshold of 5 m, iterate the matching process. For X-band data with a 3 m resolution, it can be considered that the elevation positioning accuracy of PS point is about 3 m. Since the height of the building in this paper is calculated according to the elevation estimation results of PS points, combined with the range of elevation uncertainty, an iterative height difference of 5 m is set here.

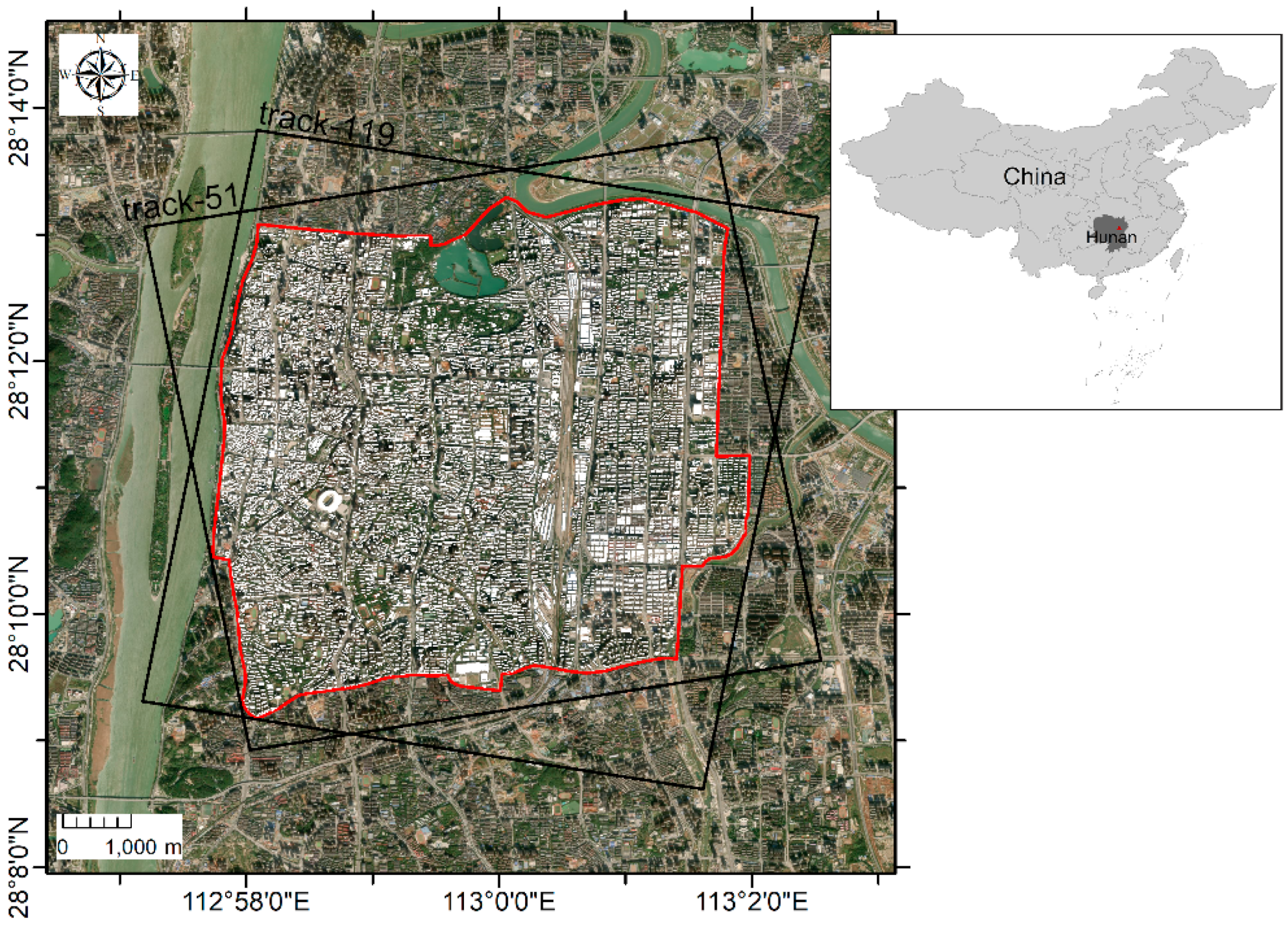
3. Study Area and Datasets

The study area selected in this article is located in the eastern part of the Xiangjiang River in Changsha City, Hunan Province, with an area of approximately 42.2 square kilometers (Figure 7). This area belongs to the earliest developed area in Changsha, with some buildings even dating back 50 years. The problem of building aging is prominent, with more new construction, dense housing, and frequent human activities.

Two sets of TerraSAR-X data were collected along the ascending (track-51, 37 scenarios) and descending (track-119, 38 scenarios) for PS-InSAR monitoring. The time range for the ascending data is 19 June 2016 to 24 June 2019, and for the descending data, it is 18 April 2016 to 2 September 2019. The cropped image size is 5000 × 4000 (range × azimuth), and the spatial coverage is indicated in black in Figure 7. The available multi-orbit datasets allow us to validate the self-consistency of the monitoring results by inter-comparison. We also obtained building contour vector data for the study area [35,36], which includes approximately 14,584 buildings, as shown in Figure 7.

4. Results

4.1. PS-InSAR Results

In this study, the block large-scale PS-InSAR algorithm proposed in reference [42] is employed for the processing of SAR data in order to overcome the atmospheric errors related to the large study area. The deformation rate maps generated from the ascending and descending data are between −10 mm/a and 8 mm/a, as shown in Figure 8. The deformation during the monitoring period is mainly settlement, related to the instability of railway tracks, engineering construction, and the instability of soft soil foundations. The deformation patterns do not significantly impact the content of this study and will not be further elaborated.

The accuracy of PS-InSAR deformation monitoring results directly affects the accuracy of PS point elevation estimation, which is crucial for accurate PS point matching. To quantitatively check the self-consistency of InSAR measurements, an inter-comparison of the deformation rates between the ascending and descending results was carried out. Due to the uncertainty in SAR geo-location, the PTs from different orbits were unlikely to be at the same locations. The resolution of the results is down-sampled with a resolution of 15 m × 15 m to reduce the effect of geo-location uncertainty. Finally, InSAR measurements from different orbits were compared (Figure 9a). The inter-comparison results between the ascending and descending InSAR-derived deformation rates showed that the correlation between the two InSAR measurements is 0.90, and the root mean square error (RMSE) of the difference between the ascending and descending orbits is 0.2 mm/a, implying that the InSAR measurements are highly self-consistent.

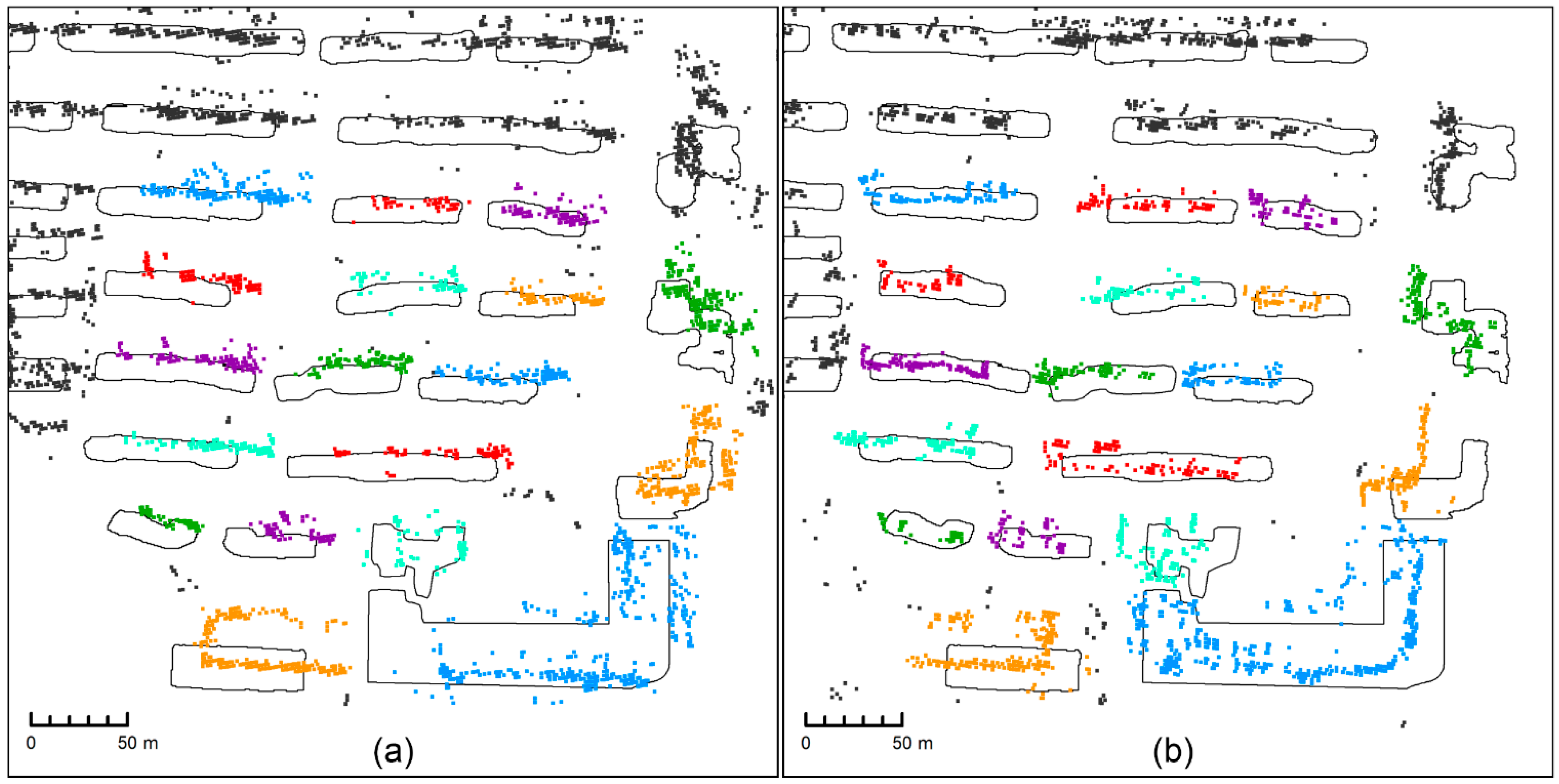
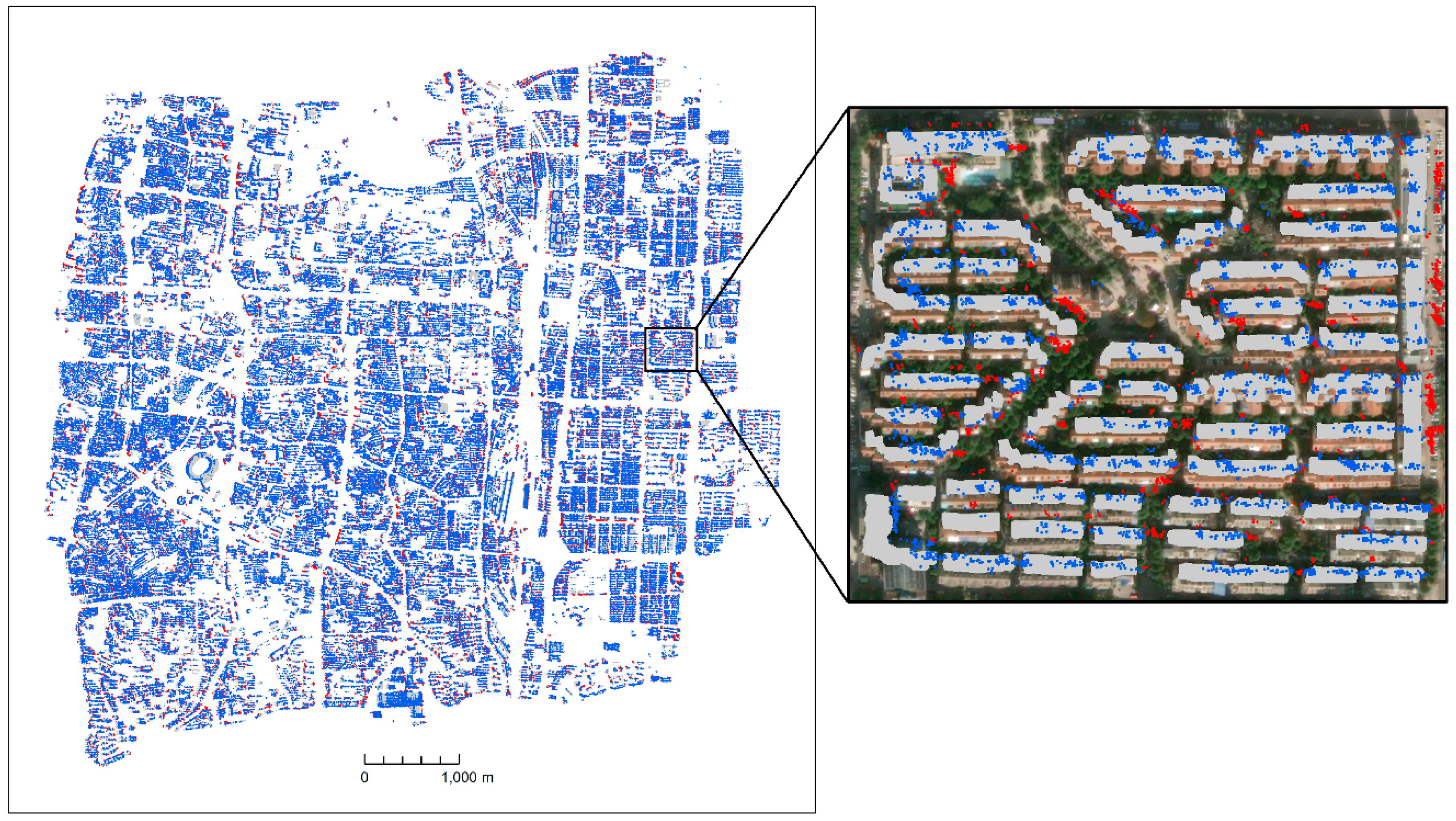
4.2. Matching Results

In our study, the spatial resolution of TerraSAR-X is 3.1 m, so $r$ is equal to 3.1. The center point incidence angle ${\theta }_0$ equals 37.28 degrees. The estimated height uncertainty of PS points is shown in Figure 9b, mainly distributed between 0.6 and 1.3. When the nearest neighbor method is used, the threshold $thd$ is set to 3 m.

Taking ascending orbit data as an example, Figure 10 shows part of the results of the adaptive buffer in the study area. The minimum buffer distance generated in the study area is 3.87 m, and the maximum buffer distance is 6.52 m. Buffers of different sizes are established for buildings of different heights. In general, the higher the actual height and the smaller the cross-sectional area of a building, the greater the deviation of the PS point, and the corresponding distance of the generated adaptive buffer zone is also larger. Compared with setting the buffer distance to the spatial resolution of the SAR satellites, the adaptive buffer has a larger range. This allows for more PS points to be obtained in the initial matching process, reducing the amount of computation needed in the supplementary selection process. Additionally, the search space for the nearest-neighbor process is enlarged, improving the matching accuracy and increasing the number of matched points.

The deformation monitoring results of the ascending and descending tracks are used to accurately match the PS points to the building contour to verify the effectiveness of the method proposed in this paper. Figure 11a,b show the partial results after matching the PS points of the ascending and descending orbits, respectively. It can be seen that the deviation direction of PS points on different orbits is different. Nevertheless, using the method proposed in this study, it is possible to match the PS point results of both the ascending and descending tracks based on the same building contour data. The results show that the matching effect is good. PS points with clustering and spatial distribution characteristics are correctly assigned to buildings. However, this can only enable a qualitative analysis of the matching effect through manual visual inspection, and quantitative evaluation cannot be conducted due to the lack of true values.

The ultimate purpose of this paper is to enhance the building risk assessments. When studying building risk assessments using PS-InSAR technology, it is crucial to precisely extract deformation information from the PS points that represent the building. This information is then transformed into the building’s assessment index. However, previous studies have primarily focused on risk assessment methods and overlooked the process of extracting PS points from buildings, i.e., the method of intersecting with building contours or intersecting with building contour buffer zones [32,43]. Meanwhile, research on the absolute localization of PS points is complex in terms of principles and algorithms. It is often treated as a separate research direction, which may hinder building risk assessments. This paper presents a strategy that contributes to building risk assessments and compares the results with those obtained using traditional intersection methods.

Figure 12 shows a comparison of the matching effect between the conventional approach and the new strategy. The traditional method used a fixed buffer distance of 3.1 m to screen out PS points located in the buffer, matching a total of 785,896 PS points. However, the new strategy matches 1,015,090 PS points, an increase of 29.2%. It is worth noting that this ratio is related to the size of the study area, the intensity of PS points, and other factors, which are not stable. It can be seen that the PS points added by the new strategy show aggregation and strong linear characteristics, meaning that it can be qualitatively determined that these PS points belong to buildings. Although the new strategy may over-match a few PS points, this over-match will not have a significant effect due to the clustering effect of the deformation features. Over-matched PS points include deformation information that does not belong to the building, and if this deformation has a large value and thus affects the risk rating of the building, it is considered overestimated. Conversely, poorly matched PS points and PS points with important deformation information are omitted, resulting in a lower risk rating for the building, which is an underestimate. From a risk perspective, overestimation can lead to overprotection and wasted resources, but underestimating safety risks can lead to incalculable losses of life and property damage. Therefore, underestimation is more serious than overestimation.

5. Discussion

In our study, we propose a strategy that uses building contour vector data to match PS point clouds. Compared with existing research methods, matching strategies aim to segment and screen PS point sets belonging to different buildings. (1) By using an external DEM with a resolution of 12.5 m to remove the terrain phase, the horizontal displacement of PS points caused by geocoding is minimized as much as possible. The accuracy of external DEM data has a direct impact on the accuracy of geocoding. The spatial resolution of DEMs is considerably lower than that of SAR satellites, which means that the use of DEMs with a higher spatial resolution can help to reduce the errors caused by geocoding. (2) Considering the difference in building height variance and establishing an adaptive buffer zone can compensate for the geographic positioning error of PS points. The PS points are offset from the building contour. The adaptive buffer reduces this offset by extending the building contour outwards to compensate for the geographic positioning errors. (3) Considering the continuity and spatial distribution characteristics of PS point elevation changes during radar side view imaging, as well as the influence of incident angle, increases the number and accuracy of PS point matching. The characteristics of the continuous change in the elevation of PS points of a single building enable the differentiation of PS points of buildings from those of roads and adjacent buildings. The PS points of buildings exhibit spatial distribution characteristics such as lines, surfaces, and aggregation. These characteristics provide a theoretical basis for accurate matching.

However, the proposed matching strategy still has limitations and needs to be improved in future research. Firstly, the source of the building contour data is constrained. At present, no large-scale orthophoto images are available for building contour data in China. The research is based on building contour data extracted from optical remote sensing images. The selected dataset takes into account the differences in optical imaging sensors, time, and environmental factors and controls the accuracy of building contour extraction to around 1 m. Nevertheless, this paper still achieved good matching results. We believe that with more accurate building contour data, the effect will be better.

Secondly, calculating building height needs to be improved. Ideally, the PS points on the roof of a building should have the same height and planar features. However, this is difficult to achieve in practice. Due to errors when estimating the height of the PS points and the structural influence of the roof of the building, it is not reasonable to use PS points with the greatest height to represent the height of the building. Consequently, the highest point of the building may lack a PS point, resulting in an inaccurate estimation of building height. Furthermore, the PS points utilized in the calculation of the building height may be incomplete until the PS points of the building are accurately matched. With this in mind, this paper uses an iterative approach to improve the accuracy of building height calculations.

Lastly, the verification method for matching results needs to be improved. In our study, a qualitative approach was used to evaluate the matching results, that is, using comparative verification and manual visual inspection methods. How to quantitatively evaluate the matching results will also be one of the key contents of subsequent research.

6. Conclusions

PS-InSAR technology has been widely used in urban fine deformation monitoring. However, the interpretation of deformation results is limited due to the geographical positioning accuracy of PS points. On the premise of not using complex means to calculate and correct the absolute position of PS points, this paper proposes a simple strategy to match the PS point target with the building contour, including the use of a convex hull to simplify the building contour, creating an adaptive buffer and, based on the spatial distribution characteristics of PS points using the nearest neighbor method, maximally recognize the PS points falling on buildings. Two sets of TerraSAR-X data for PS-InSAR monitoring in the old urban area of Changsha City were used. An inter-comparison of the InSAR measurements from different orbits showed that the correlation between these measurements is 0.90, and the RMSE of the difference between these measurements is 0.2 mm/a, implying the good self-consistency of the InSAR measurements. Qualitative validation of the matching results using different track data demonstrates that the new strategy can match ascending and descending PS points. Comparison with validation via traditional methods reveals that the number of matching points available in the new strategy increases by 29.2%. This paper provides a solid foundation for building risk assessments and improves the reliability of risk assessments. However, as pointed out in the discussion, building height errors and rough building contour data can affect the accuracy of the matching results. Furthermore, a quantitative validation of the results cannot be achieved due to the lack of real values. These limitations could serve as potential topics for future research and exploration.