Aboveground Biomass Inversion Based on Object-Oriented Classification and Pearson–mRMR–Machine Learning Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Data Acquisition and Pre-Processing
2.2.1. Sampling for Field Survey
2.2.2. Remote Sensing Image Data
2.2.3. DEM Data
2.2.4. Calculation of Feature Variables
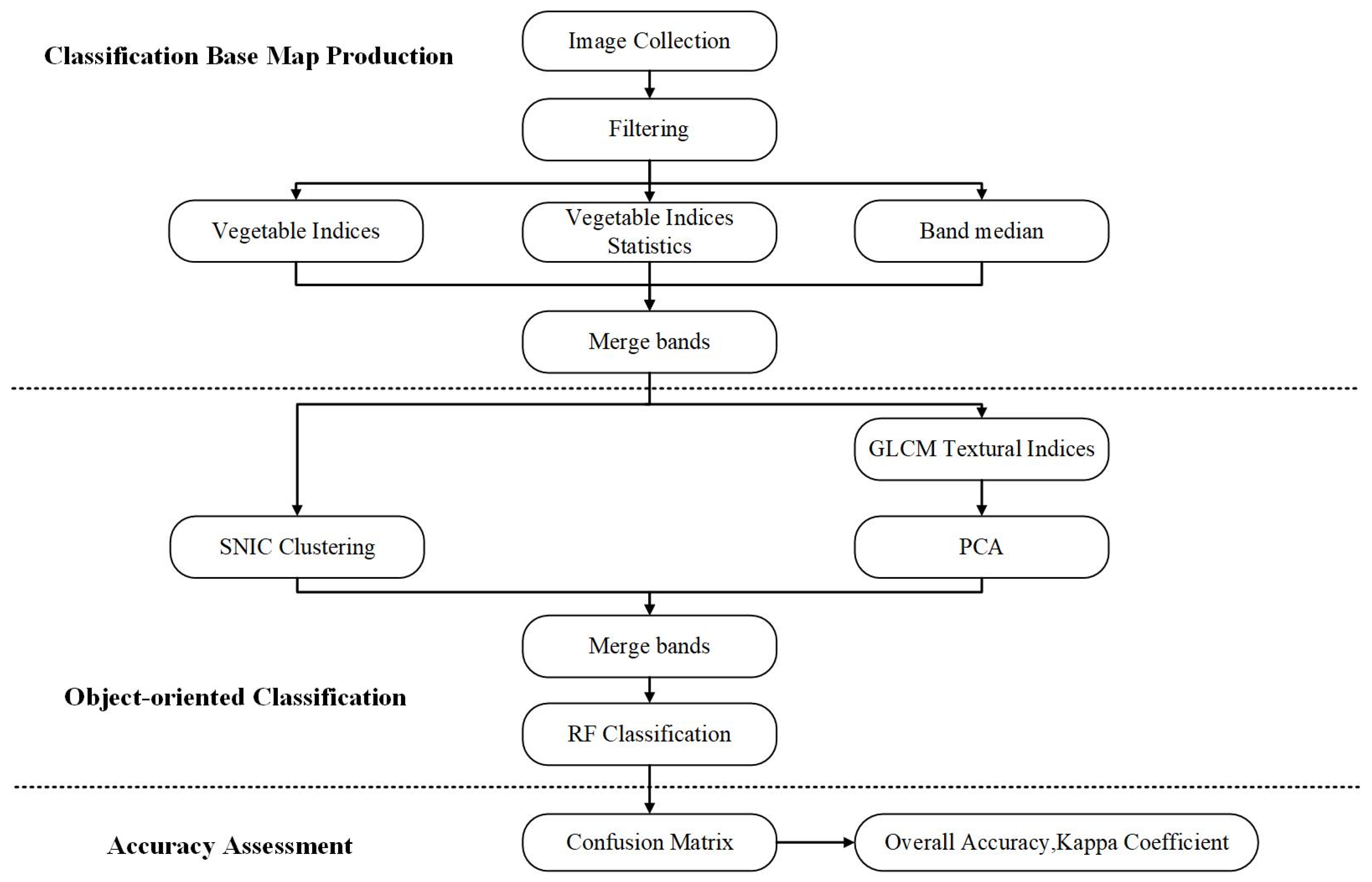
2.3. Object-Oriented Supervised Classification Algorithm
2.4. AGB Inversion Techniques
2.4.1. Machine Learning Algorithm Models
- (1)
- SV-R. The support vector regression (SV-R) model is a machine learning model for regression prediction of data, which is based on the principle of using a kernel function to map the input data into a high dimensional space, and to find a hyperplane in the high dimensional space that is closest to the sample data, in order to minimize the error between predicted and true values, and then to achieve high precision regression prediction [22].Compared with the ordinary linear model, it can better deal with nonlinear relationships and has a strong generalization ability to high dimensional data.
- (2)
- RF-R. The random forest regression (RF-R) algorithm is an integrated learning algorithm based on decision tree regression, which improves the performance and generalization ability of the model by integrating the prediction results from multiple decision trees [23]. Self-sampling and random feature selection are performed on the training sample data to generate multiple decision trees, and the final regression results are obtained by taking a weighted average of the prediction results of multiple decision trees.
- (3)
- XGBoost-R. The extreme gradient boosting regression (XGBoost-R) algorithm is a machine learning algorithm based on gradient-boost decision tree (GBDT); XGBoost is similar to GBDT and belongs to the gradient-boosting algorithm, which iteratively trains the decision tree to improve the accuracy of prediction results. However, unlike GBDT, XGBoost uses a second-order Taylor expansion to optimize the loss function, and a regularization term is added to the objective function to control the complexity of the model. The XGBoost model is the result of the integration of multiple weak learners, each of which fits the residuals of the previous one to improve the model accuracy through multiple rounds of iterations [24].
- (4)
- KNN-R. The core of the K-Nearest Neighbor Regression (KNN-R) algorithm is to achieve regression prediction by measuring the distance between sample data. Based on the calculated distance, the k feature data closest to the new sample data are selected, and the selected k feature data take the weighted average as the prediction data [25].
- (5)
- LWL-R. The Locally Weighted Linear Regression (LWL-R) algorithm is based on the introduction of a kernel function, which assigns a higher weight to the training data that are closest to the predicted data by calculating the distance between the training data and the target data [26]. The weights need to be recalculated for calculating each training data, and a weighted least squares model combined with a weight matrix is used to fit a local linear model to the predicted data.
- (6)
- Ridge-R. The Ridge Regression (Ridge-R) model is an improved linear regression model, which introduces an L2 van regularization term in the cost function to prevent overfitting as well as to improve the generalization of the model as compared to ordinary linear regression models [27]. The Ridge-R algorithm works better when the degree of feature covariance is high.
- (7)
- PLS-R. The Partial Least Squares Regression (PLS-R) model is suitable for scenarios where there are multiple correlations between variables and less modelling data; unlike a traditional regression model, which directly fits the training data to the predicted data, the PLS-R model reduces the dimensionality of the data by searching for the least squares variables to build the regression model [28].
- (8)
- Poly-R. The Polynomial Regression (Poly-R) modelling idea is more similar to ordinary linear regression; both directly use training data to fit predicted data. However, the Poly-R model also introduces higher powers of the training features, which makes the data dimensionality increase and builds a model that can better fit the nonlinear data [29].
- (9)
- Enet-R. The Elastic-net Regression (Enet-R) algorithm incorporates Lasso regression and Ridge-R regularization methods. L1 regularization and L2 regularization are introduced to control model complexity, handle covariance features, and find a balance between feature selection and model stability [30].
2.4.2. Feature Selection Algorithm
- (1)
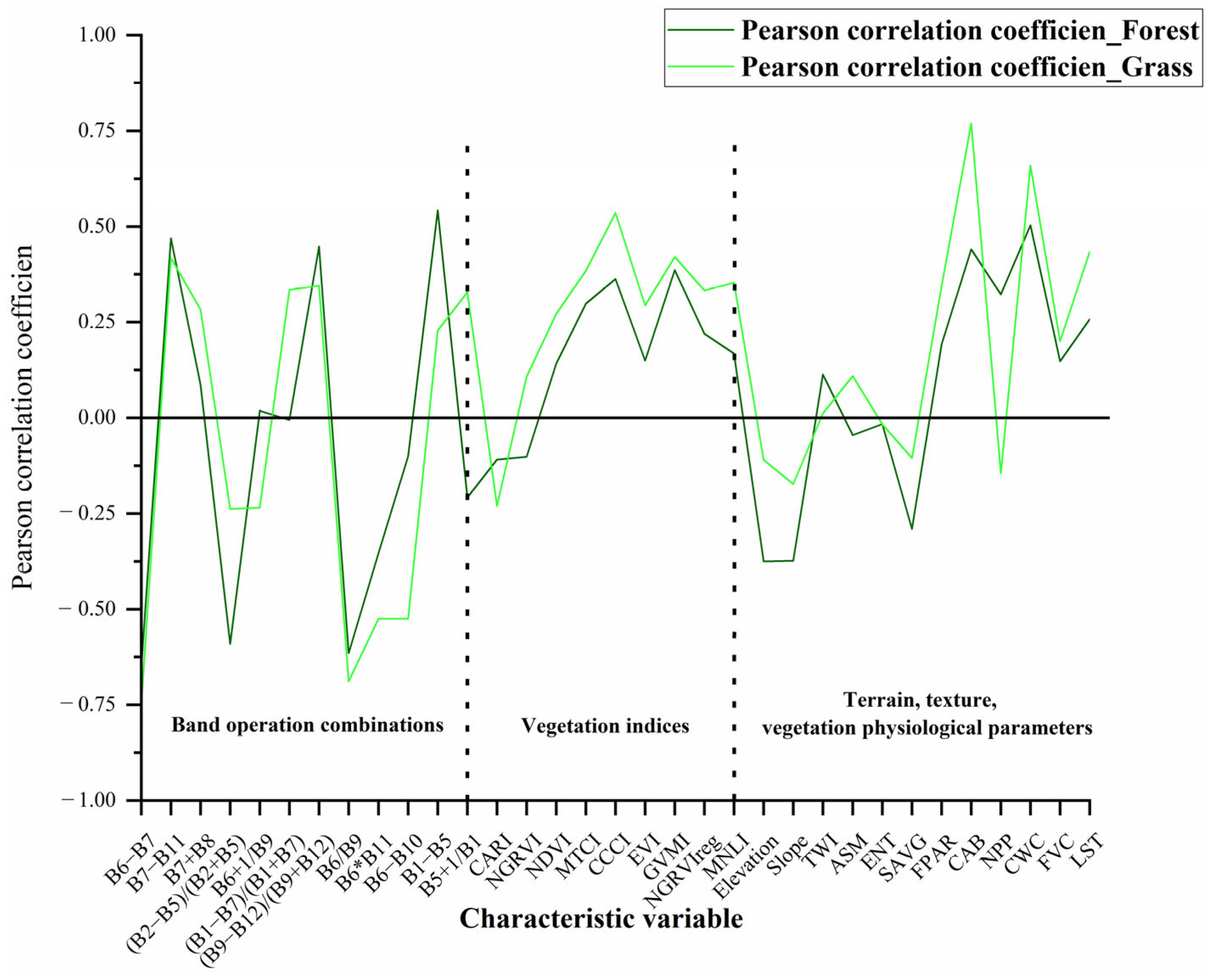
- Pearson correlation coefficient (r). The Pearson correlation coefficient can be used to assess the correlation between each feature variable and the measured real measurements, calculated as follows:where Xi and Yi are the corresponding feature variables and real measurement data of the sampling points, and are the mean value of the feature variables and the mean value of the real measurements of the sampling points, and the correlation coefficients take the values between −1 and 1; a larger absolute value represents a stronger correlation between the two variables [31].
- (2)
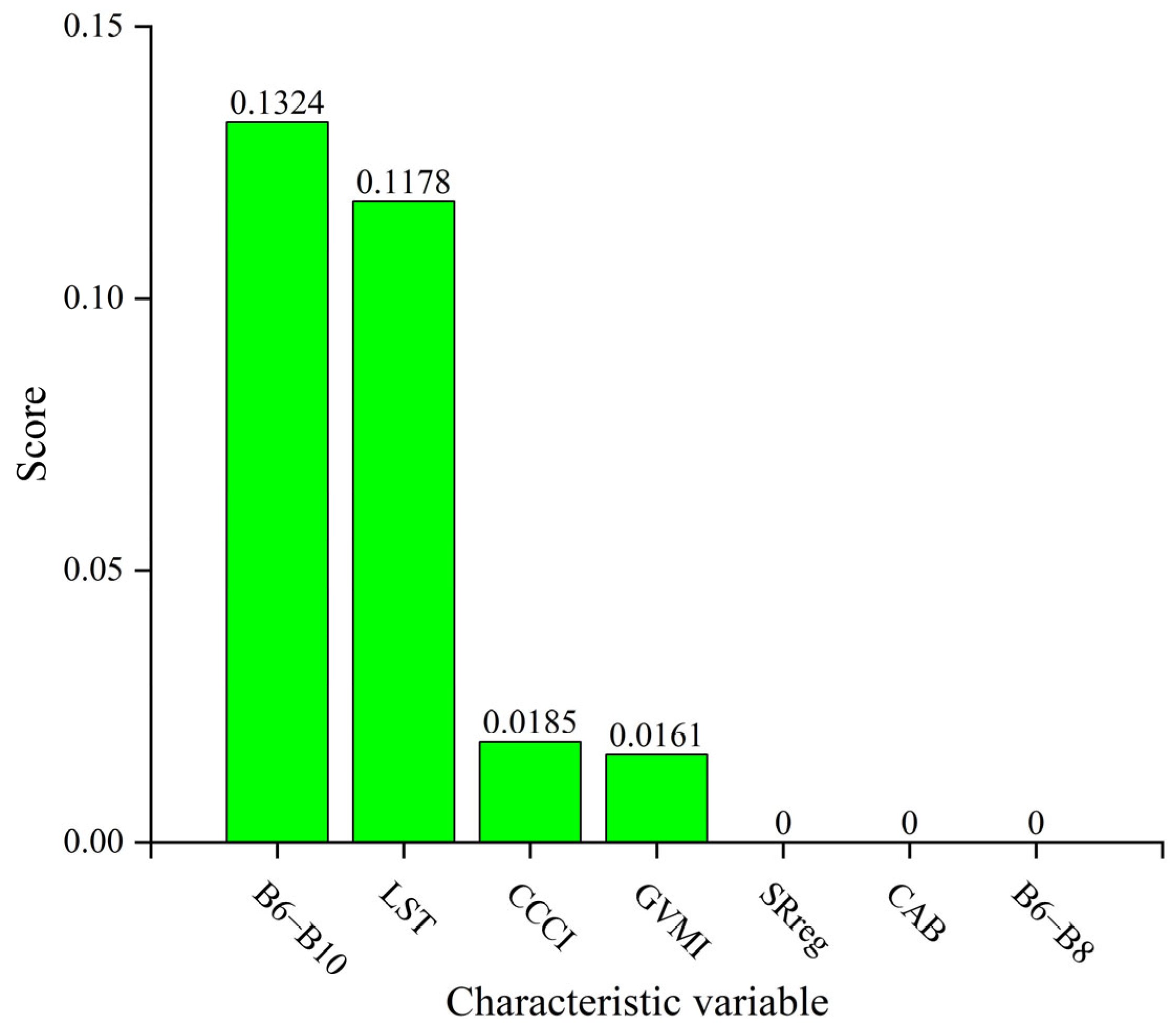
- mRMR feature selection method. The mRMR algorithm’s core is to increase the correlation between feature variables and targets while reducing the redundancy between feature variables [32]. Using mutual information as a measure of correlation between feature variables, the mutual information between feature variables can be calculated using the following equation.where p(x,y) is the joint probability density between two variables, and p(x), p(y) are the marginal probabilities of two variables, respectively. According to Equation (2), the screening condition for the minimum redundant subset is as follows:where S is the feature subset, |S| is the number of features in the subset, and gi, gj are different feature variables. In order to maximize the correlation between the subset feature variables and the target, the feature subset needs to satisfy the following conditions:where h is the target feature. mRMR algorithm’s final criterion is a linear combination of maximizing relevance and minimizing redundancy, denoted as:where λ is a regulation parameter to balance the weight of correlation combined redundancy.
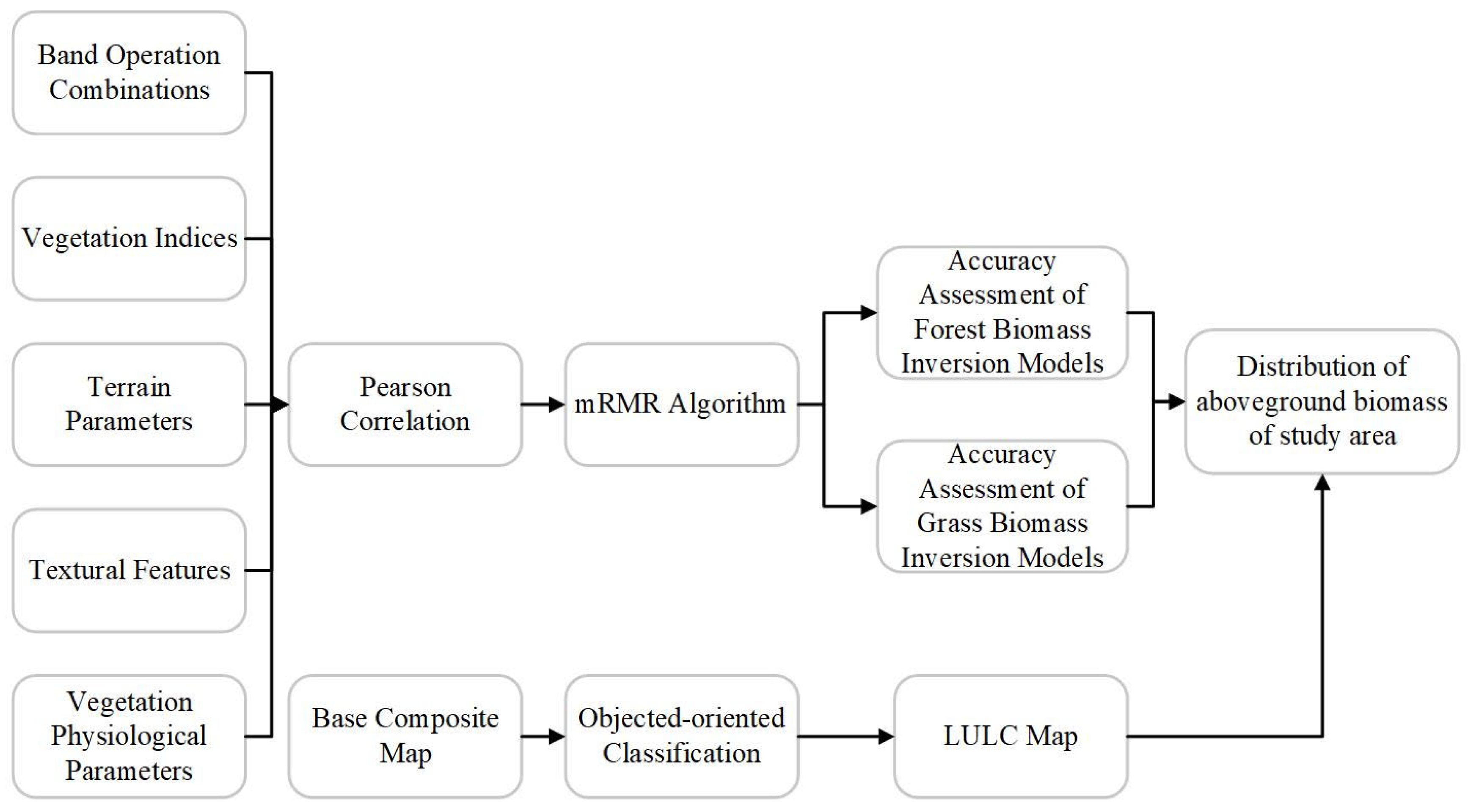
2.4.3. PmM Model for AGB Remote Sensing Inversion
- (1)
- Firstly, apply the object-oriented machine learning algorithm on GEE to classify the features in the study area, obtaining high accuracy distribution maps for forests and agri-grasses;
- (2)
- Then, calculate the combination data of the number of bands, vegetation indices, topographic data, texture characteristics, and physiological parameters of vegetation in the study area, and use the drying–weighing method to obtain the agri-grass AGB data, and use the heterogeneous growth equation to obtain the forest AGB data;
- (3)
- Preliminarily screen the feature variables with high correlation with measured AGB data of forest and agri-grass using Pearson correlation coefficient, and further screen the screened feature variables using the mRMR algorithm to obtain feature variables for final inverse modelling and application of forest and agri-grass, respectively;
- (4)
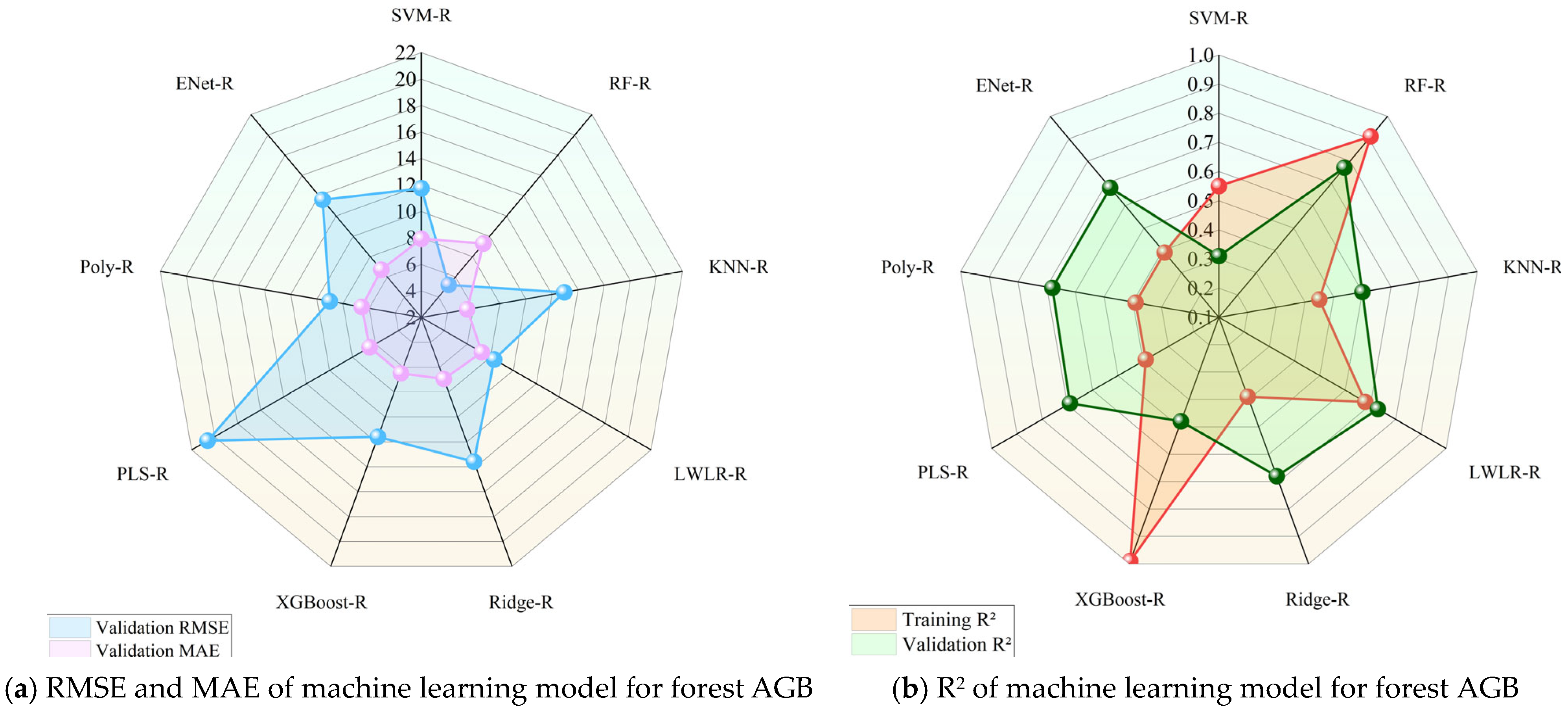
- Divide the sample dataset. Set the ratio of the training set and validation to 8:2 for both forest and agri-grass samples. Set the parameters according to the characteristics of each machine learning algorithm. Evaluate the models using the training set R2, validation set R2, and root mean square error RMSE.
- (5)
- Select the optimal machine learning model to map the distribution of forest and agri-grass AGB in the study area.
2.4.4. AGB Inversion Model Accuracy Assessment Methods
- (1)
- Data input and model parameter adjustment
- (2)
- Evaluation of model accuracy
3. Results
3.1. The Measured AGB of Different Vegetation Cover Types
3.2. Feature Classification Results and Accuracy Evaluation
3.3. Feature Correlation Analysis and Feature Selection Results
3.4. Modelling Results
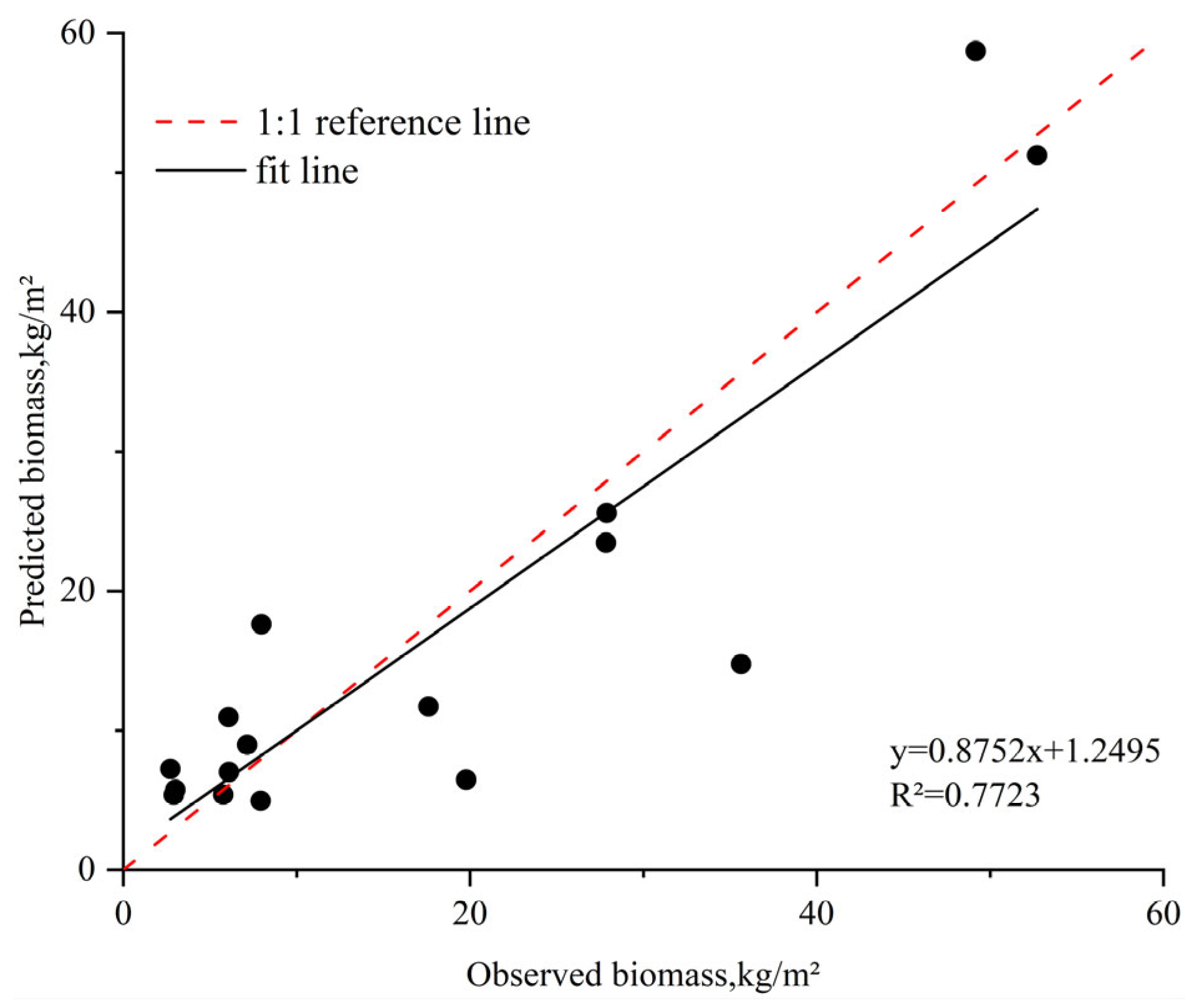
3.4.1. Forest AGB Inversion Model and Validation
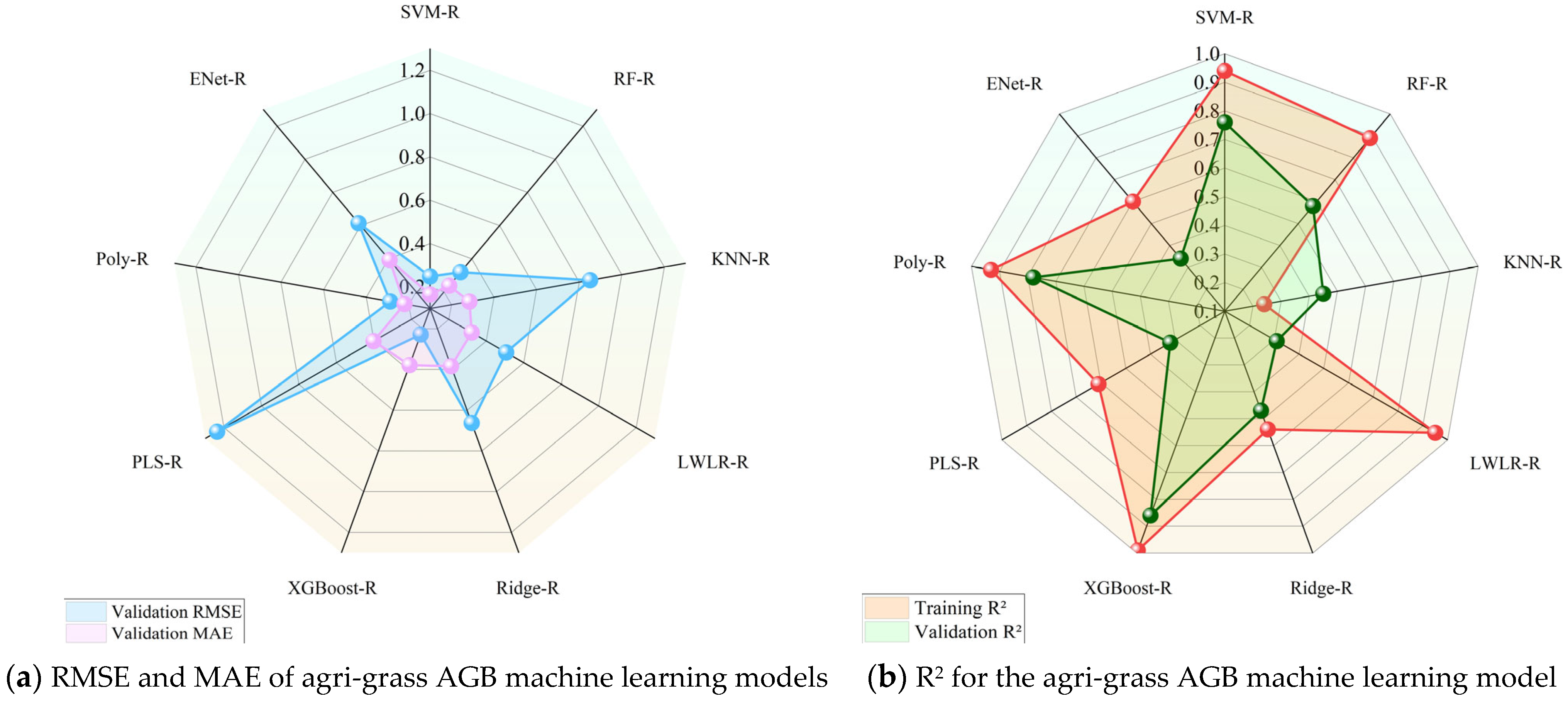
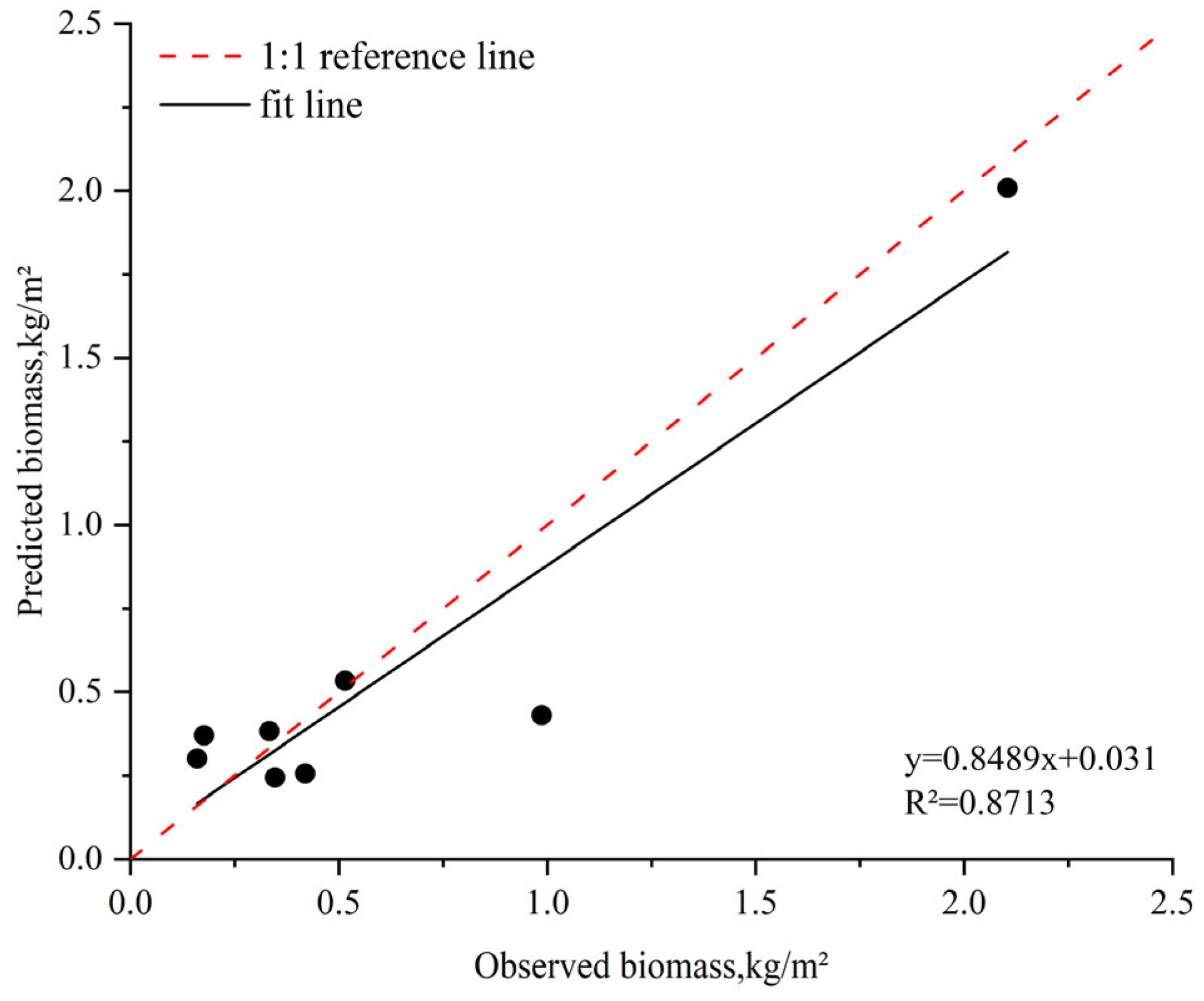
3.4.2. AGB Inversion Model and Validation on Agri-Grass Land
3.5. AGB Distribution in the Study Area
4. Discussion
5. Conclusions
- (1)
- The overall classification accuracy and Kappa coefficient of the object-oriented feature classification model are improved by 7% and 9%, respectively, compared with the classification model based on image elements; the object-oriented feature classification model is able to better distinguish between vegetation and non-vegetation as well as the boundaries between different types of vegetation.
- (2)
- For forest AGB inversion, the RF-R model is more accurate than other machine learning models, with an R2 of 0.76 and an RMSE of 5.21 kg/m2. For agri-grass AGB inversion, the XGBoost-R model achieved a higher accuracy with an R2 of 0.86 and RMSE of 0.23 kg/m2. Therefore, RF-R and XGBoost-R models were used to estimate forest and agri-grass AGB in the study area, respectively.
- (3)
- For forest AGB, the multi-band operation parameters B6 − B7, B1 − B5, B5 + 1/B1, the CCCI, and the topographic parameters elevation and slope were more highly correlated with the forest AGB. For agri-grass AGB, the multi-band operation parameters B6 − B10, the CCCI and GVMI, and vegetation physiological parameter LST were more correlated with grassland AGB.
- (4)
- The average AGB value was 4.60 kg/m2 for forests and 0.71 kg/m2 for agricultural grasslands, similar to the results of other studies. The high AGB values in the study area are mainly distributed along the water system, roads, and mountains, and the above areas are mostly distributed with tall perennial trees; lower AGB values are observed in farmlands surrounding the town, primarily consisting of herbaceous plants and crops.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blanco, E.; Pedersen Zari, M.; Raskin, K.; Clergeau, P. Urban Ecosystem-Level Biomimicry and Regenerative Design: Linking Ecosystem Functioning and Urban Built Environments. Sustainability 2021, 13, 404. [Google Scholar] [CrossRef]
- Li, L.; Zhou, X.; Chen, L.; Chen, L.; Zhang, Y.; Liu, Y. Estimating Urban Vegetation Biomass from Sentinel-2A Image Data. Forests 2020, 11, 125. [Google Scholar] [CrossRef]
- Yin, K.; Lu, D.; Tian, Y.; Zhao, Q.; Yuan, C. Evaluation of Carbon and Oxygen Balances in Urban Ecosystems Using Land Use/Land Cover and Statistical Data. Sustainability 2014, 7, 195–221. [Google Scholar] [CrossRef]
- Sullivan, P. Energetic Cities: Energy, Environment and Strategic Thinking. World Policy J. 2010, 27, 11–13. [Google Scholar] [CrossRef]
- Fang, J.; Wang, Z. Forest biomass estimation at regional and global levels, with special reference to China’s forest biomass. Ecol. Res. 2001, 16, 587–592. [Google Scholar] [CrossRef]
- Zhang, P.; Liang, Y.; Liu, B.; Ma, T.; Wu, M. Remote sensing estimation of forest aboveground biomass in Tibetan Plateau based on random forest model. Chin. J. Ecol. 2023, 42, 415–424. [Google Scholar] [CrossRef]
- Sun, S.; Wang, Y.; Song, Z.; Chen, C.; Zhang, Y.; Chen, X.; Chen, W.; Yuan, W.; Wu, X.; Ran, X.; et al. Modelling Aboveground Biomass Carbon Stock of the Bohai Rim Coastal Wetlands by Integrating Remote Sensing, Terrain, and Climate Data. Remote Sens. 2021, 13, 4321. [Google Scholar] [CrossRef]
- Li, X.; Jay, G.; Shi, Y. Aboveground Biomass Simulation and Its Temporal-Spatial Variation of Yongqu River Basin in the Alpine Meadow in the Yellow River Source Zone. Acta Agrestia Sin. 2023, 31, 1964–1976. [Google Scholar]
- Mo, Y.; Kearney, M.S.; Riter, J.C.A.; Zhao, F.; Tilley, D.R. Assessing biomass of diverse coastal marsh ecosystems using statistical and machine learning models. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 189–201. [Google Scholar] [CrossRef]
- Wang, P.; Tan, S.; Zhang, G.; Wang, S.; Wu, X. Remote Sensing Estimation of Forest Aboveground Biomass Based on Lasso-SVR. Forests 2022, 13, 1597. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, H.; Zhou, G.; Zhang, Q.; Tao, J.; Zhang, Y.; Lin, J. Aboveground mangrove biomass estimation in Bei-bu Gulf using machine learning and UAV remote sensing. Sci. Total Environ. 2021, 781, 146816. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Tassi, A.; Vizzari, M. Object-Oriented LULC Classification in Google Earth Engine Combining SNIC, GLCM, and Machine Learning Algorithms. Remote Sens. 2020, 12, 3776. [Google Scholar] [CrossRef]
- Yu, Z.; Zhao, M.; Gao, Y.; Wang, T.; Zhao, Z.; Wang, S. Spatial-Temporal Evolution and Prediction of Carbon Storage in Jiuquan City Ecosystem Based on PLUS-InVEST Model. Environ. Sci. 2024, 45, 300–313. [Google Scholar] [CrossRef]
- Zhou, G.; Yin, G. Carbon Storage in Chinese Forest Ecosystems—Biomass Equation, 1st ed.; Science Press: Beijing, China, 2018; pp. 40–80. [Google Scholar]
- Du, C.; Ren, H.; Qin, Q.; Meng, J.; Li, J. Split-Window algorithm for estimating land surface temperature from Landsat 8 TIRS data. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3578–3581. [Google Scholar] [CrossRef]
- Yu, D.; Shi, P.; Shao, H.; Zhu, W.; Pan, Y. Modelling net primary productivity of terrestrial ecosystems in East Asia based on an improved CASA ecosystem model. Int. J. Remote Sens. 2009, 30, 4851–4866. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Singh, R.; Singh, N.; Singh, S. Normalized Difference Vegetation Index (NDVI) Based Classification to Assess the Cha-nge in Land Use/Land Cover (LULC) in Lower Assam, India. Int. J. Adv. Remote Sens. GIS 2016, 5, 1963–1970. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ. 2006, 105, 142–154. [Google Scholar] [CrossRef]
- Jridi, L.; Kalaitzidis, C.; Alexakis, D.D. Quantitative Landscape Analysis Using Earth-Observation Data: An Example from Chania, Crete, Greece. Land 2023, 12, 999. [Google Scholar] [CrossRef]
- Qun’ou, J.; Lidan, X.; Siyang, S.; Meilin, W.; Huijie, X. Retrieval model for total nitrogen concentration based on UAV hyper spectral remote sensing data and machine learning algorithms—A case study in the Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar] [CrossRef]
- Li, Y.; Miao, Y.; Zhang, J.; Cammarano, D.; Li, S.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Improving Estimation of Winter Wheat Nitrogen Status Using Random Forest by Integrating Multi-Source Data Across Different Agro-Ecological Zones. Front. Plant Sci. 2022, 13, 890892. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 18–22 November 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Aguirre-Salado, C.A.; Treviño-Garza, E.J.; Aguirre-Calderón, O.A.; Jiménez-Pérez, J.; González-Tagle, M.A.; Valdéz-Lazalde, J.R.; Sánchez-Díaz, G.; Haapanen, R.; Aguirre-Salado, A.I.; Miranda-Aragón, L. Mapping aboveground biomass by integrating geospatial and forest inventory data through a k-nearest neighbor strategy in North Central Mexico. J. Arid. Land 2013, 6, 80–96. [Google Scholar] [CrossRef]
- Rahman, M.; Chen, N.; Elbeltagi, A.; Islam, M.M.; Alam, M.; Pourghasemi, H.R.; Tao, W.; Zhang, J.; Shufeng, T.; Faiz, H.; et al. Application of stacking hybrid machine learning algorithms in delineating multi-type flooding in Bangladesh. J. Environ. Manag. 2021, 295, 113086. [Google Scholar] [CrossRef] [PubMed]
- Hang, R.; Liu, Q.; Song, H.; Sun, Y.; Zhu, F.; Pei, H. Graph Regularized Nonlinear Ridge Regression for Remote Sensing Data Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 277–285. [Google Scholar] [CrossRef]
- Bi, K.; Gao, S.; Niu, Z.; Zhang, C.; Huang, N. Estimating leaf chlorophyll and nitrogen contents using active hyperspe-ctral LiDAR and partial least square regression method. J. Appl. Remote Sens. 2019, 13, 034513. [Google Scholar] [CrossRef]
- Dianat, R. Change detection in remote sensing images using modified polynomial regression and spatial multivariate alteration detection. J. Appl. Remote Sens. 2009, 3, 033561. [Google Scholar] [CrossRef]
- Li, J.; Qian, Y.; Jia, S. Regularized logistic regression method for change detection in multispectral data via Pathwise Coordinate optimization. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 2309–2312. [Google Scholar] [CrossRef]
- Chabert, M.; Tourneret, J.Y. Bivariate pearson distributions for remote sensing images. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 4038–4041. [Google Scholar] [CrossRef]
- Lv, C.; Lu, Y.; Lu, M.; Feng, X.; Fan, H.; Xu, C.; Xu, L. A Classification Feature Optimization Method for Remote Sensing Imagery Based on Fisher Score and mRMR. Appl. Sci. 2022, 12, 8845. [Google Scholar] [CrossRef]
- Moradi, F.; Darvishsefat, A.A.; Pourrahmati, M.R.; Deljouei, A.; Borz, S.A. Estimating Aboveground Biomass in Dense Hyrcanian Forests by the Use of Sentinel-2 Data. Forests 2022, 13, 104. [Google Scholar] [CrossRef]
- Wang, X. Dendroecological Studies of Dominant Tree Species Alongan Altitudinal Gradient on Changbai Lountain. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2015. [Google Scholar]
- John, R.; Chen, J.; Giannico, V.; Park, H.; Xiao, J.; Shirkey, G.; Ouyang, Z.; Shao, C.; Lafortezza, R.; Qi, J. Grassland canopy cover and aboveground biomass in Mongolia and Inner Mongolia: Spatiotemporal estimates and controlling factors. Remote Sens. Environ. 2018, 213, 34–48. [Google Scholar] [CrossRef]
- Li, F.; Miao, Y.; Feng, G.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving estimation of su-mmer maize nitrogen status with red edge-based spectral vegetation indices. Field Crops Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
- Bai, L.; Shu, Y.; Guo, Y. Estimating aboveground biomass of urban trees by high resolution remote sensing image: A case study in Hengqin, Zhuhai, China. IOP Conf. Ser. Earth Environ. Sci. 2020, 569, 012053. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison of three modeling methods for estimating forest biomass using TM, GLAS and field measurement data. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5774–5777. [Google Scholar] [CrossRef]
- Hosseiny, B.; Mahdianpari, M.; Hemati, M.; Radman, A.; Mohammadimanesh, F.; Chanussot, J. Beyond Supervised Learning in Remote Sensing: A Systematic Review of Deep Learning Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 1035–1052. [Google Scholar] [CrossRef]


| Serial Number | Tree Species | Calculation Formula | Reference | |
|---|---|---|---|---|
| 1 | Ginkgo biloba | [15] | ||
| 2 | Populus | |||
| 3 | Koelreuteria paniculata | |||
| 4 | Ligustrum lucidum | |||
| 5 | Pinus | |||
| 6 | Other Broadleaved Forests | |||
| Parameter Type | Parameter Name | Definition |
|---|---|---|
| Multi-band Operation Parameters | Band Addition | |
| Band Subtraction | ||
| Band Multiplication | ||
| Band Division | ||
| Difference Ratio Sum | ||
| SumRatio Difference | ||
| Vegetation Indices | Normalized Difference Vegetation Index (NDVI) | |
| Enhanced Vegetation Index (EVI) | ||
| Normalized Difference Greenness Red Index (NGRVI) | ||
| Canopy Chlorophyll Content Index (CCCI) | ||
| Global Vegetation Moisture Index (GVMI) | ||
| MERIS Terrestrial Chlorophyll Index (MTCI) | ||
| Normalized Difference Greenness Red-edge Index (NGRVIreg) | ||
| Modified Nonlinear Vegetation Index (MNLI) | ||
| Chlorophyll Absorption Ratio Index (CARI) | ||
| Terrain Parameters | Elevation | Elevation(m) |
| Slope | Slope (°) | |
| Topographic Wetness Index (TWI) | ||
| Textural Features | Angular Second Moment (ASM) | |
| Entropy (ENT) | ||
| Sum Average (SAVG) | is the number of grayscale levels in the represents the probability that the sum of pixelpairs in the Gray-Level Co-occurrence Matrix (GLCM) is i | |
| VegetationPhysiologicalParameters | Fraction of Photosynthetically Active Radiation (FPAR) | Proportion of photosynthetically active radiation absorbed by the vegetation canopy |
| Chlorophyll Content in the Leaf (CAB) | Vegetation leaf chlorophyll content | |
| Net Primary Productivity (NPP) | The net amount of light energy absorbed by a plant during photosynthesis | |
| Canopy Water Content (CWC) | Vegetation canopy water content | |
| Fraction of Vegetation Cover (FVC) | ||
| Land Surface Temperature (LST) | Surface temperature (°C) |
| Maximum Value (kg/m2) | Minimum Value (kg/m2) | Average Value (kg/m2) | |
|---|---|---|---|
| Observed Forest AGB | 84.27 | 2.11 | 17.77 |
| Observed Grass AGB | 5.27 | 0.10 | 0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Yang, K.; Ma, J.; Jiang, K.; Gu, X.; Peng, L. Aboveground Biomass Inversion Based on Object-Oriented Classification and Pearson–mRMR–Machine Learning Model. Remote Sens. 2024, 16, 1537. https://doi.org/10.3390/rs16091537
Chen X, Yang K, Ma J, Jiang K, Gu X, Peng L. Aboveground Biomass Inversion Based on Object-Oriented Classification and Pearson–mRMR–Machine Learning Model. Remote Sensing. 2024; 16(9):1537. https://doi.org/10.3390/rs16091537
Chicago/Turabian StyleChen, Xinyang, Keming Yang, Jun Ma, Kegui Jiang, Xinru Gu, and Lishun Peng. 2024. "Aboveground Biomass Inversion Based on Object-Oriented Classification and Pearson–mRMR–Machine Learning Model" Remote Sensing 16, no. 9: 1537. https://doi.org/10.3390/rs16091537
APA StyleChen, X., Yang, K., Ma, J., Jiang, K., Gu, X., & Peng, L. (2024). Aboveground Biomass Inversion Based on Object-Oriented Classification and Pearson–mRMR–Machine Learning Model. Remote Sensing, 16(9), 1537. https://doi.org/10.3390/rs16091537






