Author Contributions
Conceptualization, R.S.; methodology, R.S., P.Ć., P.W., M.Z. and M.P.; software, R.S. and M.P.; validation, R.S., P.Ć., P.W., M.Z. and M.P.; formal analysis, M.Z., P.W. and M.P.; investigation, R.S., M.Z., P.W., M.P. and P.Ć.; resources, P.W., M.Z., P.Ć. and M.P.; data curation, R.S. and M.Z.; writing—original draft preparation, R.S.; writing—review and editing, R.S., P.W., M.Z., M.P. and P.Ć.; visualization, R.S.; supervision, M.Z., P.W. and M.P.; project administration, P.W. and M.Z.; funding acquisition, P.W. and M.Z. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Orthophoto mosaics from Grodzisko (a) and Rybna (b) case studies from 13 July 2021.
Figure 1.
Orthophoto mosaics from Grodzisko (a) and Rybna (b) case studies from 13 July 2021.
Figure 2.
Part of the Kocinka stretch in Rybna (March 2022).
Figure 2.
Part of the Kocinka stretch in Rybna (March 2022).
Figure 3.
Schematic representation of the data set preparation workflow. Colors are for illustration purposes only and do not reflect actual data.
Figure 3.
Schematic representation of the data set preparation workflow. Colors are for illustration purposes only and do not reflect actual data.
Figure 4.
Example DSM and orthophoto dataset samples (a–d) with marked areas where the DSM equals the actual WSE ± 5 cm (red color).
Figure 4.
Example DSM and orthophoto dataset samples (a–d) with marked areas where the DSM equals the actual WSE ± 5 cm (red color).
Figure 5.
Direct regression approach—schematic representation. Numbers near arrows provide information about the dimensions of the flowing data.
Figure 5.
Direct regression approach—schematic representation. Numbers near arrows provide information about the dimensions of the flowing data.
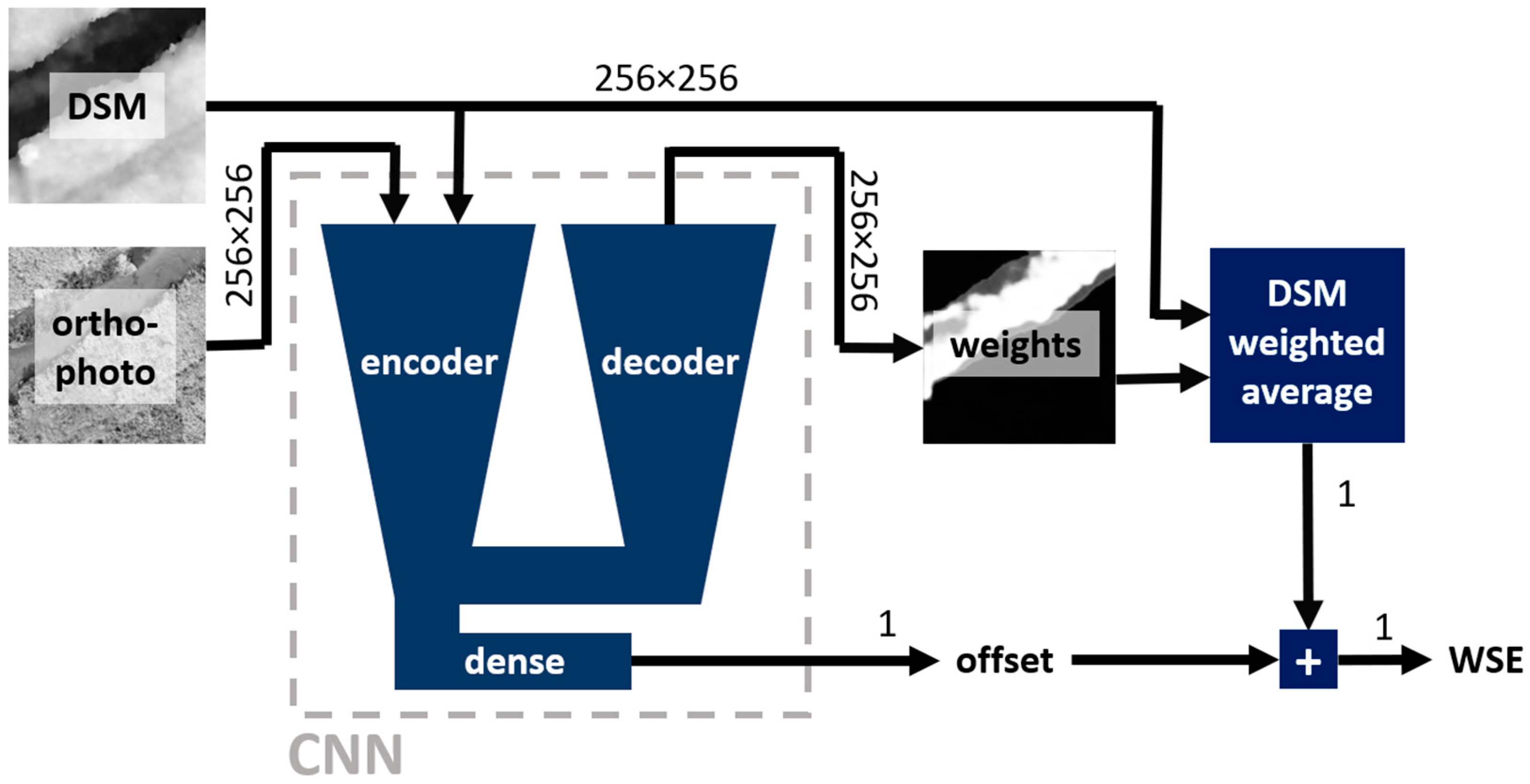
Figure 6.
Mask averaging approach—schematic representation. Numbers near arrows provide information about the dimensions of the flowing data.
Figure 6.
Mask averaging approach—schematic representation. Numbers near arrows provide information about the dimensions of the flowing data.
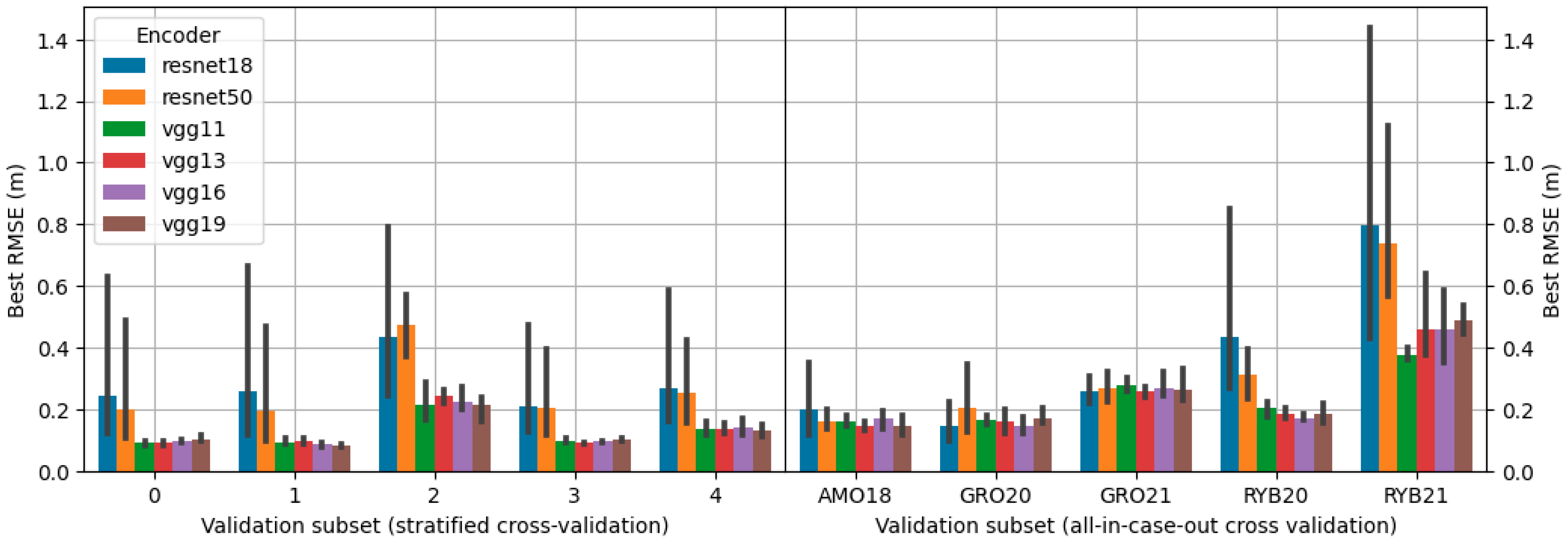
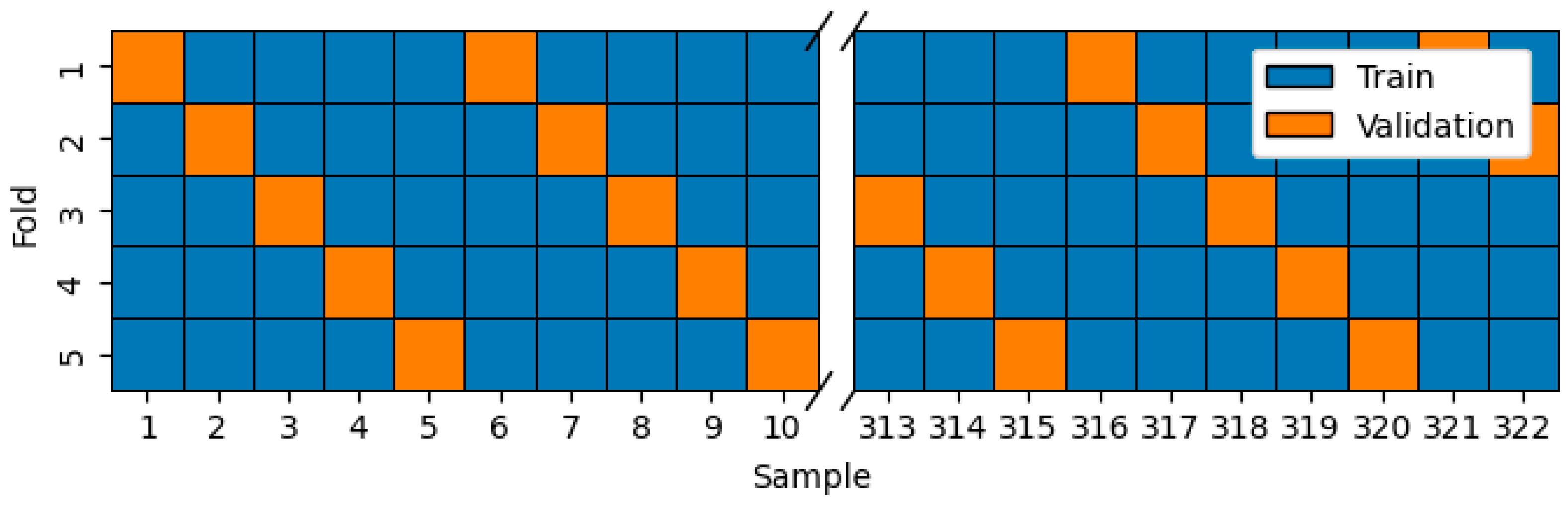
Figure 7.
The selection of validation samples for each of the 5 folds in stratified resampling.
Figure 7.
The selection of validation samples for each of the 5 folds in stratified resampling.
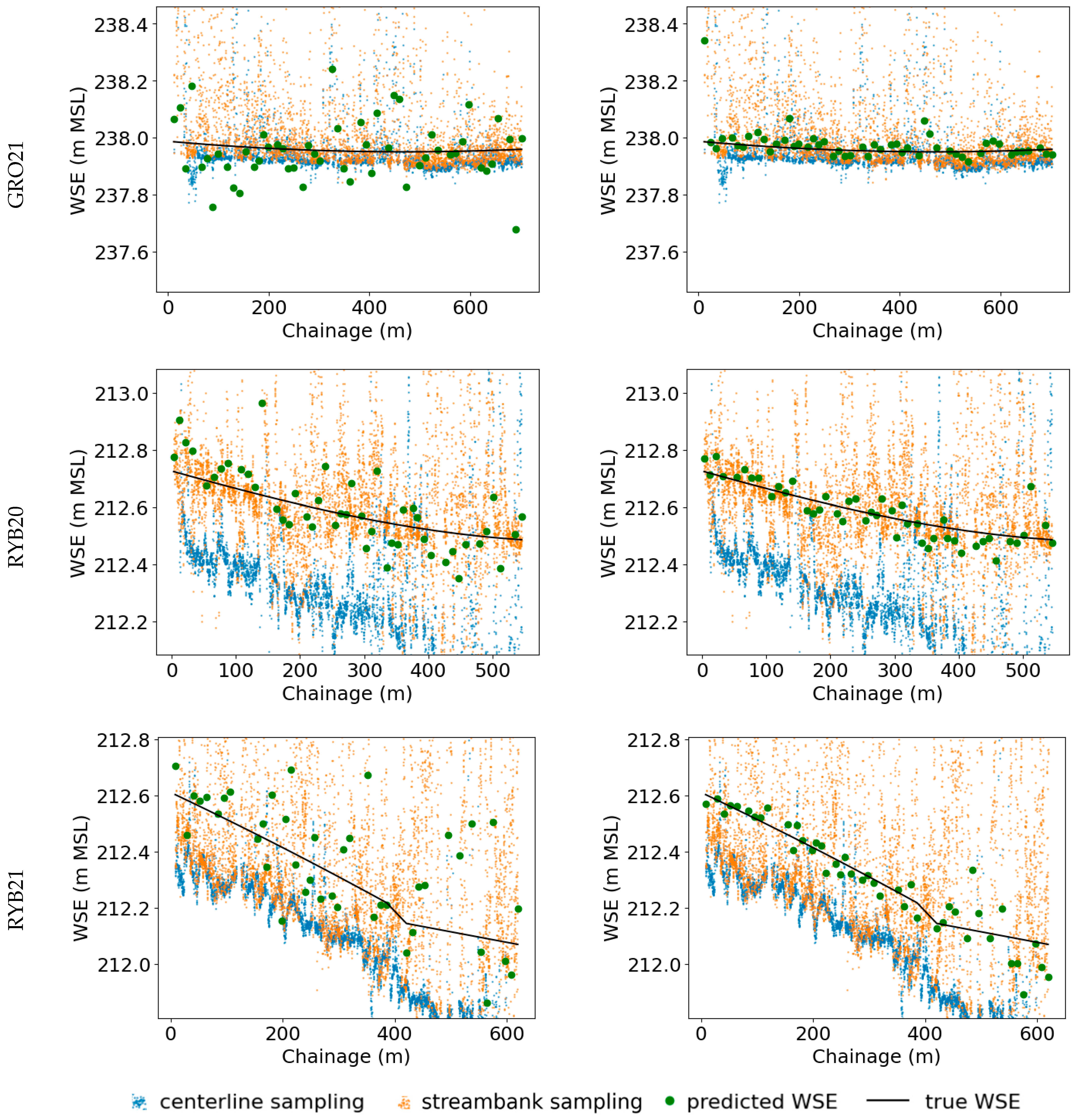
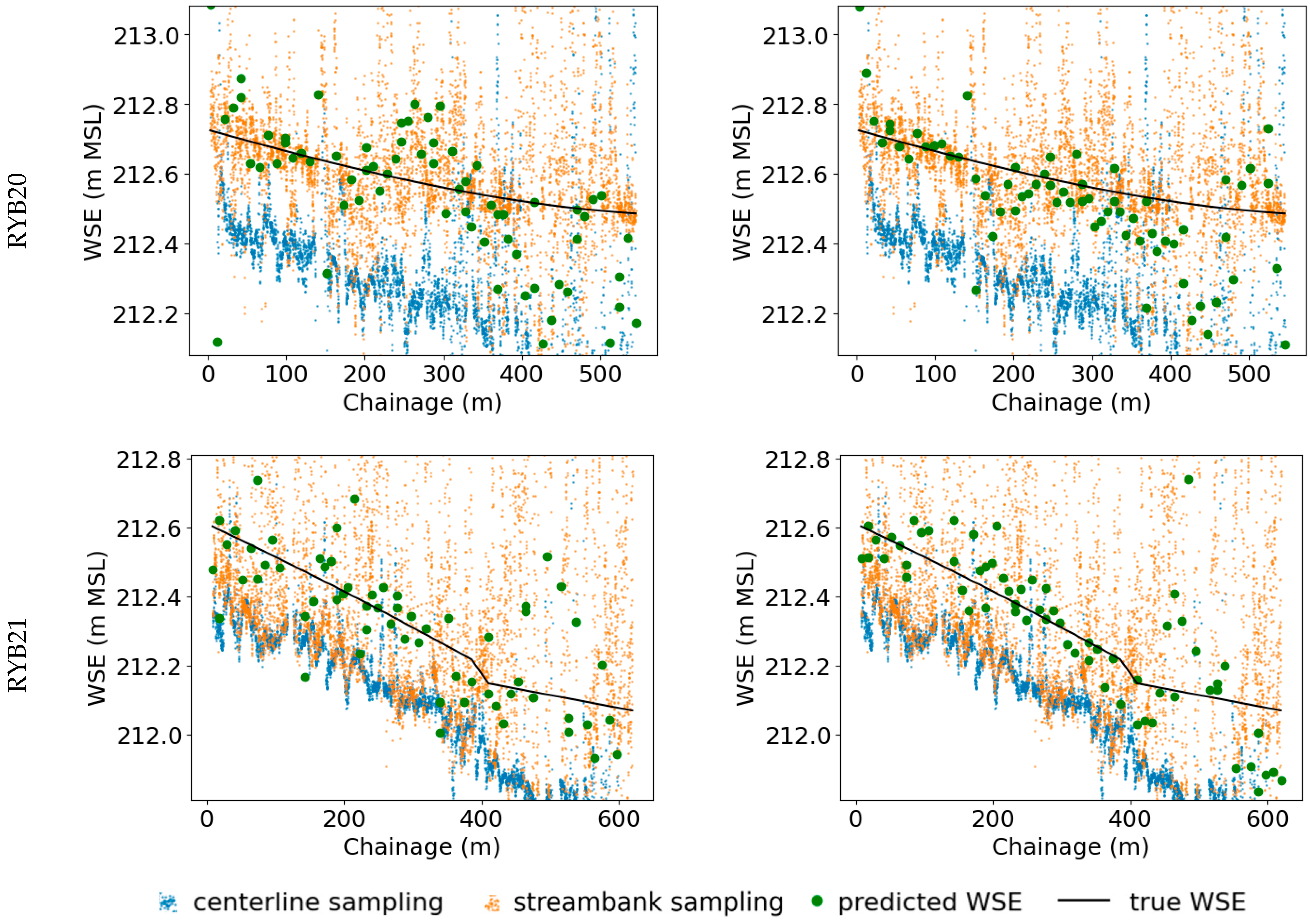
Figure 8.
Predictions of validation subsets from stratified cross-validation plotted against chainage (dark-green points). Compared with ground truth WSE (black line), DSM sampled near streambank (orange points), and DSM sampled at stream centerline (blue points). Columns denote different approaches and rows correspond to distinct case studies.
Figure 8.
Predictions of validation subsets from stratified cross-validation plotted against chainage (dark-green points). Compared with ground truth WSE (black line), DSM sampled near streambank (orange points), and DSM sampled at stream centerline (blue points). Columns denote different approaches and rows correspond to distinct case studies.
Figure 9.
Predictions of validation subsets from all-in-case-out cross-validation plotted against chainage (dark-green points). Compared with ground truth WSE (black line), DSM sampled near streambank (orange points), and DSM sampled at stream centerline (blue points). Columns denote different approaches and rows correspond to distinct case studies.
Figure 9.
Predictions of validation subsets from all-in-case-out cross-validation plotted against chainage (dark-green points). Compared with ground truth WSE (black line), DSM sampled near streambank (orange points), and DSM sampled at stream centerline (blue points). Columns denote different approaches and rows correspond to distinct case studies.
Figure 10.
Residuals (ground truth WSE minus predicted WSE) obtained during stratified and all-in-case-out cross-validations for each case study (rows) and method (columns) plotted against chainage.
Figure 10.
Residuals (ground truth WSE minus predicted WSE) obtained during stratified and all-in-case-out cross-validations for each case study (rows) and method (columns) plotted against chainage.
Figure 11.
Orthophoto, DSM, and weight masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the AMO18 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 11.
Orthophoto, DSM, and weight masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the AMO18 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 12.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the GRO20 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 12.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the GRO20 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 13.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the GRO21 case study. , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 13.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the GRO21 case study. , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
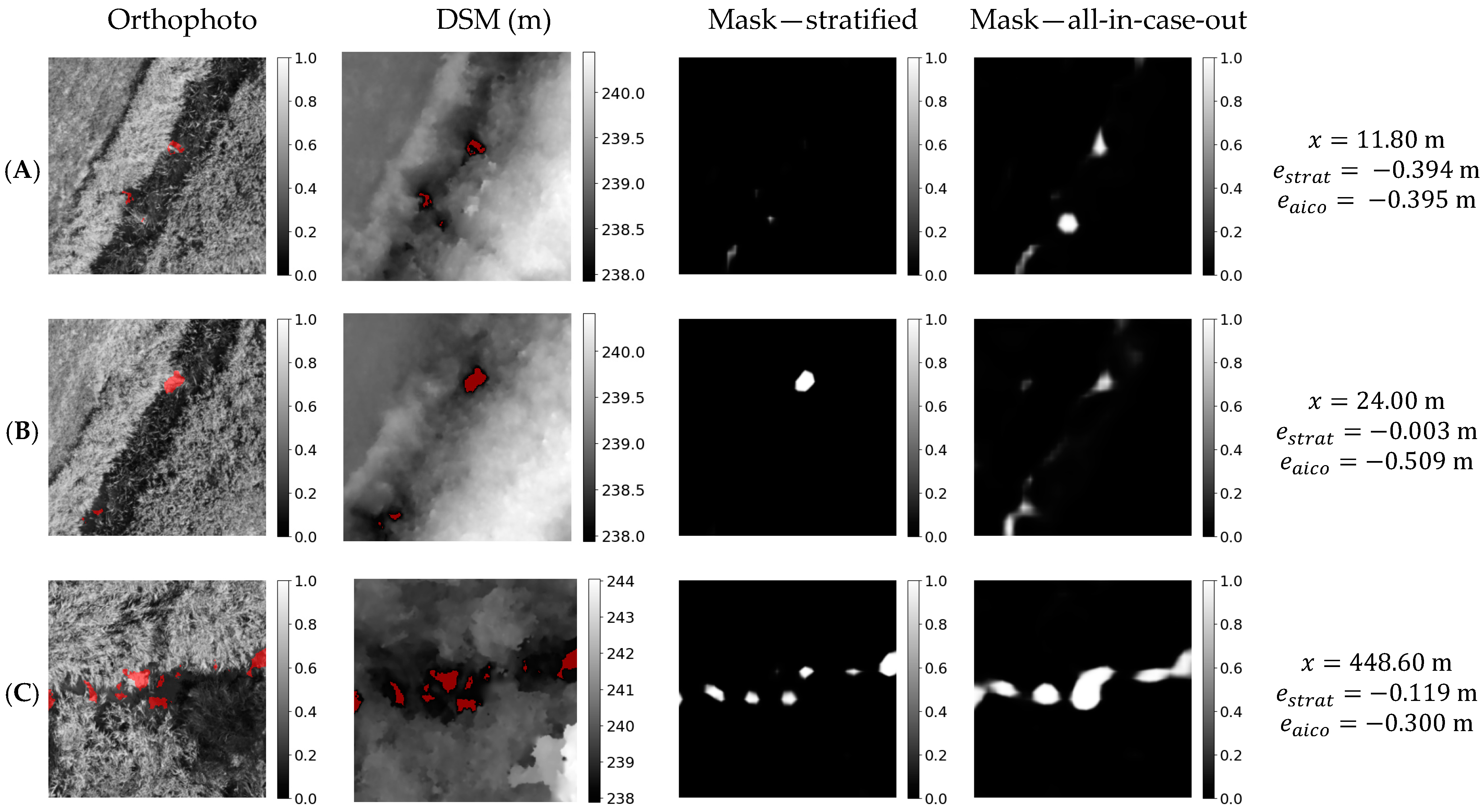
Figure 14.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the RYB20 case study. , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 14.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the RYB20 case study. , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 15.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the RYB21 case study. and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 15.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three best performing samples from the RYB21 case study. and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from most to least performing.
Figure 16.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the AMO18 case study. , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 16.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the AMO18 case study. , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 17.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the GRO20 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 17.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the GRO20 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 18.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the GRO21 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red color on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 18.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the GRO21 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red color on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 19.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the RYB20 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 19.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the RYB20 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 20.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the RYB21 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Figure 20.
Orthophoto, DSM, and masks obtained in stratified and all-in-case-out cross validations for the three worst performing samples from the RYB21 case study. , , and correspond to chainage and residuals obtained using stratified and all-in-case-out cross-validation, respectively. Areas where the DSM equals the actual WSE ± 5 cm are marked in red on the orthophoto and DSM. (A–C) samples ordered from least to most performing.
Table 1.
Number of WSE point measurements, standard error of estimate for ground truth WSE, and number of extracted data set samples for each case study.
Table 1.
Number of WSE point measurements, standard error of estimate for ground truth WSE, and number of extracted data set samples for each case study.
| Subset ID | Number of WSE Point Measurements | Standard Error of Estimate for Ground Truth WSE (m) | Number of Extracted Data Set Samples |
|---|
| GRO21 | 36 | 0.012 | 64 |
| RYB21 | 52 | 0.013 | 55 |
| GRO20 | 84 | 0.020 | 72 |
| RYB20 | 76 | 0.016 | 57 |
| AMO18 | 7235 | 0.020 | 74 |
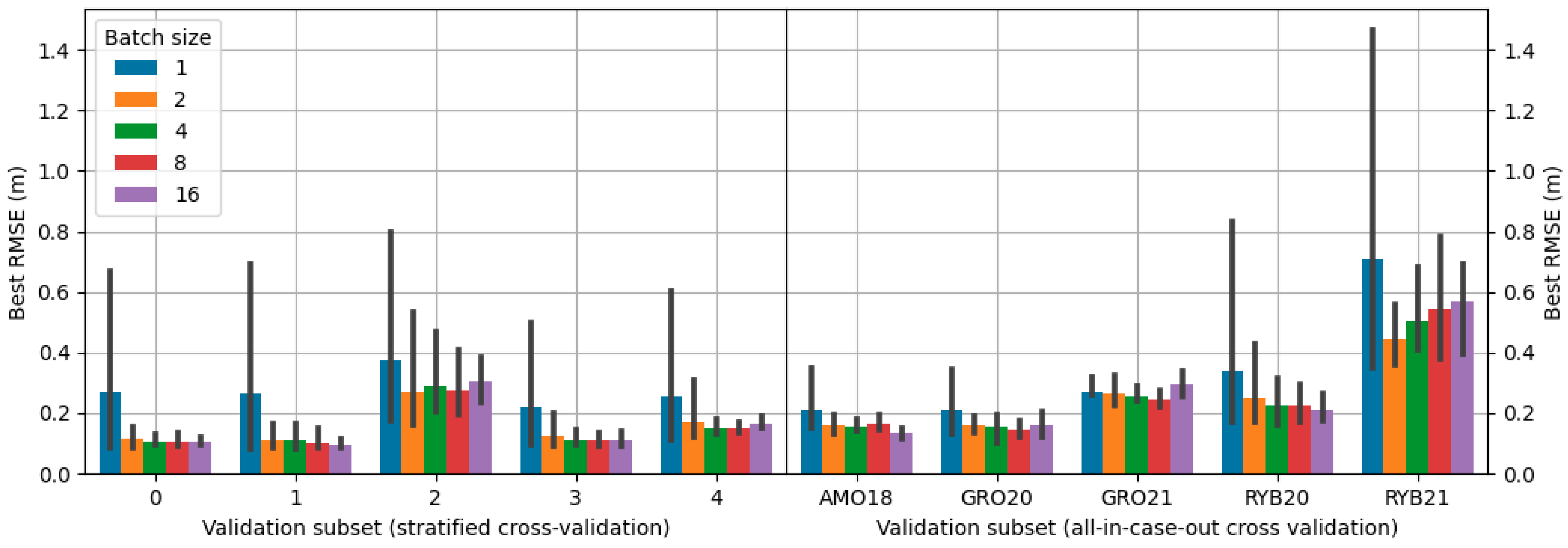
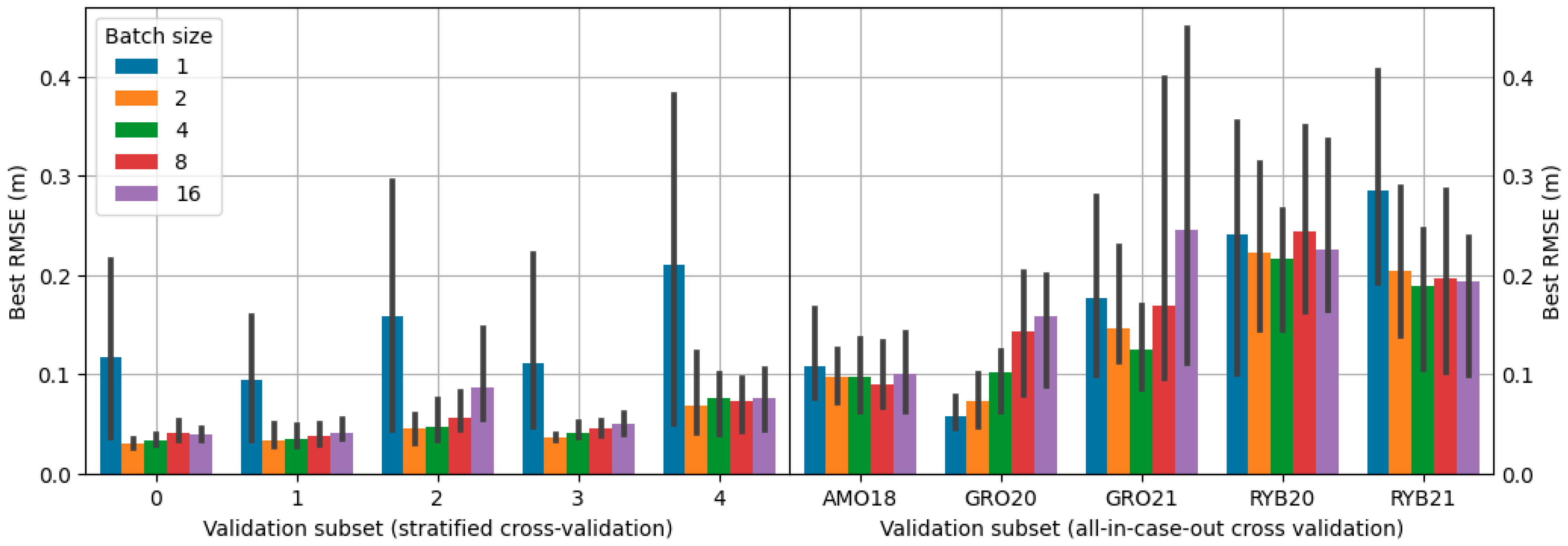
Table 2.
Propositions of architecture, encoder, and batch size used in grid search.
Table 2.
Propositions of architecture, encoder, and batch size used in grid search.
| Approach | Architectures | Encoder | Batch Size |
|---|
| Direct regression | - | ResNet18, ResNet50, VGG11, VGG13, VGG16, VGG19 | 1, 2, 4, 8, 16 |
| Mask averaging | U-Net, MA-Net, PSP-Net | VGG13, VGG16, VGG19 | 1, 2, 4, 8, 16 |
Table 3.
Best parameters configurations and achieved validation RMSEs averaged over all cross-validation folds.
Table 3.
Best parameters configurations and achieved validation RMSEs averaged over all cross-validation folds.
| | Direct | Mask |
|---|
| encoder | VGG16 | VGG19 |
| architecture | - | PSPNet |
| batch size | 1 | 4 |
| Mean RMSE | 0.170 | 0.077 |
Table 4.
RMSEs (m) achieved by proposed direct-regression and mask-averaging approaches and by straightforward sampling of DSM over centerline and near streambank. Both stratified and all-in-case-out cross-validation techniques results are given. Provided mean and sample standard deviation are calculated over all case studies.
Table 4.
RMSEs (m) achieved by proposed direct-regression and mask-averaging approaches and by straightforward sampling of DSM over centerline and near streambank. Both stratified and all-in-case-out cross-validation techniques results are given. Provided mean and sample standard deviation are calculated over all case studies.
| Cross-Validation | Stratified | All-In-Case-Out | - |
|---|
| Method | Direct | Mask | Direct | Mask | Centerline | Wateredge |
|---|
| AMO18 | 0.099 | 0.035 | 0.170 | 0.059 | 0.219 | 0.308 |
| GRO20 | 0.076 | 0.021 | 0.124 | 0.072 | 0.185 | 0.228 |
| GRO21 | 0.107 | 0.058 | 0.243 | 0.117 | 0.27 | 0.277 |
| RYB20 | 0.095 | 0.048 | 0.176 | 0.156 | 0.449 | 0.259 |
| RYB21 | 0.274 | 0.063 | 0.337 | 0.142 | 0.282 | 0.404 |
| Mean | 0.130 | 0.045 | 0.210 | 0.109 | 0.281 | 0.295 |
| Sample St. Dev. | 0.081 | 0.017 | 0.083 | 0.043 | 0.102 | 0.067 |
Table 5.
MAEs (m) achieved by proposed-direct regression and mask-averaging approaches and by straightforward sampling of DSM over centerline and near streambank. Both stratified and all-in-case-out cross-validation techniques results are given. Provided mean and sample standard deviation are calculated over all case studies.
Table 5.
MAEs (m) achieved by proposed-direct regression and mask-averaging approaches and by straightforward sampling of DSM over centerline and near streambank. Both stratified and all-in-case-out cross-validation techniques results are given. Provided mean and sample standard deviation are calculated over all case studies.
| Cross-Validation | Stratified | All-In-Case-Out | - |
|---|
| Method | Direct | Mask | Direct | Mask | Centerline | Wateredge |
|---|
| AMO18 | 0.078 | 0.026 | 0.121 | 0.045 | 0.179 | 0.176 |
| GRO20 | 0.059 | 0.015 | 0.091 | 0.06 | 0.139 | 0.104 |
| GRO21 | 0.082 | 0.028 | 0.195 | 0.072 | 0.117 | 0.138 |
| RYB20 | 0.074 | 0.037 | 0.127 | 0.111 | 0.373 | 0.157 |
| RYB21 | 0.169 | 0.045 | 0.154 | 0.096 | 0.249 | 0.276 |
| Mean | 0.092 | 0.030 | 0.138 | 0.077 | 0.211 | 0.17 |
| Sample St. Dev. | 0.044 | 0.011 | 0.039 | 0.027 | 0.103 | 0.065 |
Table 6.
MBEs (m) achieved by proposed direct-regression and mask-averaging approaches and by straightforward sampling of DSM over centerline and near streambank. Both stratified and all-in-case-out cross-validation techniques results are given. Provided mean and sample standard deviation are calculated over all case studies.
Table 6.
MBEs (m) achieved by proposed direct-regression and mask-averaging approaches and by straightforward sampling of DSM over centerline and near streambank. Both stratified and all-in-case-out cross-validation techniques results are given. Provided mean and sample standard deviation are calculated over all case studies.
| Cross-Validation | Stratified | All-In-Case-Out | - |
|---|
| Method | Direct | Mask | Direct | Mask | Centerline | Wateredge |
|---|
| AMO18 | 0.008 | −0.007 | −0.084 | −0.015 | −0.149 | 0.161 |
| GRO20 | −0.024 | −0.007 | −0.076 | −0.057 | −0.071 | 0.042 |
| GRO21 | 0.004 | −0.018 | 0.069 | −0.064 | 0.058 | 0.116 |
| RYB20 | −0.013 | 0.002 | 0.042 | 0.059 | −0.277 | 0.036 |
| RYB21 | −0.076 | 0.006 | −0.034 | −0.004 | −0.225 | 0.102 |
| Mean | −0.020 | −0.005 | −0.017 | −0.016 | −0.133 | 0.091 |
| Sample St. Dev. | 0.034 | 0.009 | 0.069 | 0.049 | 0.132 | 0.053 |
Table 7.
RMSE, MAE, and MBE from this study (using the mask-averaging method with both stratified and all-in-case-out cross-validations) compared with Bandini et al. [
25] (using radar, photogrammetry, and lidar), arranged by RMSE. All data are from the same case study of the Åmose Å stream in Denmark, collected on 21 November 2018.
Table 7.
RMSE, MAE, and MBE from this study (using the mask-averaging method with both stratified and all-in-case-out cross-validations) compared with Bandini et al. [
25] (using radar, photogrammetry, and lidar), arranged by RMSE. All data are from the same case study of the Åmose Å stream in Denmark, collected on 21 November 2018.
| Method | Source | RMSE | MAE | MBE |
|---|
| UAV radar | [25] | 0.030 | 0.033 | 0.033 |
| DL photogrammetry (stratified) | This study | 0.035 | 0.026 | −0.007 |
| DL photogrammetry (all-in-case-out) | This study | 0.059 | 0.045 | −0.015 |
| UAV photogrammetry DSM centerline | [25] | 0.164 | 0.150 | −0.151 |
| UAV photogrammetry point cloud | [25] | 0.180 | 0.160 | −0.160 |
| UAV lidar point cloud | [25] | 0.222 | 0.159 | 0.033 |
| UAV lidar DSM centerline | [25] | 0.358 | 0.238 | 0.076 |
| UAV photogrammetry DSM “water-edge” | [25] | 0.450 | 0.385 | 0.385 |