Abstract
Exploring the deformation mechanism of the 2021 Mw 7.4 Maduo Earthquake is crucial for better understanding the seismic hazard of the faults with low strain rates inside the Bayan Har block. This study leverages deformation information derived from Sentient-1 A/B images and GPS data to investigate in detail the co- and postseismic deformation mechanisms using multiple methods. The main results are as follows. First, the postseismic InSAR time series robustly identified the reactivation of the Changmahe fault, indicating the impact of the Maduo event on surrounding active faults. Second, the joint inversion of Interferometric Synthetic Aperture Radar and GPS revealed that (1) there was a complementary and partially overlapping relationship between the coseismic slip and postseismic afterslip of the main rupture; and (2) the Changmahe fault exhibited thrust compression dislocation in the early stage and experienced a sustained compressive effect from afterslip in the one year after the mainshock. Third, modeling the processes of viscoelastic relaxation and poroelastic rebound revealed that the postseismic deformation was probably caused by a combination of afterslip (near-field) and viscoelastic relaxation (near and far field). Fourth, the stress changes driven by the Maduo event revealed that the seismic gaps inside the Maqin-Maqu segment and the Kunlun Pass-Jiangcuo fault will be potential seismic risks in the future.
1. Introduction
In the past 20 years, multiple large earthquakes with a magnitude of M7 or above have occurred at the high strain rate boundary of the Bayan Har block in the Tibetan Plateau (Figure 1) [1]. However, few researchers have paid attention to the potential generation of large earthquakes inside the Bayan Har block with low strain rate. The 2021 Maduo Mw 7.4 earthquake (Maduo event), which occurred on 22 May 2021 (UTC+8), is the only large-scale earthquake that occurred on an inconspicuous fault inside the Bayan Har block in recent years, which is of great significance for in-depth insight into the stress development and fault tectonic activity inside the block.
The Maduo event generated an aftershock sequence numbering in thousands along the ~170 km length of the seismogenic rupture, which caused significant destruction to buildings and other economic losses. The event occurred on a low-slip-rate sinistral strike-slip Kunlun Pass-Jiangcuo fault (KLJF). The field investigation [2,3] and the relocated aftershock sequence [4] revealed that the seismogenic rupture zone generally trends NW280°, and a branch fault with ~40 km length appears on the eastern segment of the rupture. Geodesy observations—GPS and Interferometric Synthetic Aperture Radar (InSAR)—allow for a detailed characterization of the rupture mode and the co- and postseismic deformation behavior of seismic events [5,6,7,8]. This provides a tremendous chance to accurately depict the deformation mechanism and rupture model of the Maduo event, which is one of the main focuses of this paper.
After the Maduo event, numerous studies have explored its coseismic rupture and early postseismic deformation (e.g., [9,10,11,12,13]). Nevertheless, several issues remain, necessitating further investigation, which are as follows. Firstly, greater attention should be given to analyzing the impact of the Maduo event on the surrounding faults. Particularly, buried or known faults may be reactivated by the Maduo event. As a prominent example, field investigations after the mainshock [14,15] indicate that the eastern segment of the Tibet Dagou-Changmahe fault (the Changmahe fault), which is connected to the branch fault in the northeast of the seismogenic rupture, exhibits characteristics of compression and bulging, potentially influenced by the coseismic rupture of the Maduo event. Yang et al. [16] indicated that the Maduo event triggers the motion of the Changmahe fault. However, up to now, further exploration into the postseismic patterns of the Changmahe fault is absent, and the deformation characteristics and slip mechanisms during the early stage and one year after the mainshock remain unclear. Yang et al. [16] modeled the Changmahe fault using coseismic deformation fields spanning the early postseismic SAR image acquisition time without considering modeling based on early postseismic deformation fields. Additionally, slip behavior modeling of the Changmahe fault based on postseismic near-field GPS data is absent. Secondly, the postseismic deformation modeling of the Maduo event has been widely studied using InSAR (e.g., [7,10,17]) and dispersed GPS data [18], whereas postseismic near-field GPS data are seldom used to characterize the postseismic mechanism. Postseismic near-field GPS data can provide important constraints for exploring the postseismic deformation mechanism of the Maduo event [7]. Thirdly, the three-dimensional coseismic deformation field was calculated only utilizing the InSAR deformation fields in previous studies (e.g., [13,19]); therefore, considering the coseismic GPS measurements is indispensable to give a more precise constraint.
In the study, we introduced new postseismic near-field GPS data to better explore the properties of the seismogenic rupture and analyze the postseismic deformation mechanism. The main work of the paper includes the following: firstly, multiple methods were used to record the coseismic deformation of the Maduo event based on Sentinel-1 A/B images, and the high-precision three-dimensional coseismic deformation field was calculated by combining coseismic GPS measurements. Secondly, the SBAS-InSAR method and postseismic near-field GPS data were utilized to obtain the postseismic deformation time series (1 year) of the Maduo event. Thirdly, the joint inversion of GPS and InSAR observation was employed to constrain the co- and postseismic slip patterns, which will be beneficial for exploring the deformation mechanism of the main rupture and the Changmahe fault. Fourthly, the process of viscoelastic relaxation and poroelastic rebound were modeled to determine the relative contribution of postseismic deformation. The possible factors that control the postseismic fault slip behavior and the postseismic deformation trend were also discussed. Finally, the stress load driven by the Maduo event and the future seismic risk inside the Bayan Har block were analyzed.
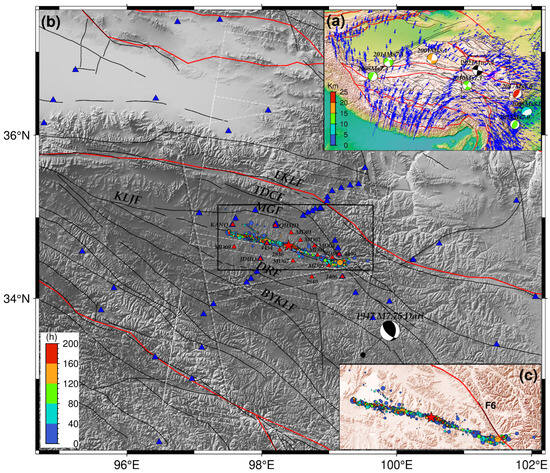
Figure 1.
The seismotectonic background around the Maduo event. The solid red line represents the boundary of blocks in the Tibetan Plateau. The solid black line represents the developed active faults [20,21]. EKLF = East Kunlun fault, KLJF = Kunlun Pass-Jiangcuo fault, DRF = Dari fault, MGF = Maduo-Gande fault, and BYKLF = Bayan Har Mountain Main Peak fault, TDCF = Tibet Dagou-Changmahe fault. (a) Major blocks and developed faults within the Tibetan Plateau. The blue-to-red beach ball sphere in (a) represents large historical earthquakes occurring at the boundary of the Bayan Har block, with color change indicating variations in depth. The black beach ball in (a) represents the Maduo event. The blue arrow indicates the interseismic GPS rate [22,23]. (b) The tectonic background around the epicenter. The white and black dashed boxes indicate the spatial coverage of Sentinel-1A/B data used to obtain co- and postseismic deformation from ascending and descending orbits, respectively. The solid black line box indicates the range of subgraph (c). The blue triangle represents the GPS station that recorded coseismic deformation, and the red triangle represents the near-field GPS station that recorded postseismic deformation. The black beach ball in (b) represents the 1947 M7.75 Dari earthquake [24]. (c) The circle represents the aftershocks after relocation [4], with color change (the color bar in (b)) representing the relative time in relation to the mainshock. The red star shows the relocated epicenter.
2. Methodology and Data Preprocessing
2.1. Coseismic Geodetic Observations
Sentinel-1 A/B data from ascending orbit 99 and descending orbit 106, spanning the period of 20 May 2021, to 26 May 2021, were used in the coseismic study. The two-pass differential InSAR (D-InSAR), pixel offset tracking (POT), and Burst-Overlap Interferometry (BOI) methods were employed to obtain the line-of-sight (LOS) deformation and azimuth offsets using the ISCE2 code [25] (Figure 2). The detailed image coverage is provided in Figure 1.
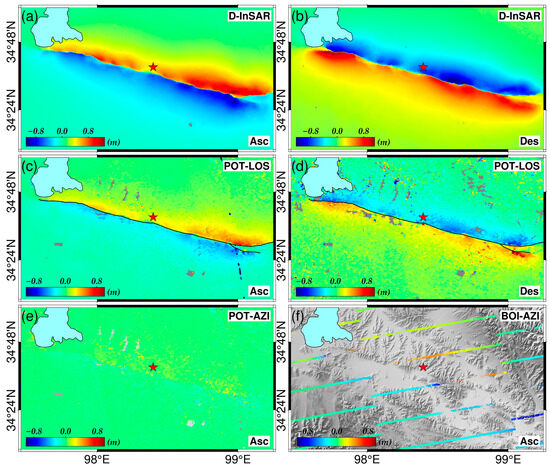
Figure 2.
Coseismic deformation fields of the Maduo event. “Asc” and “Des”, respectively, indicate the ascending and descending orbits of the satellite. (a,b) represent LOS deformation fields from ascending and descending orbits obtained by D-InSAR, respectively. (c,d) represent LOS deformation fields from ascending and descending orbits obtained by POT, respectively. (e,f) represent the azimuth deformation fields from ascending orbit obtained by POT and BOI, respectively. The solid black line indicates the seismogenic rupture trace drawn by coseismic deformation. The red star shows the relocated epicenter.
In D-InSAR processing, we applied multilook processing with azimuth direction 2 and range direction 10 to enhance the signal-to-noise ratio of the phase signal in the interferogram and reduce the influence of phase noise. In addition, we used reference DEM data (ALOS world 3D-30m) to remove the topography phase, applied Goldstein filtering [26] to remove the noise phase, and utilized the General Atmospheric Correction Online Service (GACOS) [27] to reduce the contribution of atmospheric effects. The phase unwrapping process was performed using the minimum cost flow method [28]. We selected 21 ground control points in the far-field area, away from seismic deformation, and estimated and removed the residual terrain phase and linear slope phase based on the cubic polynomial refinement method. Following phase shift and geocoding, we obtained the coseismic deformation fields in the LOS direction for both ascending and descending orbits.
In POT processing, the cross-correlation technique based on SAR image amplitude information was used to obtain the deformation fields of LOS and azimuthal offsets from ascending and descending orbits [29,30]. We employed a cross-correlation window that was 64 pixels in range and 16 pixels in azimuth. The images were oversampled by a factor of 64 in the matching process to extract offsets with a precision of 1/64 of a pixel. To further reduce the noise in the estimated offsets, we applied a median filter with a 15 × 15-pixel window to the azimuth displacement.
The BOI method, as described by Solaro et al. [31], involves several main steps. Firstly, backward and forward interferograms are generated by performing conjugate multiplication on two forward-looking and two backward-looking finely co-registered SAR images. Next, a differential process is applied between the forward and backward interferograms to extract the azimuthal deformation phase, which represents the deformation information in the azimuth direction [31]. To reduce the impact of incoherent noise, an adaptive Lee filtering method is employed to filter the azimuthal deformation phase. Finally, the entire SAR image is accurately geocoded to extract the geographic coordinates of the overlapping areas based on the geographic coordinates of the entire SAR image.
2.2. Three-Dimensional (3-D) Coseismic Deformation Field
The three-dimensional (3-D) deformation field can overcome the limitation posed by the polar-orbiting flight and side-looking imaging of spaceborne SAR sensors in the InSAR observations [32,33]. It is crucial for anatomizing seismogenic mechanisms. First, we interpolated the coseismic GPS horizontal displacements from Xiong et al. [7] (Table S1) using Kriging spatial interpolation to generate a deformation map at the same resolution as the InSAR data. Then, the complete 3-D coseismic deformation field of the Maduo event was constructed based on the SMVCE algorithm [33] with six components derived from the coseismic InSAR and coseismic GPS: one offset measurement in azimuth direction (orbit 99), two D-InSAR observations (orbits 99 and 106), one BOI measurement (orbit 99), and GPS horizontal displacements (EW and NS components) (Figure 3). In the calculation process, a window size of 21 × 21-pixel is adopted for modeling the strain model, as determined by the trial-and-error strategy.
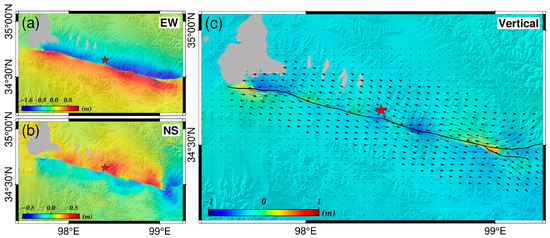
Figure 3.
The 3-D coseismic deformation field of the Maduo event. The horizontal deformation vector from the EW (a) and NS (b) deformation components of the 3-D coseismic deformation field is superimposed on the vertical (c) deformation component. Deformation values in the northward, eastward, and upward directions are positive. The red star shows the relocated epicenter. The solid black line indicates the seismogenic rupture trace drawn by coseismic deformation.
2.3. Postseismic Geodetic Observations
The postseismic InSAR deformation and GPS displacement driven by the early postseismic slip were investigated in this study (Figure 4). We collected 76 (including two frames) and 46 Sentinel-1 A/B images from ascending orbit 99 and descending orbit 106 (26 May 2021–3 May 2022), respectively, and 16 near-field GPS data (22 May 2021–25 September 2022) during the study period. The detailed Sentinel-1 A/B image coverage, the distribution of the near-field GPS stations, and data information are shown in Figure 1 and Table S1. The time series SAR images were processed using the ISCE2-StaMPS code [25,34,35]. The Small baseline subset InSAR (SBAS-InSAR) method [36] was utilized to extract the time series of postseismic InSAR deformation from interferograms (Figure 4). The Stacking InSAR method [37] was employed to obtain the LOS average deformation velocity (Figure 4d,h) The processing flowchart of SBAS-InSAR and Stacking-InSAR methods is shown in Figure S1. It is noteworthy that we employed the EW and NS components of GPS, omitting the vertical component due to its error frequently surpassing the signal [7,38].
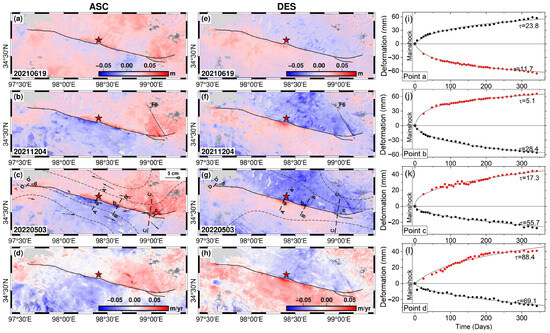
Figure 4.
The postseismic InSAR deformation fields (a–h), the postseismic GPS horizontal displacement (c), and (i–l) the time series of typical deformation points. The dashed black lines AA’–DD’ indicate the profile in Figure S3a–d. The black boxes labeled as a-d in (c,g) indicate specifically selected points in (i–l). The black dashed curve represents the isopleth with a 5 mm interval, and Figure 9a,b are overlaid as isopleth in (c) and (g), respectively. The black arrow in subgraph (c) indicates the postseismic GPS horizontal displacement in the current period. F6 represents the fault that was reactivated by the Maduo event. The coarse grey curves in (i–l) represent the best-fit curve (see Formula (2)), and the values of the decay coefficient (τ, unit in day) are labeled near the curves. The red star shows the relocated epicenter.
The main processing settings of the SBAS-InSAR method are as follows. We selected a suitable spatial–temporal baseline threshold (30 days for the time baseline and 200 m for the perpendicular baseline) to obtain a sufficient number of interferometric pairs. Figure S2 shows the distribution combination of interference pairs. To improve the signal-to-noise ratio of the interferogram, we performed multilook processing with an azimuth 20 and a range direction 4 on the original interferogram. The topography phase component contribution was removed using the ALOS WORLD 3D-30m DEM provided by the Japan Aerospace Exploration Agency. To further mitigate the impact of noise in the interferogram, we applied an adaptive Lee filtering method with a calculation window size of 32 × 32. This filtering technique significantly reduces the influence of noise on the interferogram. The unwrapping of the interferogram was performed using the minimum cost flow method [39]. A threshold of 0.6 was set to ensure sufficient deformation information during the unwrapping process. Additionally, we conducted the GACOS correction [27] to reduce the contribution of atmospheric noise to the time series data and obtain more accurate postseismic deformation information. Finally, the postseismic time series deformation was obtained (Figure 4).
The processing of near-field GPS data after the mainshock was carried out using GAMIT/GLOBK v10.6 software and the baseline calculation was performed on the original observation data to obtain a single-day relaxation solution. In the specific calculation, the latest Earth rotation parameters, solar ephemeris, lunar ephemeris, nutation parameters, and antenna phase center parameter files were used, and ionospheric model corrections were added. The IERS03 protocol model was used to deduct the effects of solid tide, ocean tide, and polar tide from phase observations. The zenith dry delay component for each station was calculated using the GPT2 model, and the tropospheric zenith wet delay component was calculated every 2h to estimate atmospheric tropospheric delay. In the network adjustment processing, the relaxation solution calculated in the previous step was combined with the global solution generated by SOPAC (http://sopac.ucsd.edu/, accessed on 10 February 2023). Under the constraints of IGS reference stations distributed globally, a seven-parameter similarity transformation was used to convert the daily solution into the ITRF2014 framework, and finally, the coordinate time series under this framework was obtained (Figure 5 and Figure 6). In addition, we used Bayesian methods to estimate the interseismic GPS rate and its uncertainty related to tectonic deformation [7].
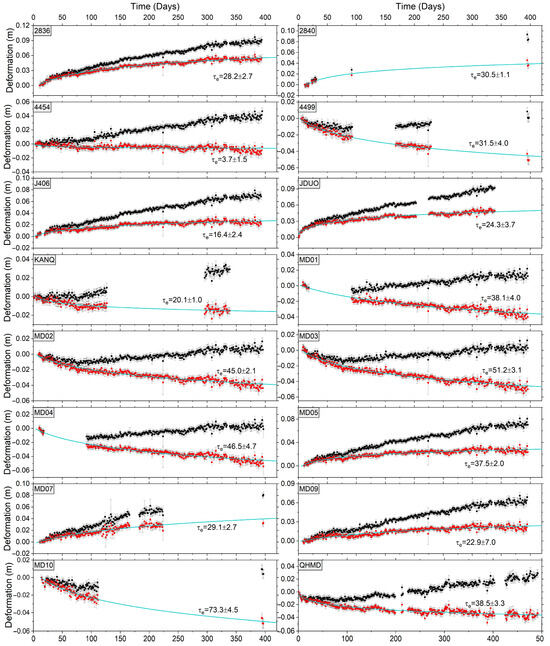
Figure 5.
The EW displacement component of the postseismic GPS time series. The red dot and the black dot represent the original and corrected GPS time series, respectively. The bluish-green curve is the logarithmic function curve with the optimal fitting (see Formula (1)), and the values of the decay coefficient (τ-τe, τn, unit in day) are labeled near the curves.
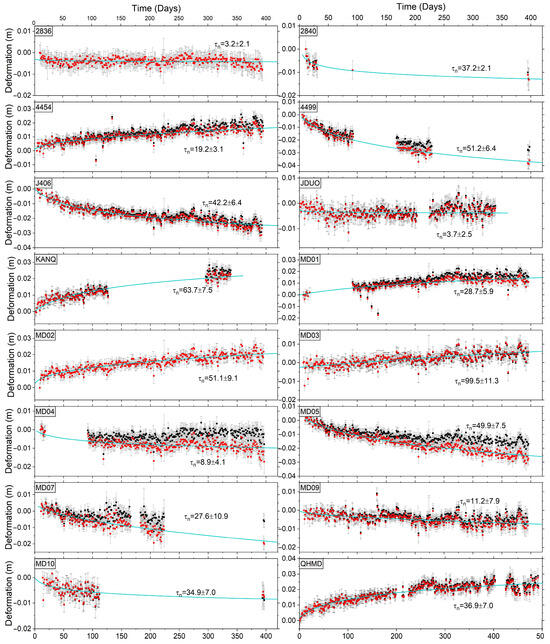
Figure 6.
The NS displacement component of the postseismic GPS time series. The red dot and the black dot represent the original and corrected GPS time series, respectively. The bluish green curve is the logarithmic function curve with the optimal fitting (see Formula (1)), the values of the decay coefficient (τ-τe, τn, unit in day) are labelled near the curves.
In order to obtain the postseismic GPS deformation trend (Figure 5 and Figure 6), we separate the linear trend and seasonal deformation signals from the original GPS time series [40]. The corresponding formula can be expressed as follows:
where F(T) represents the fitting original GPS time series (mm). T represents the observation time (days). τ represents the decay coefficient (days). a1–a7 represent the unknown coefficient to be solved. In Equation (1), the first term represents the linear trend driven by tectonic deformation, the second term represents the postseismic deformation trend, which follows a logarithmic function, the remaining trigonometric terms represent the seasonal signals present in the original GPS time series, and a7 indicates the offset term. We used an interseismic GPS rate to separate the linear trend term.
Additionally, the fitting formula for the time series of InSAR deformation points can be expressed as follows [8]:
where F indicates the fitting deformation time series. A0 is the scaling factor, T indicates the observation time (days), τ indicates the decay coefficient (unit in day), and c indicates the offset of the curve.
2.4. 2.5-Dimensional (2.5-D) Postseismic Time Series Deformation Decomposing
To further determine the postseismic deformation pattern, we measured the quasi-East-West (quasi-EW) and quasi-vertical components of the 2.5-dimensional (2.5-D) [41] deformation fields by combining LOS deformation fields from descending and ascending orbits (Figure 7). According to the imaging geometry of spaceborne SAR satellites (e.g., right-looking imaging), the LOS deformation dLOS of a target on the ground can be represented by [8,41]:
where F represents the direction of satellite flight (ascending/descending). When F is A, it represents ascending, and when D, it represents descending; indicates the LOS coseismic deformation at any given ground point; is the measurement error. de and dn denote the EW and NS deformation vectors at any given ground point, respectively, and du denotes the vertical deformation vector at any given ground point; denotes the SAR satellite incidence angle, and denotes the SAR satellite flight azimuth.
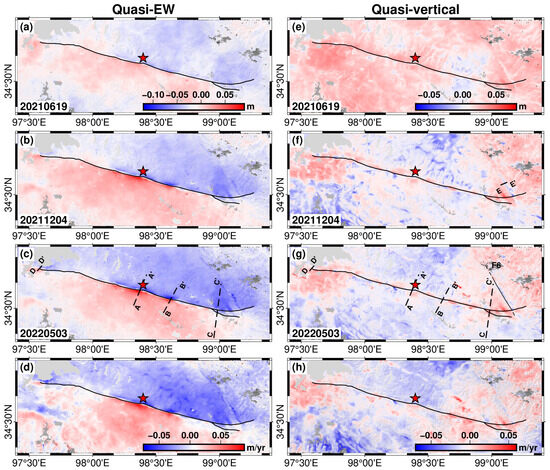
Figure 7.
The 2.5-D postseismic deformation fields (a–h). The deformation values in the quasi-E and the quasi-upward directions are positive. The black dashed lines AA′–DD′ indicate the profiles of Figure S3e–h. The black dashed line E–E′ indicates the profile of Figure 10b. The red star shows the relocated epicenter.
When the NS deformation vector is assumed to make no contribution to the LOS deformation, Formula (3) becomes Formula (4). Furthermore, the quasi-EW deformation du and quasi-vertical deformation de of ground targets can be expressed as
2.5. Co- and Postseismic Slip Modeling
We adopted the steepest descent method [42] to model the coseismic slip distribution of the Maduo event. The 67 GPS horizontal displacements [7] (Table S1) and the D-InSAR deformation from ascending and descending orbits (Figure 2a,b) were employed to jointly invert the coseismic slip (Figure 8a). To improve the operational efficiency of inversion, a non-uniform downsampling method was utilized to resample the InSAR deformation. This method was implemented by using different pixel sampling intervals for the near-field and far-field deformation regions of the coseismic rupture, respectively, in terms of rows and columns. We set the length of the seismogenic fault model to be 180 km along the strike direction, and the width extends downward along the dip direction to 30 km. The fault plane was discretized into patches with dimensions of 2 × 2 km. Considering that the deep rupture of the Maduo event reached the surface, the top edge depth of each fault segment was set to 0 km. Considering the spatial distribution of aftershocks [4] and the curvature of the seismogenic rupture trace, we divided the entire seismogenic fault into 5 fault segments (F1–F5). Referring to the relocated aftershock depth profiles [4], the dip angle for each fault segment was set differently within 80°–90°. In addition, to ensure a reasonable slip distribution, the preferred smoothing factor of 0.07 was selected through multiple inversions based on the trade-off relationship between the model roughness and the normalized misfit (Figure 8e).
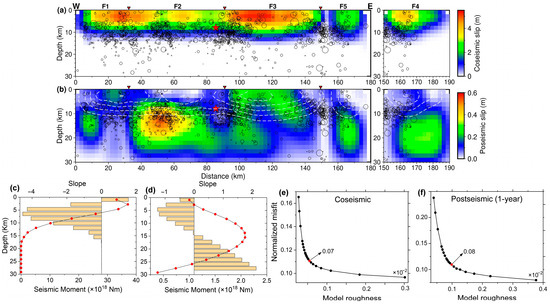
Figure 8.
The co- (a,b) postseismic (1 year) slip distribution of the Maduo event. The white dashed line denotes the coseismic slip isopleth at 1m intervals. The black circle represents the relocated aftershocks distribution. The change of geodetic moment release with depth of co- (c,d) postseismic slip. The red dots indicate the seismic moment corresponding to each depth, and the histogram indicates the slope change of the seismic moment with depth. (e,f) indicate the trade-off curve between model roughness and normalized misfit of the co- and postseismic (1 year) slip distribution, respectively. The red dots in (e,f) represent the preferred smoothing factor. The red star shows the relocated epicenter.
We applied a nearly similar inversion strategy as the coseismic slip inversion, where the postseismic LOS deformation from ascending and descending orbits and the horizontal displacements of 16 near-field GPS (Figure 5 and Figure 6) were employed for joint inversion to generate the postseismic slip model. The near-field GPS data can provide better constraints compared to near-field GPS data used by Jin et al. [18]. Here, GPS data were used within the same observation time window as InSAR. For GPS stations (e.g., 2840, 4499, and KANQ) with significant observation gaps and relatively short observation periods (<1 year), we performed optimal fitting using logarithmic functions to estimate deformations during each monitoring period (see Formula (1) and Figure 5 and Figure 6). These estimates were then utilized in the joint inversion process. Considering the contribution of viscoelastic relaxation and poroelastic rebound to the postseismic deformation within 1 year after the mainshock, the postseismic LOS deformation was obtained by subtracting the simulated LOS deformation through viscoelastic relaxation and poroelastic rebound from the cumulative LOS deformation of the last observation period obtained using SBAS-InSAR (Figure 9 and Figure S4). Meanwhile, the postseismic GPS horizontal displacements also subtract these two mechanisms-driven deformation components (Figure 9). Slip modeling was conducted for the early stage (26 May–19 June 2021) and one year after the mainshock, respectively (Figure 8b and Figure 9c,d). Considering the influence of the Maduo event on the Changmahe fault, we added an additional fault segment, F6. We utilized the nearly linear trace of fault segment F6, as depicted in the postseismic InSAR time series (see F6 in Figure 4 and Figure 7), for modeling purposes. In the detailed process, the geometry of the postseismic main rupture model was determined based on the geometry of our coseismic model. The preferred smoothing factors for the two inversions were 0.07 and 0.08, respectively, selected by considering the trade-off relationship between the model roughness and the model misfit (Figure 8f and Figure 10f).
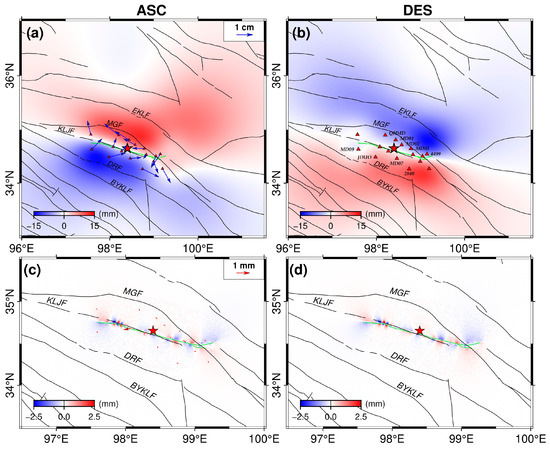
Figure 9.
The simulated LOS deformation from ascending and descending orbits and GPS horizontal displacements ~1 year after the mainshock based on the models of VR (a,b) and PR (c,d). The red triangles indicate the near-field GPS stations. The red star shows the relocated epicenter.
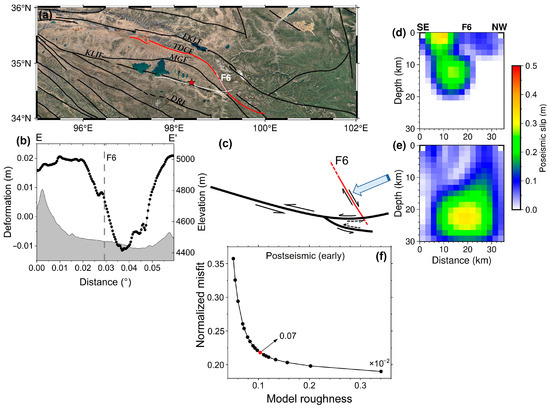
Figure 10.
The tectonic background surrounding fault F6 (a), the deformation profile across fault F6 (b), the schematic diagram illustrating the reactivation mechanism of fault F6 (c), and the slip distribution of the fault F6 during the early stage (d) and the one year (e) after the mainshock. The position of the E–E’ profile is indicated in Figure 7f. (f) illustrates the trade-off curve between model roughness and normalized misfit of the slip distribution in the early stage after the mainshock. EKLF = East Kunlun fault, KLJF = Kunlun Pass-Jiangcuo fault, DRF = Dari fault, MGF = Maduo-Gande fault, and TDCF = Tibet Dagou-Changmahe fault. The red star shows the relocated epicenter.
2.6. Modeling of Viscoelastic Relaxation and Poroelastic Rebound
Previous research on the postseismic deformation mechanism has generally neglected the effects of viscoelastic relaxation (VR) and poroelastic rebound (PR) processes, assuming that postseismic afterslip is the dominant process. However, these two mechanisms can often contribute more or less to postseismic deformation [43,44]. We modeled the VR and PR process to evaluate the simulated deformation driven.
VR typically exists in the lower crust and/or upper mantle, and high temperature and pressure enable the ductile flow of rocks [45]. Based on our coseismic slip model, the simulated LOS deformation and GPS horizontal displacements ~1 year after the mainshock driven by VR were evaluated by adopting the PSGRN/PSCMP code [46] (Figure 9a,b). The simulation utilized a multi-layer crustal model with a viscoelastic lower crust and upper mantle, as used by Xiong et al. [7], and also referenced the crustal velocity structure proposed by Wang et al. [4] and Song et al. [47]. The viscosity value (1.0 × 1018 Pa·s) used in the model is based on the value proposed by Liu et al. [48], Chen et al. [43], and Xiong et al. [7].
Earthquakes can alter the fluid pressure in the lower part of the seismogenic rupture, and the associated PR can cause time-dependent surface deformation [49]. The PEGRN/PECMP code [50] was adopted to evaluate the simulated LOS deformation and GPS horizontal displacements ~1 year after the mainshocks simulated driven by PR (Figure 9c,d), utilizing our coseismic slip model. The PR process can be modeled in a layered homogeneous half-space by considering the variation in the Poisson’s ratio of the top crustal rocks from undrained (0.28) to drained (0.241) conditions [7,49]. Following the work reported by Xiong et al. [7], we reevaluated the contribution of the PR~1 year after the mainshock. The corresponding model parameters are based on the relevant parameters in Xiong et al. [7] and Hong and Liu [40]. We assumed that the PR occurred solely within the top 7 km layer of the upper crust.
2.7. The Coulomb Failure Stress Change
We calculated the coulomb failure stress change (dCFS) driven by the coseismic rupture of the Maduo event to evaluate its effect on the surrounding fault (Figure 11). Based on the optimal coseismic slip model (Figure 8a), the PSCMP/PSGRN code [46] was employed to calculate the dCFS. The calculation of dCFS is based on a layered elastic half-space crustal and upper mantle velocity and density model reported by Xiong et al. [7], which considers the gravity effect and effectively simulates the coseismic deformation and stress change caused by the earthquake. In the study, the apparent friction coefficient was set to a value of 0.4 [51]. Different friction coefficient values affect the calculated stress values, but the distribution pattern of dCFS and the sign of stress changes (increase/decrease) remain largely the same [10,52]. The dCFS value was calculated at the same depth (7 km) as the mainshock. We select a receiving fault direction (283.9/82.7/−9) to compute stress change resolved on a nearly vertical strike-slip fault, aligning with the orientation of the Maduo event.
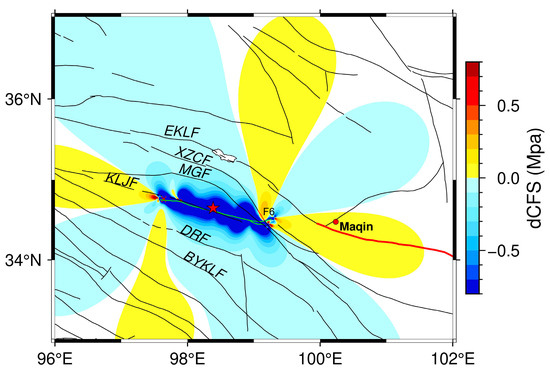
Figure 11.
The coseismic dCFS of the Maduo event. The thick red line shows the Maqin-Maqu segment. The lake filled with white color represents Donggei-Cuona Lake. EKLF = East Kunlun fault, KLJF = Kunlun Pass-Jiangcuo fault, DRF = Dari fault, MGF = Maduo-Gande fault, and TDCF = Tibet Dagou-Changmahe fault. The red star shows the relocated epicenter.
3. Results and Analyses
3.1. The Coseismic Deformation Analysis
The dense interference fringes observed in the coseismic interferogram indicate a significant deformation gradient associated with the Maduo event (Figure S5). As shown in Figure 2. The D-InSAR and POT observations have obtained a complete and wide-ranging coseismic deformation field of the Maduo event, with two main lobes of deformation separated by seismogenic rupture clearly visible. The coseismic deformation field depicts a ~282° strike rupture trace, consistent with field investigation [2,3] and relocated aftershock distribution [4]. The prominent area of deformation in the entire coseismic deformation field covers an approximately 200 km × 80 km range, with the maximum LOS deformation reaching 1.3 m. The azimuth deformation from BOI and POT reaches a maximum of 1 m. Furthermore, the discontinuity and curvature changes of deformation along the seismogenic rupture trace suggest complex geometric variations (e.g., fault bending) throughout the entire seismogenic process. The near-symmetry of the deformation lobes on the northern and southern parts of the ascending and descending deformation maps reveals the sub-vertical geometric structure of the seismogenic fault.
Figure 3 exhibits the complete 3-D coseismic deformation field. Our result demonstrates sufficient consistency in both the value range and spatial distribution of deformation compared to Liu et al. [53], Wei et al. [19], and Yang et al. [16], except for the difference in the NS component from Zhao et al. [13]. As shown in Table 1, the root mean square error (RMSE) of the EW and NS deformations was 2.3 cm and 2.9 cm, respectively, significantly lower than those reported by Liu et al. [53] (RMSE of 5.2 cm for EW and 6.4 cm for NS). Nonetheless, the small differences indicate that the 3-D coseismic deformation field calculated in this study exhibits a high level of accuracy. Figure 3 illustrates that the amplitude of deformation in the EW direction exhibited the highest magnitude, reaching a maximum of ~2.1 m, and the seismogenic fault associated with the Maduo event primarily exhibited left-lateral strike-slip motion. This implies that the horizontal deformation components in the EW and NS directions predominantly contribute to the coseismic deformation.

Table 1.
Comparison of the 3-D coseismic deformation field and coseismic GPS.
3.2. The Postseismic Deformation Analysis
InSAR observation after the mainshock displays that the deformation along the rupture trace of the Maduo event is discontinuous (Figure 4). The postseismic deformation behavior is almost identical to the coseismic, with the postseismic deformation primarily occurring on both sides of the mainshock rupture. Within 1 year after the mainshock, the maximum LOS deformations were ~0.09 m and ~0.08 m for the ascending and descending orbits, respectively (Figure 4). Similarly, the maximum deformation velocities were ~0.08 m/yr and ~0.07 m/yr, respectively (Figure 4d,h). Furthermore, the profiles A–D (Figure S3a–d) selected in the typical area, located at the two release ends of the main rupture and near the epicenter, indicate that the LOS deformations from the ascending and descending orbits reveal a large deformation amplitude, and the deformation signals from these two orbits exhibited opposite patterns. This means that the postseismic deformation is still mainly strike-slip motion. Generally, postseismic afterslip occurs within a few months or a year after the mainshock and is distributed on both sides of the seismogenic rupture [43,54]. The postseismic deformation pattern in this study (Figure 4) reveals that widespread aseismic slip reached the surface and spread around the mainshock rupture area within 1 year after the mainshock, meaning that aseismic afterslip may be the main driving factor for early postseismic deformation in the near-field of the Maduo event.
The 2.5-D time series deformations (Figure 7) showed consistency with the corresponding results in He et al. [10] regarding deformation spatial distribution and magnitude, which validates the reliability of our findings. The 2.5-D quasi-EW deformations exhibited prominent strike-slip characteristics, with a maximum deformation magnitude of ~0.085 m (Figure 7), exhibiting clear deformation patterns along the deformation profiles (Figure S3e–h). Similarly, the postseismic GPS also observed maximum horizontal displacements of ~0.05 m (EW) and 0.035 m (NS) near the mainshock (Figure 5 and Figure 6). In the 2.5-D quasi-vertical deformation, clear subsidence or uplift changes were observed near the mainshock, and the deformation distribution was not uniform (Figure 7).
3.3. The Co- and Postseismic Slip Distribution
3.3.1. The Coseismic Slip Distribution
Figure S6a–f demonstrate that the deformation driven by both InSAR and GPS measurements can be accurately reproduced in our coseismic model. The misfit is mainly observed at both ends of the seismogenic rupture, which may be attributed to the complex fault geometry and inelastic deformation [3,9,55].
As shown in Figure 8a, the inversion result reveals that (1) overall, the seismogenic fault is north-dipping, with highly segmented and sub-vertical characteristics, and a change of both dip and strike along the entire fault. (2) The rupture of the seismogenic fault reached the surface, with a maximum slip of ~5.5 m. The peak slip identified in our study is lower compared to the results reported by Fang et al. [9] (~7 m) and Zhang et al. [12] (>6 m), slightly larger than those of Yue et al. [56] (5m) and He et al. [10] (~5 m), and more consistent with the results of Jin and Fialko [57] and Xiong et al. [7]. (3) The five asperities were unevenly distributed along the fault, mainly concentrated at depths of ≤ 6 km. Coseismic slip was mainly limited to 0–12 km depth, which is less than the depth of the relocated aftershocks [4] and located within the brittle layer (~17 km) of the upper crust [47], suggesting that the seismogenic rupture did not effectively penetrate the ductile shear zone or deeper part of the seismogenic depth. Compared to previous studies (e.g., [10,13,57]), our research highlights the abovementioned characteristics of shallow fault ruptures. Furthermore, the high slip areas of fault segments F1–F6 aligned well with the surface rupture segments observed in the field investigation conducted by Yuan et al. [15].
The total seismic moment inverted in our research was 1.68 × 1020 N·m, corresponding to an Mw 7.4 earthquake. This moment magnitude is similar to the magnitude published in earlier studies, e.g., He et al. [10] and Fang et al. [9]. In addition, our total seismic moment result is significantly higher than He et al. [10] (1.58 × 1020 N·m), but lower than those of Xiong et al. [7] (1.80 × 1020 N·m) and Fang et al. [9] (1.77 × 1020 N·m), and Zhang et al. [12] (1.7 × 1020 N·m). These controversies may be related to different deformation datasets and fault geometric modeling [7,16]. Furthermore, GPS data play an essential constraint role in our coseismic slip model [7].
3.3.2. The Postseismic Slip Distribution
Figure S6g–r illustrate that the optimal afterslip model can effectively explain the majority of GPS observations. However, there are significant residuals in InSAR data, especially in the far field. This may be attributed to the residual atmospheric artifact noise and/or the low signal-to-noise ratio of postseismic deformation.
As depicted in Figure 8b, postseismic afterslip was distributed in each fault segment, mainly occurring in the updip shallow portion and the downdip direction of the coseismic slip zone. The F1 and F3 segments exhibited shallow afterslip located in the shallow part of the upper crust, with a slip of <0.3 m, overlapping with the peak area of the coseismic slip. In fault segments F2, F4, and F5, clear slip asperities were observed, with a slip magnitude from 0.2–0.6 m. These slip asperities extend into the ductile shear zone of the lower crust and manifest as deep afterslip, potentially influenced by rheological characteristics. The maximum distribution of afterslip was observed within the area where the coseismic slip deficit occurred in the F2 segment. In this segment, the peak area of the afterslip was primarily characterized by a left-lateral strike-slip, which is identical to the coseismic slip. Apart from the F3 segment, there was almost no afterslip in the coseismic slip zone, indicating a complementary relation between coseismic slip and postseismic afterslip. Overall, the postseismic slip primarily manifested as deep afterslip, with limited afterslip observed in the shallow portion of the upper crust and creeping towards the surface. Our postseismic afterslip model aligns well with the slip distribution studies conducted by He et al. [10], Xiong et al. [7], and Zhao et al. [13]. However, there are slight differences in the details of the afterslip distribution. Our results emphasize the distinctive characteristics of both shallow and deep afterslip more prominently.
We estimated the total moment release of afterslip during the study period to be ~2.544 × 1019 N·m, corresponding to the Mw 6.87 event, which accounts for ~14.62% of the coseismic moment. Our results are significantly higher than those of He et al. [10] (2.42 × 1019 N·m) and Xiong et al. [7] (1.87 × 1019 N·m), which is expected.
4. Discussion
4.1. Seismogenic Fault and Early Postseismic Mechanism
4.1.1. Early Postseismic Deformation Mechanism
The early postseismic deformation process is primarily driven by aseismic afterslip, VR, and PR [44]. Nevertheless, their relative contributions to the early postseismic deformation of the Maduo event are undetermined. We first explored the simulated deformation driven by VR using the low crustal viscosity value of 1.0 × 1018 Pa·s. Our study revealed that 1 year after the mainshock, the simulated deformation (<1.5 cm in the LOS and horizontal displacements direction) in the near and far field driven by VR was smaller than the GPS and InSAR observations (Figure 9a,b). To further analyze the discrepancy, we superimposed the simulated deformation onto the postseismic InSAR deformation field (Figure 4c,g). We found that the simulated deformation is predominantly distributed in the near and far field regions surrounding the seismogenic rupture. We separately calculated the average values of InSAR observation and simulated deformation in the overlapping area to assess the relative proportion of the two. In the near-field region, the contribution of the simulated deformation to the InSAR observations was relatively small, accounting for only ~18% of the near-field InSAR observations. The simulated GPS horizontal displacement only accounted for about 19% of the postseismic GPS observations. In the far-field region, the simulated deformation showed a good overlap with InSAR observation, both in terms of the deformation level (accounting for ~70% of the far-field InSAR deformation) and its spatial distribution. Postseismic GPS (e.g., sites QHMD, MD01, and JDUO) exhibited a similar deformation pattern to InSAR observation in the near field region (Figure 5 and Figure 6), which excluded the effect of pseudo-deformation caused by InSAR noise. This confirms the validity of comparing the simulated deformation and InSAR observation. The above-shown discussion indicates that VR dominates the far-field deformation of seismogenic rupture, with limited contribution to the near-field high-deformation area. The high near-field deformation is mainly driven by postseismic afterslip.
Poroelastic processes predominantly come into effect during the early postseismic period, generally lasting days to months, particularly in the near-field near the region of significant coseismic slip [44]. Considering the potential contribution of PR to the near-field deformation, we investigated the simulated postseismic deformation driven by PR. The result indicated that the deformation induced by PR was mainly distributed in the near-field of seismogenic rupture, with deformation amplitude in the LOS direction < 2.5 mm (the ascending and descending orbits) and in the GPS horizontal direction < 0.5 mm (Figure 9c,d), which can be ignored compared to the high near-field InSAR deformation and GPS displacements observed. Therefore, it can be concluded that the high deformation in the near-field is primarily contributed by postseismic afterslip. Postseismic deformation can be explained by a combination of aseismic afterslip (near-field) and VR effect (near- and far-field). The contribution of PR to the postseismic deformation can be neglected.
4.1.2. Seismogenic Fault and Afterslip
The slope of coseismic geodetic moment release exhibited significant differences with depth in the upper and lower crust (Figure 8c). It gradually increased in the shallow upper crust (0–5 km) and then decreased as depth increased. The slope of postseismic afterslip geodetic moment release showed two distinct peak distributions with depth, indicating a pattern of initial decrease followed by a rapid increase (Figure 8d). These characteristics reveal the heterogeneity and differences in the frictional properties of the fault materials at different depths along the seismogenic rupture.
In addition, the distribution of postseismic afterslip models is associated with the subsurface fluid properties or fault frictional properties of the seismogenic rupture [58]. In this study, postseismic afterslip is primarily distributed in the downdip region of the coseismic slip zone located in the middle-lower crust (Figure 8b), which is in close proximity to the ductile shear zone and is likely influenced by rheological characteristics. The presence of such a deep afterslip, along with the occurrence of only a few aftershocks within the afterslip zone (Figure 8b), suggests that the deep afterslip mechanism may be associated with creep within the ductile shear zone, facilitated by stress perturbations. Considering the rate-and-state friction law [59,60], the distribution of aseismic afterslip may be controlled by the friction characteristic of the rate-strengthening layer below the seismogenic fault [58]. The presence of a rate-strengthening layer could provide the necessary physical condition for deep aseismic afterslip. As the slip distribution in the deep middle-lower crust (≥15 km) may include the influence of the viscoplastic deformation mechanism in the lower crust, the phenomenon of rapid attenuation and increasing slope of seismic moment distribution in the middle-lower crust (Figure 8d) may imply the existence of a relatively weaker material layer (rate-strengthening layer) in the middle-lower crust.
In the postseismic afterslip model (Figure 8b), we observed that the distribution of afterslip was primarily located in the updip shallow portion of the upper crust. The corresponding phenomenon is the postseismic creep observed in the shallow rupture zone one year after the mainshock (Figure 4 and Figure 7). This pattern is considered to be possibly associated with the velocity strengthening in the unconsolidated material [40,61]. We found that “the unconsolidated material” corresponds to the weak sedimentary layer that covers the shallow upper crust in the Maduo rupture area. This could be one of the reasons why partial afterslip is distributed on the updip shallow portion of the upper crust.
Many earthquakes, e.g., the 2010 Maule Mw 8.8 earthquake [62], the 2011 Tohoku Mw 9.0 earthquake [63], and the 2017 Sarpol Zahāb Mw 7.3 earthquake [64], have been found to have overlapping characteristics between shallow coseismic slip and postseismic afterslip. It indicates that the overlapping area continues to release seismic energy after the mainshock. The characteristic was similarly observed in our analysis of the Maduo event (Figure 8b). In the Maduo event, the significant postseismic afterslip in the overlapping region is most likely driven by coseismic residual stress. Because for fault plane with non-uniformly distributed friction media, if all stress is not released during the coseismic stage, it will continue to be released in the postseismic stage in the form of aftershocks and/or aseismic afterslip [65]. Therefore, it is highly likely that elastic recovery of rupture bodies corresponding to stress redistribution occurs within the shallow upper crust of the postseismic rupture.
4.1.3. Postseismic Seismic Moment Release Pattern
The logarithmic trend of the postseismic deformation in the Maduo event is separated from GPS and InSAR data in Section 2.3 (Figure 4i–l and Figure 5). The optimal fitting curves of GPS and InSAR observations reflect the comparatively low delay coefficient (τ), with optimal τ values ranging from 5.1 to 93.6 days. These values are longer than those obtained by Xiong et al. [7] based on a shorter observation period. The τ values for the Maduo event, in our research and Xiong et al. [7], were lower than those estimated for other earthquakes, e.g., the 2015 Gorkha Mw 7.8 earthquake [40,66], meaning that a majority of afterslip is likely to be released in a short-term process.
4.2. Existing Fault Reactivated
We captured a particular deformation signal in the postseismic InSAR time series of the Maduo event, showing the trace of NNW lineament (F6 in Figure 4 and Figure 5). The high deformation on both sides of the lineament trace excludes the effect of topography error because it is higher than the deformation level of error noise (Figure 10b). Furthermore, the field investigation [16] did not identify any geological hazards (e.g., landslides) near the lineament, which excludes the possibility of surface deformation in the area caused by geological hazards. Therefore, we speculate that the lineament could be a preexisting fault (fault F6) that was reactivated after the Maduo event. We found that the lineament (fault F6) identified by InSAR shows a high spatial coincidence with the known Changmahe fault (Figure 10a), indicating that fault F6 belongs to the Changmahe fault.
It is noteworthy that field investigations conducted one day after the mainshock [14,15,16,67] indicate that the Changmahe fault, connected to fault segment F4, displays small field measurement deformation, and exhibits characteristics such as compression and bulging. The Maduo event may affected the Changmahe fault. However, we did not observe a clear undulation/difference on either side of the fault in the coseismic interferogram and deformation field (Figure 2 and Figure S5). Other coseismic studies, e.g., Jin and Fialko [57] and Fang et al. [9], also did not find such signals. Yet, in the early postseismic InSAR deformation field, a clear deformation trace was identified near fault F6 (Figure 4 and Figure 5). Therefore, it is plausible that subsequent motion occurred on the Changmahe fault after the initial SAR acquisition on 26 May 2021. This finding aligns with the postseismic field investigation conclusion of Yang et al. [16].
The postseismic 2.5-D quasi-vertical deformation (Figure 7e–h) reveals a meaningful difference in deformation on both sides of fault F6, with the northeastern side exhibiting uplift and the southwestern side exhibiting subsidence. The corresponding deformation profile (Figure 10b) also indicates a deformation difference of ~0.03 m on both sides of fault F6. This implies that the fault F6 may exhibit a northeast-dipping and thrusting feature. Furthermore, the deformation on both sides of fault F6 shows a clear evolutionary pattern over time (Figure 7e–g). From June 2021, the deformation on both sides of fault F6 exhibited a small deformation level (Figure 7e). By around December 2021, the deformation on both sides of fault F6 reached its peak (Figure 7f), and by May 2022, the deformation had apparently decreased (Figure 7g). This indicates that the slip of fault F6 reached its maximum around December 2021, and thereafter, the fault activity gradually weakened.
We inverted the postseismic slip patterns of fault F6 during the early stage (Figure 10d) and one year (Figure 10e) after the Maduo event to investigate its impact on this fault. As shown in Figure 10d, our inversion result exhibited a notable concordance with Yang et al. [16] in both slip magnitude and distribution, affirming the reliability of our finding. The early-stage inversion result of fault F6 reveals its characteristic of northeastward dipping with a high dip angle. The early stage slip distribution (Figure 10d) reveals that fault F6 experienced slip along its strike, with a significant dip-slip (~0.43 m) at the junction between F6 and F4 segments and a dip-slip asperity (~0.3 m) at a depth of 12 km, indicating a characteristic of thrust compression dislocation. The coseismic rupture of the Maduo event was impeded by the preexisting Changmahe fault, resulting in high-angle compression, bulging, and other features along the fault F6, thereby activating the Changmahe fault (Figure 10c). In addition, no aftershocks were observed along fault F6 (Figure 1c), indicating that the early stage postseismic motion of fault F6 is not caused by aftershocks and corresponds to aseismic slip. The early stage postseismic slip of fault F6 reveals a distinctive mechanism triggered by the mainshock. Major earthquakes can induce changes in the stress distribution within the Earth’s crust. Near the seismic rupture, the crust may accumulate new stress, leading to the reactivation of previously inactive faults influenced by the altered stress conditions. As shown in Figure 11, fault F6 is situated within a pronounced positive dCFS zone. This implies that the Maduo event resulted in an increase in dCFS near Fault F6 (stress loading), thereby promoting subsequent slip along Fault F6. Fault F6, which cuts across fault segment F4, may have acted as the termination of the dynamic rupture along fault segment F4 and the formation of its distinctive curvature during the Maduo event.
Figure 10e indicates that 1 year after the mainshock, fault F6 exhibited deep crustal dip slip (~0.39 m), with a small amount of dip-slip (~0.13 m) observed in the shallow upper crust at the junction between F6 and F4 segments. This indicates that the postseismic afterslip of the Maduo event still exerts a sustained compressive effect on the Changmahe fault. Considering the variation in slip distribution observed in the early stage and one year after the mainshock (Figure 10d,e), fault F6 may exhibit an evolutionary pattern transitioning from high slip in the shallow portion (the early stage after the mainshock) to predominantly deep slip (the one year after the mainshock).
4.3. Potential Seismic Risks around the Maduo Event
Coseismic stress adjustment can lead to the coulomb stress change on neighboring faults. Based on the loading and unloading effects of coulomb stress, seismic risk assessment of active faults can be carried out [68]. By calculating the dCFS in Section 2.7, we evaluated the seismic risk inside the Bayan Har block following the mainshock (Figure 11). We noticed that the Maduo event generated new positive stress changes (>0.1 Mpa) in the middle and eastern segments of the EKLF: the large bend segment in the eastern of Donggei-cuona Lake and the high-seismic-risk Machin-Maqu segment that has attracted widespread attention due to the seismic gap (Figure 11). Interseismic geodetic observations (GPS and InSAR) [22,23,69] indicate that the strain rate at the large bend segment in the eastern of Donggei-cuona Lake is clearly higher compared to other regions, and the faults surrounding it may exist the potential for large earthquake owing to their large locking depth and high slip rate, which should be given attention to in the future.
The KLJF is the southern extension of the EKLF, and its western segment may potentially be connected to the Kunlun Pass Fault [70,71]. The western extension of the KLJF is located at the energy release end of the Maduo event, exhibiting a significant positive stress change (Figure 11). Additionally, significant slip values have also been observed in co- and postseismic slip distributions (Figure 8). Therefore, the westward propagation of the coseismic rupture of the Maduo event may reactivate the fault-locking state of the seismic gap in this segment, increasing the risk of future seismicity in this region.
5. Conclusions
In our research, InSAR and GPS were employed to jointly invert the co- and postseismic slip patterns of the Maduo event. The SBAS-InSAR method was utilized to acquire a deformation time series ~1 year after the mainshock. The VR and PR effects after the mainshock were modeled to determine the relative contribution of early postseismic deformation processes. Modeled the slip distribution of Fault F6 in the early stage and one year after the mainshock, and analyzed its deformation mechanism. The dCFS induced by the Maduo event was calculated to assess the seismic risk on the surrounding faults within the Bayan Har block. The main conclusions are as follows:
- (1)
- Postseismic deformation can be explained by a combination of aseismic afterslip (near-field) and VR effect (near- and far-field). The contribution of PR to the postseismic deformation can be neglected;
- (2)
- The coseismic slip and postseismic afterslip exhibited a clear complementary and partially overlapping relationship. The overlapping area between coseismic slip and postseismic afterslip is likely driven by coseismic residual stress;
- (3)
- The Changmahe fault was reactivated by the Maduo event. The afterslip has continued to exert compression on it in the one year after the mainshock;
- (4)
- Stress analysis indicates that the seismic gaps in the Maqin-Maqu segment and the KLJF will be potential seismic risks in the future.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs16081399/s1, Figure S1: The processing flowchart of SBAS-InSAR and Stacking-InSAR methods; Figure S2: The distribution combination of interference pairs from ascending orbit 99 (a) and descending orbit 106 (b); Figure S3: Deformation profiles (a–h) along measuring lines A–A′, B–B′, C–C′, and D–D′ spanning seismogenic fault; Figure S4: (a,c) represent the deformation observed by InSAR, while (b,d) represent the deformation after removing the effects of viscoelastic relaxation and poroelastic rebound; Figure S5: D-InSAR interferograms (20210520–20210526) from the ascending (a,b) and descending (c,d) orbits of the Maduo event; Figure S6: Observed displacements (a,d,g,j,m,p), best-fit model predictions (b,e,h,k,n,q), and residuals (c,f,i,l,o,r) in coseismic and postseismic (the early stage and 1 year) slip models; Table S1: SAR data and GPS Stations used in co- and postseismic observations.
Author Contributions
Conceptualization, Z.M. and Q.W.; methodology, C.S. and Z.M.; software, W.X. and C.S.; validation, L.H., X.Z. and D.X.; formal analysis, W.X. and L.H.; data curation, C.S. and Z.M.; writing—original draft preparation, C.S. and Z.M.; writing—review and editing, C.S., Z.M., W.X., Q.W. and X.Z.; visualization, D.X.; supervision, Q.W.; project administration, Z.M.; funding acquisition, Z.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the National Key Research and Development Program of China, grant number 2021YFA0715104, the National Natural Science Foundation of China, grant number 42071309, the Natural Science Foundation of Jilin Province, grant number 20220101159JC, and the Graduate Innovation Fund of Jilin University, grant number 2023CX093.
Data Availability Statement
Sentinel-1A/B SAR images were downloaded from the European Space Agency (ESA) (https://scihub.copernicus.eu/dhus/#/home, accessed on 5 August 2022). The ALOS World 3D DEM was downloaded from Japan Aerospace Exploration Agency (JAXA) (https://www.eorc.jaxa.jp/ALOS/en/aw3d30/data/index.htm, accessed on 11 August 2022). The moment tensor solutions of the Maduo event and the historical earthquakes (>M7) within the boundary of the Bayan Har block come from the Global Centroid Moment Tensor project (GCMT, https://www.globalcmt.org/CMTsearch.html, accessed on 1 October 2022). All data from this study can be requested from the corresponding author (Z.M.) via email upon reasonable request.
Acknowledgments
The figures in this study were generated by adopting the Generic Mapping Tools (GMT) [72].
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviation
| SAR | Synthetic Aperture Radar |
| InSAR | Interferometric Synthetic Aperture Radar |
| D-InSAR | Two-pass differential InSAR |
| POT | Pixel offset tracking |
| BOI | Burst-Overlap Interferometry |
| LOS | Line-of-sight |
| SBAS-InSAR | Small baseline subset InSAR |
| EKLF | East Kunlun fault |
| KLJF | Kunlun Pass-Jiangcuo fault |
| DRF | Dari fault |
| MGF | Maduo-Gande fault |
| BYKLF | Bayan Har Mountain Main Peak fault |
| TDCF | Tibet Dagou-Changmahe fault |
| GACOS | General Atmospheric Correction Online Service |
| VR | Viscoelastic relaxation |
| PR | Poroelastic rebound |
| dCFS | Coulomb Failure stress change |
References
- Zhan, Y.; Liang, M.; Sun, X.; Huang, F.; Zhao, L.; Zhan, Y.; Gong, Y.; Han, J.; Li, C.; Zhang, P.; et al. Deep structure and seismogenic pattern of the 2021.5.22 Madoi (Qinghai) MS7.4 earthquake. Chin. J. Geophys. 2021, 64, 2232–2252. (In Chinese) [Google Scholar]
- Li, Z.; Li, W.; Li, T.; Xu, Y.; Su, P.; Guo, P.; Sun, H.; Ha, G.; Chen, G.; Yuan, Z. Seismogenic fault and coseismic surface deformation of the Maduo MS7.4 earthquake in Qinghai, China: A quick report. Seismol. Geol. 2021, 43, 722. [Google Scholar]
- Ren, J.; Xu, X.; Zhang, G.; Wang, Q.; Zhang, Z.; Gai, H.; Kang, W. Coseismic surface ruptures, slip distribution, and 3D seismogenic fault for the 2021 Mw 7.3 Maduo earthquake, central Tibetan Plateau, and its tectonic implications. Tectonophysics 2022, 827, 229275. [Google Scholar] [CrossRef]
- Wang, W.; Fang, L.; Wu, J.; Tu, H.; Chen, L.; Lai, G.; Zhang, L. Aftershock sequence relocation of the 2021 MS7.4 Maduo earthquake, Qinghai, China. Sci. China Earth Sci. 2021, 64, 1371–1380. [Google Scholar] [CrossRef]
- Wang, L.; Gao, H.; Feng, G.; Xu, W. Source parameters and triggering links of the earthquake sequence in central Italy from 2009 to 2016 analyzed with GPS and InSAR data. Tectonophysics 2018, 744, 285–295. [Google Scholar] [CrossRef]
- Wang, X.; Xu, C.; Xiao, Z.; Peng, Y. Source model for buried thrust-dominated earthquakes using partial InSAR displacements: The 2018 Lombok, Indonesia, earthquake sequence. Geophys. J. Int. 2022, 229, 1434–1447. [Google Scholar] [CrossRef]
- Xiong, W.; Chen, W.; Wang, D.; Wen, Y.; Nie, Z.; Liu, G.; Dijin, W.; Yu, P.; Qiao, X.; Zhao, B. Coseismic slip and early afterslip of the 2021 Mw 7.4 Maduo, China earthquake constrained by GPS and InSAR data. Tectonophysics 2022, 840, 229558. [Google Scholar] [CrossRef]
- Xu, G.; Xu, C.; Wen, Y.; Yin, Z. Coseismic and postseismic deformation of the 2016 MW 6.2 Lampa earthquake, southern Peru, constrained by interferometric synthetic aperture radar. J. Geophys. Res. Solid Earth 2019, 124, 4250–4272. [Google Scholar] [CrossRef]
- Fang, J.; Ou, Q.; Wright, T.J.; Okuwaki, R.; Amey, R.M.; Craig, T.J.; Elliott, J.R.; Hooper, A.; Lazecký, M.; Maghsoudi, Y. Earthquake Cycle Deformation Associated with the 2021 Mw 7.4 Maduo (Eastern Tibet) Earthquake: An Intrablock Rupture Event on a Slow-Slipping Fault from Sentinel-1 InSAR and Teleseismic Data. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024268. [Google Scholar] [CrossRef]
- He, L.; Feng, G.; Wu, X.; Lu, H.; Xu, W.; Wang, Y.; Liu, J.; Hu, J.; Li, Z. Coseismic and early postseismic slip models of the 2021 Mw 7.4 Maduo earthquake (western China) estimated by space-based geodetic data. Geophys. Res. Lett. 2021, 48, e2021GL095860. [Google Scholar] [CrossRef]
- Lyu, M.; Chen, K.; Xue, C.; Zang, N.; Zhang, W.; Wei, G. Overall subshear but locally supershear rupture of the 2021 Mw 7.4 Maduo earthquake from high-rate GNSS waveforms and three-dimensional InSAR deformation. Tectonophysics 2022, 839, 229542. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, W.; Du, H.; Samsonov, S.; Yi, L. Supershear rupture during the 2021 MW 7.4 Maduo, China, earthquake. Geophys. Res. Lett. 2022, 49, e2022GL097984. [Google Scholar] [CrossRef]
- Zhao, D.; Qu, C.; Chen, H.; Shan, X.; Song, X.; Gong, W. Tectonic and geometric control on fault kinematics of the 2021 Mw7.3 Maduo (China) earthquake inferred from interseismic, coseismic, and postseismic InSAR observations. Geophys. Res. Lett. 2021, 48, e2021GL095417. [Google Scholar] [CrossRef]
- Pan, J.; Bai, M.; Li, C.; Liu, F.; Li, H.; Liu, D.; Chevalier, M.; Wu, K.; Wang, P.; Lu, H. Coseismic surface rupture and seismogenic structure of the 2021-05-22 Maduo (Qinghai) MS 7.4 earthquake. Acta Geol. Sin. 2021, 95, 1655–1670. [Google Scholar]
- Yuan, Z.; Li, T.; Su, P.; Sun, H.; Ha, G.; Guo, P.; Chen, G.; Thompson Jobe, J. Large surface-rupture gaps and low surface fault slip of the 2021 Mw 7.4 Maduo earthquake along a low-activity strike-slip fault, Tibetan Plateau. Geophys. Res. Lett. 2022, 49, e2021GL096874. [Google Scholar]
- Yang, Y.; Xu, Q.; Hu, J.; Wang, Y.; Dong, X.; Chen, Q.; Zhang, Y.; Li, H. Source Model and Triggered Aseismic Faulting of the 2021 Mw 7.3 Maduo Earthquake Revealed by the UAV-Lidar/Photogrammetry, InSAR, and Field Investigation. Remote Sens. 2022, 14, 5859. [Google Scholar] [CrossRef]
- Zhao, L.; Xu, W.; Fang, N.; Liu, J.; Feng, G. Coseismic and early postseismic fault slip model and the seismogenic fault friction properties of the 2021 Qinghai Madoi MW7.3 earthquake. Chin. J. Geophys. 2023, 66, 1086–1097. (In Chinese) [Google Scholar]
- Jin, Z.; Fialko, Y.; Yang, H.; Li, Y. Transient deformation excited by the 2021 M7. 4 Maduo (China) earthquake: Evidence of a deep shear zone. J. Geophys. Res. Solid Earth 2023, 128, e2023JB026643. [Google Scholar] [CrossRef]
- Wei, S.; Zeng, H.; Shi, Q.; Liu, J.; Luo, H.; Hu, W.; Li, Y.; Wang, W.; Ma, Z.; Liu-Zeng, J. Simultaneous rupture propagation through fault bifurcation of the 2021 Mw7.4 Maduo earthquake. Geophys. Res. Lett. 2022, 49, e2022GL100283. [Google Scholar] [CrossRef]
- Deng, Q. Active tectonics and earthquake activities in China. Earth Sci. Front. 2003, 10, 66. (In Chinese) [Google Scholar]
- Qu, C. Building to the active tectonic database of China. Seismol. Geol. 2008, 30, 298–304. [Google Scholar]
- Diao, F.; Xiong, X.; Wang, R.; Walter, T.R.; Wang, Y.; Wang, K. Slip rate variation along the Kunlun fault (Tibet): Results from new GPS observations and a viscoelastic earthquake-cycle deformation model. Geophys. Res. Lett. 2019, 46, 2524–2533. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.K. Present-day crustal deformation of continental China derived from GPS and its tectonic implications. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef]
- Molnar, P.; Deng, Q. Faulting associated with large earthquakes and the average rate of deformation in central and eastern Asia. J. Geophys. Res. Solid Earth 1984, 89, 6203–6227. [Google Scholar] [CrossRef]
- Rosen, P.A.; Gurrola, E.; Sacco, G.F.; Zebker, H. The InSAR Scientific Computing Environment. In Proceedings of the EUSAR 2012: 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012; VDE: Berlin, Germany, 2012; pp. 730–733. [Google Scholar]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic atmospheric correction model for interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Pepe, A.; Lanari, R. On the extension of the minimum cost flow algorithm for phase unwrapping of multitemporal differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Gray, A.; Short, N.; Mattar, K.; Jezek, K. Velocities and flux of the Filchner Ice Shelf and its tributaries determined from speckle tracking interferometry. Can. J. Remote Sens. 2001, 27, 193–206. [Google Scholar] [CrossRef]
- Rott, H.; Stuefer, M.; Siegel, A.; Skvarca, P.; Eckstaller, A. Mass fluxes and dynamics of Moreno glacier, southern Patagonia icefield. Geophys. Res. Lett. 1998, 25, 1407–1410. [Google Scholar] [CrossRef]
- Solaro, G.; De Novellis, V.; Castaldo, R.; De Luca, C.; Lanari, R.; Manunta, M.; Casu, F. Coseismic fault model of Mw 8.3 2015 Illapel earthquake (Chile) retrieved from multi-orbit Sentinel1-A DInSAR measurements. Remote Sens. 2016, 8, 323. [Google Scholar] [CrossRef]
- Hu, J.; Liu, J.; Li, Z.; Zhu, J.; Wu, L.; Sun, Q.; Wu, W. Estimating three-dimensional coseismic deformations with the SM-VCE method based on heterogeneous SAR observations: Selection of homogeneous points and analysis of observation combinations. Remote Sens. Environ. 2021, 255, 112298. [Google Scholar] [CrossRef]
- Liu, J.; Hu, J.; Li, Z.; Zhu, J.; Sun, Q.; Gan, J. A method for measuring 3-D surface deformations with InSAR based on strain model and variance component estimation. IEEE Trans. Geosci. Remote Sens. 2017, 56, 239–250. [Google Scholar] [CrossRef]
- Agram, P.; Jolivet, R.; Riel, B.; Lin, Y.; Simons, M.; Hetland, E.; Doin, M.P.; Lasserre, C. New radar interferometric time series analysis toolbox released. Eos Trans. Am. Geophys. Union 2013, 94, 69–70. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Price, E.J. Phase gradient approach to stacking interferograms. J. Geophys. Res. Solid Earth 1998, 103, 30183–30204. [Google Scholar] [CrossRef]
- Yue, H.; Sun, J.; Wang, M.; Shen, Z.; Li, M.; Xue, L.; Lu, W.; Zhou, Y.; Ren, C.; Lay, T. The 2019 Ridgecrest, California earthquake sequence: Evolution of seismic and aseismic slip on an orthogonal fault system. Earth Planet. Sci. Lett. 2021, 570, 117066. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
- Hong, S.; Liu, M. Postseismic deformation and afterslip evolution of the 2015 Gorkha earthquake constrained by InSAR and GPS observations. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020230. [Google Scholar]
- Fujiwara, S.; Nishimura, T.; Murakami, M.; Nakagawa, H.; Tobita, M.; Rosen, P.A. 2.5-D surface deformation of M6.1 earthquake near Mt Iwate detected by SAR interferometry. Geophys. Res. Lett. 2000, 27, 2049–2052. [Google Scholar] [CrossRef]
- Wang, R.; Parolai, S.; Ge, M.; Jin, M.; Walter, T.R.; Zschau, J. The 2011 Mw 9.0 Tohoku earthquake: Comparison of GPS and strong-motion data. Bull. Seismol. Soc. Am. 2013, 103, 1336–1347. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Y.; Qian, L.; Meng, G. Early postseismic deformation of the 2010 Mw 6.9 Yushu earthquake and its implication for lithospheric rheological properties. Geophys. Res. Lett. 2022, 49, e2022GL098942. [Google Scholar] [CrossRef]
- Peña, C.; Metzger, S.; Heidbach, O.; Bedford, J.; Bookhagen, B.; Moreno, M.; Oncken, O.; Cotton, F. Role of poroelasticity during the early postseismic deformation of the 2010 Maule megathrust earthquake. Geophys. Res. Lett. 2022, 49, e2022GL098144. [Google Scholar]
- Bürgmann, R.; Dresen, G. Rheology of the lower crust and upper mantle: Evidence from rock mechanics, geodesy, and field observations. Annu. Rev. Earth Planet. Sci. 2008, 36, 531–567. [Google Scholar] [CrossRef]
- Wang, R.; Lorenzo-Martín, F.; Roth, F. PSGRN/PSCMP—A new code for calculating co-and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Comput. Geosci. 2006, 32, 527–541. [Google Scholar] [CrossRef]
- Song, X.; Wang, S.; Pan, S.; Song, J. Deep seismotectonic environment of the 2021 Madoi Ms7.4 earthquake. Seismol. Geol. 2021, 43, 757–770. [Google Scholar]
- Liu, L.; Li, Y.; Zhu, L.; Ji, L. Influence of the 1947 Dari M7.7 earthquake on stress evolution along the boundary fault of the Bayan Har block: Insights from numerical simulation. Chin. J. Geophys. 2021, 64, 2221–2231. (In Chinese) [Google Scholar]
- Peltzer, G.; Rosen, P.; Rogez, F.; Hudnut, K. Poroelastic rebound along the Landers 1992 earthquake surface rupture. J. Geophys. Res. Solid Earth 1998, 103, 30131–30145. [Google Scholar] [CrossRef]
- Wang, R.; Kümpel, H.-J. Poroelasticity: Efficient modeling of strongly coupled, slow deformation processes in a multilayered half-space. Geophysics 2003, 68, 705–717. [Google Scholar] [CrossRef]
- Chen, H.; Qu, C.; Zhao, D.; Ma, C.; Shan, X. Rupture kinematics and coseismic slip model of the 2021 Mw 7.3 Maduo (China) earthquake: Implications for the seismic hazard of the Kunlun fault. Remote Sens. 2021, 13, 3327. [Google Scholar] [CrossRef]
- Hong, S.; Liu, M.; Liu, T.; Dong, Y.; Chen, L.; Meng, G.; Xu, Y. Fault Source Model and Stress Changes of the 2021 Mw 7.4 Maduo Earthquake, China, Constrained by InSAR and GPS Measurements. Bull. Seismol. Soc. Am. 2022, 112, 1284–1296. [Google Scholar] [CrossRef]
- Liu, J.; Hu, J.; Li, Z.; Ma, Z.; Wu, L.; Jiang, W.; Feng, G.; Zhu, J. Complete three-dimensional coseismic displacements due to the 2021 Maduo earthquake in Qinghai Province, China from Sentinel-1 and ALOS-2 SAR images. Sci. China Earth Sci. 2022, 65, 687–697. [Google Scholar] [CrossRef]
- Gonzalez-Ortega, A.; Fialko, Y.; Sandwell, D.; Alejandro Nava-Pichardo, F.; Fletcher, J.; Gonzalez-Garcia, J.; Lipovsky, B.; Floyd, M.; Funning, G. El Mayor-Cucapah (Mw 7.2) earthquake: Early near-field postseismic deformation from InSAR and GPS observations. J. Geophys. Res. Solid Earth 2014, 119, 1482–1497. [Google Scholar] [CrossRef]
- Tang, X.; Guo, R.; Xu, J.; Zheng, Y. Role of Poroelasticity and Viscoelasticity during the Postseismic Deformation of the 2021 Mw 7.4 Maduo, China, Earthquake. Seismol. Res. Lett. 2023, 94, 2192–2201. [Google Scholar] [CrossRef]
- Yue, H.; Shen, Z.-K.; Zhao, Z.; Wang, T.; Cao, B.; Li, Z.; Bao, X.; Zhao, L.; Song, X.; Ge, Z. Rupture process of the 2021 M7.4 Maduo earthquake and implication for deformation mode of the Songpan-Ganzi terrane in Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2022, 119, e2116445119. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Fialko, Y. Coseismic and early postseismic deformation due to the 2021 M7.4 Maduo (China) earthquake. Geophys. Res. Lett. 2021, 48, e2021GL095213. [Google Scholar] [CrossRef]
- Dianala, J.D.B.; Jolivet, R.; Thomas, M.Y.; Fukushima, Y.; Parsons, B.; Walker, R. The relationship between seismic and aseismic slip on the Philippine Fault on Leyte Island: Bayesian modeling of fault slip and geothermal subsidence. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020052. [Google Scholar] [CrossRef]
- Dieterich, J.H. Earthquake nucleation on faults with rate-and state-dependent strength. Tectonophysics 1992, 211, 115–134. [Google Scholar] [CrossRef]
- Marone, C. Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 1998, 26, 643–696. [Google Scholar] [CrossRef]
- Marone, C.J.; Scholtz, C.; Bilham, R. On the mechanics of earthquake afterslip. J. Geophys. Res. Solid Earth 1991, 96, 8441–8452. [Google Scholar] [CrossRef]
- Bedford, J.; Moreno, M.; Baez, J.C.; Lange, D.; Tilmann, F.; Rosenau, M.; Heidbach, O.; Oncken, O.; Bartsch, M.; Rietbrock, A. A high-resolution, time-variable afterslip model for the 2010 Maule Mw = 8.8, Chile megathrust earthquake. Earth Planet. Sci. Lett. 2013, 383, 26–36. [Google Scholar] [CrossRef]
- Iinuma, T.; Hino, R.; Uchida, N.; Nakamura, W.; Kido, M.; Osada, Y.; Miura, S. Seafloor observations indicate spatial separation of coseismic and postseismic slips in the 2011 Tohoku earthquake. Nat. Commun. 2016, 7, 13506. [Google Scholar] [CrossRef]
- Liu, X.; Xu, W. Logarithmic model joint inversion method for coseismic and postseismic slip: Application to the 2017 Mw 7.3 Sarpol Zahāb earthquake, Iran. J. Geophys. Res. Solid Earth 2019, 124, 12034–12052. [Google Scholar] [CrossRef]
- Yabe, S.; Ide, S. Why do aftershocks occur within the rupture area of a large earthquake? Geophys. Res. Lett. 2018, 45, 4780–4787. [Google Scholar] [CrossRef]
- Zhao, B.; Bürgmann, R.; Wang, D.; Tan, K.; Du, R.; Zhang, R. Dominant controls of downdip afterslip and viscous relaxation on the postseismic displacements following the Mw7.9 Gorkha, Nepal, earthquake. J. Geophys. Res. Solid Earth 2017, 122, 8376–8401. [Google Scholar] [CrossRef]
- Pan, J.; Li, H.; Chevalier, M.-L.; Tapponnier, P.; Bai, M.; Li, C.; Liu, F.; Liu, D.; Wu, K.; Wang, P. Co-seismic rupture of the 2021, Mw7.4 Maduo earthquake (northern Tibet): Short-cutting of the Kunlun fault big bend. Earth Planet. Sci. Lett. 2022, 594, 117703. [Google Scholar] [CrossRef]
- Hua, J.; Zhao, D.; Shan, X.; Qu, C.; Zhang, Y.; Gong, W.; Wang, Z.; Li, C.; Zhao, L.; Li, Y.; et al. Coseismic deformation field, slip distribution and Coulomb stress disturbance of the 2021 MW7.3 Maduo earthquake using sentinel-1 InSAR observations. Seismol. Geol. 2021, 43, 677–691. [Google Scholar]
- Zhu, L.; Ji, L.; Liu, C. Interseismic slip rate and locking along the Maqin–Maqu Segment of the East Kunlun Fault, Northern Tibetan Plateau, based on Sentinel-1 images. J. Asian Earth Sci. 2021, 211, 104703. [Google Scholar] [CrossRef]
- Ha, G.; Liu, J.; Ren, Z.; Zhu, X.; Bao, G.; Wu, D.; Zhang, Z. The Interpretation of Seismogenic Fault of the Maduo Mw 7.3 Earthquake, Qinghai Based on Remote Sensing Images—A Branch of the East Kunlun Fault System. J. Earth Sci. 2022, 33, 857–868. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.K.; Wang, Y.Z.; Bürgmann, R.; Wang, F.; Zhang, P.Z.; Liao, H.; Zhang, R.; Wang, Q.; Jiang, Z.S. Postseismic deformation of the 2008 Wenchuan earthquake illuminates lithospheric rheological structure and dynamics of eastern Tibet. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022399. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).