Analytical Coherent Detection in High-Resolution Dual-Polarimetric Sea Clutter with Independent Inverse Gamma Textures

Abstract

Polarization diversity has been widely used in maritime radars to improve target detection performance. Full utilization of the polarimetric characteristics of sea clutter is the key to designing effective polarimetric detectors. For high-resolution maritime radars, the HH-HV dual-polarization is an affordable and effective mode to monitor small targets, owing to the simple configuration of single-polarimetric transmit and dual-polarimetric reception and lower clutter powers at the HH and HV polarizations. Enlightened by the analytical coherent detector in compound-Gaussian clutter with inverse Gamma texture, this paper investigates dual-polarimetric coherent detection in dual-polarimetric compound-Gaussian clutter with independent inverse Gamma distributed textures. The analytical dual-polarimetric near-optimum coherent detector is derived, which is a fusion of the generalized likelihood ratio test linear threshold detectors (GLRT-LTDs) at the two polarizations. For short, it is referred to as the P-GLRT-LTD. It is proven that the P-GLRT-LTD is of constant false alarm rate with respect to the Doppler steering vector, scale parameters of textures, and speckle covariance matrices. Moreover, the thresholds of the P-GLRT-LTD are given analytically. Experiments using simulated sea clutter data with the estimated scale and shape parameters from the two measured intelligent pixel processing radar (IPIX) datasets and two measured IPIX datasets with test targets are made to compare P-GLRT-LTD with other existing dual-polarimetric coherent detectors. The results show that the P-GLRT-LTD attains the same detection performance as the existing best-performance detector. The P-GLRT-LTD has a lower computational cost than the existing best-performing one.

1. Introduction

Multi-polarimetric joint processing is an effective approach to improving target detection and classification abilities of maritime radars because radar echoes at different polarizations provide more information on targets and sea clutter. Multi-polarimetric target detection methods for maritime radars have been developed for a long time, and many classic and simple detectors are presented [1,2,3,4,5,6,7]. For floating and low-velocity sea-surface small targets, single-polarimetric high-resolution maritime radars encounter the ‘bottleneck’ in detection ability in short coherent processing interval (CPI), due to the small and fluctuant radar cross-section (RCS) of targets, the inseparability between target echoes and sea clutter in the Doppler domain, and the strong non-Gaussianity of high-resolution sea clutter. Multi/dual-polarimetric radars provide additional dimensions to break through the bottleneck in detection ability.

Thirty years ago, polarimetric radars were successfully used in small target detection [8]. With technique development, dual-polarimetric coherent radars are an affordable and effective choice for small target detection and classification [9]. In the dual-polarimetric mode, it is a primary problem whether vertical or horizontal polarization is used at transmission. Polarimetric characteristics of sea clutter are the main foundation of selection. In high spatial resolution and low grazing angles, HH and HV polarimetric sea clutter have much lower powers than the VV polarization, from 5 to 10 decibels [10]. When horizontal polarization is employed for transmission, a disadvantage is that sea spikes are much stronger at HH than at VV polarization [11]. Owing to the long persistent time of sea spikes up to several tenths of a second and narrow Doppler bandwidths, it is difficult to exclude false alarms from sea spikes at adaptive coherent detection in CPI of several tens of milliseconds. False alarms from sea spikes are excluded by the interscan data processing [12,13,14]. Therefore, the dual-polarimetric mode of horizontal transmission and dual-polarimetric reception is a good choice for the detection of floating and low-velocity small targets in sea clutter. The work in this paper focuses on this mode.

Polarization diversity detection can trace back to the 1990s. The optimal polarization detector (OPD) and the polarimetric matched filter (PMF) are proposed under the ideal assumption of known polarization scattering matrices of target and clutter [2]. In [5], the polarization adaptive matched filter (P-AMF) detector in correlated Gaussian noise is proposed for polarized coherent radars with two reception channels. The P-AMF detector can be used only in very low-resolution maritime polarized radars because of its correlated Gaussian assumption.

High-resolution sea clutter at multiple polarization channels can be modeled by compound-Gaussian models with different amplitudes and Doppler spectral characteristics at individual channels. In this case, it is a difficult task to develop optimal or suboptimal coherent detectors. In [7], the dual-polarimetric Rao test and Wald test detectors are derived by the two-step method [7]. The two detectors have a constant false alarm rate (CFAR) with respect to the texture statistics. However, it should be noted that the shortcoming of the detectors is that the texture distributions are unavailable in design, which results in a severe loss in detection performance. In [15], the polarimetric-spatial adaptive subspace matched filter (P-ASMF) detector in compound-Gaussian clutter is constructed. The textures at individual polarizations are assumed to share an inverse Gamma distribution for analytical expression. It can be directly extended to the polarimetric-Doppler domain to derive the P-ASMF-GLRT-LTD. It is a direct extension of the GLRT-LTD, the analytical near-optimum coherent detector in single polarized compound-Gaussian clutter with inverse Gamma texture [16]. In the P-ASMF-GLRT-LTD, the block diagonal speckle covariance matrix at the HH-HV dual-polarization replaces the speckle covariance matrix in the GLRT-LTD. However, the shortcoming of the P-ASMF-GLRT-LTD is obvious. The ideal assumption that the textures at the two polarizations follow the same distribution limits its application in measured high-resolution sea clutter data. It is well known that high-resolution sea clutters have different power levels and shape parameters at different polarizations [10]. The model mismatch brings an inevitable performance loss. In a recent work [17], the dual-polarimetric GLRT and the maximum a posteriori (MAP) estimates of unknown textures are combined to construct an analytical P-MAP-GLRT detector. Owing to the full utilization of the texture distributions at the two polarizations, the P-MAP-GLRT detector achieves considerably good detection performance in the measured data [18], where the textures are assumed to be independent or uncorrelated.

In this paper, we investigate the coherent detection in dual-polarimetric compound-Gaussian clutter with different inverse Gamma textures at two polarizations, enlightened by the thinking in the GLRT-LTD [17]. When the textures at the two polarizations are assumed to be independent, the analytical dual-polarimetric near-optimum coherent detector is derived, which is referred to as the P-GLRT-LTD. In substance, the P-GLRT-LTD is a fusion of the GLRT-LTDs at the two polarizations. Further, its CFAR properties are analyzed, and the decision thresholds are derived. Moreover, the adaptive P-GLRT-LTD is compared with existing dual-polarized adaptive detectors in simulated and measured data. Experimental results show that the proposed P-GLRT-LTD achieves better detection performance.

This paper is organized as follows: Section 2 describes the dual-polarimetric coherent detection problem and reviews the dual-polarimetric compound-Gaussian sea clutter model with independent inverse Gamma textures. Section 3 proposes the P-GLRT-LTD and its adaptive version and analyzes their CFAR properties. In Section 4, simulated data and measured data from the IPIX radar database are used to evaluate the performance of the P-GLRT-LTD and its adaptive version. A comparison with other dual-polarimetric coherent detectors is given. Finally, we conclude our paper in Section 5.

2. Problem Description of Dual-Polarimetric Coherent Target Detection in Sea Clutter

For dual-polarimetric high-resolution maritime radars to find small targets, the polarization mode considers both the power level of sea clutter and affordability. Due to the lower powers of sea clutter at HH and HV polarizations, the dual-polarimetric mode of horizontal transmit and horizontal/vertical receive, as shown in Figure 1, is suitable for small target detection and implementation at a low cost.

In high-resolution maritime radars with the dual-polarimetric configuration in Figure 1, moving target detection in a coherent processing interval (CPI) boils down to the following binary hypothesis test:

$$\{\begin{array}{l}{\mathrm{H}}_0:x=c=\left[\begin{array}{c}{c}_{HH}\\ c_{HV}\end{array}\right];x_p=c_p=\left[\begin{array}{c}{c}_{HH,p}\\ c_{HV,p}\end{array}\right],p=1,2,\cdots ,P,\\ {\mathrm{H}}_1:x=s+c=\left[\begin{array}{c}{a}_{HH}p(v_R)\\ a_{HV}p(v_R)\end{array}\right]+\left[\begin{array}{c}{c}_{HH}\\ c_{HV}\end{array}\right];x_p=c_p=\left[\begin{array}{c}{c}_{HH,p}\\ c_{HV,p}\end{array}\right].\end{array}$$

(1)

where c_HH and c_HV are the N × 1 complex backscattering echoes from the sea surface received at the HH and HV channels at one cell under test (CUT), respectively; c_HH,p and c_HV,p are the complex back-scattering echoes from the sea surface at the reference cells around the CUT; s is a 2N × 1 complex target return stacked from the target returns at the two polarizations; a_HH and a_HV are the complex amplitudes of the target; and p(v_R) and ν_R are the Doppler steering vector and radial velocity of the target, respectively. Target returns are simply modeled as follows:

$$\begin{array}{l}s=\left[\begin{array}{c}{a}_{HH}p({\nu }_R)\\ a_{HV}p({\nu }_R)\end{array}\right], \\ p({\nu }_R)={\left[1,\exp \left(\frac{4\pi j{\nu }_R\Delta t}{\lambda }\right),\cdots ,\exp \left(\frac{4\pi j(N-1){\nu }_R\Delta t}{\lambda }\right)\right]}^T,\end{array}$$

(2)

where λ and Δt are the operating wavelength and pulse repetition interval (PRI) of the radar, respectively, and the superscript ‘T’ denotes the transpose. Because the complex amplitudes of target returns at the two polarizations depend on their polarimetric scattering characteristics, radars need to detect targets of various different polarimetric characteristics. Therefore, the complex amplitudes a_HH and a_HV in (2) are assumed to be unknown constants without any prior information and are estimated from the radar echoes at the CUT, like in the GLRT tests [5,6,7,15,16,17]. In this way, the key to developing dual-polarimetric analytical coherent detection is the model of dual-polarimetric high-resolution sea clutter.

At low grazing angles and high spatial resolution (for example, range resolution is high up to the order of meters), spiker sea clutter is often modeled by the compound-Gaussian model with the inverse Gamma textures or the generalized Pareto intensity distributions [16]. In a CPI of a dozen milliseconds, dual-polarimetric sea clutter vectors can be modeled by the spherically invariant random vector (SIRV) model, where the textures at the two polarizations are random variables following the inverse Gamma distributions. It should be noted that texture and speckle are sometimes correlated; their independence assumption is mainly tractability in mathematics, and the mismatch to real radar data brings some loss in detection performance [19,20,21]. The SIRV model of the HH-HV dual-polarimetric sea clutter is represented as follows [17]:

$$\begin{array}{l}c=\left[\begin{array}{c}{c}_{HH}\\ c_{HV}\end{array}\right]=\left[\begin{array}{c} \sqrt{{\tau }_{HH}}{u}_{HH}\\ \sqrt{{\tau }_{HV}}{u}_{HV}\end{array}\right], u=\left[\begin{array}{c}{u}_{HH}\\ u_{HV}\end{array}\right]\sim ℂ\mathbb{N}\left(0,\left[\begin{array}{cc}{M}_{HH}& 0\\ 0& M_{HV}\end{array}\right]\right),\\ {\tau }_{HH}\sim p_{IG}({\tau }_{HH};b_{HH},{\upsilon }_{HH}),\\ {\tau }_{HV}\sim p_{IG}({\tau }_{HV};b_{HV},{\upsilon }_{HV}),\\ b_{HH}=E\left\{{\tau }_{HH}\right\},b_{HV}=E\left\{{\tau }_{HV}\right\},{\upsilon }_{HH},{\upsilon }_{HV}>1\\ p_{IG}(\tau ;b,\upsilon )=\frac{{(\upsilon -1)}^{\upsilon }}{b\Gamma (\upsilon )}{\left(\frac{b}{\tau }\right)}^{\upsilon +1}\exp \left(-\frac{(\upsilon -1)b}{\tau }\right),\tau >0.\end{array}$$

(3)

where b_HH and b_HV are the scale parameters/powers; υ_HH and υ_HV are the shape parameters of the texture distributions at the two polarizations; and Γ(●) is the Gamma function. When the texture follows the inverse Gamma distribution in Equation (3), the amplitude probability density function (apdf) of sea clutter has an analytical expression, which is as follows:

$$p\left(z;b,\upsilon \right)=\frac{2\upsilon z}{b(\upsilon -1)}{\left[1+\frac{z^2}{b(\upsilon -1)}\right]}^{-\left(\upsilon +1\right)},z>0$$

(4)

In the model laid out in Equation (3), the independence of the speckle vectors at the HH and HV polarizations is based on the physical property of the polarimetric scattering characteristics of the sea surface [1,2,3,4,5,6]. The textures of sea clutter are mainly owing to the power modulation of long waves (swells and wind waves of long wavelength) on the sea surface for the backscattering Bragg scattering component [22,23,24]. Texture statistics are affected by many factors. In the full-polarized sea clutter IPIX radar database [18], the texture correlations of sea clutter at the HH and HV polarizations are high. Up to now, no relevant analysis on the texture polarization correlation of sea clutter has been found. In existing polarimetric coherent detection in sea clutter, textures of sea clutter at different polarization channels are assumed to be independent for tractability in mathematics. Of course, for dual-polarimetric sea clutter of correlated textures at polarimetric channels, the mismatch of the assumption brings some loss in detection performance. Here, the textures of sea clutter at the HH and HV polarizations are also assumed to be independent.

3. Near-Optimum Coherent Detector in Dual-Polarimetric SIRV Clutter with Independent Inverse Gamma Textures

This section first derives the near-optimum coherent detector in dual-polarimetric SIRV clutter with independent inverse Gamma textures along the path of the GLRT-LTD [15]. This analytical detector is abbreviated as the P-GLRT-LTD. Further, its CFAR property and CFAR thresholds are analyzed and given. At last, the adaptive P-GLRT-LTD is given, and its approximate CFAR property is testified by simulation.

3.1. Dual-Polarimetric Near-Optimum Coherent Detector

For the dual-polarimetric detection problem in (Equations (1) and (3)), when the two speckle covariance matrices, and texture distributions are known, the near-optimum coherent detector is the generalized likelihood ratio test (GLRT), given as follows:

$$\frac{\underset{a\in {ℂ}^2}{\max }{\displaystyle \underset{\tau \in {ℝ}_{+}^2}{\iint }f\left(x;{\mathrm{H}}_1,a,\tau \right)p\left(\tau \right)d\tau }}{{\displaystyle \underset{\tau \in {ℝ}_{+}^2}{\iint }f\left(x;{\mathrm{H}}_0,\tau \right)p\left(\tau \right)d\tau }}\begin{array}{c}\stackrel{H_1}{>}\\ \underset{H_0}{<}\end{array}\eta$$

(5)

where τ = [τ_HH,τ_HV]^T is the texture vector with a pdf p(τ) and a = [a_HH, a_HV]^T is the unknown complex amplitude of target returns at the two polarizations. Under the Neyman–Pearson criterion, the optimum coherent detector is the likelihood ratio test (LRT) when a signal is known [25]. When the unknown complex amplitudes of target echoes in Equation (5) are replaced by their maximum likelihood (ML) estimates, the GLRT (Equation (5)) suffers an inevitable loss in optimality, and thus the GLRT is called the near-optimum coherent detector. For most biparametric compound-Gaussian clutter, analytical near-optimum detectors have been employed [26].

In terms of the model in Equations (1) and (3), the ML estimates of the two complex amplitudes are given as follows:

$${\widehat{a}}_{HH}=\frac{p^H({\nu }_R)M_{HH}^{-1}{x}_{HH}}{p^H({\nu }_R)M_{HH}^{-1}p({\nu }_R)},{\widehat{a}}_{HV}=\frac{p^H({\nu }_R)M_{HV}^{-1}{x}_{HV}}{p^H({\nu }_R)M_{HV}^{-1}p({\nu }_R)}.$$

(6)

Substituting Equation (6) into Equation (5), the GLRT detector can be reformulated into Equation (7) on the bottom of this page, where the random variables ξ_MF,HH and ξ_MF,HV are the test statistics of the MF detectors at the HH and HV polarizations. The existence of an analytical test statistic in Equation (7) depends on the form of the joint pdf of the textures and whether the two integrations of the numerator and denominator of Equation (7) have explicit solutions. In the single polarization, the inverse Gamma texture assures the analytical GLRT-LTD [16].

$$\begin{array}{l}\frac{{\displaystyle \underset{\tau \in {ℝ}_{+}^2}{\iint }\frac{1}{{\tau }_{HH}^N{\tau }_{HV}^N}\exp \left(-\frac{x_{HH}^H{M}_{HH}^{-1}{x}_{HH}-{\xi }_{MF}(x_{HH})}{{\tau }_{HH}}-\frac{x_{HV}^H{M}_{HV}^{-1}{x}_{HV}-{\xi }_{MF}(x_{HV})}{{\tau }_{HV}}\right)p\left(\tau \right)d\tau }}{{\displaystyle \underset{\tau \in {ℝ}_{+}^2}{\iint }\frac{1}{{\tau }_{HH}^N{\tau }_{HV}^N}\exp \left(-\frac{x_{HH}^H{M}_{HH}^{-1}{x}_{HH}}{{\tau }_{HH}}-\frac{x_{HV}^H{M}_{HV}^{-1}{x}_{HV}}{{\tau }_{HV}}\right)p\left(\tau \right)d\tau }}\begin{array}{c}\stackrel{H_1}{>}\\ \underset{H_0}{<}\end{array}\eta \\ {\xi }_{MF}({\nu }_R;x_{HH})=\frac{{\left|p^H({\nu }_R)M_{HH}^{-1}{x}_{HH}\right|}^2}{p^H({\nu }_R)M_{HH}^{-1}p({\nu }_R)},\\ {\xi }_{MF}({\nu }_R;x_{HV})=\frac{{\left|p^H({\nu }_R)M_{HV}^{-1}{x}_{HV}\right|}^2}{p^H({\nu }_R)M_{HV}^{-1}p({\nu }_R)},\end{array}$$

(7)

Assume that the textures at the two polarizations are independent, as they are in most polarimetric coherent detectors. When the two independent textures follow the inverse Gamma distributions, i.e.,:

$$p\left(\tau \right)=p_{IG}({\tau }_{HH};b_{HH},{\upsilon }_{HH})p_{IG}({\tau }_{HV};b_{HV},{\upsilon }_{HV})$$

(8)

In this case, the integrated functions in the numerator and denominator in Equation (7) are variable-separable, and the double integrations are reduced to the product of the two integrations. The two independent textures bring tractability to mathematics, though independence does not always hold in complex sea clutter environments. For simplification, we consider the part relevant to a polarization on the right-hand side of Equation (7). Each part can be written into:

$$\begin{array}{l}\zeta (x;b,\upsilon )=\frac{{\displaystyle {\int }_0^{+\infty }\frac{1}{{\tau }^N}\exp \left(-\frac{x^H{M}^{-1}x-{\xi }_{MF}(x)}{\tau }\right)p_{IG}(\tau ;b,\upsilon )d\tau }}{{\displaystyle {\int }_0^{+\infty }\frac{1}{{\tau }^N}\exp \left(-\frac{x^H{M}^{-1}x}{\tau }\right)p_{IG}(\tau ;b,\upsilon )d\tau }}\\ =\frac{{\displaystyle {\int }_0^{+\infty }\frac{b^{\upsilon +1}}{{\tau }^{N+\upsilon +1}}\exp \left(-\frac{x^H{M}^{-1}x-{\xi }_{MF}(x)+(\upsilon -1)b}{\tau }\right)d\tau }}{{\displaystyle {\int }_0^{+\infty }\frac{b^{\upsilon +1}}{{\tau }^{N+\upsilon +1}}\exp \left(-\frac{x^H{M}^{-1}x+(\upsilon -1)b}{\tau }\right)d\tau }}.\end{array}$$

(9)

In terms of the property of the Gamma integral:

$${\displaystyle {\int }_0^{+\infty }\frac{1}{{\tau }^{\alpha +1}}}\exp \left(-\frac{A}{\tau }\right)d\tau =\frac{\Gamma (\alpha )}{A^{\alpha }}$$

(10)

The test statistic in Equation (9) is simplified into:

$$\begin{array}{l}\zeta (x;b,\upsilon )={\left(\frac{(\upsilon -1)b+x^H{M}^{-1}x}{(\upsilon -1)b+x^H{M}^{-1}x-{\xi }_{MF}(x)}\right)}^{N+\upsilon }=\frac{1}{{\left(1-{\xi }_{opt}(x;b,\upsilon )\right)}^{N+\upsilon }},\\ {\xi }_{opt}(x;b,\upsilon )=\frac{{\xi }_{MF}(x)}{x^H{M}^{-1}x+(\upsilon -1)b}\end{array}$$

(11)

As a result, the analytical dual-polarimetric near-optimum coherent detector is obtained as follows:

$$\begin{array}{l}{\left(1-\frac{{\xi }_{MF}({\nu }_R;x_{HH})}{({\upsilon }_{HH}-1)b_{HH}+x_{HH}^H{M}_{HH}^{-1}{x}_{HH}}\right)}^{N+{\upsilon }_{HH}}\times {\left(1-\frac{{\xi }_{MF}({\nu }_R;x_{HV})}{({\upsilon }_{HV}-1)b_{HV}+x_{HV}^H{M}_{HV}^{-1}{x}_{HV}}\right)}^{N+{\upsilon }_{HV}}\begin{array}{c}\stackrel{H_0}{>}\\ \underset{H_1}{<}\end{array}\eta \\ {\xi }_{\mathrm{P}-\mathrm{GLRT}-\mathrm{LTD}}\left(v_R\right)\equiv {\left(1-{\xi }_{opt}({\nu }_R;x_{HH})\right)}^{N+{\upsilon }_{HH}}{\left(1-{\xi }_{opt}({\nu }_R;x_{HV})\right)}^{N+{\upsilon }_{HV}}\end{array}$$

(12)

where ${\xi }_{opt}({\nu }_R;x_{HH})$ and ${\xi }_{opt}({\nu }_R;x_{HV})$ are the test statistics of the GLRT-LTDs at the HH and HV polarizations, respectively. It can be seen that the detector (12) is a simple nonlinear fusion of the two GLRT-LTDs at the two polarization channels. Enlightened by the GLRT-LTD at single polarization, it is referred to as the P-GLRT-LTD, though it fails to be expressed as the output of the matched filter compared to a linearly data-dependent threshold.

3.2. CFAR Property and Threshold of P-GLRT-LTD

At the single polarization, it has been proven that the test statistic of the GLRT-LTD has a conditional pdf under the null hypothesis independent of the Doppler steering vector, the scale parameter of the texture, and the speckle covariance matrix [16]. The conditional cumulative distribution functions (cdf) at the two polarizations are given as follows:

$$\begin{array}{l}F\left({\xi }_{opt}({\nu }_R;x_{HH});{\mathrm{H}}_0\right)=1-(1-{\xi }_{opt}({\nu }_R;x_{HH}){)}^{N+{\upsilon }_{HH}-1},\\ F\left({\xi }_{opt}({\nu }_R;x_{HV});{\mathrm{H}}_0\right)=1-(1-{\xi }_{opt}({\nu }_R;x_{HV}){)}^{N+{\upsilon }_{HV}-1},\\ 0\le {\xi }_{opt}({\nu }_R;x_{HH}),{\xi }_{opt}({\nu }_R;x_{HV})\le 1\end{array}$$

(13)

From Equation (13), the conditional cumulative distribution function of the test statistic (from Equation 12) of the P-GLRT-LTD is given in Equation (14):

$$\begin{array}{l}{P}_{fa}(\eta )=\mathrm{Prob}\left\{{\left(1-{\xi }_{opt}({\nu }_R;x_{HH},H_0)\right)}^{N+{\upsilon }_{HH}}{\left(1-{\xi }_{opt}({\nu }_R;x_{HV},H_0)\right)}^{N+{\upsilon }_{HV}}<\eta \right\} (0<\eta <1)\\ ={\eta }^{1-\frac{1}{N+{\upsilon }_{HH}}}+\{\begin{array}{l}\left(N+{\upsilon }_{HV}\right)\left(N+{\upsilon }_{HH}-1\right)\frac{{\eta }^{1-\frac{1}{N+{\upsilon }_{HV}}}-{\eta }^{1-\frac{1}{N+{\upsilon }_{HH}}}}{{\upsilon }_{HH}-{\upsilon }_{HV}},{\upsilon }_{HH}\ne {\upsilon }_{HV}\\ \left(1-\frac{1}{N+{\upsilon }_{HH}}\right){\eta }^{1-\frac{1}{N+{\upsilon }_{HH}}}\ln \frac{1}{\eta }, {\upsilon }_{HH}={\upsilon }_{HV}. \end{array}\end{array}$$

(14)

For the P-GLRT-LTD in (12), Equation (14) gives the false alarm probability when the decision threshold is taken as 0 < η < 1. Of course, for a given false alarm rate, the decision threshold can also be analytically given by using the inverse function of Equation (14). The false alarm probability at a given threshold is completely determined by the number of N integrated pulses and the two shape parameters. Therefore, the P-GLRT-LTD is the CFAR with the Doppler steering vector, the scale parameters of the dual-polarized sea clutter, and the speckle covariance matrices at the two polarizations. In this way, an analytical near-optimum coherent detector in dual-polarimetric SIRV clutter with independent inverse Gamma textures is constructed.

3.3. Adaptive P-GLRT-LTD and Approximate CFAR Property

In practical applications, speckle covariance matrices of sea clutter are known and need to be estimated from the secondary data from reference cells. In terms of Equation (1), clutter vectors at the reference cells also follow the SIRV model with independent inverse Gamma textures, i.e.,:

$$c_p=\left[\begin{array}{c}{c}_{HH,p}\\ c_{HV,p}\end{array}\right]=\left[\begin{array}{c}\sqrt{{\tau }_{HH,p}}{u}_{\mathrm{HH},p}\\ \sqrt{{\tau }_{HH,p}}{u}_{\mathrm{HV},p}\end{array}\right],p=1,2,\cdots ,P$$

(15)

Generally, the speckle vectors at the reference cells share the same speckle covariance matrix as the speckle vector at the CUT at each polarization. In terms of the texture correlation at the CUT and reference cells, the clutter environment can be classified as homogeneous, independent, identically distributed (IID), and correlated [27]. Homogeneity means that textures at the CUT and reference cells share a random constant. Correlated textures most often occur in high-resolution maritime radars, which is relevant to the spatial correlation function of sea clutter [23] and range resolution of the radar.

Owing to the independence of speckle vectors at two polarization channels, two speckle covariance matrices can be estimated by the simple normalized sample covariance matrices (NSCM) [28] or the iterative maximum likelihood (IML) estimator [29,30,31,32,33]. Taking the HH polarization channel as an example, the NSCM estimate is given as follows:

$${\widehat{M}}_{HH,NSCM}=\frac{P}{N}{\displaystyle \sum _{p=1}^P\frac{c_{HH,p}{c}_{HH,p}^H}{c_{HH,p}^H{c}_{HH,p}}}$$

(16)

Using the NSCM estimate as the initial matrix, the ML estimate of the speckle covariance matrix is iteratively computed as follows:

$$\begin{array}{l}{\widehat{M}}_{HH,0}={\widehat{M}}_{HH,\mathrm{NSCM}},\\ q_p=c_{HH,p}^H{\widehat{M}}_{HH,k}{c}_{HH,p},p=1,2,\cdots ,P\\ {\widehat{M}}_{HH,k+1}=\frac{1}{P}{\displaystyle \sum _{p=1}^P{\phi }_{GP,N}\left(q_p\right)c_{HH,p}{c}_{HH,p}^H},\\ {\phi }_{GP,N}(x)=\frac{N+{\upsilon }_{HH}}{x+({\upsilon }_{HH}-1)b_{HH}}.\end{array}$$

(17)

The iteration process is shown to be fast-convergent [31]. The speckle covariance matrix at the HV polarization is estimated by the same method. Replacing the known speckle covariance matrices in Equation (12) by their ML estimates obtains the adaptive P-GLRT-LTD. It is a difficult thing to prove that the adaptive P-GLRT-LTD is of CFAR with respect to the estimated speckle covariance matrices. We made simulation experiments to show that the adaptive version is of approximate CFAR with respect to the estimated speckle covariance matrices. Given the number N of integrated pulses, the scale and shape parameters, the number P of reference cells, and speckle covariance matrices, the received data are simulated by Equations (1) and (15), and the samples of the test statistic under the null hypothesis are computed by Equation (12). The threshold at a given false alarm rate is given by the empirical CDFs of the sample set from a large number of trails. The speckle covariance matrices are parametrized by a one-lag correlation coefficient ρ_s ∈ [0, 1):

$$M_{HH}={[{{\rho }_s}^{\left|i-j\right|}]}_{i,j=0,1,\cdots ,N-1},M_{HV}={\left[{{\rho }_s}^{\left|i-j\right|/2}\right]}_{i,j=0,1,\cdots ,N-1}$$

(18)

Note that the 1/2 on the power in the HV speckle covariance matrices is used to determine the diversity of the Doppler spectra at the two polarizations. For N = 8 and P = 16, 32, 64, and +∞ (known speckle covariance matrices), we calculate the thresholds of the adaptive P-GLRT-LTD at the false alarm rate of 10⁻⁴ by Monte Carlo tests. Figure 2 plots the decision thresholds of the adaptive detector as ρ_s varies from 0 to 0.99. The thresholds are almost invariant with ρ_s, showing that the adaptive P-GLRT-LTD is approximately CFAR with respect to estimated speckle covariance matrices. Note that the threshold gets smaller when the number of reference cells reduces, due to the special structure of the detector.

In this way, the decision threshold of the adaptive P-GLRT-LTD is a function of N, P, and the shape parameters υ_HH and υ_HV. This function can be built in advance by a mass of Monte Carlo tests as a four-dimensional table on N, P, υ_HH, and υ_HV at different false alarm rates. In applications, the decision threshold is looked up from the table in terms of the parameters of the detector and the parameters of sea clutter.

4. Experimental Results and Performance Comparison

In this section, the adaptive P-GLRT-LTD is verified by simulated experiments and real-measured data from the IPIX radar database [18]. Firstly, the polarimetric characteristics of sea clutter and target echoes are analyzed using measured data. Secondly, based on the characteristics of target returns and the polarimetric sea clutter model, simulated data are generated to compare the proposed detector with other detectors. Third, experimental results on two measured datasets are reported for full performance comparison.

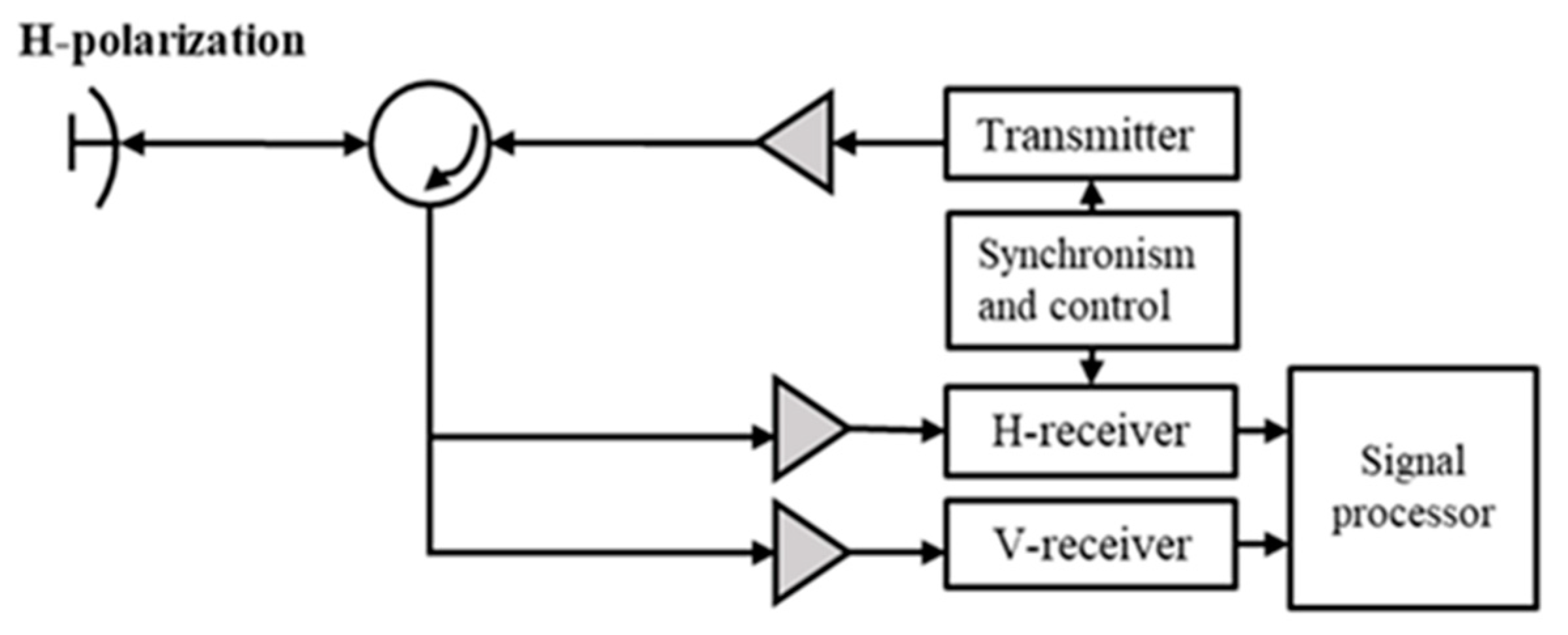
4.1. Characteristics Analysis of Dual-Polarimetric Data

In the full-polarimetric IPIX radar database, 1993 datasets often contain radar echoes of a dozen contiguous range cells, which are unsuitable for adaptive detection. 1998 datasets often contain radar echoes of thirty range cells or so, which are suitable for the evaluation of adaptive detectors in a short CPI. Therefore, two 1998 datasets with a PRF of 1000 Hz are used for analysis. In the two datasets, test targets are floating small boats. The amplitude distributions of sea clutter at the HH and HV polarizations are analyzed, where the case after sea spikes are excluded. The texture correlation coefficients at the two polarizations are computed, and the average SCRs of the test targets at the two polarizations are analyzed. Taking the dataset of 19980223-184853-ANTSTEP as an example, the amplitude maps of the dataset at the two polarizations are plotted in Figure 3a, b, where the test floating small boat is located on the 20–24th range cells. It can be observed that in the HH and HV polarimetric sea clutter data, there are a few sea spikes at the same time intervals and positions, which are labeled by a red circle in the HH polarimetric power map. Due to the much longer lifetimes of sea spikes than the CPI, false alarms from sea spikes have been removed during sequent multiscan data processing. Hence, false alarms in sea spike regions are not counted in the false alarms of adaptive coherent detection. Sea spikes can be extracted by the method in terms of the average amplitude of sea clutter and persistence duration [34].

High-resolution sea clutter data at each polarization are modeled by the generalized Pareto intensity distributions. From the power map of the data, a clean region with target echoes and few sea spikes is used to estimate the scale and shape parameters of the GP distributions by the outlier-robust iterative truncated maximum likelihood (TML) estimator with a truncation ratio of 0.85 [35]. The outlier-robust TML estimator can mitigate the influence of outliers in the data. For the sea clutter data in Figure 3a,b, the empirical amplitude pdf and fitted pdf using the estimated parameters are plotted in Figure 3c,d. The scale and shape parameters in the GP distributions of the two dual-polarimetric datasets are listed in

Table 1. Scale and shape parameters, the texture correlation coefficients at the two polarizations, and the average SCRs in the two datasets.

Dataset	19980223_184853	19980223_190106
Resolution	3 m	9 m
PRF	1000 Hz	1000 Hz
vHH	8.8	4.3
vHV	3.5	1.9
bHH	1.887 × 103	2.366 × 104
bHV	4.598 × 102	1.045 × 104
ρ	0.76	0.82
SCRHH	3.2 dB	4.2 dB
SCRHV	16.7 dB	18.1 dB

. It can be seen that the clutter powers at the HV polarization are smaller, about 5–10 dB, than those at the HH polarization. Sea clutter data at HV polarization have much smaller shape parameters and are much spikier than that at HH polarization. Hence, the assumption that sea clutter at two polarizations follows the same amplitude distribution is unrealistic. Furthermore, the textures at the two polarizations are estimated in terms of the texture coherent length of 0.1 s. The texture correlation coefficients of the two polarizations are calculated and listed in Table 1. Additionally, another dataset with a range resolution of 9 m is listed in Table 1, which has strong non-Gaussianity at the two polarizations. In the datasets, texture correlation coefficients at the two polarizations are relatively large, which is due to that the textures at the two polarizations are closely related to the tilting modulation of long waves on the sea surface to the power of radar returns from the sea surface [22]. Hence, the independence assumption of texture at the two polarizations is for tractability in mathematics instead of physical reality. In fact, in the absence of unavailable dual-polarimetric texture knowledge and models, the independence assumption can help to design effective coherent detectors, though the mismatch probably brings some loss in performance. In addition, the average SCRs of the test boats at the two polarizations are calculated and listed in Table 1. It is found that the average SCRs at the HV polarization are about 15 dB larger than those at the HH polarization, which is because of the lower clutter power level and the larger RCS of the special test targets at the HV polarization.

At last, we analyze the time-Doppler characteristics of the radar echoes of the test boats and sea clutter in the two datasets. Due to higher SCRs, HV-polarized data are available. Figure 4a,b illustrate the time-frequency distributions (TFD) and the average Doppler spectrum (on the left side of the image) of the radar echoes at a range cell occupied by the test target and a clutter-only cell in the first dataset. The Doppler offsets of the floating boat exhibit quasi-periodic fluctuation in (−50 Hz, 50 Hz), and the behavior is relevant to the influence of swells and wind waves on the floating boat. Sea clutter has a Doppler offset of about 100 Hz and a bandwidth of about 250 Hz. In the Doppler domain, the radar echoes of the test boat are partly overlapped with sea clutter. Figure 4c,d illustrate the situation of the second dataset, and the situation is similar. The detection experiment using the two datasets can evaluate the detection performance of the detector in the main clutter region, the clutter boundary, and the noise region of the Doppler domain.

4.2. Performance Evaluation Using Simulated Data

For dual-polarized detection, in addition to the P-GLRT-LTD, there are many detectors available, including the P-Rao and P-Wald detectors [7], the P-ASMF-GLRT-LTD [15], and the recent P-MAP-GLRT detector [17]. These detectors all assume independent textures at the two polarizations, though this does not accord with the physical reality of the measured data. In simulation, the textures at the two polarizations are independent. Each is modeled by the inverse Gamma distribution, and the dual-polarized sea clutter is modeled by the GPIDs with independent textures. The speckle covariance matrices are generated as follows:

$$\begin{array}{l}{M}_{HH}={\left[{{\rho }_{s,HH}}^{\left|i-j\right|}\right]}_{i,j=0,1,\cdots ,N-1},\\ M_{HV}={\left[{{\rho }_{s,HV}}^{\left|i-j\right|/2}\right]}_{i,j=0,1,\cdots ,N-1},\\ {\rho }_{s,HH}=0.95,{\rho }_{s,HV}=0.92\end{array}$$

(19)

where N is the number of integrated pulses.

In this way, the average Doppler spectra of sea clutter at the two polarizations are given as follows:

$$S_{*}(f_d)=\frac{b_{*}\left(1-{\left|{\rho }_{s,*}\right|}^2\right)}{1+{\left|{\rho }_{s,*}\right|}^2-2\left|{\rho }_{s,*}\right|\cos \left(2\pi f_d\right)},*\in \{HH,HV\},f_d\in [-0.5,0.5]$$

(20)

where f_d is the normalized Doppler frequency. The clutter power nonuniformly distributes in the Doppler domain. To remove the Doppler dependency of detection probability at each SCR level, the SCR of the HH polarization at each Doppler frequency f_d is specified as follows:

$$SC{R}_{HH}(f_d)=10{\log }_{10}\left(\frac{{\left|a_{HH}\right|}^2}{S_{HH}(f_d)}\right)(dB)$$

(21)

When the SCR_HH(f_d) is given, the SCR at the HV polarization is determined as follows:

$$\begin{array}{l}SC{R}_{HV}(f_d)=10{\log }_{10}\left(\frac{{\left|a_{HH}\varsigma \right|}^2}{S_{HV}(f_d)}\right)(dB),\\ \varsigma =\frac{\left|a_{HV}\right|}{\left|a_{HH}\right|}\end{array}$$

(22)

where ς is the amplitude ratio of target returns at the HV and HH polarizations.

In terms of the CFAR property of the P-GLRT-LTD detector with respect to the Doppler steering vector and the approximate CFAR property with respect to estimated speckle covariances, their decision thresholds at a given false alarm rate are first determined by the Monte Carlo tests when the number N of integrated pulses and the number P of reference cells are given. For other detectors for comparison, the decision thresholds are determined by the Monte Carlo tests. In the Monte Carlo tests to calculate detection probability, for a given SCR_HH, at each trial, the normalized Doppler frequency of target returns is randomly generated in terms of the uniform distribution in (−0.05, 0.05), and then the amplitudes of target returns at the two polarizations are generated in terms of Equations (21) and (22) and the amplitude ratio ς. From a mass of independent trials, the detection probabilities of the detectors at a given SCR_HH can be obtained. The performance curves of the SCR_HH versus detection probability are obtained for each detector.

In experiments, set N = 8, P = 24, and P_fa = 10⁻⁴, the scale and shape parameters in simulation are setup in terms of the two datasets in Table 1. The performance curves of the five detectors are plotted in Figure 5a,c for ς = 1 and Figure 5b,d for ς = 1.5, where (a) and (b) use the scale and shape parameters of the first dataset and (c) and (d) use those of the second dataset.

Several important facts can be revealed from the simulation experiments. Firstly, the P-MAP-GLRT detector [17] and the proposed P-GLRT-LTD have almost overlapped performance curves and obtain the largest detection probabilities in all four cases. Though the two detectors use quite different derivation paths and have quite different forms, both detectors fully exploit the texture distributions at the two polarizations. The former combines the near-optimum coherent test statistic in known textures with the MAP estimates of textures. The latter directly derives the analytical coherent detector from the likelihood ratio test. Secondly, the P-ASMF-GLRT-LTD is slightly poorer in the first case and much poorer in the second case than the two best detectors. In the experiments, the textures at the two polarizations follow different inverse Gamma distributions. Thus, the mismatch between the clutter model and the assumption makes the P-ASMF-GLRT-LTD poor and unstable in detection performance. Thirdly, the early P-Rao and P-Wald detectors in [7] behave the worst because the texture distributions at the two polarizations are unavailable in derivation. It is found that the textures at the two polarizations are correlated in the measured sea clutter datasets. All five detectors encounter a mismatch in texture correlation. In the mismatch cases, their performance is compared by using the two measured datasets.

4.3. Performance Comparison Using Measured Data

In this subsection, the dual-polarized coherent detectors are examined and compared using the two IPIX radar databases in Table 1. For each dual-polarimetric dataset, 6 × 10⁴ pulses at 34 contiguous range cells are segmented into 34 × 7500 range-time cells. Each range-time cell contains the radar returns from eight pulses. The number of integrated pulses N = 8, and the number of reference cells P = 24. For each adaptive coherent detector, taking the P-GLRT-LTD as an example, at each range-time cell, the test statistic is computed as follows:

$$\xi (r,t)\equiv \underset{{\nu }_R\in [-7.5,7.5]}{\min }\left\{{\xi }_{\mathrm{P}-\mathrm{GLRT}-\mathrm{LTD}}\left(v_R|{\widehat{M}}_{HH},{\widehat{M}}_{HV}\right)\right\}$$

(23)

where (r, t) denotes the range-time cell, [−7.5 m/s, 7.5 m/s] is the maximal unambiguous interval of the radial velocity, and ${\widehat{M}}_{HH}$ and ${\widehat{M}}_{HV}$ are the estimated speckle covariance matrices at the two polarizations from the secondary data from the 24 reference cells. The speckle covariance matrices are separately estimated at the two polarizations by the iterative maximum likelihood estimator [28,29,30,31,32,33]. Due to the unavailability of the joint texture distribution at the two polarizations, the decision thresholds for every detector fail to be determined by the indirect Monte Carlo tests, like in the simulation experiments in Section 4.2. Hence, the direct Monte Carlo tests on the measured data are used to control the false alarm rate on all the range-time cells of the data. In each dataset, the range cells are divided into clutter-only cells, the primary cells occupied by the floating boat, and the secondary cells affected by the floating boat. The samples of the test statistic (from Equation (23)) on the range-time cells on the clutter-only cells are used to determine the decision threshold at a given false alarm rate on the range-time cells, where the range-time cells occupied by sea spikes detected by the method in [34] do not count for false alarms. Later, the number of range-time cells on the primary cell whose values of the test statistic exceed the decision threshold is used to calculate the detection probability of the detector. In the experiment, the false alarm rate on the range-time cells is set at 10⁻³, and the numbers of clutter-only cells in the two datasets are 27 and 30, meaning that 203 and 225 false alarms are allowed in the two datasets.

For the two datasets, the detection results of the six detectors are illustrated in Figure 6 and Figure 7. The adaptive HV-GLRT-LTD is considered to show the benefit of dual-polarization in detection performance. The HH-polarimetric one is not employed for lower SCRs at HH polarizations. The three dual-polarimetric coherent detectors except the early P-Rao/Wald detectors obtain better performance than the adaptive HV-GLRT-LTD, though the HH polarization is lower by over 14 dB than the HV polarization. For the two measured datasets, the early P-Rao/Wald detectors have obviously lower detection probabilities than the other four detectors. The reason is that the texture distributions are not exploited in the design of the detectors. The P-MAP-GLRT detector and P-GLRT-LTD attain the comparable and largest detection probabilities in the two datasets. The P-ASMF-GLRT-LTD attains slightly poorer detection performance than the best two detectors because its texture assumption mismatches the real datasets.

Moreover, considering that the detection probabilities of the P-MAP-GLRT detector and P-GLRT-LTD are almost equal, we calculate their decision time for a full comparison. Their average decision times on a personal computer are 1.35 ms and 1.12 ms, respectively. The two detectors take the same time in speckle covariance matrices estimation. Differently, the P-MAP-GLRT detector takes more time on the MAP estimation of textures for its complex expressions.

At last, it is worthy to note that the textures at the two polarizations are correlated in the measured datasets, meaning that the five polarimetric coherent detectors are derived under the mismatch assumption of independent textures at the two polarizations. Hence, modeling and exploitation of joint texture distribution on multiple polarizations are potential and interesting problems to further improve detection performance.

5. Conclusions

It is always an important approach to use the polarization diversity of target returns and sea clutter to improve the detection performance of low-velocity small targets on maritime radars. In the HH-HV dual-polarimetric high-resolution mode, this paper proposes the dual-polarimetric near-optimum coherent detector, the P-GLRT-LTD, under the assumption that the textures at the two polarizations follow different inverse Gamma distributions and are independent. The P-GLRT-LTD is proven to be of CFAR with respect to the Doppler steering vector, scale parameters of textures, and speckle covariance matrices. Moreover, its CFAR thresholds are given analytically. The performance of the P-GLRT-LTD is evaluated by using simulated data and measured IPIX datasets. The results show that the P-GLRT-LTD achieves the best detection performance, which is competitive with the existing best-performance P-MAP-GLRT detector. In addition, it is found from measured datasets that the textures at the two polarizations are often highly correlated. Therefore, the modeling of dual-polarimetric sea clutter with correlated textures and the exploitation of the texture polarimetric correlation will be a potential approach to further improve the performance of polarimetric maritime radars.