Abstract
Remote sensing datasets offer a unique opportunity to observe spatial and temporal trends in water quality indicators (WQIs), such as chlorophyll-a, salinity, and turbidity, across various aquatic ecosystems. In this study, we used available in situ WQI measurements (chlorophyll-a: 17, salinity: 478, and turbidity: 173) along with Landsat-8 surface reflectance data to examine the capability of empirical and machine learning (ML) models in retrieving these indicators over Matagorda Bay, Texas, between 2014 and 2023. We employed 36 empirical models to retrieve chlorophyll-a (12 models), salinity (2 models), and turbidity (22 models) and 4 ML families—deep neural network (DNN), distributed random forest, gradient boosting machine, and generalized linear model—to retrieve salinity and turbidity. We used the Nash–Sutcliffe efficiency coefficient (NSE), correlation coefficient (r), and normalized root mean square error (NRMSE) to assess the performance of empirical and ML models. The results indicate that (1) the empirical models displayed minimal effectiveness when applied over Matagorda Bay without calibration; (2) once calibrated over Matagorda Bay, the performance of the empirical models experienced significant improvements (chlorophyll-a—NRMSE: 0.91 ± 0.03, r: 0.94 ± 0.04, NSE: 0.89 ± 0.06; salinity—NRMSE: 0.24 ± 0, r: 0.24 ± 0, NSE: 0.06 ± 0; turbidity—NRMSE: 0.15 ± 0.10, r: 0.13 ± 0.09, NSE: 0.03 ± 0.03); (3) ML models outperformed calibrated empirical models when used to retrieve turbidity and salinity, and (4) the DNN family outperformed all other ML families when used to retrieve salinity (NRMSE: 0.87 ± 0.09, r: 0.49 ± 0.09, NSE: 0.23 ± 0.12) and turbidity (NRMSE: 0.63± 0.11, r: 0.79 ± 0.11, NSE: 0.60 ± 0.20). The developed approach provides a reference context, a structured framework, and valuable insights for using empirical and ML models and Landsat-8 data to retrieve WQIs over aquatic ecosystems. The modeled WQI data could be used to expand the footprint of in situ observations and improve current efforts to conserve, enhance, and restore important habitats in aquatic ecosystems.
1. Introduction
Collecting and analyzing water quality (WQ) data are crucial for assessing spatiotemporal trends in the health of aquatic ecosystems. WQ has a substantial impact on the wellbeing of the human population and the species that rely on these ecosystems [,,,]. Water quality indicators (WQIs) are specific parameters used to assess the WQ in various ecosystems [,]. These indicators include parameters such as temperature, dissolved oxygen (DO), pH (hydrogen ion concentration), salinity, turbidity, suspended solids, nutrients, and heavy metals [,,,,]. The ultimate purpose of monitoring WQIs is to identify changes in aquatic conditions and to provide data to decision makers, which they can use to inform their environmental management and protection practices [,,].
In situ observations involve collecting measurements of WQIs directly at a location of interest within an aquatic ecosystem. These observations provide a common approach to monitoring WQIs across ecosystems [,]. However, these observations are relatively expensive and time-consuming, and are spatially and temporally limited [,,,]. Some areas are difficult to access for sampling purposes and/or have very limited resources. In addition, periodic WQ sampling stations might also miss the short-lived magnitudes, trends, and gradients in WQIs. Moreover, permanent field WQ stations are vulnerable to damage from extreme climate events.
Remote sensing datasets (e.g., visible, thermal, and radar) in the public domain provide a unique and cost-effective opportunity to monitor WQIs, especially in large and inaccessible aquatic ecosystems [,,]. These space-based observations offer a wealth of data with excellent spectral, spatial, and temporal resolutions that facilitate the calculation of WQIs. Landsat images, for example, have been extensively used to estimate optical and non-optical WQIs, such as turbidity [,,,], total nitrogen (TN) and total phosphorus (TP) [,,,,,], chlorophyll-a [,,,], DO [], total suspended solids (TSSs) [,], salinity [,], and ammonium []. Moderate Resolution Imaging Spectroradiometer images have been used to retrieve salinity [,], chlorophyll-a [,,,], colored dissolved organic material [,,], TSS [,], TN [,,,], and TP [,,]. Sentinel-2 images have been used to retrieve salinity [,], chlorophyll-a [,,,], TN [,], TP [,], colored dissolved organic material [,,], turbidity [,,], and electrical conductivity (EC) []. Thermal infrared data have been used to retrieve water temperature [,,]. Radar data have been used to retrieve EC [,], salinity [,], and total dissolved salts [,]. Previous efforts that used remote sensing products to monitor WQIs over multiple ecosystems commonly used empirical models [,,,,,,]. However, determining the appropriate model for extracting WQIs in a specific area of interest, along with the factors to be considered while selecting such a model, presents a significant challenge.
With the rise in artificial intelligence techniques, modeling capabilities have made great advances [,]. Machine learning (ML) algorithms have been used to analyze complex linear and nonlinear patterns between remote sensing datasets and WQI data [,,,]. Several studies have used convoluting neural networks, artificial neural networks, and deep neural networks (DNNs) to retrieve salinity [,], TN [,,], TP [,,], chlorophyll-a [,], DO [,], and turbidity [,] data. Other ML families, such as Extreme Gradient Boosting, Gradient Boosting Machine (GBM), Regression Tree, and Multi-Layer Perceptron, have been implemented to retrieve EC [], DO [,], pH [,], TN [], TP [,], chlorophyll-a [], and turbidity [] data. However, determining the most suitable ML model family for a specific area of interest remains challenging.
Matagorda Bay, also called the Lavaca–Colorado estuary, is one of seven major estuarine systems located on the Texas coast (Figure 1; inset a). As the second largest estuary in Texas, Matagorda Bay is known for its vital role in supporting diverse ecosystems, serving as a critical habitat for marine life, and providing a foundation for commercial and recreational activities [,,,].
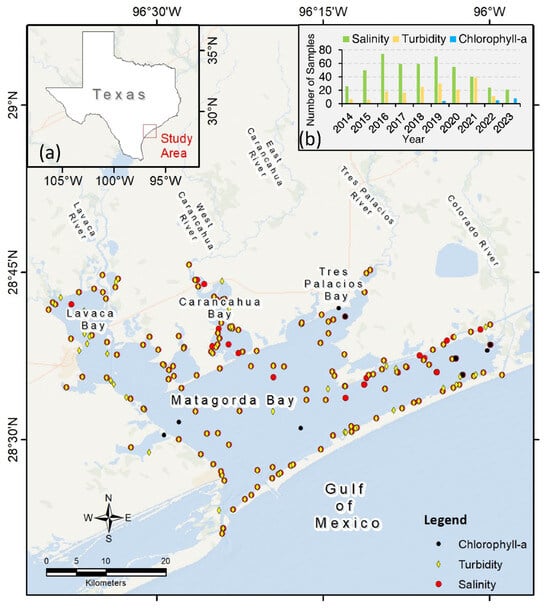
Figure 1.
The spatial distribution of Matagorda Bay along the Texas Gulf Coast, and the locations of the in situ WQIs measurements used in this study. (a) The location of the study area along the Texas coast. (b) The yearly distribution of in situ WQI measurements during the study period (2014–2023).
In this study, turbidity, chlorophyll-a, and salinity WQIs were retrieved from Landsat-8 images over Matagorda Bay during the period from 2014 to 2023. Because they exhibit complex spatiotemporal patterns and trends, these three WQIs have been established in several studies as significant markers of the health of Matagorda Bay [,]. Along with water depth, current conditions, and temperature, several studies have found these WQIs to be the most significant in controlling the growth of oysters in Matagorda Bay [,,,]. Both empirical and ML models were used. Specific questions to be addressed in this study include the following: (1) Which empirical model(s) could perform well in extracting chlorophyll-a, salinity, and turbidity data over Matagorda Bay? (2) Which model(s) witness a significant performance enhancement once recalibrated over Matagorda Bay? (3) Do ML models usually outperform empirical models in extracting WQI data? (4) Which ML model family performs well in extracting salinity and turbidity data over Matagorda Bay?
A total of 36 empirical models, documented in previous research, were applied to retrieve turbidity, chlorophyll-a, and salinity data over Matagorda Bay, Texas (Figure 1). Specifically, 12 models were employed for chlorophyll-a, 2 models for salinity, and 22 models for turbidity estimation. In addition, four distinct ML algorithm families—DNN, GBM, Distributed Random Forest (DRF), and Generalized Linear Model (GLM)—were employed to retrieve salinity and turbidity data over Matagorda Bay.
2. Data
2.1. Study Area
Matagorda Bay (area: 1070 km2) comprises a primary bay (Matagorda Bay) and several subsystems, including Lavaca Bay, Tres Palacios Bay, and East Matagorda Bay (Figure 1) [,,]. Matagorda Bay holds diverse ecological significance as an estuarine ecosystem, nurturing a wide range of flora and fauna and functioning as a habitat and breeding ground for various fish, shellfish, and aquatic organisms that enhance local biodiversity and support fisheries [,,,]. This ecological richness translates into substantial economic value, driven by thriving fisheries, recreational pursuits, and the potential for shipping and transportation. Both commercial and recreational fishing bolster the local economy, and the bay attracts tourists for activities like boating, birdwatching, and outdoor exploration [,,].
Oysters are commercially harvested in Matagorda Bay []. They also play a crucial role in maintaining WQ, supporting local fisheries, and enhancing the overall ecological resilience of Matagorda Bay [,,]. Studies have highlighted the oyster reefs in Matagorda Bay as important nurseries for various commercially valuable species, such as spotted seatrout and red drum []. The threats these oyster populations face include habitat degradation, reduced water flow, and disease, which are directly related to the WQ in Matagorda Bay [,,]. Monitoring WQIs is significant for developing effective conservation measures that are crucial to preserving the ecological and economic benefits that oysters in Matagorda Bay provide.
Matagorda Bay’s ecosystem is significantly shaped by its connectivity to neighboring water bodies, primarily the Gulf of Mexico for the main bay and river connections for the secondary bays []. The estuary is fed by four major rivers: the Colorado River, the Lavaca River, the Carancahua River, and the Tres Palacios River [,]. The Colorado River is the primary source of freshwater, supplying an estimated 34% of the total freshwater inflow for the bay system [,,,,,]. Freshwater input plays a pivotal role in determining the overall health of Matagorda Bay [,,,,]; it supplies nutrients to the bay [,], regulates salinity [,,,,], and is responsible for the transportation of sediment [,].
2.2. In situ Data
We gathered in situ measurements over Matagorda Bay for the period from 2014 to 2023 (Inset b; Figure 1). These data were collected from the public databases of the Texas Commission on Environmental Quality (TCEQ) [], Lower Colorado River Association (LCRA) [], and Texas Wildlife Parks Department (TWPD). TCEQ sampling procedures have been adopted by both LCRA and TWPD [,]. For sampling within estuaries, water samples were obtained at a depth of 0.30 m. Salinity was measured using a multiprobe instrument and recorded to the nearest 0.10 psu (practical salinity unit) []. Turbidity is measured using the benchtop turbidity meter instrument and reported to the nearest 0.02 NTU (nephelometric turbidity unit) [,]. Chlorophyll-a concentrations were measured on collected water samples [] using a spectrophotometer and recorded in µg/L [].
The locations of in situ measurements are shown in Figure 1. A total of 17 measurements were collected for chlorophyll-a, 478 for salinity, and 173 for turbidity. These are the only measurements that align in time with the dates of the Landsat-8 acquisition during the investigated period (2014–2023). Table 1 provides statistics for these measurements. Table 1 indicates that over Matagorda Bay, chlorophyll-a concentrations ranged from 0.04 µg/L in August 2023 to 25.50 µg/L in September 2019. Salinity ranged from 0.10 psu in May 2021 to 35.91 psu in October 2022. Turbidity ranged from 2.0 NTU in November 2017 to 91.0 NTU in July 2020. The average (± standard deviation) is estimated at 17.37 ± 8.22 psu, 25.18 ± 18.60 NTU, and 5.11 ± 7.55 µg/L for salinity, turbidity, and chlorophyll-a, respectively.

Table 1.
Statistics for in situ WQIs (salinity, turbidity, and chlorophyll-a) collected over Matagorda Bay, at locations shown in Figure 1, from 2014 to 2023 1.
2.3. Remote Sensing Data
In this study, we used Landsat-8 (Collection 2, Level 2, Tier 1) images from 2014 to 2023 over Matagorda Bay. These images cover path 26 and row 40 of the Landsat worldwide reference system. Landsat-8 launched on 11 February 2013, as a joint mission between the U.S. Geological Survey and the National Aeronautics and Space Administration [,]. Landsat-8 carries two instruments: the Operational Land Imager (OLI) and the Thermal Infrared Sensor (TIR). These instruments record data over 11 spectral bands. OLI records apparent radiance in nine optical bands in wavelengths ranging from optical to shortwave infrared at a spatial resolution of 30 m. The TIR instrument records in thermal infrared wavelengths at a 120 m spatial resolution. Landsat-8 has 16-day temporal resolution and a 185 km swath width. A total of five Landsat-8 images were used to retrieve chlorophyll-a. Salinity required 121 images, while turbidity required 43 images.
3. Methods
3.1. Surface Reflectance
Surface reflectance data were extracted from Landsat-8 images in a Google Earth Engine (GEE) environment. In the GEE editor, the scale factor was applied to Landsat-8′s band 1 through band 7 (B1–B7) to generate surface reflectance data. These surface reflectance data were corrected for the temporally, spatially, and spectrally varying scattering and absorbing effects of atmospheric gases, aerosols, and water vapor [,]. For modeling purposes, surface reflectance data were extracted over locations of in situ observations (Figure 1) and times where in situ observations align with the dates of Landsat-8 acquisition during the investigated period (2014–2023). Due to the inherently low surface reflectance of water, some pixels showed negative surface reflectance values [,]. These pixels were deleted and not considered for further analyses. Surface reflectance values for pixels in cloud-contaminated areas were also removed. Figure 2 displays scatterplots depicting the relationship between surface reflectance data across each band (B1–B7) and the WQIs. The correlation coefficient between chlorophyll-a and surface reflectance, from all bands, was estimated to be 0.89 ± 0.07 (average ± standard deviation). B6 and B7 exhibited the highest positive correlation (0.96 and 0.98, respectively) with chlorophyll-a, while B1 and B2 demonstrated the lowest positive correlations (0.80 and 0.81, respectively). The correlation coefficient between salinity and surface reflectance was weak. It was estimated at −0.11 ± 0.04. B4 and B5 showed the maximum negative correlation of -0.16, whereas B7 showed the minimum negative correlation (−0.05). The correlation coefficient between turbidity and surface reflectance was estimated to be 0.05 ± 0.04. B4 exhibited the highest correlation of 0.12, whereas B7 demonstrated the lowest correlation of −0.02.
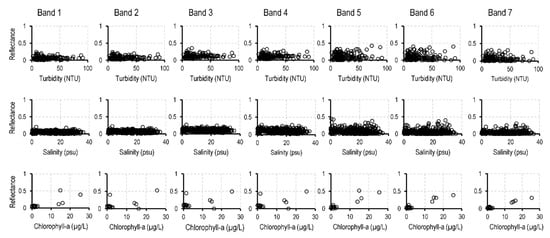
Figure 2.
Scatterplots of turbidity (top panel), salinity (middle panel), and chlorophyll-a (bottom panel), and Landsat-8-derived surface reflectance data at each band (B1–B7).
Table 2 presents statistics for surface reflectance data generated from B1 through B7 during the periods when in situ observations correspond with Landsat-8 acquisition dates. The surface reflectance data used for salinity retrieval displayed mean values ranging from 0.04 to 0.11, with corresponding standard deviations ranging from 0.03 to 0.07. For turbidity, the surface reflectance data revealed average values spanning from 0.06 to 0.12, accompanied by standard deviations ranging from 0.04 to 0.09. The surface reflectance data used for chlorophyll-a retrieval demonstrated average and standard deviation values ranging from 0.07 to 0.15 and 0.09 to 0.16, respectively.

Table 2.
Statistics for surface reflectance data extracted at in situ locations 1.
3.2. Empirical Models
A total of 36 empirical models, documented in previous studies, were applied to Landsat-8 surface reflectance data to extract WQI data for Matagorda Bay. We reported all empirical models that were published and used to retrieve WQIs from Landsat-8 data. These models along with their geographic origins and sources are presented in Table 3. Salinity retrieval used 2 models (Sn1 and Sn2), turbidity retrieval involved 22 models (T1–T22), and chlorophyll-a estimation used 12 models (C1–C12) (Table 3). The empirical models for chlorophyll-a used B1, B2, B3, B4, B5, B6, and B7. Salinity made use of B1, B2, B3, and B4, while turbidity models employed B1, B2, B3, B4, and B5. These models were initially used with their original weights (Table 3), i.e., uncalibrated models. Additionally, we performed recalibration specifically tailored to Matagorda Bay, resulting in the generation of new weights for each of these models (i.e., calibrated models). Empirical models over Matagorda Bay were calibrated using the ordinary least squares package in a geographic information system environment [,].

Table 3.
Empirical model coefficients published in previous studies along with the locations they were applied to and their respective sources. Models over Matagorda Bay were calibrated.
3.3. Machine Learning (ML) Models
3.3.1. ML Model Families
In this study, the open-source H2O-AML (automated ML) platform was employed (accessible at: https://docs.h2o.ai/h2o/latest-stable/h2o-docs/automl.html; accessed on 1 June 2023). H2O-AML provides user-friendly, fully automated supervised learning algorithms, catering to both those well versed in the field and those without expertise []. Within the realm of H2O-AML, various ML families are used in this study, including DNN, DRF, GBM, and GLM.
DNN is a feedforward network that uses multiple hidden layers composed of neurons to analyze complex relationships between inputs and target features [,,,]. DRF combines multiple weak decision trees to produce a strong ensemble forest [,]. The GBM family generates an ensemble model using parallel regression trees [,]. The GLM algorithm produces regression models using exponential distributions [,]. Comprehensive descriptions regarding structures and hyperparameters for H2O-AML families can be found on the H2O-AML website (https://docs.h2o.ai/h2o/latest-stable/h2o-docs/automl.html; accessed on 1 June 2023).
3.3.2. ML Model Setup and Structure
For both turbidity and salinity, the input data for the ML models comprised seven Landsat-8 bands (Figure 3). The organization of the input data aimed to facilitate a more straightforward comparison between ML and empirical models. Due to the limited data availability, ML models were not created for chlorophyll-a.
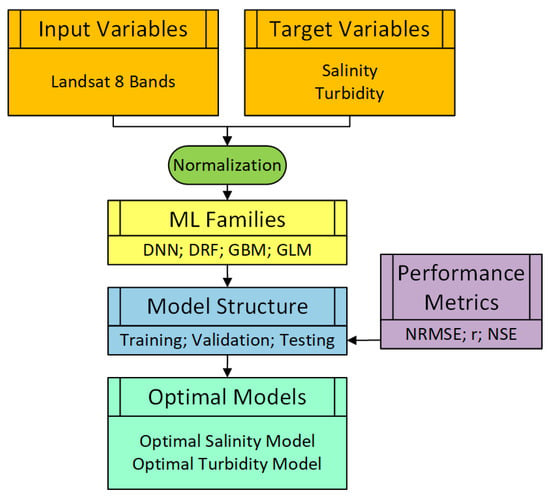
Figure 3.
Input and target variables and structures of the ML families used to retrieve salinity and turbidity data over Matagorda Bay.
To guarantee equal consideration of all input variables, the following equation was employed to normalize model inputs within the range of 0 to 1 (Figure 3):
where represents the normalized value for a specific input x, while and represent the maximum and minimum recorded values of x, respectively.
For each model family (DNN, DRF, GBM, and GLM), the input and target data were divided into training (64%), validation (16%), and testing (20%) sets (Figure 3). The process of dividing the input/target data followed a random format. This method of generating random data ensures unique input values for each model run.
To prevent overfitting in each model, early stopping criteria were enforced, employing the mean-squared error as the stopping metric. This involved setting a stopping round value of 5 and a stopping tolerance of 0.0001. This option specifies the tolerance value by which an ML model must improve before training ceases. In this case, the moving average for last six simulation rounds is calculated, where the first moving average is the reference value for comparison with the other five moving averages. The model will stop training if the ratio between the best moving average and the reference moving average is more than or equal to 0.0001. These stopping options are used to increase model performance by restricting the number of models that are built. To improve the simulation accuracy, we ran each simulation for 50 runs. The model with the highest testing performance, based on the Nash–Sutcliffe efficiency (NSE) coefficient, was selected as an optimal model. An optimal model was selected for salinity and for turbidity from each ML model family (e.g., DNN, DRF, GBM, and GLM) (Figure 3).
3.4. Model Performance Measures
Performance for both empirical and ML models was assessed using the NSE coefficient, correlation coefficient (r), and normalized root mean square error (NRMSE). These measures were used to evaluate the performance of similar models worldwide [,,,]. The standard variation in the 50 ML model simulations was used to quantify errors in each performance metric.
The NSE measures the relative magnitude of residual variance to the variance in the observed data. NSE values range from −∞ to 1, with optimal performance at 1:
The r value measures the strength of the linear relationship between predicted and observed data with value ranges between −1 and 1. An r value of 0 means there is no correlation, and positive (negative) values mean positive (negative) correlations, with 1 (−1) indicating perfect positive (negative) correlations between predicted and observed values:
The NRMSE is the RMSE normalized by the standard deviation of the observed data with value ranges from 0 to ∞, given by the following equation:
where and represent the predicted value and observed (e.g., in situ) values, respectively; and are the mean predicted and observed values; n represents the input data size; and σ is the standard deviation of the observed data.
4. Results
4.1. Empirical Models
Figure 4 and Table 4 present the performance metrics of the 36 uncalibrated and calibrated empirical models implemented in this study. Performance varied in the 12 uncalibrated empirical chlorophyll-a models (Figure 4a; Table 4), with the NRMSE ranging from 0.32 to 1475.10, r from −0.88 to 0.96, and NSE from −23,527,276.57 to −0.12. Among these uncalibrated models, model C8 had the highest performance, based on NSE values, (NRMSE: 0.32, r: 0.65, NSE: −0.12); model C7 displayed the lowest performance (NRMSE: 1475.10, r: 0.80, NSE: −23,527,276.57) (Figure 4a; Table 4). Statistical assessments of the uncalibrated chlorophyll-a models indicate poor performance (NRMSE: 126.91 ± 424.70, r: 0.42 ± 0.67, NSE: −1,961,890 ± 6,791,336). After calibration over Matagorda Bay, the chlorophyll-a models demonstrated enhanced performance (NRMSE: 0.91 ± 0.03, r: 0.94 ± 0.04, NSE: 0.89 ± 0.06). These calibrated models also demonstrated comparable performance when compared to one another (Figure 4a; Table 4). The NRMSE for the calibrated models ranged from 0.85 to 0.96, with corresponding r values from 0.88 to 0.99 and NSE values from 0.88 to 0.98. Notably, calibrated model C2 exhibited the highest performance (optimal model) with NRMSE, r, and NSE values of 0.96, 0.99, and 0.98, respectively. A scatterplot of the calibrated model C2 demonstrates an overall acceptable performance (Figure 5a). Calibrated model C9 displayed the lowest performance, with NRMSE, r, and NSE values of 0.85, 0.88, and 0.77, respectively.
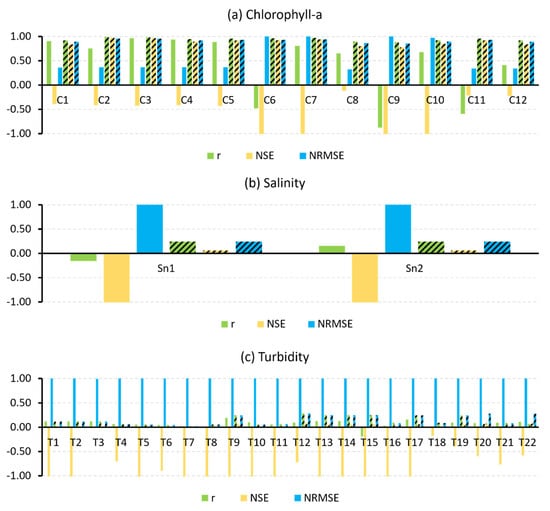
Figure 4.
Performance statistics for (a) chlorophyll-a, (b) salinity, and (c) turbidity uncalibrated (solid colors) and calibrated (dashed lines) empirical models. Note the y-axis is fitted to ±1 for display purposes; actual higher and lower values are listed in Table 4.

Table 4.
Performance metrics for 36 uncalibrated and calibrated empirical models (equations shown in Table 3) applied over Matagorda Bay.
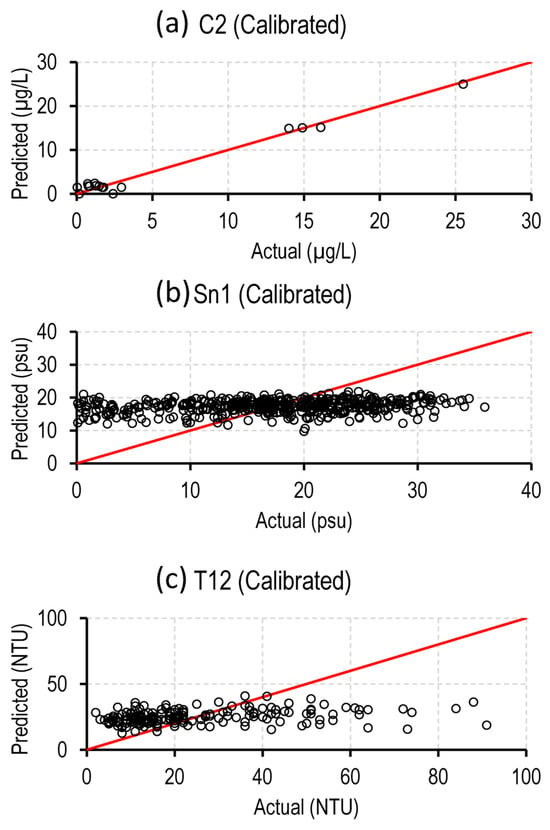
Figure 5.
Observed and modeled (a) chlorophyll-a, (b) salinity, and (c) turbidity values generated from calibrated empirical models over Matagorda Bay. Red lines indicate a 1:1 relationship.
The performance of the uncalibrated empirical salinity models varied across the matrices, with NRMSE ranging from 180.47 to 180.48, r from -0.16 to 0.16, and NSE from −32,638.62 to −32,635.55 (Figure 4b; Table 4). Notably, neither of the uncalibrated empirical salinity models produced statistically significant performances (NRMSE: 180.47 ± 0.01, r: 0.16 ± 0.22, NSE: −32,635 ± 2.18). The calibrated empirical salinity model exhibited a slight improvement with NRMSE, r, and NSE values of 0.24, 0.24, and 0.06, respectively (Figure 4b; Table 4). However, the scatterplot for the calibrated salinity model indicates poor performance (Figure 5b). It is important to note that since the same bands (B1–B4) were used to generate the uncalibrated salinity models, only one calibrated model was generated for salinity.
The performance of uncalibrated turbidity models varied with NRMSE values ranging from 0.99 to 85.15, r from −0.19 to 0.19, and NSE from −7292.28 to 0.01 (Figure 4c; Table 4). Among the 22 models, uncalibrated model T3 demonstrated the highest performance (NRMSE: 0.99, r: 0.12, NSE: 0.01), while uncalibrated model T13 had the least favorable performance (NRMSE: 85.15, r: −0.13, NSE: −7292.28) (Figure 4c; Table 4). None of the uncalibrated empirical turbidity models yielded significant performance metrics (NRMSE: 5.86 ± 17.78, r: 0.07 ± 0.08, NSE: −337.09 ± 1553.51). The calibrated empirical turbidity models displayed a relatively improved performance (NRMSE: 0.15 ± 0.10, r: 0.13 ± 0.09, NSE: 0.03 ± 0.03). The calibrated models showed NRMSE values ranging from 0.02 to 0.29, r values from 0.00 to 0.29, and NSE values from 0.02 to 0.08 (Figure 4c; Table 4). Among the models, calibrated model T12 showed the highest performance with NRMSE, r, and NSE values of 0.29, 0.29, and 0.08, respectively. However, the scatterplot depicting the calibrated turbidity model T12 shows inadequate performance (Figure 5c). Calibrated model T7 exhibited the lowest performance, with NRMSE, r, and NSE values of 0.02, 0.02, and 0.00, respectively.
4.2. ML Models
Figure 6 and Table 5 present the statistical measures for the optimal salinity models (selected based on testing the NSE value) generated from various ML families during the training and testing phases. Among the diverse ML families, a trend of closely competitive performances emerges. However, DNN stands out as the most effective family for salinity simulations. The optimal DNN achieved a training performance of NRMSE: 0.90 ± 0.08, r: 0.45 ± 0.10, NSE: 0.19 ± 0.13, and a testing performance of NRMSE: 0.87 ± 0.06, r: 0.49 ± 0.09, NSE: 0.23 ± 0.12. The most significant input variables for this model were B3, B4, B6, B7, and B1. The relative importance for these inputs were 22%, 15%, 14%, 13%, and 13%, respectively.
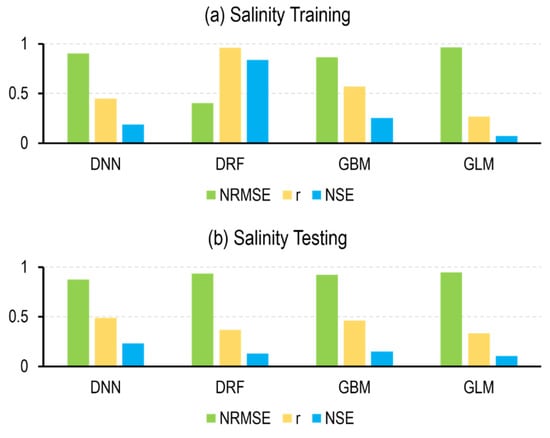
Figure 6.
Performance metrics for optimal salinity models derived from different ML model families (e.g., DNN, DRF, GBM, GLM). Metrics are displayed for (a) training and (b) testing phases.

Table 5.
Performance metrics for optimal ML model generated for salinity and turbidity during training and testing phases.
Following DNN closely in performance, GBM ranks as the second best performing family. The optimal GBM model, showcased training performance metrics of NRMSE: 0.86 ± 0.04, r: 0.57 ± 0.07, and NSE: 0.25 ± 0.07, and testing performance metrics of NRMSE: 0.92 ± 0.03, r: 0.46 ± 0.10, and NSE: 0.15 ± 0.07. DRF presents a slightly weaker performance, being the second least effective family. The optimal DRF model exhibited a training performance of NRMSE: 0.40 ± 0.01, r: 0.96 ± 0.00, and NSE: 0.84 ± 0.01, and a testing performance of NRMSE: 0.93 ± 0.04, r: 0.37 ± 0.08, and NSE: 0.13 ± 0.08. Finally, GLM ranks as the least proficient model. The optimal GLM model resulted in a training performance of NRMSE: 0.96 ± 0.01, r: 0.27 ± 0.02, and NSE: 0.07 ± 0.01, and a testing performance of NRMSE: 0.95 ± 0.03, r: 0.33 ± 0.08, and NSE: 0.10 ± 0.05. Overall, these results underscore the superiority of DNN, GBM, and DRF for salinity simulation while highlighting the limitations of GLM (Figure 6; Table 5). Figure 7 presents scatterplots illustrating observed and modeled salinity values generated for the optimal model in each ML family during both the training and testing phases. As depicted in Figure 7, the DRF model is performing well during training compared to other models.
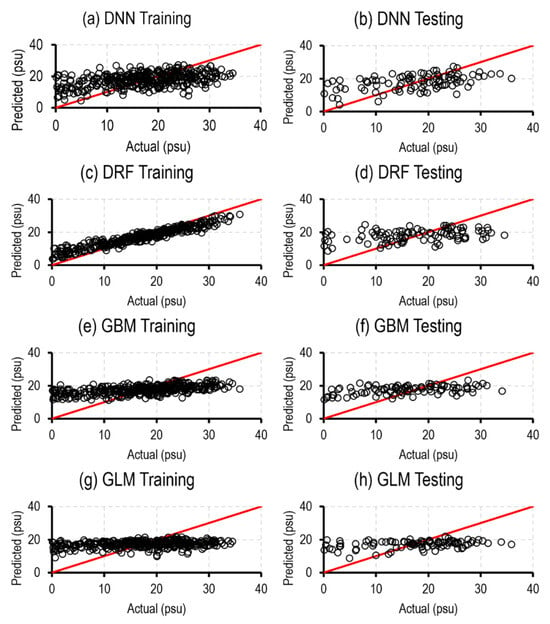
Figure 7.
The observed and modeled salinity values generated for the optimal model in each ML family during the training and testing phases. The red lines indicate a 1:1 relationship.
Figure 8 and Table 5 present the optimal turbidity models from the various ML families. All DNN, GBM, and DRF turbidity models demonstrated closely competitive performances. The optimal DNN model achieved a training performance of NRMSE: 0.59 ± 0.13, r: 0.81 ± 0.06, and NSE: 0.65 ± 0.11, and a testing performance of NRMSE: 0.63 ± 0.11, r: 0.79 ± 0.11, and NSE: 0.60 ± 0.20 (Figure 8; Table 5). The most significant input variables for this model were B4, B5, B3, B7, and B1. The relative importance for these inputs were 20%, 16%, 14%, 14%, and 14%, respectively. The GBM family provided the second-best performance. The optimal GBM model has a training performance of NRMSE: 0.66 ± 0.17, r: 0.79 ± 0.07, and NSE: 0.56 ± 0.14, and a testing performance of NRMSE: 0.73 ± 0.10, r: 0.73 ± 0.13, and NSE: 0.47 ± 0.20. The performance of the DRF was slightly weaker than the DNN and GBM families. The optimal DRF model produced training performances of NRMSE: 0.36 ± 0.02, r: 0.95 ± 0.01, and NSE: 0.87 ± 0.01, and testing performances of NRMSE: 0.76 ± 0.10, r: 0.65 ± 0.11, and NSE: 0.42 ± 0.18. Once more, the GLM family produced models with the lowest performance. The optimal GLM model produced training performance metrics of NRMSE: 0.93 ± 0.03, r: 0.36 ± 0.08, and NSE: 0.13 ± 0.05, and testing performance of NRMSE: 0.86 ± 0.07, r: 0.63 ± 0.16, and NSE: 0.25 ± 0.14 (Figure 8; Table 5). Figure 9 depicts scatterplots that illustrate the relationship between the observed and modeled turbidity values produced by the optimal model from each ML family during both the training and testing phases. All model families tend to overpredict turbidity values during the training phase. The performances of the DNN, GBM, and DRF models are close for both training and testing.
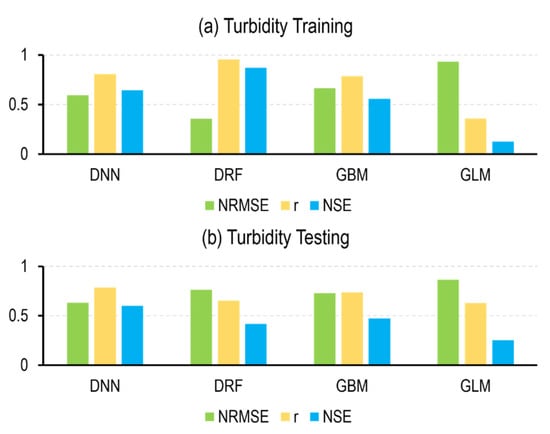
Figure 8.
Performance metrics for different turbidity ML model families (e.g., DNN, DRF, GBM, and GLM). Metrics are displayed for the (a) training and (b) testing phases.
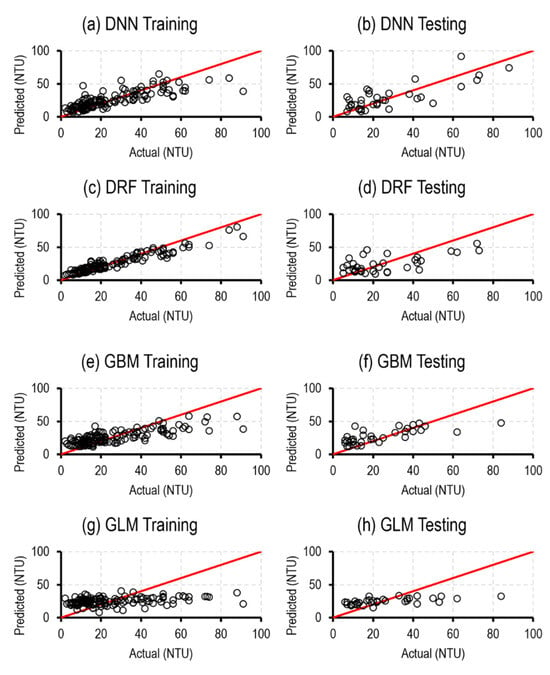
Figure 9.
The observed and modeled turbidity values generated for the optimal model in each ML family during the training and testing phases. The red lines indicate a 1:1 relationship.
4.3. Applications of Optimal Models
The optimal model for chlorophyll-a was determined to be the calibrated empirical C2 model. However, for salinity and turbidity, the optimal models were identified as DNN models. These models were then used to retrieve WQI data across all of Matagorda Bay. Figure 10 provides examples of the retrieved products for August and November of 2018.
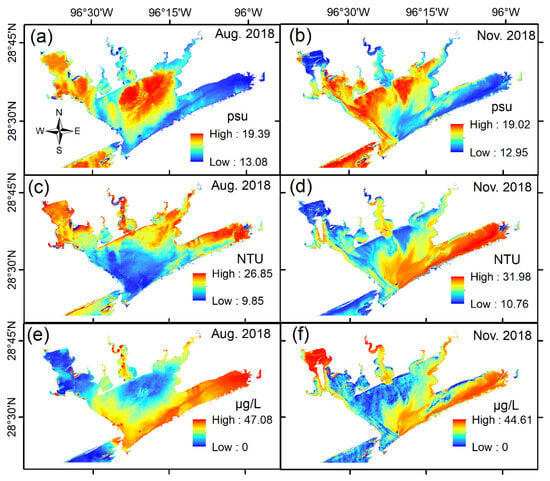
Figure 10.
Modeled WQI data produced using optimal salinity, turbidity, and chlorophyll-a models over Landsat-8 images acquired on (a,c,e) 22 August 2018 and (b,d,f) 26 November 2018.
Spatial and temporal variations in WQIs are outside the scope of this study. However, turbidity reflects the clarity and suspended particle levels in the water [], chlorophyll-a is a key indicator of phytoplankton and algae levels [,,], and salinity is crucial for understanding the bay’s conditions and the organisms it can support [,,].
The high spatial resolution of WQI data, such as those produced in this study, provides opportunities to analyze and monitor trends in the health of aquatic systems, significantly contributing to previous conservation and pollution assessment efforts [,]. Specifically, these data could be used to (1) expand in situ observational footprints and improve current efforts to conserve, enhance, and restore important aquatic habitats; (2) define areas of “anomalous” WQIs that may need further future investigation; (3) enable a demonstration and use of satellite observations to improve the understanding of factors controlling spatial and temporal variability in WQs across complex aquatic systems; and (4) help realize an opportunity and process to enable standard WQ monitoring protocols to be expanded and complemented by free satellite products.
5. Discussion
The performances of the implemented empirical and ML models are influenced by the quality of input datasets. Landsat-8 surface reflectance data showed reasonable quality over Matagorda Bay. Relevant studies indicate a significant correlation (r: 0.70) between Landsat-8-derived and in-situ-derived surface reflectance data []. In addition, we removed pixels over cloud-contaminated regions and those with negative surface reflectance. Atmospheric conditions can significantly affect the quality of Landsat-8 imagery. Aerosols, clouds, and water vapor in the atmosphere can scatter and absorb light, leading to errors in the measured surface reflectance values [,]. However, the Landsat-8 level 2 data used in this study are atmospherically corrected [,]. Landsat 8, like any satellite, has a calibration process to ensure the accuracy of its radiometric measurements [,]. The angle of the sun and the presence of sun glint (sunlight reflecting directly off the water’s surface) can impact the reflectance measurements [,,]. To reduce these effects, we removed these pixels from our modeling exercise.
Matagorda Bay is influenced by four major rivers: the Colorado River, the Lavaca River, the Carancahua River, and the Tres Palacios River. Suspended solids and dissolved organic matter from these rivers can directly affect water turbidity, salinity, and reflectance in the area []. Colored, dissolved organic matter, a yellow substance, contains inherently optical properties that affect surface reflectance [,]. In addition, previous studies have reported significant negative correlations between salinity and total suspended solids []. In this study, correlations of 0.05 ± 0.04 were estimated between salinity and turbidity. Turbidity, dissolved organic matter, and suspended solids directly influence water color and spectral reflectance. This indirect relationship between salinity and spectral bands motivated the use of Landsat-8 data to estimate salinity, a non-optical WQI. Similar principles have been applied in several studies utilizing Landsat-5 [,,,,,], MODIS [], and Landsat-8 [,,] data for salinity retrieval. However, the relatively lower correlation between Landsat-8-derived spectral reflectance and salinity might explain the significantly lower performance of empirical models and the relatively lower performance of the ML over Matagorda Bay.
5.1. Empirical Models
Most uncalibrated empirical models produced poor performance measures. The inadequacies of these models are more likely due to their application in water bodies, for which they were not originally designed. These models were initially developed across geographic regions encompassing lakes, rivers, and estuaries, each with distinct surface areas, hydrological conditions, and surface reflectance signatures. These discrepancies between the model’s training conditions and the environmental characteristics of Matagorda Bay contribute to their poor performance.
The empirical models, however, demonstrated improved performance when calibrated over Matagorda Bay. The calibrated chlorophyll-a models showed the most significant improvement. The average ± standard deviation of the NRMSE, r, and NSE measures increased from 126.91 ± 424.70, 0.42 ± 0.67, and −1,961,890.27 ± 6,791,336.75 for uncalibrated models to 0.91 ± 0.03, 0.94 ± 0.04, and 0.89 ± 0.06 for calibrated models, respectively. The highest performance of the calibrated models was reported for Model C2, which used B1, B3, B5, B6, and B7. These bands were all highly correlated (r > 0.80) with in situ chlorophyll-a values, which likely made it easier for this model to generalize a linear relationship between surface reflectance and chlorophyll-a measurements. The metrics of the calibrated C2 model outperform the metrics published in previous studies (0.74 ± 0.12) [].
It is notable that the number of data points utilized in creating the empirical models for chlorophyll-a (total: 17) may raise concerns. However, these measurements were the only ones available that coincided with Landsat-8 overpasses over Matagorda Bay. They represent the sole data points temporally synchronized with the dates of Landsat-8 acquisition throughout the 10-year study period (2014–2023). Some of these in situ chlorophyll-a data were gathered in the field when weather conditions allowed, while others were obtained from historical records (e.g., TCEQ, TWPD, and LCRA). The results of our chlorophyll-a models should be used with caution. We acknowledge that a larger sample size would undoubtedly enhance the robustness of the empirical models, and we are actively pursuing efforts to acquire additional data to expand the sample size in future studies. Despite the limited sample size, our primary objective was to evaluate the feasibility of empirical models in estimating chlorophyll-a using the available data. The empirical salinity models also experienced improvements after calibration over Matagorda Bay. The RMSE, r, and NSE measures increased from 180.47 ± 0.01, 0.00 ± 0.22, and −32,637.09 ± 2.18 for uncalibrated models to 0.24, 0.24, and 0.06 for the calibrated model, respectively. The calibrated salinity models, Sn1 and Sn2, used B1, B2, B3, and B4. These bands indicated a weakly inverse relationship (r: −0.16 to −0.09) with in situ salinity measurements. This weak relationship likely hinders the empirical models in establishing meaningful linear relationships between in situ salinity observations and surface reflectance. In addition, the performance of calibrated salinity models was significantly lower than the performance reported for the original study. In its original applications, the r values for Sn1 and Sn2 were 0.84 [] and 0.77 [], respectively. However, the original studies only used 33 data points, which might have led to overfitting and produced misleading performance measures.
The calibrated turbidity models demonstrated some improvements in performance. The NRMSE, r, and NSE measures increased from 5.86 ± 17.78, 0.07 ± 0.08, and −337.09 ± 1553.51 for uncalibrated models to 0.15 ± 0.10, 0.13 ± 0.09, and 0.03 ± 0.03 for calibrated models, respectively. The highest-performing calibrated empirical turbidity model is T12, which used B2, B3, B4, and B5. These bands had a positive, but low, correlation with in situ turbidity (r: 0.05 − 0.12). Model T12 had higher performances reported in its original studies (r: 0.85 ± 0.18) compared to that calibrated to Matagorda Bay []. This might be due to the complex turbidity patterns over Matagorda Bay.
5.2. ML Models
ML algorithms performed better for both salinity and turbidity compared to empirical models. ML algorithms are much more complex, and equipped to ascertain intricate relationships between inputs (surface reflectance) and target (salinity and turbidity) datasets []. In addition, ML algorithms are better able to map nonlinear relationships, such as those between salinity and turbidity and surface reflectance (correlation between salinity and surface reflectance: −0.10 ± 0.04; correlation between turbidity and surface reflectance: 0.04 ± 0.04).
The DNN, GBM, and DRF families examined in this study demonstrated acceptable performance when used to retrieve turbidity and salinity over Matagorda Bay. Notably, DNN performed better than the other families when simulating both salinity and turbidity. DNN is widely recognized for its efficacy in modeling high-dimensional and complex datasets, particularly those characterized by intricate nonlinear associations between input and target variables [,]. DNNs excel in extracting hierarchical features from input and target data, endowing them with stronger modeling capabilities relative to alternative ML families [,,]. The GBM family consistently secured the second-highest model performance when simulating salinity and turbidity. However, no large differences were found in the performance of both DRF and GBM. Remarkably, the GLM family consistently produced the poorest-performing models for both salinity and turbidity simulations. GLM models adopt a straightforward linear regression approach and lack the intricacy required to dissect the multifaceted relationships inherent in the multidimensional and nonlinear datasets used in this study. Consequently, the limitations of GLM models prevent them from effectively capturing the complexities in the data.
Most of the ML models exhibited a slight decrease in performance during the testing phase compared to the training phase. This relatively modest reduction in testing performance can be attributed to the limited number of training samples [,]. For instance, the salinity models were trained with only 382 data points, while the turbidity models had a training set of 138 data points. Another potential explanation for the variation in performance between the training and testing sets may stem from differences in the input/target patterns within the model inputs in the testing set compared to those in the training set. Salinity models were tested with 96 data points, while turbidity was tested with 35. Attempts to model chlorophyll-a using ML models were unsuccessful, likely due to a lack of in situ data. Chlorophyll-a measurements have only 17 data points. It is likely that this dataset did not provide large enough target time series to allow the ML algorithms to adequately analyze the complex relationship between surface reflectance and the provided chlorophyll-a observations.
6. Conclusions
The integration of public-domain remote sensing data-modeling techniques has significantly enhanced WQI monitoring capabilities. Landsat-8 offers a unique opportunity to observe the spatiotemporal trends of WQ within expansive aquatic ecosystems. With advances in modeling techniques, numerous inquiries have arisen regarding the most effective approaches to model WQIs. This study examines the capabilities of both empirical and ML models to determine optimal methods for retrieving salinity, turbidity, and chlorophyll-a from Landsat-8 data over Matagorda Bay, Texas.
The uncalibrated empirical models exhibited poor performance when applied to Matagorda Bay. The unique environmental characteristics of Matagorda Bay contributed to the failure of these uncalibrated models to produce WQIs. However, when calibrated over Matagorda Bay, model performance improved when used to retrieve chlorophyll-a data. ML models, on the other hand, yielded meaningful results for both salinity and turbidity. Among the implemented ML families, DNN demonstrated the highest performance. This model was able to successfully map complex nonlinear relationships between Landsat-8 reflectance datasets and salinity and turbidity.
Our methodology offers a point of reference, a structured framework, and valuable insights for employing empirical and ML models on Landsat-8 data to characterize WQIs. This approach encourages broader, enhanced use of remote sensing datasets by the scientific community, end-users, and decision makers. Given the higher performance of calibrated C2 empirical models for chlorophyll-a and DNN models for both salinity and turbidity, the modeled WQIs could be used to expand the footprint of in situ observations and improve current efforts to conserve, enhance, and restore important habitats in aquatic ecosystems. The developed approach serves as a guide to enhance monitoring procedures for aquatic ecosystems.
Author Contributions
Conceptualization, M.A. and M.B.; methodology, M.A. and M.B.; software, M.A. and M.B.; validation, M.A. and M.B.; formal analysis and investigation, and data curation, M.A. and M.B.; resources, M.A.; writing—original draft preparation, M.A. and M.B.; writing—review and editing, M.A. and M.B.; visualization, M.A. and M.B.; supervision, M.A.; project administration, M.A.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by a Texas Coastal Management Program grant approved by the Texas Land Commissioner, providing financial assistance under the Coastal Zone Management Act of 1972, as amended, awarded by the National Oceanic and Atmospheric Administration (NOAA), Office for Coastal Management, pursuant to NOAA Award No. NA21NOS4190136. The views expressed herein are those of the author(s) and do not necessarily reflect the views of NOAA, the U.S. Department of Commerce, or any of their subagencies. The authors thank the Mary and Jeff Bell Library at Texas A&M University-Corpus Christi (TAMU-CC) for providing the Open Access Publication Fund.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank Muhamed Elshalkany for his help with collecting the empirical models’ equations from the previously published studies, as well as Michael Alcala for his assistance with Google Earth Engine (GEE) coding.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Bugica, K.; Sterba-Boatwright, B.; Wetz, M.S. Water Quality Trends in Texas Estuaries. Mar. Pollut. Bull. 2020, 152, 110903. [Google Scholar] [CrossRef]
- Silva, G.M.; Campos, D.F.; Brasil, J.A.T.; Tremblay, M.; Mendiondo, E.M.; Ghiglieno, F. Advances in Technological Research for Online and In Situ Water Quality Monitoring—A Review. Sustainability 2022, 14, 5059. [Google Scholar] [CrossRef]
- Strobl, R.O.; Robillard, P.D. Network Design for Water Quality Monitoring of Surface Freshwaters: A Review. J. Environ. Manag. 2008, 87, 639–648. [Google Scholar] [CrossRef]
- Wilber, D.H.; Bass, R. Effect of the Colorado River Diversion on Matagorda Bay Epifauna. Estuar. Coast. Shelf Sci. 1998, 47, 309–318. [Google Scholar] [CrossRef]
- Misaghi, F.; Delgosha, F.; Razzaghmanesh, M.; Myers, B. Introducing a Water Quality Index for Assessing Water for Irrigation Purposes: A Case Study of the Ghezel Ozan River. Sci. Total Environ. 2017, 589, 107–116. [Google Scholar] [CrossRef]
- Kumar, A.; Dua, A. Water Quality Index for Assessment of Water Quality of River Ravi at Madhopur (India). Glob. J. Environ. Sci. 2009, 8, 49–57. [Google Scholar] [CrossRef]
- Lim, J.; Choi, M. Assessment of Water Quality Based on Landsat 8 Operational Land Imager Associated with Human Activities in Korea. Environ. Monit. Assess. 2015, 187, 384. [Google Scholar] [CrossRef] [PubMed]
- Kannel, P.R.; Lee, S.; Lee, Y.-S.; Kanel, S.R.; Khan, S.P. Application of Water Quality Indices and Dissolved Oxygen as Indicators for River Water Classification and Urban Impact Assessment. Environ. Monit. Assess. 2007, 132, 93–110. [Google Scholar] [CrossRef]
- Poshtegal, M.K.; Mirbagheri, S.A. Simulation and Modelling of Heavy Metals and Water Quality Parameters in the River. Sci. Rep. 2023, 13, 3020. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.P.; Khali, H.; Singh, S.; Pande, C.B.; Singh, R.; Chaurasia, S.K. An Assessment of In-Situ Water Quality Parameters and Its Variation with Landsat 8 Level 1 Surface Reflectance Datasets. Int. J. Environ. Anal. Chem. 2021, 103, 1–23. [Google Scholar] [CrossRef]
- Wong, M.-S.; Lee, K.-H.; Kim, Y.-J.; Nichol, J.E.; Li, Z.; Emerson, N. Modeling of Suspended Solids and Sea Surface Salinity in Hong Kong Using Aqua/MODIS Satellite Images. Korean J. Remote Sens. 2007, 23, 161–169. [Google Scholar] [CrossRef]
- AL-Fahdawi, A.A.H.; Rabee, A.M.; Al-Hirmizy, S.M. Water Quality Monitoring of Al-Habbaniyah Lake Using Remote Sensing and in Situ Measurements. Environ. Monit. Assess. 2015, 187, 367. [Google Scholar] [CrossRef] [PubMed]
- Behmel, S.; Damour, M.; Ludwig, R.; Rodriguez, M.J. Water Quality Monitoring Strategies—A Review and Future Perspectives. Sci. Total Environ. 2016, 571, 1312–1329. [Google Scholar] [CrossRef]
- Ighalo, J.O.; Adeniyi, A.G. A Comprehensive Review of Water Quality Monitoring and Assessment in Nigeria. Chemosphere 2020, 260, 127569. [Google Scholar] [CrossRef] [PubMed]
- González-Márquez, L.C.; Torres-Bejarano, F.M.; Torregroza-Espinosa, A.C.; Hansen-Rodríguez, I.R.; Rodríguez-Gallegos, H.B. Use of LANDSAT 8 Images for Depth and Water Quality Assessment of El Guájaro Reservoir, Colombia. J. S. Am. Earth Sci. 2018, 82, 231–238. [Google Scholar] [CrossRef]
- Peterson, K.T.; Sagan, V.; Sloan, J.J. Deep Learning-Based Water Quality Estimation and Anomaly Detection Using Landsat-8/Sentinel-2 Virtual Constellation and Cloud Computing. GIScience Remote Sens. 2020, 57, 510–525. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Dailloux, D.; White, M.; Bowers, D. Fundamentals of in Situ Digital Camera Methodology for Water Quality Monitoring of Coast and Ocean. Sensors 2009, 9, 5825–5843. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Alikas, K.; Anstee, J.; Barbosa, C.; Binding, C.; Bresciani, M.; Cremella, B.; Giardino, C.; Gurlin, D.; et al. Simultaneous Retrieval of Selected Optical Water Quality Indicators from Landsat-8, Sentinel-2, and Sentinel-3. Remote Sens. Environ. 2022, 270, 112860. [Google Scholar] [CrossRef]
- Carpenter, D.J.; Carpenter, S.M. Modeling Inland Water Quality Using Landsat Data. Remote Sens. Environ. 1983, 13, 345–352. [Google Scholar] [CrossRef]
- Sharaf El Din, E. A Novel Approach for Surface Water Quality Modelling Based on Landsat-8 Tasselled Cap Transformation. Int. J. Remote Sens. 2020, 41, 7186–7201. [Google Scholar] [CrossRef]
- Vakili, T.; Amanollahi, J. Determination of Optically Inactive Water Quality Variables Using Landsat 8 Data: A Case Study in Geshlagh Reservoir Affected by Agricultural Land Use. J. Clean. Prod. 2020, 247, 119134. [Google Scholar] [CrossRef]
- Wei, Z.; Wei, L.; Yang, H.; Wang, Z.; Xiao, Z.; Li, Z.; Yang, Y.; Xu, G. Water Quality Grade Identification for Lakes in Middle Reaches of Yangtze River Using Landsat-8 Data with Deep Neural Networks (DNN) Model. Remote Sens. 2022, 14, 6238. [Google Scholar] [CrossRef]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.; Dimitriou, E. Analysis on the Feasibility of Landsat 8 Imagery for Water Quality Parameters Assessment in an Oligotrophic Mediterranean Lake. Int. J. Geol. Environ. Eng. 2017, 11, 906–914. [Google Scholar]
- Sudheer, K.P.; Chaubey, I.; Garg, V. Lake Water Quality Assessment from Landsat Thematic Mapper Data Using Neural Network: An Approach to Optimal Band Combination Selection1. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 1683–1695. [Google Scholar] [CrossRef]
- Zhang, H.; Xue, B.; Wang, G.; Zhang, X.; Zhang, Q. Deep Learning-Based Water Quality Retrieval in an Impounded Lake Using Landsat 8 Imagery: An Application in Dongping Lake. Remote Sens. 2022, 14, 4505. [Google Scholar] [CrossRef]
- González-Márquez, L.C.; Torres-Bejarano, F.M.; Rodríguez-Cuevas, C.; Torregroza-Espinosa, A.C.; Sandoval-Romero, J.A. Estimation of Water Quality Parameters Using Landsat 8 Images: Application to Playa Colorada Bay, Sinaloa, Mexico. Appl. Geomat. 2018, 10, 147–158. [Google Scholar] [CrossRef]
- Ansari, M.; Akhoondzadeh, M. Mapping Water Salinity Using Landsat-8 OLI Satellite Images (Case Study: Karun Basin Located in Iran). Adv. Space Res. 2020, 65, 1490–1502. [Google Scholar] [CrossRef]
- Bayati, M.; Danesh-Yazdi, M. Mapping the Spatiotemporal Variability of Salinity in the Hypersaline Lake Urmia Using Sentinel-2 and Landsat-8 Imagery. J. Hydrol. 2021, 595, 126032. [Google Scholar] [CrossRef]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. An Appraisal of the Potential of Landsat 8 in Estimating Chlorophyll-a, Ammonium Concentrations and Other Water Quality Indicators. Remote Sens. 2018, 10, 1018. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Z.; Clayton, T.D.; Swarzenski, P.; Brock, J.C.; Muller–Karger, F.E. Assessment of Estuarine Water-Quality Indicators Using MODIS Medium-Resolution Bands: Initial Results from Tampa Bay, FL. Remote Sens. Environ. 2004, 93, 423–441. [Google Scholar] [CrossRef]
- Kim, H.-C.; Son, S.; Kim, Y.H.; Khim, J.S.; Nam, J.; Chang, W.K.; Lee, J.-H.; Lee, C.-H.; Ryu, J. Remote Sensing and Water Quality Indicators in the Korean West Coast: Spatio-Temporal Structures of MODIS-Derived Chlorophyll-a and Total Suspended Solids. Mar. Pollut. Bull. 2017, 121, 425–434. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Mukherjee, D.; Chen, S. Assessment of Hurricane Ivan Impact on Chlorophyll-a in Pensacola Bay by MODIS 250 m Remote Sensing. Mar. Pollut. Bull. 2011, 62, 490–498. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Yu, S.; Cao, Z.; Qi, T.; Duan, H. Process-Oriented Estimation of Column-Integrated Algal Biomass in Eutrophic Lakes by MODIS/Aqua. Int. J. Appl. Earth Obs. Geoinf. 2021, 99, 102321. [Google Scholar] [CrossRef]
- Schaeffer, B.A.; Conmy, R.N.; Duffy, A.E.; Aukamp, J.; Yates, D.F.; Craven, G. Northern Gulf of Mexico Estuarine Coloured Dissolved Organic Matter Derived from MODIS Data. Int. J. Remote Sens. 2015, 36, 2219–2237. [Google Scholar] [CrossRef]
- Yu, X.; Yi, H.; Liu, X.; Wang, Y.; Liu, X.; Zhang, H. Remote-Sensing Estimation of Dissolved Inorganic Nitrogen Concentration in the Bohai Sea Using Band Combinations Derived from MODIS Data. Int. J. Remote Sens. 2016, 37, 327–340. [Google Scholar] [CrossRef]
- Mathew, M.M.; Srinivasa Rao, N.; Mandla, V.R. Development of Regression Equation to Study the Total Nitrogen, Total Phosphorus and Suspended Sediment Using Remote Sensing Data in Gujarat and Maharashtra Coast of India. J. Coast. Conserv. 2017, 21, 917–927. [Google Scholar] [CrossRef]
- Singh, A.; Jakubowski, A.R.; Chidister, I.; Townsend, P.A. A MODIS Approach to Predicting Stream Water Quality in Wisconsin. Remote Sens. Environ. 2013, 128, 74–86. [Google Scholar] [CrossRef]
- Arıman, S. Determination of Inactive Water Quality Variables by MODIS Data: A Case Study in the Kızılırmak Delta-Balik Lake, Turkey. Estuar. Coast. Shelf Sci. 2021, 260, 107505. [Google Scholar] [CrossRef]
- Hossen, H.; Mahmod, W.E.; Negm, A.; Nakamura, T. Assessing Water Quality Parameters in Burullus Lake Using Sentinel-2 Satellite Images. Water Resour. 2022, 49, 321–331. [Google Scholar] [CrossRef]
- Sent, G.; Biguino, B.; Favareto, L.; Cruz, J.; Sá, C.; Dogliotti, A.I.; Palma, C.; Brotas, V.; Brito, A.C. Deriving Water Quality Parameters Using Sentinel-2 Imagery: A Case Study in the Sado Estuary, Portugal. Remote Sens. 2021, 13, 1043. [Google Scholar] [CrossRef]
- Virdis, S.G.P.; Xue, W.; Winijkul, E.; Nitivattananon, V.; Punpukdee, P. Remote Sensing of Tropical Riverine Water Quality Using Sentinel-2 MSI and Field Observations. Ecol. Indic. 2022, 144, 109472. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First Experiences in Mapping Lake Water Quality Parameters with Sentinel-2 MSI Imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef]
- Guo, H.; Huang, J.J.; Chen, B.; Guo, X.; Singh, V.P. A Machine Learning-Based Strategy for Estimating Non-Optically Active Water Quality Parameters Using Sentinel-2 Imagery. Int. J. Remote Sens. 2021, 42, 1841–1866. [Google Scholar] [CrossRef]
- Torres-Bejarano, F.; Arteaga-Hernández, F.; Rodríguez-Ibarra, D.; Mejía-Ávila, D.; González-Márquez, L.C. Water Quality Assessment in a Wetland Complex Using Sentinel 2 Satellite Images. Int. J. Environ. Sci. Technol. 2021, 18, 2345–2356. [Google Scholar] [CrossRef]
- Gorokhovich, Y.; Cawse-Nicholson, K.; Papadopoulos, N.; Oikonomou, D. Use of ECOSTRESS Data for Measurements of the Surface Water Temperature: Significance of Data Filtering in Accuracy Assessment. Remote Sens. Appl. Soc. Environ. 2022, 26, 100739. [Google Scholar] [CrossRef]
- Shi, J.; Hu, C. Evaluation of ECOSTRESS Thermal Data over South Florida Estuaries. Sensors 2021, 21, 4341. [Google Scholar] [CrossRef]
- Ding, H.; Elmore, A.J. Spatio-Temporal Patterns in Water Surface Temperature from Landsat Time Series Data in the Chesapeake Bay, U.S.A. Remote Sens. Environ. 2015, 168, 335–348. [Google Scholar] [CrossRef]
- Shareef, M.A.; Khenchaf, A.; Toumi, A. Integration of Passive and Active Microwave Remote Sensing to Estimate Water Quality Parameters. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–4. [Google Scholar]
- Shareef, M.A.; Toumi, A.; Khenchaf, A. Estimation and Characterization of Physical and Inorganic Chemical Indicators of Water Quality by Using SAR Images. In Proceedings of the SAR Image Analysis, Modeling, and Techniques XV, SPIE, Toulouse, France, 15 October 2015; Volume 9642, pp. 140–150. [Google Scholar]
- He, Y.; Jin, S.; Shang, W. Water Quality Variability and Related Factors along the Yangtze River Using Landsat-8. Remote Sens. 2021, 13, 2241. [Google Scholar] [CrossRef]
- Trinh, R.C.; Fichot, C.G.; Gierach, M.M.; Holt, B.; Malakar, N.K.; Hulley, G.; Smith, J. Application of Landsat 8 for Monitoring Impacts of Wastewater Discharge on Coastal Water Quality. Front. Mar. Sci. 2017, 4, 329. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, Y.; Huang, C.; Wang, Z.; Huang, Q.; Yin, F.; Guo, Y.; Cao, L. Inland Lakes Mapping for Monitoring Water Quality Using a Detail/Smoothing-Balanced Conditional Random Field Based on Landsat-8/Levels Data. Sensors 2020, 20, 1345. [Google Scholar] [CrossRef]
- Pu, F.; Ding, C.; Chao, Z.; Yu, Y.; Xu, X. Water-Quality Classification of Inland Lakes Using Landsat8 Images by Convolutional Neural Networks. Remote Sens. 2019, 11, 1674. [Google Scholar] [CrossRef]
- Jakovljević, G.; Govedarica, M.; Álvarez-Taboada, F. Assessment of Biological and Physic Chemical Water Quality Parameters Using Landsat 8 Time Series. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XX, SPIE, Berlin, Germany, 10 October 2018; Volume 10783, pp. 349–361. [Google Scholar]
- Bormudoi, A.; Hinge, G.; Nagai, M.; Kashyap, M.P.; Talukdar, R. Retrieval of Turbidity and TDS of Deepor Beel Lake from Landsat 8 OLI Data by Regression and Artificial Neural Network. Water Conserv. Sci. Eng. 2022, 7, 505–513. [Google Scholar] [CrossRef]
- Krishnaraj, A.; Honnasiddaiah, R. Remote Sensing and Machine Learning Based Framework for the Assessment of Spatio-Temporal Water Quality in the Middle Ganga Basin. Environ. Sci. Pollut. Res. 2022, 29, 64939–64958. [Google Scholar] [CrossRef] [PubMed]
- Wagle, N.; Acharya, T.D.; Lee, D.H. Comprehensive Review on Application of Machine Learning Algorithms for Water Quality Parameter Estimation Using Remote Sensing Data. Sens. Mater. 2020, 32, 3879. [Google Scholar] [CrossRef]
- Li, N.; Ning, Z.; Chen, M.; Wu, D.; Hao, C.; Zhang, D.; Bai, R.; Liu, H.; Chen, X.; Li, W.; et al. Satellite and Machine Learning Monitoring of Optically Inactive Water Quality Variability in a Tropical River. Remote Sens. 2022, 14, 5466. [Google Scholar] [CrossRef]
- Caillier, J. An Assessment of Benthic Condition in the Matagorda Bay System Using a Sediment Quality Triad Approach. Master’s Thesis, Texas A&M University, Corpus Christi, TX, USA, 2023. [Google Scholar]
- Brody, S.D.; Highfield, W.; Arlikatti, S.; Bierling, D.H.; Ismailova, R.M.; Lee, L.; Butzler, R. Conflict on the Coast: Using Geographic Information Systems to Map Potential Environmental Disputes in Matagorda Bay, Texas. Environ. Manag. 2004, 34, 11–25. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, D.N. Salinity Disturbance Affects Community Structure and Organic Matter on a Restored Crassostrea Virginica Oyster Reef in Matagorda Bay, Texas. Master’s Thesis, Texas A&M University, Corpus Christi, TX, USA, 2017. [Google Scholar]
- Onabule, O.A.; Mitchell, S.B.; Couceiro, F. The Effects of Freshwater Flow and Salinity on Turbidity and Dissolved Oxygen in a Shallow Macrotidal Estuary: A Case Study of Portsmouth Harbour. Ocean Coast. Manag. 2020, 191, 105179. [Google Scholar] [CrossRef]
- Ward, G.H.; Armstrong, N.E. Matagorda Bay, Texas, Its Hydrography, Ecology, and Fishery Resources; Fish and Wildlife Service, U.S. Department of the Interior: Washington, DC, USA, 1980.
- Kinsey, J.; Montagna, P.A. Response of Benthic Organisms to External Conditions in Matagorda Bay; University of Texas, Marine Science Institute: Port Aransas, TX, USA, 2005. [Google Scholar] [CrossRef]
- Marshall, D.A.; Lebreton, B.; Palmer, T.; De Santiago, K.; Beseres Pollack, J. Salinity Disturbance Affects Faunal Community Composition and Organic Matter on a Restored Crassostrea Virginica Oyster Reef. Estuar. Coast. Shelf Sci. 2019, 226, 106267. [Google Scholar] [CrossRef]
- McBride, M.R. Influence of Colorado River Discharge Variability on Phytoplankton Communities in Matagorda Bay, Texas. Master’s Thesis, Texas A&M University, Corpus Christi, TX, USA, 2022. [Google Scholar]
- Armstrong, N. Studies Regarding the Distribution and Biomass Densities of, and the Influences of Freshwater Inflow Variations on Finfish Populations in the Matagorda Bay System, Texas; University of Texas at Austin: Austin, TX, USA, 1987. [Google Scholar]
- Olsen, Z. Quantifying Nursery Habitat Function: Variation in Habitat Suitability Linked to Mortality and Growth for Juvenile Black Drum in a Hypersaline Estuary. Mar. Coast. Fish. 2019, 11, 86–96. [Google Scholar] [CrossRef]
- Renaud, M.; Williams, J. Movements of Kemp’s Ridley (Lepidochelys kempii) and Green (Chelonia mydas) Sea Turtles Using Lavaca Bay and Matagorda Bay; Environmental Protection Agency Office of Planning and Coordination: Dallas, TX, USA, 2023.
- Ropicki, A.; Hanselka, R.; Cummins, D.; Balboa, B.R. The Economic Impacts of Recreational Fishing in the Matagorda Bay System. Available online: https://repository.library.noaa.gov/view/noaa/43595 (accessed on 5 November 2023).
- Haby, M. A Review of Palacios Shrimp Landings, Matagorda Bay Oyster Resources and Statewide Economic Impacts from the Texas Seafood Supply Chain and Saltwater Sportfishing; Sea Grant College Program, Texas A&M University: Corpus Christi, TX, USA, 2016. [Google Scholar]
- Culbertson, J.C. Spatial and Temporal Patterns of Eastern Oyster (Crassostrea virginica) Populations and Their Relationships to Dermo (Perkinsus marinus) Infection and Freshwater Inflows in West Matagorda Bay, Texas. Ph.D. Thesis, Texas A&M University, Corpus Christi, TX, USA, 2008. [Google Scholar]
- Kim, H.-C.; Montagna, P.A. Implications of Colorado River (Texas, USA) Freshwater Inflow to Benthic Ecosystem Dynamics: A Modeling Study. Estuar. Coast. Shelf Sci. 2009, 83, 491–504. [Google Scholar] [CrossRef]
- Grabowski, J.H.; Brumbaugh, R.D.; Conrad, R.F.; Keeler, A.G.; Opaluch, J.J.; Peterson, C.H.; Piehler, M.F.; Powers, S.P.; Smyth, A.R. Economic Valuation of Ecosystem Services Provided by Oyster Reefs. BioScience 2012, 62, 900–909. [Google Scholar] [CrossRef]
- Palmer, T.A.; Montagna, P.A.; Pollack, J.B.; Kalke, R.D.; DeYoe, H.R. The Role of Freshwater Inflow in Lagoons, Rivers, and Bays. Hydrobiologia 2011, 667, 49–67. [Google Scholar] [CrossRef]
- Kucera, C.J.; Faulk, C.K.; Holt, G.J. The Effect of Spawning Salinity on Eggs of Spotted Seatrout (Cynoscion nebulosus, Cuvier) from Two Bays with Historically Different Salinity Regimes. J. Exp. Mar. Biol. Ecol. 2002, 272, 147–158. [Google Scholar] [CrossRef]
- Montagna, P. Inflow Needs Assessment: Effect of the Colorado River Diversion on Benthic Communities; Research Technical Final Report; The University of Texas at Austin: Austin, TX, USA, 1994. [Google Scholar] [CrossRef]
- Armstrong, N. The Ecology of Open-Bay Bottoms of Texas: A Community Profile; U.S. Department of the Interior, Fish and Wildlife Service, Research and Development, National Wetlands Research Center: Washington, DC, USA, 1987.
- TCEQ Surface Water Quality Viewer. Available online: https://tceq.maps.arcgis.com/apps/webappviewer/index.html?id=b0ab6bac411a49189106064b70bbe778 (accessed on 17 August 2023).
- LCRA. Waterquality.Lcra.Org. Available online: https://waterquality.lcra.org/ (accessed on 17 August 2023).
- LCRA. 2022 Guidance for Assessing and Reporting Surface Water Quality in Texas; LCRA: Austin, TX, USA, 2022. [Google Scholar]
- LCRA. Water Quality Parameters—LCRA—Energy, Water, Community; LCRA: Austin, TX, USA, 2023. [Google Scholar]
- TCEQ. Surface Water Quality Monitoring Procedures, Volume 1: Physical and Chemical Monitoring Methods; TCEQ: Austin, TX, USA, 2012.
- Texas Secretary of State Texas Administrative Code. Available online: https://texreg.sos.state.tx.us/public/readtac%24ext.TacPage?sl=T&app=9&p_dir=F&p_rloc=183310&p_tloc=29466&p_ploc=14656&pg=3&p_tac=&ti=30&pt=1&ch=290&rl=111 (accessed on 6 November 2023).
- Dunne, R.P. Spectrophotometric Measurement of Chlorophyll Pigments: A Comparison of Conventional Monochromators and a Reverse Optic Diode Array Design. Mar. Chem. 1999, 66, 245–251. [Google Scholar] [CrossRef]
- Danbara, T.T. Deriving water quality indicators of lake tana, Ethiopia, from Landsat-8. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar]
- Kuhn, C.; de Matos Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 Surface Reflectance Products for River Remote Sensing Retrievals of Chlorophyll-a and Turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef]
- Mondejar, J.P.; Tongco, A.F. Near Infrared Band of Landsat 8 as Water Index: A Case Study around Cordova and Lapu-Lapu City, Cebu, Philippines. Sustain. Environ. Res. 2019, 29, 16. [Google Scholar] [CrossRef]
- Cabral, P.; Santos, J.A.; Augusto, G. Monitoring Urban Sprawl and the National Ecological Reserve in Sintra-Cascais, Portugal: Multiple OLS Linear Regression Model Evaluation. J. Urban Plan. Dev. 2011, 137, 346–353. [Google Scholar] [CrossRef]
- Peprah, M.S.; Mensah, I.O. Performance Evaluation of the Ordinary Least Square (OLS) and Total Least Square (TLS) in Adjusting Field Data: An Empirical Study on a DGPS Data. S. Afr. J. Geomat. 2017, 6, 73–89. [Google Scholar] [CrossRef]
- Elangovan, A.; Murali, V. Mapping the Chlorophyll-a Concentrations in Hypereutrophic Krishnagiri Reservoir (India) Using Landsat 8 Operational Land Imager. Lakes Reserv. Res. Manag. 2020, 25, 377–387. [Google Scholar] [CrossRef]
- Vargas-Lopez, I.A.; Rivera-Monroy, V.H.; Day, J.W.; Whitbeck, J.; Maiti, K.; Madden, C.J.; Trasviña-Castro, A. Assessing Chlorophyll a Spatiotemporal Patterns Combining In Situ Continuous Fluorometry Measurements and Landsat 8/OLI Data across the Barataria Basin (Louisiana, USA). Water 2021, 13, 512. [Google Scholar] [CrossRef]
- Buditama, G.; Damayanti, A.; Giok Pin, T. Identifying Distribution of Chlorophyll-a Concentration Using Landsat 8 OLI on Marine Waters Area of Cirebon. IOP Conf. Ser. Earth Environ. Sci. 2017, 98, 012040. [Google Scholar] [CrossRef]
- Masocha, M.; Dube, T.; Nhiwatiwa, T.; Choruma, D. Testing Utility of Landsat 8 for Remote Assessment of Water Quality in Two Subtropical African Reservoirs with Contrasting Trophic States. Geocarto Int. 2018, 33, 667–680. [Google Scholar] [CrossRef]
- Yang, Z.; Anderson, Y. Estimating Chlorophyll-A Concentration in a Freshwater Lake Using Landsat 8 Imagery. J. Environ. Earth Sci. 2016, 6, 134–142. [Google Scholar]
- Zhao, J.; Temimi, M. An Empirical Algorithm for Retreiving Salinity in the Arabian Gulf: Application to Landsat-8 Data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4645–4648. [Google Scholar]
- Zhao, J.; Temimi, M.; Ghedira, H. Remotely Sensed Sea Surface Salinity in the Hyper-Saline Arabian Gulf: Application to Landsat 8 OLI Data. Estuar. Coast. Shelf Sci. 2017, 187, 168–177. [Google Scholar] [CrossRef]
- Snyder, J.; Boss, E.; Weatherbee, R.; Thomas, A.C.; Brady, D.; Newell, C. Oyster Aquaculture Site Selection Using Landsat 8-Derived Sea Surface Temperature, Turbidity, and Chlorophyll a. Front. Mar. Sci. 2017, 4, 190. [Google Scholar] [CrossRef]
- Quang, N.H.; Sasaki, J.; Higa, H.; Huan, N.H. Spatiotemporal Variation of Turbidity Based on Landsat 8 OLI in Cam Ranh Bay and Thuy Trieu Lagoon, Vietnam. Water 2017, 9, 570. [Google Scholar] [CrossRef]
- Liu, L.-W.; Wang, Y.-M. Modelling Reservoir Turbidity Using Landsat 8 Satellite Imagery by Gene Expression Programming. Water 2019, 11, 1479. [Google Scholar] [CrossRef]
- Allam, M.; Yawar Ali Khan, M.; Meng, Q. Retrieval of Turbidity on a Spatio-Temporal Scale Using Landsat 8 SR: A Case Study of the Ramganga River in the Ganges Basin, India. Appl. Sci. 2020, 10, 3702. [Google Scholar] [CrossRef]
- Pereira, L.S.F.; Andes, L.C.; Cox, A.L.; Ghulam, A. Measuring Suspended-Sediment Concentration and Turbidity in the Middle Mississippi and Lower Missouri Rivers Using Landsat Data. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 440–450. [Google Scholar] [CrossRef]
- Truong, A.; Walters, A.; Goodsitt, J.; Hines, K.; Bruss, C.B.; Farivar, R. Towards Automated Machine Learning: Evaluation and Comparison of AutoML Approaches and Tools. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 1471–1479. [Google Scholar]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep Learning in Agriculture: A Survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Mathew, A.; Amudha, P.; Sivakumari, S. Deep Learning Techniques: An Overview. In Proceedings of the Advanced Machine Learning Technologies and Applications, Jaipur, India, 13–15 February 2020; Hassanien, A.E., Bhatnagar, R., Darwish, A., Eds.; Springer: Singapore, 2021; pp. 599–608. [Google Scholar]
- Oyebisi, S.; Alomayri, T. Artificial Intelligence-Based Prediction of Strengths of Slag-Ash-Based Geopolymer Concrete Using Deep Neural Networks. Constr. Build. Mater. 2023, 400, 132606. [Google Scholar] [CrossRef]
- Tang, C.; Luktarhan, N.; Zhao, Y. SAAE-DNN: Deep Learning Method on Intrusion Detection. Symmetry 2020, 12, 1695. [Google Scholar] [CrossRef]
- Asgari, M.; Yang, W.; Farnaghi, M. Spatiotemporal Data Partitioning for Distributed Random Forest Algorithm: Air Quality Prediction Using Imbalanced Big Spatiotemporal Data on Spark Distributed Framework. Environ. Technol. Innov. 2022, 27, 102776. [Google Scholar] [CrossRef]
- Shrivastav, L.K.; Kumar, R. An Ensemble of Random Forest Gradient Boosting Machine and Deep Learning Methods for Stock Price Prediction. J. Inf. Technol. Res. (JITR) 2022, 15, 1–19. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient Boosting Machines, a Tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- Pekár, S.; Brabec, M. Generalized Estimating Equations: A Pragmatic and Flexible Approach to the Marginal GLM Modelling of Correlated Data in the Behavioural Sciences. Ethology 2018, 124, 86–93. [Google Scholar] [CrossRef]
- Osawa, T.; Mitsuhashi, H.; Uematsu, Y.; Ushimaru, A. Bagging GLM: Improved Generalized Linear Model for the Analysis of Zero-Inflated Data. Ecol. Inform. 2011, 6, 270–275. [Google Scholar] [CrossRef]
- Masocha, M.; Mungenge, C.; Nhiwatiwa, T. Remote Sensing of Nutrients in a Subtropical African Reservoir: Testing Utility of Landsat 8. Geocarto Int. 2018, 33, 458–469. [Google Scholar] [CrossRef]
- Davies-Colley, R.J.; Smith, D.G. Turbidity Suspeni)Ed Sediment, and Water Clarity: A Review1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 1085–1101. [Google Scholar] [CrossRef]
- Boyer, J.N.; Kelble, C.R.; Ortner, P.B.; Rudnick, D.T. Phytoplankton Bloom Status: Chlorophyll a Biomass as an Indicator of Water Quality Condition in the Southern Estuaries of Florida, USA. Ecol. Indic. 2009, 9, S56–S67. [Google Scholar] [CrossRef]
- Kasprzak, P.; Padisák, J.; Koschel, R.; Krienitz, L.; Gervais, F. Chlorophyll a Concentration across a Trophic Gradient of Lakes: An Estimator of Phytoplankton Biomass? Limnologica 2008, 38, 327–338. [Google Scholar] [CrossRef]
- Rakocevic-Nedovic, J.; Hollert, H. Phytoplankton Community and Chlorophyll a as Trophic State Indices of Lake Skadar (Montenegro, Balkan) (7 Pp). Environ. Sci. Poll. Res. Int. 2005, 12, 146–152. [Google Scholar] [CrossRef]
- El-Zeiny, A.; El-Kafrawy, S. Assessment of Water Pollution Induced by Human Activities in Burullus Lake Using Landsat 8 Operational Land Imager and GIS. Egypt. J. Remote Sens. Space Sci. 2017, 20, S49–S56. [Google Scholar] [CrossRef]
- Schild, K.M.; Hawley, R.L.; Chipman, J.W.; Benn, D.I. Quantifying Suspended Sediment Concentration in Subglacial Sediment Plumes Discharging from Two Svalbard Tidewater Glaciers Using Landsat-8 and in Situ Measurements. Int. J. Remote Sens. 2017, 38, 6865–6881. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D.; Gordon, H.R.; Nakajima, T.; Lenoble, J.; Frouin, R.; Grassl, H.; Herman, B.M.; King, M.D.; Teillet, P.M. Passive Remote Sensing of Tropospheric Aerosol and Atmospheric Correction for the Aerosol Effect. J. Geophys. Res. Atmos. 1997, 102, 16815–16830. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary Analysis of the Performance of the Landsat 8/OLI Land Surface Reflectance Product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Misra, A.; Chapron, B.; Nouguier, F.; Ramakrishnan, B.; Yurovskaya, M. Sun-Glint Imagery of Landsat 8 for Ocean Surface Waves. In Proceedings of the Remote Sensing of the Open and Coastal Ocean and Inland Waters, SPIE, Honolulu, HI, USA, 24 October 2018; Volume 10778, pp. 86–94. [Google Scholar]
- Wei, J.; Lee, Z.; Garcia, R.; Zoffoli, L.; Armstrong, R.A.; Shang, Z.; Sheldon, P.; Chen, R.F. An Assessment of Landsat-8 Atmospheric Correction Schemes and Remote Sensing Reflectance Products in Coral Reefs and Coastal Turbid Waters. Remote Sens. Environ. 2018, 215, 18–32. [Google Scholar] [CrossRef]
- Pahlevan, N.; Schott, J.R.; Franz, B.A.; Zibordi, G.; Markham, B.; Bailey, S.; Schaaf, C.B.; Ondrusek, M.; Greb, S.; Strait, C.M. Landsat 8 Remote Sensing Reflectance (Rrs) Products: Evaluations, Intercomparisons, and Enhancements. Remote Sens. Environ. 2017, 190, 289–301. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Y.J. Development and Application of a Remote Sensing-Based Salinity Prediction Model for a Large Estuarine Lake in the US Gulf of Mexico Coast. J. Hydrol. 2008, 360, 184–194. [Google Scholar] [CrossRef]
- Binding, C.E.; Bowers, D.G. Measuring the Salinity of the Clyde Sea from Remotely Sensed Ocean Colour. Estuar. Coast. Shelf Sci. 2003, 57, 605–611. [Google Scholar] [CrossRef]
- Bowers, D.G.; Brett, H.L. The Relationship between CDOM and Salinity in Estuaries: An Analytical and Graphical Solution. J. Mar. Syst. 2008, 73, 1–7. [Google Scholar] [CrossRef]
- Fang, L.; Chen, S.; Wang, H.; Qian, J.; Zhang, L. Detecting Marine Intrusion into Rivers Using EO-1 ALI Satellite Imagery: Modaomen Waterway, Pearl River Estuary, China. Int. J. Remote Sens. 2010, 31, 4125–4146. [Google Scholar] [CrossRef]
- Lavery, P.; Pattiaratchi, C.; Wyllie, A.; Hick, P. Water Quality Monitoring in Estuarine Waters Using the Landsat Thematic Mapper. Remote Sens. Environ. 1993, 46, 268–280. [Google Scholar] [CrossRef]
- Vuille, M.; Baumgartner, M.F. Hydrologic Investigations in the North Chilean Altiplano Using Landsat-MSS and -TM Data. Geocarto Int. 1993, 8, 35–45. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z.; Roberts, C.; Berry, L.; Chen, G. Salinity Assessment in Northeast Florida Bay Using Landsat TM Data. Southeast. Geogr. 2012, 52, 267–281. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, C.; Berry, L. Geographically Weighted Modelling of Surface Salinity in Florida Bay Using Landsat TM Data. Remote Sens. Lett. 2013, 4, 75–83. [Google Scholar] [CrossRef]
- Khorram, S. Development of Water Quality Models Applicable throughout the Entire San Francisco Bay and Delta. Photogramm. Eng. Remote Sens. 1985, 51, 53–62. [Google Scholar]
- Nazeer, M.; Bilal, M. Evaluation of Ordinary Least Square (OLS) and Geographically Weighted Regression (GWR) for Water Quality Monitoring: A Case Study for the Estimation of Salinity. J. Ocean Univ. China 2018, 17, 305–310. [Google Scholar] [CrossRef]
- Urquhart, E.; Zaitchik, B.; Hoffman, M.; Guikema, S.; Geiger, E. Remotely Sensed Estimates of Surface Salinity in the Chesapeake Bay: A Statistical Approach. Remote Sens. Environ. 2012, 123, 522–531. [Google Scholar] [CrossRef]
- Nguyen, P.; Koedsin, W.; McNeil, D.; Van, T. Remote Sensing Techniques to Predict Salinity Intrusion: Application for a Data-Poor Area of the Coastal Mekong Delta, Vietnam. Int. J. Remote Sens. 2018, 39, 6676. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, J.; Yang, X.; Zhang, Y.; Zhang, L.; Ren, H.; Wu, B.; Ye, L. A Review of the Application of Machine Learning in Water Quality Evaluation. Eco-Environ. Health 2022, 1, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Tian, S.; Jeanne Huang, J.; Zhu, X.; Wang, B.; Zhang, Z. Performance of Deep Learning in Mapping Water Quality of Lake Simcoe with Long-Term Landsat Archive. ISPRS J. Photogramm. Remote Sens. 2022, 183, 451–469. [Google Scholar] [CrossRef]
- Sun, A.; Scanlon, B.; Save, H.; Rateb, A. Reconstruction of GRACE Total Water Storage Through Automated Machine Learning. Water Resour. Res. 2021, 57, e2020WR028666. [Google Scholar] [CrossRef]
- Fallatah, O.; Ahmed, M.; Gyawali, B.; Alhawsawi, A. Factors Controlling Groundwater Radioactivity in Arid Environments: An Automated Machine Learning Approach. Sci. Total Environ. 2022, 830, 154707. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).