The Crack Diffusion Model: An Innovative Diffusion-Based Method for Pavement Crack Detection
Abstract
1. Introduction
- This study introduces a novel framework for pavement crack detection based on the diffusion model, CrackDiff, which is capable of learning both surface and deep features related to the distribution and spatial relationships of cracks, leading to accurate and continuous crack segmentation results.
- This study proposes a diffusion model structure based on multi-task UNet, which enhances the guidance effect on the original image by predicting image segmentation results, resulting in robust crack segmentation.
- Through experiments conducted on the Crack500 and DeepCrack datasets, CrackDiff achieves state-of-the-art results in pavement crack detection.
2. Related Works
2.1. Pavement Crack Detection
2.2. Diffusion Model
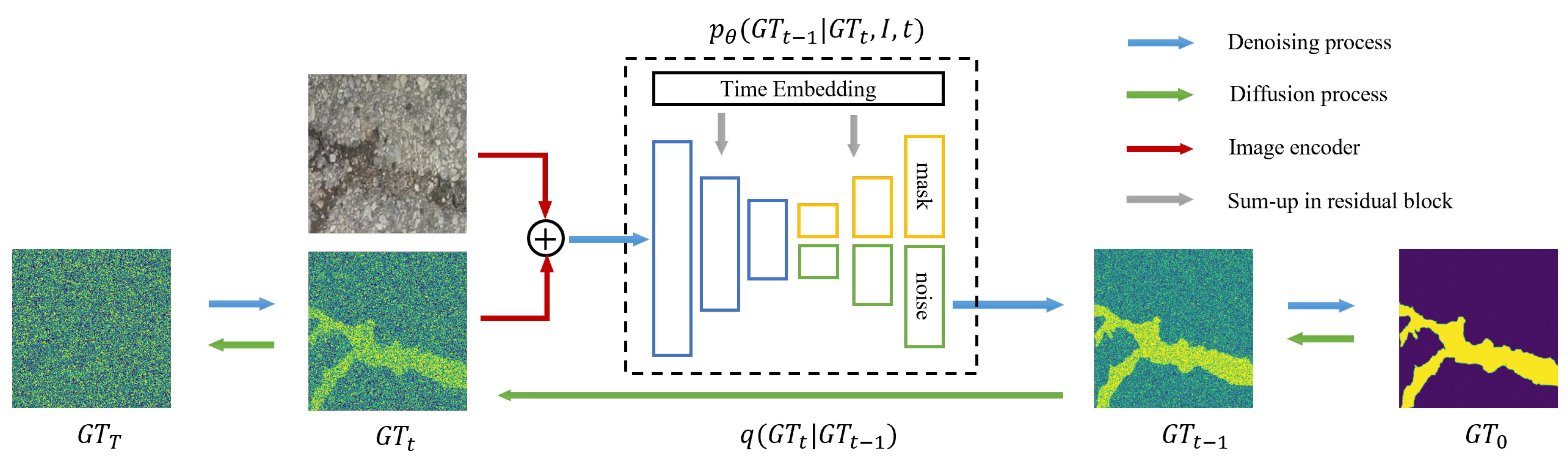
3. Methodology
3.1. Diffusion Model
3.2. Crack Diffusion Model
| Algorithm 1 Training Algorithm |
| Input: images and masks , total diffusion steps T repeat Sample Calculate according to Equations (3) and (11) Calculate loss and gradient according to Equation (12) Backward until iteration stop |
| Algorithm 2 Inference Algorithm |
| Input: image I, total diffusion steps T Sample for do Sample Calculate Calculate noise prediction Calculate according to Equation (7) end for return |
3.3. Structure of the Denoising Network
4. Experiments
4.1. Experimental Settings
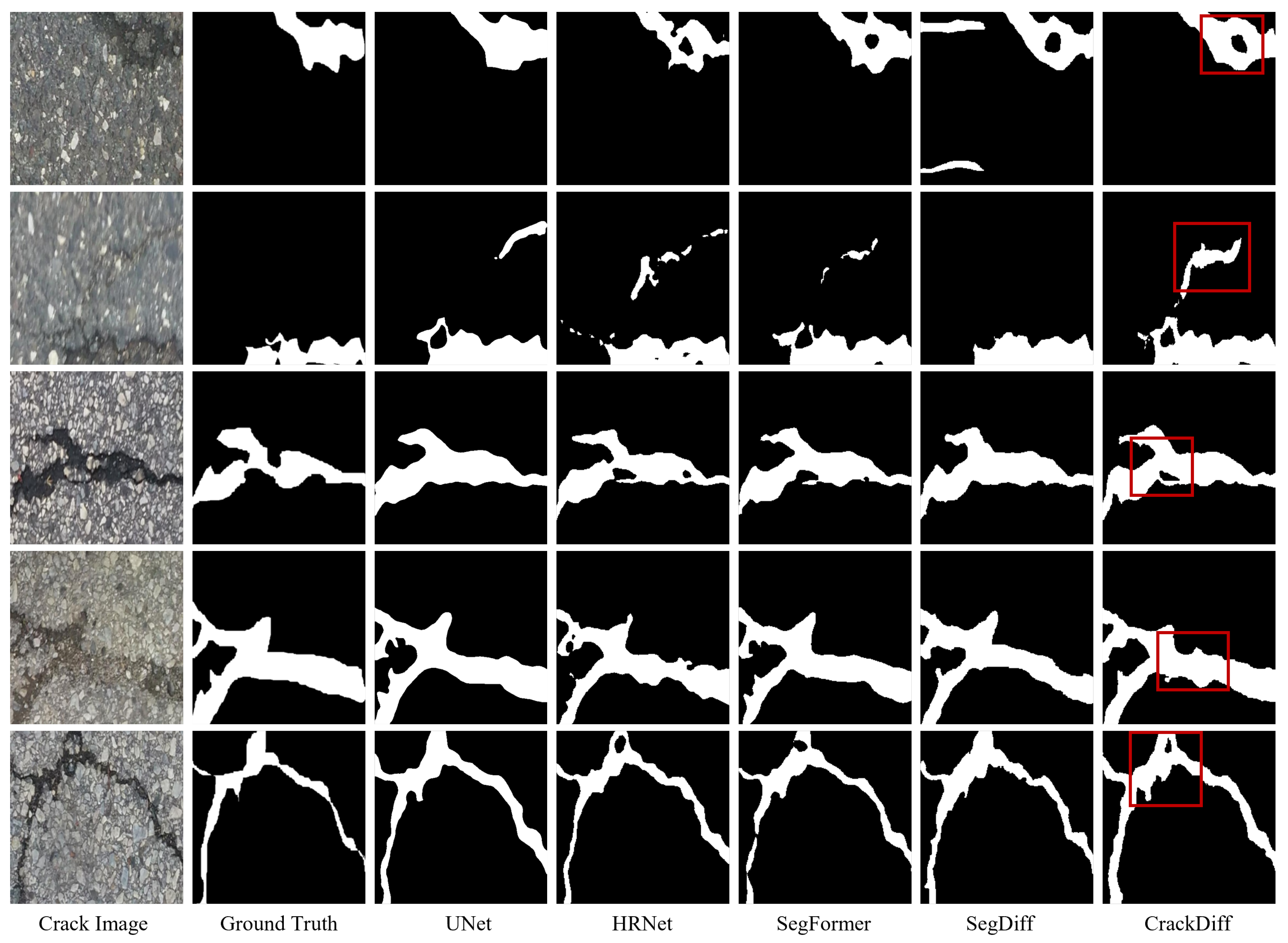
4.2. Experiment Results
4.3. Model Analysis
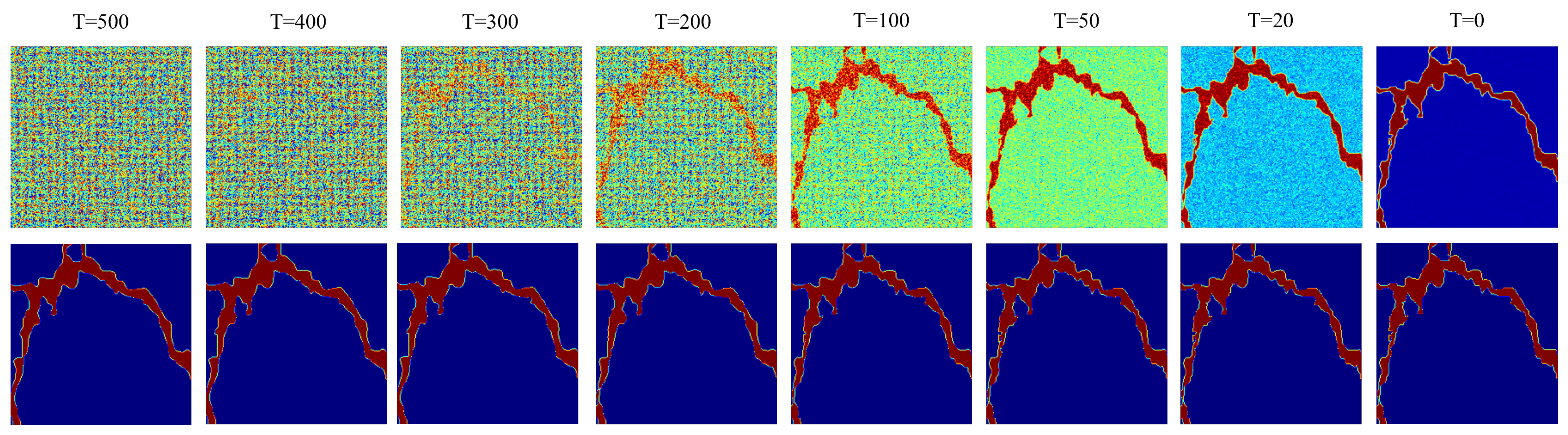
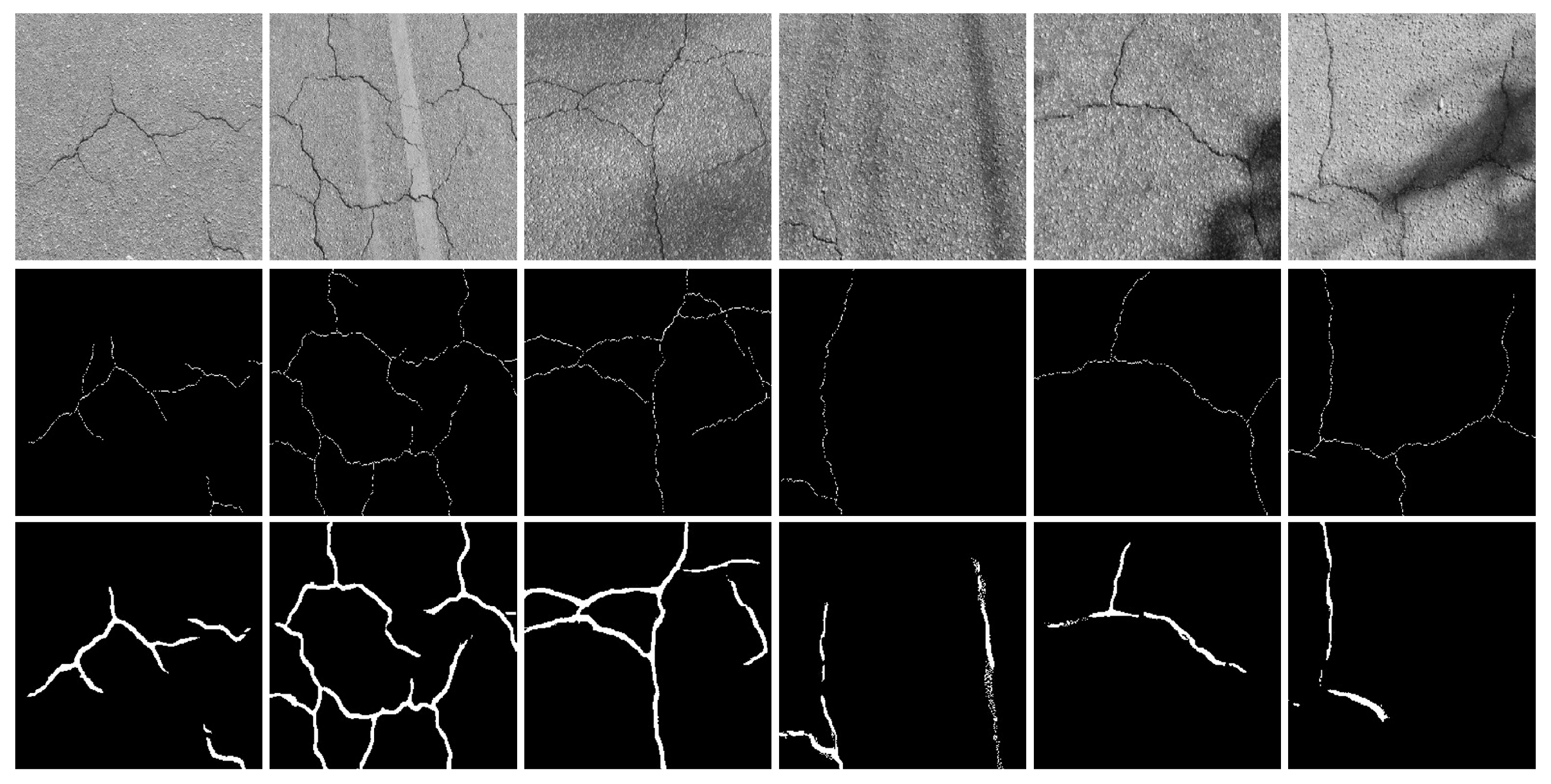
4.3.1. Visualization of Diffusion Steps
4.3.2. Ablation Study
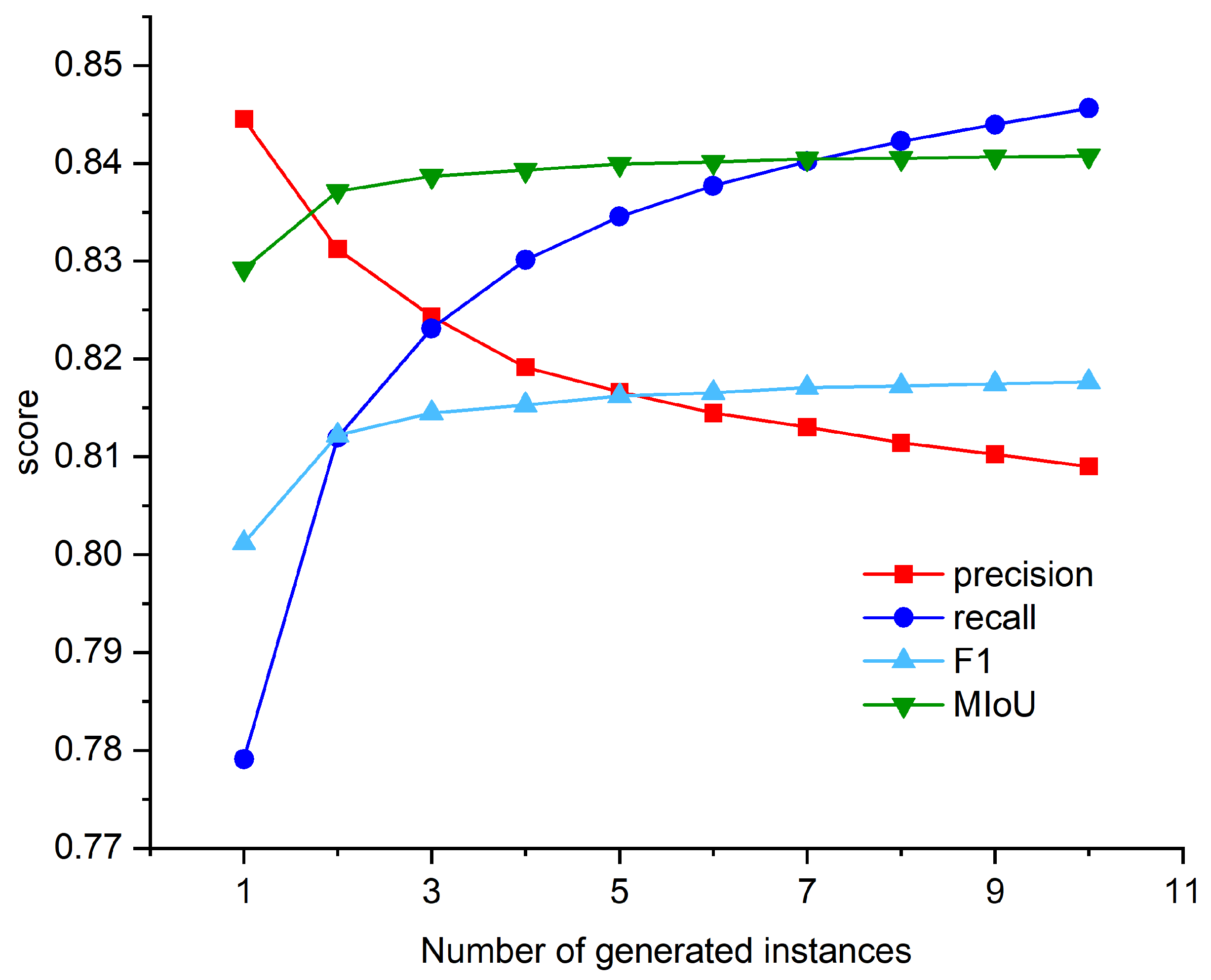
4.3.3. Impact of the Number of Generations
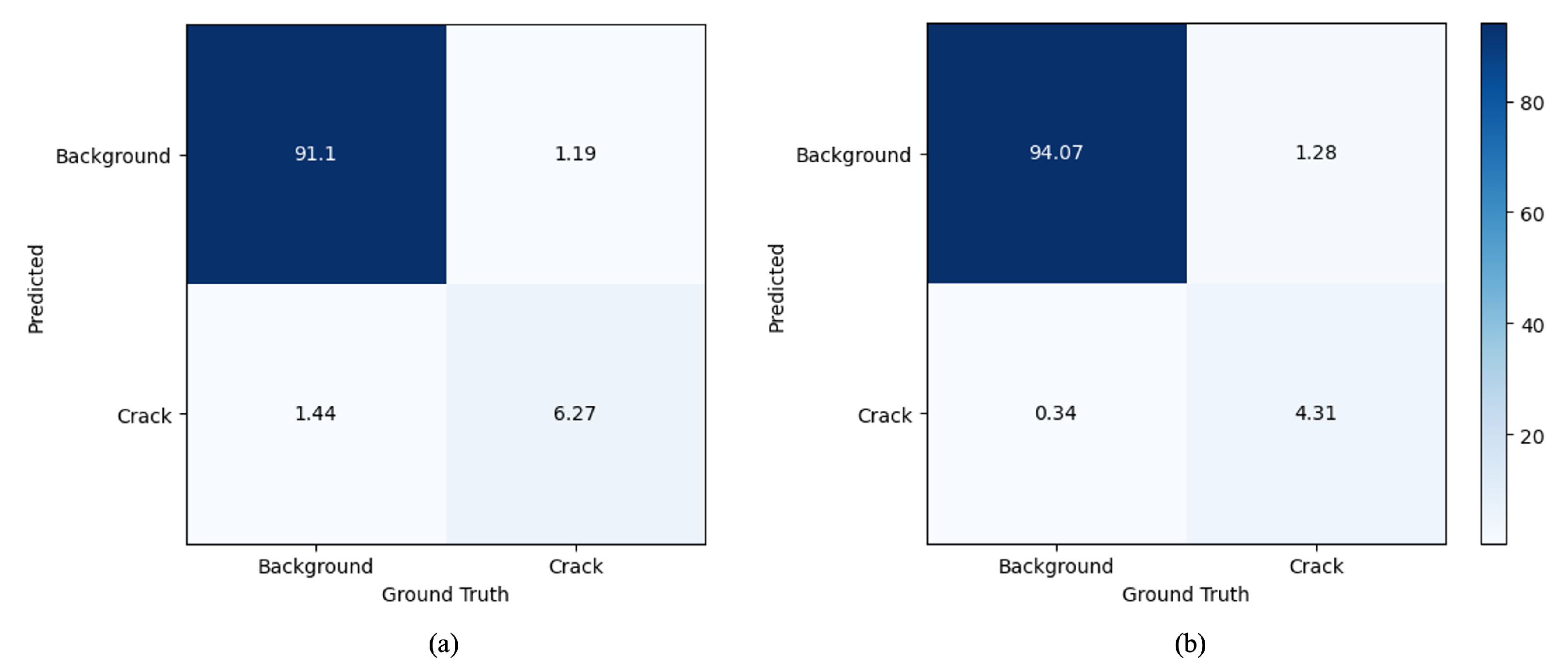
4.3.4. Robustness of CrackDiff
4.3.5. Model Generalization
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature pyramid and hierarchical boosting network for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1525–1535. [Google Scholar] [CrossRef]
- Yang, J.; Wang, W.; Lin, G.; Li, Q.; Sun, Y.; Sun, Y. Infrared Thermal Imaging-Based Crack Detection Using Deep Learning. IEEE Access 2019, 7, 182060–182077. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, D.; Zou, Q.; Lin, H. 3D laser imaging and sparse points grouping for pavement crack detection. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 2036–2040. [Google Scholar] [CrossRef]
- Kheradmandi, N.; Mehranfar, V. A critical review and comparative study on image segmentation-based techniques for pavement crack detection. Constr. Build. Mater. 2022, 321, 126162. [Google Scholar] [CrossRef]
- Zhao, H.; Qin, G.; Wang, X. Improvement of canny algorithm based on pavement edge detection. In Proceedings of the 2010 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; Volume 2, pp. 964–967. [Google Scholar] [CrossRef]
- Hoang, N.D.; Nguyen, Q.L. Metaheuristic optimized edge detection for recognition of concrete wall cracks: A comparative study on the performances of roberts, prewitt, canny, and sobel algorithms. Adv. Civ. Eng. 2018, 2018, 7163580. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Y.; Duan, Y.; Wei, D.; Zhu, X.; Zhang, B.; Pang, B. Robust surface crack detection with structure line guidance. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103527. [Google Scholar] [CrossRef]
- Lin, J.; Liu, Y. Potholes detection based on SVM in the pavement distress image. In Proceedings of the International Symposium DCABES, Hong Kong, China, 10–12 August 2010; pp. 544–547. [Google Scholar] [CrossRef]
- O’Byrne, M.; Schoefs, F.; Ghosh, B.; Pakrashi, V. Texture analysis based damage detection of ageing infrastructural elements. Comput.-Aided Civ. Infrastruct. Eng. 2013, 28, 162–177. [Google Scholar] [CrossRef]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic road crack detection using random structured forests. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- David Jenkins, M.; Carr, T.A.; Iglesias, M.I.; Buggy, T.; Morison, G. A Deep Convolutional Neural Network for Semantic Pixel-Wise Segmentation of Road and Pavement Surface Cracks. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Roma, Italy, 3–7 September 2018; pp. 2120–2124. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, J.; Lu, X.; Xie, R.; Li, L. DeepCrack: A deep hierarchical feature learning architecture for crack segmentation. Neurocomputing 2019, 338, 139–153. [Google Scholar] [CrossRef]
- Alipour, M.; Harris, D.K.; Miller, G.R. Robust pixel-level crack detection using deep fully convolutional neural networks. J. Comput. Civ. Eng. 2019, 33, 04019040. [Google Scholar] [CrossRef]
- Chen, T.; Cai, Z.; Zhao, X.; Chen, C.; Liang, X.; Zou, T.; Wang, P. Pavement crack detection and recognition using the architecture of segNet. J. Ind. Inf. Integr. 2020, 18, 100144. [Google Scholar] [CrossRef]
- Sun, X.; Xie, Y.; Jiang, L.; Cao, Y.; Liu, B. DMA-Net: DeepLab with multi-scale attention for pavement crack segmentation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18392–18403. [Google Scholar] [CrossRef]
- Ji, A.; Xue, X.; Wang, Y.; Luo, X.; Xue, W. An integrated approach to automatic pixel-level crack detection and quantification of asphalt pavement. Autom. Constr. 2020, 114, 103176. [Google Scholar] [CrossRef]
- Jiang, X.; Mao, S.; Li, M.; Liu, H.; Zhang, H.; Fang, S.; Yuan, M.; Zhang, C. MFPA-Net: An efficient deep learning network for automatic ground fissures extraction in UAV images of the coal mining area. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103039. [Google Scholar] [CrossRef]
- Xiao, S.; Shang, K.; Lin, K.; Wu, Q.; Gu, H.; Zhang, Z. Pavement crack detection with hybrid-window attentive vision transformers. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103172. [Google Scholar] [CrossRef]
- Ali, R.; Chuah, J.H.; Talip, M.S.A.; Mokhtar, N.; Shoaib, M.A. Structural crack detection using deep convolutional neural networks. Autom. Constr. 2022, 133, 103989. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 6–12 December 2020. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Han, L.; Zhao, Y.; Lv, H.; Zhang, Y.; Liu, H.; Bi, G.; Han, Q. Enhancing Remote Sensing Image Super-Resolution with Efficient Hybrid Conditional Diffusion Model. Remote Sens. 2023, 15, 3452. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the Computer Vision—ECCV 2018: 15th European Conference, Berlin/Heidelberg, Germany, 8–14 September 2018; pp. 833–851. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Los Alamitos, CA, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar] [CrossRef]
- Ren, M.; Zhang, X.; Chen, X.; Zhou, B.; Feng, Z. YOLOv5s-M: A deep learning network model for road pavement damage detection from urban street-view imagery. Int. J. Appl. Earth Obs. Geoinf. 2023, 120, 103335. [Google Scholar] [CrossRef]
- Song, W.; Jia, G.; Zhu, H.; Jia, D.; Gao, L. Automated pavement crack damage detection using deep multiscale convolutional features. J. Adv. Transp. 2020, 2020, 6412562. [Google Scholar] [CrossRef]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Liu, D.; Mu, Y.; Tan, M.; Wang, X.; et al. Deep high-resolution representation learning for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3349–3364. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, G.; Zhang, L. A spatial-channel hierarchical deep learning network for pixel-level automated crack detection. Autom. Constr. 2020, 119, 103357. [Google Scholar] [CrossRef]
- Cui, X.; Wang, Q.; Dai, J.; Xue, Y.; Duan, Y. Intelligent crack detection based on attention mechanism in convolution neural network. Adv. Struct. Eng 2021, 24, 1859–1868. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, H.; Eastwood, J.; Qi, X.; Jia, J.; Cao, Y. Concrete crack detection using lightweight attention feature fusion single shot multibox detector. Knowl.-Based Syst. 2023, 261, 110216. [Google Scholar] [CrossRef]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. Proc. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar] [CrossRef]
- Liu, H.; Miao, X.; Mertz, C.; Xu, C.; Kong, H. Crackformer: Transformer network for fine-grained crack detection. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 3763–3772. [Google Scholar] [CrossRef]
- Xu, Z.; Guan, H.; Kang, J.; Lei, X.; Ma, L.; Yu, Y.; Chen, Y.; Li, J. Pavement crack detection from CCD images with a locally enhanced transformer network. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102825. [Google Scholar] [CrossRef]
- Tao, H.; Liu, B.; Cui, J.; Zhang, H. A Convolutional-Transformer Network for Crack Segmentation with Boundary Awareness. In Proceedings of the 2023 IEEE International Conference on Image Processing (ICIP), Kuala Lumpur, Malaysia, 9–12 October 2023; pp. 86–90. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Cheng, H.D. CrackGAN: Pavement Crack Detection Using Partially Accurate Ground Truths Based on Generative Adversarial Learning. IEEE Trans. Intell. Transp. Syst. 2021, 22, 1306–1319. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, W.; Zhao, T.; Wang, Z.; Wang, Z. A Rapid Bridge Crack Detection Method Based on Deep Learning. Appl. Sci. 2023, 13, 9878. [Google Scholar] [CrossRef]
- Kyslytsyna, A.; Xia, K.; Kislitsyn, A.; Abd El Kader, I.; Wu, Y. Road Surface Crack Detection Method Based on Conditional Generative Adversarial Networks. Sensors 2021, 21, 7405. [Google Scholar] [CrossRef]
- Song, Y.; Durkan, C.; Murray, I.; Ermon, S. Maximum likelihood training of score-based diffusion models. Adv. Neural Inf. Process. Syst. 2021, 34, 1415–1428. [Google Scholar] [CrossRef]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-based generative modeling through stochastic differential equations. arXiv 2020, arXiv:2011.13456. [Google Scholar]
- Song, J.; Meng, C.; Ermon, S. Denoising diffusion implicit models. arXiv 2020, arXiv:2010.02502. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Volume 139, pp. 8162–8171. [Google Scholar] [CrossRef]
- Ranzato, M.; Beygelzimer, A.; Dauphin, Y.; Liang, P.; Vaughan, J.W. D2C: Diffusion-decoding models for few-shot conditional generation. Adv. Neural Inf. Process. Syst. 2021, 34, 12533–12548. [Google Scholar] [CrossRef]
- Peebles, W.; Xie, S. Scalable diffusion models with transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 4195–4205. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Chang, M.; Chen, S.; Feng, H.; Xu, Z.; Li, Q.; Chen, Y. Srdiff: Single image super-resolution with diffusion probabilistic models. Neurocomputing 2022, 479, 47–59. [Google Scholar] [CrossRef]
- Amit, T.; Shaharbany, T.; Nachmani, E.; Wolf, L. Segdiff: Image segmentation with diffusion probabilistic models. arXiv 2021, arXiv:2112.00390. [Google Scholar]
- Saharia, C.; Chan, W.; Chang, H.; Lee, C.; Ho, J.; Salimans, T.; Fleet, D.; Norouzi, M. Palette: Image-to-image diffusion models. In Proceedings of the ACM SIGGRAPH 2022 Conference Proceedings, Vancouver, BC, Canada, 7–11 August 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Meng, Q.; Shi, W.; Li, S.; Zhang, L. PanDiff: A Novel Pansharpening Method Based on Denoising Diffusion Probabilistic Model. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5611317. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar] [CrossRef]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar] [CrossRef]
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]





| Method | Precision | Recall | F1 | mIoU |
|---|---|---|---|---|
| UNet [24] | 76.00 | 87.53 | 80.20 | 83.00 |
| FCN [25] | 77.58 | 84.17 | 79.67 | 82.64 |
| DeepLabV3+ [26] | 77.99 | 85.88 | 80.72 | 83.39 |
| PSPNet [28] | 76.01 | 73.45 | 72.93 | 78.01 |
| HRNet [31] | 85.04 | 74.83 | 78.49 | 81.56 |
| MFPANet [17] | 75.73 | 86.88 | 80.92 | 82.83 |
| SegFormer [35] | 85.89 | 78.00 | 80.84 | 83.32 |
| CrackFormer [36] | 84.06 | 79.19 | 81.55 | 82.47 |
| CT-crackseg [38] | 68.51 | 76.37 | 72.14 | 74.89 |
| DeepCrack [12] | 81.17 | 78.97 | 78.21 | 81.66 |
| SegDiff [49] | 80.47 | 79.63 | 80.05 | 80.90 |
| CrackDiff (ours) | 81.34 | 84.10 | 81.78 | 84.09 |
| Method | Precision | Recall | F1 | mIoU |
|---|---|---|---|---|
| UNet [24] | 79.76 | 88.08 | 81.82 | 84.62 |
| FCN [25] | 78.68 | 82.08 | 77.90 | 82.02 |
| DeepLabV3+ [26] | 68.93 | 88.56 | 74.98 | 80.10 |
| PSPNet [28] | 63.93 | 48.23 | 51.46 | 66.84 |
| HRNet [31] | 89.58 | 68.51 | 78.42 | 82.13 |
| MFPANet [17] | 81.82 | 85.67 | 83.70 | 84.62 |
| SegFormer [35] | 91.79 | 71.09 | 79.42 | 82.56 |
| CrackFormer [36] | 88.32 | 78.11 | 82.90 | 85.46 |
| CT-crackseg [38] | 87.43 | 79.87 | 83.48 | 85.83 |
| DeepCrack [12] | 81.56 | 84.02 | 80.49 | 83.85 |
| SegDiff [49] | 85.60 | 68.10 | 75.85 | 84.07 |
| CrackDiff (ours) | 91.93 | 79.45 | 84.06 | 86.24 |
| Method | Precision | Recall | F1 | mIoU | |
|---|---|---|---|---|---|
| Crack500 | Backbone | 76.00 | 87.53 | 80.20 | 83.00 |
| Single task | 80.47 | 79.63 | 80.05 | 80.90 | |
| CrackDiff | 81.34 | 84.10 | 81.78 | 84.09 | |
| DeepCrack | Backbone | 79.76 | 88.08 | 81.82 | 84.62 |
| Single task | 85.60 | 68.10 | 75.85 | 84.07 | |
| Crackdiff | 91.93 | 79.45 | 84.06 | 86.24 |
| Precision | Recall | F1 | mIoU | |
|---|---|---|---|---|
| Single | 0.514 | 0.63 | 0.508 | 0.289 |
| Multi | 0.112 | 0.084 | 0.095 | 0.067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Chen, N.; Li, M.; Mao, S. The Crack Diffusion Model: An Innovative Diffusion-Based Method for Pavement Crack Detection. Remote Sens. 2024, 16, 986. https://doi.org/10.3390/rs16060986
Zhang H, Chen N, Li M, Mao S. The Crack Diffusion Model: An Innovative Diffusion-Based Method for Pavement Crack Detection. Remote Sensing. 2024; 16(6):986. https://doi.org/10.3390/rs16060986
Chicago/Turabian StyleZhang, Haoyuan, Ning Chen, Mei Li, and Shanjun Mao. 2024. "The Crack Diffusion Model: An Innovative Diffusion-Based Method for Pavement Crack Detection" Remote Sensing 16, no. 6: 986. https://doi.org/10.3390/rs16060986
APA StyleZhang, H., Chen, N., Li, M., & Mao, S. (2024). The Crack Diffusion Model: An Innovative Diffusion-Based Method for Pavement Crack Detection. Remote Sensing, 16(6), 986. https://doi.org/10.3390/rs16060986







