1. Introduction
Point clouds obtained from LiDAR scans have become an essential tool in fields such as civil engineering, urban planning, archaeology, geology, and even autonomous driving. The adoption of this technology in such a variety of fields has led to a rapid evolution of the technology, procedures and support software. Technology has improved to the point of reaching scanning speeds of up to one million points per second, with precision in the range of 3–5 mm. Due to this rapid escalation, efficient methods for its storage, transmission, visualization, editing, analysis and comparison, among others, are required. Change detection (CD) of terrestrial information is fundamental in many topics: environmental monitoring and landscape transformation, climate change, disaster assessment, urban dynamics, etc. Typically, change detection has been solved using different techniques on sets of images taken at different times. Then, image-processing methods (such as classic ones based on deep learning) are used [
1]. However, they all have the same problems: the images usually have differences due to changes in weather, seasonal variations, and, in general, changes in lighting intensity between the two images due to changes in color and not due to changes in geometry. For this reason, images have currently been replaced by point clouds because the resolution obtained with these is higher than that obtained with images. So, change detection of point clouds (3DCD) is one of the major topics in remote sensing, and it refers to the process of identifying differences in the state of an object or phenomenon by observing it at different times [
2].
Usually, the methods used in 3DCD can be classified into two categories [
3]: volumetric grid methods and point-based methods. The first type of solution converts the point cloud into a grid-based volumetric structure, and then uses some methods to compare the grids. The second category uses the point cloud and some criteria to detect the CD: distance, normal, etc. Unlike image-based methods, where deep learning-based techniques are promising, DL-based 3DCD methods are still under development. This is due to the absence of a network that extracts general features and takes into account the difference in data structure between 2D images and 3D point clouds. Another important issue in point clouds is the huge size of the datasets. Because of this, the Open Geospatial Consortium (OGC) Testbed-14, in the Point Cloud Data Handling Engineering Report [
4], identifies some applications and tasks that need spatially accelerated accesses, including change detection. In this case, the use of hierarchical structures to speed up the performance of the algorithms is very usual (see [
5,
6]).
Current and most widespread approaches focus on the analysis of individual geometric features such as the distance between points of the compared clouds. However, the natural uncertainty of the scanning process implies that the points do not always have the same density or spatial coordinates. This can cause, for example, significant inconsistencies if distance-based methods are used, which will produce very imprecise results if the clouds do not have similar densities. Moreover, when using hierarchical structures, the CD problem is hardest for distance-based methods because it is necessary to study the differences between every node of the hierarchical structure for every point cloud.
This paper presents a new approach for locating and identifying the differences between two overlapping point clouds, presumably taken at different moments, using a mixed approach of volumetric methods and point-based methods. This method has the following innovations. First, it uses the fractal dimension (FD), which is a more invariant measure that captures a high-level feature of a set of points as is the complexity of its distribution in 3D space. As it is a morphological metric, FD is useful to identify similarities and differences in partially sampled objects as is often the case with point clouds. Second, the algorithm uses a hierarchical spatial data structure, which allows parallel processing of point clouds. Because of this, the box-counting dimension (BCD) is estimated on the internal nodes of the structure using the intermediate results for the child nodes, which dramatically improves performance. These intermediate levels of detail, provided by the hierarchical structure, are not used by other approaches. Moreover, we can precompute the FD of every node of the hierarchical data structure of every point cloud, storing it as an additional attribute of the node. Therefore, the calculation of CD between point clouds can be solved in O(1) because the FD is invariant to rigid transformations and depends only on the size and geometry of the boxes used in the hierarchical decomposition.
Our method has several advantages over the state of the art. It is robust in the presence of environmental and sensor factors that produce abnormal results with other methods. It is more stable than others in cases where there is no significant displacement of points but there is a local alteration of the structure of the point cloud. Furthermore, the precision can be adapted to the complexity and density of the point cloud. Finally, our solution is faster than other CD methods such as distance-based methods and can run at O(1) under some conditions, which is important when working with large datasets.
The document is organized as follows. In
Section 2, different approaches in the scientific literature for the comparison of point clouds are shown.
Section 3 explains the fractal dimension (FD) and its use for the characterization of point clouds. Our algorithm estimates the FD of a point cloud using the box-counting method and uses it for comparing point clouds.
Section 4 describes the experimentation performed to test this new method and a discussion of the results. Finally,
Section 5 presents the conclusions and future work.
2. Previous Work
Two point clouds of a target structure, captured through LiDAR scanning at different times, differ in a natural way due to the sources of uncertainty implicit in the scanning process derived from the use of a different sensor technology or survey planning (different number of scans or scanning positions). Apart from this, more significant changes have their origin in human activities, geological processes or natural disasters. Detecting these changes is relevant in a wide variety of applications, such as map updating [
7,
8], environmental monitoring [
9] or disaster detecting and analyzing [
10,
11].
Change detection is one of the major topics in remote sensing, and as a result, has received considerable attention in remote and close-range sensing in the last decades, driven by its importance [
12]. Traditionally, most approaches have addressed the problem using visible or spectral 2D images acquired from satellite or airborne sensors, applying a wide range of techniques [
13,
14,
15]. The advent of affordable LiDAR systems that allowed the acquisition of accurate 3D data from terrestrial (TLS), mobile (MLS), or airborne (ALS) laser scanning sparked interest in developing specific methods for 3D point cloud comparison. In the case of ALS, several approaches focus on converting the 3D point clouds produced into 2D rasters, known as digital surface models (DSMs), where each pixel stores the elevation information. Then, well-known comparison methods for 2D images can be applied. However, these methods usually use low resolutions in the images, which provide much less information than the point clouds generated using TLS and MLS, which is why they have been restricted to very specific uses.
As we said previously, 3DCD can be solved using volumetric grid methods or point-based methods. In [
11], a complete revision of both methods is presented. We are interested in point-based methods because the volumetric-based methods imply a reduction in the density of the original cloud, losing information and precision. Qin et al. [
16] made an exhaustive review of the existing methods and organized them into two main categories: those based on geometric comparison (Euclidean distance, height differences or DSM projection differences), and those based on geometry-spectrum analysis (post-refinement of DSM methods, direct feature fusion and post-classification). One of its main conclusions is that methods based on different metrics are difficult to compare, and the use to be given to the results must be considered when choosing one method or another. Another important contribution to this field is that of de Gélis et al. [
17], where they presented an experimental comparison of six different point cloud change detection methods. The authors divided the methods according to the historical evolution of this work area and to the technique used according to the taxonomy described below.
2.1. Direct Methods
The CD strategies based on the point cloud directly use geometric features (Euclidean distance, height differences, etc.) in order to make the comparison between the clouds. These methods work on the 3D point cloud and therefore are suitable for processing dense and complex point clouds, mainly from TLS and MLS that cannot be handled by DSM-based methods. They rely on geometric features of the points, and one of the first approaches in this category is the one presented by Girardeau-Montaut et al. [
18] called C2C (cloud to cloud). It organizes the point clouds spatially by using an octree and calculates for each point of the first cloud the Hausdorff distance to the closest one in the second cloud.
Another approach is the M3C2 method (multi-scale model-to-model cloud comparison) proposed by Lague et al. [
19]. This method first determines a set of core points (a sub-sampled version of the reference cloud that can also be viewed as a kind of region of interest), then it calculates their normal vectors by fitting a plane taking into account its neighbors at a certain scale. The comparison is performed by computing the mean surface change along the normal direction between both point clouds with the calculation of a local confidence interval. Compared to C2C, it has three major advantages: it is less affected by missing data, changes in point density or point cloud roughness, is capable of detecting positive and negative changes in the cloud, and as shown in the work from [
20] requires less computing time.
2.2. Detection Methods Based on DSM
The CD strategies based on DSM convert the point cloud to a surface model and then use surface-based approaches in order to identify the differences between the clouds. They are especially useful in homogeneous point clouds (ALS) and low-density clouds because the process to obtain the surface is simpler. For example, Murakami et al. [
21] developed a straightforward method for detecting the differences between the point clouds by computing and subtracting their DSM to calculate a new difference cloud. This approach has been extensively used in urban environments and more recently in earth sciences [
22]. Once the differences (DSMd) have been calculated, it is necessary to establish a threshold from which to detect the changes. This threshold can be set empirically as in the original paper of Murakami et al., or calculated from the DSMd histogram by using Otsu’s algorithm as in [
23].
A DSM contains artifacts that need to be handled by adding one or more pre-processing or post-processing stages. For example, Choi et al. [
24] segmented the DSMd by using filters and grouping to identify areas with changes, then classified these areas into three categories (land, vegetation and buildings), and finally computed the differences between the point clouds by comparing these categories. Other approaches apply morphological filters (erosion and dilation) to remove noise, outliers or vegetation for the detection of changes in buildings, such as [
25]. Another approach based on DSMd is that of Pang et al. [
26], which extracts possible changes in buildings by setting a threshold in the DSMd and applying random sample consensus (RANSAC) to distinguish buildings from trees. The buildings identified are then classified into four categories: newly built, demolished, taller, and shorter. New approaches make use of statistical techniques to segment the DSMd and compute attributes related to shape similarity in order to obtain changes and highlight them by using a k-means algorithm as in [
1].
2.3. Detection Methods Based on Machine Learning
These approaches extract information from the point clouds, classify it (semantic segmentation) and finally compare the results of the generated classes. Among these methods, we can highlight the one from Awrangjeb et al. [
27], which extracts building edges from LiDAR scans and aerial images, and compares those edges on a 2D map. A very similar proposal is that of Siddiqui et al. [
28], which generates 3D models of buildings to compare their dimensions and categorize changes into five types of classes. Xu et al. [
5] also works with point clouds to detect changes, using geometric methods to calculate the distance from each point in one cloud to the nearest plane in the other cloud. With these data, a 3D map of the differences is generated, and points are classified as belonging to roofs, walls, dormers, vehicles, rooftop structures, and undefined objects. Almost all changes were detected, and approximately 80% of changes were correctly classified. In the work from Gao et al. [
29], they used a new labeled dataset to make an evaluation of point cloud change detection approaches. They used three Siamese neural networks, one based on geometry context aware (GCA), another using the voxel feature encoding architectures, and a third one using a Siamese KPConv network to detect changes between two point clouds at different chronological times.
There is another group of noteworthy methods, which first identify the changes and then characterize them. The approach used by Xu et al. [
30] first filters ground points from non-ground points and then generates an octree with the non-ground points of the reference point cloud, identifying the changes in the empty or non-existing leaves whose space is occupied by points of the cloud to be compared. These selected nodes are clustered to remove noise and categorize changes according to local terrain features. Tran et al. [
31] combined classification and change detection in the same step. To do this, the authors extracted features related to the distribution of points, terrain elevation, multi-target capabilities of LiDAR systems (such as the number of echoes of the emitted laser shots), and a special feature called stability that relates the points of both clouds. This feature is defined as the ratio of the number of points in the spherical neighborhood to the number of points in the vertical cylindrical neighborhood (oriented along the vertical axis) in the other point cloud. This ratio will be close to 100% when there are no changes and 0% otherwise. Subsequently, a random forest algorithm is applied to obtain a supervised classification of the changes in eight classes (lost tree, new tree, lost building, new building, changed ground, unchanged building, unchanged tree, and unchanged ground).
Finally, there are other methods that use neural networks, among which we can cite the work of Fang et al. [
32]. First, a point cloud semantic segmentation network is developed under the classic PointNet++ frame to provide semantic labeling for change detection. Secondly, the point cloud is voxelized based on an octree, where the label of each voxel is determined by the result of semantic segmentation. Finally, the change detection result is obtained by comparing the changes in voxel coordinates and semantic information of the two point clouds. The accuracy of the change detection rate reached is near 91%.
3. Materials and Methods
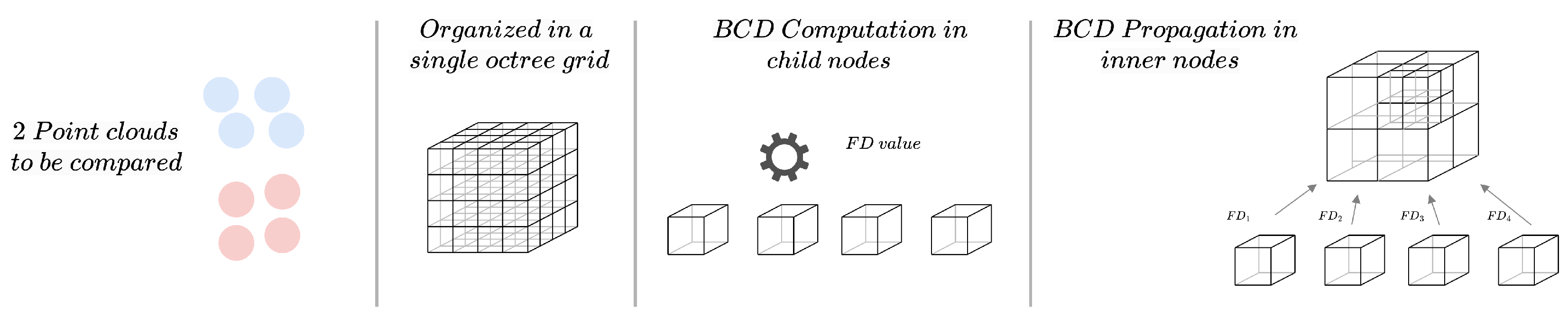
In this section, we discuss the key ideas of our proposal: the FD as a method for the morphological characterization of a point cloud, the application of the box-counting dimension (BCD) to estimate the FD for the comparison of point clouds, and the hierarchical spatial data structure used for partitioning the point clouds and calculating the FD at different scales. An overall flowchart representing the method steps is depicted in
Figure 1. Each entry point cloud is organized hierarchically (if it was not previously). Next, for each leaf node, the FD is calculated. After that, the FD of the interior nodes is calculated from bottom to top. The comparison is performed by calculating the difference between the values stored in the node at the desired depth level.
3.1. Fractal Dimension
As mentioned above, previous direct methods focus on geometric features of the points (mean distance, best fitting plane orientation, Hausdorff distance, Chamfer distance, etc.). However, these approaches are sensitive to variations in the sampling of the points between scans. Also, as pointed out by [
18], the distance between a point in cloud A and its closest point in cloud B does not always indicate a real change between the objects represented by the two point clouds.
In 1967, Mandelbrot introduced the concept of the fractal dimension (FD) and its ability to characterize complex systems with a high degree of self-similarity, further estimating in his study the FD of the coast of Great Britain [
33]. The FD has been successfully used in many practical problems related to astronomy [
34], acoustics [
35,
36], diagnostics imaging [
3,
37,
38,
39,
40], image analysis [
41,
42], or neuroscience [
43,
44], among others. Related to the analysis of point cloud models, we can highlight the approaches of Zhang et al. [
45] and Zhang et al. [
46], where they classify trees based on the FD of their corresponding point clouds.
The FD is a morphological descriptor, either two-dimensional or three-dimensional, that quantifies the complexity of a system as the ratio of the change in detail to the change in scale (see Equation (
1)). It is invariant to translation, rotation, or changes in scale or resolution in the case of sampled objects (within certain limits). Applied to a point cloud, the FD is a measure of the distribution of the points in space, providing a statistical index of the degree of occupation of the 3D volume covered by the point cloud. To a certain extent, the FD can be used to characterize an object: Ref. [
46] made use of the FD applied to a point cloud in order to classify different types of independent tree species.
The core idea of the present work is to compare two point clouds by comparing their FDs. However, two morphologically different objects can have the same FD: for instance, the Hilbert, Sierpiński, and Peano curves all have FD = 2 [
47]. For this reason, in order to reveal the morphological differences between the point clouds, we apply a top–down approach in which the FDs are computed at progressively smaller regions, starting with the bounding box of the two clouds. Therefore, our method works in a mixed way between methods based on volumetric decomposition and those based on the full cloud. First, we use a top–down approach with the point clouds, organizing all the points hierarchically, which provides speed in the solution. Second, since all the points of the original cloud are preserved (unlike volumetric methods), we can adjust the solution to obtain the desired precision. The advantage of this approach is that in a coarse partition of space, the comparison of the FDs provides a general idea of the degree of similarity of the clouds. As the partition gets finer, it highlights differences in specific areas of the clouds. Both the method of calculating the FD of a point cloud and the method for space partitioning are described in the next two sections.
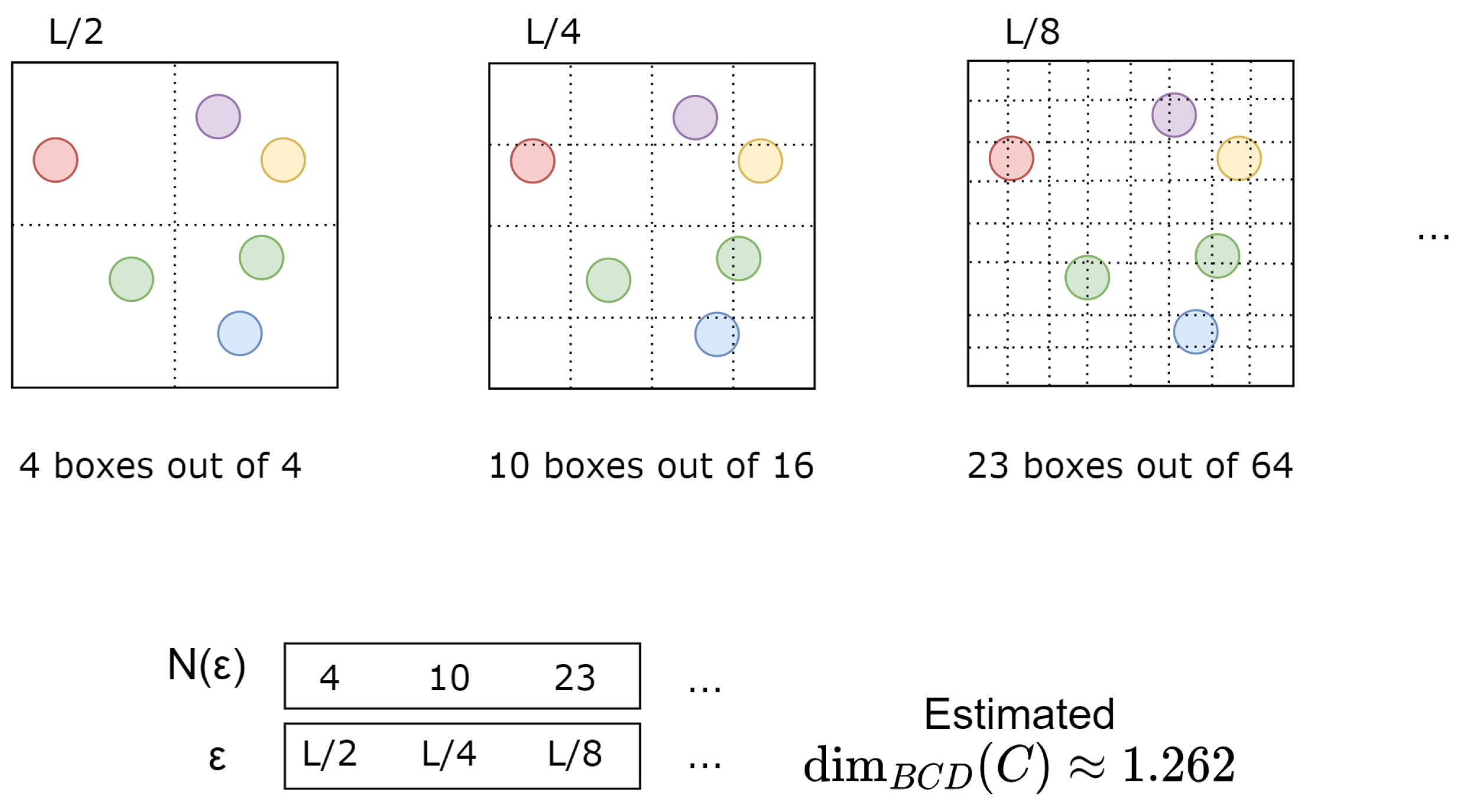
3.2. 3D Box Counting
The Minkowski–Bouligand dimension or box-counting dimension is the most used estimation for the FD [
6]. In order to calculate it, space (2D or 3D) is subdivided using an evenly spaced grid, counting the number of cells or boxes required to cover the entire object, or, in our case, the number of boxes with at least one point of the cloud. The FD is estimated by studying how this number changes as the grid gets thinner until a maximum division level determined by the parameter
is reached (see Algorithms 1 and 2). The grid is divided from 2 × 2 cells to
cells. Formally, the BCD is defined as:
where
is the box size, and
is the number of boxes needed to cover the entire point cloud
C.
Figure 2 illustrates the calculation of the BCD for a set of points.
In practice, the infinitesimal calculation in Equation (
1) cannot be computed; therefore, approximation techniques are used. A line is fitted to the 2D points
for different
values using the least square approach, and its slope is taken as an estimation for the BCD.
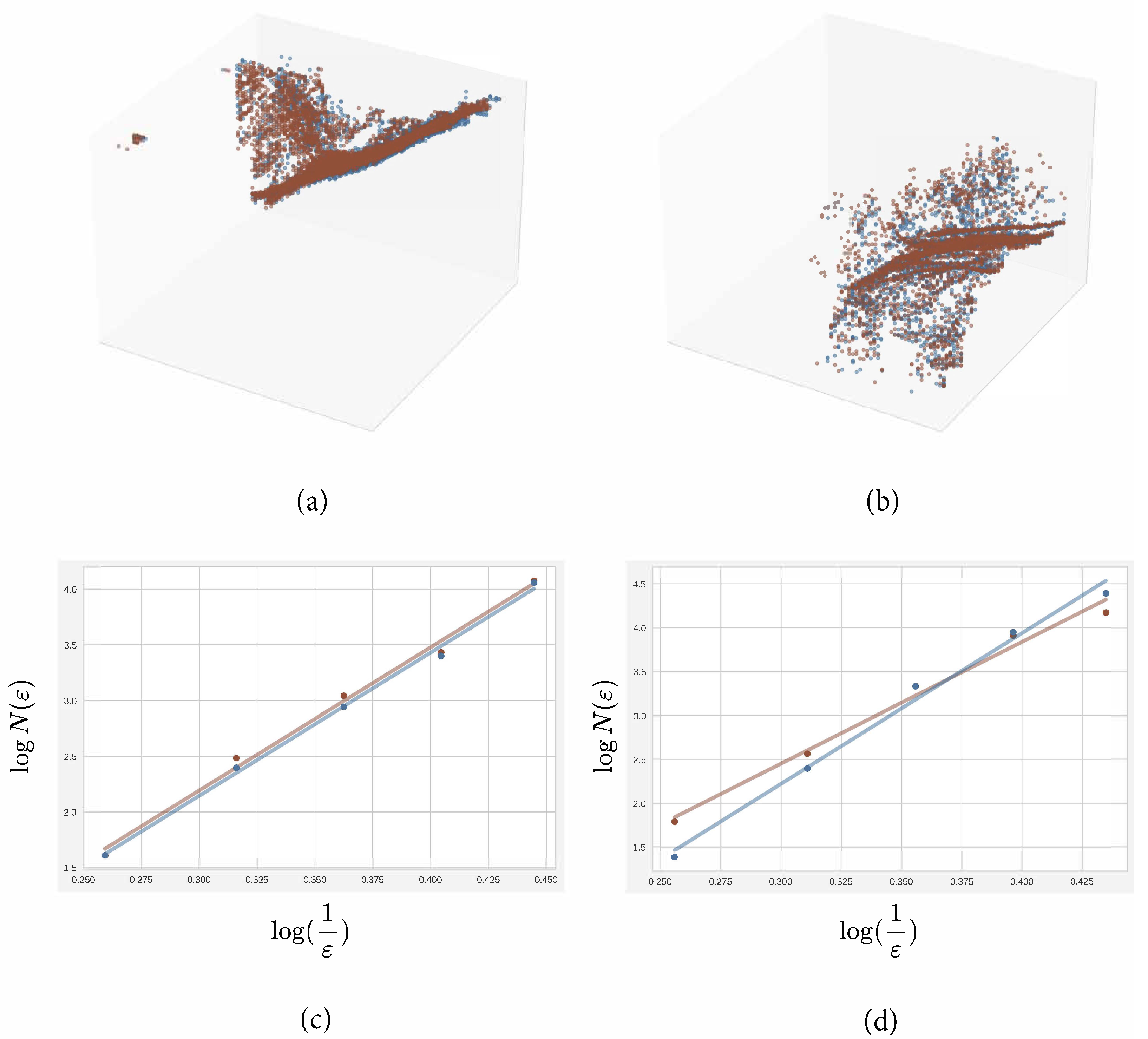
Figure 3 depicts a real use case scenario involving two sets of similar and different point clouds and their corresponding BCD plot. Each of these sets of point clouds represents a partition of a larger pair of point clouds compared between themselves.
A simple implementation for the box-counting method for point clouds is detailed in Algorithm 1. The set
H is implemented through a hash table, making this algorithm very efficient. The code shows a possible cell hash function, but many more are possible, provided they are injective. For instance, we implemented it using fast bit rotations instead of power products. This implementation runs in
time but with a large hidden constant. Alternatively, a faster but somewhat more elaborate implementation based on the
algorithm of [
48] can be used.
Based on the BCD, the approach for comparing point clouds works as follows. Given a region of space enclosing the point clouds, their FDs are estimated and compared. If they differ substantially, the point clouds are also proportionally different. Conversely, if the FDs are similar, the point clouds will most likely be similar, but this cannot be guaranteed. In both cases, further subdivisions of the region following the same approach would reveal more details about the parts of the clouds that differ or that are reasonably similar. As the region gets smaller and contains fewer points, the FD better characterizes the morphology of the point cloud. The error of this approach is therefore bounded by the size of the smallest regions reached during the subdivision process. Within one of these regions, point clouds could differ and not be detected by the method. These regions are similar to the regions of interest defined by the core points of the M3C2 method [
19], where the actual comparison between the two point clouds is performed.
| Algorithm 1 BCD: Computation of the BCD for a point cloud. |
Input: A node n storing a subset of point cloud C enclosed in a cubic box in 3D space. Output: BCD d of the point cloud in the node box.
for to MAX_DIV do # Cube size for iteration. : node box dimensions for each point p in do # Cell containing the point # : box corner with minimum coords.
# Cell hash end for # Add point to log-log plot end for slope(linearRegression(P)) |
| Algorithm 2 BCDInner: BCD derivation for inner nodes. |
Input: An inner node n of an octree organizing point cloud C. Node n represents a cubic box that contains a subset of C. Its children nodes have already calculated their box counting for the predefined number of subdivisions. Output: BCD d of the point cloud enclosed in the node box.
# : dimensions of node box B # : Iverson bracket (1 if P is true; 0 otherwise)
for to MAX_DIV do end for slope(linearRegression(P)) |
3.3. Hierarchical Spatial Data Structure
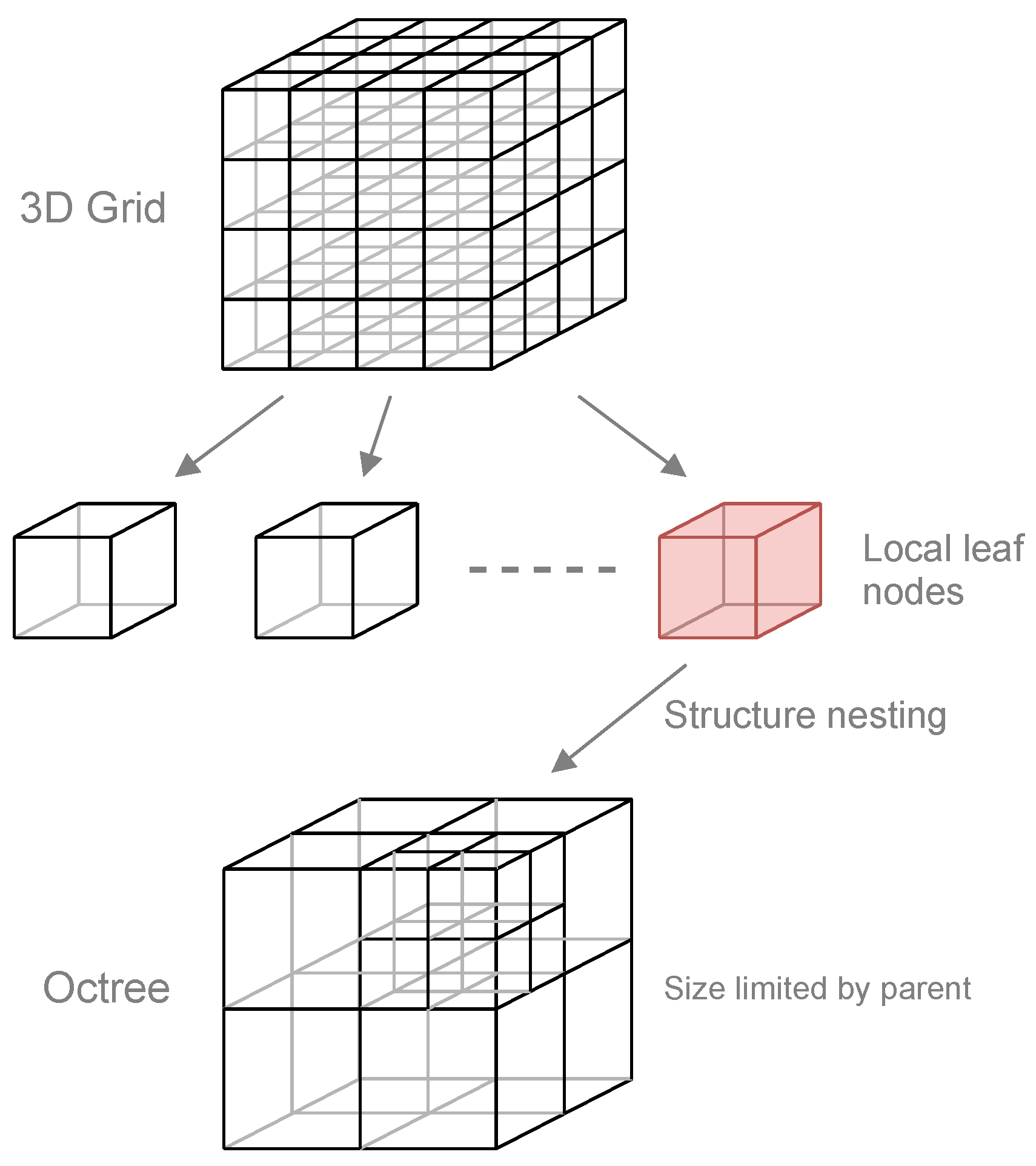
In order to calculate the FD, following the general approach outlined in the previous section, we use a grid of octrees as the spatial data structure as depicted in
Figure 4. Although a single octree would also be adequate to implement the space partition described in
Section 3.1, using a grid of octrees has two significant advantages: first, it allows building the octrees and computing the BCDs in parallel, and second, and more importantly, if the grid is a subset of a consistent 3D spatial partition of the earth’s surface, it allows precomputing the BCDs for an ALS or TLS point cloud, which makes comparisons against other point clouds extremely fast. We expand on this idea below.
The data structure is built as follows. First, the points of the two clouds to be compared are organized in a regular 3D grid of cube-shaped cells. Then, each grid cell is hierarchically subdivided by an octree. We use a regular subdivision of space that generates cubic node boxes. A node is subdivided if it contains points of both clouds in the node box, up to a maximum number of recursive divisions. This defines the minimum octree node box size and therefore the maximum error of the comparison as we explained in
Section 3.2.
Once the data structure has been built, the nodes of the octrees are iterated estimating the BCD of the points of each cloud enclosed in the node box, and calculating their difference as described in Algorithm 3. When a node contains points from only one of the clouds, the FD difference is assigned the fixed value 3, corresponding to the maximum possible difference between the BCDs of the clouds.
At the leaf nodes of the octree, the BCD is estimated by using the box-counting algorithm described in Algorithm 1, but at the inner nodes, the box counting can be computed at a negligible cost by using the intermediate results of the box counting of the children nodes. Given an inner node representing a box in space with size
L, each child node represents an octant with size
. This implies that
can be computed simply by counting the number of non-empty children, or equivalently, the number of children with a box-counting different from zero. Following the same approach,
can be computed by counting the number of non-empty boxes with a size equal to half the octant represented by each child node, which was already computed by the box counting in each of them.
Figure 5 illustrates this with an example, and Algorithm 2 shows the pseudocode of the BCD derivation for inner nodes.
| Algorithm 3 Cloud comparison based on local BCD. |
Input: grid G containing point clouds and . Output: grid G with BCD differences for and stored at each octree node n as .
for each octree O in grid G do for each node n in bottom-up traversal of O do if isLeaf(n) then BCD() BCD() else BCDInner() BCDInner() end if if and then else # Default BCD difference end if end for end for |
The data structure described above can be used for a single point cloud, calculating and storing the BCD in each node. Then, the comparison of two clouds is reduced to simply iterating the octrees in the two data structures and calculating the BCD differences, with a negligible cost. However, this is only possible if the same grid or two grids from the same 3D space partition are used since, otherwise, the regions associated with the octrees of the two clouds would not match. The octree structures used for comparing two clouds need to be geo-referenced to make the method work on arbitrary point clouds. This approach is particularly useful for large-scale LiDAR data repositories storing many point clouds. The BCDs can be precomputed for each point cloud, uploaded to the repository, and used in future comparisons. The requirement of a consistent space partition for the storage of the clouds seems logical in this type of system.
4. Experimentation and Results
The experimentation carried out seeks to demonstrate the validity of the proposed method, as well as comparing it with other known state-of-the-art methods. We carried out different executions on the same datasets to obtain a qualitative and quantitative comparison of the results at the level of location of differences. Once the validity of the method is demonstrated, in the sense that it finds the same differences or similarities as other methods, we present an assessment of the performance of the method. We perform a comparison of the proposed approach with the most common methods based on distance: C2C [
18] and M3C2 [
19]. We analyze the time of execution, the spatial location of the changes, and the extremes of the histograms of the comparisons as described below. The dataset used in the experiments is bildstein1 from Semantic3D, and it is publicly available through its download portal [
49]. This dataset, depicted in
Figure 6, comprises almost 30 M points of an area of 225 × 250 m around the church of Bildstein (Austria). The experiments are performed on a system with an Intel Core i7-10510U CPU with 4 cores and 32 GB RAM. Our algorithm is implemented as a plugin of the Cloud Compare v.2.12.3 (Kyiv) [
50] software, which already includes implementations of the C2C and M3C2 methods, making comparison easier. These implementations use octrees and kd-trees, respectively, to accelerate the distance computation. Both C2C and M3C2, as well as our method, take advantage of multithreading to speed up the execution.
The implementation of our approach (FD) uses a grid cell size of 100 m and octrees with a maximum depth of 6, corresponding to a maximum resolution of 3.125 m. The BCD is estimated by using 10 iterations of the box-counting algorithm, that is, computing , where L is the dimension of the node box. This configuration is set taking into account the point cloud density and size. There are 500 points/m2 approximately, so with a size of the grid of 3.125 m in the leaves, there will be 45,000 points in every node. The number of iterations is obtained empirically. We carry out four experiments in which we artificially reproduce different common situations when comparing LiDAR data. In each experiment, the point cloud is compared to the following:
- E1
The same cloud where each point is randomly displaced a maximum distance
0.01 m in each axis. This experiment tests the performance of the algorithms against noise. Also, it can be useful when two clouds of the same place are captured from very near positions.
- E2
A subsampled version of the point cloud at 50%, that is, with half of its points chosen randomly. This experiment allows to test the behavior of the algorithms with different model densities.
- E3
The same cloud with an artificial hole in the center. In this way, it is possible to test the behavior of the algorithms in the event of missing information due to capture problems (occlusions, low/high reflectivity surfaces, etc).
- E4
A modified version of the point cloud, where three flower beds of the entrance area are artificially removed, restoring the ground level (
Figure 7). The intention of this experiment is to test the behavior of the algorithms when there are only slight differences between the clouds.
Table 1 shows the running times of the three algorithms tested in the four experiments carried out. The initialization stage includes the construction of the data structures required by each method. The load of the point clouds from local disk files or a network repository is not considered here. The computation phase comprises the estimation of the BCDs in each node and the calculation of the differences between the point clouds. As it can be seen from
Table 1, the FD method is faster than the other method in all cases. The initialization time for the FD method uses a depth of 6, so it could be reduced by using a lower depth. But with that depth, a good balance is achieved between the number of node points and the processing cost. For the M3C2 method, this cost cannot be adjusted since it is the one provided directly by the plugin used. If we consider the total cost (initialization and computation) our method, compared to M3C2, is 1.23× faster for E1, 1.55× faster for E2, 2.46× faster for E3, and 1.38× faster for E4. If we exclude the initialization time, then the benefit of our method reaches up to 10.9× for E3. So, we can conclude that the performance of the proposed method is higher than that of distance-based methods.
When octrees are used to organize large point clouds, it is common to use, as an early stopping criterion, the subdivision of nodes only if they exceed a predefined number of points. This prunes the octree, decreasing the average depth and ensuring that all leaf nodes have a minimum number of points, which has an overall positive effect on cloud storage and visualization. In order to assess the impact of this stopping criterion on the FD calculation, we include the execution times in the last row of
Table 1, using an octree with a threshold of 10,000 points per node for both clouds and keeping the maximum depth of 6 levels.
It is interesting to highlight the inconsistencies found in the distance-based methods due to the different point densities used in the comparison. This fact is easily verified by combining experiments E1 and E2. In E1, both clouds have a similar density, but the position of the points is disturbed. As can be seen, the distance maps obtained by C2C for experiments E1 and E2 are very different because they are based only on the distances between points. This proves that the C2C method is very sensitive to the density of the point clouds used. On the other hand, with the proposed method, the values found in E1 and E2 are practically the same as should correspond to two clouds that are practically identical. The M3C2 method also behaves like the FD method at the cost of setting the maximum value when it cannot compare points, although its computational cost is much higher than the FD. As can be seen, our method is more robust in the presence of point density and distance variations that produce inaccurate results with other methods.
Additionally, we show the results in a qualitative way based on the analysis of the histograms and the visual results (
Figure 8,
Figure 9,
Figure 10 and
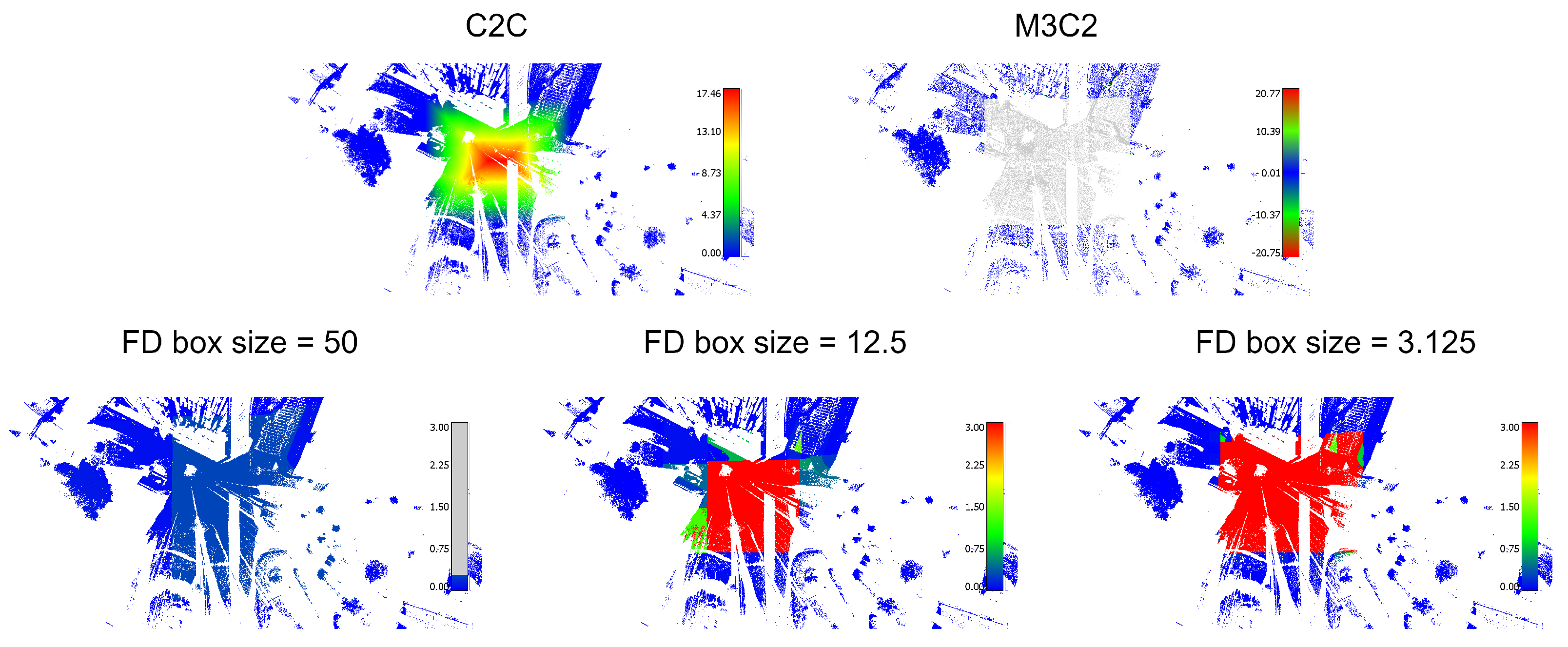
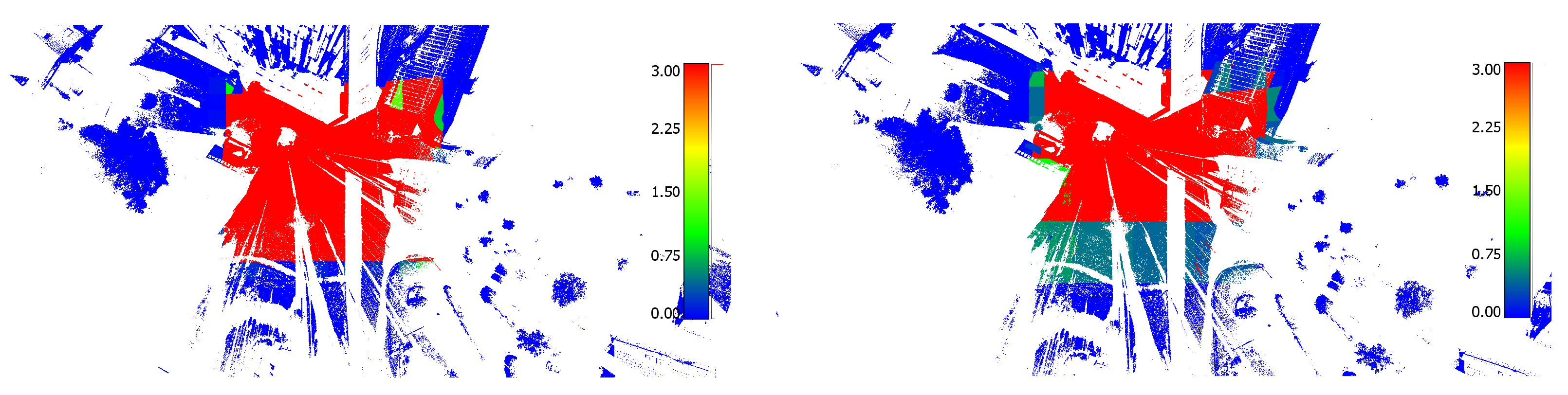
Figure 11). As the M3C2 algorithm uses a signed distance, we modify its color scale to make it symmetrical. A fixed color scale [0–3] is also used with our method to facilitate the comparison. By using different metrics associated with each method, the units are different; therefore, it is not possible to establish a common color scale for the values obtained. What is shown are the gradients, which indicate the degree of difference detected in each case. We show the results of the comparison at different octree depth levels: 2, 4, and 6, corresponding to node box sizes of 50 m, 12.5 m, and 3.125 m, respectively. This allows to compare the results of the FD-based method with different accuracy levels. Examining differences in FD at an intermediate octree level can be useful to detect relevant changes beyond errors arising from capturing points at slightly different positions or different sampling resolutions. Also, it can be used to avoid expanding a node of the octree, and therefore calculating the BCD for its descendants if no further detail is required. An interesting aspect is shown in experiment E4. As can be seen, with the methods based on distances, no difference is seen. In contrast, the FD method finds differences with a resolution box of 3.125 m (the modified area has been zoomed in at the bottom right of the figure to highlight this). Consequently, the method is more sensitive to morphological modifications. In addition,
Figure 12 compares the results of the FD-based method calculated using an octree without or with pruning for the datasets of experiment E3.
5. Conclusions
In this work, a novel approach for comparing point clouds based on the fractal dimension (FD) has been presented. For this purpose, the two point clouds are adaptively subdivided by using a grid of octrees and the FDs are estimated at each node by the box-counting distance. At each node, the differences between the FD of each point cloud reveal the local changes between them. In the experiments, the results of the proposed method are comparable to that of distance-based approaches, but it stands out when there are changes that, although they do not involve a significant displacement of points, do alter the structure of the point cloud locally. The computation times are overall faster than those of the rest of the approaches, and it has the added advantage that the FD can be computed for a point cloud once and used in multiple comparisons.
The validity of the method has been shown. Firstly, verifying that the same differences identified by other methods based on distance are found in different situations: small variations of the clouds, differences in densities, holes or artifacts in the cloud, and finally, slight, very localized differences. In all cases, the proposed method behaves similarly to the other methods studied. But also, in terms of performance, the computing speed is much higher than the others, ranging from 1.23× to 12× at best. In addition to all these advantages, the FD can be precomputed and stored in the point cloud as an additional attribute of the hierarchical storage structure. In fact, the FD characterizes the cloud of points according to a specific partition, so if the same coordinate system is used for all the stored clouds, it could serve as a characteristic element of the cloud itself.
Future work includes the implementation of the FD-based comparison in GPU, using the CUDA implementation of the box-counting algorithm of [
48] provided by [
51]. However, large clouds may not fit in GPU memory, so a strategy must be developed to process them in chunks. The partition of the point clouds into a grid of octrees facilitates this. We also plan to use our method in applications related to tracking changes over time in urban environments, land surface due to geological processes, and archaeological sites during excavation. In all these cases, it is very important to have a fast method to identify slight differences between point clouds. We think that the proposed method will be very useful in that context.
Author Contributions
Conceptualization, P.N., R.J.S.-S., A.J.R.-R., J.M.F., C.D. and C.J.O.-A.; methodology, R.J.S.-S., A.J.R.-R., J.M.F., C.D. and C.J.O.-A.; software, J.C.C.-R. and A.L.-R.; validation, P.N., A.L.-R., R.J.S.-S. and A.J.R.-R.; writing—original draft preparation, J.C.C.-R., R.J.S.-S. and A.J.R.-R.; writing—review and editing, A.L.-R., R.J.S.-S., A.J.R.-R., J.M.F., C.D. and C.J.O.-A.; project administration, R.J.S.-S. and C.J.O.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This result is part of the research project RTI2018-099638-B-I00 funded by “MCIN/AEI/10.13039/501100011033/” and ERDF funds “A way of doing Europe”. Also, the work has been funded by the University of Jaén (via ERDF funds) through the research project 1265116/2020. Pablo Navarro has been funded through the research project FEDER-UJA 1381115/2022.
Data Availability Statement
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lyu, X.; Hao, M.; Shi, W. Building Change Detection Using a Shape Context Similarity Model for LiDAR Data. ISPRS Int. J. Geo-Inf. 2020, 9, 678. [Google Scholar] [CrossRef]
- Singh, A. Review article digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Yu, S.; Lakshminarayanan, V. Fractal Dimension and Retinal Pathology: A Meta-Analysis. Appl. Sci. 2021, 11, 2376. [Google Scholar] [CrossRef]
- Boehler, W.; Bordas Vicent, M.; Marbs, A. OGC Testbed-14: Point Cloud Data Handling Engineering Report; Technical Report; i3mainz, Institute for Spatial Information and Surveying Technology, FH Mainz: Mainz, Germany, 2018. [Google Scholar]
- Xu, S.; Vosselman, G.; Oude Elberink, S. Detection and Classification of Changes in Buildings from Airborne Laser Scanning Data. Remote Sens. 2015, 7, 17051–17076. [Google Scholar] [CrossRef]
- Russell, D.A.; Hanson, J.D.; Ott, E. Dimension of Strange Attractors. Phys. Rev. Lett. 1980, 45, 1175–1178. [Google Scholar] [CrossRef]
- Rottensteiner, F. Automated updating of building data bases from digital surface models and multi-spectral images: Potential and limitations. In Proceedings of the ISPRS Congress, Beijing, China, 3–11 July 2008; Volume 37, pp. 265–270. [Google Scholar]
- Champion, N.; Boldo, D.; Pierrot-Deseilligny, M.; Stamon, G. 2D building change detection from high resolution satelliteimagery: A two-step hierarchical method based on 3D invariant primitives. Pattern Recognit. Lett. 2010, 31, 1138–1147. [Google Scholar] [CrossRef]
- Li, X.; Gong, P.; Liang, L. A 30-year (1984–2013) record of annual urban dynamics of Beijing City derived from Landsat data. Remote Sens. Environ. 2015, 166, 78–90. [Google Scholar] [CrossRef]
- Sofina, N.; Ehlers, M. Building Change Detection Using High Resolution Remotely Sensed Data and GIS. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3430–3438. [Google Scholar] [CrossRef]
- Vetrivel, A.; Gerke, M.; Kerle, N.; Nex, F.; Vosselman, G. Disaster damage detection through synergistic use of deep learning and 3D point cloud features derived from very high resolution oblique aerial images, and multiple-kernel-learning. ISPRS J. Photogramm. Remote Sens. 2018, 140, 45–59. [Google Scholar] [CrossRef]
- Xiao, W.; Cao, H.; Tang, M.; Zhang, Z.; Chen, N. 3D urban object change detection from aerial and terrestrial point clouds: A review. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103258. [Google Scholar] [CrossRef]
- Si Salah, H.; Ait-Aoudia, S.; Rezgui, A.; Goldin, S.E. Change detection in urban areas from remote sensing data: A multidimensional classification scheme. Int. J. Remote Sens. 2019, 40, 6635–6679. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondízio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, M.; Zhang, R.; Chen, S.; Zhan, Z. Change Detection Based on Artificial Intelligence: State-of-the-Art and Challenges. Remote Sens. 2020, 12, 1688. [Google Scholar] [CrossRef]
- Qin, R.; Tian, J.; Reinartz, P. 3D change detection—Approaches and applications. ISPRS J. Photogramm. Remote Sens. 2016, 122, 41–56. [Google Scholar] [CrossRef]
- de Gélis, I.; Lefèvre, S.; Corpetti, T. Change Detection in Urban Point Clouds: An Experimental Comparison with Simulated 3D Datasets. Remote Sens. 2021, 13, 2629. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change detection on point cloud data acquired with a ground laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, W19. [Google Scholar]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Shirowzhan, S.; Sepasgozar, S.M.E.; Li, H.; Trinder, J.; Tang, P. Comparative analysis of machine learning and point-based algorithms for detecting 3D changes in buildings over time using bi-temporal lidar data. Autom. Constr. 2019, 105, 102841. [Google Scholar] [CrossRef]
- Murakami, H.; Nakagawa, K.; Hasegawa, H.; Shibata, T.; Iwanami, E. Change detection of buildings using an airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 1999, 54, 148–152. [Google Scholar] [CrossRef]
- Okyay, U.; Telling, J.; Glennie, C.L.; Dietrich, W.E. Airborne lidar change detection: An overview of Earth sciences applications. Earth-Sci. Rev. 2019, 198, 102929. [Google Scholar] [CrossRef]
- Vu, T.T.; Matsuoka, M.; Yamazaki, F. LIDAR-based change detection of buildings in dense urban areas. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 5, pp. 3413–3416. [Google Scholar] [CrossRef]
- Choi, K.; Lee, I.; Kim, S. A feature based approach to automatic change detection from LiDAR data in urban areas. ISPRS Archives – Volume XXXVIII-3/W8, Laserscanning’09 2009, 38, 259–264. [Google Scholar]
- Stal, C.; Tack, F.; De Maeyer, P.; De Wulf, A.; Goossens, R. Airborne photogrammetry and lidar for DSM extraction and 3D change detection over an urban area—A comparative study. Int. J. Remote Sens. 2013, 34, 1087–1110. [Google Scholar] [CrossRef]
- Pang, S.; Hu, X.; Wang, Z.; Lu, Y. Object-Based Analysis of Airborne LiDAR Data for Building Change Detection. Remote Sens. 2014, 6, 10733–10749. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Fraser, C.S.; Lu, G. Building Change Detection from LIDAR Point Cloud Data Based on Connected Component Analysis. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W5, 393–400. [Google Scholar] [CrossRef]
- Siddiqui, F.U.; Awrangjeb, M. A Novel Building Change Detection Method Using 3D Building Models. In Proceedings of the International Conference on Digital Image Computing: Techniques and Applications (DICTA), Sydney, Australia, 29 November–1 December 2017; pp. 1–8. [Google Scholar]
- Gao, Y.; Yuan, H.; Ku, T.; Veltkamp, R.C.; Zamanakos, G.; Tsochatzidis, L.; Amanatiadis, A.; Pratikakis, I.; Panou, A.; Romanelis, I.; et al. SHREC 2023: Point cloud change detection for city scenes. Comput. Graph. Pergamon 2023, 115, 35–42. [Google Scholar] [CrossRef]
- Xu, H.; Cheng, L.; Li, M.; Chen, Y.; Zhong, L. Using Octrees to Detect Changes to Buildings and Trees in the Urban Environment from Airborne LiDAR Data. Remote Sens. 2015, 7, 9682–9704. [Google Scholar] [CrossRef]
- Tran, T.H.G.; Ressl, C.; Pfeifer, N. Integrated Change Detection and Classification in Urban Areas Based on Airborne Laser Scanning Point Clouds. Sensors 2018, 18, 448. [Google Scholar] [CrossRef]
- Fang, L.; Liu, J.; Pan, Y.; Ye, Z.; Tong, X. Semantic supported urban change detection using ALS point clouds. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103271. [Google Scholar] [CrossRef]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Caicedo-Ortiz, H.E.; Santiago-Cortes, E.; López-Bonilla, J.; Castañeda, H.O. Fractal dimension and turbulence in Giant HII Regions. J. Phys. Conf. Ser. 2015, 582, 012049. [Google Scholar] [CrossRef]
- Burns, T.; Rajan, R. A Mathematical Approach to Correlating Objective Spectro-Temporal Features of Non-linguistic Sounds With Their Subjective Perceptions in Humans. Front. Neurosci. 2019, 13, 459438. [Google Scholar] [CrossRef]
- Maragos, P.; Potamianos, A. Fractal dimensions of speech sounds: Computation and application to automatic speech recognition. J. Acoust. Soc. Am. 1999, 105, 1925–1932. [Google Scholar] [CrossRef] [PubMed]
- Landini, G.; Murray, P.I.; Misson, G.P. Local connected fractal dimensions and lacunarity analyses of 60 degrees fluorescein angiograms. Investig. Ophthalmol. Vis. Sci. 1995, 36, 2749–2755. [Google Scholar]
- Cheng, Q. Multifractal Modeling and Lacunarity Analysis. Math. Geol. 1997, 29, 919–932. [Google Scholar] [CrossRef]
- Popescu, D.P.; Flueraru, C.; Mao, Y.; Chang, S.; Sowa, M.G. Signal attenuation and box-counting fractal analysis of optical coherence tomography images of arterial tissue. Biomed. Opt. Express 2010, 1, 268–277. [Google Scholar] [CrossRef]
- Velázquez-Ameijide, J.; García-Vilana, S.; Sánchez-Molina, D.; Llumà, J.; Martínez-González, E.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Prediction of mechanical properties of human rib cortical bone using fractal dimension. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 506–516. [Google Scholar] [CrossRef] [PubMed]
- Al-Kadi, O.S.; Watson, D. Texture Analysis of Aggressive and Nonaggressive Lung Tumor CE CT Images. IEEE Trans. Biomed. Eng. 2008, 55, 1822–1830. [Google Scholar] [CrossRef]
- Gorsich, D.J.; Tolle, C.R.; Karlsen, R.E.; Gerhart, G.R. Wavelet and fractal analysis of ground-vehicle images. In Proceedings of the Wavelet Applications in Signal and Image Processing IV, Denver, CO, USA, 5–9 August 1996; International Society for Optics and Photonics: Bellingham, WA, USA, 1996; Volume 2825, pp. 109–119. [Google Scholar] [CrossRef]
- Gómez, C.; Mediavilla, A.; Hornero, R.; Abásolo, D. Use of the Higuchi’s fractal dimension for the analysis of MEG recordings from Alzheimer’s disease patients. Med. Eng. Phys. 2008, 31, 306–313. [Google Scholar] [CrossRef]
- King, R.D.; George, A.T.; Jeon, T.; Hynan, L.S.; Youn, T.S.; Kennedy, D.N.; Dickerson, B.a. Characterization of Atrophic Changes in the Cerebral Cortex Using Fractal Dimensional Analysis. Brain Imaging Behav. 2009, 3, 154–166. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, N.; Feng, X.; Wang, D.; Yang, L.; Wang, Z. Shape Representation of Fractal Dimension on Point Cloud. In Proceedings of the 2019 Nicograph International (NicoInt), Yangling, China, 5–7 July 2019; pp. 102–105. [Google Scholar]
- Zhang, J.; Hu, Q.; Wu, H.; Su, J.; Zhao, P. Application of Fractal Dimension of Terrestrial Laser Point Cloud in Classification of Independent Trees. Fractal Fract. 2021, 5, 14. [Google Scholar] [CrossRef]
- Gulick, D. Encounters with Chaos and Fractals, Second Edition, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2012; pp. 253–254. [Google Scholar]
- Hou, X.J.; Gilmore, R.; Mindlin, G.B.; Solari, H.G. An efficient algorithm for fast O(Nln(N)) box counting. Phys. Lett. A 1990, 151, 43–46. [Google Scholar] [CrossRef]
- ETH Zürich. Semantic3D–Data. 2017. Available online: http://www.semantic3d.net/ (accessed on 13 March 2024).
- Cloud Compare. 3D Point Cloud and Mesh Processing Software Open Source Project. 2022. Available online: https://www.danielgm.net/cc/ (accessed on 13 March 2024).
- Jiménez, J.; Ruiz de Miras, J. Fast box-counting algorithm on GPU. Comput. Methods Programs Biomed. 2012, 108, 1229–1242. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Overall flowchart of the FD method.
Figure 1.
Overall flowchart of the FD method.
Figure 2.
Computation of the BCD of a point cloud in a 2D plane.
Figure 2.
Computation of the BCD of a point cloud in a 2D plane.
Figure 3.
Two pairs of sub clouds, red and blue, belonging to a real use case, with similar (a) and different (b) shapes and distributions. Below each pair of clouds, the BCD of both clouds is estimated as the slope of the line fitting the points in a log–log plot, where the x-axis represents the inverse of the size of the boxes and the y-axis the number of non-empty boxes (c,d). Each point in the plots represents one of the values used for the linear regression, required for the BCD computation.
Figure 3.
Two pairs of sub clouds, red and blue, belonging to a real use case, with similar (a) and different (b) shapes and distributions. Below each pair of clouds, the BCD of both clouds is estimated as the slope of the line fitting the points in a log–log plot, where the x-axis represents the inverse of the size of the boxes and the y-axis the number of non-empty boxes (c,d). Each point in the plots represents one of the values used for the linear regression, required for the BCD computation.
Figure 4.
Three-dimensional regular grid of nested octrees used for space partitioning and point cloud indexing.
Figure 4.
Three-dimensional regular grid of nested octrees used for space partitioning and point cloud indexing.
Figure 5.
Example of box-counting calculation for an inner node using the box-counting of its children.
Figure 5.
Example of box-counting calculation for an inner node using the box-counting of its children.
Figure 6.
Top and perspective views of the bildstein1 dataset of Semantic3D used in the experiments, with almost 30 million points scattered over 50,000 m2 around the area of Bildstein church (Austria).
Figure 6.
Top and perspective views of the bildstein1 dataset of Semantic3D used in the experiments, with almost 30 million points scattered over 50,000 m2 around the area of Bildstein church (Austria).
Figure 7.
Modified version of the bildstein1 dataset for experiment E4.
Figure 7.
Modified version of the bildstein1 dataset for experiment E4.
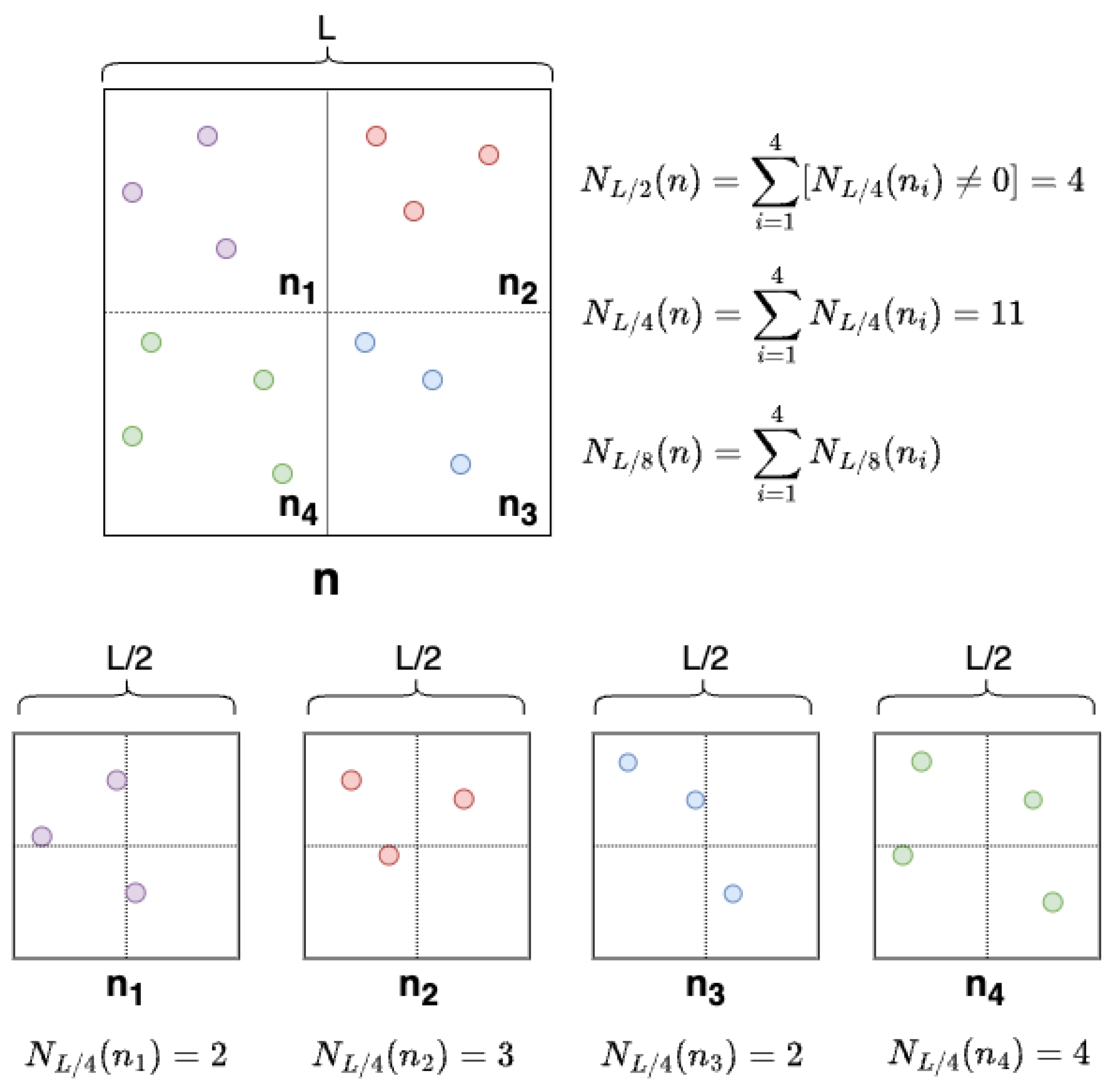
Figure 8.
Experiment E1. The second cloud is an artificially modified version of the first one by perturbing the location of the points. FD box size units are meters.
Figure 8.
Experiment E1. The second cloud is an artificially modified version of the first one by perturbing the location of the points. FD box size units are meters.
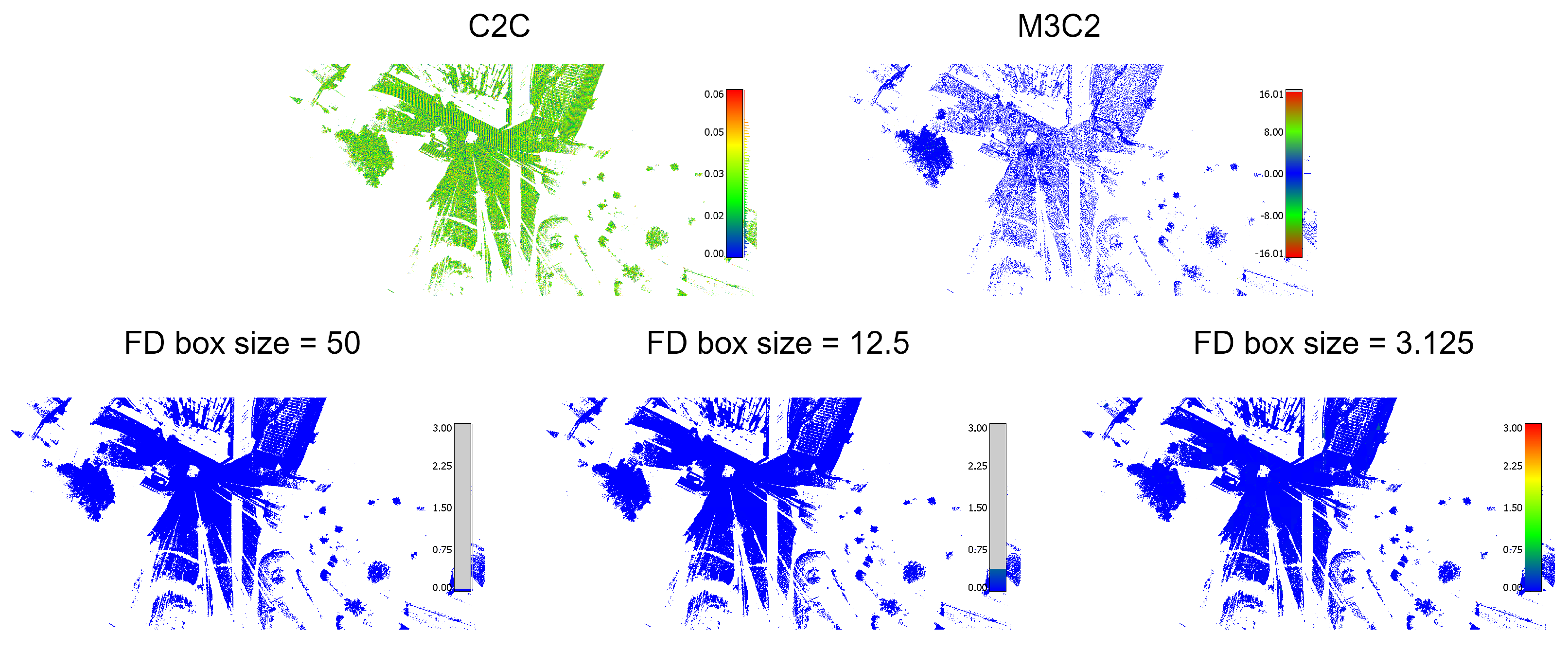
Figure 9.
Experiment E2. The second cloud is a subsample random version (50%) of the first one. FD box size units are meters.
Figure 9.
Experiment E2. The second cloud is a subsample random version (50%) of the first one. FD box size units are meters.
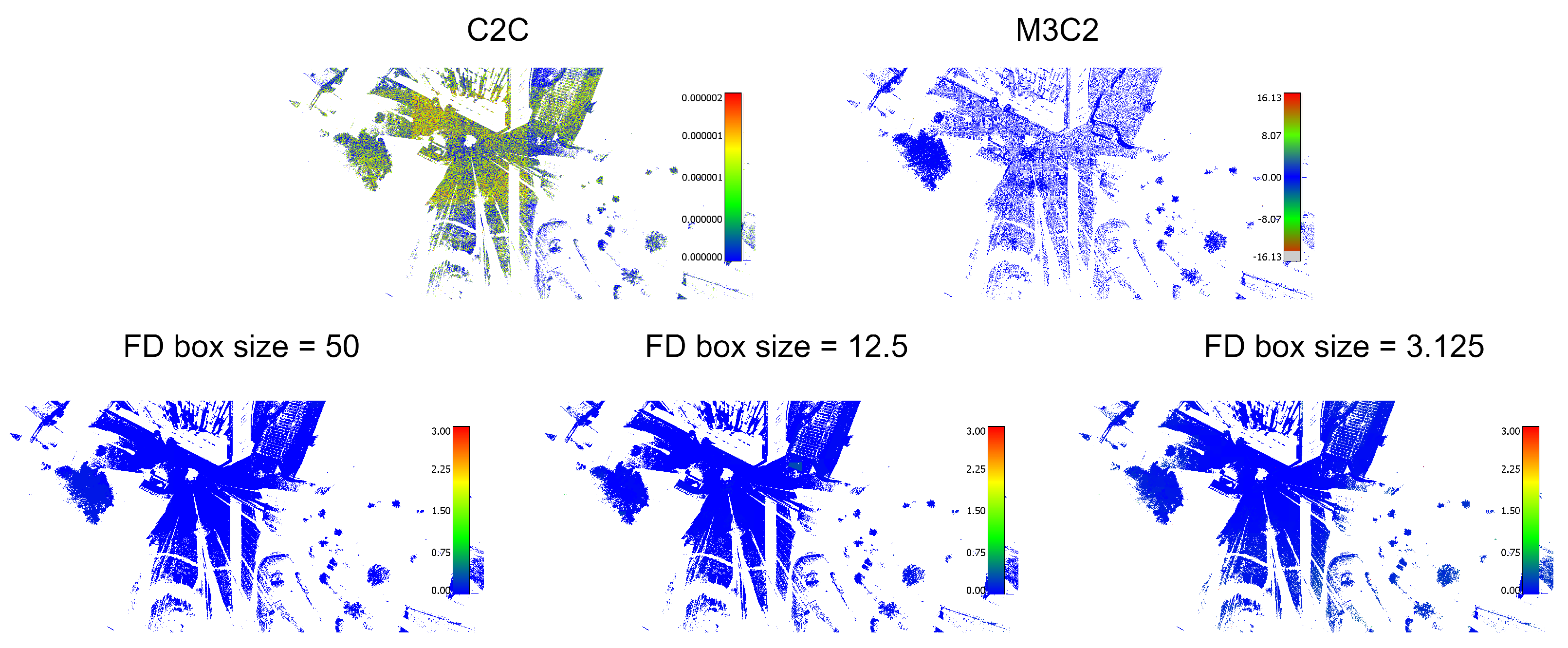
Figure 10.
Experiment E3. The second cloud is a copy of the first one but with a hole in the middle area. FD box size units are meters.
Figure 10.
Experiment E3. The second cloud is a copy of the first one but with a hole in the middle area. FD box size units are meters.
Figure 11.
Experiment E4. The second cloud is a modified version of the first point cloud where several objects have been removed. The FD box size units are meters.
Figure 11.
Experiment E4. The second cloud is a modified version of the first point cloud where several objects have been removed. The FD box size units are meters.
Figure 12.
Visual comparison of the results of the FD-based method in the experiment E3 calculated in an octree without pruning (left) or with pruning (right).
Figure 12.
Visual comparison of the results of the FD-based method in the experiment E3 calculated in an octree without pruning (left) or with pruning (right).
Table 1.
Time (in seconds) of execution of the algorithms tested with the four experiments proposed. The final row includes the benefit of performing the new method compared with M3C2.
Table 1.
Time (in seconds) of execution of the algorithms tested with the four experiments proposed. The final row includes the benefit of performing the new method compared with M3C2.
| Method Tested | Stage | E1 | E2 | E3 | E4 |
|---|
| C2C | Computation | 639.14 | 3.40 | 6377.12 | 2507.61 |
| M3C2 | Initialization | 19.30 | 12.53 | 13.01 | 13.24 |
| Computation | 28.32 | 33.63 | 19.21 | 30.33 |
| FD | Initialization | 26.44 | 20.46 | 12.78 | 22.96 |
| Computation | 12.24 | 9.53 | 1.76 | 9.44 |
| Initialization | 23.21 | 17.55 | 10.51 | 19.07 |
| Computation | 12.09 | 9.24 | 1.85 | 9.45 |
| Performance factor | Init + Comp | 1.23× | 1.54× | 2.22× | 1.34× |
| (FD vs. M3CD2) | Only Comput. | 2.31× | 3.53× | 10.91× | 3.21× |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).