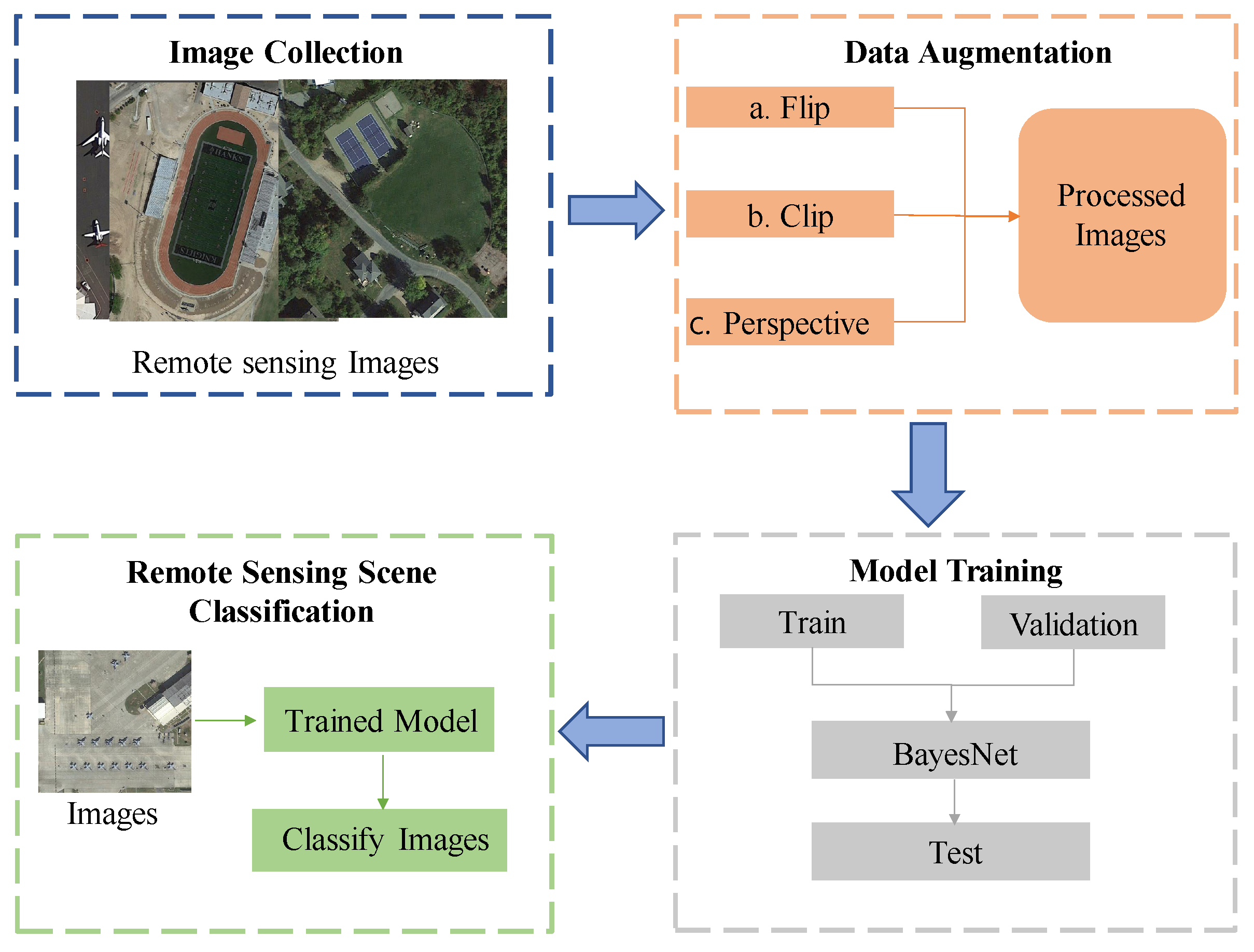
Figure 1.
The overall architecture of the proposed remote sensing image scene understanding classification system based on BayesNet.
Figure 1.
The overall architecture of the proposed remote sensing image scene understanding classification system based on BayesNet.
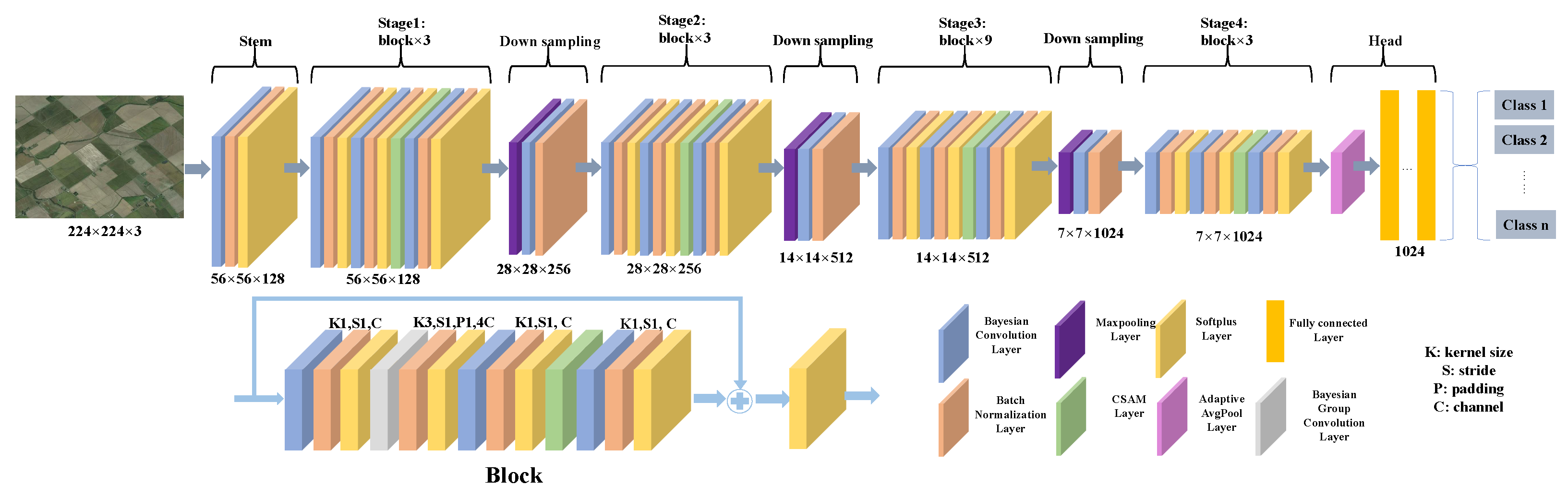
Figure 2.
The overall structure of the BayesNet model, which consists of stem, body, and head parts.
Figure 2.
The overall structure of the BayesNet model, which consists of stem, body, and head parts.
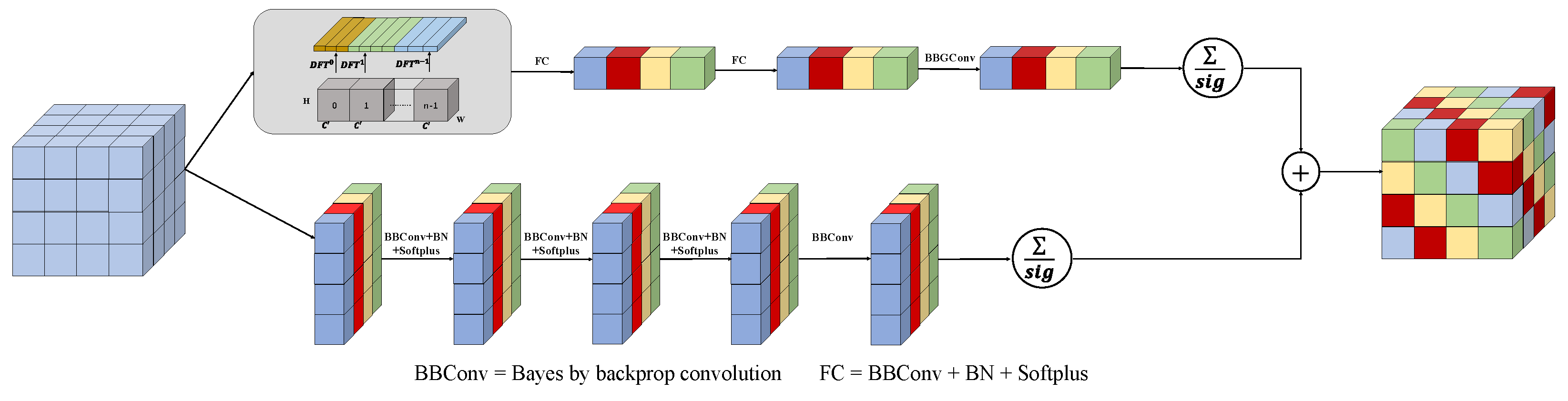
Figure 3.
The architecture of the CSAM block from the individual block, showcasing its detailed structure and components.
Figure 3.
The architecture of the CSAM block from the individual block, showcasing its detailed structure and components.
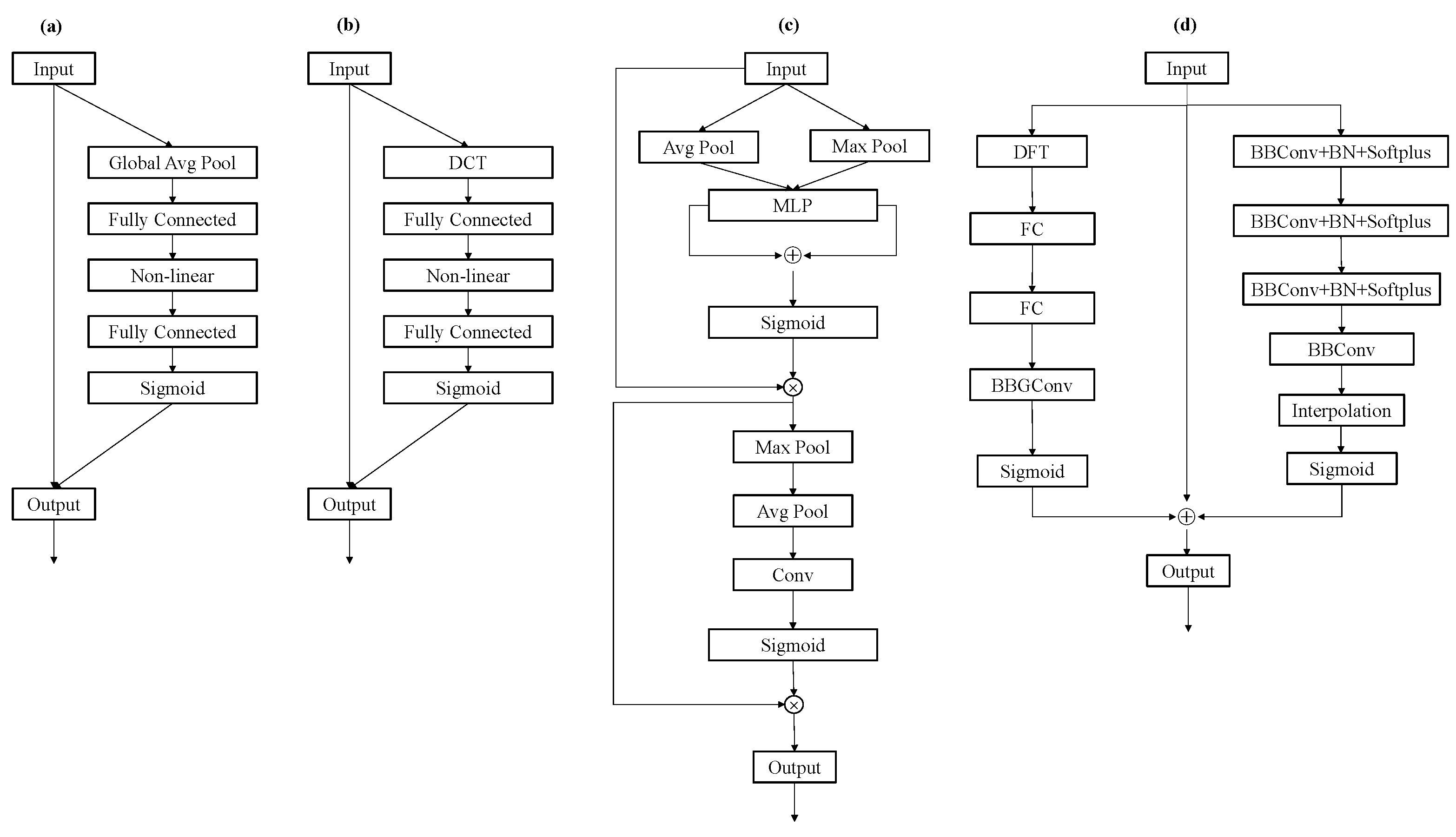
Figure 4.
The comparison of different structure of attention modules. (a) SE attention module, (b) FcaNet attention module, (c) CBAM attention network, (d) proposed CSAM attention module.
Figure 4.
The comparison of different structure of attention modules. (a) SE attention module, (b) FcaNet attention module, (c) CBAM attention network, (d) proposed CSAM attention module.
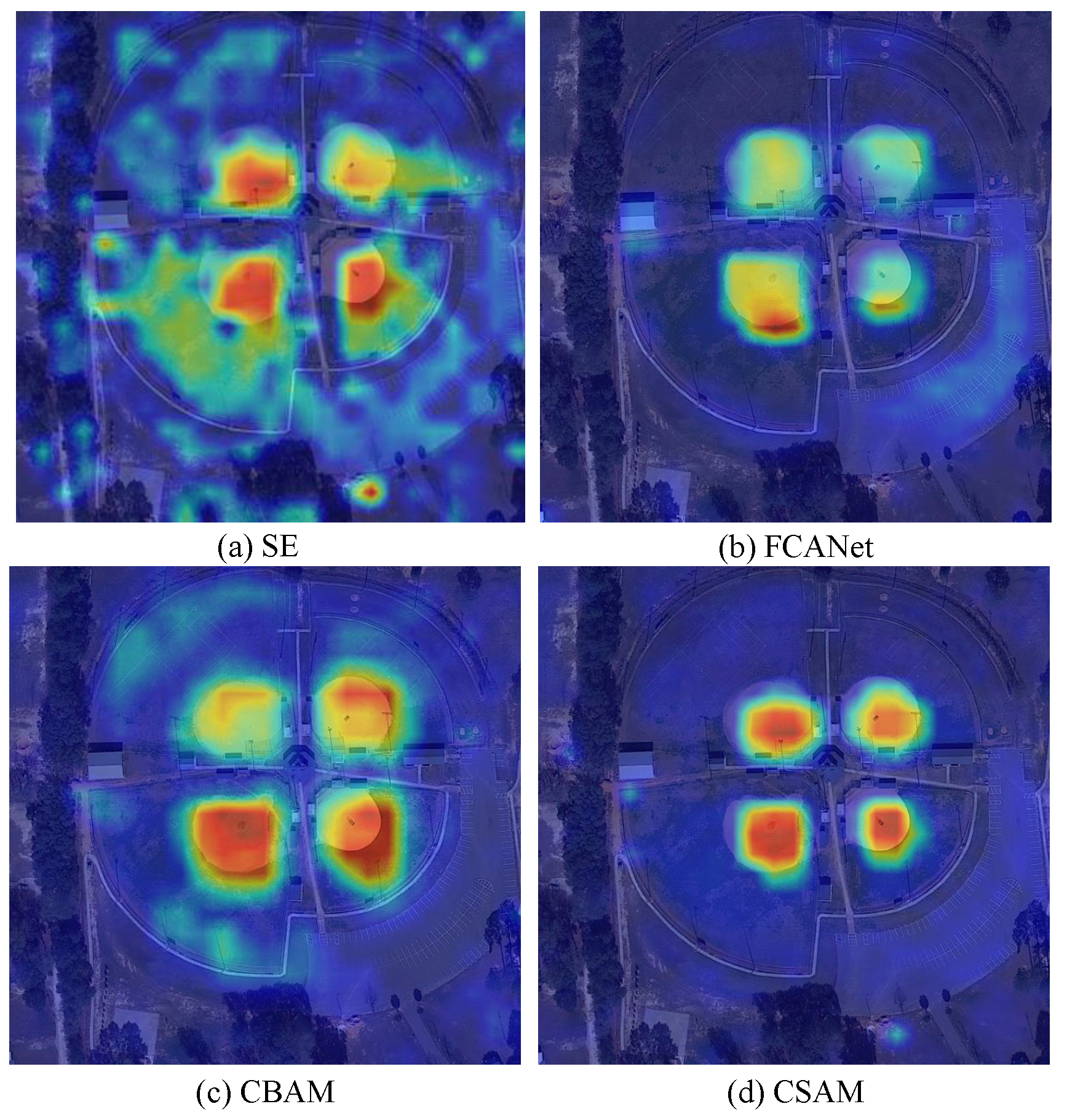
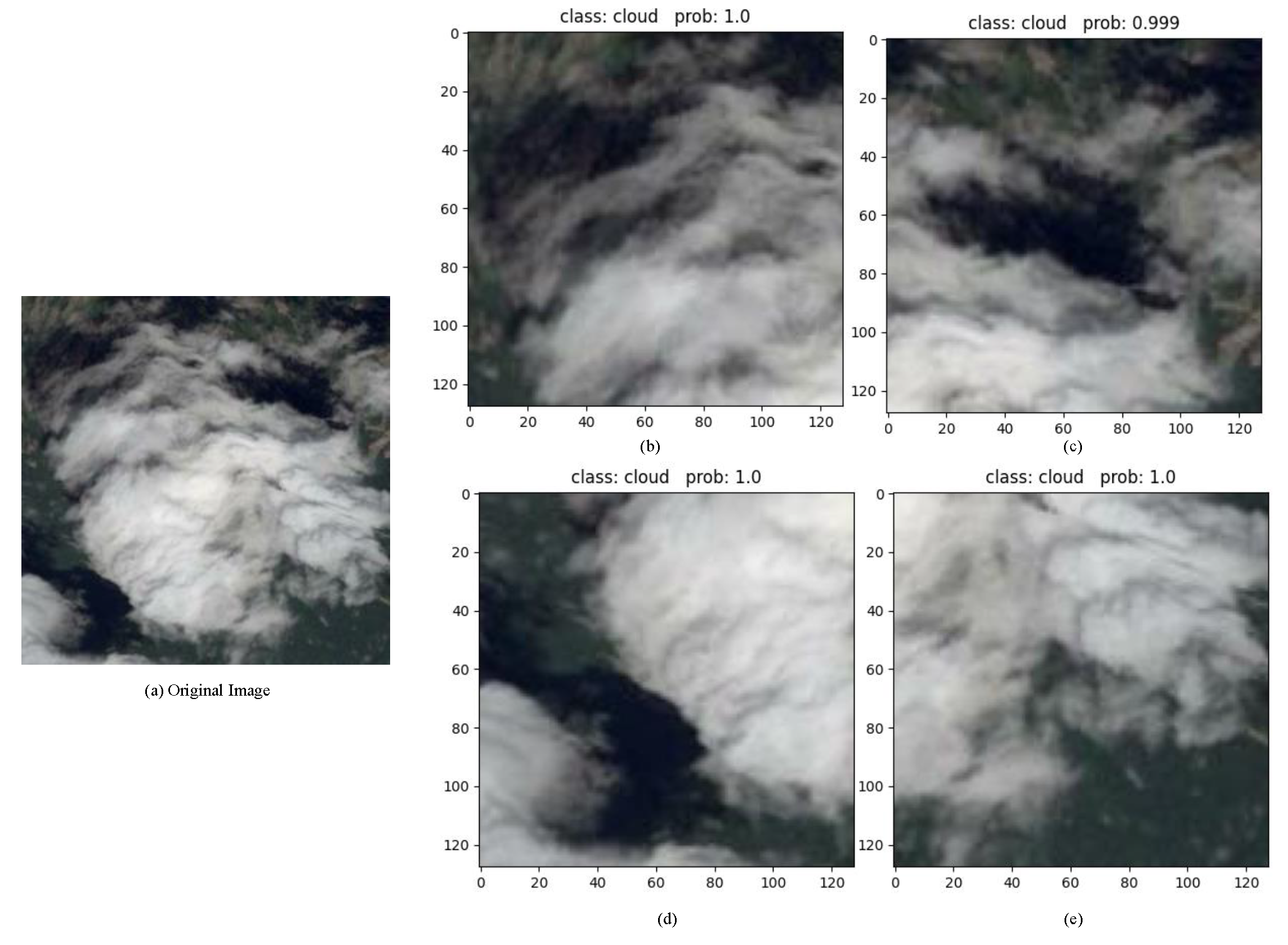
Figure 5.
The visual comparison of different methods using GradCam.
Figure 5.
The visual comparison of different methods using GradCam.
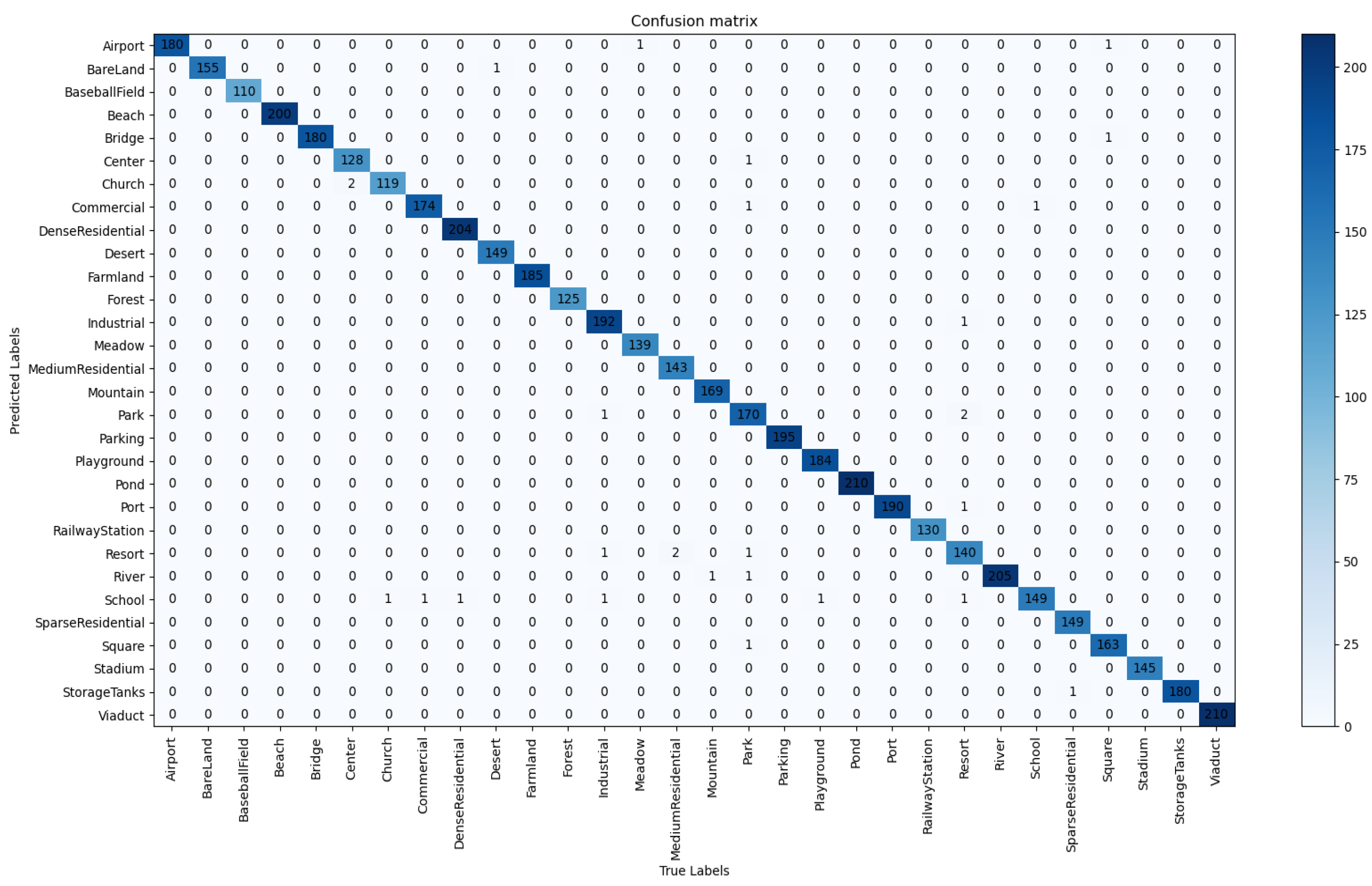
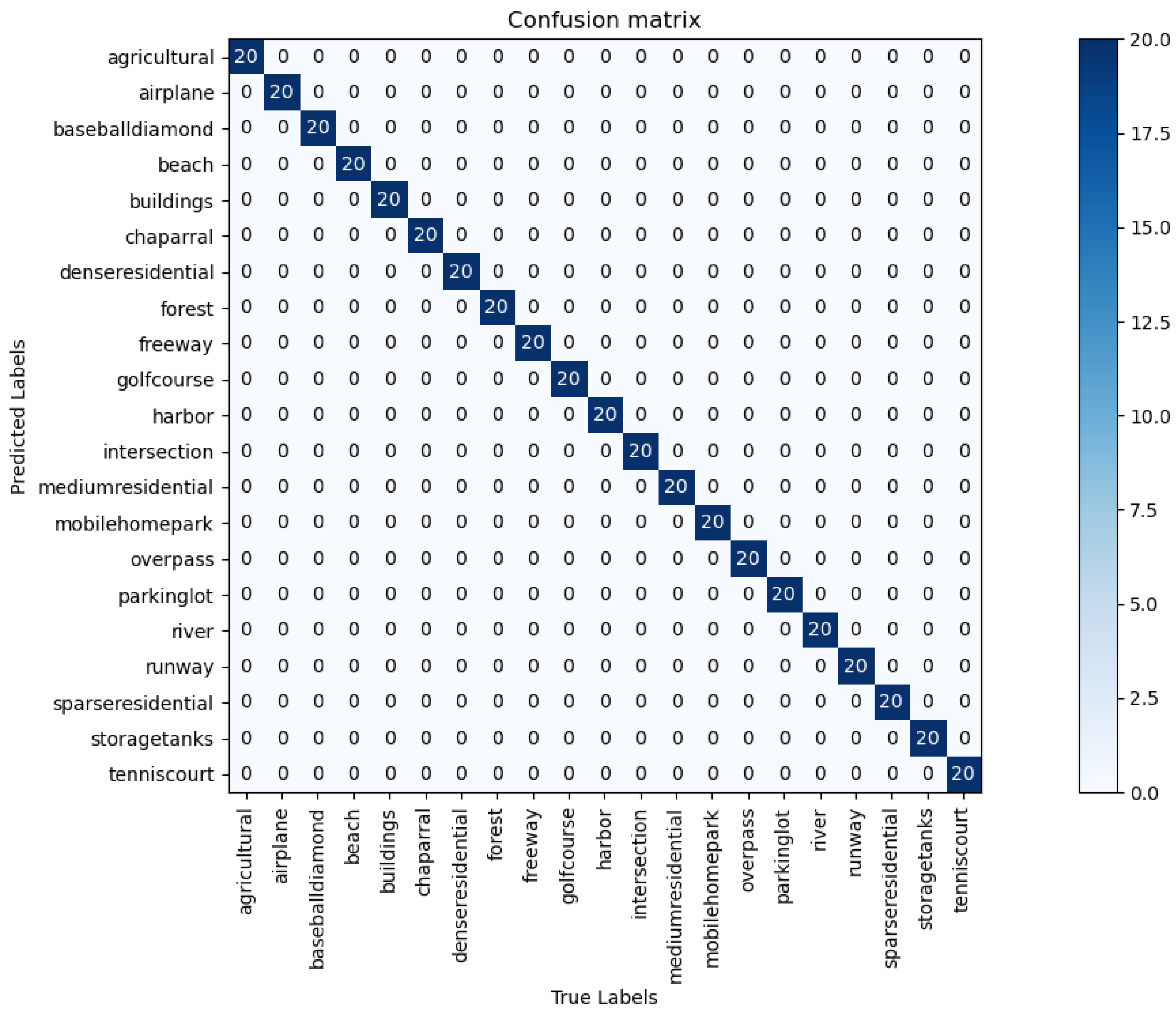
Figure 6.
The calculated confusion matrix on AID (50:50) dataset using BayesNet.
Figure 6.
The calculated confusion matrix on AID (50:50) dataset using BayesNet.
Figure 7.
Visualization of the efficient classification results of the BayesNet on the AID dataset.
Figure 7.
Visualization of the efficient classification results of the BayesNet on the AID dataset.
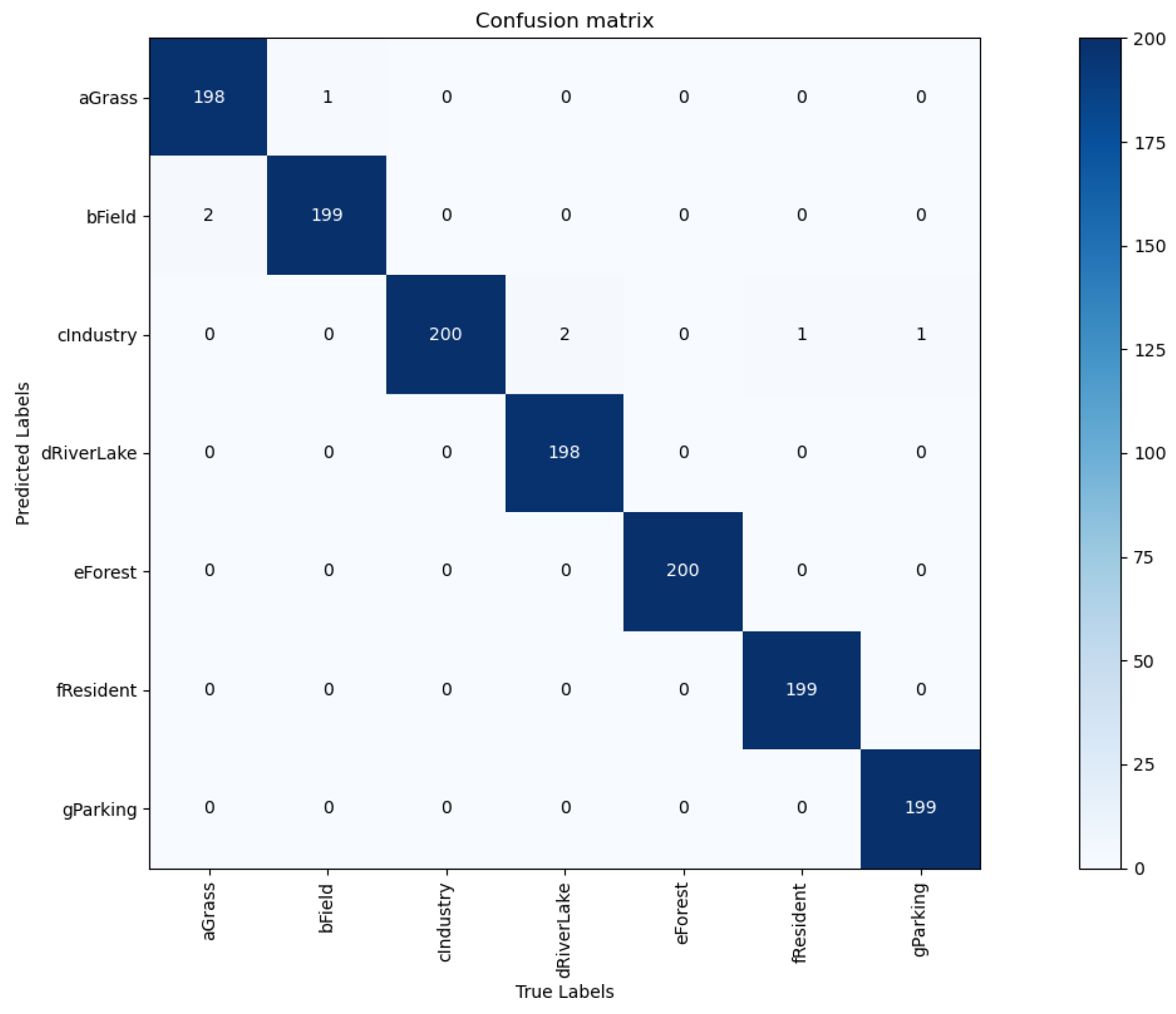
Figure 8.
The calculated confusion matrix on RSSCN7 (50:50) dataset using BayesNet.
Figure 8.
The calculated confusion matrix on RSSCN7 (50:50) dataset using BayesNet.
Figure 9.
Illustration of the robust classification performance of the BayesNet using the RSSCN7 dataset.
Figure 9.
Illustration of the robust classification performance of the BayesNet using the RSSCN7 dataset.
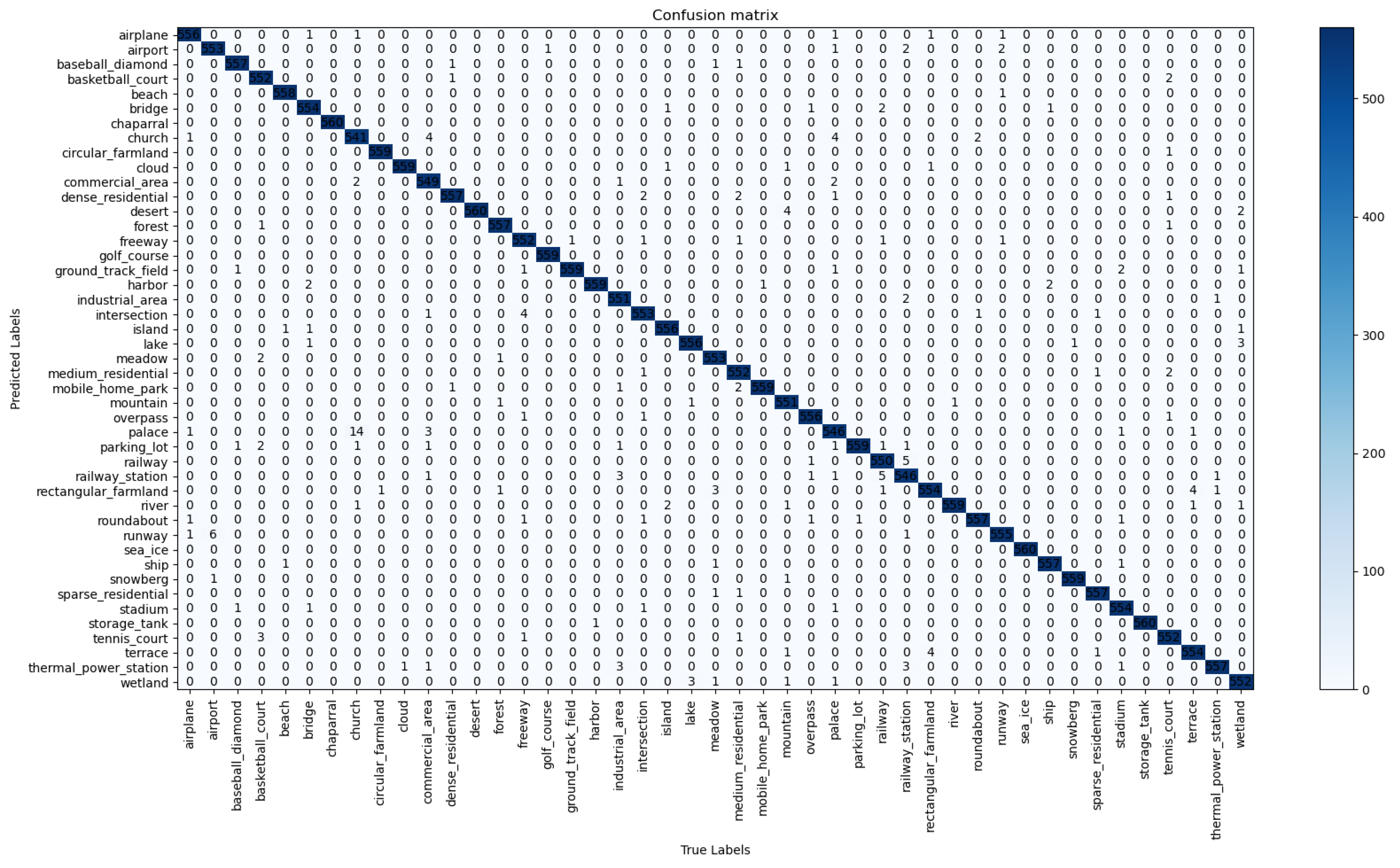
Figure 10.
The calculated confusion matrix on NWPU45 (20:80) dataset using BayesNet.
Figure 10.
The calculated confusion matrix on NWPU45 (20:80) dataset using BayesNet.
Figure 11.
Visualization of the efficient classification results of the BayesNet on the NWPU dataset.
Figure 11.
Visualization of the efficient classification results of the BayesNet on the NWPU dataset.
Figure 12.
The calculated confusion matrix on UCM21 (20:80) dataset using BayesNet.
Figure 12.
The calculated confusion matrix on UCM21 (20:80) dataset using BayesNet.
Figure 13.
Demonstration of the distinctive classification capabilities of the proposed BayesNet on UCM21 dataset.
Figure 13.
Demonstration of the distinctive classification capabilities of the proposed BayesNet on UCM21 dataset.
Figure 14.
The predictions of BayesNet on the cropped images. Cropped images were used to evaluate the performance of the BayesNet. (a) original image, (b) prediction on cropped top left of the original image, (c) prediction on cropped top right of the original image, (d) prediction on cropped bottom left of the image, (e) prediction on cropped bottom right of the original image.
Figure 14.
The predictions of BayesNet on the cropped images. Cropped images were used to evaluate the performance of the BayesNet. (a) original image, (b) prediction on cropped top left of the original image, (c) prediction on cropped top right of the original image, (d) prediction on cropped bottom left of the image, (e) prediction on cropped bottom right of the original image.
Figure 15.
The predictions of BayesNet on the rotated images. Different rotated angle images were used to evaluate the performance of the BayesNet. (a) original image, (b) prediction on 90 degrees rotated image, (c) prediction on 180 degrees rotated image, (d) prediction on 270 degrees rotated image, (e) prediction on 360 degrees rotated images.
Figure 15.
The predictions of BayesNet on the rotated images. Different rotated angle images were used to evaluate the performance of the BayesNet. (a) original image, (b) prediction on 90 degrees rotated image, (c) prediction on 180 degrees rotated image, (d) prediction on 270 degrees rotated image, (e) prediction on 360 degrees rotated images.
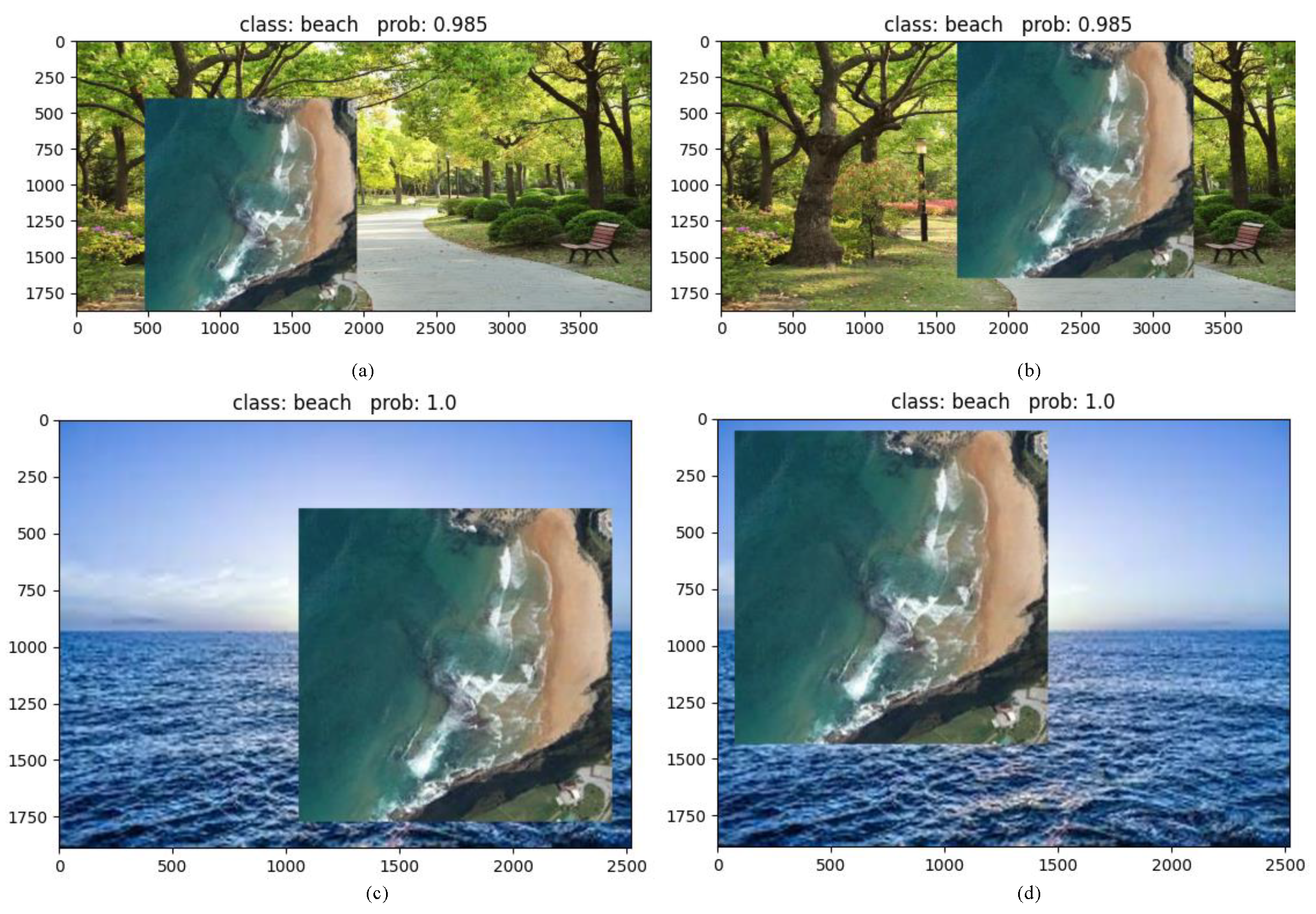
Figure 16.
The predictions of BayesNet on the partially overlapping images to evaluate the performance of the BayesNet in constrained environments. (a,b) prediction of beach class partially overlapped on park image; (c,d) prediction of beach class partially overlapped on sea image.
Figure 16.
The predictions of BayesNet on the partially overlapping images to evaluate the performance of the BayesNet in constrained environments. (a,b) prediction of beach class partially overlapped on park image; (c,d) prediction of beach class partially overlapped on sea image.
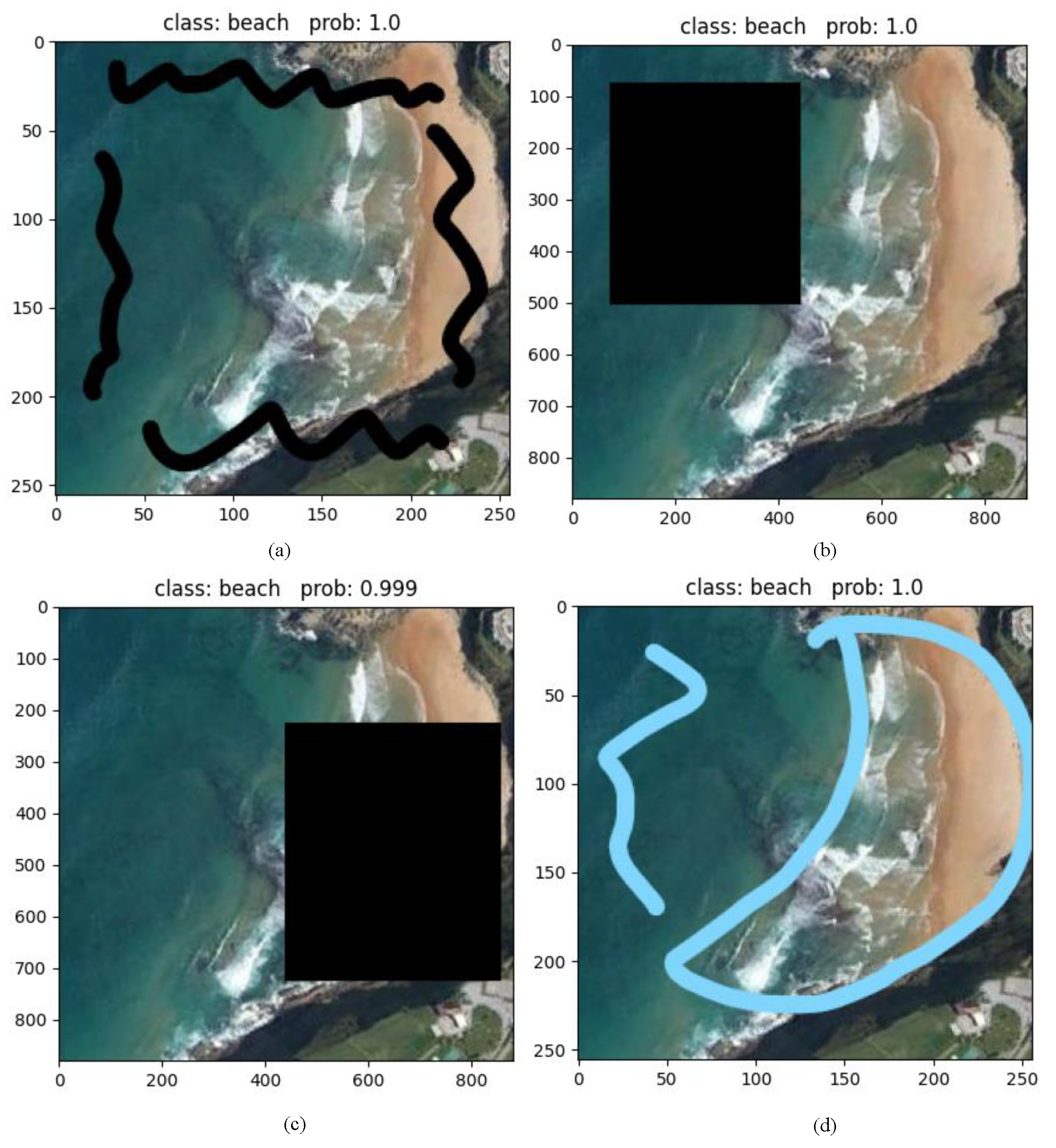
Figure 17.
The predictions of BayesNet on the noisy images, where black screen and random line noise were utilized to evaluate the performance of the BayesNet. (a) prediction of beach class with black line noise; (b) prediction of beach class with left aligned black screen noise; (c) prediction of beach class with right aligned black screen noise; (d) prediction of beach class with blue line noise.
Figure 17.
The predictions of BayesNet on the noisy images, where black screen and random line noise were utilized to evaluate the performance of the BayesNet. (a) prediction of beach class with black line noise; (b) prediction of beach class with left aligned black screen noise; (c) prediction of beach class with right aligned black screen noise; (d) prediction of beach class with blue line noise.
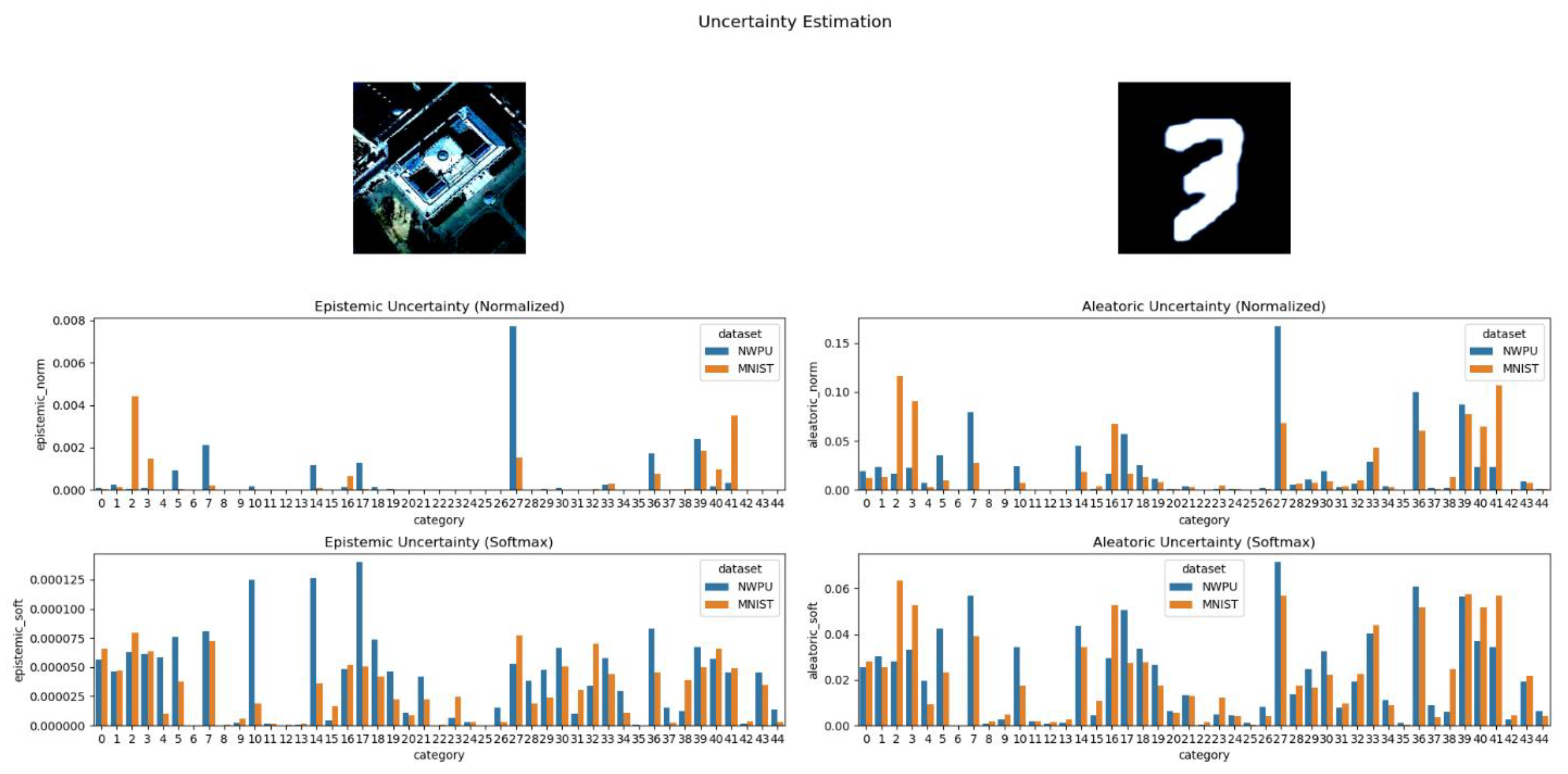
Figure 18.
The normalized and SoftMax aleatoric and epistemic uncertainty estimation for NWPU dataset using BayesNet.
Figure 18.
The normalized and SoftMax aleatoric and epistemic uncertainty estimation for NWPU dataset using BayesNet.
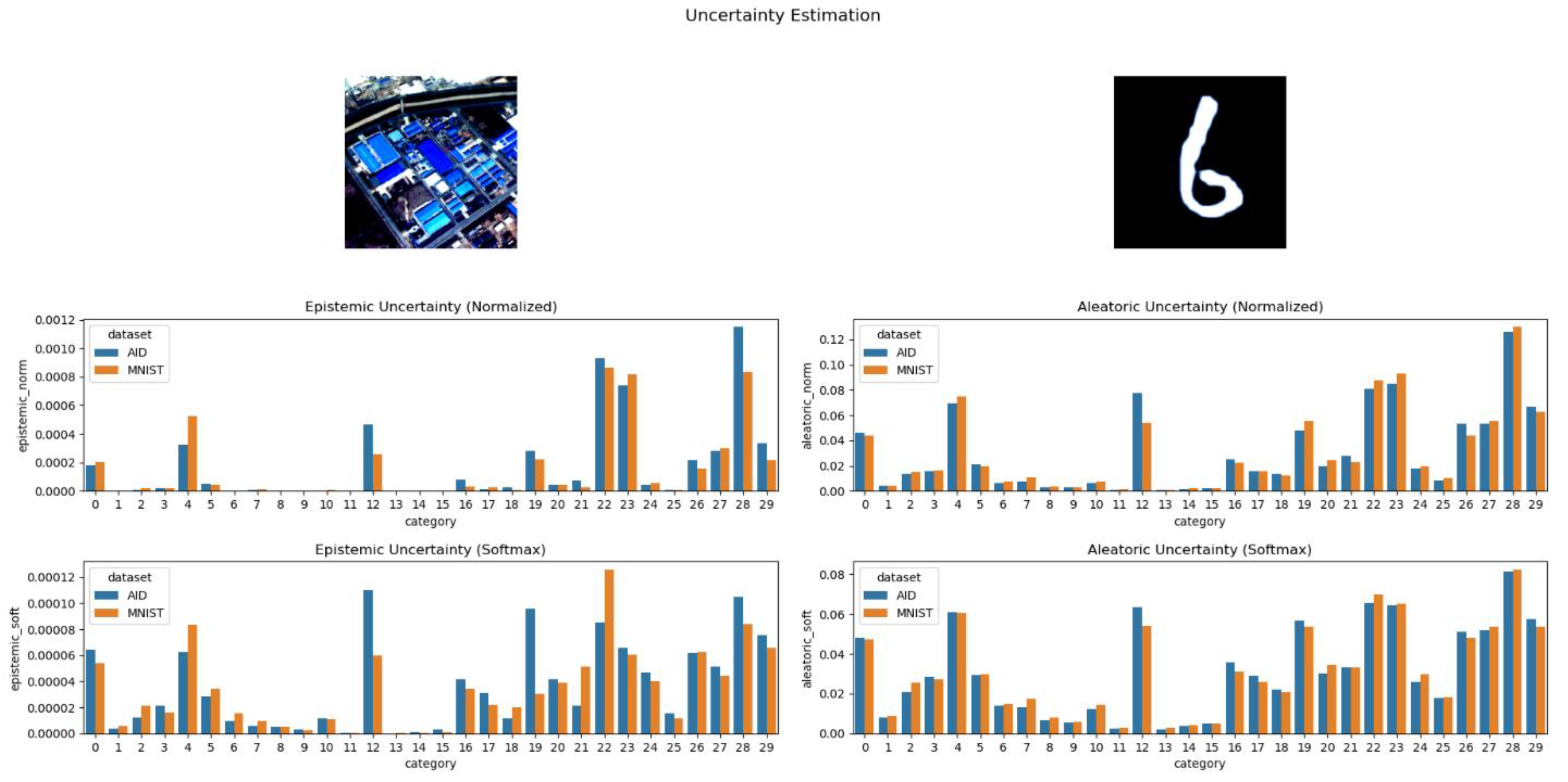
Figure 19.
Normalized and SoftMax-processed estimation of aleatoric and epistemic uncertainty for the AID dataset, utilizing BayesNet.
Figure 19.
Normalized and SoftMax-processed estimation of aleatoric and epistemic uncertainty for the AID dataset, utilizing BayesNet.
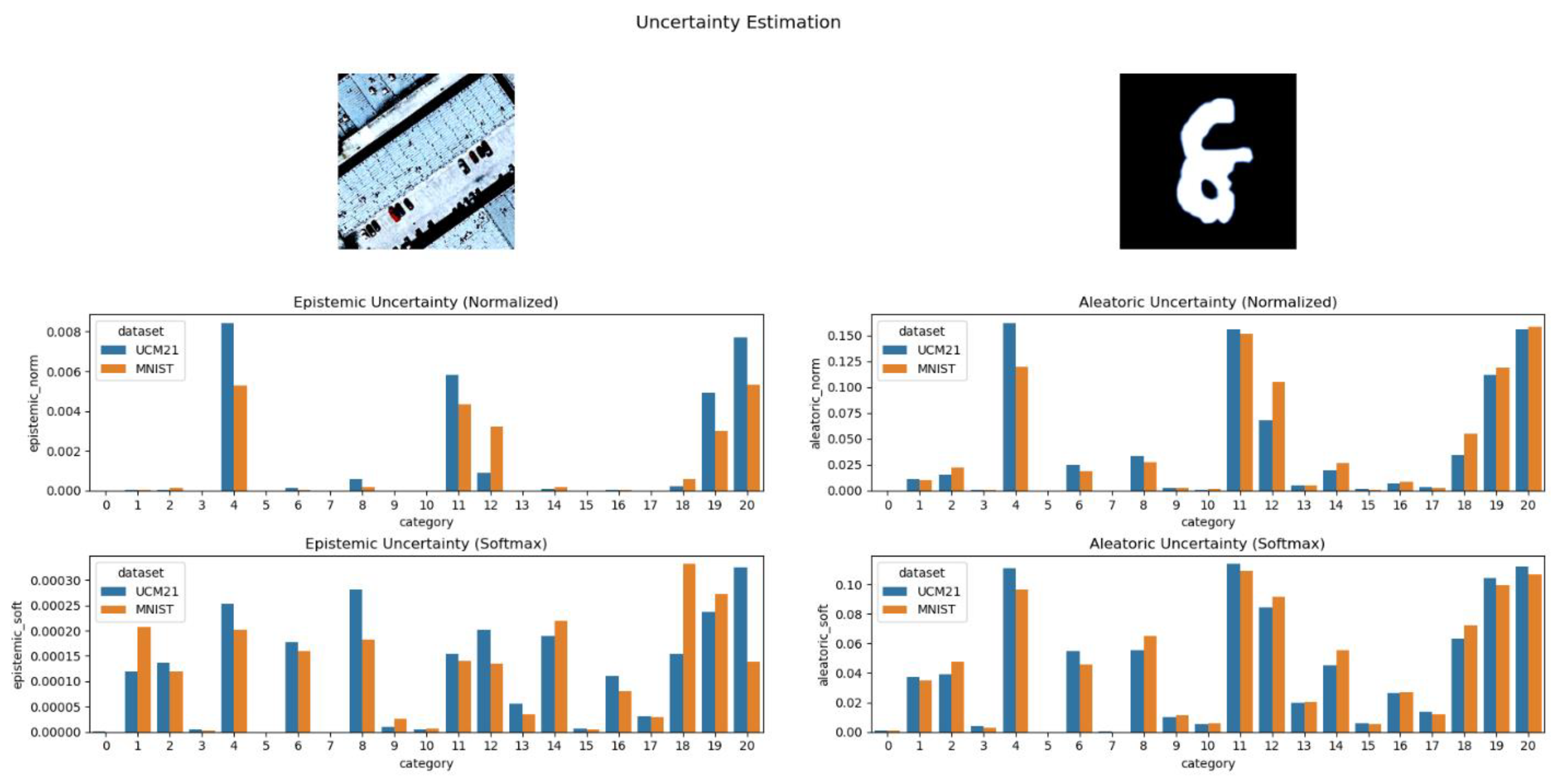
Figure 20.
Normalized and SoftMax-transformed representation of aleatoric and epistemic uncertainty estimation for the UCM-21 dataset, using BayesNet.
Figure 20.
Normalized and SoftMax-transformed representation of aleatoric and epistemic uncertainty estimation for the UCM-21 dataset, using BayesNet.
Figure 21.
Visualization of normalized and SoftMax-adjusted aleatoric and epistemic uncertainty estimations for the RSSCN7 dataset, leveraging BayesNet.
Figure 21.
Visualization of normalized and SoftMax-adjusted aleatoric and epistemic uncertainty estimations for the RSSCN7 dataset, leveraging BayesNet.
Figure 22.
Sample images from the testing dataset to evaluate the performance of BayesNet on unseen data.
Figure 22.
Sample images from the testing dataset to evaluate the performance of BayesNet on unseen data.
Figure 23.
Prediction visualization using BayesNet on our introduced remote sensing testing dataset which comprises complex backgrounds.
Figure 23.
Prediction visualization using BayesNet on our introduced remote sensing testing dataset which comprises complex backgrounds.
Table 1.
The detailed description of four remote sensing scene image datasets used in this study.
Table 1.
The detailed description of four remote sensing scene image datasets used in this study.
| Datasets | Scene Class Number | Image Number | Image Resolution | Image Size |
|---|
| UCM21 [23] | 21 | 2100 | 0.3 | |
| RSSCN7 [24] | 7 | 2800 | - | - |
| AID [25] | 30 | 10,000 | 0.5–0.8 | |
| NWPU45 [26] | 45 | 31,500 | 0.2–30 | |
Table 2.
Comparative analysis of the accuracy (Acc) rates for different augmentation methods, including None, Auto-Augment, and the Proposed BayesNet (Flip, Clip, Perspective), across four datasets: UCM-21, RSSCN7, AID, and NWPU.
Table 2.
Comparative analysis of the accuracy (Acc) rates for different augmentation methods, including None, Auto-Augment, and the Proposed BayesNet (Flip, Clip, Perspective), across four datasets: UCM-21, RSSCN7, AID, and NWPU.
| Augmentation Method | UCM21 [23] | RSSCN7 [24] | AID [25] | NWPU [26] |
|---|
| None | 99.87 | 97.25 | 97.46 | 95.32 |
| Auto-Augment | 99.93 | 97.34 | 97.51 | 95.39 |
| BayesNet (Flip, Clip, Perspective) | 99.99 | 97.30 | 97.57 | 95.44 |
Table 3.
The training and testing accuracy of the BayesNet and the different deep learning models.
Table 3.
The training and testing accuracy of the BayesNet and the different deep learning models.
| Model Name | UCM21 [23] | RSSCN7 [24] | AID [25] | NWPU [26] |
|---|
| AlexNet [30] | 88.13 | 87.00 | 85.70 | 87.34 |
| VGG16 [31] | 95.44 | 87.18 | 89.64 | 93.56 |
| GoogLeNet [32] | 93.12 | 85.84 | 86.39 | 86.02 |
| ResNet50 [33] | 94.76 | 91.45 | 94.69 | 91.86 |
| VIT [34] | 99.01 | 90.89 | 95.27 | 93.31 |
| RegNet [35] | 97.93 | 94.33 | 94.61 | 95.03 |
| Bayesian RegNet | 95.72 | 95.24 | 94.93 | 95.05 |
| BayesNet | 99.99 | 97.30 | 97.57 | 95.44 |
Table 4.
Comparative analysis of proposed models’ overall accuracy on AID dataset (50:50) over the last few years.
Table 4.
Comparative analysis of proposed models’ overall accuracy on AID dataset (50:50) over the last few years.
| Method | Year | Overall Accuracy |
|---|
| Bidirectional Adaptive Feature Fusion [36] | 2019 | 93.56 |
| Feature Aggregation CNN [37] | 2019 | 95.45 |
| Aggregated Deep Fisher Feature [38] | 2019 | 95.26 |
| Skip-connected covariance network [39] | 2019 | 93.30 |
| EfficientNet [40] | 2020 | 88.35 |
| InceptionV3 [41] | 2020 | 95.07 |
| Branch Feature Fusion [42] | 2020 | 94.53 |
| Gated Bidirectional Network with global feature [43] | 2020 | 95.48 |
| Deep Discriminative Representation Learning [44] | 2020 | 94.08 |
| Hierarchical Attention and Bilinear Fusion [45] | 2020 | 96.75 |
| VGG-VD16 with SAFF [46] | 2021 | 95.98 |
| EfficientNetB3-CNN [47] | 2021 | 95.39 |
| Multiscale attention network [48] | 2021 | 96.76 |
| Channel Multi-Group Fusion [49] | 2021 | 97.54 |
| Multiscale representation learning [50] | 2022 | 96.01 |
| Global-local dual-branch structure [51] | 2022 | 97.01 |
| Multilevel feature fusion networks [52] | 2022 | 95.06 |
| Multi-Level Fusion Network [53] | 2022 | 97.38 |
| MGSNet [54] | 2023 | 97.18 |
| BayesNet | - | 97.57 |
Table 5.
Comparative analysis of proposed models’ overall accuracy on RSSCN7 dataset (50:50) over the last few years.
Table 5.
Comparative analysis of proposed models’ overall accuracy on RSSCN7 dataset (50:50) over the last few years.
| Method | Year | Overall Accuracy |
|---|
| Aggregated Deep Fisher Feature [38] | 2019 | 95.21 |
| SE-MDPMNet [55] | 2019 | 92.64 |
| Positional Context Aggregation [56] | 2019 | 95.98 |
| Feature Variable Significance Learning [57] | 2019 | 89.1 |
| Branch Feature Fusion [42] | 2020 | 94.64 |
| Coutourlet CNN [58] | 2021 | 95.54 |
| Channel Multi-Group Fusion [49] | 2022 | 97.50 |
| GLFFNet [59] | 2023 | 94.82 |
| CRABR-Net [60] | 2023 | 95.43 |
| BayesNet | - | 97.30 |
Table 6.
Comparative analysis of proposed models’ overall accuracy on NWPU45 (20:80) dataset over the last few years.
Table 6.
Comparative analysis of proposed models’ overall accuracy on NWPU45 (20:80) dataset over the last few years.
| Method | Year | Overall Accuracy |
|---|
| Rotation invariant feature learning [61] | 2019 | 91.03 |
| Positional Context Aggregation [56] | 2019 | 92.61 |
| Feature Variable Significance Learning [57] | 2019 | 89.13 |
| Multi-Granualirty Canonical Appearance Pooling [62] | 2020 | 91.72 |
| EfficientNet [40] | 2020 | 81.83 |
| ResNet50 with transfer learning [41] | 2020 | 88.93 |
| MobileNet with tranfer learning [41] | 2020 | 83.26 |
| Branch Feature Fusion [42] | 2020 | 91.73 |
| Multi-Structure Deep features fusion [63] | 2020 | 93.55 |
| Coutourlet CNN [58] | 2021 | 89.57 |
| Channel Multi-Group Fusion [49] | 2022 | 94.18 |
| Multi-Level Fusion Network [53] | 2022 | 94.90 |
| MGSNet [54] | 2023 | 94.57 |
| BayesNet | - | 95.44 |
Table 7.
Comparative analysis of proposed models’ overall accuracy on UCM21 (80:20) dataset over the last few years.
Table 7.
Comparative analysis of proposed models’ overall accuracy on UCM21 (80:20) dataset over the last few years.
| Method | Year | Overall Accuracy |
|---|
| Skip connected covariance network [39] | 2019 | 97.98 |
| Feature aggregation CNN [37] | 2019 | 98.81 |
| Aggregated Deep Fisher Feature [38] | 2019 | 98.81 |
| Scale-Free Network [64] | 2019 | 99.05 |
| SE-MDPMNet [55] | 2019 | 99.09 |
| Multiple resolution BlockFeature method [65] | 2019 | 94.19 |
| Branch Feature Fusion [42] | 2020 | 99.29 |
| Gated Bidirectional Network with global feature [43] | 2020 | 98.57 |
| Positional Context Aggregation [56] | 2020 | 99.21 |
| Feature Variable Significance Learning [57] | 2020 | 98.56 |
| Deep Discriminative Representation Learning [44] | 2020 | 99.05 |
| ResNet50 with transfer learning [41] | 2020 | 98.76 |
| VGG-VD16 with SAFF [46] | 2021 | 97.02 |
| Coutourlet CNN [58] | 2021 | 99.25 |
| EfficientNetB3 [47] | 2021 | 99.21 |
| Channel Multi-Group Fusion [49] | 2022 | 99.52 |
| Inception-ResNet-v2 [66] | 2023 | 99.05 |
| MGSNet [54] | 2023 | 99.76 |
| BayesNet | - | 99.99 |
Table 8.
The ablation study of the proposed model on four remote sensing datasets.
Table 8.
The ablation study of the proposed model on four remote sensing datasets.
| Method | UCM21 [23] | RSSCN7 [24] | AID [25] | NWPU [26] |
|---|
| RegNet [35] | 97.93 | 94.33 | 94.61 | 95.03 |
| Bayesian + RegNet | 95.72 | 95.24 | 94.93 | 95.05 |
| RegNet + CSAM | 99.14 | 96.73 | 96.31 | 95.18 |
| BayeNet (Bayesian + Bayes Block + CSAM) | 99.99 | 97.30 | 97.57 | 95.44 |
Table 9.
The comparison of testing accuracy on our proposed dataset with AID dataset trained model.
Table 9.
The comparison of testing accuracy on our proposed dataset with AID dataset trained model.
| Method | Accuracy |
|---|
| AlexNet [30] | 89.32 |
| VGG16 [31] | 92.79 |
| GoogLeNet [32] | 91.46 |
| ResNet50 [33] | 94.57 |
| ViT [34] | 95.35 |
| RegNet [35] | 94.88 |
| BayesNet | 96.39 |
Table 10.
Comparison of parameters and complexity of different deep learning models implemented in this study.
Table 10.
Comparison of parameters and complexity of different deep learning models implemented in this study.
| Method | Parameters (M) | Complexity (G) |
|---|
| AlexNet [30] | 61.1 | 0.715 |
| VGG16 [31] | 138.36 | 15.5 |
| GoogleNet [32] | 13.0 | 1.51 |
| ResNet50 [33] | 25.56 | 4.12 |
| VIT [34] | 306.54 | 15.39 |
| Bayesian RegNet | 900.3 | 92.3 |
| BayesNet | 949.85 | 93.1 |