Non-Cooperative LEO Satellite Orbit Determination Using Single Station for Space-Based Opportunistic Positioning
Abstract
1. Introduction
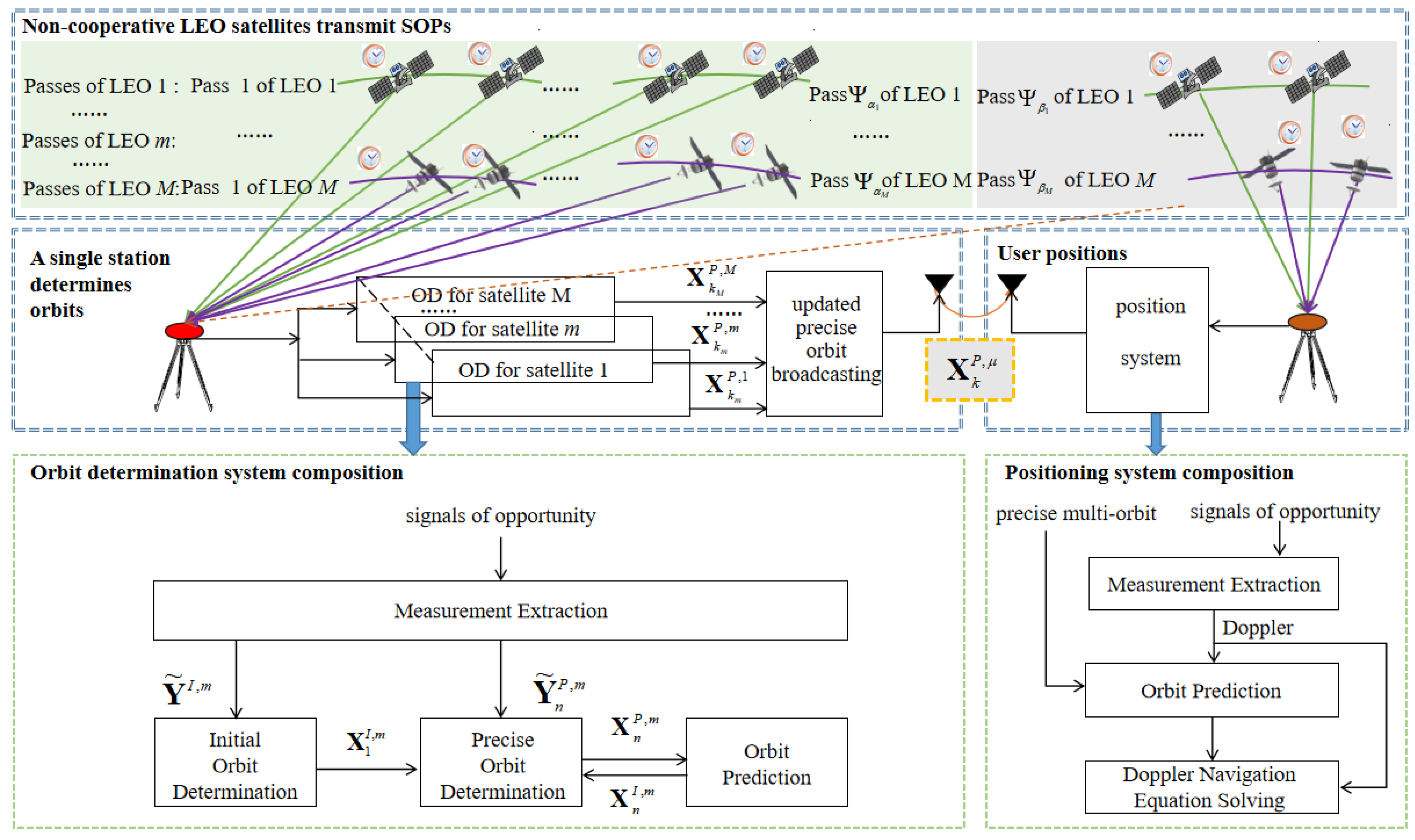
2. Non-Cooperative LEO Satellite Orbit Determination Using a Single Station for Opportunistic Positioning Framework
2.1. Overview
2.2. System Composition and Process of Orbit Determination
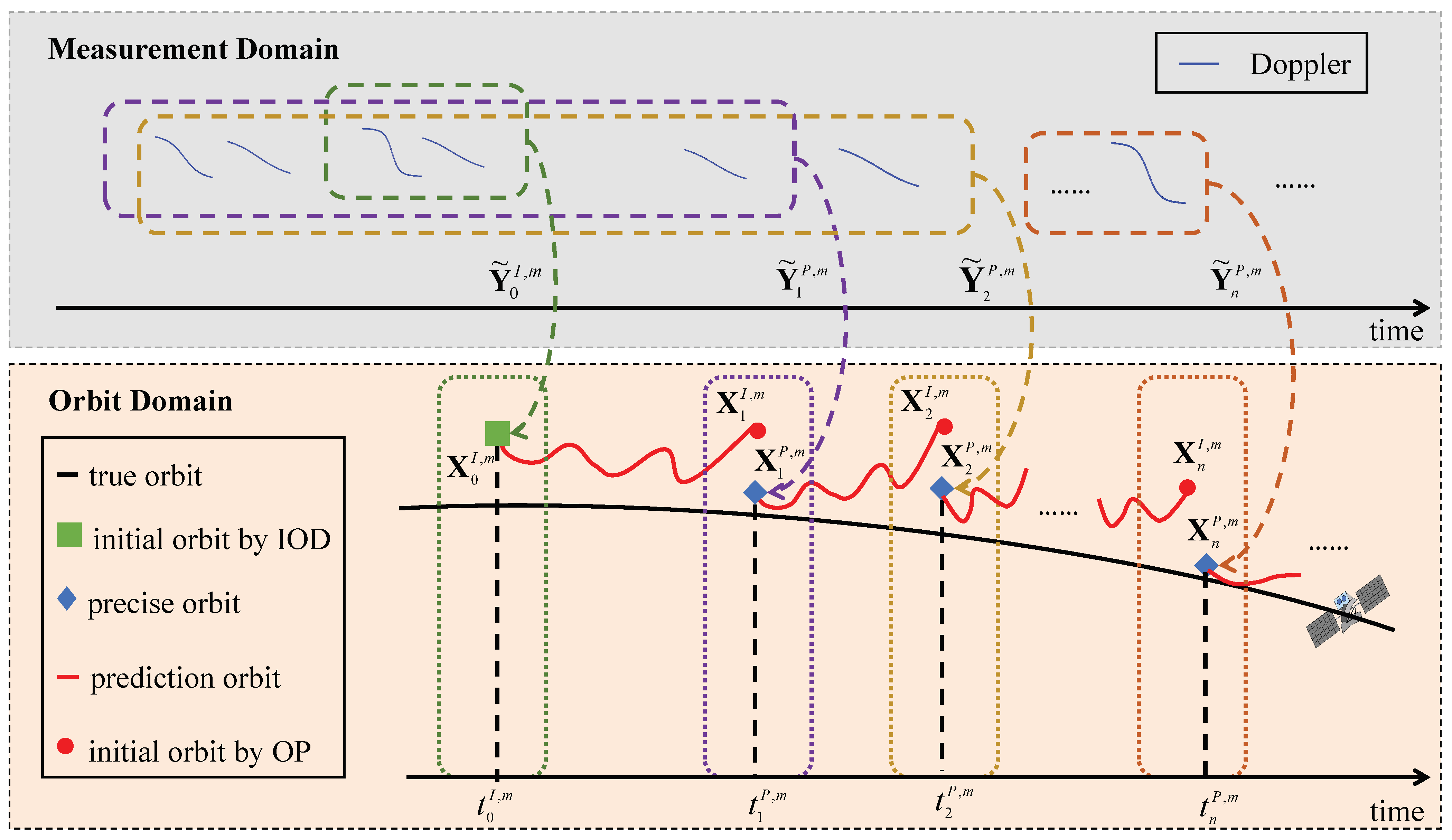
3. Initial Orbit Determination
3.1. Problem Description
3.2. Three-Step Initial Orbit Determination Algorithm
3.2.1. Coarse Orbit Estimation
3.2.2. Data Association
3.2.3. Initial Orbit Estimation
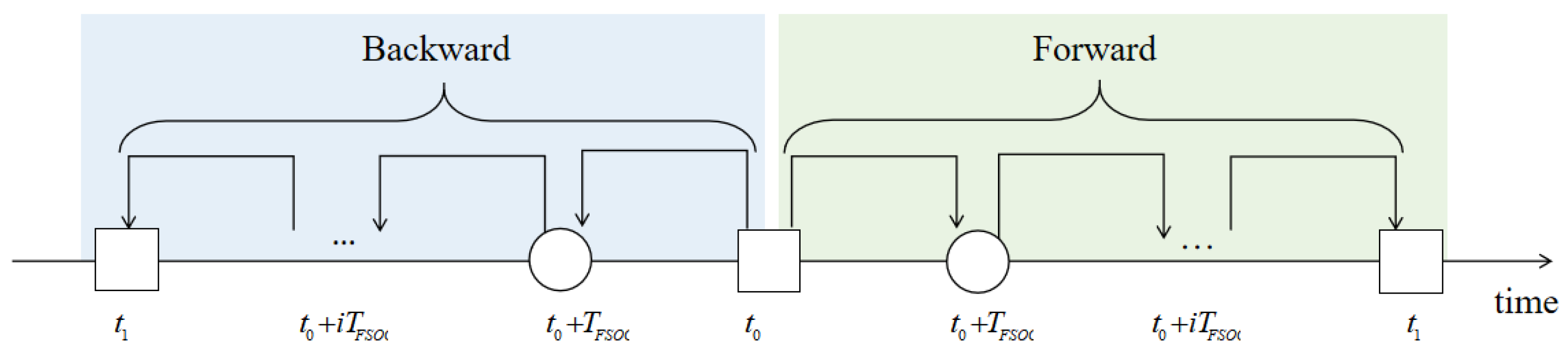
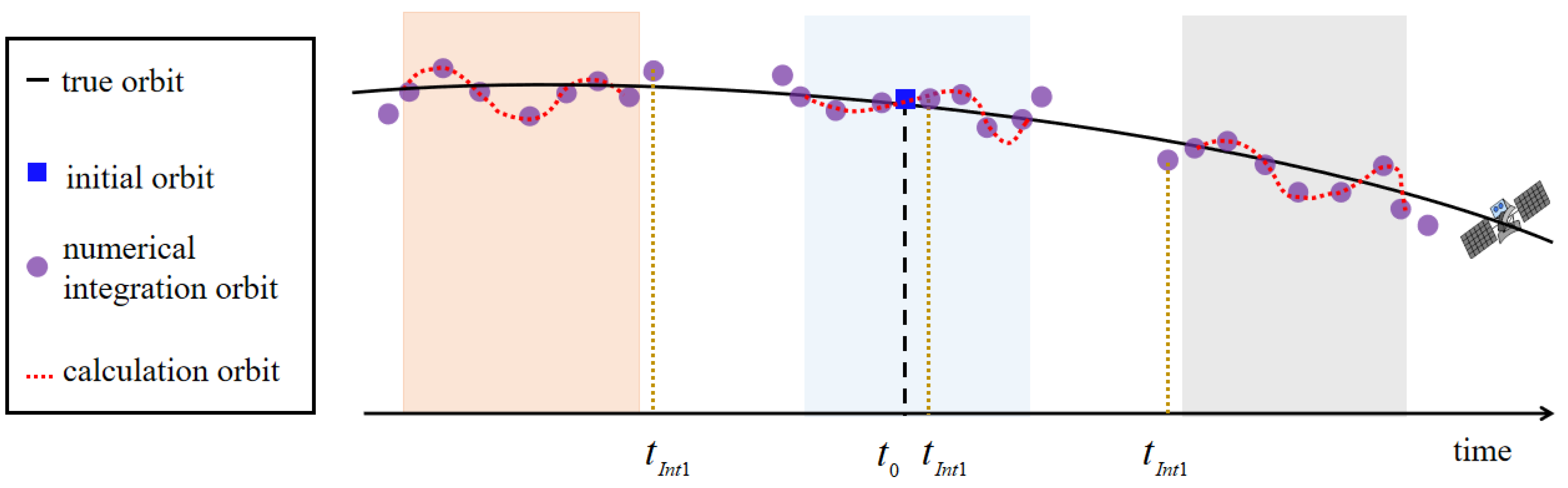
4. Fast Orbit Calculation
4.1. Problem Description
4.2. Fast Single-Orbit Calculation Algorithm
4.3. Fast Multi-Orbit Calculation Algorithm
5. Experimental Results
5.1. Experimental Environment and Basic Settings
5.2. Results and Discussion
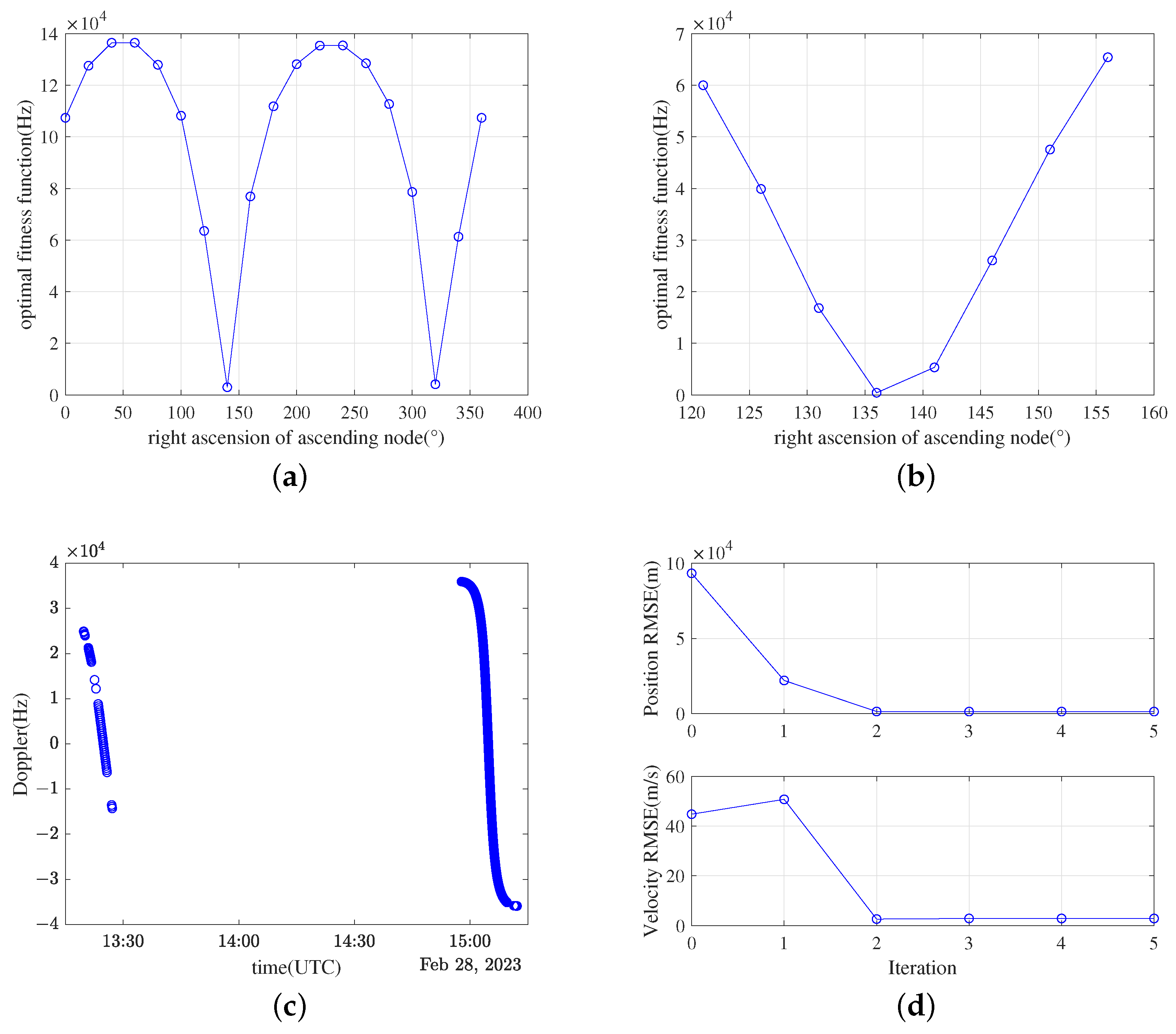
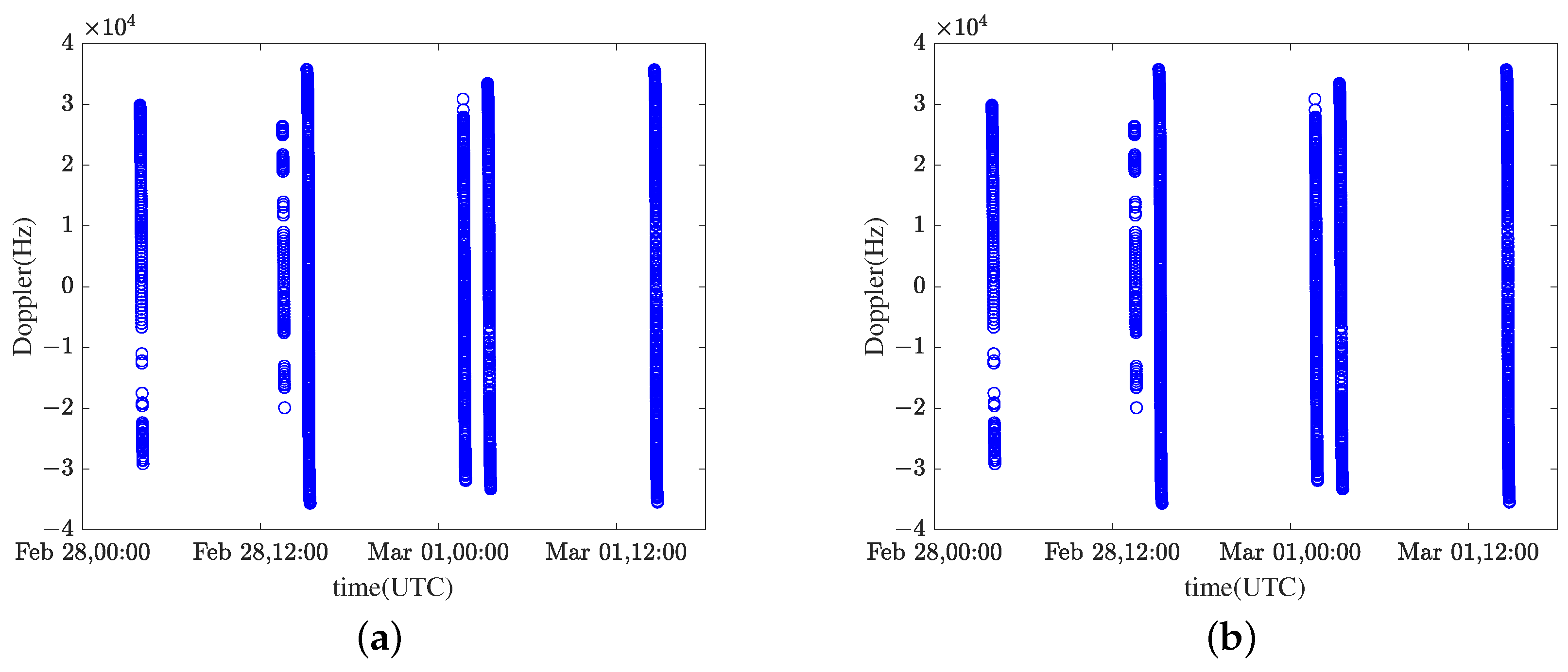
5.2.1. Acquired Doppler Results
5.2.2. Initial Orbit Determination
5.2.3. Orbit Calculation
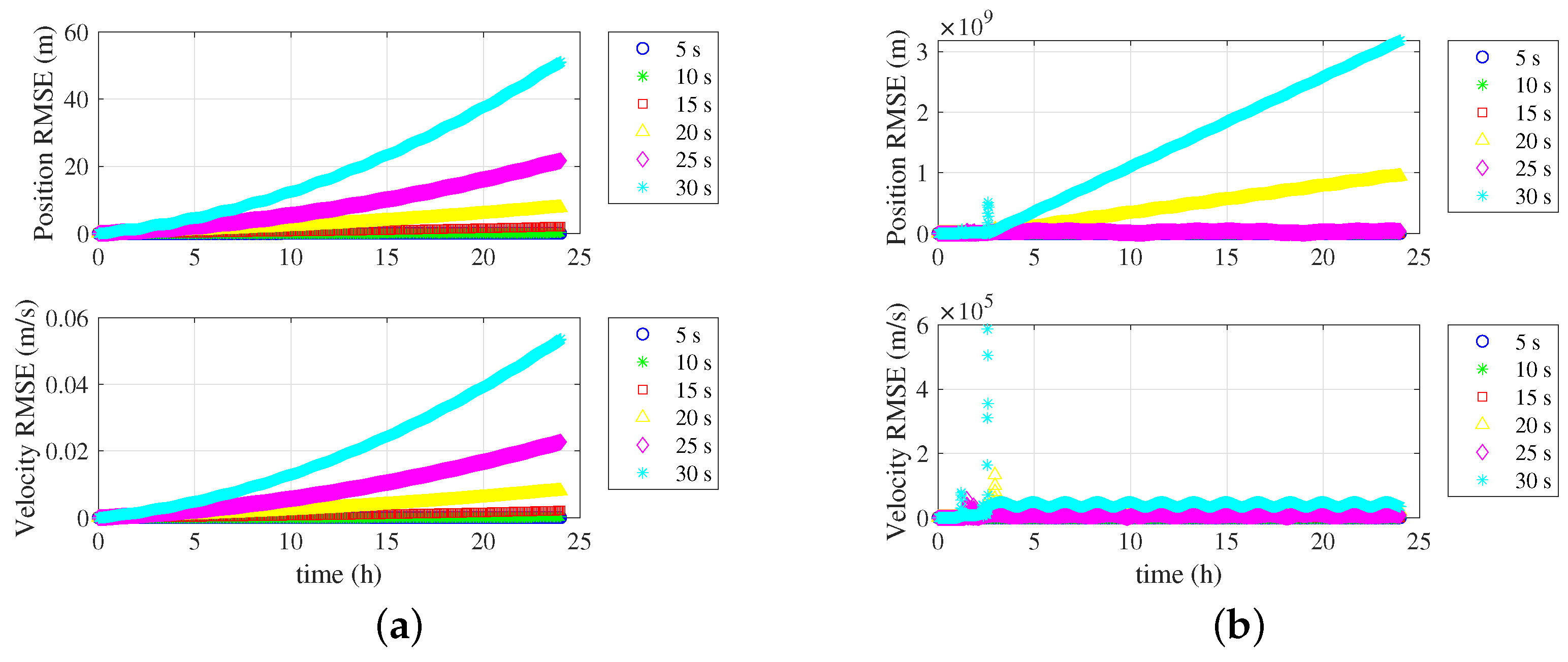
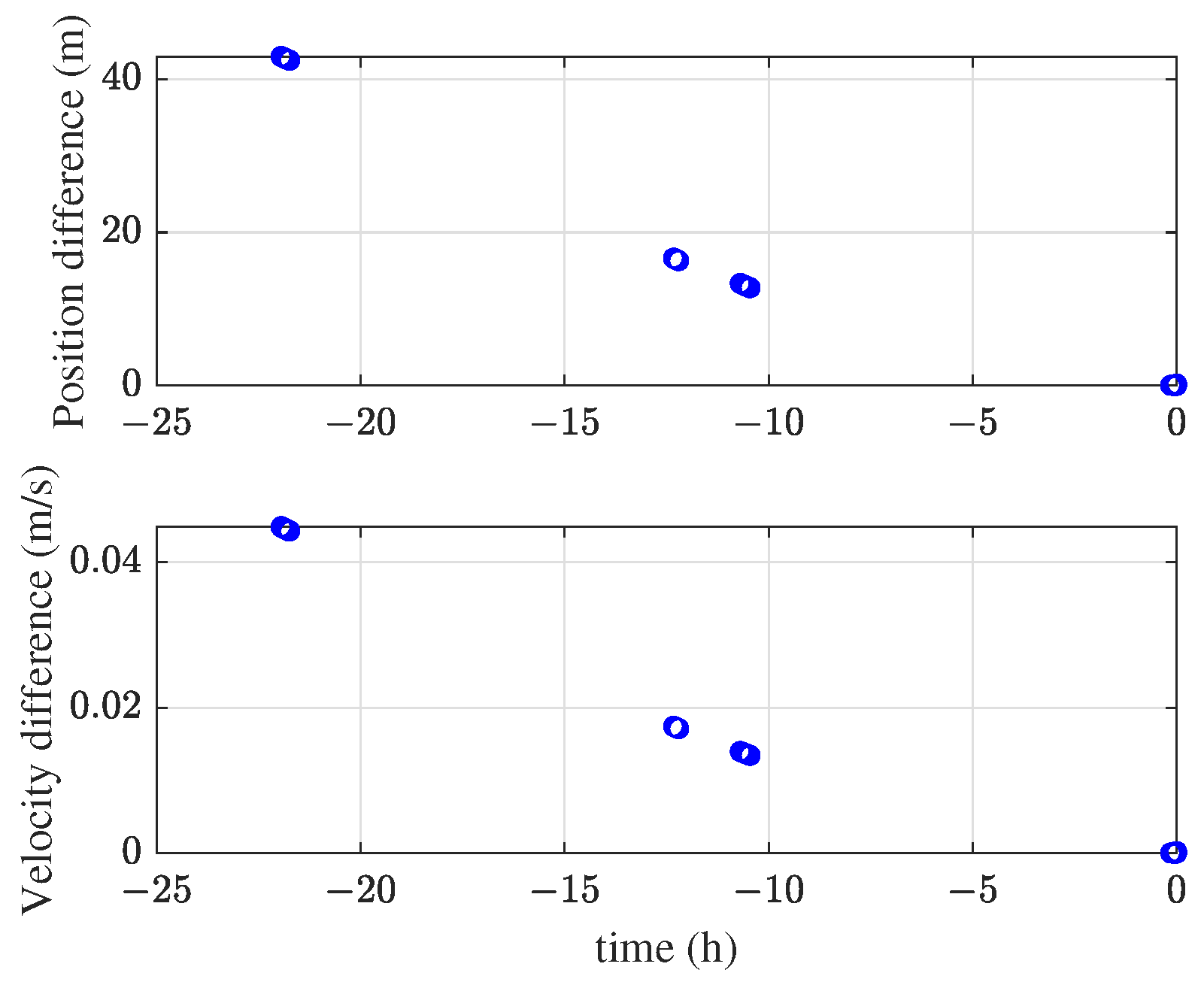
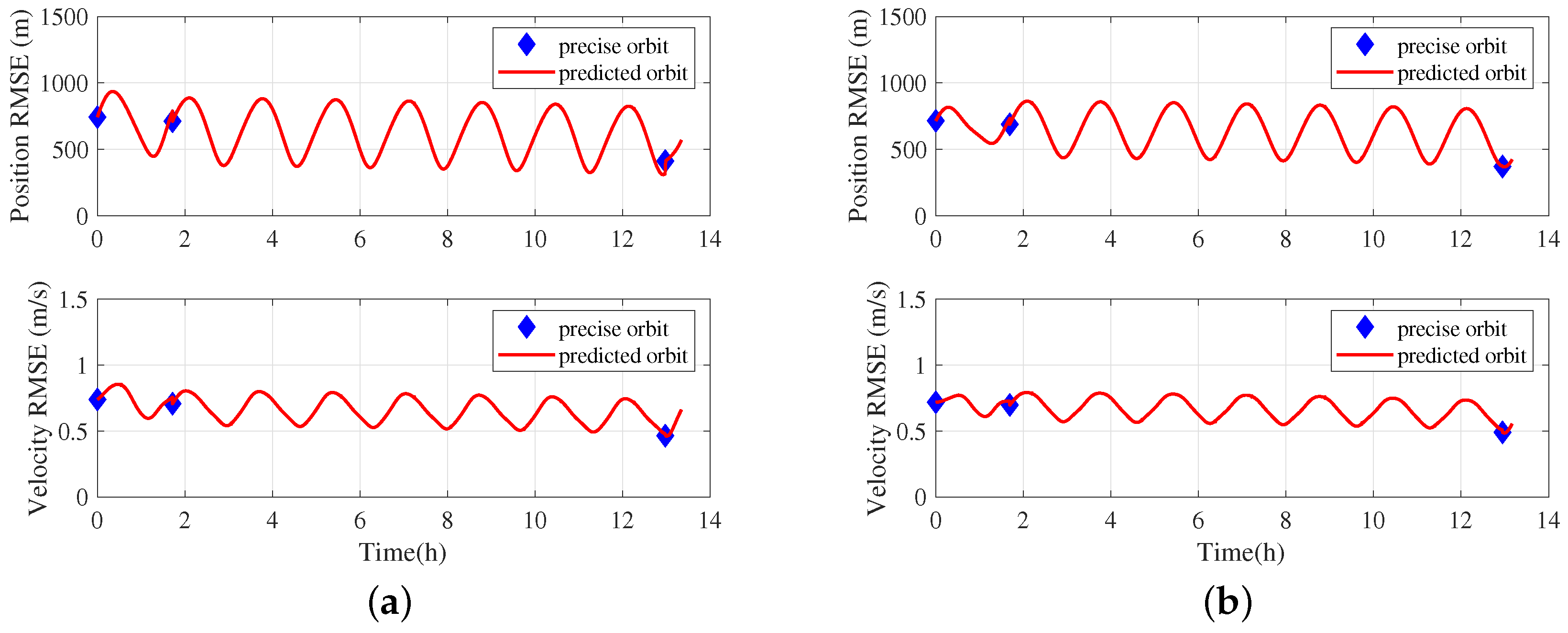
5.2.4. Precise Orbit Determination and Orbit Prediction
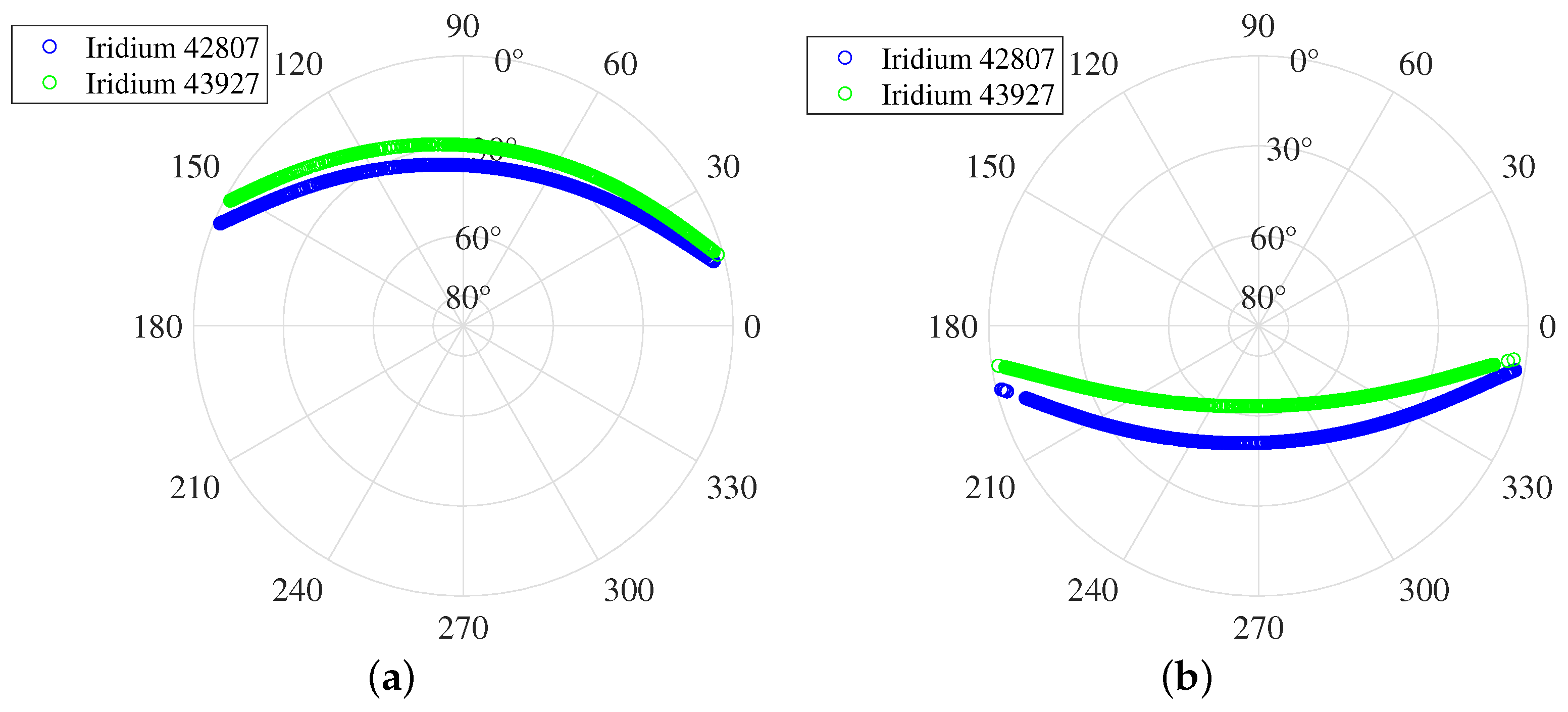
5.2.5. Opportunistic Positioning
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morton, Y.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021; Volume 1, pp. 3–4. [Google Scholar]
- Winter, A.; Morrison, A.; Sokolova, N. Analysis of 5G and LTE Signals for Opportunistic Navigation and Time Holdover. Sensors 2024, 24, 213. [Google Scholar] [CrossRef]
- Zhao, C.; Qin, H.; Li, Z. Doppler measurements from multiconstellations in opportunistic navigation. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Iannucci, P.A.; Humphreys, T.E. Fused low-Earth-orbit GNSS. IEEE Trans. Aerosp. Electron. Syst. 2022, 1. [Google Scholar] [CrossRef]
- Prol, F.S.; Ferre, R.M.; Saleem, Z.; Välisuo, P.; Pinell, C.; Lohan, E.S.; Elsanhoury, M.; Elmusrati, M.; Islam, S.; Çelikbilek, K.; et al. Position, navigation, and timing (PNT) through low earth orbit (LEO) satellites: A survey on current status, challenges, and opportunities. IEEE Access 2022, 10, 83971–84002. [Google Scholar] [CrossRef]
- Khairallah, N.; Kassas, Z.M. Ephemeris closed-loop tracking of LEO satellites with pseudorange and Doppler measurements. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021. [Google Scholar]
- Zhao, C.; Qin, H.; Wu, N.; Wang, D. Analysis of Baseline Impact on Differential Doppler Positioning and Performance Improvement Method for LEO Opportunistic Navigation. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Neinavaie, M.; Khalife, J.; Kassas, Z.M. Acquisition, Doppler tracking, and positioning with Starlink LEO satellites: First results. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2606–2610. [Google Scholar] [CrossRef]
- Lee, B.-S. NORAD TLE conversion from osculating orbital element. Korean Space Sci. Soc. 2002, 19, 395–402. [Google Scholar] [CrossRef]
- Krag, H.; Klinkrad, H.; Alarcon-Rodriguez, J.R. Assessment of orbit uncertainties for collision risk predictions at ESA. In Proceedings of the Second IAASS Conference “Space Safety in a Global World”, Chicago, IL, USA, 14–16 May 2007. [Google Scholar]
- Vallado, D.; Crawford, P. SGP4 orbit determination. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honoluly, HI, USA, 18–21 August 2008. [Google Scholar]
- Wang, R.; Liu, J.; Zhang, Q.M. Propagation errors analysis of TLE data. Adv. Space Res. 2009, 43, 1065–1069. [Google Scholar] [CrossRef]
- Speretta, S.; Sundaramoorthy, P.P.; Gill, E.K.A. Long-term performance analysis of NORAD Two-Line Elements for CubeSats and PocketQubes. In Proceedings of the Small Satellites for Earth Observation, Berlin, Germany, 24–28 April 2017. [Google Scholar]
- Kassas, Z.; Morales, J.; Khalife, J. New-age satellite-based navigation–STAN: Simultaneous tracking and navigation with LEO satellite signals. Inside GNSS Mag. 2019, 14, 56–65. [Google Scholar]
- Mortlock, T.R.; Kassas, Z.M. Performance analysis of simultaneous tracking and navigation with LEO satellite. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), Manassas, VA, USA, 21–25 September 2020. [Google Scholar]
- Kozhaya, S.E.; Haidar-Ahmad, J.A.; Abdallah, A.A.; Kassas, Z.M.; Saab, S.S. Comparison of neural network architectures for simultaneous tracking and navigation with LEO satellites. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021. [Google Scholar]
- Haidar-Ahmad, J.; Khairallah, N.; Kassas, Z.M. A hybrid analytical-machine learning approach for LEO satellite orbit prediction. In Proceedings of the 25th International Conference on Information Fusion (FUSION), Linköping, Sweden, 4–7 July 2022. [Google Scholar]
- Li, B.; Liu, L.; Sang, J.-Z. Tracklet-to-object Matching for Climbing Starlink Satellites through Recursive Orbit Determination and Prediction. Res. Astron. Astrophys. 2022, 22, 115010. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Nishio, M. Orbit determination using radio interferometer of small-diameter antennas for LEO satellites. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2111–2118. [Google Scholar] [CrossRef]
- Deng, R.; Qin, H.; Li, H.; Wang, D.; Lyu, H. Non-cooperative LEO Satellite Orbit Determination Based on Single Pass Doppler Measurements. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1096–1106. [Google Scholar] [CrossRef]
- Patton, R.B. Orbit determination from single pass Doppler observations. IRE Trans. Mil. Electron. 1960, 2, 336–344. [Google Scholar] [CrossRef]
- Li, W.; Yuan, J. Optimal algorithm of orbit tracking and determination by single station dopper radar. J. Astronaut. 2001, 22, 69–73. [Google Scholar]
- Christian, J.; Ertl, C.; Horneman, K.; Lovell, A. Doppler-Only Initial Orbit Determination for an Orbiting Transmitter. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Sakamoto, Y.; Yoneyama, A. Orbit determination system with reasonable performance using low-cost ground station for nanosatellite projects. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2012, 10, 9–14. [Google Scholar] [CrossRef]
- Morales, J.J.; Khalife, J.; Cruz, U.S.; Kassas, Z.M. Orbit Modeling for Simultaneous Tracking and Navigation using LEO Satellite Signals. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Applications; Springer: Berlin, Germany, 2005; pp. 169–190. [Google Scholar]
- Iridium Next Engineering Statement. Available online: https://fcc.report/IBFS/SAT-MOD-20131227-00148/1031348.pdf (accessed on 16 February 2024).
- Ma, Z. Research on Particle Swarm Optimization for High-Dimensionaland Multi-Obiective Optimization Problems. Master’s Thesis, Dalian University of Technology, Dalian, China, 2014. [Google Scholar]
- Song, X.F.; Zhang, Y.; Guo, Y.N.; Sun, X.Y.; Wang, Y.L. Variable-size cooperative coevolutionary particle swarm optimization for feature selection on high-dimensional data. IEEE Trans. Evol. Comput. 2020, 24, 882–895. [Google Scholar] [CrossRef]
- Wu, Z. Autonomous Real-Time Orbit Determination for Low-Earth-Orbit Satellite Using on-Board GPS. Ph.D. Thesis, Beihang University, Beijing, China, 2008. [Google Scholar]
- Zhao, Q. Research on Precision Orbit Determination Theory and Software of both GPS Naviagation Constellation and LEO Satellites. Ph.D. Thesis, Wuhan University, Wuhan, China, 2003. [Google Scholar]
- Shen, X. Adaptive Particle Swarm Optimization Algorithm and Its Applications; Tsinghua University Press: Beijing, China, 2015. [Google Scholar]
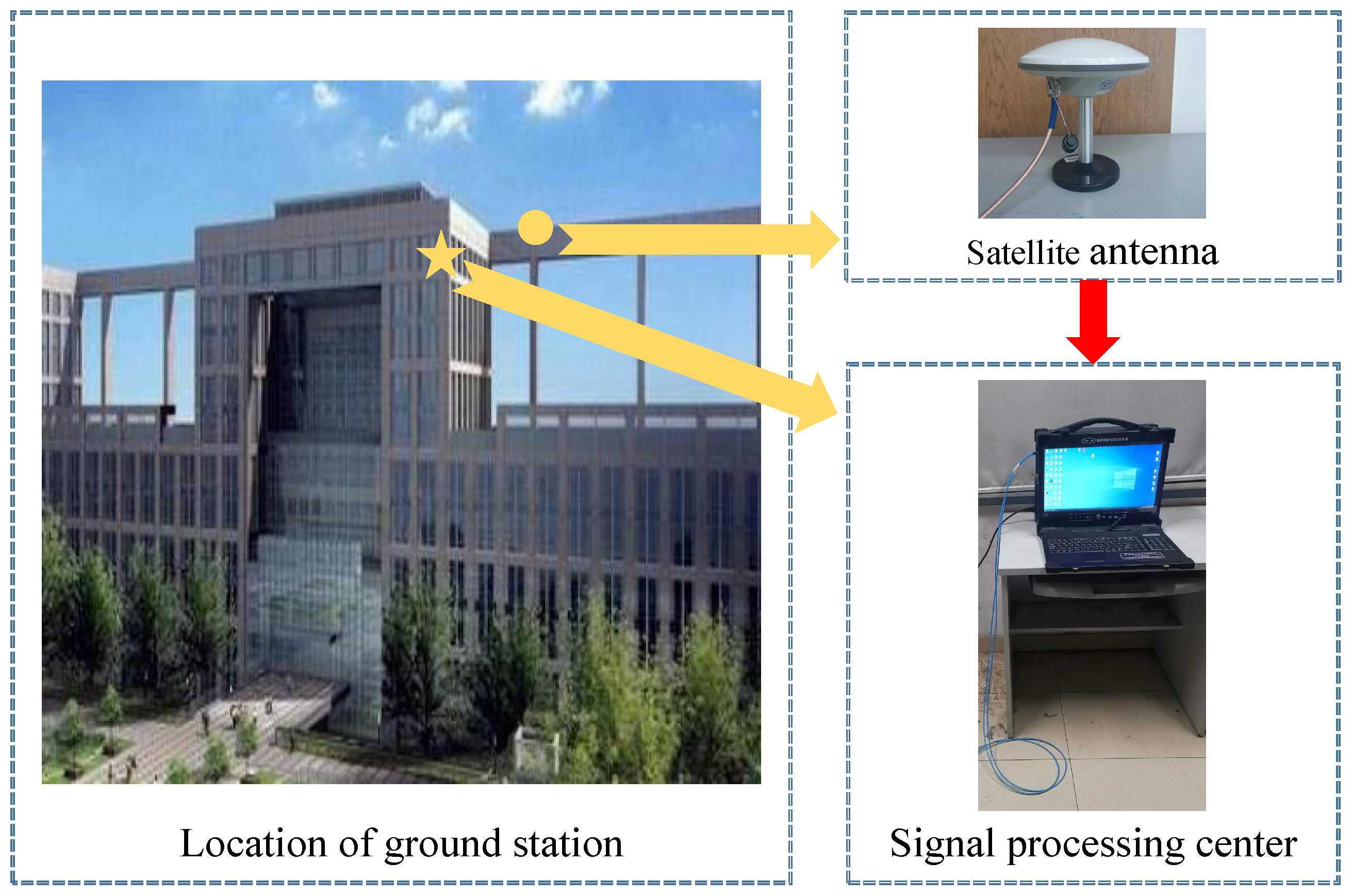
| Operation | Start Time (UTC) | End Time (UTC) |
|---|---|---|
| Observation | 28 February 2023, 03:40 | 1 March 2023, 14:09 |
| IOD | 28 February 2023, 03:40 | 28 February 2023, 15:22 |
| POD-OP | 1 March 2023, 01:39 | 1 March 2023, 15:00 |
| The first position | 1 March 2023, 03:09 | 1 March 2023, 03:31 |
| The second position | 1 March 2023, 14:24 | 1 March 2023, 14:46 |
| Experiment Number | Positioning RMSE Using TLE (m) | Positioning RMSE Using Precise Orbit (m) |
|---|---|---|
| 1 | 441 | 100 |
| 2 | 191 | 149 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, R.; Qin, H.; Zhang, Y. Non-Cooperative LEO Satellite Orbit Determination Using Single Station for Space-Based Opportunistic Positioning. Remote Sens. 2024, 16, 912. https://doi.org/10.3390/rs16050912
Deng R, Qin H, Zhang Y. Non-Cooperative LEO Satellite Orbit Determination Using Single Station for Space-Based Opportunistic Positioning. Remote Sensing. 2024; 16(5):912. https://doi.org/10.3390/rs16050912
Chicago/Turabian StyleDeng, Ruofan, Honglei Qin, and Yu Zhang. 2024. "Non-Cooperative LEO Satellite Orbit Determination Using Single Station for Space-Based Opportunistic Positioning" Remote Sensing 16, no. 5: 912. https://doi.org/10.3390/rs16050912
APA StyleDeng, R., Qin, H., & Zhang, Y. (2024). Non-Cooperative LEO Satellite Orbit Determination Using Single Station for Space-Based Opportunistic Positioning. Remote Sensing, 16(5), 912. https://doi.org/10.3390/rs16050912





