A Novel SV-PRI Strategy and Signal Processing Approach for High-Squint Spotlight SAR
Abstract
1. Introduction
2. SV-PRI Sequences for High-Squint Spotlight SAR
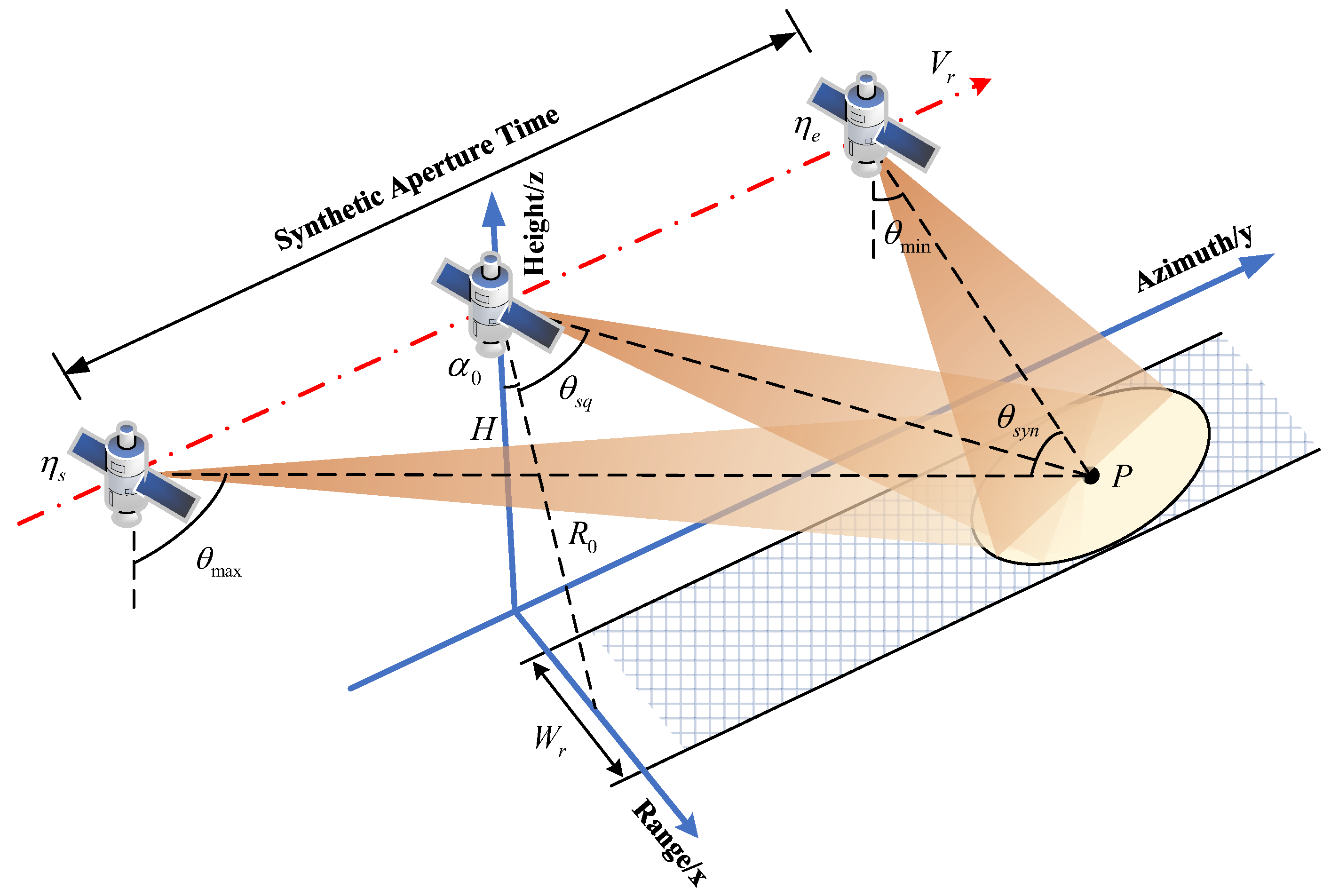
2.1. Acquisition Geometry
2.2. Design of the SV-PRI Sequence
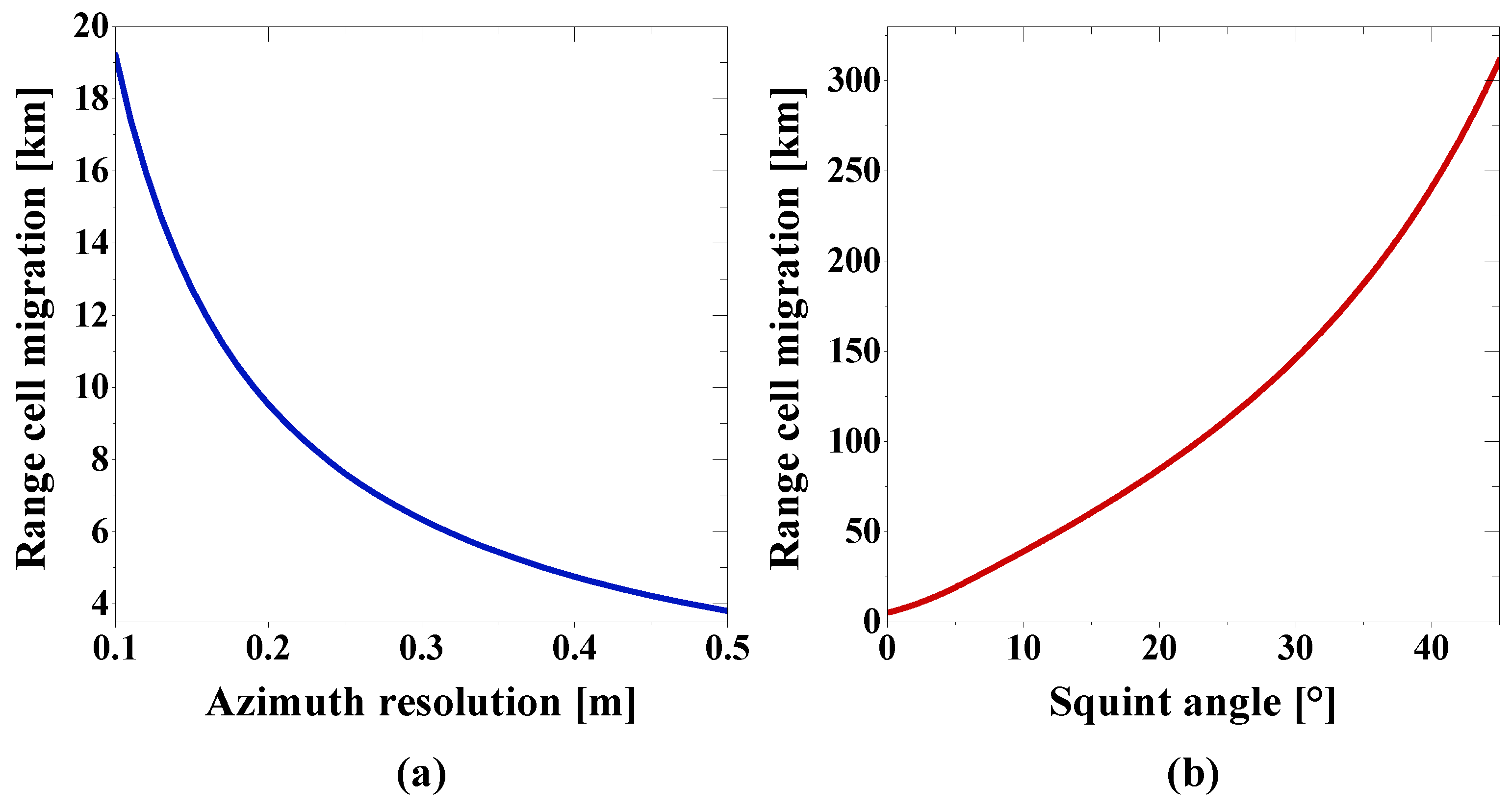
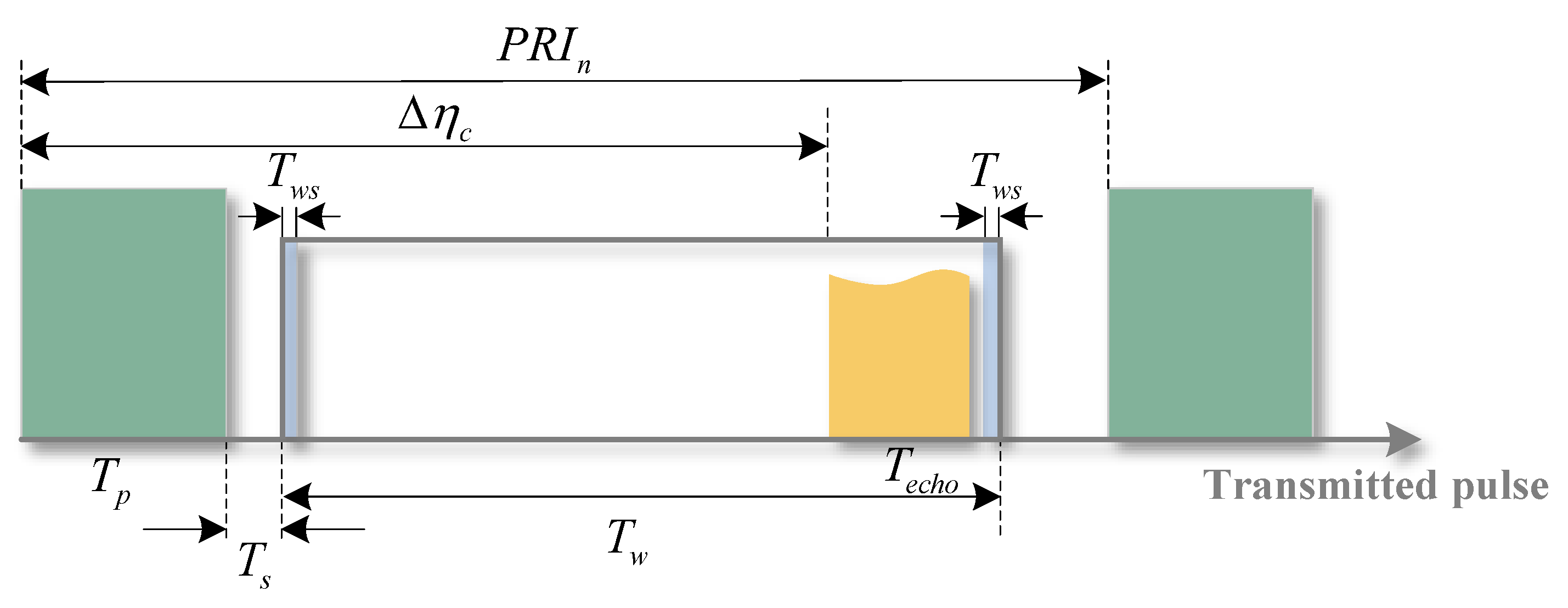
2.3. Analysis of Echo Data Loss
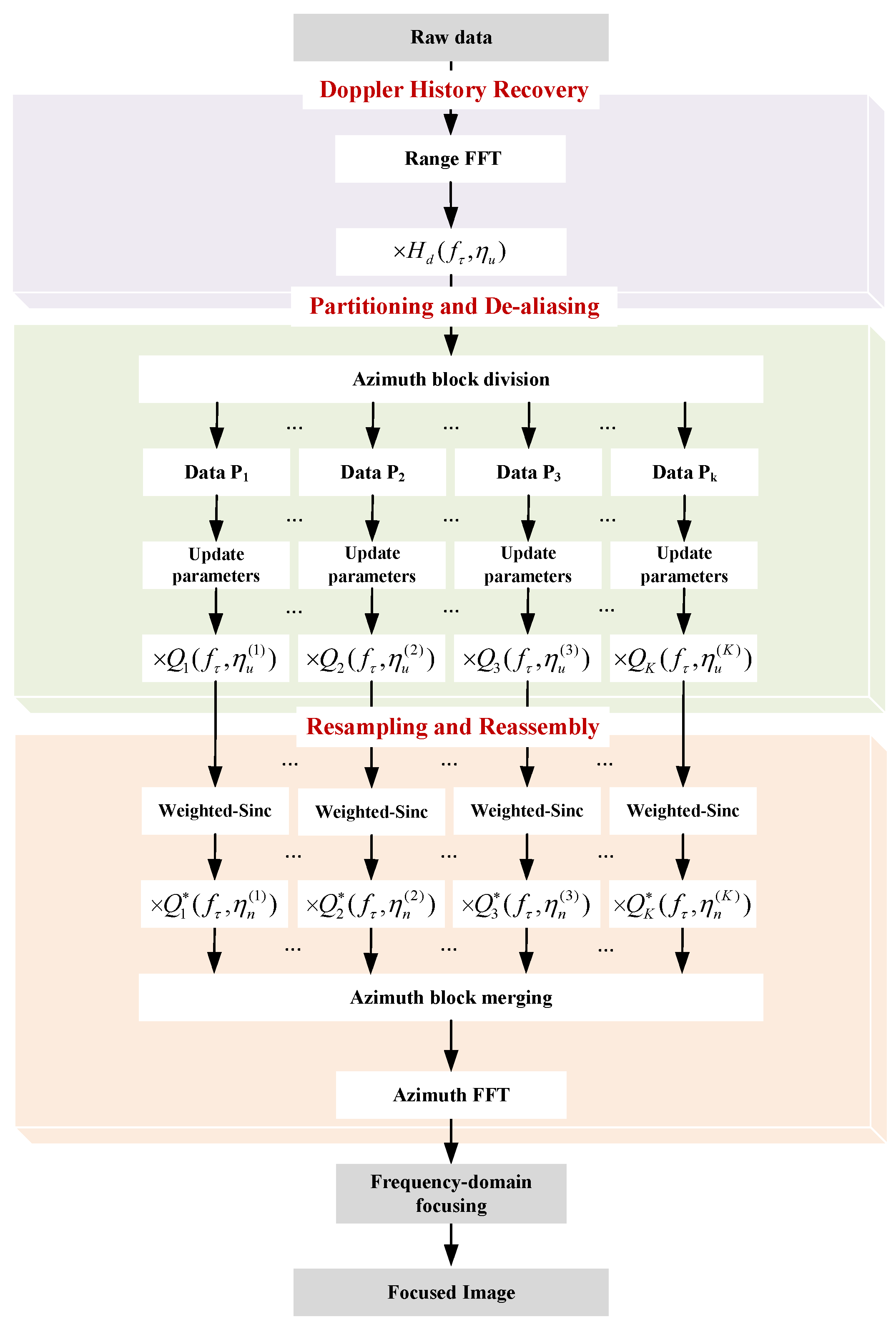
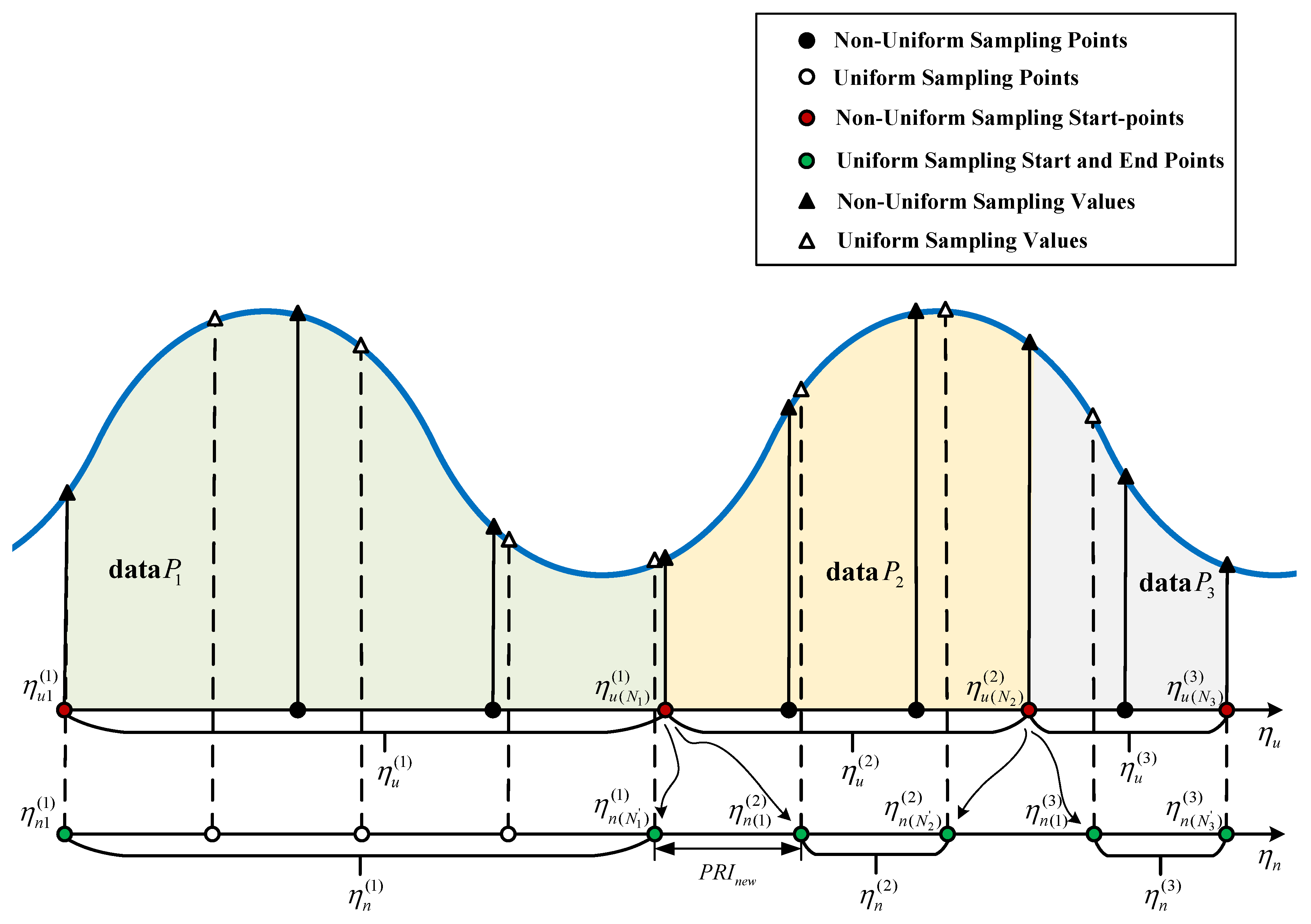
3. Processing of Non-Uniformly Sampled Data
3.1. Doppler History Recovery
3.2. TPR-Based Azimuth Partitioning and De-Aliasing
3.3. Azimuth Resampling and Reassembly
4. Simulation Results
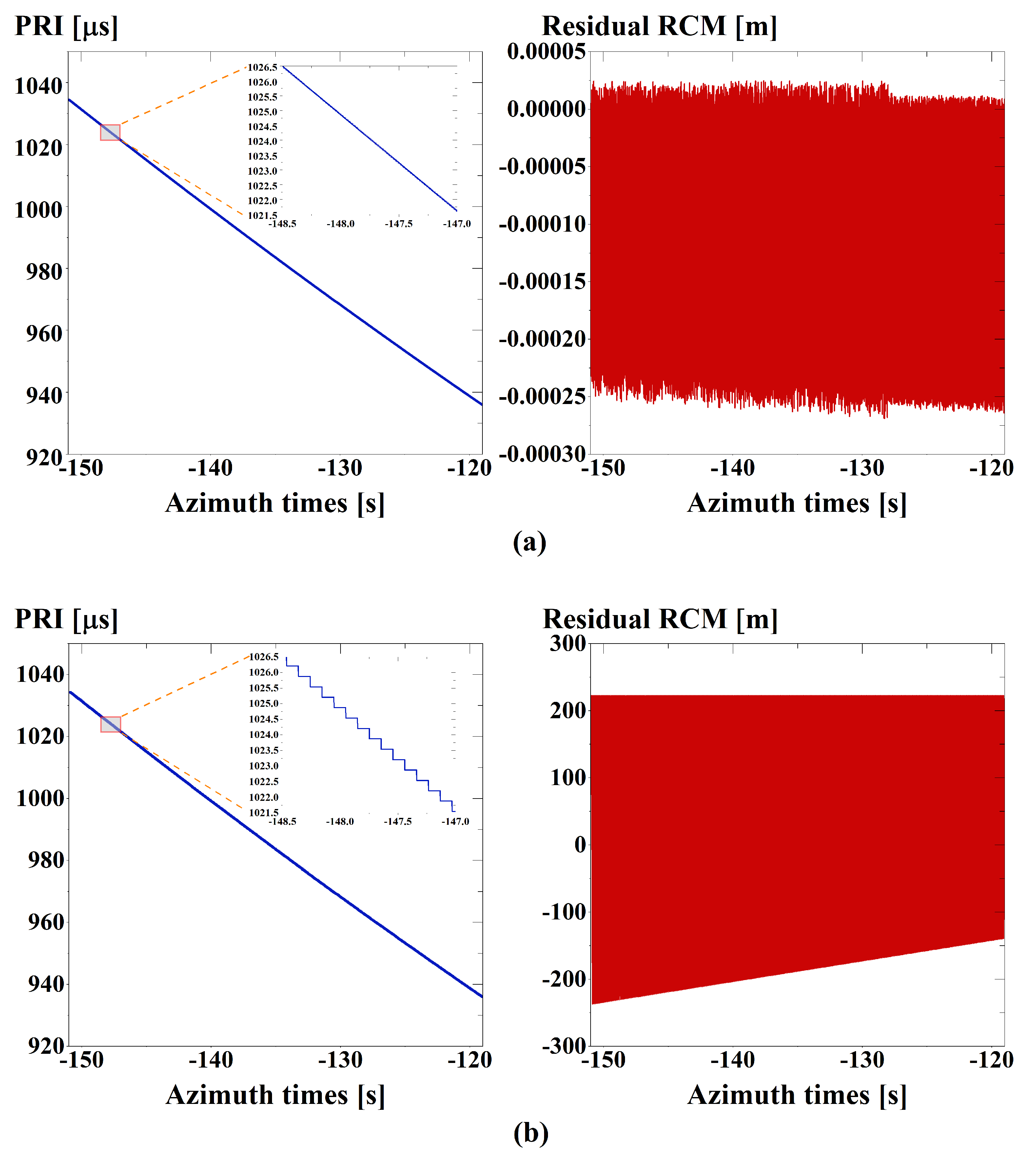
4.1. Performance Analysis of the SV-PRI Sequence
4.1.1. Granularity Factor and Residual RCM
4.1.2. Resampling Relative Error
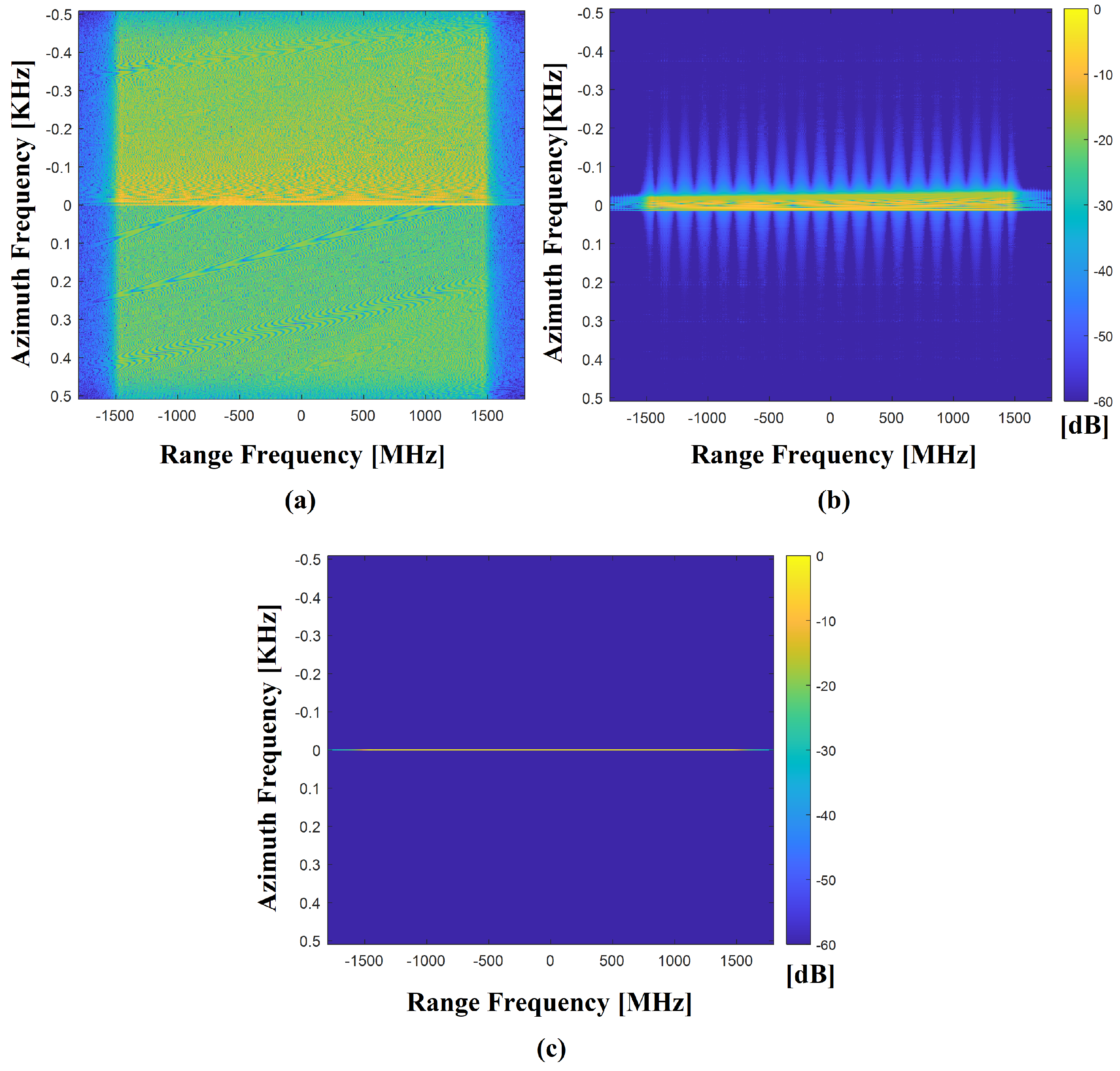
4.2. Analysis of Uniform Signal Reconstruction Processing
4.3. Focusing Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. Papathanassiou A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Jakowatz, C.V.; Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Thompson, P.A. Spotlight-Mode Synthetic Aperture Radar: A Signal Processing Approach, 1st ed.; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Boerner, E.; Lord, R.; Mittermayer, J.; Bamler, R. Evaluation of TerraSAR-X spotlight processing accuracy based on a new spotlight raw data simulator. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 2, pp. 1323–1325. [Google Scholar] [CrossRef]
- Reigber, A.; Scheiber, R.; Jager, M.; Prats-Iraola, P.; Hajnsek, I.; Jagdhuber, T.; Papathanassiou, K.P.; Nannini, M.; Aguilera, E.; Baumgartner, S.; et al. Very-high-resolution airborne synthetic aperture radar imaging: Signal processing and applications. Proc. IEEE 2012, 101, 759–783. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Scheiber, R.; Rodriguez-Cassola, M.; Mittermayer, J.; Wollstadt, S.; de Zen, F.; Bräutigam, B.; Schwerdt, M.; Reigber, A.; Moreira, A. On the processing of very high resolution spaceborne SAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6003–6016. [Google Scholar] [CrossRef]
- de Almeida, F.Q.; Younis, M.; Prats-Iraola, P.; Rodriguez-Cassola, M.; Krieger, G.; Moreira, A. Slow Pulse Repetition Interval Variation for High-Resolution Wide-Swath SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5665–5686. [Google Scholar] [CrossRef]
- Dong, B.; Li, G.; Zhang, Q. High-Resolution and Wide-Swath Imaging of Spaceborne SAR via Random PRF Variation Constrained by the Coverage Diagram. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5241016. [Google Scholar] [CrossRef]
- Wang, P.; Liu, W.; Chen, J.; Niu, M.; Yang, W. A High-Order Imaging Algorithm for High-Resolution Spaceborne SAR Based on a Modified Equivalent Squint Range Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1225–1235. [Google Scholar] [CrossRef]
- Zhu, D.; Xiang, T.; Wei, W.; Ren, Z.; Yang, M.; Zhang, Y.; Zhu, Z. An Extended Two Step Approach to High-Resolution Airborne and Spaceborne SAR Full-Aperture Processing. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8382–8397. [Google Scholar] [CrossRef]
- Sun, X.; Yeo, T.S.; Zhang, C.; Lu, Y.; Kooi, P.S. Time-varying step-transform algorithm for high squint SAR imaging. IEEE Trans. Geosci. Remote Sens. 1999, 6, 2668–2677. [Google Scholar] [CrossRef]
- Davidson, G.W.; Cumming, I. Signal properties of spaceborne squint-mode SAR. IEEE Trans. Geosci. Remote Sens. 1997, 3, 611–617. [Google Scholar] [CrossRef]
- Zeng, H.C.; Chen, J.; Liu, W.; Yang, W. Modified Omega-k algorithm for high-speed platform highly-squint staggered SAR based on azimuth non-uniform interpolation. Sensors 2015, 15, 3750–3765. [Google Scholar] [CrossRef] [PubMed]
- An, D.; Huang, X.; Jin, T.; Zhou, Z. Extended two-step focusing approach for squinted spotlight SAR imaging. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2889–2900. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, M.; Li, J.; Wei, P. Modified Range-Doppler Algorithm for High Squint SAR Echo Processing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 422–426. [Google Scholar] [CrossRef]
- Zeng, L.; Liang, Y.; Xing, M.; Li, Z. A Novel Motion Compensation Approach for Airborne Spotlight SAR of High-Resolution and High-Squint Mode. IEEE Geosci. Remote Sens. Lett. 2016, 13, 429–433. [Google Scholar] [CrossRef]
- Xuying, X.; Gen, L.; Yanheng, M.; Lina, C. New slant range model and azimuth perturbation resampling based high-squint maneuvering platform SAR imaging. J. Syst. Eng. Electron. 2021, 32, 545–558. [Google Scholar] [CrossRef]
- Ding, Z.; Zheng, P.; Li, H.; Zhang, T.; Li, Z. Spaceborne High-Squint High-Resolution SAR Imaging Based on Two-Dimensional Spatial-Variant Range Cell Migration Correction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5240114. [Google Scholar] [CrossRef]
- Chen, X.; Sun, G.-C.; Xing, M.; Li, B.; Yang, J.; Bao, Z. Ground Cartesian Back-Projection Algorithm for High Squint Diving TOPS SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5812–5827. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Z.; Li, C. Effects of PRF variation on spaceborne SAR imaging. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, VC, Australia, 21–26 July 2013; pp. 1336–1339. [Google Scholar] [CrossRef]
- Xu, H.; Gao, J.; Li, J. A variable PRF imaging method for high squint diving SAR. Prog. Electromagn. Res. 2013, 135, 215–229. [Google Scholar] [CrossRef]
- Yin, W.; Ding, Z.; Yang, S.; Li, Y.; Zeng, T.; Long, T. A continuous PRI variation method for geosynchronous SAR with elliptical orbit. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4582–4585. [Google Scholar] [CrossRef]
- Luo, X.; Xu, W.; Han, L. The Application of Staggered PRF Technology in Slant-Focus SAR. J. Radars 2015, 4, 70–77. [Google Scholar]
- Wang, Y.; Li, J.; Yang, J.; Sun, B. A novel spaceborne sliding spotlight range sweep synthetic aperture radar: System and imaging. Remote Sens. 2017, 9, 783. [Google Scholar] [CrossRef]
- Wang, P.; Xu, W.; Li, N.; Dong, W. Research on spaceborne high squint spotlight SAR imaging technology with variable PRI. J. Electron. Inf. Technol. 2018, 40, 2470–2477. [Google Scholar]
- Zou, H.; Zhao, F.; Jia, X.; Wang, W.; Zhang, H. Continuous pulse repetition interval variation for highly squint high-resolution spotlight SAR imaging. Remote Sens. Lett. 2021, 12, 209–218. [Google Scholar] [CrossRef]
- Zhou, Z.X.; Deng, Y.; Wang, W.; Jia, X.; Wang, R. Analysis of Varying-PRI Spotlight SAR Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5221020. [Google Scholar] [CrossRef]
- Meng, D.; Ding, C.; Hu, D.; Qiu, X.; Huang, L.; Han, B.; Liu, J.; Xu, N. On the processing of very high resolution spaceborne SAR data: A chirp-modulated back projection approach. IEEE Trans. Geosci. Remote Sens. 2017, 56, 191–201. [Google Scholar] [CrossRef]
- Chen, S.; Huang, L.; Yu, L. An Improved Sinc Interpolation-Based Staggered PRF Sampling for Beamforming SAR Imaging. J. Radars 2019, 8, 527–536. [Google Scholar]
- Zhang, Z.; Xu, W.; Huang, P.; Tan, W.; Qi, Y. Azimuth Preprocessing of Squinted Sliding Spotlight Synthetic Aperture Radar Data with Block Varying PRF. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium, Hangzhou, China, 21–25 November 2021. [Google Scholar]
- Villano, M.; Krieger, G.; Jäger, M.; Moreira, A. Staggered SAR: Performance analysis and experiments with real data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6617–6638. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Orbit height | 1000 km |
| Antenna length | 12 m |
| Carrier frequency | 9.6 GHz |
| Pulse bandwidth | 3 GHz |
| Off-nadir angle | 30° |
| Squint angle | 40° |
| Cross-range resolution | 0.1 m |
| Initialized PRF | 1018.1 Hz |
| Types of PRI | Resampling Error (dB) |
|---|---|
| CV-PRI in [24] | −33.73 |
| CV-PRI in [25] | −32.96 |
| SV-PRI ( = 1) | −42.77 |
| SV-PRI ( = 2) | −35.01 |
| SV-PRI ( = 5) | −34.98 |
| SV-PRI ( = 10) | −35.03 |
| Method of Uniform Reconstruction | Resampling Error (dB) | |
|---|---|---|
| = 1 | = 10 | |
| Method in [9] | 2.97 | 2.98 |
| Method in [29] | −42.76 | −34.33 |
| Proposed method | −42.77 | −35.03 |
| PSLR (dB) | ISLR (dB) | IRW | |
|---|---|---|---|
| Uniformly sampling | −13.2546 | −10.0466 | 0.8696 |
| Proposed method | −13.2549 | −10.0468 | 0.8696 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Wang, W.; Wu, X.; Deng, Y.; Xiao, D. A Novel SV-PRI Strategy and Signal Processing Approach for High-Squint Spotlight SAR. Remote Sens. 2024, 16, 871. https://doi.org/10.3390/rs16050871
Hu Y, Wang W, Wu X, Deng Y, Xiao D. A Novel SV-PRI Strategy and Signal Processing Approach for High-Squint Spotlight SAR. Remote Sensing. 2024; 16(5):871. https://doi.org/10.3390/rs16050871
Chicago/Turabian StyleHu, Yuzhi, Wei Wang, Xiayi Wu, Yunkai Deng, and Dengjun Xiao. 2024. "A Novel SV-PRI Strategy and Signal Processing Approach for High-Squint Spotlight SAR" Remote Sensing 16, no. 5: 871. https://doi.org/10.3390/rs16050871
APA StyleHu, Y., Wang, W., Wu, X., Deng, Y., & Xiao, D. (2024). A Novel SV-PRI Strategy and Signal Processing Approach for High-Squint Spotlight SAR. Remote Sensing, 16(5), 871. https://doi.org/10.3390/rs16050871







