Estimating Winter Arctic Sea Ice Motion Based on Random Forest Models
Abstract
1. Introduction
2. Data
2.1. Target and Input Variables for the RF Model
2.1.1. The Target Variable
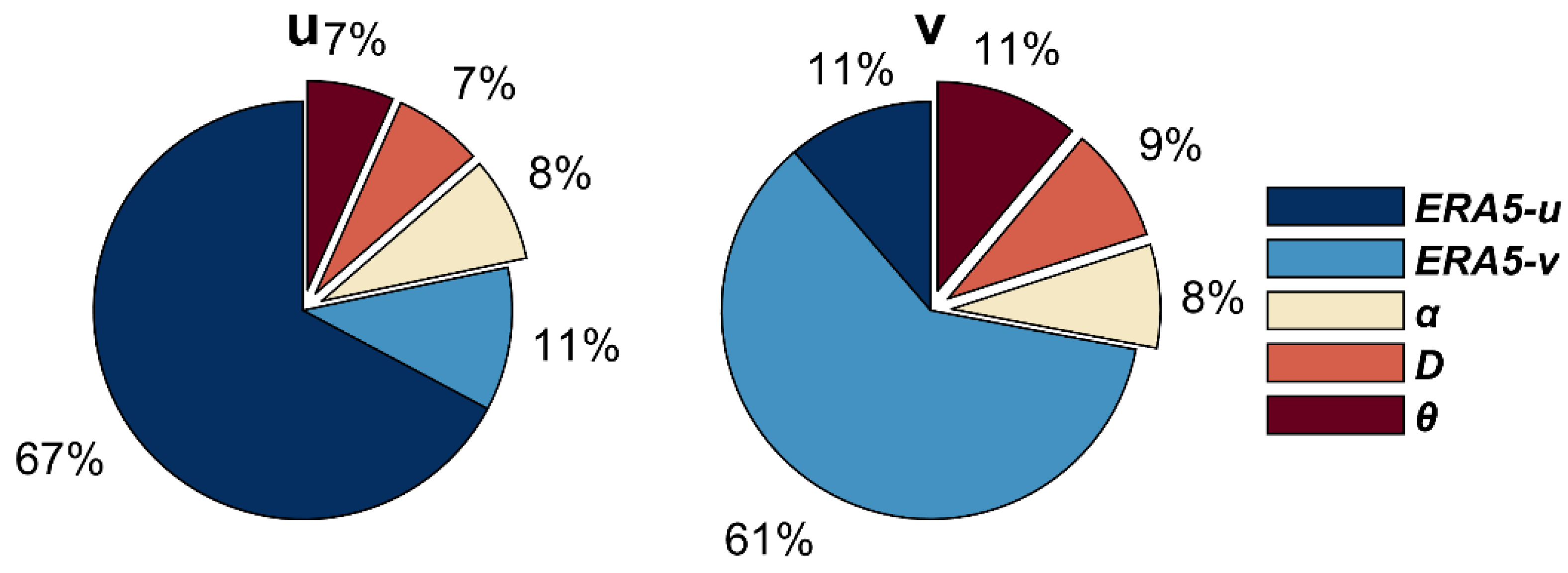
2.1.2. Input Variables
2.2. Comparison Datasets
3. Methods
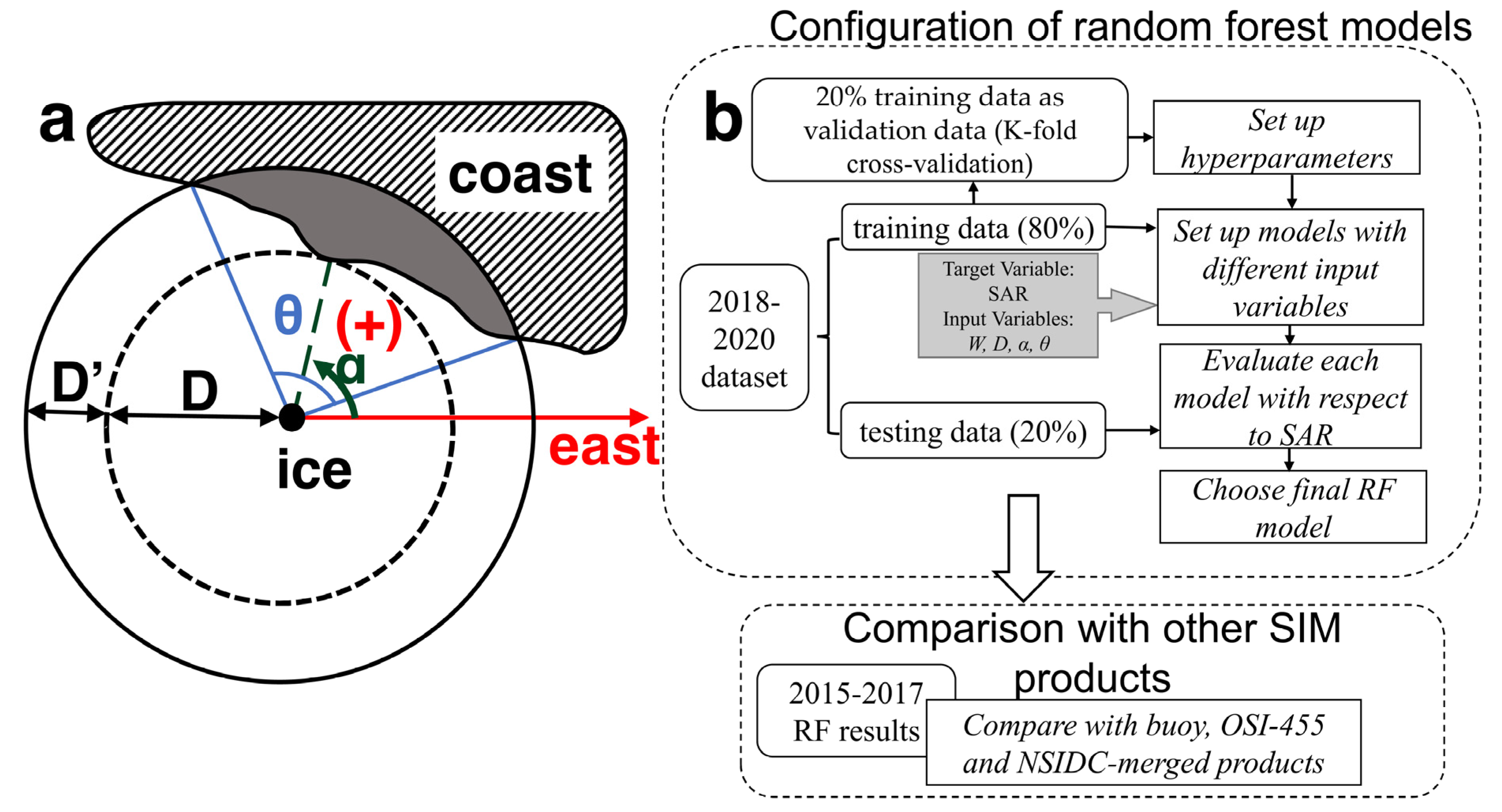
3.1. Configuration of Random Forest Models
3.2. Constructing Training DatasetDatasets
3.3. Method of Evaluation
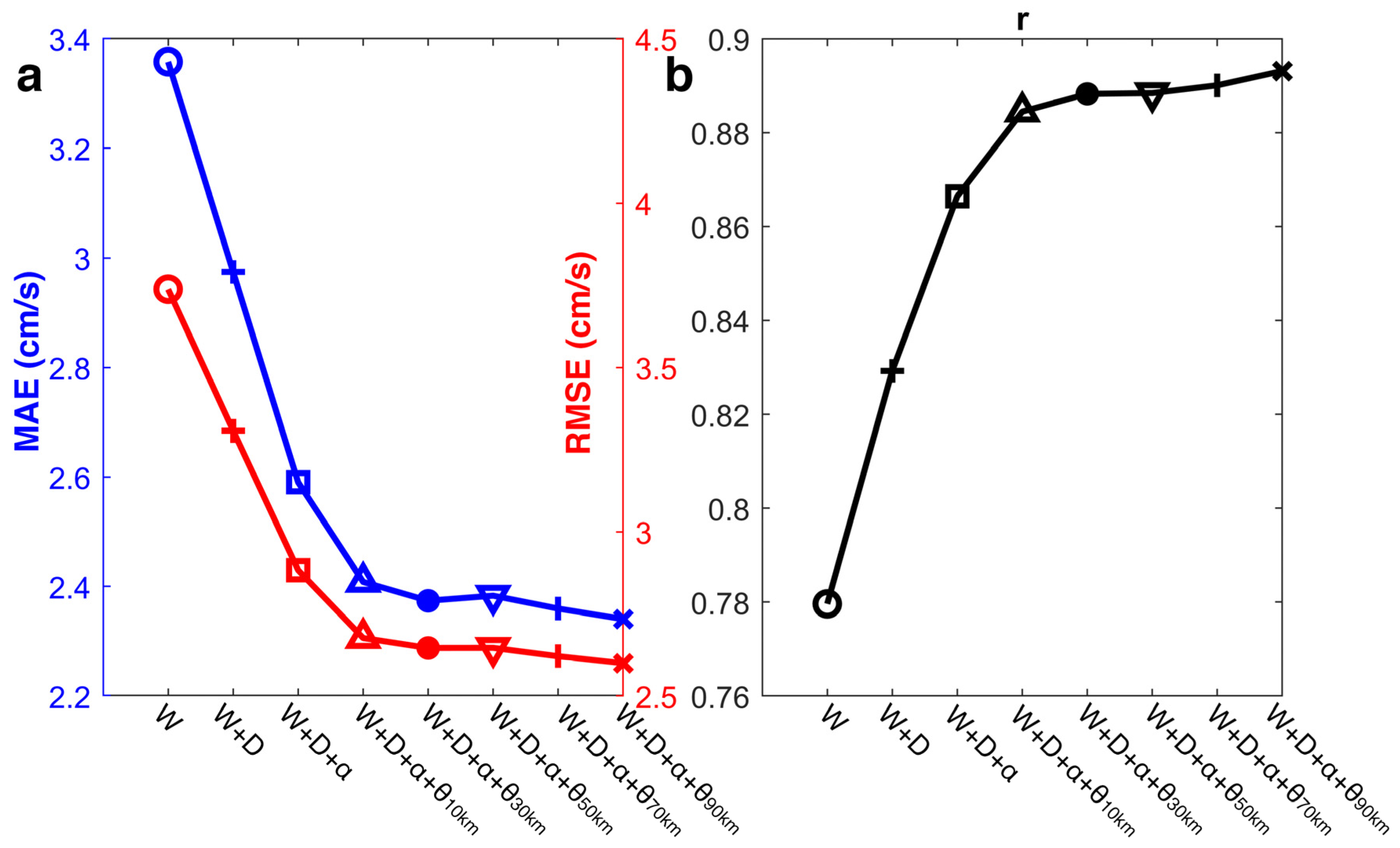
3.4. Sensitivity Experiments of Hyperparameters and Setting up Input Variables
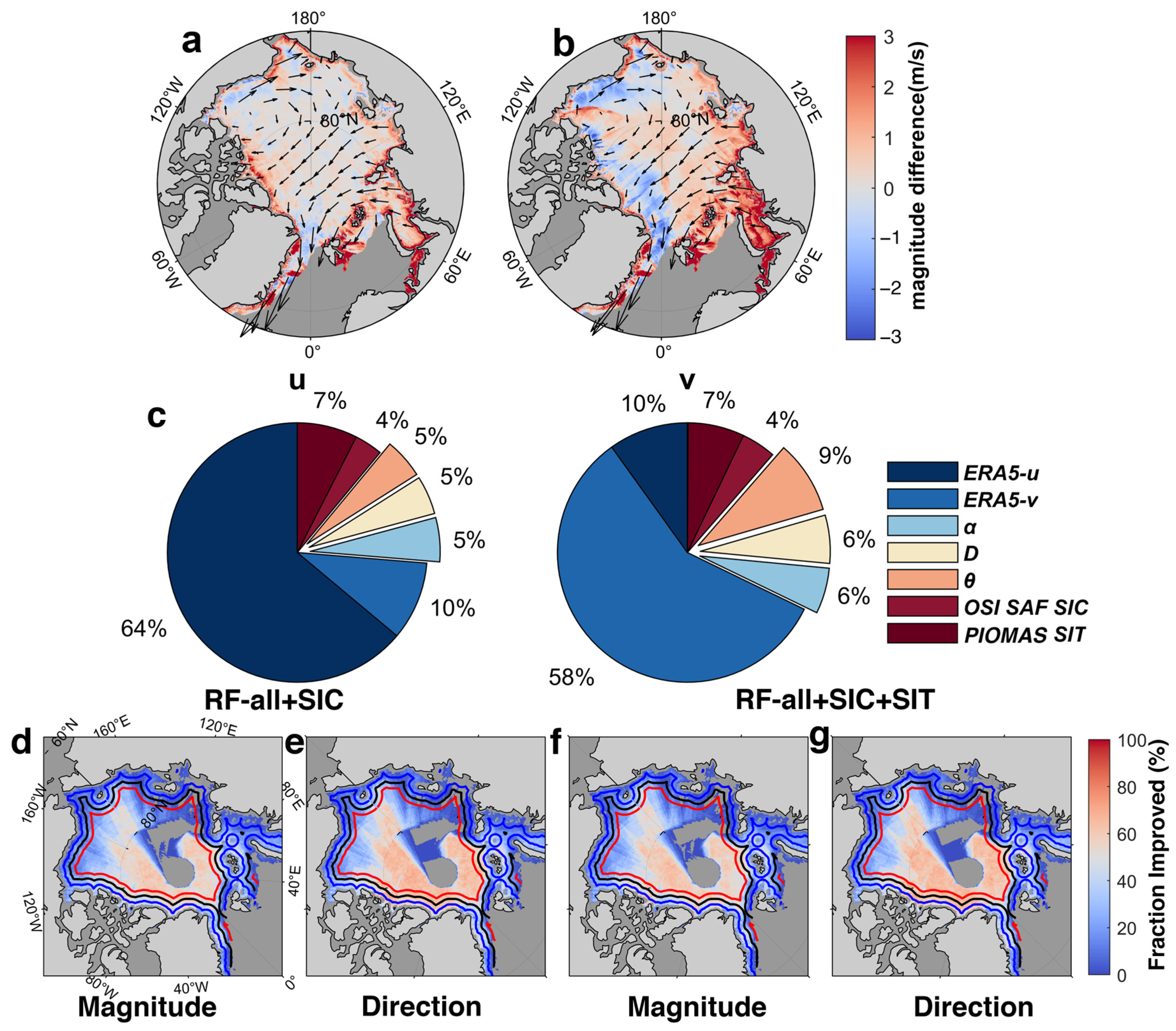
4. Results and Analysis
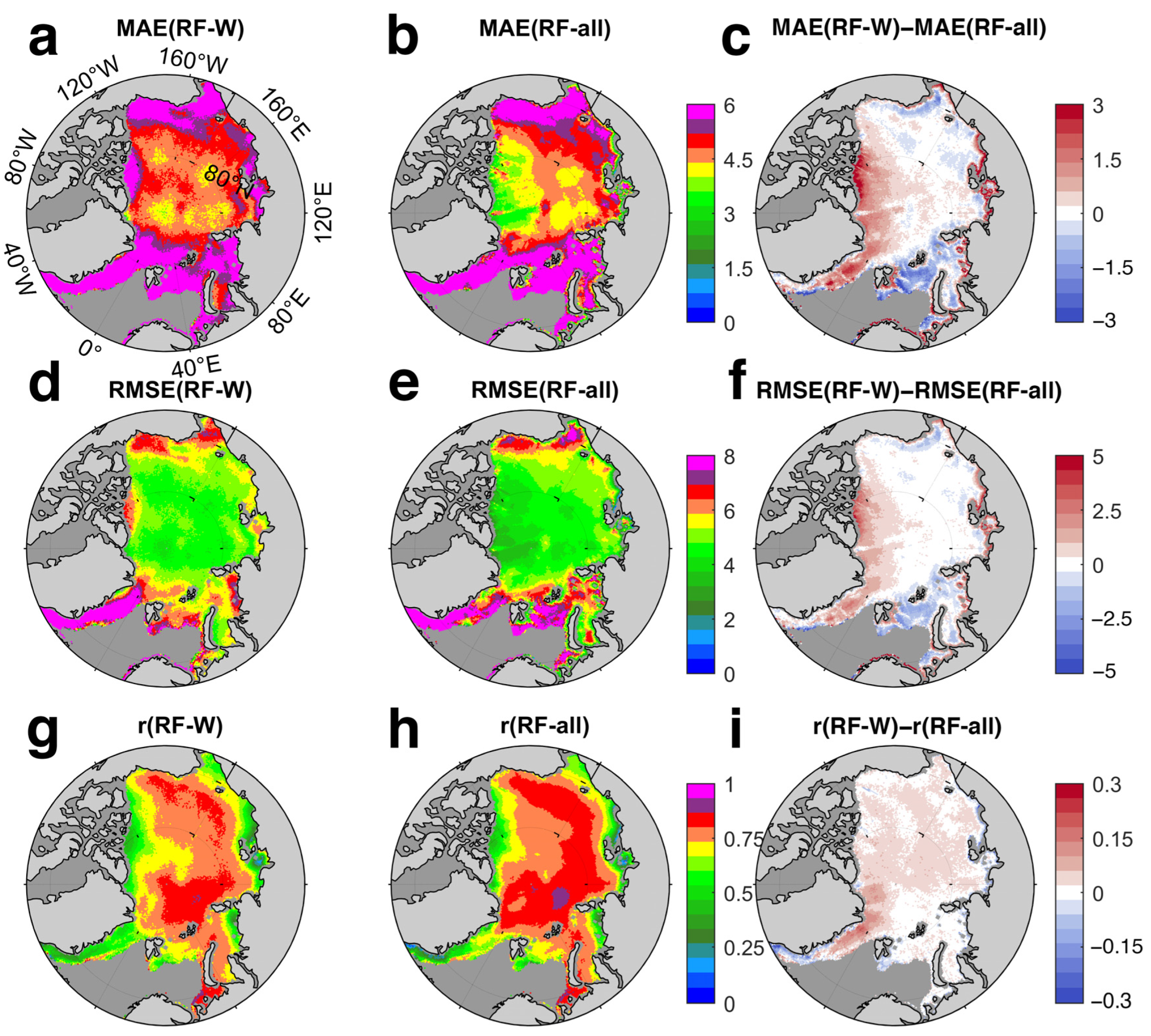
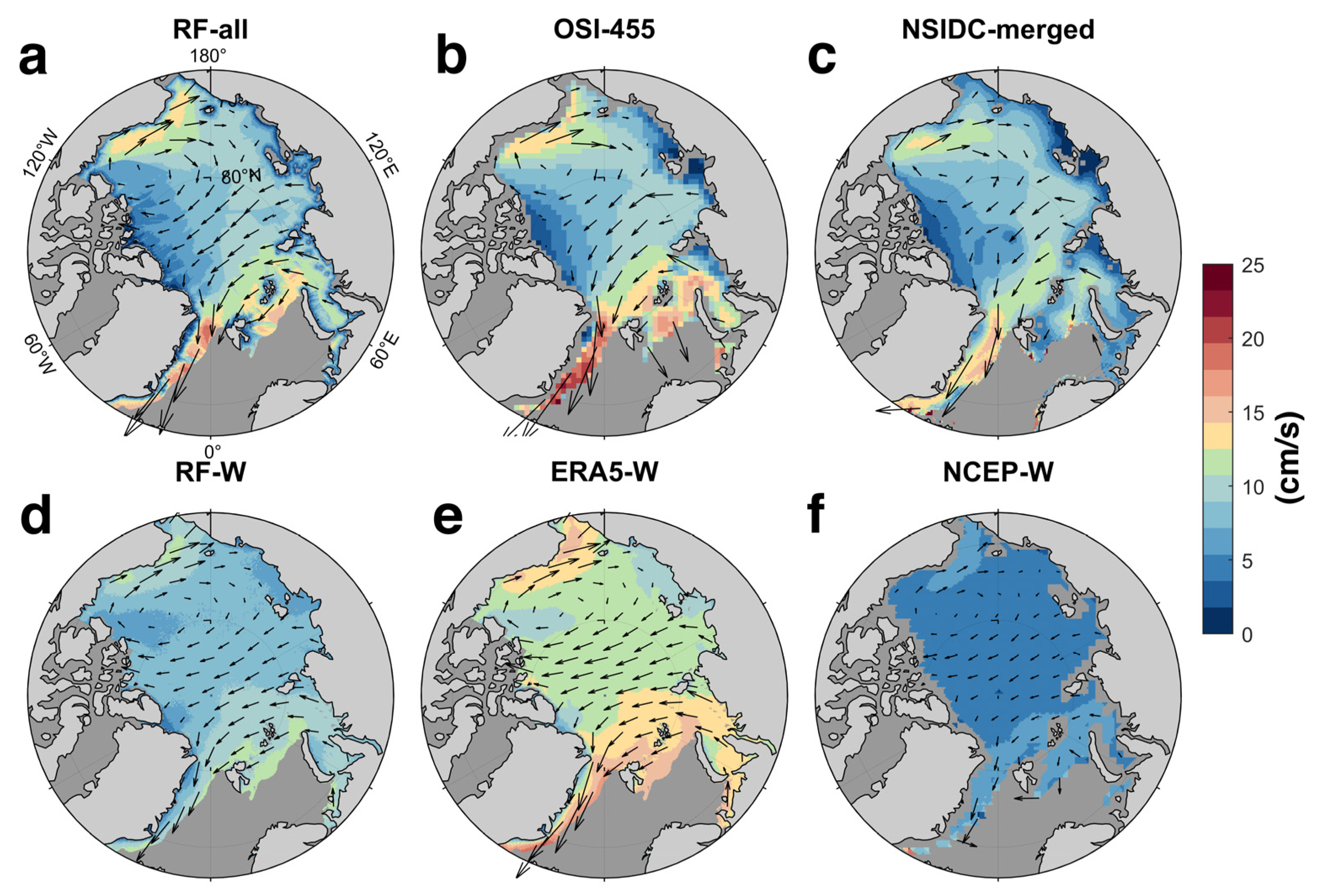
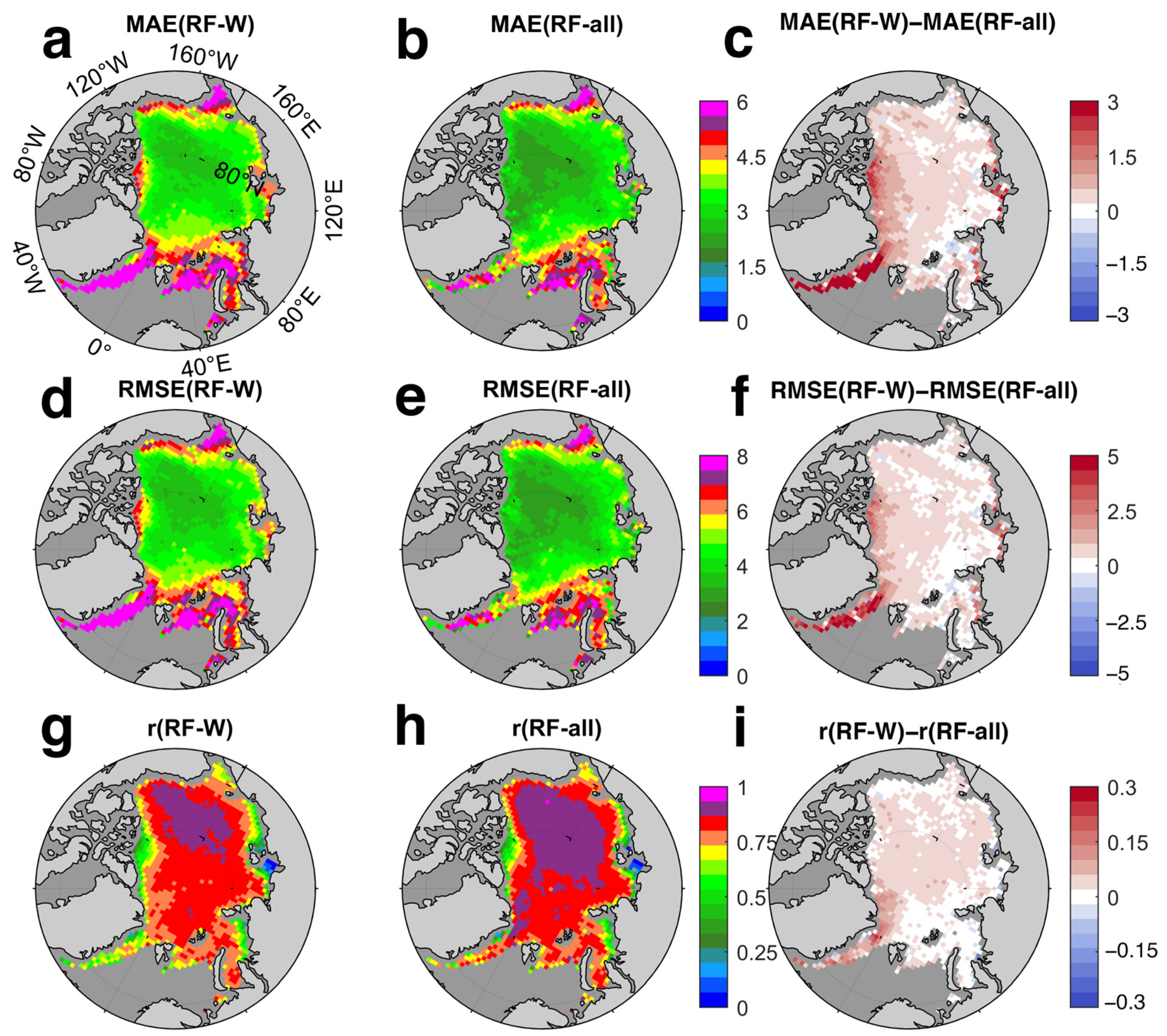
4.1. Comparison with Reference Dataset
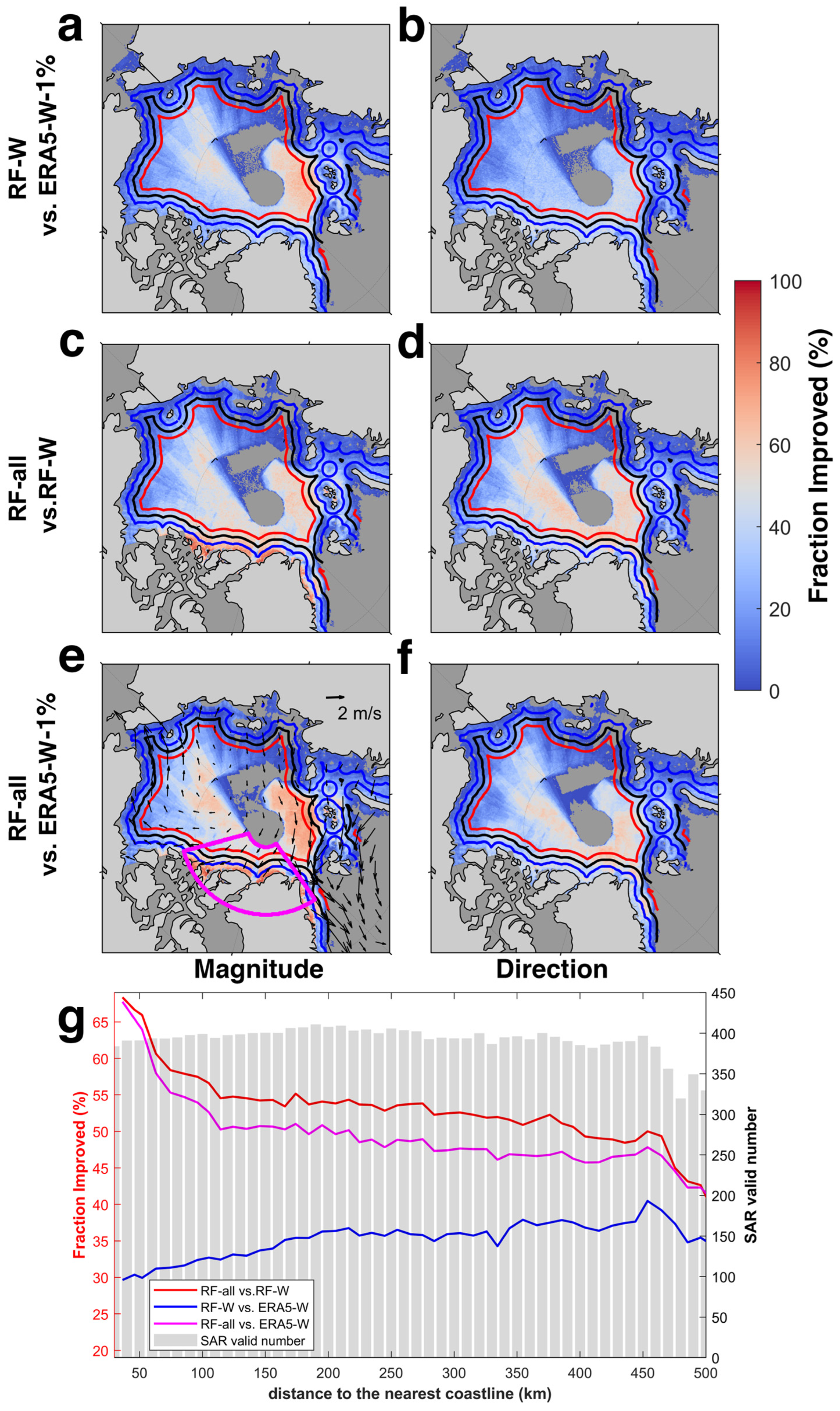
4.2. Relationship between RF-Derived SIM and Coastline Parameters
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Bias (cm/s) | MAE (cm/s) | r | RMSE (cm/s) | Skill | |
|---|---|---|---|---|---|
| Reference Dataset: Buoys | |||||
| RF-all + SIC | 0.23 | 3.77 | 0.76 | 4.18 | 0.45 |
| RF-all + SIC + SIT | 0.47 | 3.70 | 0.76 | 4.11 | 0.46 |
| Reference dataset: OSI-455 | |||||
| RF-all + SIC | 0.08 | 3.32 | 0.84 | 3.69 | 0.56 |
| RF-all + SIC + SIT | 0.24 | 3.21 | 0.85 | 3.57 | 0.58 |
| Reference dataset: NSIDC-merged | |||||
| RF-all + SIC | −0.01 | 3.77 | 0.78 | 4.19 | 0.44 |
| RF-all + SIC + SIT | 0.14 | 3.68 | 0.79 | 4.08 | 0.45 |
| r | (RF-All) | (RF-All) | (NSIDC-Merged) |
|---|---|---|---|
| - | - | - | |
| (OSI-455) | (NSIDC-Merged) | (OSI-455) | |
| 2015 | 0.82 | 0.76 | 0.72 |
| 2016 | 0.82 | 0.78 | 0.79 |
| 2017 | 0.84 | 0.80 | 0.75 |
References
- Coon, M.D. A Review of AIDJEX Modeling. Sea Ice Process. Models 1980, 12, 25. [Google Scholar] [CrossRef]
- Hibler, W.D. A Dynamic Thermodynamic Sea Ice Model. J. Phys. Ocean. 1979, 9, 815–846. [Google Scholar] [CrossRef]
- Leppäranta, M. The Drift of Sea Ice; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; ISBN 3642046835. [Google Scholar]
- Watkins, D.M.; Bliss, A.C.; Hutchings, J.K.; Wilhelmus, M.M. Evidence of Abrupt Transitions Between Sea Ice Dynamical Regimes in the East Greenland Marginal Ice Zone. Geophys. Res. Lett. 2023, 50, e2023GL103558. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, A.K. Arctic sea-ice motion and its relation to pressure field. J. Oceanogr. 2007, 63, 505–515. [Google Scholar] [CrossRef]
- Lavergne, T.; Eastwood, S.; Teffah, Z.; Schyberg, H.; Breivik, L. Sea Ice Motion from Low-resolution Satellite Sensors: An Alternative Method and Its Validation in the Arctic. J. Geophys. Res. Ocean. 2010, 115, C10. [Google Scholar] [CrossRef]
- Ezraty, R.; Girard-Ardhuin, F.; Piollé, J.-F.; Kaleschke, L.; Heygster, G. Arctic and Antarctic Sea Ice Concentration and Arctic Sea Ice Drift Estimated from Special Sensor Microwave Data; Département d’Océanographie Physique et Spatiale, IFREMER; University of Bremen Germany: Bremen, Germany, 2007; Volume 2. [Google Scholar]
- Tschudi, M.A.; Meier, W.N.; Scott Stewart, J. An Enhancement to Sea Ice Motion and Age Products at the National Snow and Ice Data Center (NSIDC). Cryosphere 2020, 14, 1519–1536. [Google Scholar] [CrossRef]
- Karvonen, J. Operational SAR-Based Sea Ice Drift Monitoring over the Baltic Sea. Ocean. Sci. 2012, 8, 473–483. [Google Scholar] [CrossRef]
- Frost, A.; Jacobsen, S.; Singha, S. High Resolution Sea Ice Drift Estimation Using Combined TerraSAR-X and RADARSAT-2 Data: First Tests. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 342–345. [Google Scholar]
- Howell, S.E.L.; Brady, M.; Komarov, A.S. Generating Large-Scale Sea Ice Motion from Sentinel-1 and the RADARSAT Constellation Mission Using the Environment and Climate Change Canada Automated Sea Ice Tracking System. Cryosphere 2022, 16, 1125–1139. [Google Scholar] [CrossRef]
- Lavergne, T.; Down, E. Product User’s Manual for the Global Sea Ice Drift Climate Data Record v1. Available online: https://osisaf-hl.met.no/sites/osisaf-hl/files/user_manuals/osisaf_cdop3_ss2_pum_sea-ice-drift-lr-cdr_v1p0.pdf (accessed on 31 January 2024).
- Petrou, Z.I.; Tian, Y. Prediction of Sea Ice Motion with Convolutional Long Short-Term Memory Networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6865–6876. [Google Scholar] [CrossRef]
- Palerme, C.; Müller, M. Calibration of Sea Ice Drift Forecasts Using Random Forest Algorithms. Cryosphere 2021, 15, 3989–4004. [Google Scholar] [CrossRef]
- Zhai, J.; Bitz, C.M. A Machine Learning Model of Arctic Sea Ice Motions. arXiv 2021, arXiv:2108.10925. [Google Scholar]
- Hoffman, L.; Mazloff, M.R.; Gille, S.T.; Giglio, D.; Bitz, C.M.; Heimbach, P.; Matsuyoshi, K. Machine Learning for Daily Forecasts of Arctic Sea Ice Motion: An Attribution Assessment of Model Predictive Skill. Artif. Intell. Earth Syst. 2023, 2, 230004. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.-L.; Zeileis, A.; Hothorn, T. Bias in Random Forest Variable Importance Measures: Illustrations, Sources and a Solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Thorndike, A.S.; Colony, R. Sea Ice Motion in Response to Geostrophic Winds. J. Geophys. Res. Ocean. 1982, 87, 5845–5852. [Google Scholar] [CrossRef]
- Kimura, N.; Wakatsuchi, M. Relationship between Sea-ice Motion and Geostrophic Wind in the Northern Hemisphere. Geophys. Res. Lett. 2000, 27, 3735–3738. [Google Scholar] [CrossRef]
- Maeda, K.; Kimura, N.; Yamaguchi, H. Temporal and Spatial Change in the Relationship between Sea-Ice Motion and Wind in the Arctic. Polar Res. 2020, 39. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Sakov, P.; Counillon, F.; Bertino, L.; Lisæter, K.A.; Oke, P.R.; Korablev, A. TOPAZ4: An Ocean-Sea Ice Data Assimilation System for the North Atlantic and Arctic. Ocean. Sci. 2012, 8, 633–656. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Thomson, R.E.; Emery, W.J. Data Analysis Methods in Physical Oceanography; Newnes: Boston, MA, USA, 2014; ISBN 0123877830. [Google Scholar]
- Sumata, H.; Lavergne, T.; Girard-Ardhuin, F.; Kimura, N.; Tschudi, M.A.; Kauker, F.; Karcher, M.; Gerdes, R. An Intercomparison of Arctic Ice Drift Products to Deduce Uncertainty Estimates. J. Geophys. Res. Ocean. 2014, 119, 4887–4921. [Google Scholar] [CrossRef]
- Hwang, B. Inter-Comparison of Satellite Sea Ice Motion with Drifting Buoy Data. Int. J. Remote Sens. 2013, 34, 8741–8763. [Google Scholar] [CrossRef]
- Wang, X.; Chen, R.; Li, C.; Chen, Z.; Hui, F.; Cheng, X. An Intercomparison of Satellite Derived Arctic Sea Ice Motion Products. Remote Sens. 2022, 14, 1261. [Google Scholar] [CrossRef]
- Leppäranta, M.; Hibler, W.D., III. The role of plastic ice interaction in marginal ice zone dynamics. J. Geophys. Res. Ocean. 1985, 90, 11899–11909. [Google Scholar] [CrossRef]
- Baordo, F.; Vargas, L.F.; Howe, E. OSI SAF Product User Manual for Global Sea Ice Concentration Level 2 and Level 3, OSI-410-a, OSI-401-d, OSI-408-a. Version 1.2, 14/6/2023. Available online: https://osisaf-hl.met.no/sites/osisaf-hl/files/user_manuals/osisaf_pum_ice-conc_l2-3_v1p2.pdf (accessed on 9 October 2023).
- Zhang, J.; Rothrock, D.A. Modeling Global Sea Ice with a Thickness and Enthalpy Distribution Model in Generalized Curvilinear Coordinates. Mon. Weather. Rev. 2003, 131, 845–861. [Google Scholar] [CrossRef]
- Schweiger, A.; Lindsay, R.; Zhang, J.; Steele, M.; Stern, H.; Kwok, R. Uncertainty in Modeled Arctic Sea Ice Volume. J. Geophys. Res. Ocean. 2011, 116, C8. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, X.; Chen, Z. Arctic daily 1 km sea ice drift product: 2018–2020, version 1.0[DS/OL]. V1. Science Data Bank 2023. Available online: https://www.scidb.cn/en/detail?dataSetId=8cf81c7a69004c2ebc94b12ddbb7ae72 (accessed on 31 January 2024).
- Liang, K.; Wang, J.; Luo, H.; Yang, Q. The Role of Atmospheric Rivers in Antarctic Sea Ice Variations. Geophys. Res. Lett. 2023, 50, e2022GL102588. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, G.; Ting, M.; Ruby, L.L.; Guan, B.; Li, L. More frequent atmospheric rivers slow the seasonal recovery of Arctic sea ice. Nat. Clim. Chang. 2023, 13, 266–273. [Google Scholar] [CrossRef]


| Input Variable | Target Variable | ||||||
|---|---|---|---|---|---|---|---|
| ERA5 10 m Wind (W) | Distance (D) | Azimuth Angle (α) | Sector Angle of Coastline Based on a Maximum Extend of 90 km (θ90 km) | OSI SAF OSI-401-d Ice Concentration (SIC) | PIOMAS Sea Ice Thickness (SIT) | SAR SIM | |
| RF-W | √ * | √ | |||||
| RF-all | √ | √ | √ | √ | √ | ||
| RF-all + SIC | √ | √ | √ | √ | √ | ||
| RF-all + SIC + SIT | √ | √ | √ | √ | √ | √ | √ |
| Bias (cm/s) | MAE (cm/s) | r | RMSE (cm/s) | Skill | |
|---|---|---|---|---|---|
| Reference Dataset: Buoys | |||||
| RF-all | 0.23 | 3.83 | 0.75 | 4.26 | 0.45 |
| RF-W | 0.12 | 4.95 | 0.57 | 5.50 | 0.39 |
| ERA5-W | 0.04 | 5.87 | 0.58 | 6.52 | 0.28 |
| NCEP-W | 0.44 | 5.26 | 0.79 | 7.51 | 0.19 |
| OSI-455 | −0.04 | 3.71 | 0.74 | 5.33 | 0.42 |
| NSIDC-merged | −0.04 | 1.26 | 0.97 | 1.98 | 0.79 |
| Reference dataset: OSI-455 | |||||
| RF-all | 0.13 | 3.31 | 0.84 | 3.68 | 0.56 |
| RF-W | 0.10 | 3.87 | 0.77 | 4.30 | 0.49 |
| ERA5-W | 0.39 | 4.93 | 0.78 | 6.27 | 0.28 |
| NCEP-W | 0.91 | 5.00 | 0.75 | 6.63 | 0.24 |
| Reference dataset: NSIDC merged | |||||
| RF-all | −0.01 | 3.91 | 0.78 | 5.07 | 0.31 |
| RF-W | 0.02 | 3.99 | 0.72 | 4.43 | 0.39 |
| ERA5-W | −0.11 | 5.27 | 0.70 | 5.84 | 0.18 |
| NCEP-W | 0.54 | 3.59 | 0.79 | 4.81 | 0.33 |
| r | (RF-All) - (OSI-455) | (RF-All) - (NSIDC-Merged) | (NSIDC-Merged) - (OSI-455) |
|---|---|---|---|
| January | 0.83 | 0.75 | 0.68 |
| February | 0.85 | 0.78 | 0.73 |
| March | 0.82 | 0.74 | 0.70 |
| April | 0.82 | 0.75 | 0.71 |
| December | 0.86 | 0.80 | 0.76 |
| all | 0.84 | 0.78 | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Shi, Q.; Leppäranta, M.; Liu, J.; Yang, Q. Estimating Winter Arctic Sea Ice Motion Based on Random Forest Models. Remote Sens. 2024, 16, 581. https://doi.org/10.3390/rs16030581
Zhang L, Shi Q, Leppäranta M, Liu J, Yang Q. Estimating Winter Arctic Sea Ice Motion Based on Random Forest Models. Remote Sensing. 2024; 16(3):581. https://doi.org/10.3390/rs16030581
Chicago/Turabian StyleZhang, Linxin, Qian Shi, Matti Leppäranta, Jiping Liu, and Qinghua Yang. 2024. "Estimating Winter Arctic Sea Ice Motion Based on Random Forest Models" Remote Sensing 16, no. 3: 581. https://doi.org/10.3390/rs16030581
APA StyleZhang, L., Shi, Q., Leppäranta, M., Liu, J., & Yang, Q. (2024). Estimating Winter Arctic Sea Ice Motion Based on Random Forest Models. Remote Sensing, 16(3), 581. https://doi.org/10.3390/rs16030581







