1. Introduction
Over the course of more than half a century, the field of Earth observation technology has witnessed remarkable advancements. Fueled by a series of Earth Observation pro-grams worldwide, artificial satellites equipped with sensors spanning the spectrum from visible and infrared to microwave bands have proliferated at various orbital altitudes. These sensors are employed on aircraft, ground-based platforms, and diverse Earth orbit satellites, contributing significantly to the study of Earth’s atmosphere, oceans, and terrestrial surfaces. Earth observation technology has emerged as a robust tool, facilitating the collection of copious remote sensing data that underpins crucial areas such as resource surveying, environmental monitoring, and climate change studies. However, despite the considerable strides made in Earth observation, the growing need to deepen our understanding of the Earth system and its impact on the human habitat has compelled the development of fresh Earth observation platforms and technologies. Existing Earth observation satellites, while effective, possess limitations in their capacity to provide a comprehensive, systematic perspective on our planet, thus constraining scientific investigations in Earth system science [
1,
2,
3]. Low Earth Orbit (LEO) satellites offer high spatial resolution and versatile viewing angles, yet they struggle to deliver global data with both temporal consistency and spatial continuity. Conversely, Geostationary Earth Orbit (GEO) satellites maintain continuous regional coverage but are limited in their ability to observe the Polar Regions. Recognizing that no single satellite platform can fully meet the diverse demands of Earth observation, it becomes imperative to explore the merits of distinct platforms and develop new Earth observation systems that integrate these various platforms [
3,
4,
5,
6].
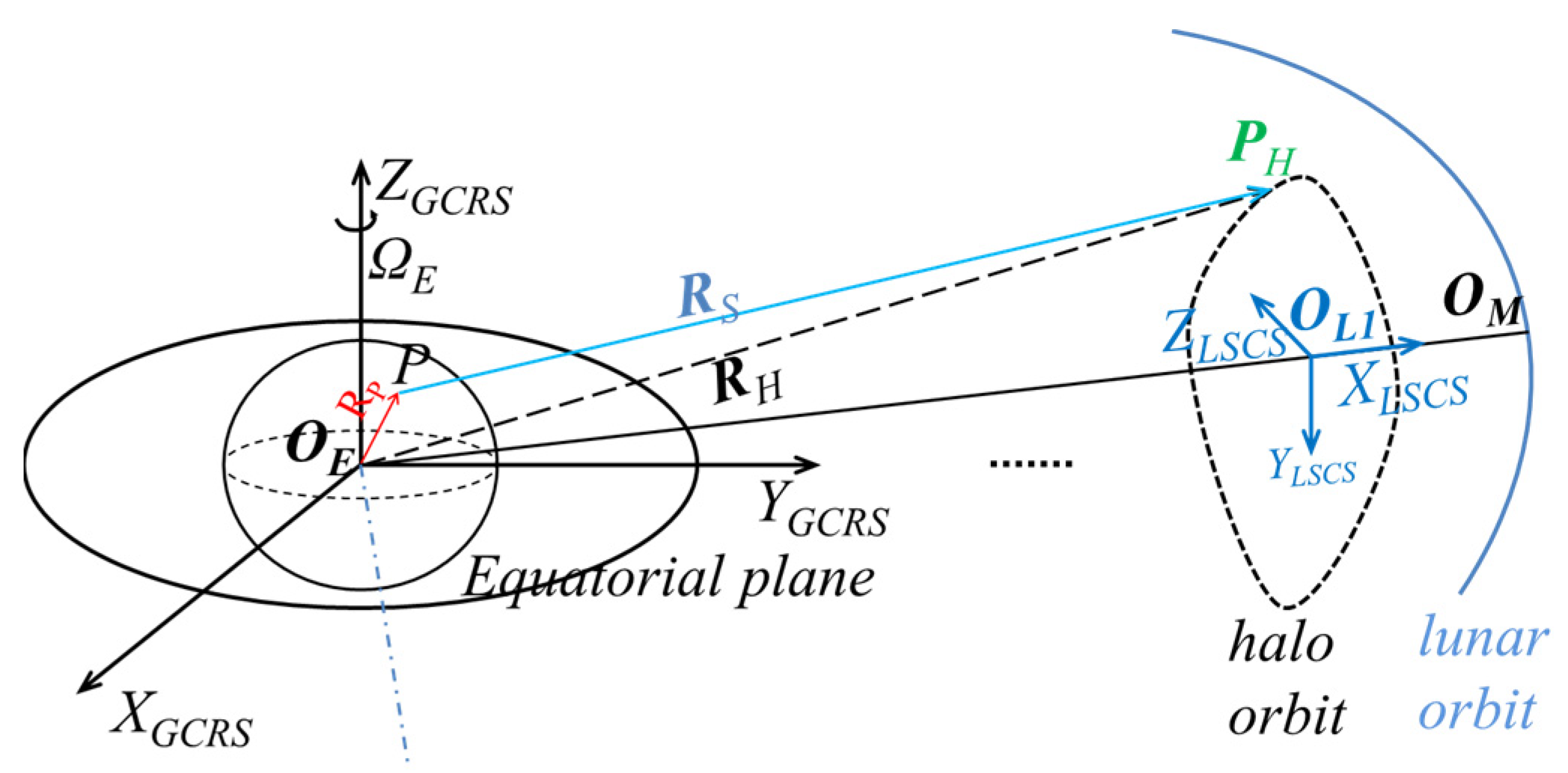
Lagrange points represent a class of gravitational equilibrium positions within a rotating two-body celestial system, such as the Earth-Moon system or the Sun-Earth system. Spacecraft stationed at Lagrange points within the Earth-Moon system offers the unique advantage of achieving full coverage of celestial bodies while maintaining a relatively stable geometric relationship with both the Earth and the Moon, leading to reduced propellant consumption. Moreover, there are low energy transfer orbits from the Earth to the Earth-Moon L1 point. This means that the cost of space transportation is much lower compared with other locations at the same altitude, which is conducive to the construction of high-orbit Earth observation platforms [
7,
8]. In the past century, the application of Lagrange points within the Sun-Earth system predates that of the Earth-Moon system. Successful missions to Sun-Earth L-points date back to the launch of ISEE-3 in 1978, the first artificial satellite to orbit L1. These missions were primarily designed for space observation, such as solar observatories, while a few were dedicated to Earth observation. Notable examples include ISEE-3 and WIND at L1 within the Sun-Earth system, which served in part to monitor the Earth’s magnetosphere. A joint mission in 2015, DSCOVR, contributed data on Earth’s albedo, ozone, and aerosols [
9,
10,
11,
12]. Aboard DSCOVR, the National Institute of Standards and Technology Advanced Radiometer (NISTAR) observed the entire dayside hemisphere of the Earth, providing a broadband spectral signature of the Earth to support planetary measurements and exoplanet studies [
13].
Recent years have witnessed a resurgence of interest in lunar exploration, with a corresponding upsurge in attention directed toward the Lagrange points within the Earth-Moon system. Earth-lunar space exploration is of great significance in relay communications, autonomous navigation and positioning, space science and space exploration, manned space stations, earth remote sensing, and situational awareness. For instance, China’s “Magpie Bridge” mission in 2018, which orbits in a halo configuration around L2 in cislunar space, serves as a vital relay satellite for communication with Earth. NASA’s Artemis mission also has plans to establish the Lunar Orbital Platform-Gateway (LOP-G) around L1 [
14,
15,
16]. Presently, research pertaining to the L1 point within the Earth-Moon system primarily centers on lunar station development, space gateway exploration, low-energy transfer orbits, and navigation service systems [
7,
17,
18,
19,
20,
21]. Recent endeavors have also explored the potential of Earth observation from the L1 point. For example, Zhang et al. introduced a novel Earth observation system featuring a radiometer designed to capture Earth’s radiation budget, operating from the L1 point within the Earth-Moon system, yielding simulation results that exhibit high-quality imaging [
22].
However, it is worth noting that the three collinear Lagrange points (L1, L2, and L3) along the Earth-Moon line are inherently unstable, requiring spacecraft to employ active control to remain in position, whereas the equilateral Lagrange points (L4, L5) are stable [
23]. This inherent instability suggests that spacecraft are more likely to occupy periodic orbits, such as halo orbits, rather than a precise L1 point position [
24]. Thus, this study aims to conduct a more scientifically rigorous analysis of the general characteristics of Earth observation, introducing the concept of halo orbits around L1 as opposed to relying on the simplification that sensors remain static at the L1 point. Additionally, considering the changing distance between the Moon and Earth, which fluctuates from approximately 363,000 km to 405,000 km over time, this study employs ephemeris data to describe the Earth-Moon movement rather than relying on a simplified, uniform circular motion, thereby reducing potential errors in orbit determination [
25]. Moreover, we conduct numerical simulations employing various time steps and periods following geometric analysis to effectively demonstrate accurate characteristics.
Furthermore, due to the similarity in motion between the Moon and the L1 point within the Earth-Moon system—both revolving around the Earth at the same angular velocity and maintaining a close proximity, approximately 0.15 times the Earth-Moon distance—it is plausible that there are both differences and similarities in their Earth observation capabilities. While a substantial body of the literature has explored Earth observation from Moon-based platforms [
6,
26,
27], minimal attention has been devoted to studying the Lagrange points in cislunar space, which represent unique spatial resources and an ideal location for lunar exploration, offering distinctive potential as a supplementary Earth observation platform. Thus, this paper undertakes a comparative analysis, considering periodic halo orbits around L1 within the Earth-Moon system and elucidating the distinctions in Earth observation characteristics between Moon-based platforms and the L1 point.
The remainder of this paper is structured as follows:
Section 2 introduces the data used in our analysis, including JPL ephemeris data and methods for calculating periodic halo orbits. The subsequent section elucidates the primary coordinate systems employed in this study, alongside the derivation of transformation matrices that facilitate the calculation of relative motions between the sensor and ground targets. Building upon the geometric model of the halo orbit and the Earth’s surface, we derive pertinent geometric parameters.
Section 3 conducts a numerical analysis of the variation in nadir point tracks, as characterized by the proposed temporal complexity curve—a critical factor influencing other Earth observation characteristics, such as the distribution of viewing angles and spatiotemporal ground coverage. To facilitate comparison, we also analyze and present data for Moon-based platforms.
Section 4 discusses the experimental results, highlights the principal differences between Moon-based platforms and the L1 point, and envisions the potential for joint Earth observation using lunar surfaces and halo orbits around the L1 point. Finally, we draw a conclusion summarizing the findings of this study and delineating the sources of error encountered.
3. Results
The track of nadir points and altitude are often utilized to present the features of Earth satellites of different kinds of Earth orbits and play an influential role in the further performance of observation characteristics. The angular and spatiotemporal coverage characteristics are the two commonly concerned features in Earth observation, which have been studied carefully in many previous studies on Moon-based Earth observation [
34,
35]. Thus, the first step of this work is to compare the different performances of halo orbits in these aspects.
3.1. Nadir Point Track and FOV
Variation of the nadir point is the key factor that induces a temporal variation of ground coverage and revisit cycles and repeat cycles. As one of the most different characteristics between the lunar and halo orbits, it is also the main factor that affects the differences in their Earth observation characteristics, such as the ground coverage and diversity of viewing angle.
Figure 3 shows the nadir point tracks of the Moon (left) and a halo orbit (right) at 00:00:00 UTC each day from 20 March 2024 to 20 March 2025 when the lunar orbital inclination reaches the maximum of 28°. Similar to the nominal orbit of “Magpie Bridge”, whose Z-direction amplitude is around 13,000 km, here the amplitude parameter, which denotes the deviation of the halo orbit from L1, is set at 20,000 km, corresponding to the normalization parameter of 0.3457. Note that since the latitude variation of the nadir point track is relatively small during the daily cycle, the real-time nadir point may reach the whole area with different longitudes and the same latitude. As presented in the figure, the latitude range of the nadir point track of the Moon is limited to around 28°N and 28°S, which. together with the period of less than one day, forms one of the Moon’s most important features. In fact, as a result of the declination of the Moon varying between 18.3° and 28.6° with a period of around 18.6 years, the maximum latitude varies from 18.3° to 28.6° both north and south of the equator [
36]. In the case of a 20,000-km halo orbit, on the one hand, the variation of nadir points behaves more complicatedly during a period of one month or one year. The maximum latitude is extended to around 42°N induced by the halo motion, which in a way induces more diversity of viewing angles and is advantageous to the observation of the polar zone with a similar observation performance to the Moon-based platform. On the other hand, as the Moon’s orbital period is as long as a sidereal month, the repeat cycle of the Moon is fixed. While the orbital period of the family of halo orbits around L1, it is less than half of a sidereal month and is designable and alterable.
As demonstrated in
Figure 3, the latitude and longitude variations of the nadir point become more complex induced by the halo motion, while the longitude variation produces a more significant effect.
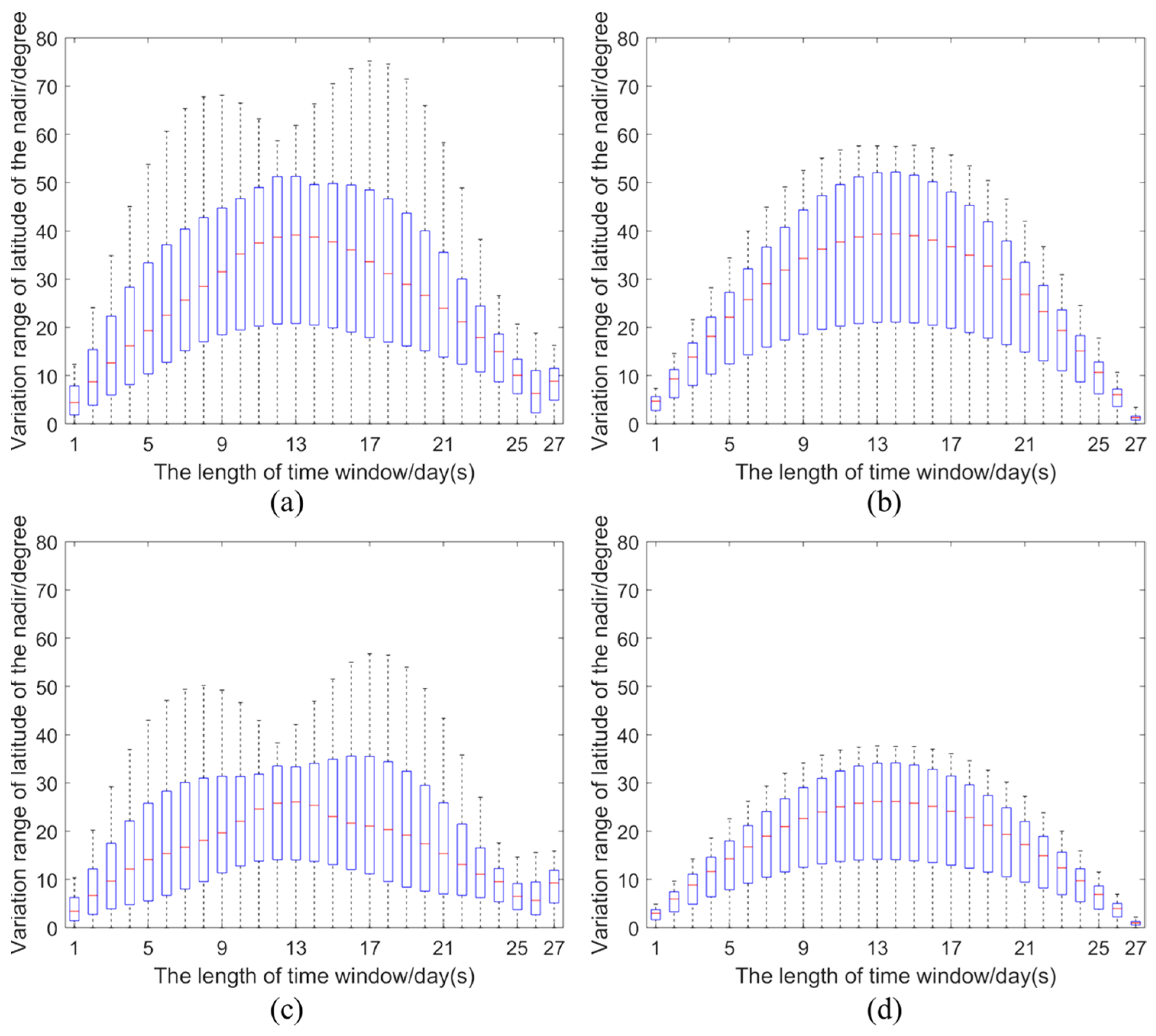
Figure 4 presents the temporal complexity of the latitude variation of the nadir point of the 20,000-km halo orbit (left) and Moon (right). The horizontal axis represents the length of the sliding time window, and the vertical axis represents the range of latitude variation within the time window. Each plotted box counts the changing values of the latitude of the nadir point calculated using one-hour time steps over a one-year period from 20 March 2024 to 20 March 2025 (a,b) and from March 2033 to March 2034 (c,d). Note that (a,b) is during the year when the lunar orbital inclination reaches its maximum, i.e., around 28°, while (c,d) is during the year when the lunar orbital inclination reaches its minimum value, i.e., around 18°. The temporal complexity curve of latitude variation is derived from the concept of Approximate Entropy, which is usually used to characterize the irregularity and complexity of time series and it works for both stochastic processes and deterministic processes (the case of this study). The temporal complexity curve provides a good description of the pattern and complexity of the nadir point’s latitude variation with the length of time windows; in the meantime, it can also quantify the distribution of latitude variation values within a certain time window, which is useful for assessing the ground coverage of different latitudes with respect to hemispheric-scale Earth observations. The time window is taken from one day to 27 days because the revisiting period of the Moon and L1 with respect to Earth is approximately one day and the orbit period of the halo orbit is always less than half of the lunar orbit. One year of data as a calculation period is sufficient to show the main patterns of the nadir point’s latitude variation.
Figure 4a–d revealed that in different years, which means different inclinations of the lunar orbit, the temporal complexity curves of latitude variation have similar shapes in both cases of the Moon and halo orbits, thus, they are independent of the inclination of the lunar orbit. On the one hand, considering the complexity patterns manifested by the shape of the curve, it is obvious that the shape of curves in the case of the Moon is an inerratic near sinusoidal curve which is determined by the approximate uniform circular motion of the Moon around the Earth, while the shape of curves in case of the halo orbit shows two peaks when the time window is around 8 days and 17 days. On the other hand, for each time window, the quartiles and medians of latitude variation in the case of a halo orbit are approximately equal to that of the Moon; while the maximum variation of latitude for each time window in the case of a halo orbit is greater than that of Moon especially around the peaks, which is around 14° and 21°, respectively, for a 20,000-km halo orbit. The above demonstrates that the halo orbit induced complexity of the nadir point’s latitude variation by splitting one peak into two while it can also extend the range of latitude variation for each time period.
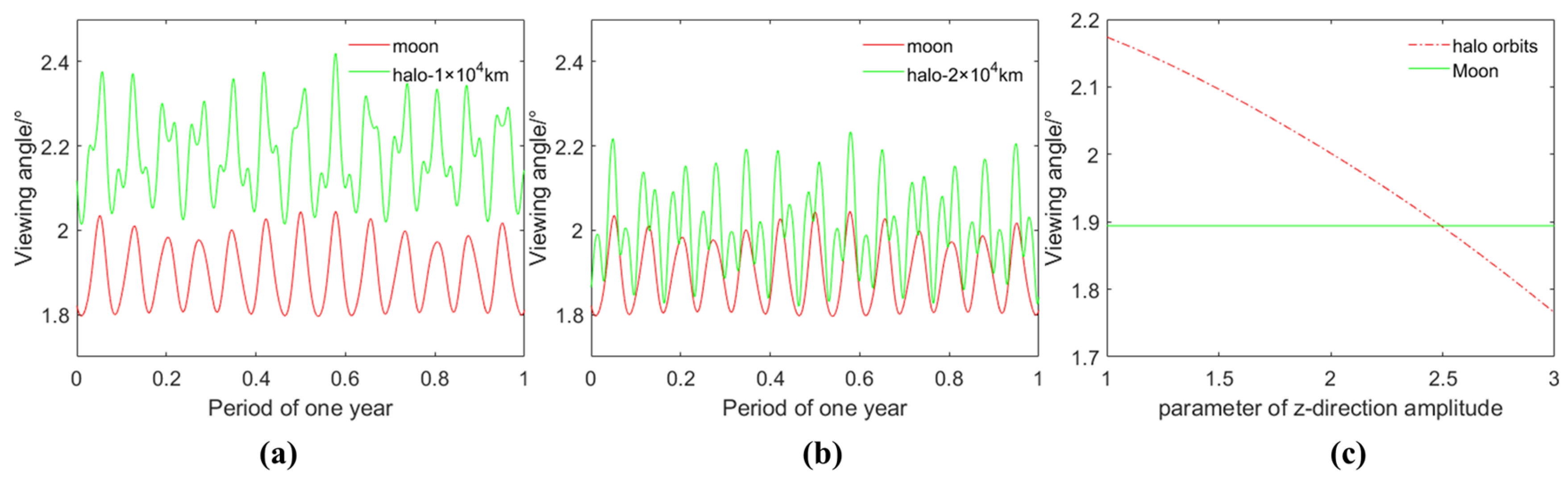
As the name suggests, the halo orbits are like lunar aureole viewing from the perspective of the Earth due to the same angular momentum around the Earth, and the distance of the L1 to the Moon is much smaller than to the Earth, which leads to a similar field of view of the Earth.
Figure 5 shows the variation of the field of view (FOV) of the Earth from halo orbits with z-directional amplitudes of 10,000 km (a) and 20,000 km (b) and the mean FOV (c) in a year from 20 March 2024 to 20 March 2025 varying with z-directional amplitude, respectively. It can be seen that in the general range, both have roughly the same FOV and only when the orbit is very large will there be a significant difference. Thus, there is not much difference from the perspective of observing the Earth as a whole.
3.2. Distribution of Viewing Angles
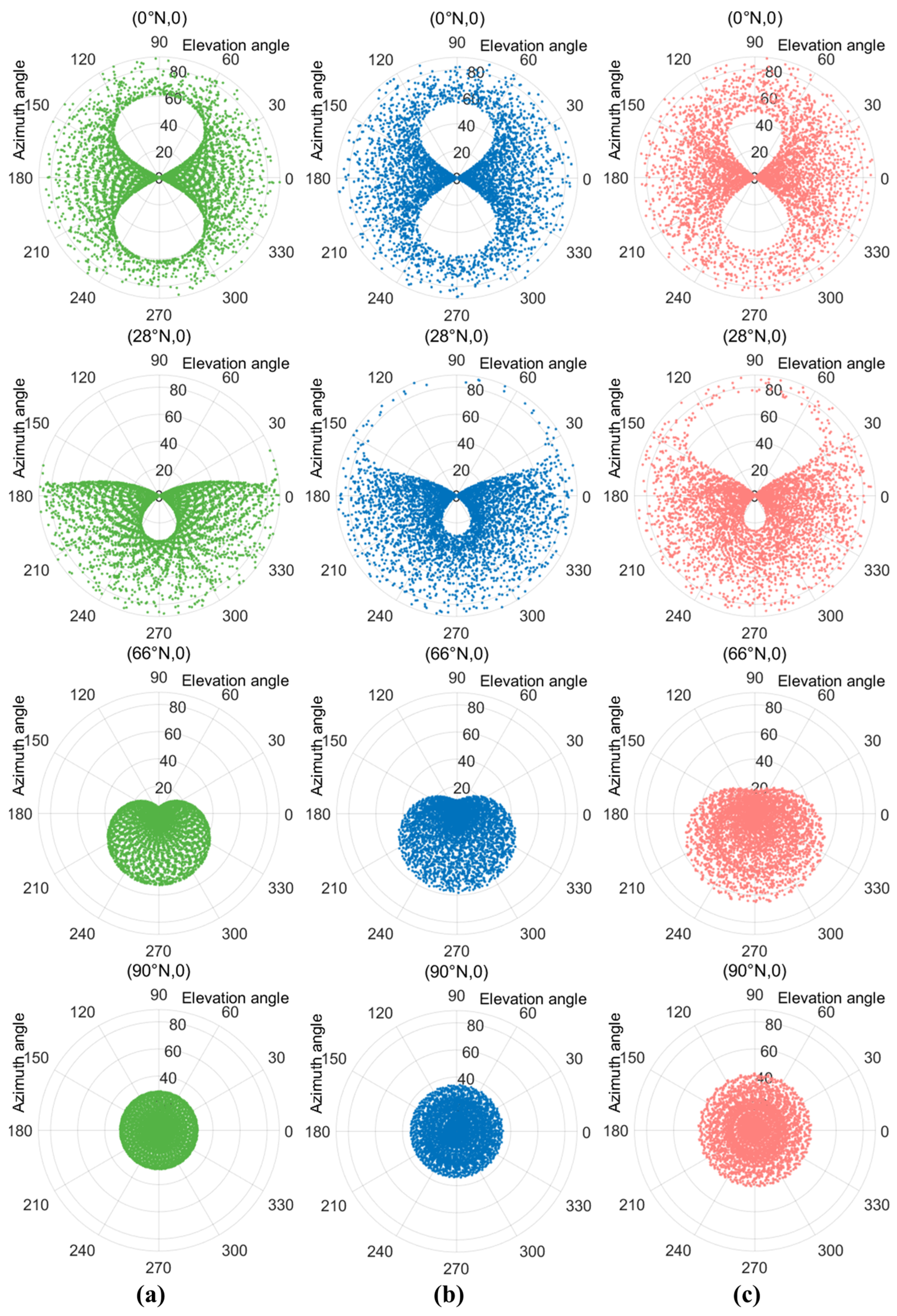
The elevation angle and azimuth angle are very important angular parameters in remote sensing observation of the Earth, both for optical and radar remote sensing. The elevation angle is the angle between the line-of-sight direction and the local horizontal plane, which is the residual angle of the zenith angle. As defined above, the azimuth angle is the angle between the projection of the line-of-sight direction on the local horizontal plane and the reference direction, which is set as east for the convenience of visualization.
In this section, a series of experiments was carried out to analyze the distributions of viewing elevation angle and azimuth angle during the period from 20 March 2024 to 20 March 2025 at four locations with different attitudes on the prime meridian. As contrasted with the Moon-based platform (a), the viewing angular characteristics of two representative halo orbits, of which the parameters of orbital amplitude are set at 10,000 km (b) and 20,000 km (c), are shown in
Figure 6. The pre-test shows that the differences in angular distribution between different longitudes are small, and it is symmetrical in the northern and southern hemispheres. Thus, with the sampling interval set at an hour, the distribution of the combination of elevation angle and azimuth angle at four representative locations with different latitudes, namely 0°N, 28°N, 66°N, and 90°N, are presented in the polar coordinate system, where the polar radius and polar angle corresponds to elevation angle and azimuth angle, respectively.
In order to maximize the observation angle combination of Moon-based Earth observation in the polar region, the one-year period selected in this experiment is when the lunar orbital inclination is close to the maximum value of 28.5°. On the one hand, the results demonstrated that at low latitudes, there is little difference in the combination of angular distribution between Moon-based platforms and halo orbits throughout the year, where for both of them, the azimuth angle during one year covers the whole range from 0° to 360° and the elevation angle during one year also covers the whole range from 0° to 90°. While at critical latitude near 28°N, the viewing azimuth angle of the Moon-based platform is limited from 180° to 360°. Moreover, for areas of interest exceeding 28°N, the data observed from the whole north side is missing. In the case of a halo orbit, especially of greater z-directional amplitude, the critical latitude could be extended to over 42°N, depending on the designed orbit. Thus, generally, the range of elevation angle and azimuth angle can both be extended by halo orbits. On the other hand, the period of the halo orbit around L1 of the Earth-Moon system is shorter than half of the Moon’s orbital period (e.g., the period for the chosen halo orbit with a 20,000 km amplitude is approximately 12 days), as a result of which the revisiting period of the nadir point can be reduced compared to the Moon-based platform.
Generally, the Moon’s halo orbits around L1 are expected to enhance the ability of Moon-based Earth observation to some extent with the complementation of an extended viewing angle and a shortened period of nadir point revisiting. For example, one of the scientific aims of Moon-based Earth observation is to understand the Earth’s radiation budget and its interaction with global climate change, which is focused on the changes in outgoing radiation at the top of the atmosphere (TOA). In order to establish a reliable global Angular Distribution Model (ADM) to reconstruct the actual total outgoing radiation from TOA, it is necessary to acquire a mass of continuous data from the Earth disk with a diversity of configurations of viewing angles and a short data acquisition period. Therefore, the improvements provided by the Moon’s halo orbits in these aspects may provide supplementary Earth disk data.
3.3. Spatiotemporal Coverage
In general, a high earth orbit can offer extensive ground coverage and a relatively short revisit period in the meantime. For example, a Moon-based platform can implement continuous observations of the Earth on a hemispherical scale with a period of approximately one day due to the Earth’s rotation and the moon’s revolution. As for optical Earth remote sensing, in the case of observing the Earth’s facing-Moon disk, most areas of the Earth’s hemisphere are visible both at Moon-based platforms and halo orbits, between which a slight difference may exist in the viewing angular characteristics of the Earth disk. However, when it comes to broadside-looking synthetic aperture radar (SAR), the incident angle and azimuth angle need to be limited for data quality. There are relatively many historical studies focused on the spatiotemporal coverage of Moon-based Earth observation [
34,
35]. In this section, the effects of the limitations of elevation angle and azimuth angle on the global spatiotemporal coverage of Moon-based SAR as well as the halo orbits are analyzed for comparison.
Most of the present spaceborne SAR systems are configured with an incident angle between 20° and 60°, e.g., RADARSAT-1, RADARSAT-2, TerraSAR-X, and TanDEM-X [
37]. This is a little bit harsh for Moon-based SAR. Nevertheless, there are still several satellites configured with a wider range of incident angle, such as ALOS-2, whose range of incident angle is designed between 8° and 70°. As adopted in previous studies focused on Moon-based SAR [
35,
38], for the quality of imaging data, here the incident angle is limited between 15° and 70° as an assumption. Moreover, the velocity of halo motion is relatively small compared to the Moon; thus, according to the inverse synthetic aperture imaging mode of Moon-based SAR, the reference azimuth angle, which is the main factor that affects the squint angle, is limited between 30° and 150° or between 210° and 330°. Therefore, with the limitation of incident angle and azimuth angle, the spatiotemporal coverage of the Moon-based platform and halo orbits is calculated.
Figure 7 presents the accumulated coverage time of Moon-based platforms (a,b) and halo orbits with a z-direction amplitude of 20,000 km (c,d) during one year from March 2024 to March 2025 (a,c) and from March 2033 to March 2034 (b,d). Results demonstrate the differences induced by the varying declination of lunar orbit in different years and by the halo motion. On the one hand, the comparison of (a) and (b), where the declination of the moon almost reaches the maximum 28.6° and the minimum 18.3°, reveals the different annual patterns of ground coverage: when the declination of the lunar orbit reaches the maximum, the area with low latitudes from 15°S to 15°N are covered most intensively, the mid-latitude zone from 30° to 50° is also covered for a considerable time, and the polar area can be observed in at least 755 h during one year. However, when the declination of the lunar orbit reaches the minimum, the ground coverage in a year behaves with a complete pattern, and the coverage time of low-latitude area decreases greatly from 1743 h to 900 h, especially in the equatorial region. Reduction happens in the near-polar region as well, where the north and south poles can be hardly covered during the year. Instead, the mid-latitude area can be covered almost every day with a significantly increased coverage time during the whole year, and the range of latitudes is also extended to 20° and 60°. On the other hand, the results of (c) and (d) compared with (a) and (b) show that the ground coverage pattern in the case of a Moon-based platform is not impacted by the halo motion, which is more likely to play a role in extending the intensively covered area and slightly increasing the coverage time of the equatorial region and polar area.
As mentioned above, the halo motion can contribute to the revisiting cycle of the nadir point, which is an advantage for ground coverage frequency compared to the Moon-based platform due to the fact that the repeating period of the nadir-point track for the Moon is as long as about 27 days. Thus, without loss of generality, the following section takes several locations on prime meridians with different latitudes as examples to analyze the differences in coverage frequency during two typical years.
The segments of lines in
Figure 8 depict the annual coverage cycle and frequency of eleven typical locations of different latitudes during the annual period from March 2024 to March 2025 (a) and from March 2033 to March 2034 (b). The black segments of each line with different latitudes indicate the moment able to be covered while the white intervals between segments indicate a non-covered period. In a similar definition, the segments of lines with different colors and intervals under the black ones indicate the same in the case of halo orbit. Moreover, the grid of the time axis refers to the orbital period of the lunar, which is regarded as a sidereal month inconsistent with the commonly used Gregorian month. Note that due to the density of the scatter, there are still invisible intervals in what seemingly looks like a segment, thus the line of Moon in (b) with a latitude of 28° is not a completely continuous line. As is presented, the total pattern of the coverage cycle for the Moon and halo orbit is almost the same both in (a) and (b). However, (a) shows that the shortest gap period occurs in the equatorial region and the gap length increases with hoisting latitude, while (b) shows that the shortest gap period occurs at low latitudes around 28° and decreases towards high latitudes and the equator. Similarly, the halo motion does not influence the overall trend of the coverage cycle in the dimension of latitude; instead, it plays a role in extending the coverage segment under a monthly scale, especially in areas with shorter coverage time, such as the polar region and slightly reducing the interval inter-monthly.
4. Discussion
As Earth’s sole natural satellite, the Moon and its several special Lagrange points in the cis-lunar space provide significant opportunities for lunar and deep space exploration, space weather and Earth observation, communication relay, and navigation service. Known scientific missions to Lagrange points have mainly focused on the Sun-Earth system while missions within the Earth-Moon system are relatively rare, but recently lunar exploration has led to an increase in the exploitation of Earth-moon Lagrange points especially L1 and L2. However, as for Earth observation, there have been limited studies on the L1 point of the Earth-Moon system in Earth observation in contrast to either Moon-based Earth observation or the L1 point of the Sun-Earth system. Recent investigations into Earth radiation monitoring at the L1 point have made the unrealistic assumption that a sensor could remain stationary at this location—an improbable scenario. Hence, this study endeavors to analyze the fundamental characteristics of the L1 point with respect to Earth observation.
This study has three main improvements. The first, as mentioned above, is the determination of periodic halo orbits around the L1 point of the Earth-Moon system, which is designed for spacecraft to maintain its adjacent position in the neighborhood of the L1 point with lower energy consumption compared to the in situ maintenance. As for the calculation of halo orbit, it is still an idealized problem in the field of astronautics as there are many perturbation sources resulting in orbital errors such as the solar gravitational perturbation, thus it is necessary for spacecraft to carry out real-time orbit control. Therefore, the precise orbit determination in this paper is impossible as well as unnecessary. Anyway, this paper still considered the perturbation effect of main sources by adopting ephemeris data to accurately determine the position and relative motion of the Moon and Earth. Note that a common assumption in the N-body problem is that the mass of spacecraft can be considered to be zero relative to other main and perturbing celestial bodies. Thus this paper considers the perturbation from main sources to the motion of the Earth and Moon by means of ephemeris data while the direct gravitational perturbation to massless spacecraft is ignored, which is the second main improvement of this study. The final contribution of this study lies in the proposal of a “temporal complexity curve” describing the latitude variation at the nadir point, which effectively captures the intricate dynamics induced by halo motion, especially in contrast to the Moon’s nadir point. This curve not only reveals patterns and complexities in latitude variation over specified time windows but also quantifies latitude variation values within those windows. Such quantification proves valuable for assessing ground coverage at different latitudes in the context of hemispheric-scale Earth observations.
Leveraging the aforementioned enhancements, this study undertakes a comprehensive analysis of the general geometric characteristics of the L1 point in Earth observation, juxtaposed with Moon-based platforms for comparison. The results and subsequent analysis, focusing on nadir point variation, angular distribution, and spatial and temporal coverage in
Section 3, affirm the strikingly similar Earth observation capabilities of L1 and Moon-based platforms. Both are adept at near-hemispheric-scale coverage of the Earth’s surface within approximately one day and complete global coverage within a month. Notably, both achieve nearly daily revisits for mid-to-low latitudes—an unattainable feat for low Earth orbit and geostationary satellites. However, the introduction of halo motion, depending on its amplitude, engenders a more intricate nadir point variation pattern and a broader latitude range within specific time windows, constituting the primary source of differences in viewing angle distribution and spatiotemporal ground coverage when compared to Moon-based platforms. Although halo motion slightly increases the range of nadir point latitudes (spanning over 28°S to 28°N) and widens the distribution range of viewing angles, it does not confer a decisive advantage in complementing Earth observation. Furthermore, over the course of a year, halo motion exerts a slight averaging effect on global coverage along latitudes. While it enhances observation time in Polar Regions, it does not distinctly improve observation frequency.
The hallmark advantage of Lagrange points within the Earth-Moon system lies in their unique spatial location and dynamical properties in cislunar space. They can function as observatories for space observations encompassing the entirety of cislunar space, as well as transit stations for low-energy interplanetary transmissions [
39,
40]. In comparison to geostationary Earth orbit (GEO), access to Lagrange points is cost-competitive, if not more economical, due to low-energy transfer orbits, and the maintenance costs are significantly lower than those associated with sustaining the north-south position of GEO orbits. This makes Lagrange points a viable option for Earth observation. It should be noted that when designing the halo orbit, the amplitude outside and inside the plane of the halo orbit, orbital period, and phase relative to the lunar orbit need to be considered to ensure the coverage of the polar region. Nevertheless, in contrast to Moon-based platforms, the L1 point exhibits remarkably similar geometric characteristics for Earth observation. Yet, considering the unique advantages of the Moon—such as its extensive lunar surface, marked by exceptional geological stability and protracted life cycles—the L1 point does not demonstrate a distinctive advantage. Consequently, lunar surfaces remain the preferred choice for Earth observation within the cislunar space.
Nonetheless, it is essential to acknowledge that there are limitations and avenues for future improvements in this field. In fact, the actual orbital data cannot be accurately predicted due to the interference of various perturbations such as the solar gravitational force, the Earth’s aspherical gravity, and the solar photopressure. Enhancing the determination of halo orbits is necessary for in-depth research. One potential avenue for achieving greater precision lies in adopting a realistic force model of the solar system to more accurately determine orbits, such as the doubly synchronous binary asteroid model [
41] and the numerical continuation method [
42]. However, it is crucial to balance precision with practicality, as overly precise orbit determination is often unnecessary. Additionally, the exploration of other periodic and quasi-periodic orbits, such as Lissajous orbits, which have found utility in space observation, warrants consideration for future research.
5. Conclusions
This paper conducts preliminary comparative studies between Moon-based platforms and halo orbits around the L1 point in the Earth-Moon system, with a specific focus on Earth observation. We carried out numerical analyses using Ephemeris data to elucidate the Earth observation characteristics of halo orbits, encompassing variations in the nadir point, distribution of viewing angles, and spatiotemporal ground coverage. The findings of this study suggest that halo motion around the L1 point does indeed have a role in modestly expanding the range of nadir point latitudes and introducing higher and more intricate rates of variation in nadir point latitudes. In conclusion, the geometric characteristics of halo orbits for Earth observation closely resemble those of Moon-based platforms. However, considering the distinct advantages of Moon-based platforms, such as their vast lunar surface with remarkable stability and nearly eternal operational lifespans, Moon-based platforms remain the optimal choice for Earth observation in the cislunar space. Nonetheless, L1, along with other Lagrange points, still holds promise as an extension of the Moon-based platform, contributing to the formation of a comprehensive globally-coverage network for Earth observation in cislunar space. This network would be characterized by its ability to conduct hemisphere-scale observations and offer a unique observational perspective. This study has contributed to a broader understanding of the future of Moon-based Earth observation, encompassing not only the lunar surface and orbit but also the Lagrange points within the entire cislunar space.