A Multichannel, Multipulse, Multiweight Block-Adaptive Quantization (3MBAQ) Algorithm Based on Space-Borne Multichannel SAR Doppler Domain A-BAQ

Abstract

Amid the conflict between the current huge data volumes and the requirement for large-compression-ratio compression in space-borne multichannel SAR, this paper proposes a data compression method that uses the adaptive bit allocation BAQ method in the Doppler domain of space-borne multichannel SAR. Specifically, 3MBAQ, which denotes multichannel, multipulse, multiweight block-adaptive quantization, performs signal reconstruction through a Krieger filter to obtain the Doppler spectrum under azimuthal multichannel and multipulse conditions and then achieves nonuniform bit allocation by using the multiple weight contributions between subband spectra. Furthermore, large-compression-ratio compression can be realized in homogeneous scenarios by using the adaptive bit allocation BAQ method together with the improved bit error control (BEC) algorithm. In this paper, the effectiveness of the 3MBAQ method is verified on GF3 measured data. Moreover, compared to the SQNR and NMSE of the BAQ, A-BAQ, A-BAQ-BEC, MCBAQ-ASQ, and MCBAQ-BEC methods under the same conditions, it is shown that there is an optimal 1.3434 dB improvement in SQNR and a 0.0241 improvement in NMSE using the 3MBAQ algorithm, and the complexity of the algorithm for 3MBAQ is $\mathrm{O}\left({\mathrm{N}}^2\mathrm{l}\mathrm{o}\mathrm{g}\right(\mathrm{N}\left)\right)$, which is within acceptable limits, clearly proving the superiority of the 3MBAQ method.

1. Introduction

Synthetic aperture radar (SAR), with its all-day, all-weather ground observation capability, has a wide range of applications in resource surveys, military reconnaissance, disaster monitoring, and other aspects. In order to provide broader and more detailed target information, the SAR system is rapidly developing in the direction of a high resolution and wide swath. However, for single-channel SAR, an ultralarge width and high resolution are conflicting metrics: the large width of the ground-mapping band requires a low pulse repetition frequency (PRF), and the high resolution in the azimuth direction requires a sufficiently large PRF. The conflicting nature of the PRF is inherent in the limitation of the minimum antenna area [1].

The conflict of PRF cannot be avoided in single-channel SAR systems, but azimuth multichannel SAR (MC-SAR), which is composed of multiple receiving apertures along the azimuth direction, can easily overcome this problem. The coherent superposition of the echo signals received from each channel in the azimuth direction can effectively suppress the Doppler spectral blurring and thus realize a high resolution and ultralarge bandwidth [2]. Such an SAR system causes great hardware design pressure while improving the operating performance; in particular, the size of the data volume is proportional to the number of channels, leading to a rapid increase in the data acquisition, storage, and transmission bandwidth requirements, which in turn imposes more stringent requirements for on-satellite storage and downlink transmission. In this case, the SAR data compression method will directly affect the subsequent processing of SAR data and the quality of SAR products, such as SAR image ship identification, data analysis, and imaging processing. Therefore, a higher-performance SAR raw data compression method is needed to reduce the data transmission rate, taking into account the need for a high compression ratio and low signal distortion.

To date, many SAR raw data compression algorithms have been proposed [3,4]: scalar quantization algorithms [5,6] and vector quantization algorithms [7,8,9] in the time domain [10] take advantage of the statistical properties and intrinsic correlation of the raw data; wavelet transform compression in the transform domain [11,12], the subband coding method, and FFT transform compression [13,14] have better performance but at the same time have greater complexity; and there is also lattice coding quantization [15], predictive coding [16,17,18], compressed sensing [19,20], and entropy-limited quantization [21,22]. Among them, block-adaptive quantization (BAQ) has been the mainstream for single-channel SAR due to the simplicity of its algorithm and hardware implementation [5,23].

Thus far, BAQ is still widely used in the SAR field, but the wide application of BAQ does not indicate its excellent performance in all types of SAR radar. The various variants of the BAQ algorithm also imply that it does not have the advantage of data compression performance in specific SARs. Moreover, with regard to multichannel SAR, as analyzed in the following section, methods such as BAQ are not satisfactory. The purpose of this paper is to propose a method for an azimuthal multichannel SAR system that can utilize the intrinsic connection between azimuthal multichannel data to achieve smaller data distortion in the same scenario and the same data compression ratio, or to achieve a larger data compression ratio under the same data distortion, in order to alleviate the pressure on data storage and transmission in multichannel SAR and to further promote the progress of SAR products.

This paper is organized as follows. In Section 2, the related work performed by the authors prior to the generation of the method in this paper is presented, including the multichannel data compression idea and several data compression methods inspired by and utilized from it. Section 3 presents some basic information about the 3MBAQ method, including a process overview and several key innovations. Section 4 validates the method of this paper on GF data to determine the effectiveness of the method. In Section 5, the test results from Section 4 are illustrated, and the superiority of the 3MBAQ method is determined through analysis and comparison. This paper ends in Section 6 with a conclusion, which briefly describes the key advantages, limitations, and future perspectives of 3MBAQ.

2. Related Work

2.1. Multichannel SAR Data Compression Idea

The difference between the study of data compression under multichannel SAR and several existing single-channel data compression methods lies in the need to consider the connection between multichannel data. As is well known, multichannel SAR is driven by the contradiction between a high resolution and large mapping width, which inevitably generates a large amount of data and spreads them across multiple channels. Therefore, it is obvious that the scenarios corresponding to the data from each channel will overlap, which creates a possibility for the realization of multichannel data compression.

Before exploring the intrinsic correlation of multichannel data, the problem of uniform sampling between the azimuthal multichannel data is inevitable. For an $N$ channel SAR with a pulse repetition frequency of ${PRF}_{sys}$, adapting the BAQ to this system requires that the raw data satisfy a uniform distribution of azimuth samples:

$$PR{F}_{sys}=\frac{2v_{sat}}{L_{az}}$$

(1)

where $v_{sat}$ is the speed of the on-board radar platform, $l_{az}$ is the phase center spacing of the azimuth antenna sub-aperture, and $L_{az}$ is the total azimuth antenna length and satisfies the relation $L_{az}=l_{az}\times N$. However, in the actual SAR system design, in order to avoid receiving down-star point echoes or receiving echo signals in the transmitting pulse window [24], the ${PRF}_{sys}$ does not satisfy the above equation in many cases, and the deviation of the ${PRF}_{sys}$ leads to the azimuth sampling points presenting periodic nonuniform distributions, which results in the emergence of false targets [2], as well as azimuth spectral aliasing. The signal reconstruction of azimuthal multichannel nonuniform sampled data can be achieved by the Krieger filter [2,25], which realizes the transition from multichannel to single-channel, with the equivalent pulse repetition frequency ${PRF}_{eff}={PRF}_{sys}\times N$.

For each aperture of the N-channel SAR-received echo data, considering the correlation of its antenna direction diagrams and azimuth Doppler spectra, a form of intrinsic correlation is introduced to the azimuth data between the channels. For MC-SAR, the ${PRF}_{sys}$ is less than the Doppler processing bandwidth $PBW$. Moreover, the ${PRF}_{eff}$ is greater than the $PBW$, which indicates that there is a large amount of out-of-bandwidth clutter information in the collected data after reconstruction [26], and these unnecessary data take up a larger portion of the transmission bandwidth in the downlink. Therefore, 3MBAQ selectively compresses the Doppler spectrum based on the existing antenna direction diagrams as well as the relationship between ${PRF}_{eff}$ and $PBW$.

2.2. BAQ

The block-adaptive quantization [27] algorithm is the most widespread and mainstream method in space-borne SAR data compression, having the advantages of a simple principle, convenient hardware implementation, great compression performance, and fast computation speed. Meanwhile, the drawbacks are obvious: one is the quantization limitation of the integer number of bits, and the other is the limitation of the compression performance caused by the homogeneous quantization. The BAQ algorithm uses an adaptive quantizer, according to the estimated standard deviation of each small block of input data, to control the optimal quantizer and to achieve the effective compression of the input data, as shown in Figure 1. The raw data received by the radar are sampled by an $n$-bit high-precision ADC to obtain digital signals, and the block-adaptive quantizer encodes and processes the signals of $n$ bits per sample into the signals of $m$ bits per sample, thus realizing the compression of the raw data. The data compressed by the SAR system after BAQ are packaged and then downlinked to the ground or stored on the satellite. In the earth station, the data decoding operation can be carried out to recover the radar data according to each corresponding block of data. Generally, the size of the block is $32\times 32$ or $64\times 64$ (samples of azimuth $\times$ range). The coding principle of BAQ is shown in Figure 1.

$$b_i=\frac{y_{i-1}+y_i}{2}$$

(2)

$$y_i=\frac{{\int }_{b_i}^{b_{i+1}}x·f\left(x\right)dx}{{\int }_{b_i}^{b_{i+1}}f\left(x\right)dx}$$

(3)

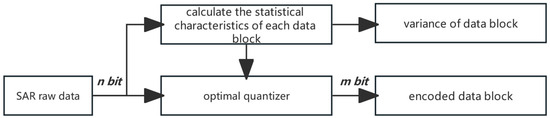
Figure 1. Flowchart of BAQ algorithm. The $n$-bit raw data are quantized and compressed using the statistical characteristics of the block itself (i.e., variance), together with the optimal quantizer, to quantize and compress the data block. The data quantized by m bits and the variance information are preserved as results.

For the SAR raw data, the data distribution generally conforms to a slow-varying memoryless Gaussian distribution, and, based on this characteristic, the selection of the optimal quantizer is shifted from the uniform linear quantizer to the Max-Lloyd optimal quantizer [28]. The Max-Lloyd quantizer finds a set of quantization levels (i.e., $y_i$) and a set of decision thresholds (i.e., $b_i$) for Gaussian-distributed data such that the original data fall within different judgment intervals with the same probability distribution. According to the nearest neighbor condition shown in Equation (2) and the center of mass condition shown in Equation (3), the quantization levels and decision thresholds can be obtained as shown in Table 1.

Table 1. The Max-Lloyd quantizer under standard Gaussian distribution, positive semi-axis section.

i	1 Bit		2 Bit		3 Bit		4 Bit		5 Bit
	${\mathit{b}}_{\mathit{i}}$	${\mathit{y}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{y}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{y}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{y}}_{\mathit{i}}$	${\mathit{b}}_{\mathit{i}}$	${\mathit{y}}_{\mathit{i}}$
1	0	0.7979	0	0.4528	0	0.2451	0	0.1284	0	0.0660
2			0.9816	1.5104	0.5006	0.7560	0.2583	0.3881	0.1332	0.1983
3					1.0500	1.3439	0.5225	0.6569	0.2651	0.3319
4					1.7480	2.1520	0.7997	0.9425	0.3996	0.4673
5							1.0994	1.2564	0.5366	0.6057
6							1.4373	1.6182	0.6770	0.7481
7							1.8437	2.0692	0.8219	0.8957
8							2.4010	2.7327	0.9729	1.0500
9									1.1316	1.2131
10									1.3004	1.3877
11									1.4827	1.5776
12									1.6832	1.7886
13									1.9094	2.0301
14									2.1746	2.3191
15									2.5058	2.6923
16									2.9771	3.2618

In addition, in order to reduce the complexity of calculating the standard deviation of blocks, BAQ calculates the amplitude means of the block signal and then looks up the table to obtain the standard deviations of the blocks.

The mapping relationship [5,10,29] between the means of the absolute values and the standard deviations under the standard Gaussian distribution is given in Equation (4), and the mapping curve between the means of the sampled signal amplitude and the standard deviations of the input signal is shown in Figure 2.

$$\left|\overline{I}\right|=\left|\overline{Q}\right|=127.5-\sum _{n=0}^{N}erf\left(\frac{n+1}{\sqrt{2}\sigma }\right)$$

(4)

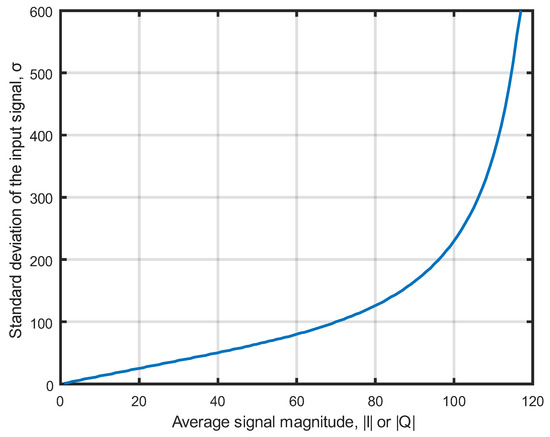
Figure 2. Mapping curve of the means of the sampled signal amplitude to the standard deviations of the input signal. The horizontal coordinate is the average of sub-block elements after taking the magnitude, and the vertical coordinate is the standard deviation of the corresponding sub-block elements. This is the inverse function curve obtained from Equation (4). By obtaining the average signal magnitude of the sub-blocks and using them as addresses, the standard deviations of the sub-blocks can be easily obtained through the correspondence shown in Figure 2. The one-to-one correspondence shown in Figure 2 can be used to create a look-up table, reducing the amount of computation.

2.3. Adaptive Bit Allocation BAQ

Due to the different antenna direction map modulations of the SAR system and the different ground scattering characteristics, the echo signal power of each block of data varies when block coding is implemented, and the adaptive bit allocation BAQ (A-BAQ) data compression algorithm proposes a variable bit rate method to study the adaptive selection of the quantization bit rates for different data blocks. The bit rate selection mechanism is based on the signal power magnitude of the blocks of data, and it can adaptively select quantizers with different bit rates, without the need for a priori knowledge [30] of the scattering characteristics of the features in the imaging region. Compared with the traditional BAQ, it can effectively improve the data signal-to-quantization noise ratio and reduce the complex image phase error, and its computational complexity increases very little; thus, it can be adapted to the data transmission needs of different communication bandwidths.

The basic idea of A-BAQ is to allocate more bits to the sub-blocks with a larger standard deviation and less bits to the sub-blocks with a smaller standard deviation, so that the total quantization distortion is minimized under the condition of certain average bits. Using the Lagrange multiplier method and Gaussian source rate distortion function as detailed in Equations (10)–(16), the sub-blocks are assigned different fractional bits, and the fractional quantization bit per sub-block is further integerized using a bit error control algorithm. A-BAQ compresses the original data in the time domain. The problem is twofold: firstly, there exists a non-adaptation to the multichannel SAR system, thus not obtaining high compression performance; secondly, it is not adapted to the data compression in the uniform target scenarios, including nonuniform bit allocation non-adaptation and bit error control algorithm non-adaptation.

2.4. Multichannel BAQ

A cutting-edge multichannel compression algorithm for MC-SAR is MCBAQ, proposed by Michele Martone et al. [31]. In MC-SAR, data are transferred from the time domain to the transform domain by an interchannel discrete Fourier transform (DFT), and the optimization of the quantization bit rate is applied to the transformed coefficient matrices in order to obtain a bit allocation scheme between the coefficient matrices, with the aim of improving the compression performance according to the spectral energy. The fractional bit rate on the coefficient matrix is achieved by azimuth switch quantization (ASQ) [32] using the standard BAQ for sub-block data compression. The details of the MCBAQ algorithm are shown in Figure 3.

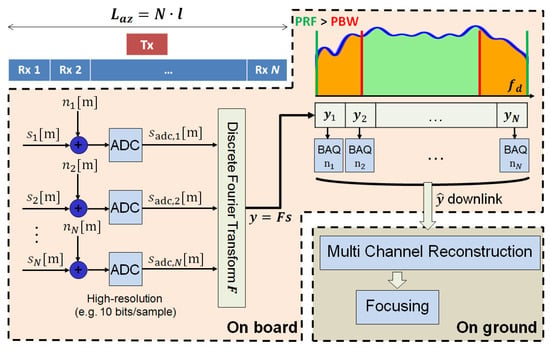
Figure 3. Schematic diagram of the MCBAQ process used in the literature [31]. MCBAQ compresses the echo data of $N$-channel SAR: at each moment $m$, the $i$th channel receives the signal $s_i$ quantized by the high-precision ADC, and then MCBAQ decomposes the multichannel data of length $N$ by the DFT method; finally, the transformed coefficients are assigned appropriate $n_i$ bits to obtain the optimized compression performance.

MCBAQ can adapt azimuthal multichannel SAR [33,34,35], and its advantages are obvious. On the one hand, MCBAQ obtains the $N$-point DFT spectrum between the azimuth channels to avoid the problem of uneven slow-time sampling; on the other hand, it optimizes the compression performance according to the allocation of bits on the coefficient matrices in the spectrum. Problems in MCBAQ also exist: firstly, ASQ can only realize a fractional bit rate without considering the inter-sub-block characteristics, which may cause a performance degradation; secondly, for the result of the $N$-point DFT of MC-SAR with fewer channels (e.g., $N$= 2), its quantization noise is close to the order of magnitude of the FFT noise floor; lastly, spectral coefficients coupled with a larger range of bandwidth information will also result in misallocation on bits.

On this basis, this paper proposes the 3MBAQ method (multichannel, multipulse, multiweight block-adaptive quantization) to obtain nonuniform bit allocation between frequency bands by azimuth multipulse orthogonal transformation and multiweight contribution on multichannel SAR. Specifically, 3MBAQ can effectively avoid the FFT noise floor problem and the problem of spectrum integration to one point of the MCBAQ when the number of channels is small in quantity, and it can extend the application scenario of A-BAQ to the uniform target scenario by utilizing the improved bit error control algorithm. In this paper, it can be concluded, by comparing the compression performance with that of BAQ, A-BAQ, A-BAQ-BEC, MCBAQ-ASQ, and MCBAQ-BEC, that the 3MBAQ method can significantly improve the data signal-to-quantization noise ratio; moreover, the complexity analysis illustrates that 3MBAQ successfully addresses the problem of complexity increasing caused by the reconstruction.

3. Materials and Methods

3.1. Multichannel, Multipulse, Multiweight Block-Adaptive Quantization Summary and Preprocessing

Figure 4 summarizes the data compression flowchart of the 3MBAQ algorithm for echo data with an $N$-channel SAR. Specifically, 3MBAQ obtains the multichannel raw data matrices from the high-precision ADC, obtains the equivalent single-channel Doppler-domain data matrix through the Krieger reconstruction algorithm [2,36], divides it into subbands and then obtains the nonuniform bit allocation among the subbands through the multiweighted contribution, and performs the A-BAQ data compression within the subband matrices. The final result is downloaded to the earth station for processing.

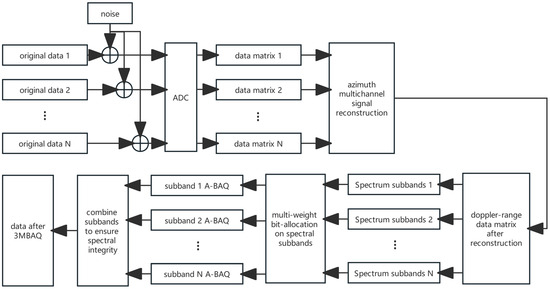
Figure 4. Flowchart of the 3MBAQ algorithm. The high-precision ADC data are obtained from the original distortion-free data, and then the multichannel signal is reconstructed by a Krieger filter to obtain the equivalent single-channel azimuth frequency–distance time-domain matrix. The Doppler-domain data are divided into multiple subband matrices, and the A-BAQ algorithm is implemented on the subbands by obtaining a nonuniform bit allocation scheme between the subbands through multiple weighted contributions.

It is assumed that each azimuth pulse, after being received, is sampled by a high-precision ADC to obtain $N_r$ samples of distance range data, and each channel aperture retains $N_{as}$ slow-time sampled data. The time-domain complementary zero Fourier transform of $N_{am}=N_{as}\times N$ points is performed, filtered, and merged on the azimuth multichannel signals, respectively, by a Krieger filter. The Krieger reconstruction filter [2] is shown in Equation (5).

$$\begin{array}{c}P\left(f\right)={\mathrm{H}}^{-1}\left(f\right)\hfill \\ =\left[\begin{array}{ccc}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{j}\mathsf{\pi }\left(\frac{∆x_1^2}{2\lambda r_0}+\frac{∆x_1}{v_{sat}}f\right)\right)& \cdots & \mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{j}\mathsf{\pi }\left(\frac{∆x_N^2}{2\lambda r_0}+\frac{∆x_N}{v_{sat}}f\right)\right)\\ ⋮& \ddots & ⋮\\ \mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{j}\mathsf{\pi }\left(\frac{∆x_1^2}{2\lambda r_0}+\frac{∆x_1}{v_{sat}}(f+(N-1)\times {PRF}_{sys})\right)\right)& \cdots & -\mathrm{j}\mathsf{\pi }\left(\frac{∆x_N^2}{2\lambda r_0}+\frac{∆x_N}{v_{sat}}(f+(N-1)\times {PRF}_{sys})\right)\end{array}\right]\hfill \end{array}$$

(5)

where $f$ is ${[PRF}_{eff}/2,{PRF}_{eff}/2+{PRF}_{sys}]$, which is the range of azimuth frequencies indicated by a single channel; $∆x$ is the distance between the equivalent phase center of the $k$th receiving antenna channel and the phase center of the transmitting antenna; $\lambda$ is the wavelength of the carrier frequency; and $r$ is the slant distance corresponding to the range bin.

The process and results of the Krieger filter reconstruction are tested with point target simulation, and the image results are shown schematically in Figure 5. Comparing the multichannel imaging results after reconstruction, the multichannel nonuniform sampling information without reconstruction processing is manifested in the image as the appearance of false targets, and the single-channel imaging results are manifested as Doppler spectral aliasing. The parameters for the reconstruction simulation with point target signals are the same as the GF3 data in Section 4.

Figure 5. Schematic of the effect of the Krieger filter: (a) is the result of multichannel signal imaging after using the reconstruction algorithm; (b) is the result of multichannel imaging without reconstruction, which produces obvious false targets in the image; and (c) is the result of imaging after utilizing single-channel complementary zeroing, which produces severe azimuth spectral aliasing due to the fact that the ${PRF}_{sys}$ is smaller than the $PBW$.

3.2. Transform-Domain Compression Effectiveness Analysis

The SAR raw data, while conforming to an approximate zero-mean Gaussian distribution, have low correlations in the distance and azimuth directions, respectively. Orthogonal decorrelation transforms the strongly correlated spatial samples into uncorrelated or weakly correlated transform coefficients, which removes the data redundancy that exists in the correlation. Under certain conditions, such as increasing the transform size, it is even possible to make these coefficients independent of each other, resulting in a memoryless source, so that each coefficient can be quantized independently [11]. The azimuth signal is reconstructed to obtain uniformly sampled echo data, and the azimuth $N_{am}$ pulses are used to obtain the azimuth spectrum by the orthogonal transformation of the DFT, as shown in the following equation, which realizes the decorrelation of the azimuth direction into the Doppler range domain.

$$y_{k_{rg}}[k_{az}]={\displaystyle \sum _{n=0}^{Nam-1}(s_{k_{rg}}[n])}{e}^{-j\pi n{k}_{az}/Nam}$$

(6)

$k_{rg}=[\mathrm{1,2},\cdots ,N_r]$ denotes the range-oriented position and $k_{az}=[\mathrm{1,2},\cdots ,N_{am}]$ denotes the azimuth-oriented position.

According to the ratio of the Doppler bandwidth $PBW$ to the sampling rate ${PRF}_{eff}$, the number of subbands in the frequency domain can be selected appropriately, and it is generally the same as the original channel number $N$ due to the consideration of the oversampling rate and the number of channels in the design of the whole system. Due to the decorrelation effect of the orthogonal transform, the DFT redistributes and concentrates the energy, so the energy distribution of each subband coefficient is different, and the inverse Fourier transform reconstructs the time-domain data with different contributions to the original data. In order to achieve the purpose of optimal compression, different frequency subband coefficients need to be allocated different bits. Optimal bit allocation aims to find a reasonable bit allocation scheme to minimize the total coding error given the total bit rate under some error measure [11].

The transform encoder decomposes the signal and optimizes the compression of the decomposition coefficients under the discrete Fourier transform orthonormal basis $B=\left\{F_{k_{az}}\right\}$, $0\le k_{az}<N_{am}$. Assuming that the probability distribution of the one-dimensional signal $s_{k_{rg}}\left[n\right]$ is known and its IQ decomposition data have a zero-mean slow-variable memoryless Gaussian distribution with length $Nam$, the decomposition of $s_{k_{rg}}$ under $B$ has

$$s_{k_{rg}}={\displaystyle \sum _{k_{az}=0}^{Nam-1}{y}_{k_{rg}}[k_{az}]\cdot F_{k_{az}}}$$

(7)

$$y_{k_{rg}}[k_{az}]=⟨s_{k_{rg}},F_{k_{az}}⟩={\displaystyle \sum _{n=0}^{Nam-1}{s}_{k_{rg}}[n]\cdot F_{k_{az}}^{\ast }[n]}$$

(8)

Scalar quantization is taken for the coefficients of the decomposition, and we let the quantized coefficients be ${\tilde{y}}_{k_{rg}}\left[k_{az}\right]$. The quantized reconstructed signal is then

$${\tilde{s}}_{k_{rg}}={\displaystyle \sum _{k_{az}=0}^{Nam-1}{\tilde{y}}_{k_{rg}}[k_{az}]F_{k_{az}}}$$

(9)

Using the mean square error distortion measure and based on the nature of the orthogonal bases, the average coding distortion due to the above quantization process is

$$d=E\left\{{\Vert s_{k_{rg}}-{\tilde{s}}_{k_{rg}}\Vert }^2\right\}={\displaystyle \sum _{k_{az}=0}^{Nam-1}E\left\{{\left|y_{k_{rg}}[k_{az}]-{\tilde{y}}_{k_{rg}}[k_{az}]\right|}^2\right\}}$$

(10)

The above equation shows that the total coding distortion of the signal after canonical orthogonal basis decomposition depends on the sum of the coding distortion of all its transform coefficients, and it also proves that the optimization process of bit allocation and data quantization can be carried out only for the transform coefficients for the discrete Fourier transform, and the methodology used in Equation (6) is valid.

3.3. Nonuniform Bit Distribution

It is known that the SAR raw data are decorrelated by the azimuth discrete Fourier transform, and the statistical properties of the Doppler distance domain data obtained are consistent with the assumption of a continuously distributed memoryless Gaussian source; therefore, its rate distortion function is utilized to implement the process of bit allocation.

$$R_n=\frac{1}{2}{\log }_2\left(\frac{{\sigma }_n^2}{d_n}\right)$$

(11)

$$d_n={\sigma }_n^2\times 4^{-R_n}$$

(12)

It should be noted that ${\sigma }_n^2$ denotes the source variance, i.e., the signal energy, in the SAR raw data domain; according to Paswal’s theorem, it should denote the frequency domain integral, i.e., the signal energy, in the Doppler frequency domain, and the denotation is detailed in Equation (19). Moreover, the average distortion of all subband data quantization is

$$\overline{d}\left(\overline{R}\right)=\frac{1}{N}{\displaystyle \sum _{n=0}^{N-1}{d}_n\left(R_n\right)}$$

(13)

$\overline{R}$ is the preset average number of quantization bits, and $d_n\left(R_n\right)$ denotes the mean square quantization error under the condition that the number of subband quantization bits is $R_n$. Thus, we have

$$\overline{d}\left(\overline{R}\right)=\frac{1}{N}{\displaystyle \sum _{n=0}^{N-1}{\sigma }_n^2\times 4^{-R_n}}$$

(14)

Thus, the optimal bit allocation problem is described as follows: under the condition that the average number of quantization bits is fixed, find the allocation of the quantization bits that minimizes the average quantization distortion defined by Equation (14). According to the Lagrange multiplier method, the objective function as well as the optimal solution for nonuniform bit allocation can be obtained as

$$\underset{R_n,n=1,\cdots ,N}{\arg \min }J=\underset{R_n,n=1,\cdots ,N}{\arg \min }\left[\frac{1}{N}{\displaystyle \sum _{n=0}^{N-1}{\sigma }_n^2\times 4^{-R_n}+\lambda \left(\frac{1}{N}{\displaystyle \sum _{n=0}^{N-1}{R}_n-\overline{R}}\right)}\right]$$

(15)

$$R_n=\overline{R}+\frac{1}{2}\left[{\log }_2{\sigma }_n^2-\frac{1}{N}{\displaystyle \sum _{m=0}^{N-1}{\log }_2{\sigma }_m^2}\right]=\overline{R}+\Delta R_n$$

(16)

The nonuniform bit allocation in the Doppler domain obtained from Equation (16) is illustrated by the following two points.

(1) According to Paswal’s theorem, ${\sigma }_n^2$ should represent the frequency-domain integral, i.e., the signal energy, $P_n$ in the Doppler frequency domain; considering the relationship between the $PBW$ and subbands in the Doppler frequency domain, ${\sigma }_n^2$ should be proportional to the effective integral of the subband Doppler power spectrum, i.e., to the integral $I$ of the corresponding frequency band Dirichlet kernel [31] within the effective bandwidth. By means of multiple weighted contributions, the following can be obtained:

$$P_n=\frac{1}{Nas\cdot Nr}{\displaystyle \sum _{k=1}^{Nr}{\displaystyle \sum _{m=1}^{Nas}{\left|y_{n,k}\left[m\right]\right|}^2}}$$

(17)

$$I_n={\displaystyle \underset{-PBW/2}{\overset{PBW/2}{\int }}\left|\frac{\sin \left(\pi N\frac{f+PRF\left(N/2-n\right)/N}{PRF}\right)}{\sin \left(\pi \frac{f+PRF\left(N/2-n\right)/N}{PRF}\right)}\right|}df$$

(18)

$${\sigma }_n^2=\frac{P_n\cdot I_k}{N^2}$$

(19)

where $y_{n,k}\left[m\right]$ denotes the Doppler distance-domain data for the $n$th frequency band corresponding to position $(m,k)$, and $1/N^2$ serves as a scale variation factor and does not contribute to the actual bit allocation.

(2) Equation (16) is applicable under compression scenario conditions with high bit rates, whereas $R_n=\overline{R}+∆R_n$ may occur at large compression ratios, which is not allowed by the practical situation [13]. In the case whereby the preset average number of quantization bits $\overline{R}$ is small, a simple compromise is taken to limit the upper and lower bounds of the bit rate by restricting the minimum number of quantization bits of the subband data to 0 bit according to the proportional scaling of the bit allocation scheme, and this restriction is reflected in both the Doppler-domain nonuniform bit allocation and the bit error control algorithm.

The fractional inter-subband nonuniform bit allocation is obtained by the previous steps, the improved A-BAQ algorithm is further utilized to obtain the integer variable bit rate among the subbands sub-blocks, and BAQ is applied to each sub-block, which finally results in a compressed data matrix in the complete frequency domain.

3.4. Improved Bit Error Control Algorithm

Considering the fact that the uniformity of the actual target scenario will lead to less high-frequency information in the Doppler spectrum, a small-amplitude dynamic range of the sub-block, and uniform energy of the sub-block, it is necessary to adjust the bit error control (BEC) part of the A-BAQ in order to ensure the requirement of the fixed-length coding of the integer number of bits of the BAQ quantizer, as well as the realization of the fractional bit rate coding in the homogeneous scenario. The flow of the improved bit error control coding is shown in Figure 6 below. The symbols defined in Figure 6 are shown in Table 2.

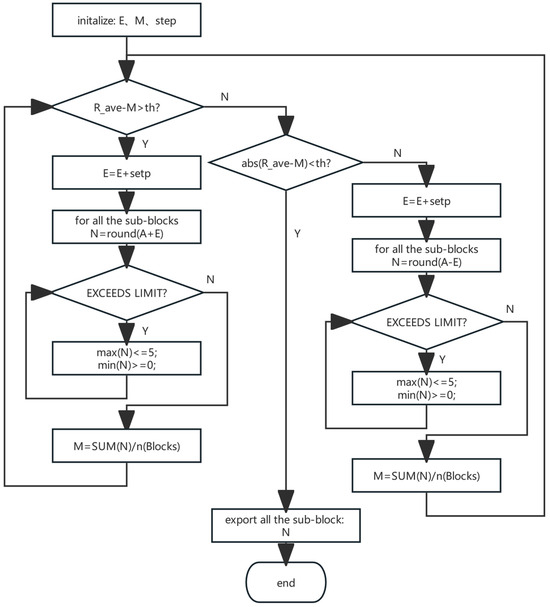
Figure 6. Improved bit error control algorithm. The BEC algorithm considers the cases of exceeding and falling below the average number of bits, respectively, and strictly controls the average number of bits in the threshold range.

Table 2. Bit error control symbol description.

Symbol	Statement
$E$	Bit rate error that needs to be adjusted
$M$	Average bits for all current sub-blocks
$R\_ave$	Preset average bits
$A$	Theoretical fractional bit number matrix
$N$	Sub-block bit matrix after adjustment to integers
$th$	Error thresholds for M and R_ave

Compared with the bit error control algorithms proposed in the literature [3], the bit error control algorithm in Figure 6 has the advantage of realizing adaptive bit allocation in the uniform target scenario. In the homogeneous scenario, the low dynamic range of the sub-block data and the slow change characteristics between sub-blocks are obvious. Utilizing the old bit error control algorithm centered on the floor() function (rounding to negative infinity) in such a context leads to a degradation in the overall quantization bit count and compression performance in the threshold range, i.e., $0\le R\_ave-M\le th$, where the optimization upper limit is BAQ. The BEC algorithm used by 3MBAQ utilizes the round() function (round to nearest integer), which fits the idea of nonuniform bit allocation, as the core, considering the strict control of the upper limit of the transmission bandwidth. It strengthens the bit error threshold $th=0.005 bit$, which can reach a maximum relative error of 0.25% with the number of 2-bit quantization bits. It can be regarded as not affecting the transmission bandwidth, thus solving the problem that the round() function exceeds the bandwidth limitation and highlighting its effective allocation in the case of a homogeneous scenario, a small bit transformation range $∆R_n$, and a degradation to the quantization performance of the classical BAQ in the worst case.

Taking the average bit quantization target of 2 bits as an example, the effect of bit allocation is shown in Figure 7. When utilizing the bit error control algorithm with the floor() function as the core, the average number of bits actually fails to reach the preset target in the uniform target scenario, while the BEC algorithm with the round() function as the core proves the effectiveness of its difference quantization.

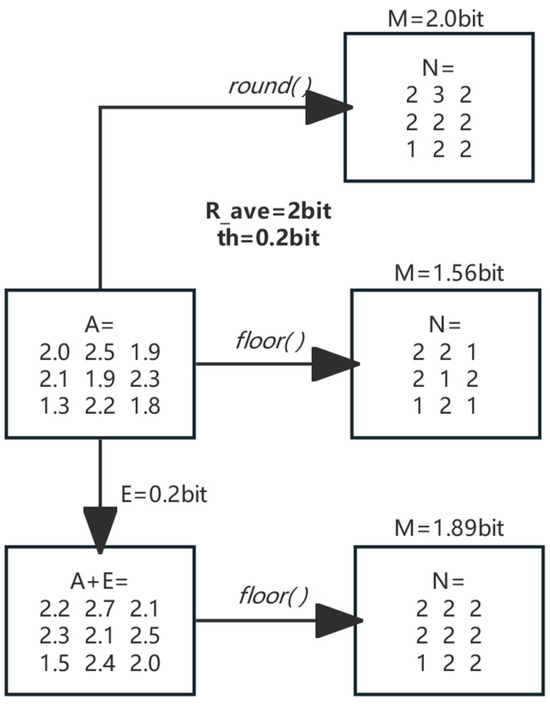
Figure 7. Illustration of the failure of the bit error control algorithm based on floor() as the core and the effectiveness of the bit error control algorithm based on round() as the core in the homogeneous scenario.

4. Result

4.1. Definition of Data Compression Evaluation Metrics

4.1.1. Signal-to-Quantization Noise Ratio (SQNR)

SQNR [37] is the signal-to-noise ratio when the distortion of the signal before and after compression is considered as noise, reacting to the effect of the data compression algorithm on the signal, and the larger its value is, the smaller the effect of data compression on the signal.

$$SQNR=10{\log }_{10}\frac{{\displaystyle \sum _{i=1}^{Nam}{\displaystyle \sum _{j=1}^{Nr}{\left|s_{ij}\right|}^2}}}{{\displaystyle \sum _{i=1}^{Nam}{\displaystyle \sum _{j=1}^{Nr}{\left|s_{ij}-{\tilde{s}}_{ij}\right|}^2}}}$$

(20)

where $s_{ij}$ is the value of the uncompressed signal at $(i,j)$, ${\tilde{s}}_{ij}$ is the value of the signal at $(i,j)$ after data compression, and $i$ and $j$ are the number of sampling points in the azimuth and range.

4.1.2. Normalized Mean Square Error (NMSE)

NMSE indicates the signal energy distortion introduced by compression; the smaller the value of this index, the smaller the error introduced by compression.

$$NMSE=\frac{{\displaystyle \sum _{i=1}^{Nam}{\displaystyle \sum _{j=1}^{Nr}{\left|s_{ij}-{\tilde{s}}_{ij}\right|}^2}}}{{\displaystyle \sum _{i=1}^{Nam}{\displaystyle \sum _{j=1}^{Nr}{\left|s_{ij}\right|}^2}}}$$

(21)

4.2. Homogeneous Scenario Data Test

Since the distortion-free SAR raw data acquired by the space-borne SAR system in real time cannot be obtained, this paper adopts the raw data acquired by GF3 [38] as the experimental data, and the data are quantized by high-precision ADC into the float32 format. Table 3 shows the parameters of the SAR carried by the GF3 satellite.

Table 3. Parameters of GF3.

Parameter	Value
Number of azimuth channels, $N$	2
Frequency band	$C$
Azimuth antenna length, $L_{az}$	7.5 m
Pulse repetition frequency, ${PRF}_{sys}$	2179 Hz
Total processed bandwidth, $PBW$	2466 Hz
Minimum slant range, $R_c$	902,273 m
Effective radar velocity, $V_r$	7133 m/s
Range sample frequency, $f_s$	133 MHz
Range bandwidth, $B_r$	120 MHz

The nonuniform bit allocation results for MCBAQ and 3MBAQ are ${∆R}_n=[-\mathrm{0.857,0.857}]$ and ${∆R}_n=[-\mathrm{1.0036,1.0036}]$, respectively, and a limit on the number of compressed bits is needed when the overall number of quantization bits is small. In the following, 3MBAQ-BEC also denotes the algorithm 3MBAQ proposed in this paper with consistency.

Table 4 shows the performance comparison of the SQNR and NMSE metrics obtained after using a total of six data compression methods, namely BAQ, ABAQ, ABAQ-BEC, MCBAQ-ASQ, MCBAQ-BEC, and 3MBAQ, on the GF3 data with 2 bits on average. The SQNR and NMSE for different average quantization bits using different quantization schemes in the GF3 homogeneous scenario are shown in Figure 8 and Figure 9. Because of the limitation of A-BAQ-BEC in the homogeneous scenario, its quantization performance is identical to that of BAQ, so it is uniformly represented by the curve of A-BAQ-BEC. Figure 10 shows the original scenario of the GF3 data. The comparison of each compression scheme in the image domain for the localized scenario of GF3 is shown in Figure 11, and it can be seen from the 3D noise map that the image noise of BAQ, MCBAQ-BEC, and 3MBAQ decreases sequentially and the compression quality gradually improves. It should be noted that when the overall number of quantization bits is an integer, the quantization effect of A-BAQ-BEC is the same as that of BAQ, which cannot use noninteger quantization, so the BAQ method is used in Figure 11 for comparison, while the A-BAQ-BEC method is used in Figure 8 and Figure 9 instead, which is essentially the same.

Table 4. Evaluation results of methods on GF3 real data under the overall quantization bit size of 2 bits.

INDEX	BAQ	A-BAQ	A-BAQ-BEC	MCBAQ-ASQ	MCBAQ-BEC	3MBAQ
SQNR	9.4566	9.4253	9.4566	9.3951	9.6458	10.7385
NMSE	0.1133	0.1141	0.1133	0.1149	0.1085	0.0844

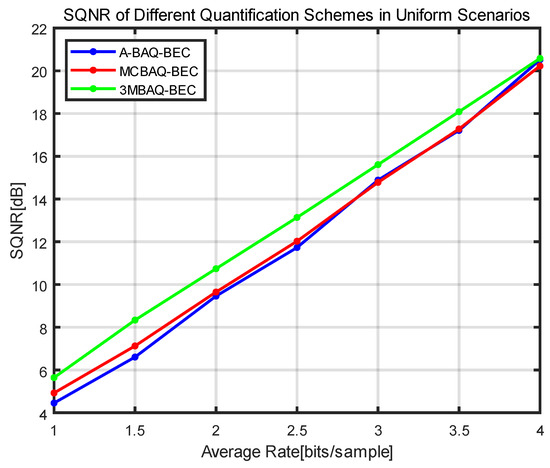
Figure 8. SQNR of homogeneous scenarios under different quantization schemes as a function of the average rate: 3MBAQ in green, MCBAQ-BEC in red, and A-BAQ-BEC in blue.

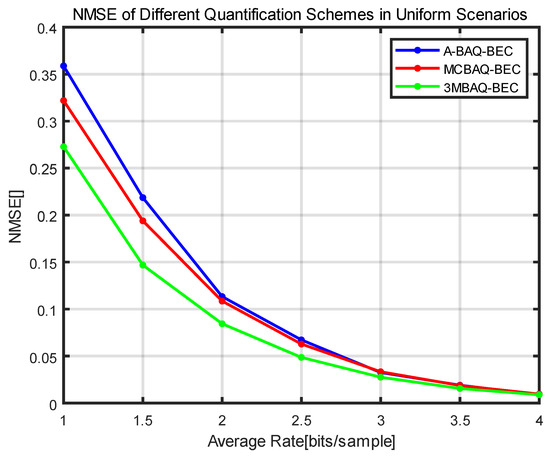
Figure 9. NMSE of homogeneous scenarios under different quantization schemes as a function of the average rate: 3MBAQ in green, MCBAQ-BEC in red, and A-BAQ-BEC in blue.

Figure 10. On the left is an uncompressed raw image of the GF3 test data (a), and on the right is a zoomed-in view of a localized lake area from the GF3 data (b).

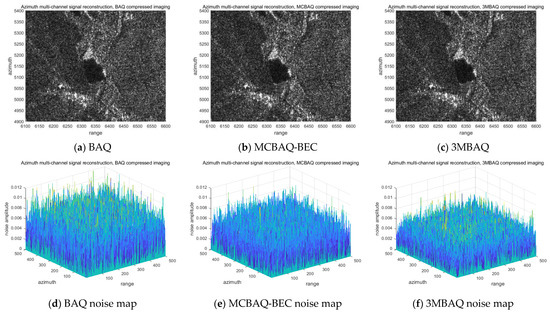
Figure 11. Performance of BAQ, MCBAQ-BEC, and 3MBAQ in the image domain at 2 bits. (a) Image after data compression and then restoration by the BAQ method; (b) image after compression and then restoration by the MCBAQ-BEC method; (c) image after compression and then restoration by the 3MBAQ method; (d) quantization noise generated by the BAQ method; (e) quantization noise generated by the MCBAQ method; (f) quantization noise generated by the 3MBAQ method.

5. Discussion

5.1. SQNR Upper Bound

The literature [22] discusses conventional single-channel BAQ performance with a effective 0.225-bit difference, but it is clearly not applicable here. Due to the similarity between radar chirp signals and sinusoidal signals, the SQNR of the radar echo data is discussed as if it were a sinusoidal signal, and the RMS of the full-scale input sinusoidal signal, as well as the RMS of the quantization noise, is given by

$$rm{s}_{in}=\frac{q\cdot 2^R}{2\sqrt{2}}$$

(22)

$$rm{s}_n=\frac{q}{\sqrt{12}}$$

(23)

where $q$ denotes the lowest significant bit.

$$\begin{array}{cc}\hfill SQNR& =10{\log }_{10}{\left(\frac{rm{s}_{in}}{rm{s}_n}\right)}^2\hfill \\ & =20{\log }_{10}\frac{q{2}^R/2\sqrt{2}}{q/\sqrt{12}}\hfill \\ & =20{\log }_{10}{2}^R+20{\log }_{10}\sqrt{\frac{3}{2}}\hfill \\ & =6.02R+1.76\hfill \end{array}$$

(24)

Since the conversion between the frequency and time domains does not affect the final evaluation metrics on the original data domain, the upper limit of the SQNR of the BAQ, A-BAQ, A-BAQ-BEC, MCBAQ-ASQ, MCBAQ-BEC, and 3MBAQ algorithms based on BAQ at 2 bits is 13.8 dB, instead of 10.6 dB as shown in the literature [22].

5.2. Original and Improved Bit Error Control Algorithm

As shown in the results in Table 4, the SQNR of the A-BAQ algorithm in the GF3 scenario is 9.4253 dB, which is smaller than that of the classical BAQ, which is 9.4566 dB, and the NMSE of A-BAQ is inferior to that of BAQ. The nature of the failure of the A-BAQ algorithm in the homogeneous target scenario, in terms of algorithmic data, is that the small energy difference of the sub-blocks of the original data of the GF3 leads to the mismatch of the variable bit allocation formulae derived using the rate distortion function and the Lagrange multiplier method, which results in the extremely small magnitude of the variation in the bit allocation through Equation (16). The original bit error control algorithm is centered on the floor() function, which leads to an upper limit of performance optimization of the A-BAQ algorithm in a homogeneous target scenario at the level of BAQ. A-BAQ-BEC utilizes the round() function as the core of the method improvement, which, together with adaptive bit allocation, can achieve an SQNR of 9.4566 dB, which is better than the effect of the original bit error control algorithm. Since the uniformity of the original data is not fundamentally solved, the optimization effect of A-BAQ-BEC is limited, and, from the algorithmic point of view, it can only achieve the worst performance optimization at the equivalent BAQ level. This is the limitation of the varying bit algorithm in homogeneous target scenarios, while the effectiveness in nonuniform target scenarios is proven by the results in the literature [3].

5.3. MCBAQ-ASQ and MCBAQ-BEC

The literature [31,32] uses the azimuth switch quantization to achieve a fractional bit rate. ASQ achieves fractional quantization bits with alternating azimuth quantization bits $⌈R_n⌉$ and $⌊R_n⌋$ and fixing bits for all distance-oriented sub-blocks, which achieves a fractional bit rate according to mathematical laws rather than intrinsic logic. This paper compares MCBAQ-ASQ and MCBAQ-BEC; the latter realizes bit allocation according to the energy distribution and concentrates the sub-blocks with small quantization bits in the azimuth high-frequency clutter portion. It couples the quantization noise into signals outside of the bandwidth and reduces the effect of the quantization noise on the effective information, so MCBAQ-BEC quantization is superior to all methods other than 3MBAQ under the same conditions. The SQNR of MCBAQ-BEC is 9.6458 dB, while that of MCBAQ-ASQ is 9.3961 dB. ASQ, as a fractional bit rate implementation algorithm, has a lower SQNR than BAQ when used with MCBAQ.

5.4. MCBAQ and 3MBAQ

MCBAQ-BEC concentrates the azimuth subband spectral information to one point by interchannel orthogonal transformation; the uniformity of the final coefficient matrix is strengthened, and the effect of utilizing adaptive bit allocation BAQ on this matrix is limited, with an SQNR of 9.6458 dB. In addition, according to the University of California at Berkeley’s IC course, when the number of interchannel FFT points is 2, the 32-bit quantization noise SQNR obtained from the distortion-free data on the satellite after sampling through the high-precision ADC data will be of the same order of magnitude as the FFT noise floor, and too few points in the FFT will have a certain effect on the noise floor.

Meanwhile, 3MBAQ obtains the Doppler spectrum information under the $N_{am}$ points FFT result by azimuth multipulse reconstruction, which is decorrelated by FFT orthogonal basis conversion on one hand and converted to the spectrum on the other hand, in order to expand the dynamic range of the data and the magnitude of the variance change among the sub-blocks, which is helpful for the use of the varying bit algorithm. Inter-subband bit allocation is realized on the Doppler spectrum using the multi-weighted contribution of information such as the subband to total bandwidth ratio, subband energy, etc., which is more in line with practical experience and the variable bit allocation requirements. Compared to BAQ, the 3MBAQ algorithm has a 1.3 dB improvement in SQNR, and this improvement overcomes the limitation of homogeneous scenarios.

Figure 8 and Figure 9 show the performance of different quantization schemes in the homogeneous scenario. The 3MBAQ algorithm consistently outperforms A-BAQ-BEC and MCBAQ-BEC within the range of 1 bit to 4 bits, and the optimization effect of SQNR is greatest within the range of 1.5 bits to 2.5 bits. As the average bit rate increases, the performance of MCBAQ-BEC and 3MBAQ gradually approaches that of A-BAQ-BEC, both because the effect of the upper limit of the bit allocation makes the range of variable bits smaller and smaller and because, as the number of preset bits rises, the bit allocation scheme accounts for a smaller and smaller proportion of the overall number of quantization bits. Therefore, 3MBAQ has a diminishing effect on the SQNR of the image. By comparing the image domain effects of different quantization schemes and the quantization noise image under 2-bit compression in Figure 11, it can be seen that, among BAQ(A-BAQ-BEC), MCBAQ-BEC, and 3MBAQ, 3MBAQ is able to obtain better image quality and the smallest overall quantization noise under a large compression ratio. The comparison results of the 3MBAQ images with different compression ratios shown in Figure 12 indicate that the SQNR of 3MBAQ is 9.4430 dB at 1.72 bits, and its image quality is comparable to that of the BAQ-compressed SAR image at 2 bits, which can also be verified in Figure 8.

Figure 12. Taking the original image (a) and the image domain effect of BAQ algorithm at 2 bits (f) as a reference, (b–e) demonstrate the image domain compression effect of the 3MBAQ algorithm at different bits. The 3MBAQ algorithm achieves well-compressed results at all compression ratios, and the compression effect of the 1.72-bit 3MBAQ is similar to that of the 2-bit BAQ.

The GF3 data test results show that 3MBAQ can effectively improve the SAR raw data compression performance. It can exceed the performance of A-BAQ-BEC in the homogeneous target scenario and exceed the performance of MCBAQ-BEC in the case of fewer channels, and it provides more diversified choices for the real-time data compression of the multichannel space-borne SAR system.

5.5. Algorithm Complexity Analysis

Assuming that the number of channels is $N$, the single channel is compressed once every $N_a\times N_r$ sampling points. Because the flight parameters are fixed, the Krieger reconstruction filter can be calculated in advance, which does not account for the complexity. Moreover, in the reconstruction process, only $N$ times $N_a\times N=N_{am}$ points of the complementary zero FFT process and one addition operation are added in each range unit, the obtained $N_{am}\times N_r$ points of the Doppler-distance domain data can be used directly as azimuth multipulse FFT results, and the arithmetic complexity is mainly increased in the complementary zero FFT of $O\left(N_{am}{N}_{r}log\right(N_{am}\left)\right)$. The multi-weighted contribution part requires a summation of the subband spectral energies, and the complexity is proportional to the amount of data $O\left(N_{am}{N}_r\right)$, while the integration of the Dirichlet kernel can be obtained in advance and does not account for the computational complexity.

Overall, the complexity of 3MBAQ is $O\left(N_{am}{N}_{r}log\right(N_{am}\left)\right)$, which is an acceptable increase compared to the complexity of BAQ, $O\left(N_{am}{N}_r\right)$ and is much reduced compared to the complexity of FFT-BAQ, $O\left(N_{am}{N}_{r}log\right(N_{am}{N}_r\left)\right)$. In engineering, the satellite multichannel calibration unit, a fast intelligent imaging unit, will include azimuth signal amplitude-phase calibration and channel signal reconstruction. The preparation of 3MBAQ is covered, so that there is no need to take into account the complexity expenditure of the reconstruction; thus, the complexity of the algorithm is of the same order of magnitude as that of A-BAQ.

6. Conclusions

In this paper, a space-borne multichannel SAR Doppler-domain A-BAQ algorithm, 3MBAQ, is proposed on the basis of MCBAQ and A-BAQ. In particular, 3MBAQ obtains data compression results through azimuth multichannel reconstruction, the FFT of multipulses, nonuniform bit allocation for multibands and sub-blocks, bit error control algorithms, and BAQ, and it shows a maximum 1.3434 dB improvement in SQNR and 0.0241 improvement in NMSE compared to BAQ, A-BAQ, A-BAQ-BEC, MCBAQ, and MCBAQ-BEC. Moreover, in addition to innovatively proposing 3MBAQ, a BEC algorithm that can be used with A-BAQ in a homogeneous targeting scenario is also well developed, and the validity of 3MBAQ for the compression of multichannel space-borne SAR raw data in a homogeneous targeting scenario is verified on the data of GF3. In terms of application prospects, 3MBAQ reduces the computational process to the overall complexity $O\left(N^{2}log\right(N\left)\right)$, and its complexity can be further reduced due to the overlap of the preparation work of reconstruction by multichannel calibration and the fast intelligent processing unit.

However, the content of this paper is constrained by the limited samples of 3MBAQ test data, including the limited amount of data and the limited number of azimuth channels, and the advantages of 3MBAQ obtained in this way are yet to be proven by subsequent experiments. Moreover, when realizing engineering applications, problems such as data matrix storage, the determination of the number of points of the multipulse FFT, the conflict of pipelining, and the poor price–performance ratio of compression schemes may be encountered. With the continuous development of hardware, these problems will no longer be experienced, and we believe that the algorithm has great development prospects.