Deep-Learning Gravity Inversion Method with Depth-Weighting Constraints and Its Application in Geothermal Exploration
Abstract
1. Introduction
2. Method
2.1. Regularized Gravity Inversion Theory
2.2. Deep-Learning Inversion Theory
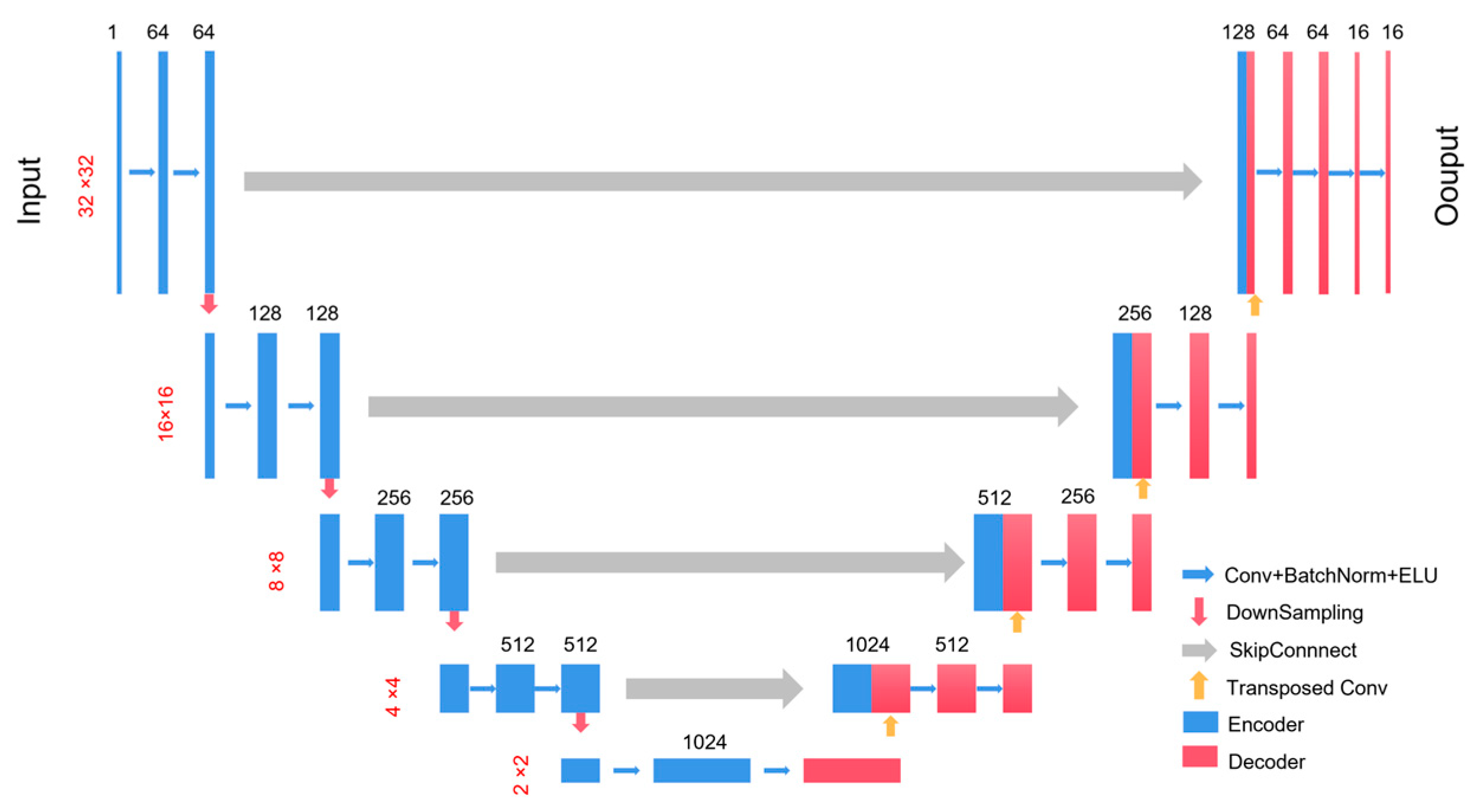
2.2.1. Introduction to U-Net Network
2.2.2. Loss Function
3. Model Testing
3.1. Dataset
3.2. Model Testing
3.2.1. Model I
3.2.2. Model II
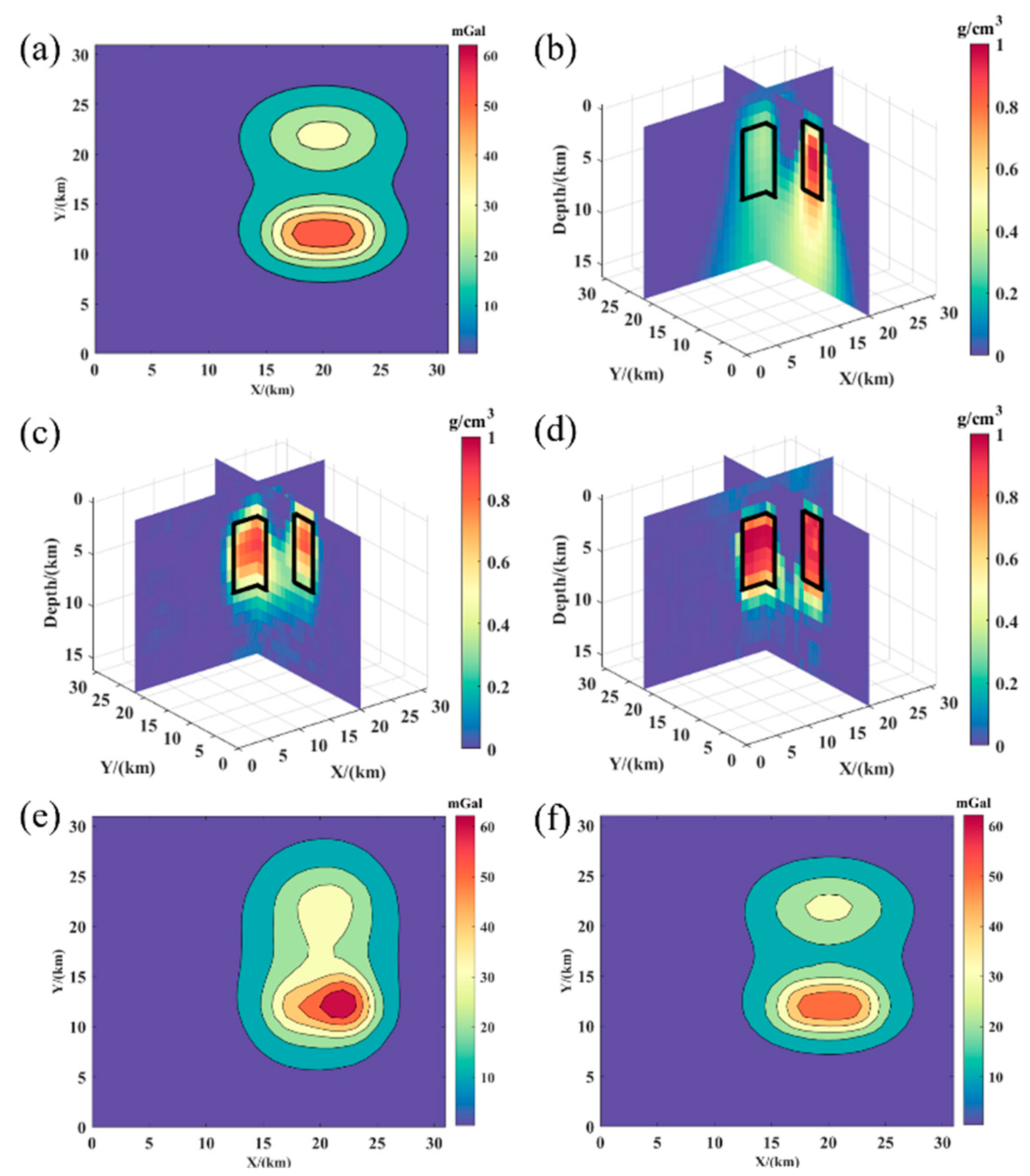
3.2.3. Model III
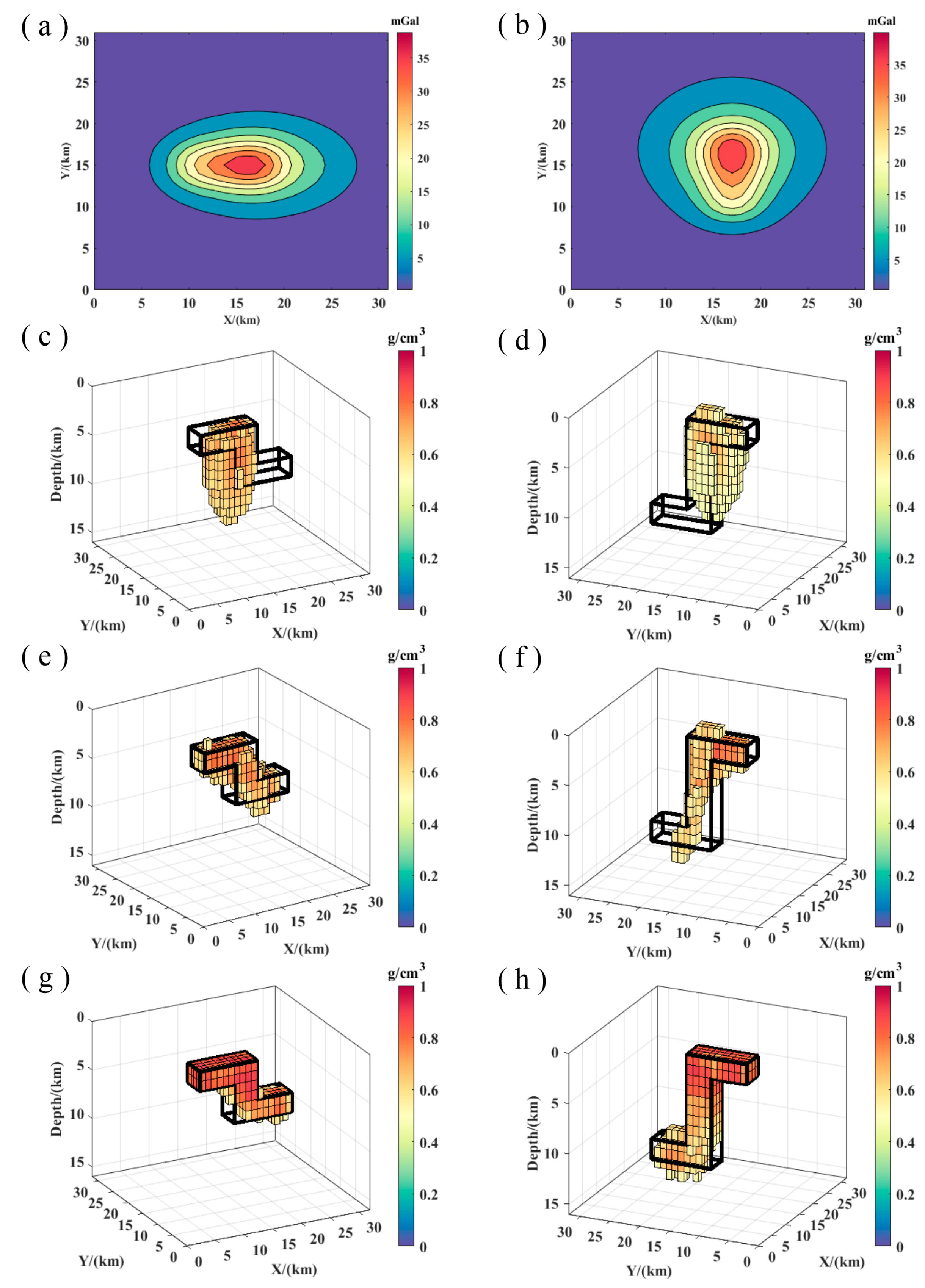
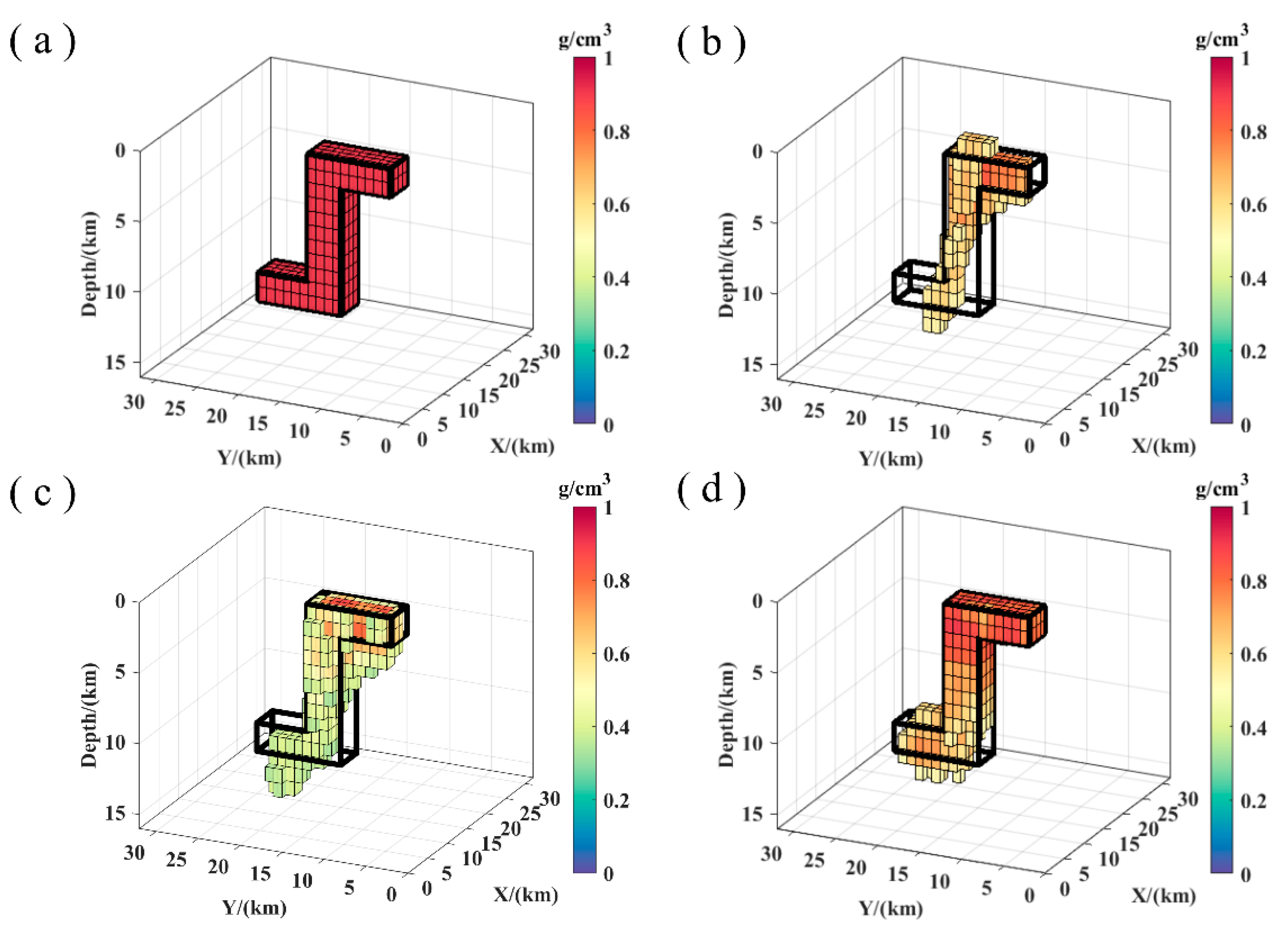
3.2.4. Model IV
3.2.5. Model V
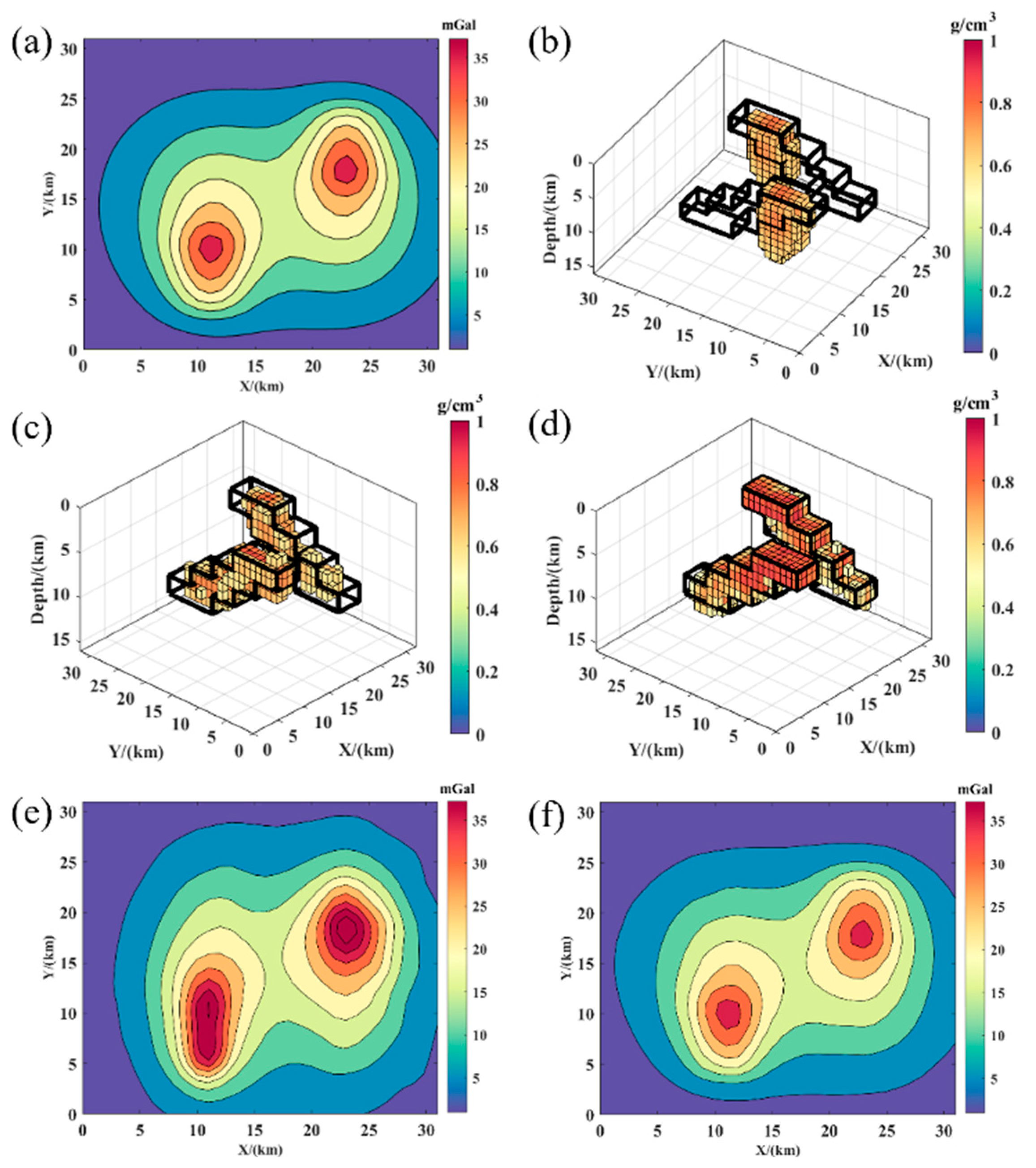
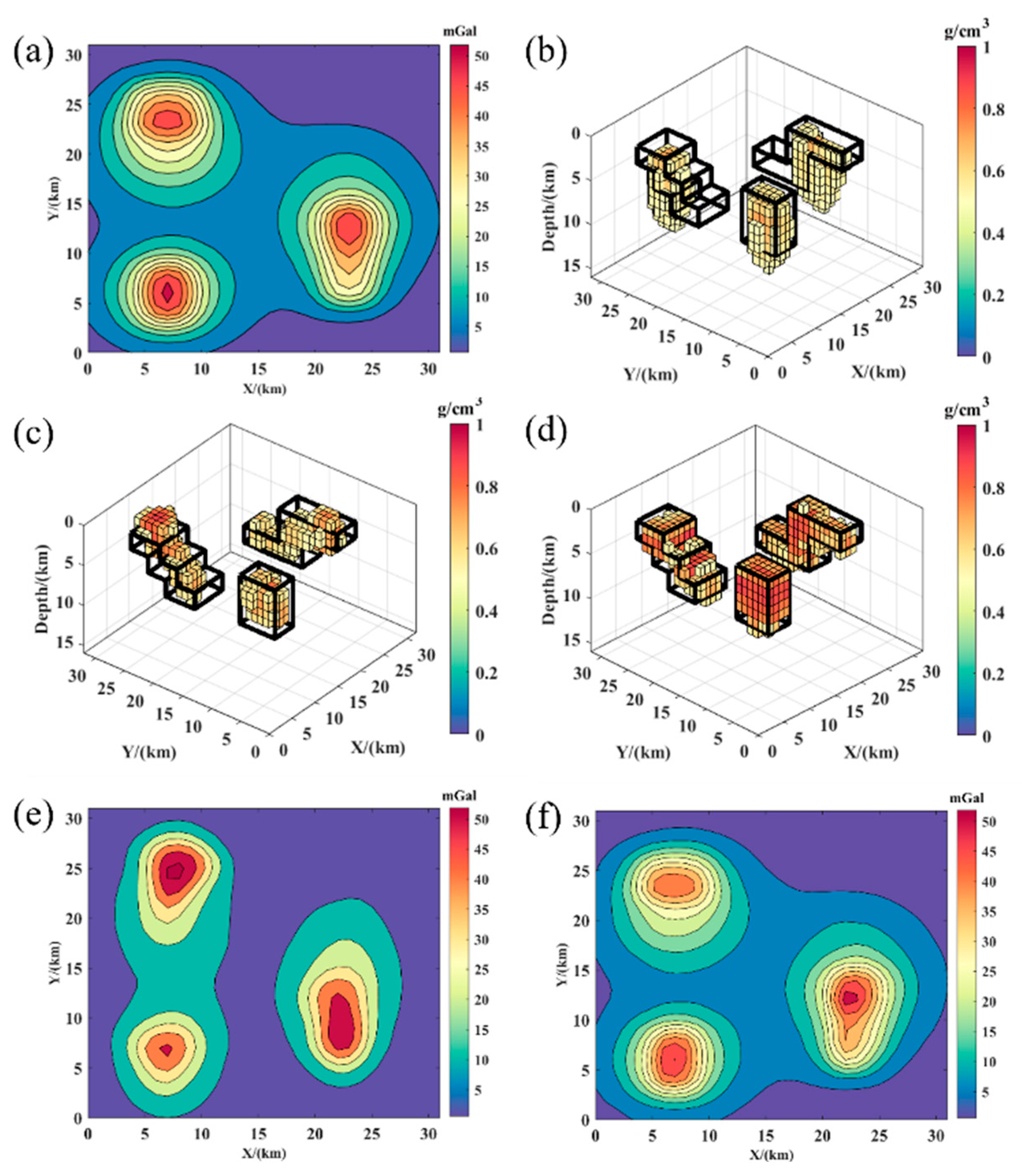
3.3. Multi-Density Model
3.4. Analytical Metrics
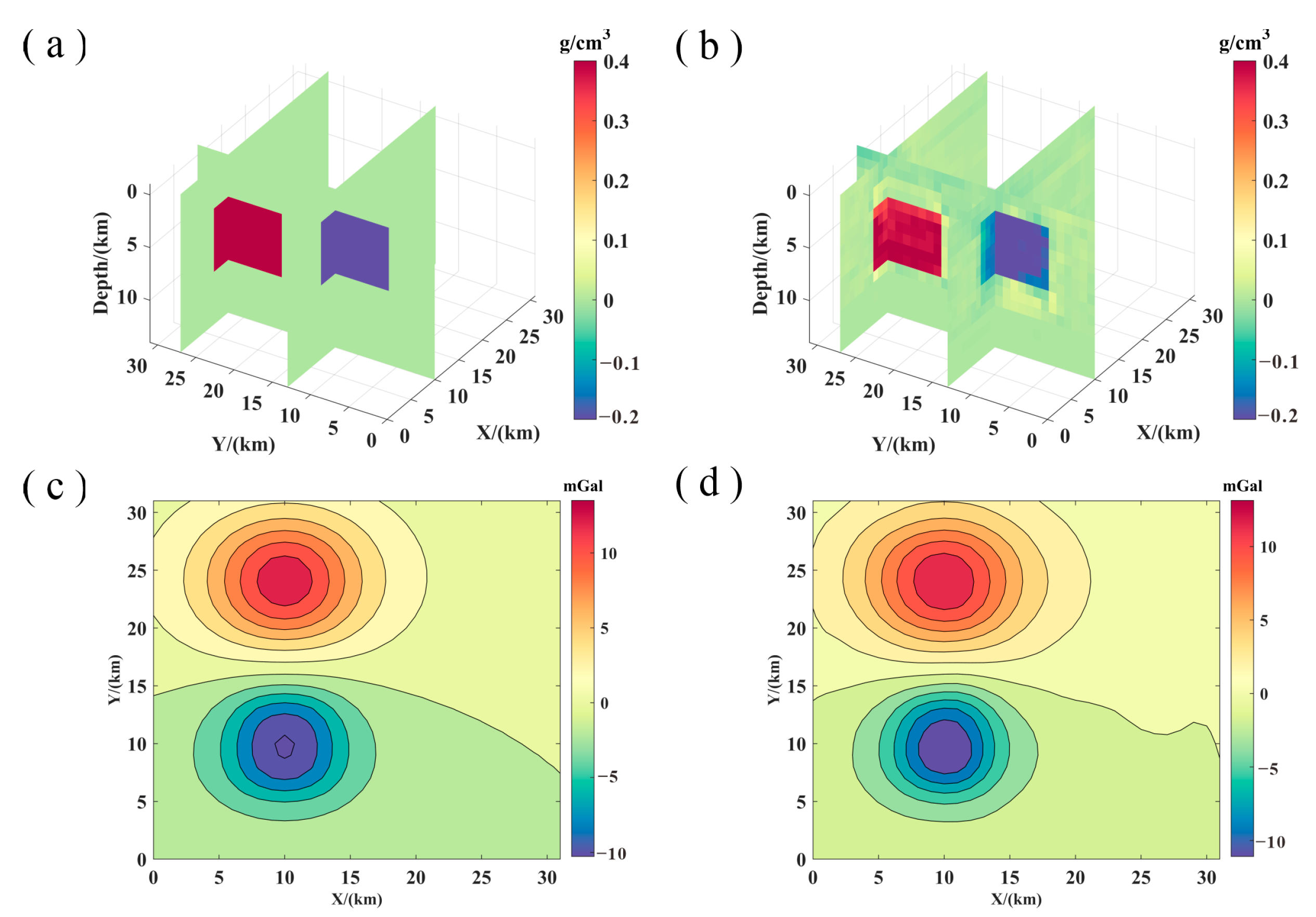
3.5. Ablation Experiment
3.6. Regularization Parameter Selection
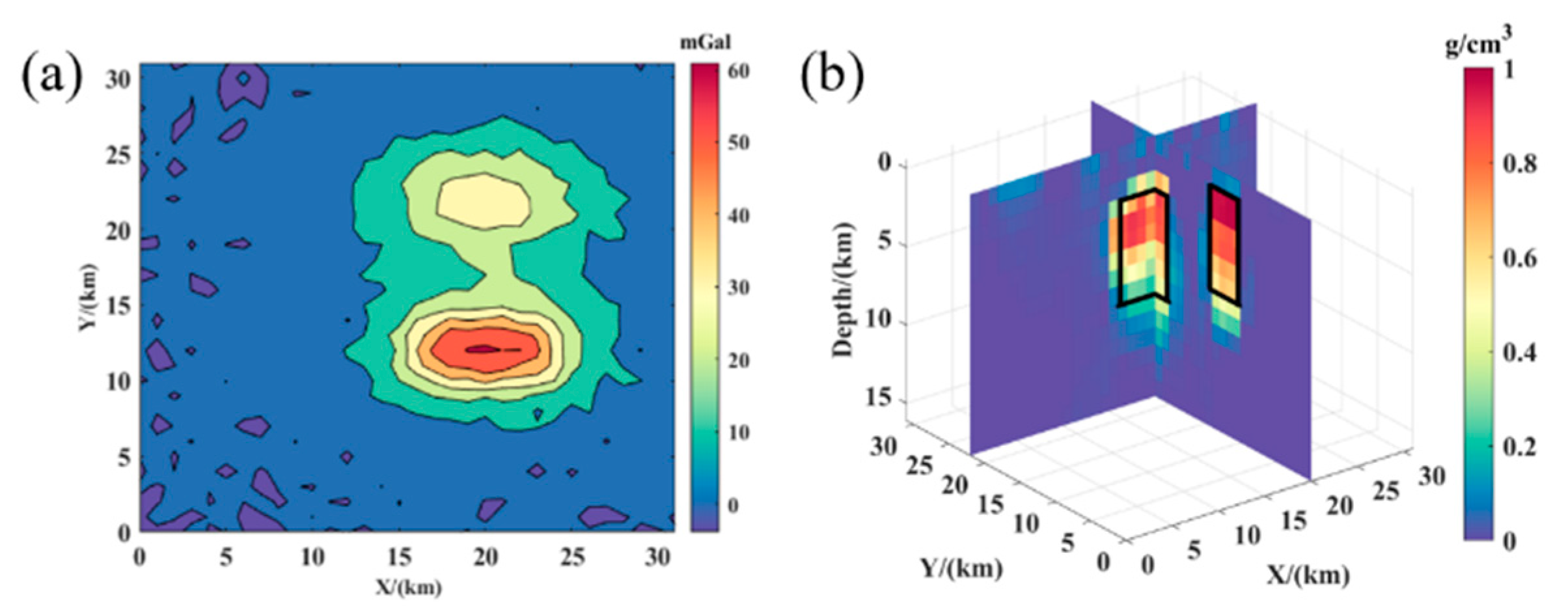
4. Application of Actual Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhdanov, M.S. Inverse Theory and Applications in Geophysics; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Jian, W.; Chongyang, S.; Hui, I.; Shaoan, S.; Lelin, X. Gravity inversion of deep-crust and mantle interfaces in the Three Gorges area. Geod. Geodyn. 2012, 3, 7–17. [Google Scholar] [CrossRef]
- Yang, G.; Wang, J.; Yan, H. Application of modeling inversion of Bouguer gravity anomalies to oil and gas exploration in the Erlian Basin. Chin. J. Geophys. 2019, 62, 316–330. [Google Scholar]
- Hinze, W.J. The role of gravity and magnetic methods in engineering and environmental studies. In Geotechnical an Environmental Geophysics: Volume I: Review and Tutorial; Ward, S.H., Ed.; SEG: Tulsa, OK, USA, 1990; pp. 75–126. [Google Scholar]
- Geng, M.; Huang, D.; Yang, Q.; Liu, Y. 3D inversion of airborne gravity-gradiometry data using cokriging. Geophysics 2014, 79, G37–G47. [Google Scholar] [CrossRef]
- Vatankhah, S.; Ardestani, V.E.; Renaut, R.A. Application of the χ2 principle and unbiased predictive risk estimator for determining the regularization parameter in 3-D focusing gravity inversion. Geophys. J. Int. 2015, 200, 265–277. [Google Scholar] [CrossRef][Green Version]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2002, 67, 1532–1541. [Google Scholar] [CrossRef]
- Commer, M. Three-dimensional gravity modelling and focusing inversion using rectangular meshes. Geophys. Prospect. 2011, 59, 966–979. [Google Scholar] [CrossRef]
- Boulanger, O.; Chouteau, M. Constraints in 3D gravity inversion. Geophys. Prospect. 2001, 49, 265–280. [Google Scholar] [CrossRef]
- Pilkington, M. 3D magnetic data-space inversion with sparseness constraints. Geophysics 2009, 74, L7–L15. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Li, Y. Inversion for Applied Geophysics: A Tutorial. In Near-Surface Geophysics; Society of Exploration Geophysicists: Tulsa, OK, USA, 2005; pp. 89–150. [Google Scholar] [CrossRef]
- Namaki, L.; Gholami, A.; Hafizi, M.A. Edge-preserved 2-D inversion of magnetic data: An application to the Makran arc-trench complex. Geophys. J. Int. 2011, 184, 1058–1068. [Google Scholar] [CrossRef]
- Cheyney, S.; Fishwick, S.; Hill, I.A.; Linford, N.T. Successful adaptation of three-dimensional inversion methodologies for archaeological-scale, total-field magnetic data sets. Geophys. J. Int. 2015, 202, 1271–1288. [Google Scholar] [CrossRef]
- Rezaie, M. A sigmoid stabilizing function for fast sparse 3D inversion of magnetic data. Near Surf. Geophys. 2020, 18, 149–159. [Google Scholar] [CrossRef]
- Yang, Q.; Hu, X.; Liu, S.; Jie, Q.; Wang, H.; Chen, Q. 3-D Gravity Inversion Based on Deep Convolution Neural Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3001305. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, G.; Liu, Y.; Fan, Z. Deep Learning for 3-D Inversion of Gravity Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5905918. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Yin, C.; Su, Y.; Zhang, B.; Ren, X. Flexible and Accurate Prior Model Construction Based on Deep Learning for 2-D Magnetotelluric Data Inversion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5902511. [Google Scholar] [CrossRef]
- Qin, P.; Zhang, C.; Meng, Z.; Zhang, D.; Hou, Z. Three Integrating Methods for Gravity and Gravity Gradient 3-D Inversion and Their Comparison Based on a New Function of Discrete Stability. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4505712. [Google Scholar] [CrossRef]
- Bhangale, K.B.; Kothandaraman, M. Survey of Deep Learning Paradigms for Speech Processing. Wirel. Pers. Commun. 2022, 125, 1913–1949. [Google Scholar] [CrossRef]
- Lin, Y.; Wu, Y. InversionNet: A real-time and accurate full waveform inversion with convolutional neural network. J. Acoust. Soc. Am. 2018, 144, 1683. [Google Scholar] [CrossRef]
- Ren, Y.; Nie, L.; Yang, S.; Jiang, P.; Chen, Y. Building Complex Seismic Velocity Models for Deep Learning Inversion. IEEE Access 2021, 9, 63767–63778. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Ren, Z.; Tang, J.; Xu, Z.; Chen, Y.; Liu, X. Deep learning audio magnetotellurics inversion using residual-based deep convolution neural network. J. Appl. Geophys. 2021, 188, 104309. [Google Scholar] [CrossRef]
- Ren, Y.; Xu, X.; Yang, S.; Nie, L.; Chen, Y. A Physics-Based Neural-Network Way to Perform Seismic Full Waveform Inversion. IEEE Access 2020, 8, 112266–112277. [Google Scholar] [CrossRef]
- Li, Y.; Song, J.; Lu, W.; Monkam, P.; Ao, Y. Multitask learning for super-resolution of seismic velocity model. IEEE Trans. Geosci. Remote Sens. 2020, 59, 8022–8033. [Google Scholar] [CrossRef]
- Li, Y.; Jia, Z.; Lu, W. Self-Supervised Deep Learning for 3D Gravity Inversion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, Y. Data-Driven Seismic Waveform Inversion: A Study on the Robustness and Generalization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6900–6913. [Google Scholar] [CrossRef]
- Puzyrev, V. Deep learning electromagnetic inversion with convolutional neural networks. Geophys. J. Int. 2019, 218, 817–832. [Google Scholar] [CrossRef]
- Wu, S.; Huang, Q.; Zhao, L. Convolutional neural network inversion of airborne transient electromagnetic data. Geophys. Prospect. 2021, 69, 1761–1772. [Google Scholar] [CrossRef]
- Liu, B.; Yu, A.; Yu, X.; Wang, R.; Gao, K.; Guo, W. Deep Multiview Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7758–7772. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]
- Wu, X.; Ma, J.; Si, X.; Bi, Z.; Yang, J.; Gao, H.; Xie, D.; Guo, Z.; Zhang, J. Sensing prior constraints in deep neural networks for solving exploration geophysical problems. Proc. Natl. Acad. Sci. USA 2023, 120, e2219573120. [Google Scholar] [CrossRef]
- Di, H.; Li, C.; Smith, S.; Li, Z.; Abubakar, A. Imposing interpretational constraints on a seismic interpretation convolutional neural network. Geophysics 2021, 86, IM63–IM71. [Google Scholar] [CrossRef]
- Kong, Q.; Wang, R.; Walter, W.R.; Pyle, M.; Koper, K.; Schmandt, B. Combining Deep Learning with Physics Based Features in Explosion-Earthquake Discrimination. Geophys. Res. Lett. 2022, 49, e2022GL098645. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Rasht-Behesht, M.; Huber, C.; Shukla, K.; Karniadakis, G.E. Physics-Informed Neural Networks (PINNs) for Wave Propagation and Full Waveform Inversions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023120. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Q.; Lu, W.; Li, H. Physics-Constrained Seismic Impedance Inversion Based on Deep Learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Huang, R.; Liu, S.; Qi, R.; Zhang, Y. Deep Learning 3D Sparse Inversion of Gravity Data. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022476. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Zhang, Y.-J.; Fu, L.-H.; Li, H.-W. Three-dimensional gravity inversion based on 3D U-Net++. Appl. Geophys. 2021, 18, 451–460. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Hu, X.; Fu, L.; Qu, J.; Wang, H.; Chen, Q. Inversion of magnetic data using deep neural networks. Phys. Earth Planet. Inter. 2021, 311, 106653. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, C.; Cao, X.; Sun, S.; Liu, Y.; Ren, X. DecNet: Decomposition network for 3D gravity inversion. Geophysics 2022, 87, G103–G114. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, X.; Guan, Q.; Lin, Y. Making Invisible Visible: DataDriven Seismic Inversion with SpatioTemporally Constrained Data Augmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar]
- Celaya, A.; Denel, B.; Sun, Y.; ArayaPolo, M.; Price, A. Inversion of TimeLapse Surface Gravity Data for Detection of 3D CO2 Plumes via Deep Learning. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Liu, W.L. Drilling technical difficulties and solutions in development of Hot dry Rock geothermal energy. Adv. Pet. Explor. Dev. 2017, 13, 63–69. [Google Scholar]
- Zhang, C.; Jiang, G.; Jia, X.; Li, S.; Zhang, S.; Hu, D.; Hu, S. Parametric study of the production performance of an enhanced geothermal system, A case study at the Qiabuqia geothermal area, northeast Tibetan plateau. Renew. Energy 2018, 132, 959–978. [Google Scholar] [CrossRef]
- Samrock, F.; Kuvshinov, A.; Bakker, J.; Jackson, A.; Fisseha, S. 3-D analysis and interpretation of magnetotelluric data from the Aluto-Langano geothermal field, Ethiopia. Geophys. J. Int. 2015, 202, 1923–1948. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, H.; Zhang, S.; Chen, X.; Cheng, Z.; Jia, X.; Li, S.; Fu, L.; Gao, L.; Xin, H. Three-dimensional magnetotelluric imaging of the geothermal system beneath the Gonghe Basin, Northeast Tibetan Plateau. Geothermics 2018, 76, 15–25. [Google Scholar] [CrossRef]
- Maithya, J.; Fujimitsu, Y.; Nishijima, J. Analysis of gravity data to delineate structural features controlling the Eburru geothermal system in Kenya. Geothermics 2020, 85, 101795. [Google Scholar] [CrossRef]







| Model | Method I | Method II | Method III | ||||
|---|---|---|---|---|---|---|---|
| Em | Ed | Em | Ed | Em | Ed | ||
| single prism | 27.0880 | 0.0102 | 8.8881 | 60.0225 | 5.9523 | 17.8810 | |
| horizontal adjacent superimposed prisms | 26.0842 | 0.0099 | 11.4264 | 97.7662 | 7.7077 | 17.7445 | |
| inclined steps | 25.9457 | 0.0095 | 15.4075 | 93.1364 | 10.7526 | 12.5255 | |
| Z-shaped model | I | 17.2367 11.9710 | 0.0088 0.0099 | 8.8974 11.5936 | 47.4270 61.2051 | 5.9650 7.8873 | 9.1144 9.7404 |
| II | |||||||
| complex combination model | 30.2815 | 0.4608 | 16.0528 | 154.2097 | 12.0304 | 39.3747 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Wei, Y.; Lu, P.; Jiao, J.; Jia, H. Deep-Learning Gravity Inversion Method with Depth-Weighting Constraints and Its Application in Geothermal Exploration. Remote Sens. 2024, 16, 4467. https://doi.org/10.3390/rs16234467
Zhou S, Wei Y, Lu P, Jiao J, Jia H. Deep-Learning Gravity Inversion Method with Depth-Weighting Constraints and Its Application in Geothermal Exploration. Remote Sensing. 2024; 16(23):4467. https://doi.org/10.3390/rs16234467
Chicago/Turabian StyleZhou, Shuai, Yue Wei, Pengyu Lu, Jian Jiao, and Hongfa Jia. 2024. "Deep-Learning Gravity Inversion Method with Depth-Weighting Constraints and Its Application in Geothermal Exploration" Remote Sensing 16, no. 23: 4467. https://doi.org/10.3390/rs16234467
APA StyleZhou, S., Wei, Y., Lu, P., Jiao, J., & Jia, H. (2024). Deep-Learning Gravity Inversion Method with Depth-Weighting Constraints and Its Application in Geothermal Exploration. Remote Sensing, 16(23), 4467. https://doi.org/10.3390/rs16234467






