Optimal-Transport-Based Positive and Unlabeled Learning Method for Windshear Detection
Abstract
1. Introduction
2. Optimal Transport and Positive and Unlabeled Learning
2.1. Optimal Transport
2.2. Positive and Unlabeled Learning
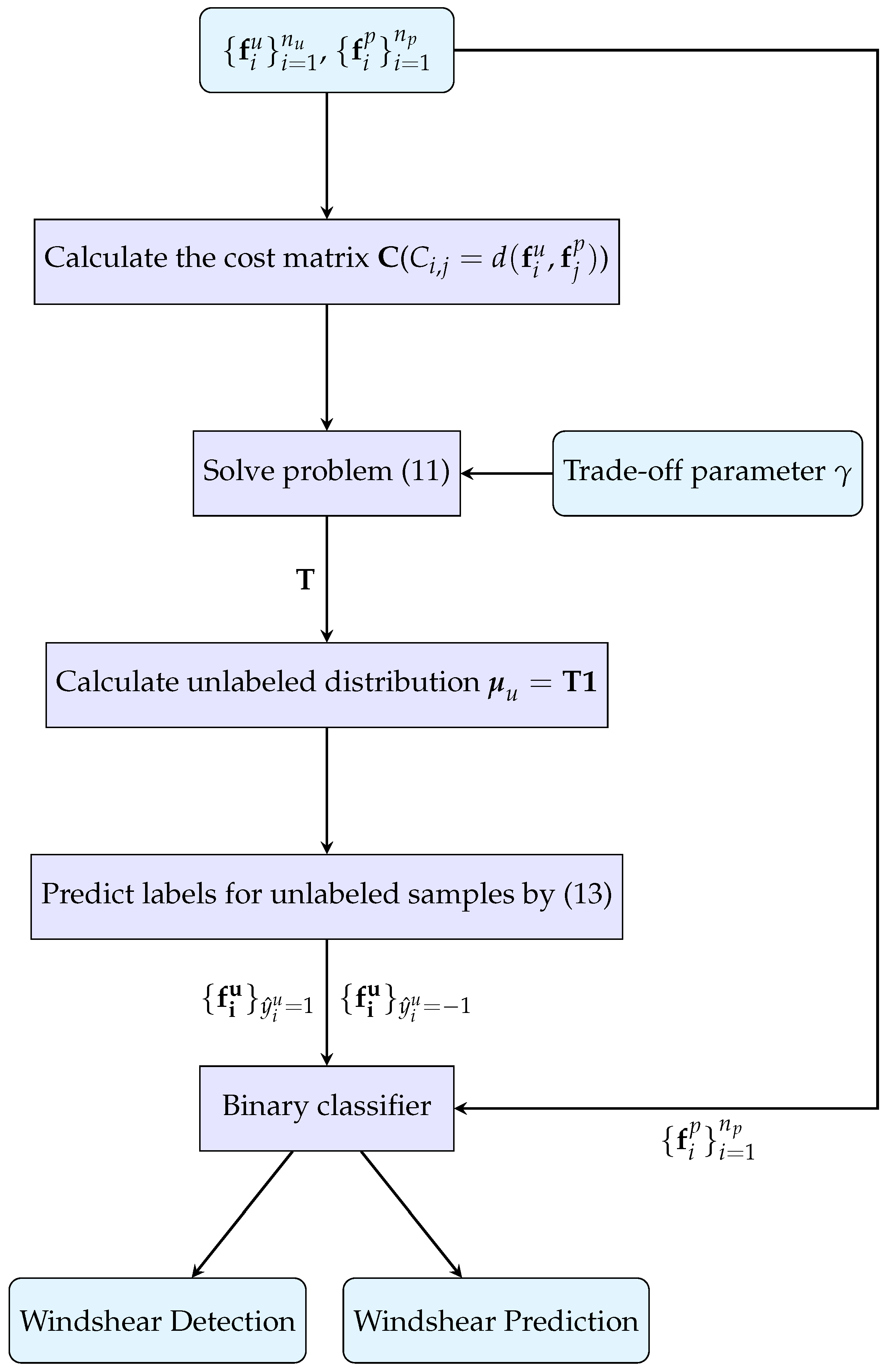
3. Proposed Method
3.1. LiDAR Observational Data and Pilots’ Reports
3.2. Analysis of Learning-Based Windshear Detection
- (i)
- We do not know the exact location and range of windshear occurrence, making it challenging to explicitly extract the windshear features from LiDAR observational wind velocity data. In other words, windshear features might be missed by inappropriate feature extraction methods. Hence, it could be better to extract the windshear features globally based on all the wind velocity data collected by LiDAR in the region that covers the flight path and touch-down zone. Details about the specific region discussed in this paper are provided in Section 3.1.
- (ii)
- Although windshear occurrence can be recorded by pilot reports, the exact onset time of windshear is unknown. Taking pilots’ recording delays in actual operations into account, the previous learning-based windshear detection methods that extract the windshear features from the wind velocity data collected at the timestamp nearest to the reported time spot might miss windshear features. It could be better to extract windshear features from all LiDAR observational wind velocity data collected several minutes around the reported time spot.
- (iii)
- We cannot determine whether windshear occurs during non-flight times. Namely, in the learning procedure, we have precise knowledge from some positive-labeled samples (i.e., windshear cases reported by pilots) but have no information for negative-labeled samples, constituting a positive and unlabeled learning problem.
3.3. Windshear Features
- ▶
- Dissimilarity:
- ▶
- Contrast:
- ▶
- Correlation:where and denote the mean values and standard deviation values, respectively.
3.4. Learning Model
3.5. Optimization Algorithm
- ▶
- Determination of update direction:The direction update is mainly based on the minimization of the linear approximation of the problem given by the first-order Taylor approximation of around .Specifically, the corresponding sub-problem is given as follows:Substituting the derivative of the objective function at point , the sub-problem can be written asThis is a linear programming method, and one can solve it efficiently by using the dual simplex method.
- ▶
- Line-search for the step-size:The step-size can be determined by the following optimization problem:Specifically, the objective function for problem (16) isThis is obviously a convex function, so problem (16) is a convex optimization problem of . The first-order optimality condition is
- ▶
- Update :The update rule for is defined as
| Algorithm 1 Frank–Wolfe algorithm for problem (11). |
| Input: The cost matrix C, the trade-off parameter . Initialize: The initial point . |
4. Numerical Experiments
4.1. Experimental Setting
- Euclidean distance: ;
- Squared Euclidean distance: ;
- City block distance: ,
4.2. Windshear Detection
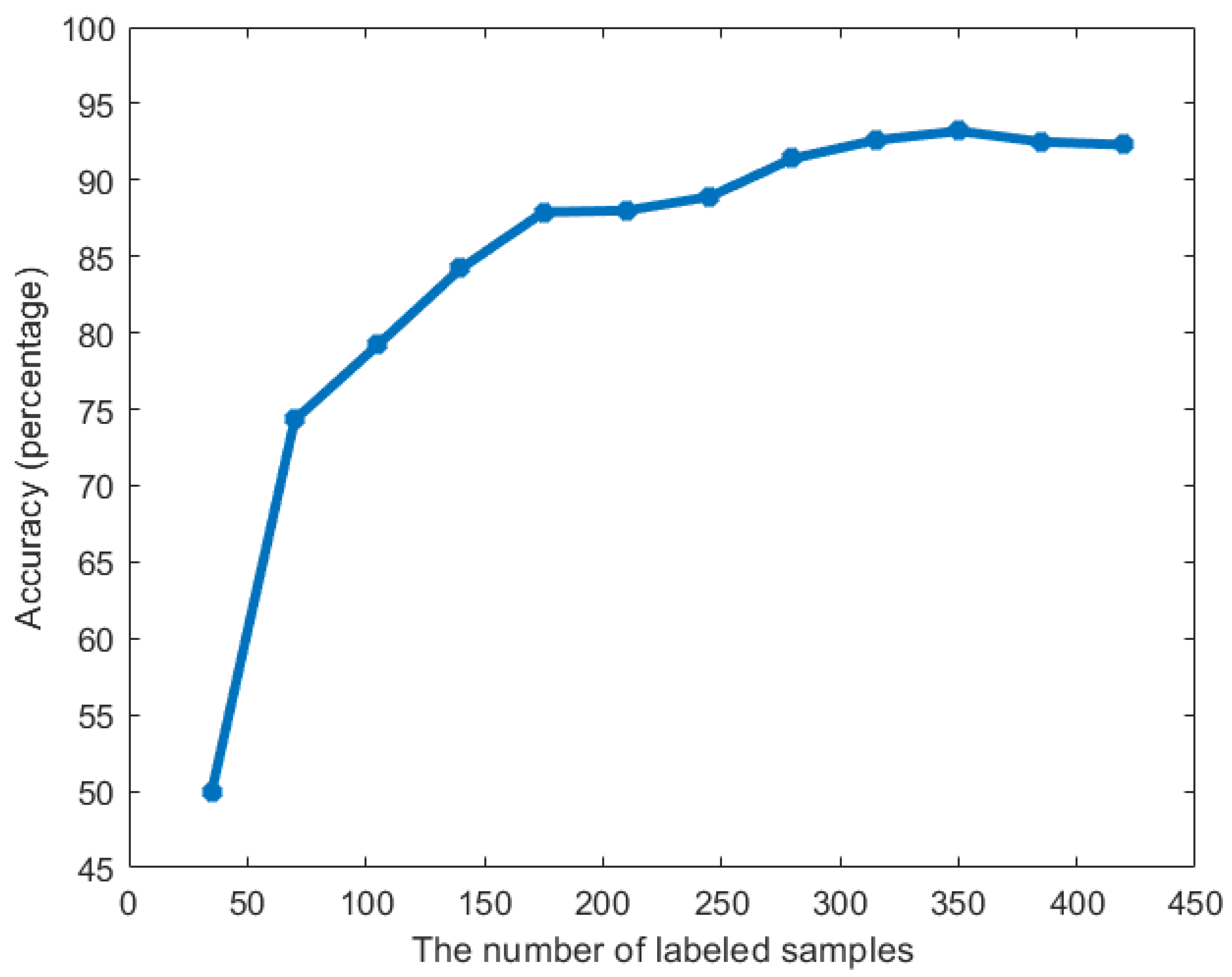
4.2.1. Accuracy Results
4.2.2. Data Transportation
4.3. Windshear Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chan, P.; Shun, C.; Wu, K. Operational LIDAR-based system for automatic windshear alerting at the Hong Kong International Airport. In Proceedings of the 12th Conference on Aviation, Range, and Aerospace Meteorology, Atlanta, GA, USA, 29 January–2 February 2006; Volume 6. [Google Scholar]
- Thobois, L.; Cariou, J.; Gultepe, I. Review of lidar-based applications for aviation weather. Pure Appl. Geophys. 2019, 176, 1959–1976. [Google Scholar] [CrossRef]
- ICAO. Manual on Low-Level Wind Shear; Technical Report; International Civil Aviation Organization: Montréal, QC, Canada, 2005. [Google Scholar]
- Weipert, A.; Kauczok, S.; Hannesen, R.; Ernsdorf, T.; Stiller, B. Wind shear detection using radar and lidar at Frankfurt and Munich airports. In Proceedings of the 8th European Conference on Radar in Meteorology and Hydrology, Garmisch-Partenkirchen, Germany, 1–5 September 2014; pp. 1–5. [Google Scholar]
- Li, M.; Xu, J.; Xiong, X.l.; Ma, Y.; Zhao, Y. A novel ramp method based on improved smoothing algorithm and second recognition for windshear detection using lidar. Curr. Opt. Photonics 2018, 2, 7–14. [Google Scholar]
- Jones, J.; Haynes, A. A Peakspotter Program Applied to the Analysis of Increments in Turbulence Velocity; Technical Report; RAE: Madrid, Spain, 1984.
- Woodfield, A.; Woods, J. Worldwide Experience of Wind Shear During 1981–1982; Technical Report; Royal Aircraft EstablIshment Bedford: Bedford, UK, 1983. [Google Scholar]
- Hon, K.; Chan, P. Improving Lidar Windshear Detection Efficiency by Removal of “Gentle Ramps”. Atmosphere 2021, 12, 1539. [Google Scholar] [CrossRef]
- Hinton, D.A. Airborne Derivation of Microburst Alerts from Ground-Based Terminal Doppler Weather Radar Information: A Flight Evaluation; Technical Report; National Aeronautics and Space Administration, Langley Research Center Hampton: Hampton, VA, USA, 1993.
- Chan, P.; Hon, K.; Shin, D. Combined use of headwind ramps and gradients based on LIDAR data in the alerting of low-level windshear/turbulence. Meteorol. Z. 2011, 20, 661. [Google Scholar] [CrossRef]
- Chan, P. Application of LIDAR-based F-factor in windshear alerting. Meteorol. Z. 2012, 21, 193. [Google Scholar] [CrossRef]
- Lee, Y.; Chan, P. LIDAR-based F-factor for wind shear alerting: Different smoothing algorithms and application to departing flights. Meteorol. Appl. 2014, 21, 86–93. [Google Scholar] [CrossRef]
- Wu, T.; Hon, K. Application of spectral decomposition of LIDAR-based headwind profiles in windshear detection at the Hong Kong International Airport. Meteorol. Z. 2018, 27, 33–42. [Google Scholar] [CrossRef]
- Li, L.; Shao, A.; Zhang, K.; Ding, N.; Chan, P. Low-Level Wind Shear Characteristics and Lidar-Based Alerting at Lanzhou Zhongchuan International Airport, China. J. Meteorol. Res. 2020, 34, 633–645. [Google Scholar] [CrossRef]
- Ma, Y.; Li, S.; Lu, W. Recognition of partial scanning low-level wind shear based on support vector machine. Adv. Mech. Eng. 2018, 10, 1687814017754151. [Google Scholar] [CrossRef]
- Huang, J.; Ng, M.; Chan, P. Wind Shear Prediction from Light Detection and Ranging Data Using Machine Learning Methods. Atmosphere 2021, 12, 644. [Google Scholar] [CrossRef]
- Monge, G. Mémoire sur la théorie des déblais et des remblais. In Histoire de l’Académie Royale des Sciences de Paris; Imprimerie royale: Paris, France, 1781. [Google Scholar]
- Kantorovitch, L. On the Translocation of Masses. Manag. Sci. 1958, 5, 1–4. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. Adv. Neural Inf. Process. Syst. 2013, 26, 2292–2300. [Google Scholar]
- Altschuler, J.; Niles-Weed, J.; Rigollet, P. Near-linear time approximation algorithms for optimal transport via Sinkhorn iteration. Adv. Neural Inf. Process. Syst. 2017, 30, 1961–1971. [Google Scholar]
- Dvurechensky, P.; Gasnikov, A.; Kroshnin, A. Computational optimal transport: Complexity by accelerated gradient descent is better than by Sinkhorn’s algorithm. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 1367–1376. [Google Scholar]
- Lin, T.; Ho, N.; Jordan, M. On the Efficiency of Entropic Regularized Algorithms for Optimal Transport. J. Mach. Learn. Res. 2022, 23, 1–42. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational optimal transport: With applications to data science. Found. Trends® Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, T.; Tao, D. An Optimal Transport Analysis on Generalization in Deep Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 2842–2853. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Liu, S.; Li, G.; Xu, G. Causal optimal transport for treatment effect estimation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 6, 2842–2853. [Google Scholar] [CrossRef]
- Amores, J. Multiple instance classification: Review, taxonomy and comparative study. Artif. Intell. 2013, 201, 81–105. [Google Scholar] [CrossRef]
- Flamary, R.; Cuturi, M.; Courty, N.; Rakotomamonjy, A. Wasserstein discriminant analysis. Mach. Learn. 2018, 107, 1923–1945. [Google Scholar] [CrossRef]
- Su, B.; Zhou, J.; Wu, Y. Order-preserving wasserstein discriminant analysis. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9885–9894. [Google Scholar]
- Su, B.; Zhou, J.; Wen, J.; Wu, Y. Linear and Deep Order-Preserving Wasserstein Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3123–3138. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Tolstikhin, I.; Bousquet, O.; Gelly, S.; Schölkopf, B. Wasserstein Auto-Encoders. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Courty, N.; Flamary, R.; Tuia, D.; Rakotomamonjy, A. Optimal transport for domain adaptation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1853–1865. [Google Scholar] [CrossRef] [PubMed]
- Courty, N.; Flamary, R.; Habrard, A.; Rakotomamonjy, A. Joint distribution optimal transportation for domain adaptation. Adv. Neural Inf. Process. Syst. 2017, 30, 3733–3742. [Google Scholar]
- Zhang, Z.; Wang, M.; Nehorai, A. Optimal transport in reproducing kernel hilbert spaces: Theory and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1741–1754. [Google Scholar] [CrossRef] [PubMed]
- Chapel, L.; Alaya, M.; Gasso, G. Partial optimal tranport with applications on positive-unlabeled learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2903–2913. [Google Scholar]
- Cao, N.; Zhang, T.; Shi, X.; Jin, H. Posistive-Unlabeled Learning via Optimal Transport and Margin Distribution. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, IJCAI-22, Vienna, Austria, 23–29 July 2022; pp. 2836–2842. [Google Scholar]
- Bekker, J.; Davis, J. Learning from positive and unlabeled data: A survey. Mach. Learn. 2020, 109, 719–760. [Google Scholar] [CrossRef]
- Li, F.; Dong, S.; Leier, A.; Han, M.; Guo, X.; Xu, J.; Wang, X.; Pan, S.; Jia, C.; Zhang, Y.; et al. Positive-unlabeled learning in bioinformatics and computational biology: A brief review. Briefings Bioinform. 2022, 23, bbab461. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Liu, Z.; Li, M. Semi-Supervised Disease Classification based on Limited Medical Image Data. IEEE J. Biomed. Health Inform. 2024, 28, 1575–1586. [Google Scholar] [CrossRef]
- Gong, C.; Shi, H.; Yang, J.; Yang, J. Multi-manifold positive and unlabeled learning for visual analysis. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 1396–1409. [Google Scholar] [CrossRef]
- de Souza, M.C.; Nogueira, B.M.; Rossi, R.G.; Marcacini, R.M.; Dos Santos, B.N.; Rezende, S.O. A network-based positive and unlabeled learning approach for fake news detection. Mach. Learn. 2022, 111, 3549–3592. [Google Scholar] [CrossRef]
- Wang, J.; Qian, S.; Hu, J.; Hong, R. Positive Unlabeled Fake News Detection Via Multi-Modal Masked Transformer Network. IEEE Trans. Multimed. 2023, 26, 234–244. [Google Scholar] [CrossRef]
- Li, X.; Liu, B. Learning to classify texts using positive and unlabeled data. In Proceedings of the 18th International Joint Conference on Artificial Intelligence, IJCAI-03, Acapulco, Mexico, 9–15 August 2003; pp. 587–592. [Google Scholar]
- Liu, B.; Dai, Y.; Li, X.; Lee, W.; Yu, P. Building text classifiers using positive and unlabeled examples. In Proceedings of the Third IEEE International Conference on Data Mining, IEEE, Melbourne, FL, USA, 19–22 November 2003; pp. 179–186. [Google Scholar]
- Gong, C.; Shi, H.; Liu, T.; Zhang, C.; Yang, J.; Tao, D. Loss decomposition and centroid estimation for positive and unlabeled learning. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 918–932. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Ormerod, J.; Liu, W.; Ma, C.; Zomaya, A.; Yang, J. AdaSampling for positive-unlabeled and label noise learning with bioinformatics applications. IEEE Trans. Cybern. 2018, 49, 1932–1943. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Zhang, T.; Jin, H. Entropy Weight Allocation: Positive-unlabeled Learning via Optimal Transport. In Proceedings of the 2022 SIAM International Conference on Data Mining (SDM), SIAM, Alexandria, VA, USA, 28–30 April 2022; pp. 37–45. [Google Scholar]
- Zhang, J.; Chan, P.; Ng, M. LiDAR-Based Windshear Detection via Statistical Features. Adv. Meteorol. 2022, 2022. [Google Scholar] [CrossRef]
- Xu, H. Convergence analysis of the Frank-Wolfe algorithm and its generalization in Banach spaces. arXiv 2017, arXiv:1710.07367. [Google Scholar]


| Dataset Name | Dataset Size | Description |
|---|---|---|
| 535 | Non-reported cases collected at the most likely non-windshear timestamps. | |
| 535 | Non-reported cases collected at randomly selected timestamps. | |
| 731 | Non-reported cases collected at the most likely non-windshear timestamps. | |
| 719 | Non-reported cases collected at randomly selected timestamps. |
| Cost Matrix Construction | ||||
|---|---|---|---|---|
| Euclidean distance | ||||
| Squared Euclidean distance | ||||
| City block distance |
| Methods | Accuracy | ||||
|---|---|---|---|---|---|
| SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average |
| Methods | Accuracy | ||||
|---|---|---|---|---|---|
| SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + LDA | Windshear detection | 89.40% | 86.40% | 89.60% | 79.40% |
| Non-windshear detection | |||||
| Average | |||||
| KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average |
| Methods | Accuracy | ||||
|---|---|---|---|---|---|
| SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average |
| Methods | Accuracy | ||||
|---|---|---|---|---|---|
| SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average |
| Group | Result | Windshear | Non-Windshear | Accuracy |
|---|---|---|---|---|
| Ground Truth Windshear | 86 | 14 | ||
| Ground Truth Non-Windshear | 13 | 87 | ||
| Ground Truth Windshear | 75 | 25 | ||
| Ground Truth Non-Windshear | 4 | 96 | ||
| Ground Truth Windshear | 86 | 14 | ||
| Ground Truth Non-Windshear | 11 | 89 | ||
| Ground Truth Windshear | 75 | 25 | ||
| Ground Truth Non-Windshear | 2 | 98 |
| Group | Cost Matrix Construction | ||||
|---|---|---|---|---|---|
| Euclidean distance | 132 | 130 | 125 | 113 | |
| Squared Euclidean distance | 133 | 131 | 123 | 110 | |
| City Block Distance | 133 | 136 | 124 | 112 | |
| Euclidean distance | 202 | 186 | 177 | 175 | |
| Squared Euclidean distance | 223 | 184 | 166 | 181 | |
| City Block Distance | 187 | 178 | 179 | 168 | |
| Euclidean distance | 158 | 150 | 151 | 153 | |
| Squared Euclidean distance | 139 | 149 | 145 | 137 | |
| City Block Distance | 150 | 170 | 138 | 142 | |
| Euclidean distance | 239 | 242 | 234 | 201 | |
| Squared Euclidean distance | 223 | 245 | 233 | 232 | |
| City Block Distance | 223 | 207 | 221 | 200 |
| Methods | Accuracy | ||||
|---|---|---|---|---|---|
| SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average |
| Methods | Accuracy | ||||
|---|---|---|---|---|---|
| SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + SVM | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + LDA | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (squared Euclidean) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average | |||||
| OT (city block) + KNN | Windshear detection | ||||
| Non-windshear detection | |||||
| Average |
| Group | Result | Windshear | Non-Windshear | Accuracy |
|---|---|---|---|---|
| Ground Truth Windshear | 83 | 17 | ||
| Ground Truth Non-Windshear | 4 | 96 | ||
| Ground Truth Windshear | 82 | 17 | ||
| Ground Truth Non-Windshear | 4 | 96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Chan, P.-W.; Ng, M.K.-P. Optimal-Transport-Based Positive and Unlabeled Learning Method for Windshear Detection. Remote Sens. 2024, 16, 4423. https://doi.org/10.3390/rs16234423
Zhang J, Chan P-W, Ng MK-P. Optimal-Transport-Based Positive and Unlabeled Learning Method for Windshear Detection. Remote Sensing. 2024; 16(23):4423. https://doi.org/10.3390/rs16234423
Chicago/Turabian StyleZhang, Jie, Pak-Wai Chan, and Michael Kwok-Po Ng. 2024. "Optimal-Transport-Based Positive and Unlabeled Learning Method for Windshear Detection" Remote Sensing 16, no. 23: 4423. https://doi.org/10.3390/rs16234423
APA StyleZhang, J., Chan, P.-W., & Ng, M. K.-P. (2024). Optimal-Transport-Based Positive and Unlabeled Learning Method for Windshear Detection. Remote Sensing, 16(23), 4423. https://doi.org/10.3390/rs16234423







