A Planar Feature-Preserving Texture Defragmentation Method for 3D Urban Building Models
Abstract
1. Introduction
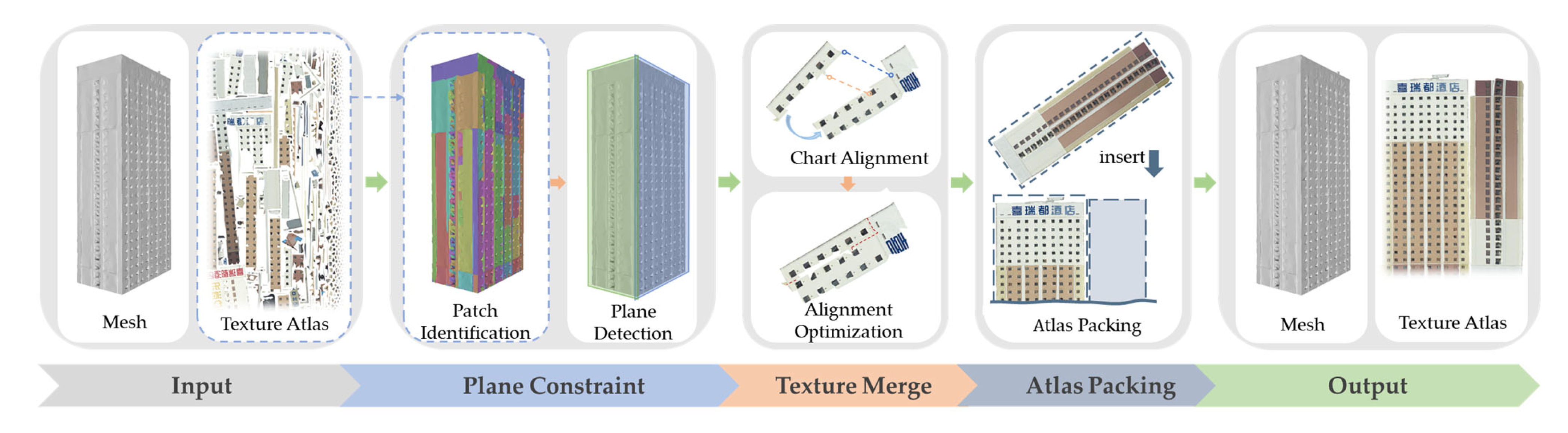
2. Materials and Methods
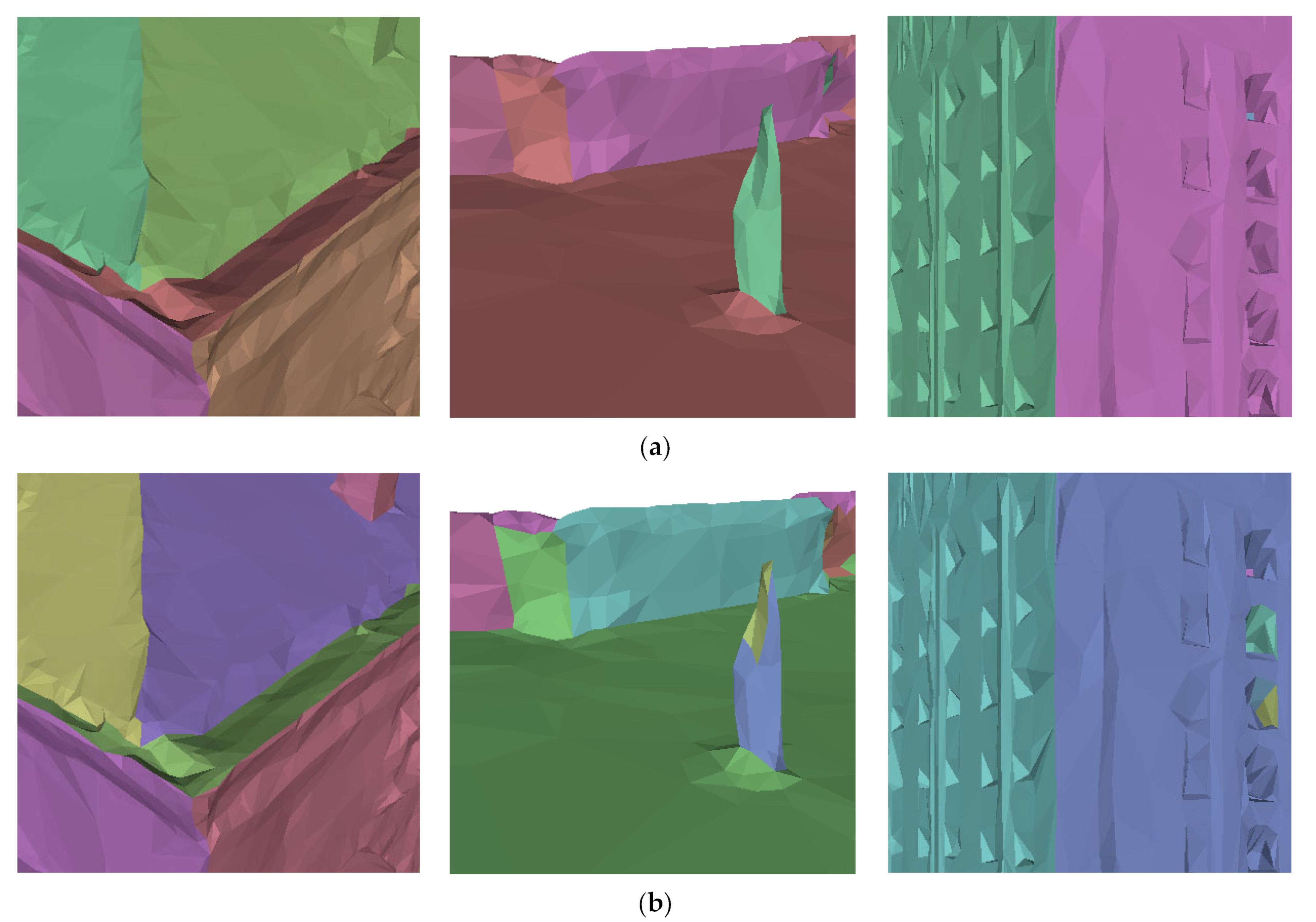
2.1. Enhanced Planar Feature Detection
2.1.1. Patch Identification
2.1.2. Patch-Based Region Growing
- Sort all patches to be partitioned in the global set in descending area order;
- Choose a patch as the seed, add it to the seed set, remove it from the global set, and simultaneously initialize a new planar region;
- Expand the region by including adjacent patches that meet angle criteria, simultaneously adding them to the seed set, and removing them from the global set;
- Select a new seed from the seed set and repeat until no seeds remain;
- If patches are left unassigned, restart with a new seed.
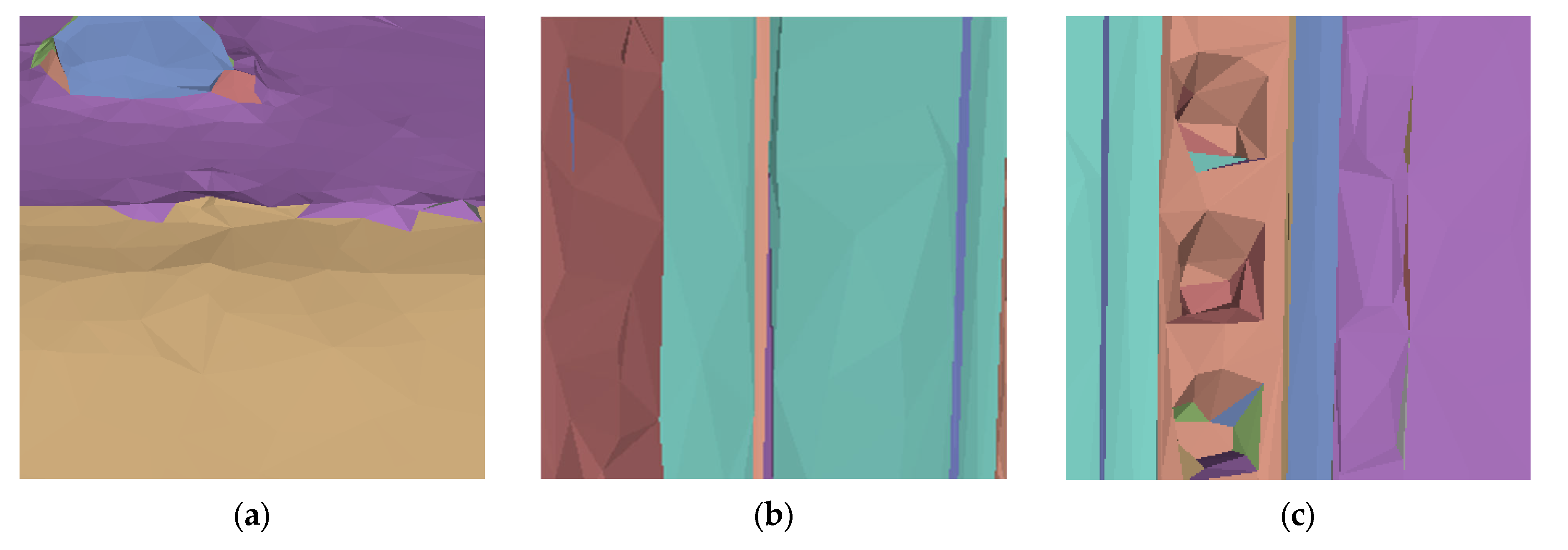
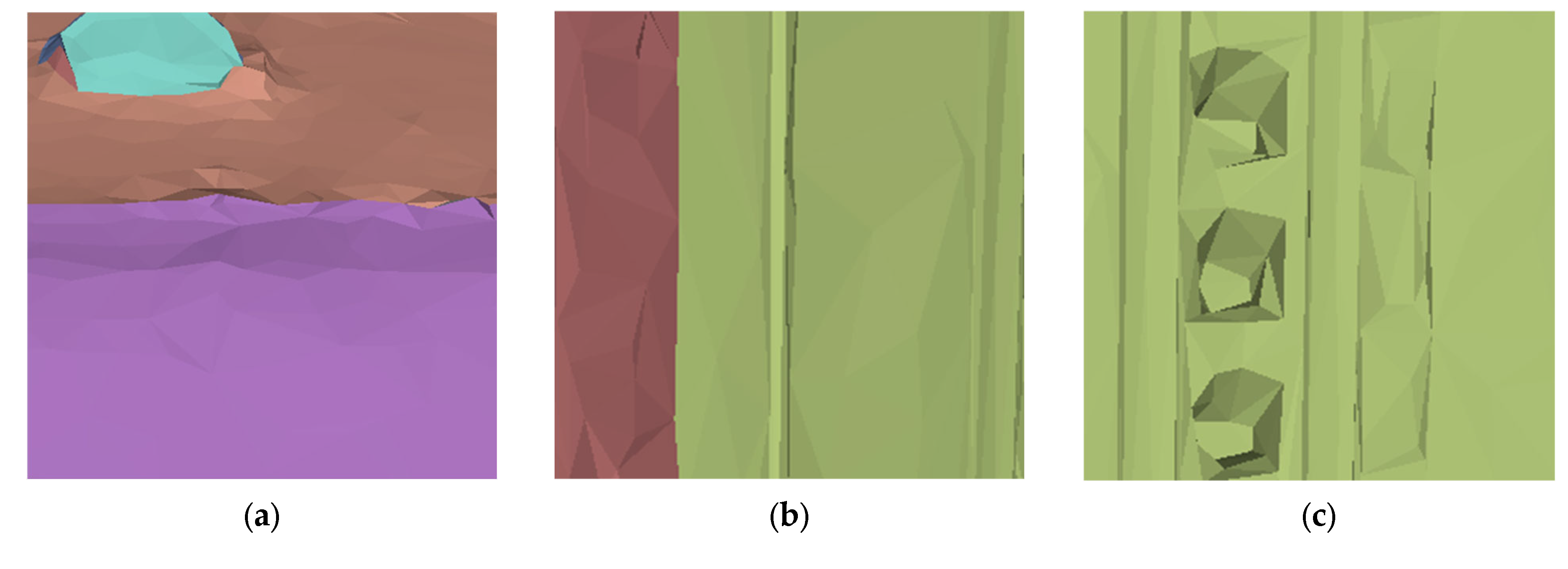
2.1.3. Region Growing Refinements
- Jagged borders: These may arise due to irregularities in the original surface geometry, and may contribute to the overall integrity of the plane;
- Elongated strip-like regions: The presence of elongated strip-like regions may be attributed to elongated features in the building structure, such as beams or columns, which can cause the bending or curvature of the textures;
- Small components with smooth curvature: The traditional region growing method faces significant challenges when handling models with smooth curvature [17]. Small components with smooth curvature might be caused by architectural details or decorative elements that deviate from the assumed planarity.
2.2. Texture Merging Methods
2.2.1. Specifying Sequence for Texture Merging
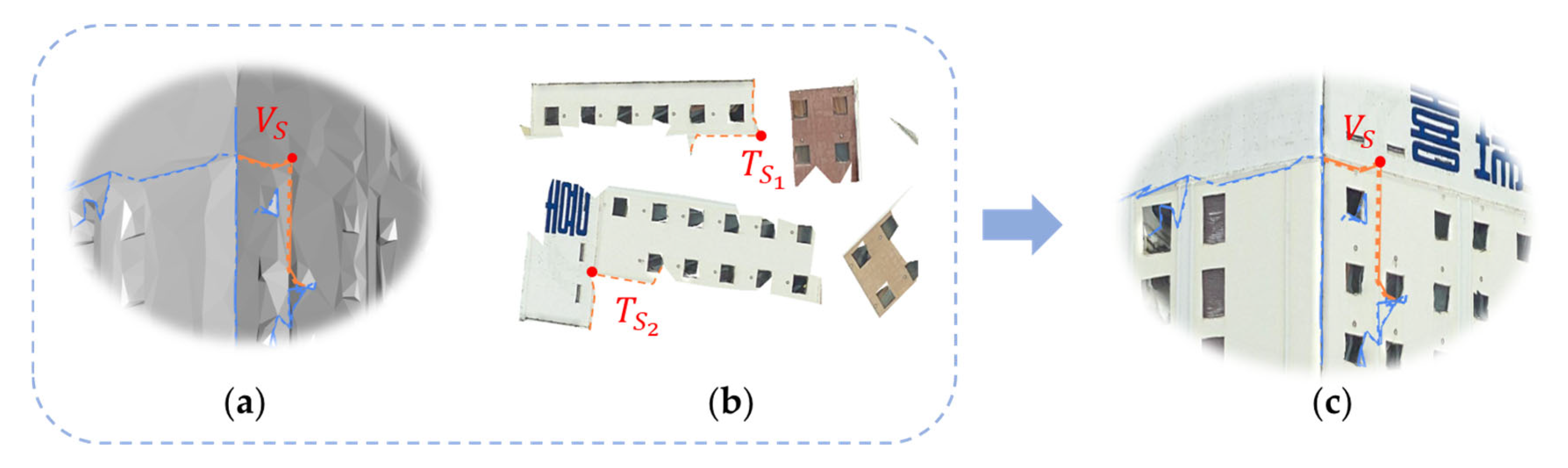
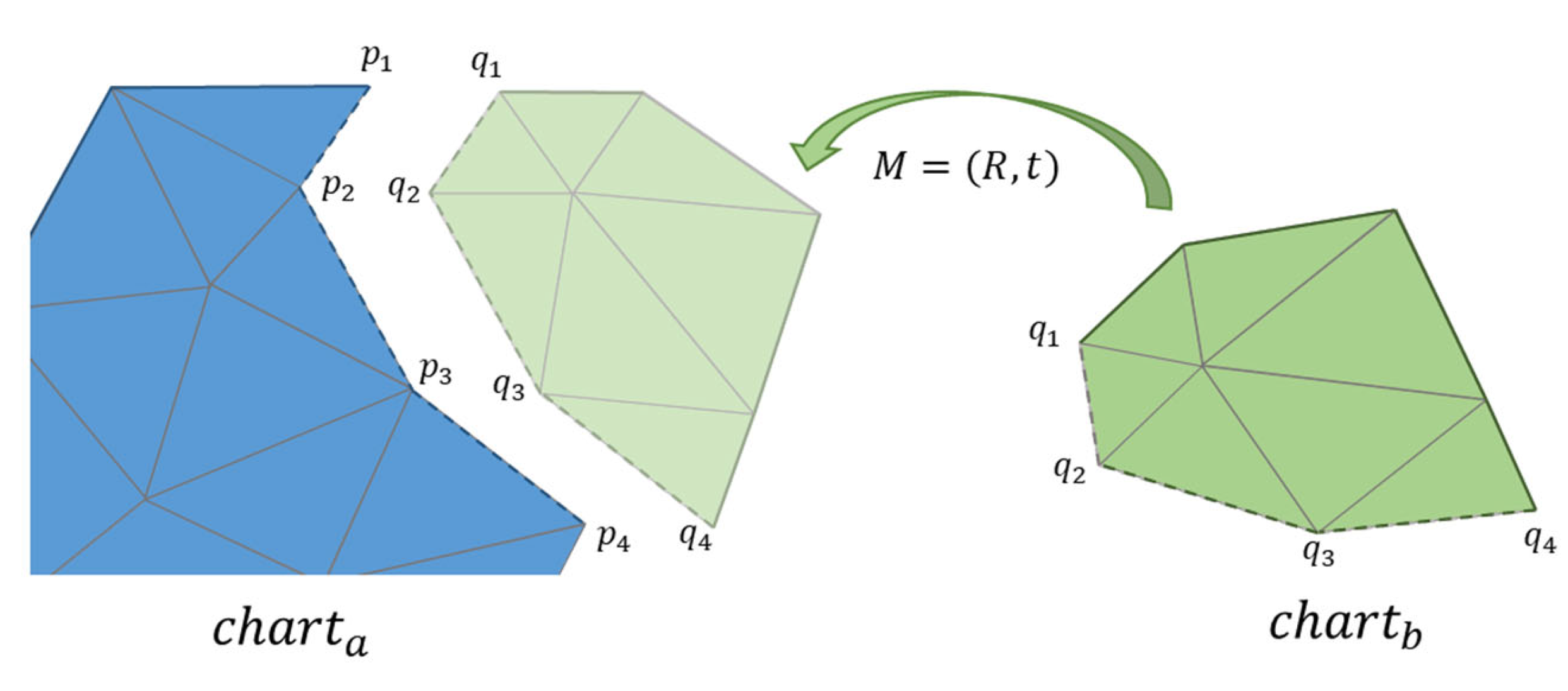
2.2.2. Chart Alignment
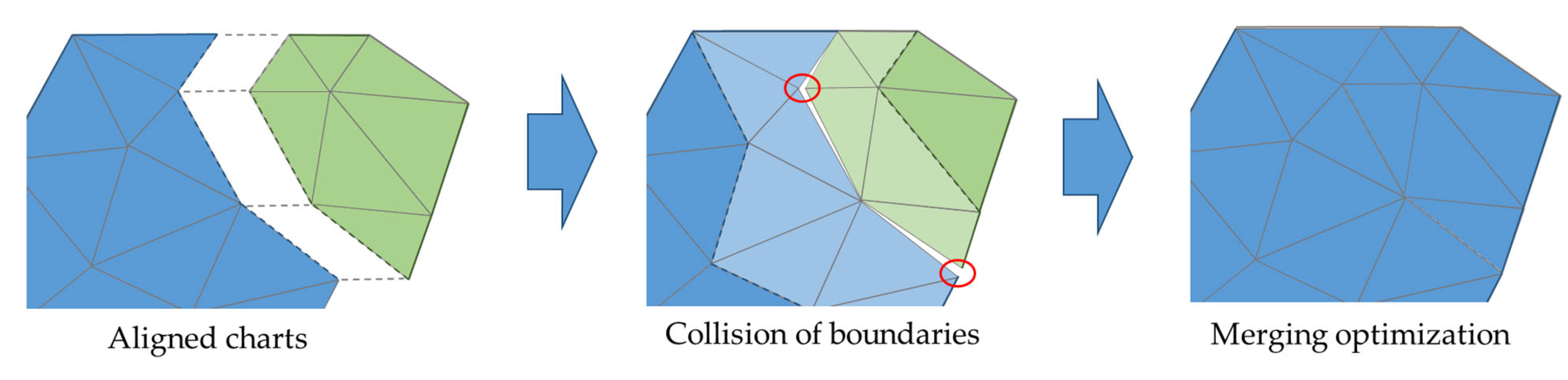
2.2.3. Merging Optimization
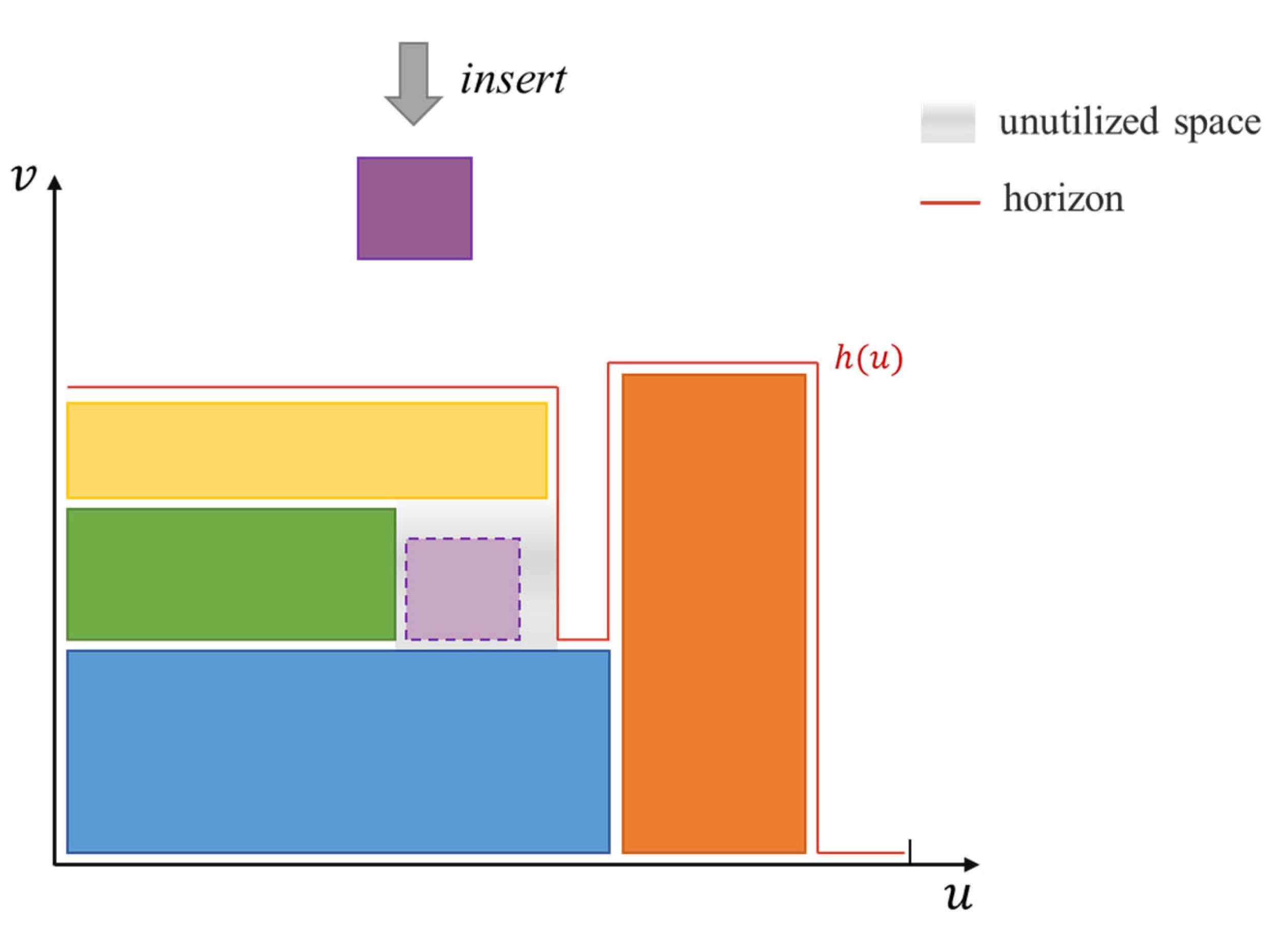
2.3. Texture Atlas Packing Strategy
- Initially, we position all texture atlases within their minimum bounding rectangles (MBRs). These MBRs will replace the actual texture atlases in the calculation of their packing positions in the (u, v) space.
- The MBRs can be placed horizontally or vertically, and they are sorted in decreasing order of area.
- As shown in the diagram, we retain the concept of a horizon from traditional Tetris methods and maintain it using a simpler piecewise linear function, h(u). Additionally, for unutilized space, we allow the next inserted rectangle to prioritize detecting and filling that area.
- The placement of the MBRs will follow the subsequent method. Initially, we sort the enclosed unutilized space in descending order by area to obtain . For each chart’s bounding rectangle square, we assess if it can be placed within . If not, we position the lower-left corner of the square on the horizon from left to right to minimize the peak value of after placement, and update . If placement is feasible, h(u) remains unchanged, and we update Ls. The position where the bounding rectangle is placed represents the final packing position of the corresponding texture atlas.
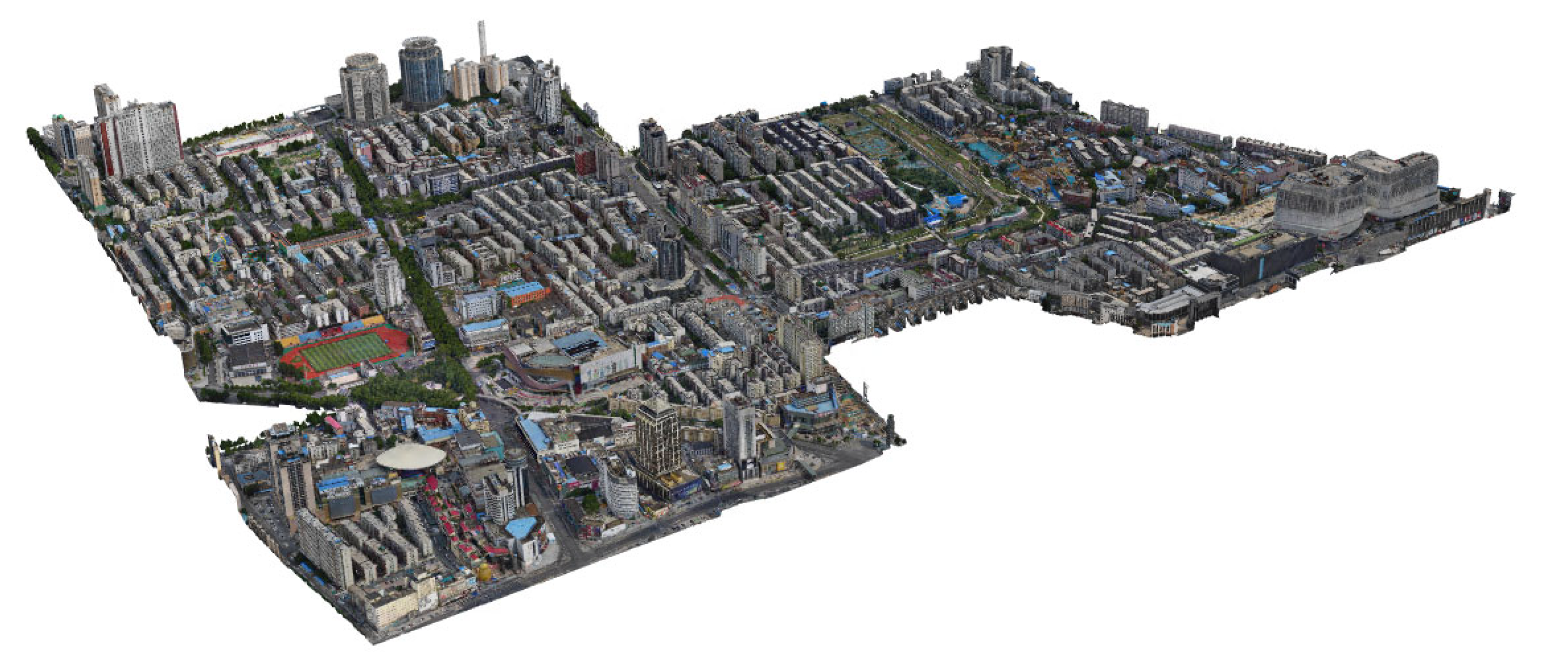
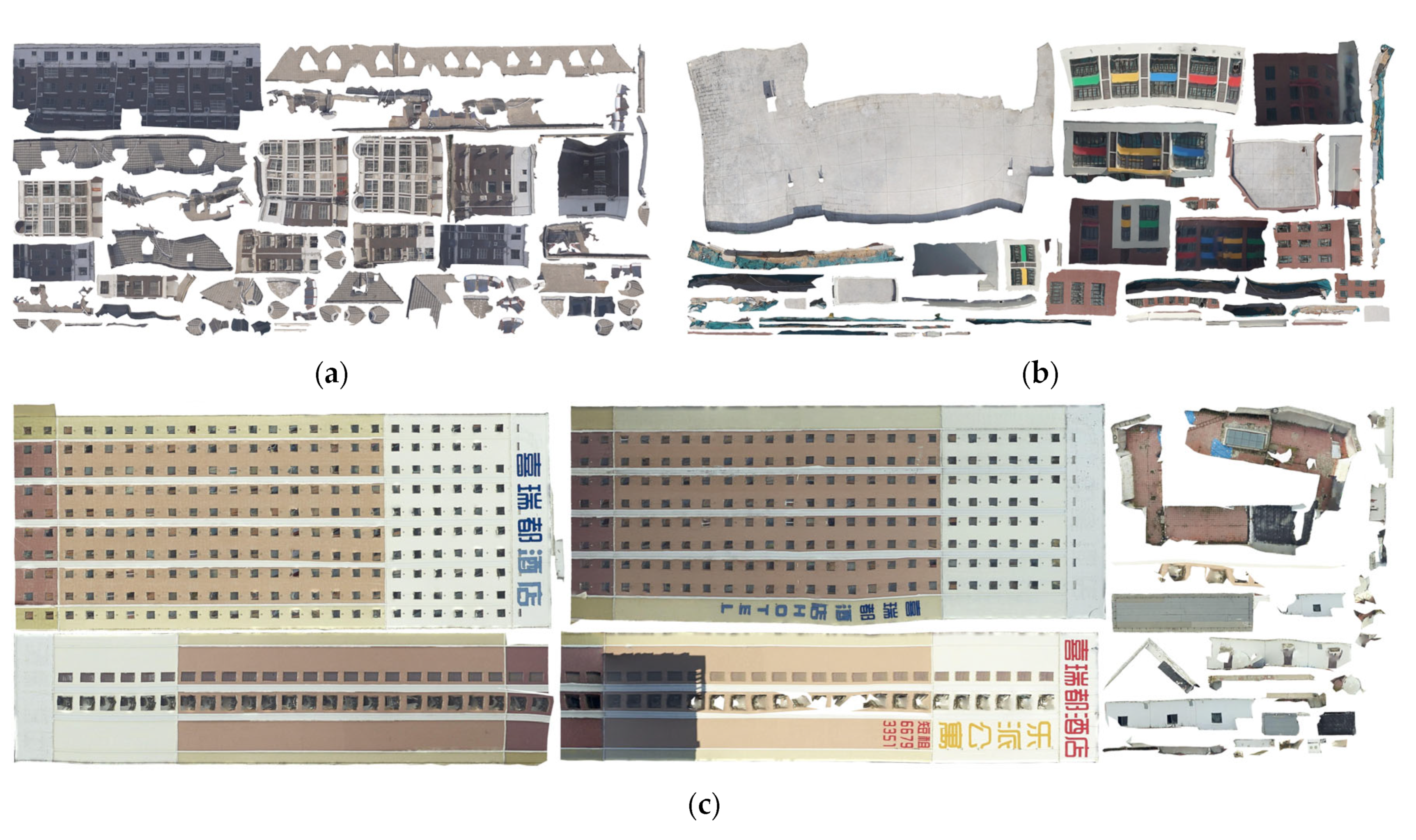
3. Experiments and Discussion
3.1. Qualitative Assessment
3.2. Quantitative Analysis
3.2.1. Measurements for Defragmented Models
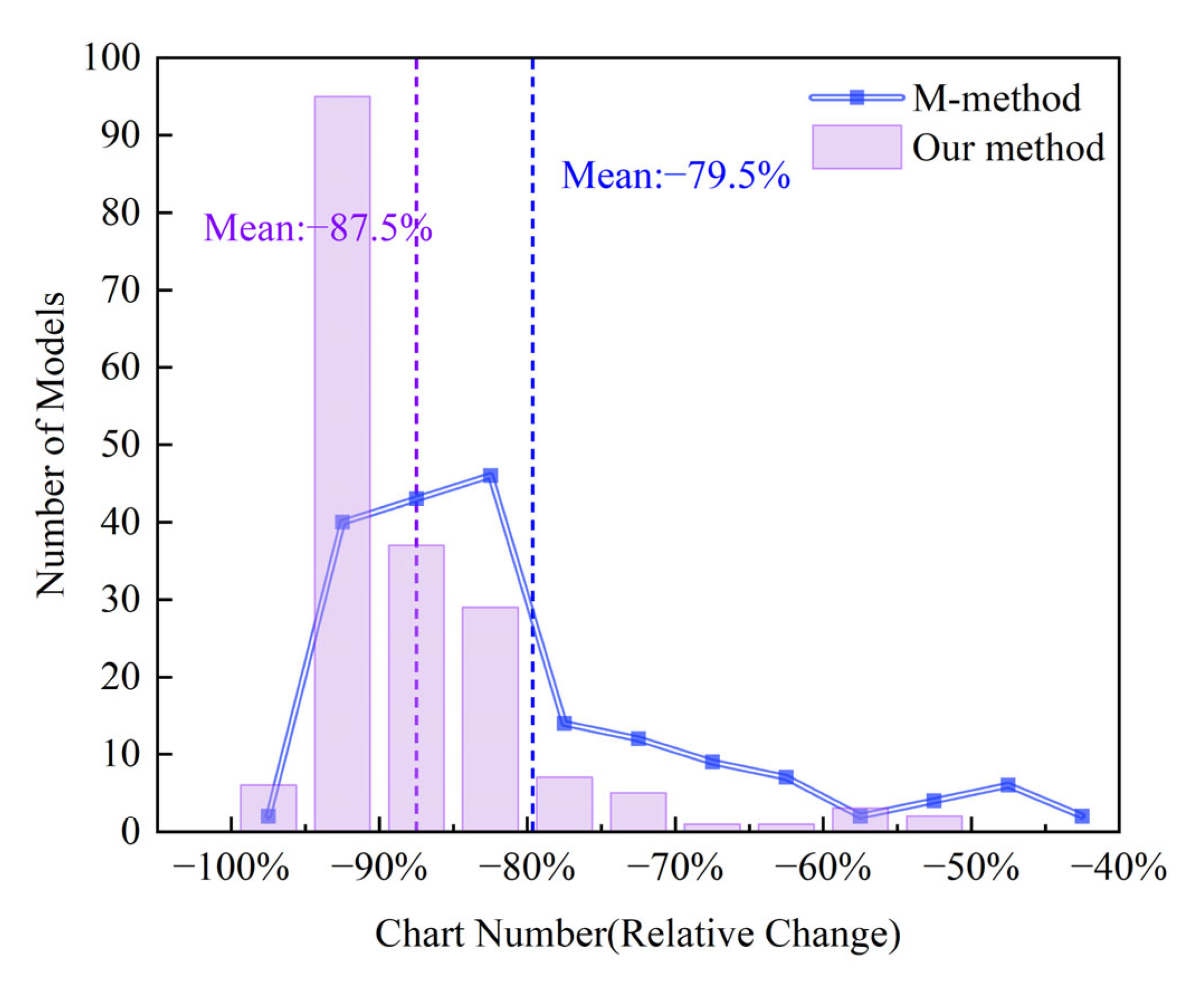
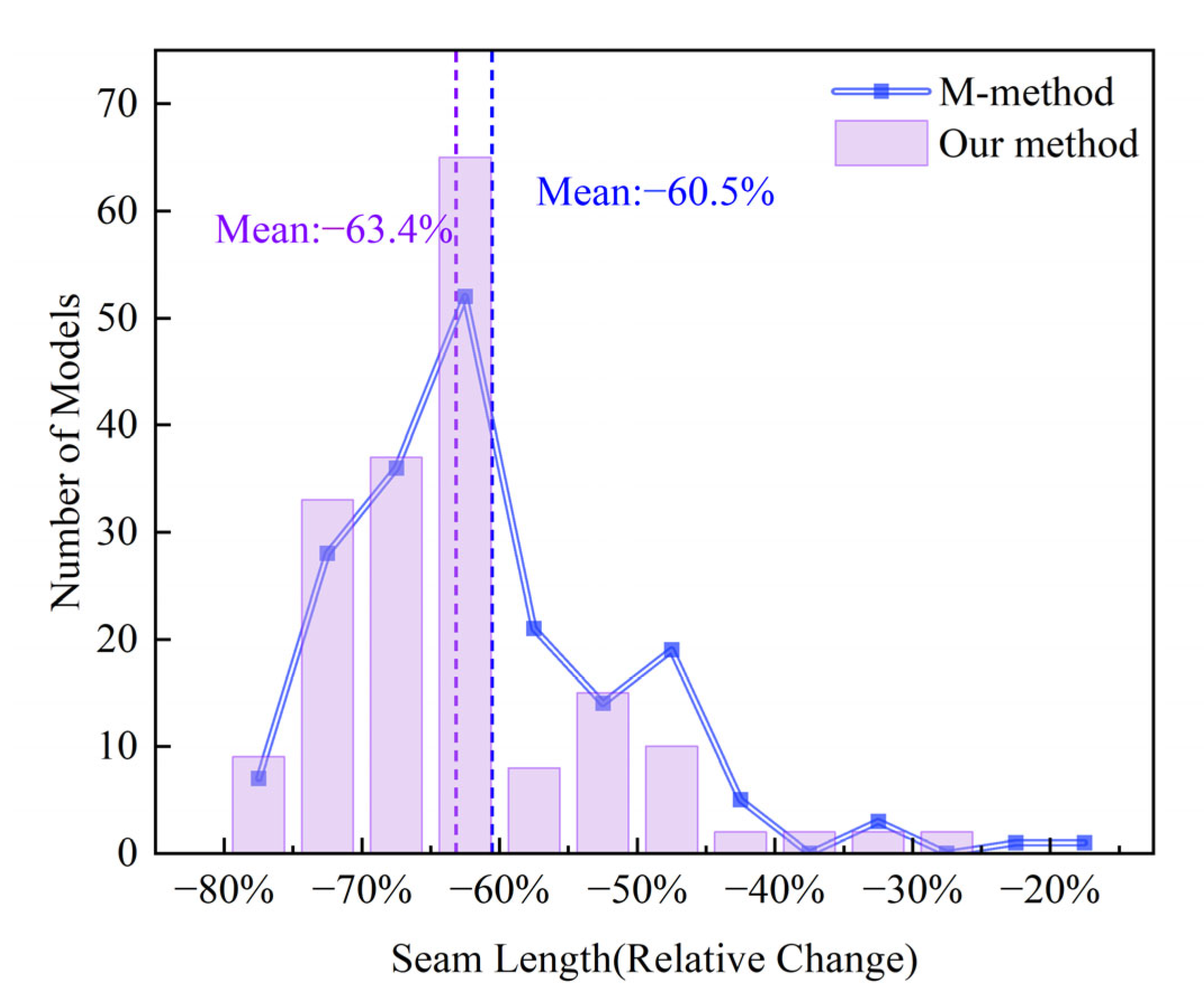
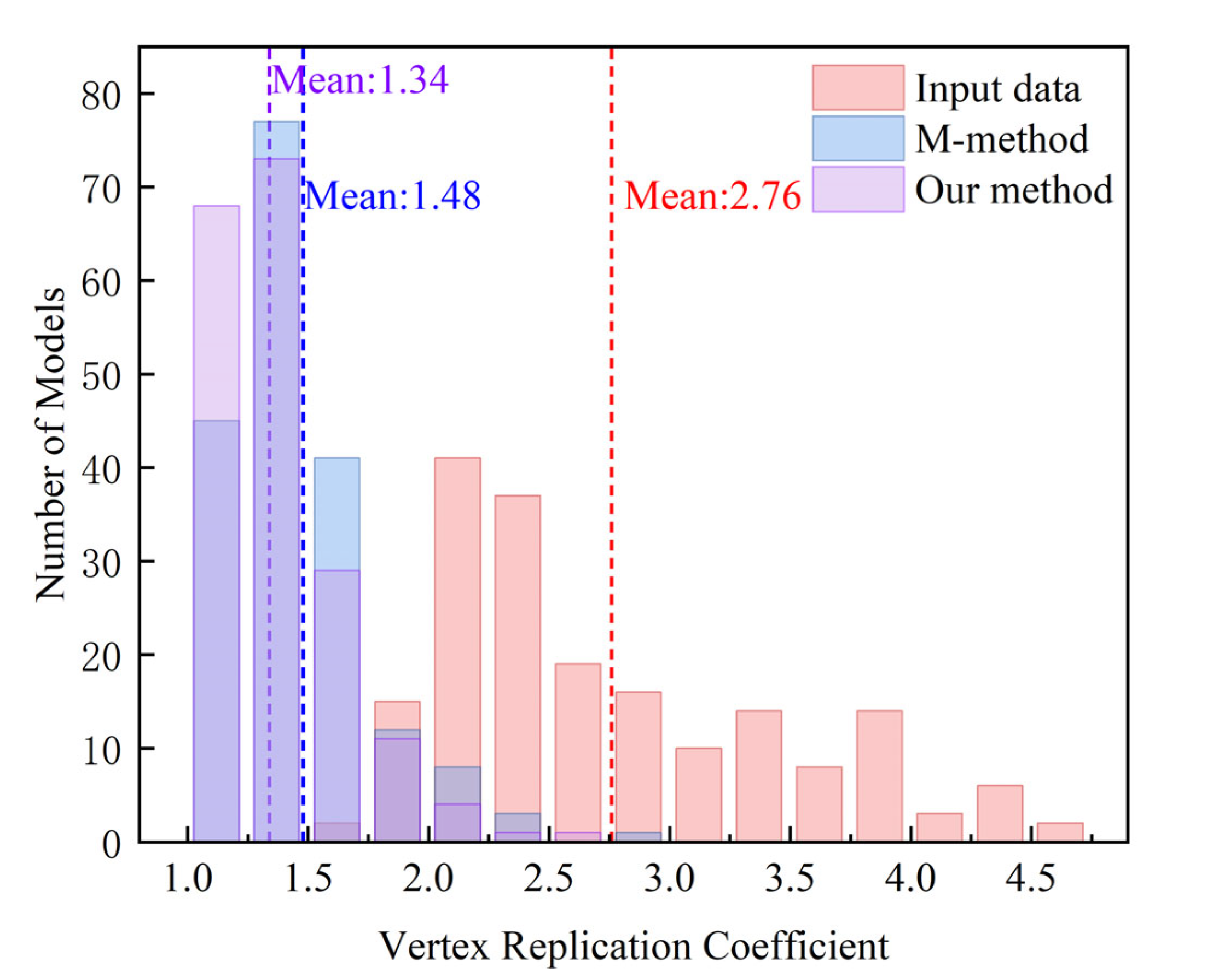
3.2.2. Comparison of Fragmentation Improvement
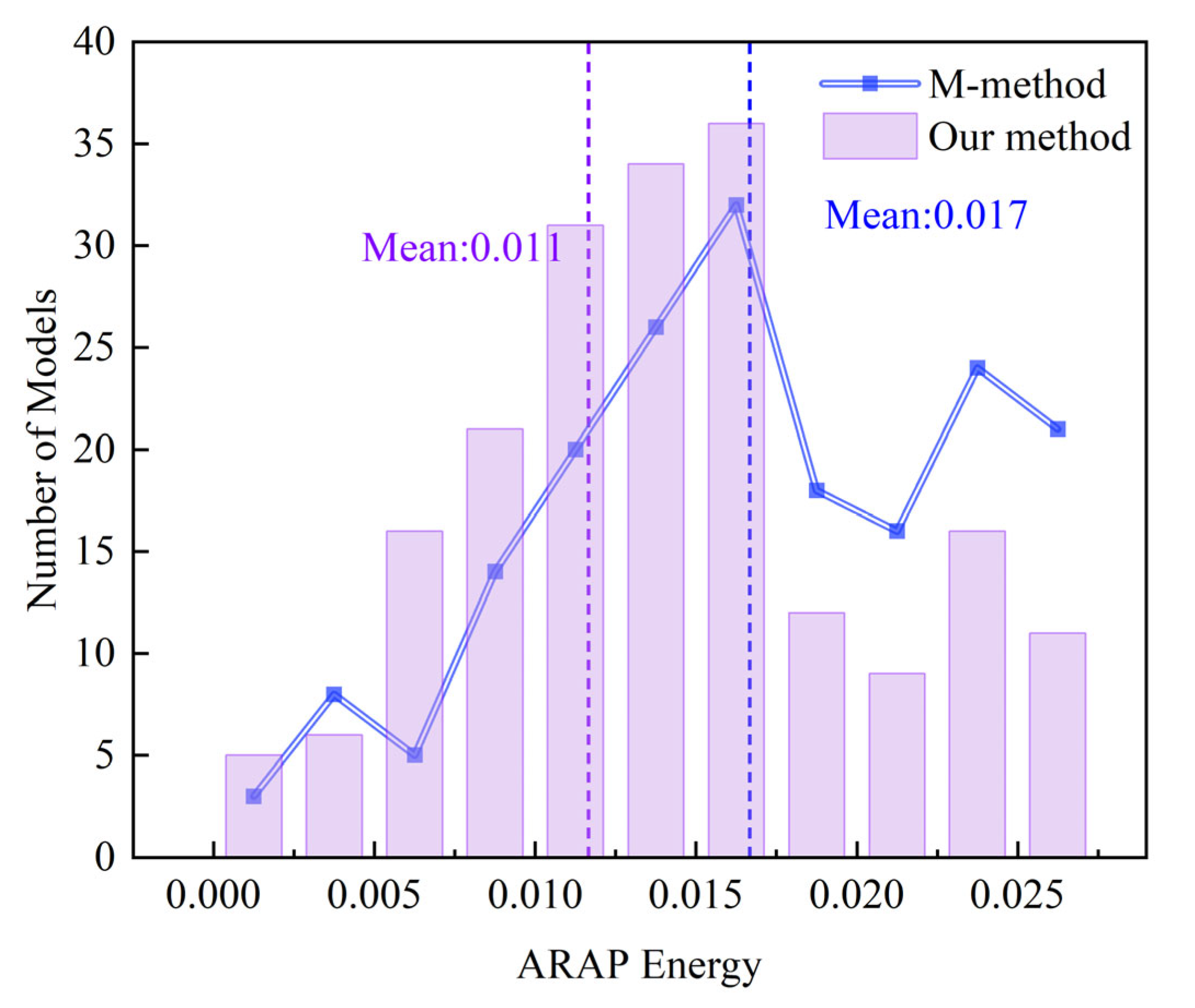
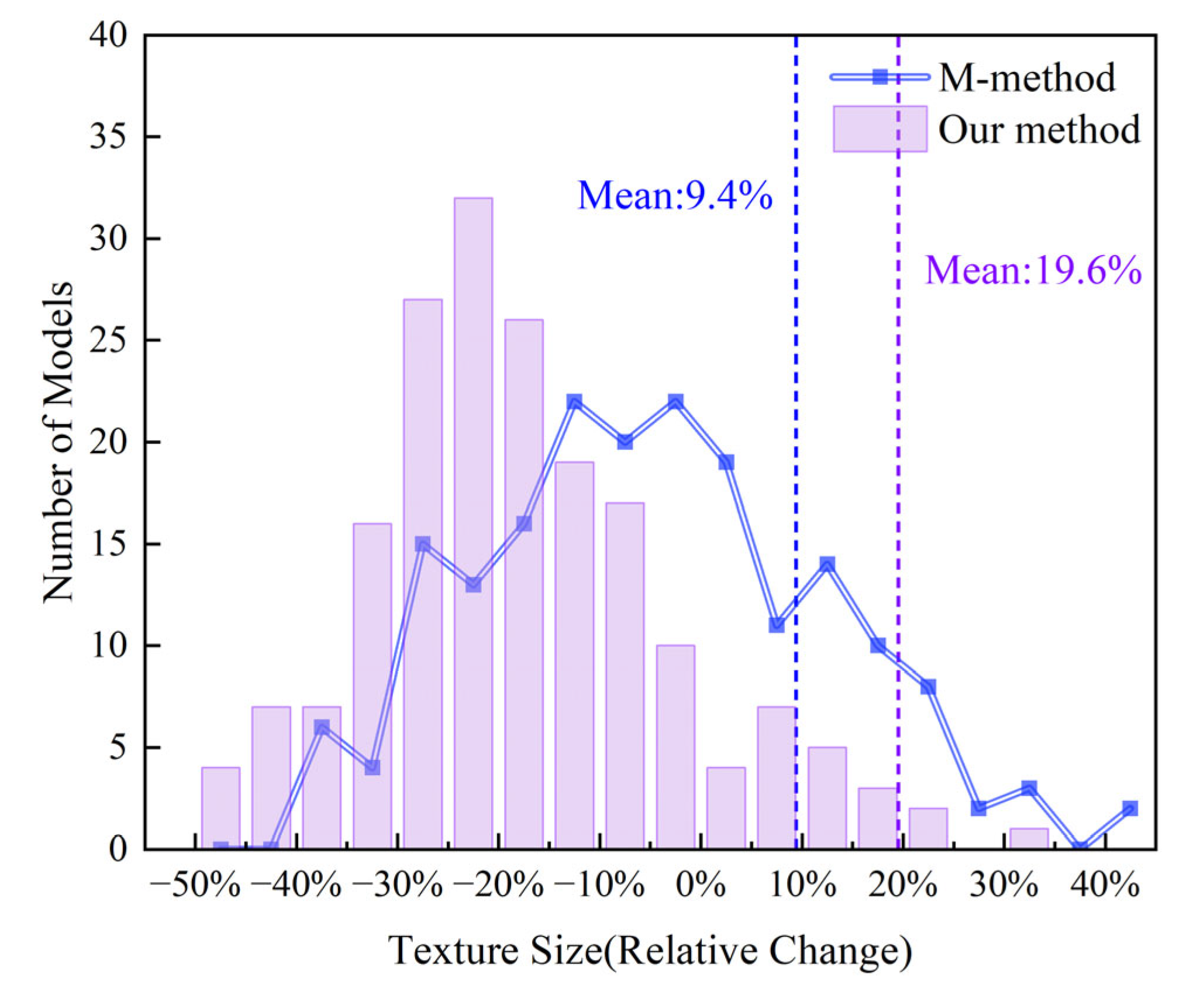
3.2.3. Evaluation of Global Distortion
3.2.4. Evaluation of Memory Usage
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Yuxuan, L.; Yangjie, S.; Chaozhen, L.; Haibin, A.; Zhongli, F. A Review of Developments in the Theory and Technology of Three-Dimensional Reconstruction in Digital Aerial Photogrammetry. Acta Geod. Cartogr. Sin. 2022, 51, 1437. [Google Scholar]
- Maggiordomo, A.; Ponchio, F.; Cignoni, P.; Tarini, M. Real-World Textured Things: A Repository of Textured Models Generated with Modern Photo-Reconstruction Tools. Comput. Aided Geom. Des. 2020, 83, 101943. [Google Scholar] [CrossRef]
- Yuksel, C.; Lefebvre, S.; Tarini, M. Rethinking Texture Mapping. Comput. Graph. Forum 2019, 38, 535–551. [Google Scholar] [CrossRef]
- Li, M.; Kaufman, D.M.; Kim, V.G.; Solomon, J.; Sheffer, A. OptCuts: Joint Optimization of Surface Cuts and Parameterization. ACM Trans. Graph. 2018, 37, 247. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, L.; Xu, Y.; Gotsman, C.; Gortler, S.J. A Local/Global Approach to Mesh Parameterization. Comput. Graph. Forum 2008, 27, 1495–1504. [Google Scholar] [CrossRef]
- Aigerman, N.; Lipman, Y. Orbifold Tutte Embeddings. ACM Trans. Graph. 2015, 34, 190:1–190:12. [Google Scholar] [CrossRef]
- Sawhney, R.; Crane, K. Boundary First Flattening. ACM Trans. Graph. 2017, 37, 5. [Google Scholar] [CrossRef]
- Claici, S.; Bessmeltsev, M.; Schaefer, S.; Solomon, J. Isometry-Aware Preconditioning for Mesh Parameterization. Comput. Graph. Forum 2017, 36, 37–47. [Google Scholar] [CrossRef]
- Rabinovich, M.; Poranne, R.; Panozzo, D.; Sorkine-Hornung, O. Scalable Locally Injective Mappings. ACM Trans. Graph. 2017, 36, 16. [Google Scholar] [CrossRef]
- Jiang, Z.; Schaefer, S.; Panozzo, D. Simplicial Complex Augmentation Framework for Bijective Maps. ACM Trans. Graph. 2017, 36, 186:1–186:9. [Google Scholar] [CrossRef]
- Chu, L.; Pan, H.; Liu, Y.; Wang, W. Repairing Man-Made Meshes via Visual Driven Global Optimization with Minimum Intrusion. ACM Trans. Graph. 2019, 38, 158. [Google Scholar] [CrossRef]
- Maggiordomo, A.; Cignoni, P.; Tarini, M. Texture Defragmentation for Photo-Reconstructed 3D Models. Comput. Graph. Forum 2021, 40, 65–78. [Google Scholar] [CrossRef]
- Li, Y.; Gong, G.; Liu, C.; Zhao, Y.; Qi, Y.; Lu, C.; Li, N. Hybrid Method of Connection Evaluation and Framework Optimization for Building Surface Reconstruction. Remote Sens. 2024, 16, 792. [Google Scholar] [CrossRef]
- Lempitsky, V.; Ivanov, D. Seamless Mosaicing of Image-Based Texture Maps. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Gal, R.; Wexler, Y.; Ofek, E.; Hoppe, H.; Cohen-Or, D. Seamless Montage for Texturing Models. Comput. Graph. Forum 2010, 29, 479–486. [Google Scholar] [CrossRef]
- Fu, Y.; Yan, Q.; Liao, J.; Xiao, C. Joint Texture and Geometry Optimization for RGB-D Reconstruction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5949–5958. [Google Scholar] [CrossRef]
- Li, S.; Xiao, X.; Guo, B.; Zhang, L. A Novel OpenMVS-Based Texture Reconstruction Method Based on the Fully Automatic Plane Segmentation for 3D Mesh Models. Remote Sens. 2020, 12, 3908. [Google Scholar] [CrossRef]
- Xiang, H.; Huang, X.; Lan, F.; Yang, C.; Gao, Y.; Wu, W.; Zhang, F. A Shape-Preserving Simplification Method for Urban Building Models. ISPRS Int. J. Geo-Inf. 2022, 11, 562. [Google Scholar] [CrossRef]
- Drobnyi, V.; Hu, Z.; Fathy, Y.; Brilakis, I. Construction and Maintenance of Building Geometric Digital Twins: State of the Art Review. Sensors 2023, 23, 4382. [Google Scholar] [CrossRef]
- Oechsle, M.; Mescheder, L.; Niemeyer, M.; Strauss, T.; Geiger, A. Texture Fields: Learning Texture Representations in Function Space. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4530–4539. [Google Scholar] [CrossRef]
- Sander, P.V.; Snyder, J.; Gortler, S.J.; Hoppe, H. Texture Mapping Progressive Meshes. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’01), Los Angeles, CA, USA, 12–17 August 2001; Association for Computing Machinery: New York, NY, USA, 2001; pp. 409–416. [Google Scholar] [CrossRef]
- Vo, A.-V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-Based Region Growing for Point Cloud Segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for Point-Cloud Shape Detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Wang, X.; Zou, L.; Shen, X.; Ren, Y.; Qin, Y. A Region-Growing Approach for Automatic Outcrop Fracture Extraction from a Three-Dimensional Point Cloud. Comput. Geosci. 2017, 99, 100–106. [Google Scholar] [CrossRef]
- Smith, J.; Schaefer, S. Bijective Parameterization with Free Boundaries. ACM Trans. Graph. 2015, 34, 70. [Google Scholar] [CrossRef]
- Milenkovic, V.J. Rotational Polygon Containment and Minimum Enclosure Using Only Robust 2D Constructions. Comput. Geom. 1999, 13, 3–19. [Google Scholar] [CrossRef]
- Sander, P.V.; Wood, Z.J.; Gortler, S.J.; Snyder, J.; Hoppe, H. Multi-Chart Geometry Images. In Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Aachen, Germany, 23–25 June 2003; Eurographics Association: Goslar, Germany, 2003; pp. 146–155. [Google Scholar]
- Lévy, B.; Petitjean, S.; Ray, N.; Maillot, J. Least Squares Conformal Maps for Automatic Texture Atlas Generation. ACM Trans. Graph. 2002, 21, 362–371. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Liu, W.; Lei, Z.; Zhang, F.; Huang, X.; Awwad, T.M. A Planar Feature-Preserving Texture Defragmentation Method for 3D Urban Building Models. Remote Sens. 2024, 16, 4154. https://doi.org/10.3390/rs16224154
Liu B, Liu W, Lei Z, Zhang F, Huang X, Awwad TM. A Planar Feature-Preserving Texture Defragmentation Method for 3D Urban Building Models. Remote Sensing. 2024; 16(22):4154. https://doi.org/10.3390/rs16224154
Chicago/Turabian StyleLiu, Beining, Wenxuan Liu, Zhen Lei, Fan Zhang, Xianfeng Huang, and Tarek M. Awwad. 2024. "A Planar Feature-Preserving Texture Defragmentation Method for 3D Urban Building Models" Remote Sensing 16, no. 22: 4154. https://doi.org/10.3390/rs16224154
APA StyleLiu, B., Liu, W., Lei, Z., Zhang, F., Huang, X., & Awwad, T. M. (2024). A Planar Feature-Preserving Texture Defragmentation Method for 3D Urban Building Models. Remote Sensing, 16(22), 4154. https://doi.org/10.3390/rs16224154





