Boosting Point Set-Based Network with Optimal Transport Optimization for Oriented Object Detection
Abstract
1. Introduction
- An effective remote sensing image object detector is proposed, which can significantly optimize the point set localization supervision process through a one-to-many matching method.
- A novel comprehensive quality evaluation scheme for point set representation methods is proposed, which contributes to the selection of high-quality candidate point sets.
2. Related Work
2.1. Oriented Object Detection Based on Point Set Representation
2.2. Quality Assessment and Sample Assignment for Object Detection
3. Proposed Method
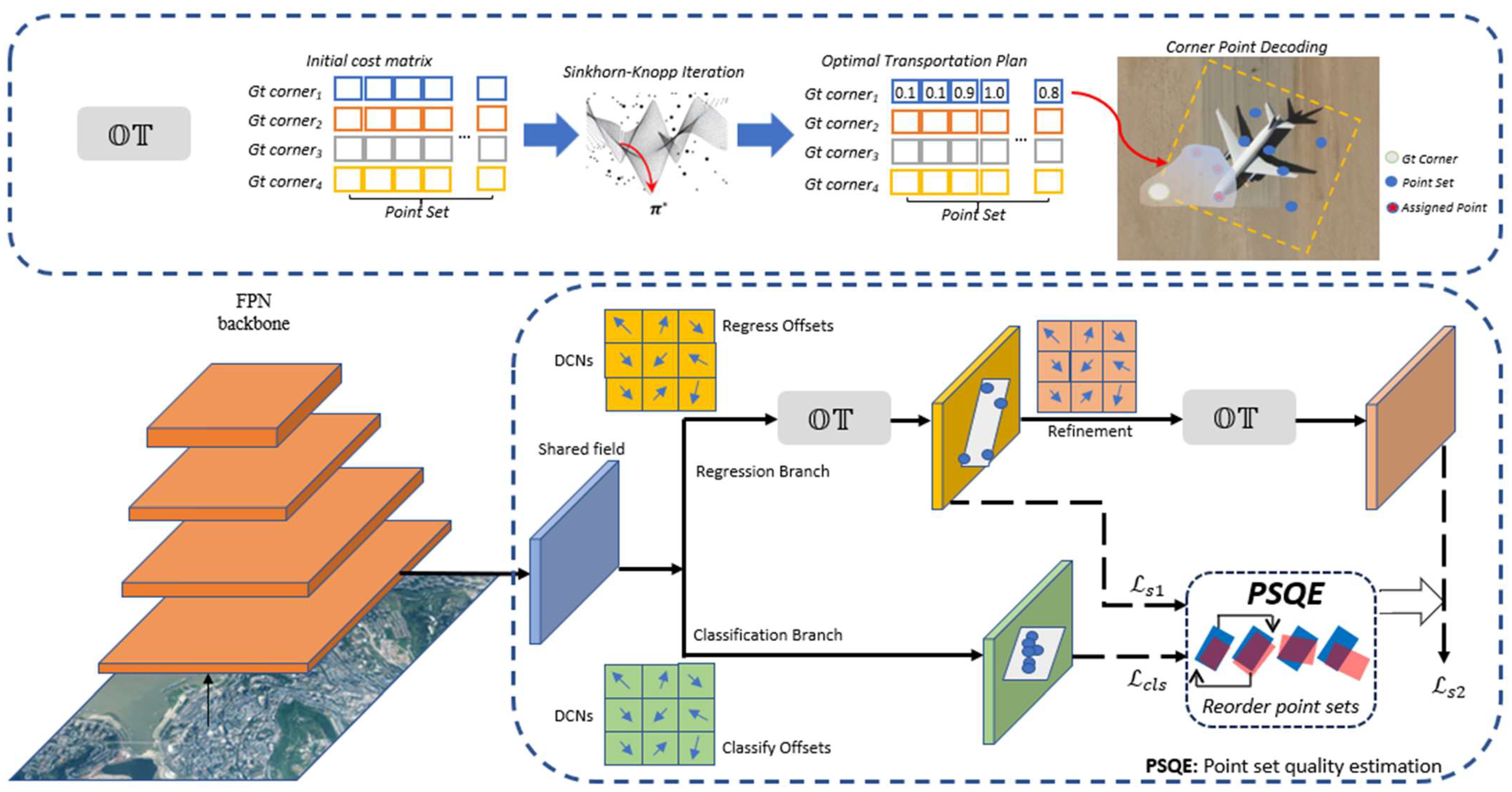
3.1. Overview
3.2. Point Set Representation
3.3. OT for Conversion Function
3.3.1. Optimal Transport
3.3.2. Conversion Function Construction
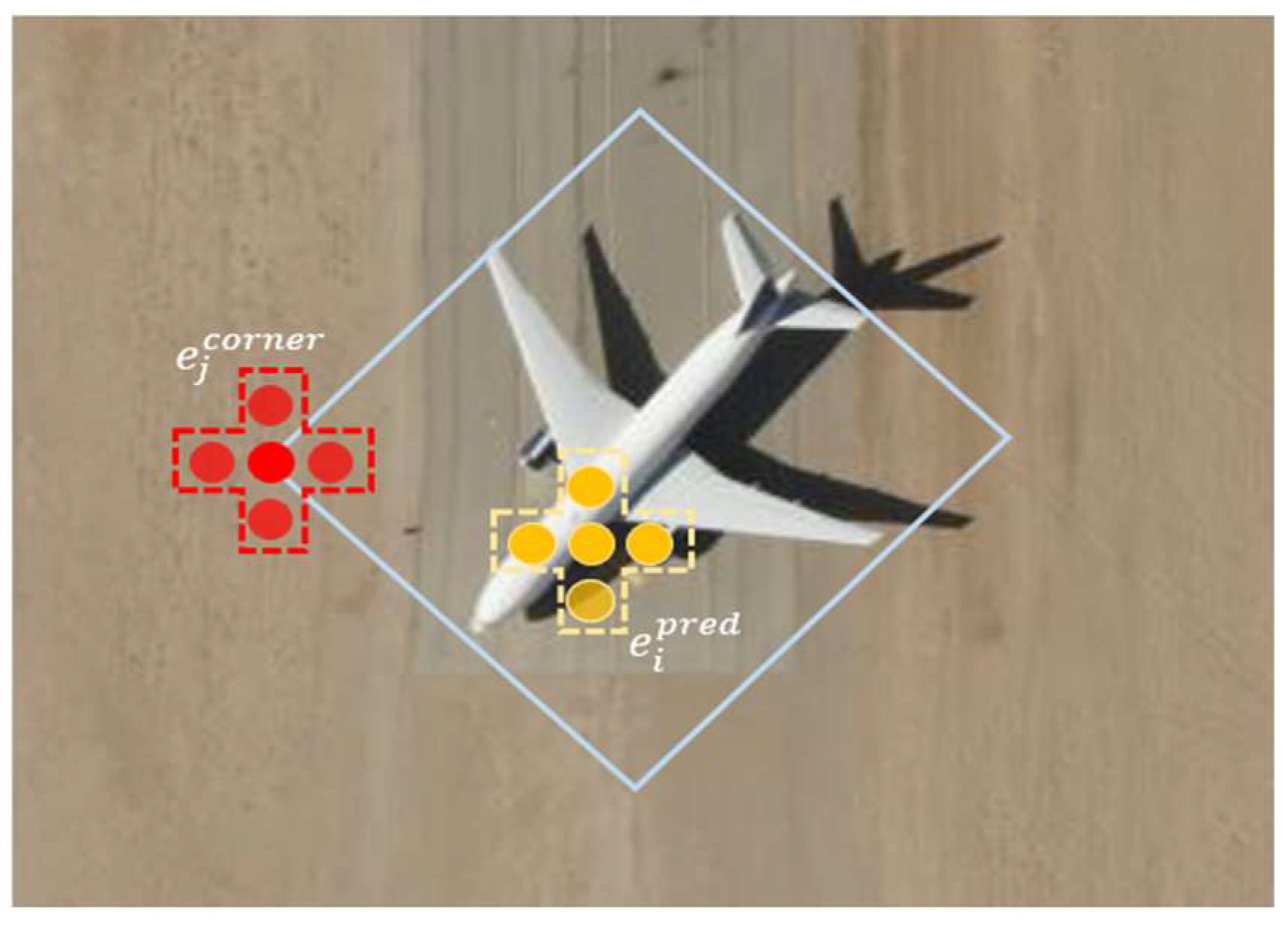
| Algorithm 1: The pseudo-code of the optimal transport conversion strategy |
| Input: |
| I is an input image R is a point set |
| G represents the gt corner points for each object |
| T is the number of iterations in Sinkhorn–Knopp iteration |
| is the balanced coefficient |
| Output: |
| is the optimal assigning plan |
| 1: |
| 2: pairwise localization cost: |
| 3: |
| 4: pairwise correlation cost: |
| 5: compute final cost matrix: |
| 6: |
| 7: for t = 0 to T do: |
| 8: |
| 9: compute optimal assigning plan |
| 10: |
| 11: return |
3.3.3. Dynamic Estimation
3.3.4. Spatial Decoupled Sampling Strategy
3.4. Point Set Quality Evaluation
4. Experimental Results
4.1. Datasets and Evaluation Metrics
4.2. Implementation Details
4.3. Ablation Study
4.4. Time Cost Analysis
4.5. Comparison with the State-of-the-Art Methods
4.6. More Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, X.; Yang, J.; Yan, J.; Zhang, Y.; Zhang, T.; Guo, Z.; Xian, S.; Fu, K. SCRDet: Towards More Robust Detection for Small, Cluttered and Rotated Objects. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Zhang, G.; Lu, S.; Zhang, W. CAD-Net: A Context-Aware Detection Network for Objects in Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10015–10024. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Ming, Q.; Wang, W.; Zhang, X.; Tian, Q. Rethinking Rotated Object Detection with Gaussian Wasserstein Distance Loss. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022. [Google Scholar]
- Pan, X.; Ren, Y.; Sheng, K.; Dong, W.; Yuan, H.; Guo, X.; Ma, C.; Xu, C. Dynamic Refinement Network for Oriented and Densely Packed Object Detection. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 11204–11213. [Google Scholar]
- Yang, X.; Yan, J.; Feng, Z.; He, T. R3Det: Refined Single-Stage Detector with Feature Refinement for Rotating Object. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 3163–3171. [Google Scholar] [CrossRef]
- Han, J.; Ding, J.; Xue, N.; Xia, G.-S. ReDet: A Rotation-Equivariant Detector for Aerial Object Detection. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2785–2794. [Google Scholar]
- Dai, L.; Liu, H.; Tang, H.; Wu, Z.; Song, P. AO2-DETR: Arbitrary-Oriented Object Detection Transformer. Available online: https://arxiv.org/abs/2205.12785v1 (accessed on 5 September 2024).
- Lyu, C.; Zhang, W.; Huang, H.; Zhou, Y.; Wang, Y.; Liu, Y.; Zhang, S.; Chen, K. RTMDet: An Empirical Study of Designing Real-Time Object Detectors. arXiv 2022, arXiv:2212.07784. [Google Scholar] [CrossRef]
- Li, Y.; Hou, Q.; Zheng, Z.; Cheng, M.-M.; Yang, J.; Li, X. Large Selective Kernel Network for Remote Sensing Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 16794–16805. [Google Scholar]
- Xie, X.; Cheng, G.; Wang, J.; Yao, X.; Han, J. Oriented R-CNN for Object Detection. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 3500–3509. [Google Scholar]
- Xu, Y.; Fu, M.; Wang, Q.; Wang, Y.; Chen, K.; Xia, G.-S.; Bai, X. Gliding Vertex on the Horizontal Bounding Box for Multi-Oriented Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 1452–1459. [Google Scholar] [CrossRef] [PubMed]
- Qian, W.; Yang, X.; Peng, S.; Yan, J.; Guo, Y. Learning Modulated Loss for Rotated Object Detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 2458–2466. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J. Arbitrary-Oriented Object Detection with Circular Smooth Label. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 12353, pp. 677–694. ISBN 978-3-030-58597-6. [Google Scholar]
- Zeng, Y.; Chen, Y.; Yang, X.; Li, Q.; Yan, J. ARS-DETR: Aspect Ratio-Sensitive Detection Transformer for Aerial Oriented Object Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Yang, X.; Yang, X.; Yang, J.; Ming, Q.; Wang, W.; Tian, Q.; Yan, J. Learning High-Precision Bounding Box for Rotated Object Detection via Kullback-Leibler Divergence. Adv. Neural Inf. Process. Syst. 2022, 34, 18381–18394. [Google Scholar]
- Lee, H.; Song, M.; Koo, J.; Seo, J. Hausdorff Distance Matching with Adaptive Query Denoising for Rotated Detection Transformer. arXiv 2023, arXiv:2305.07598. [Google Scholar]
- Yang, Z.; Liu, S.; Hu, H.; Wang, L.; Lin, S. RepPoints: Point Set Representation for Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Guo, Z.; Liu, C.; Zhang, X.; Jiao, J.; Ji, X.; Ye, Q. Beyond Bounding-Box: Convex-Hull Feature Adaptation for Oriented and Densely Packed Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8792–8801. [Google Scholar]
- Li, W.; Chen, Y.; Hu, K.; Zhu, J. Oriented RepPoints for Aerial Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Hou, L.; Lu, K.; Yang, X.; Li, Y.; Xue, J. G-Rep: Gaussian Representation for Arbitrary-Oriented Object Detection. Remote Sens. 2023, 15, 757. [Google Scholar] [CrossRef]
- Merugu, S.; Jain, K.; Mittal, A.; Raman, B. Sub-scene Target Detection and Recognition Using Deep Learning Convolution Neural Networks. In Proceedings of the ICDSMLA 2019, Proceedings of the 1st International Conference on Data Science, Machine Learning and Applications, Lecture Notes in Electrical Engineering, Hyderabad, India, 26–27 December 2021; Springer: Singapore, 2019; Volume 601, pp. 1082–1101. [Google Scholar] [CrossRef]
- Haq, M.A.; Rahim Khan, M.A. DNNBoT: Deep Neural Network-Based Botnet Detection and Classification. Comput. Mater. Contin. CMC 2022, 71, 1729–1750. [Google Scholar] [CrossRef]
- Merugu, S.; Tiwari, A.; Sharma, S.K. Spatial–Spectral Image Classification with Edge Preserving Method. J. Indian Soc. Remote Sens. 2021, 49, 703–711. [Google Scholar] [CrossRef]
- Zhang, X.; Wan, F.; Liu, C.; Ji, R.; Ye, Q. FreeAnchor: Learning to Match Anchors for Visual Object Detection. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Zhang, S.; Chi, C.; Yao, Y.; Lei, Z.; Li, S.Z. Bridging the Gap Between Anchor-Based and Anchor-Free Detection via Adaptive Training Sample Selection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Kim, K.; Lee, H.S. Probabilistic Anchor Assignment with IoU Prediction for Object Detection. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 12370, pp. 355–371. ISBN 978-3-030-58594-5. [Google Scholar]
- Ming, Q.; Zhou, Z.; Miao, L.; Zhang, H.; Li, L. Dynamic Anchor Learning for Arbitrary-Oriented Object Detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 2355–2363. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Dayoub, F.; Sunderhauf, N. VarifocalNet: An IoU-Aware Dense Object Detector. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8510–8519. [Google Scholar]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Curran Associates, Inc.: New York, NY, USA, 2020; Volume 33, pp. 21002–21012. [Google Scholar]
- Ge, Z.; Liu, S.; Li, Z.; Yoshie, O.; Sun, J. OTA: Optimal Transport Assignment for Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- De Plaen, H.; De Plaen, P.-F.; Suykens, J.A.K.; Proesmans, M.; Tuytelaars, T.; Van Gool, L. Unbalanced Optimal Transport: A Unified Framework for Object Detection. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 3198–3207. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Cuturi, M. Sinkhorn Distances: Lightspeed Computation of Optimal Transport. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; Curran Associates, Inc.: New York, NY, USA, 2013; Volume 26. [Google Scholar]
- Huang, Z.; Li, W.; Xia, X.-G.; Wang, H.; Tao, R. Task-Wise Sampling Convolutions for Arbitrary-Oriented Object Detection in Aerial Images. IEEE Trans. Neural Netw. Learn. Syst. 2024. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Su, H.; Guibas, L. A Point Set Generation Network for 3D Object Reconstruction from a Single Image. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2463–2471. [Google Scholar]
- Liu, Z.; Yuan, L.; Weng, L.; Yang, Y. A High Resolution Optical Satellite Image Dataset for Ship Recognition and Some New Baselines. In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods, Porto, Portugal, 24–26 February 2017; SCITEPRESS—Science and Technology Publications: Setúbal, Portugal, 2017; pp. 324–331. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ding, J.; Xue, N.; Long, Y.; Xia, G.-S.; Lu, Q. Learning RoI Transformer for Oriented Object Detection in Aerial Images. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2844–2853. [Google Scholar]
- Yi, J.; Wu, P.; Liu, B.; Huang, Q.; Qu, H.; Metaxas, D. Oriented Object Detection in Aerial Images with Box Boundary-Aware Vectors. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020. [Google Scholar]
- Han, J.; Ding, J.; Li, J.; Xia, G.-S. Align Deep Features for Oriented Object Detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]



| Methods | Conversion Function | mAP(07) |
|---|---|---|
| Oriented RepPoints | NearestGTCorner | 87.12 |
| ConvexHull | 88.56 | |
| BE-Det | Optimal Transport | 89.14 |
| Methods | Oriented RepPoints | BE-Det | ||
|---|---|---|---|---|
| \ | 1 | 2 | dynamic | |
| mAP(07) | 87.12 | 87.19 | 88.82 | 90.59 |
| Ablation Studies on Each Component in BE-Det | ||||
|---|---|---|---|---|
| baseline | √ | |||
| OT | √ | √ | √ | |
| √ | √ | |||
| √ | ||||
| mAP(07) | 87.12 | 89.14 | 89.79 | 90.59 |
| Methods | mAP | Params | Speed |
|---|---|---|---|
| Oriented RepPoints | 90.29 | 36.4 M | 22.3 fps |
| ReDet | 87.83 | 40.2 M | 18.4 fps |
| BE-Det | 92.37 | 36.8 M | 21.9 fps |
| Methods | Backbone | mAP(07) | mAP(12) |
|---|---|---|---|
| Rotated Faster-rcnn RoI-Transformer [39] | R-50-FPN | 84.30 | - |
| R-101-FPN | 86.20 | - | |
| BBAVectors [40] | R-101-FPN | 88.60 | - |
| R3Det | R-101-FPN | 89.26 | 96.01 |
| ReDet | ReR-50 | 89.92 | 96.63 |
| S2A-Net [41] | R-101-FPN | 90.17 | 95.01 |
| Oriented RepPoints | R-50-FPN | 90.38 | 97.26 |
| BE-Det | R-50-FPN | 90.59 | 97.88 |
| BE-Det | R-101-FPN | 90.63 | 97.95 |
| Methods | Backbone | mAP | FAR |
|---|---|---|---|
| RoI-Transformer R3Det | R-101-FPN | 85.88 | 9.69 |
| R-101-FPN | 87.62 | 8.06 | |
| ReDet | ReR-50 | 87.83 | 7.98 |
| S2A-Net | R-101-FPN | 88.17 | 7.38 |
| Oriented RepPoints | R-50-FPN | 90.29 | 5.01 |
| BE-Det | R-50-FPN | 92.37 | 3.92 |
| BE-Det | R-101-FPN | 92.67 | 3.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, B.; Zhi, X.; Hu, J.; Zhang, W. Boosting Point Set-Based Network with Optimal Transport Optimization for Oriented Object Detection. Remote Sens. 2024, 16, 4133. https://doi.org/10.3390/rs16224133
Yuan B, Zhi X, Hu J, Zhang W. Boosting Point Set-Based Network with Optimal Transport Optimization for Oriented Object Detection. Remote Sensing. 2024; 16(22):4133. https://doi.org/10.3390/rs16224133
Chicago/Turabian StyleYuan, Binhuan, Xiyang Zhi, Jianming Hu, and Wei Zhang. 2024. "Boosting Point Set-Based Network with Optimal Transport Optimization for Oriented Object Detection" Remote Sensing 16, no. 22: 4133. https://doi.org/10.3390/rs16224133
APA StyleYuan, B., Zhi, X., Hu, J., & Zhang, W. (2024). Boosting Point Set-Based Network with Optimal Transport Optimization for Oriented Object Detection. Remote Sensing, 16(22), 4133. https://doi.org/10.3390/rs16224133







