Abstract
The time of a satellite navigation system is primarily generated by the main control station of the ground system. Consequently, when ground stations fail, there is a risk to the continuous provision of time services to the equipment and users. Furthermore, the anticipated launch of additional satellites will further strain the satellite–ground link. Next-generation satellite navigation systems will rely on time deviation measurements from inter-satellite links to independently establish and maintain a space-based time reference, enhancing the system’s reliability and robustness. The increasing number of low-Earth-orbit satellite navigation constellations provides ample resources for establishing a space-based time reference. However, this also introduces challenges, including extensive time scale computations, increased link noise, and low clock resource utilization. To address these issues, this paper proposes a Distributed Kalman Plus Weight (D-KPW) algorithm, which combines the benefits of Kalman filtering and the weighted average algorithm, balancing the performance with computational resources. Furthermore, an adaptive clock control algorithm, D-KPW (Control), is developed to account for both the short-term and long-term frequency stability of the time reference. The experimental results demonstrate that the frequency stability of the time reference established by the D-KPW (Control) algorithm reaches and for sampling intervals of 1000 s and 1,000,000 s, respectively, outperforming traditional algorithms such as ALGOS. The 20-day prediction error of the time reference is 1.55 ns. Compared to traditional algorithms such as AT1, ALGOS, Kalman, and D-KPW, the accuracy improves by 65%, 65%, 66%, and 67%, respectively.
1. Introduction
Satellite navigation systems provide accurate positioning, navigation, and timing services around the clock, playing a crucial role in transportation, communications, national defense, energy management, and other fields. Time synchronization is fundamental to the ability of satellite navigation systems to deliver these services. To ensure high-precision time synchronization and satisfy the internal user requirements of each system, every navigation system establishes and maintains its time reference, known as the GNSS time [1]. For multi-system compatibility and interoperability, navigation satellites broadcast signals that include conversion parameters, allowing for the translation between different systems’ time references. Additionally, the time references of the four major navigation systems are regularly traced back to Universal Time Coordinated (UTC), thereby better serving human production and daily life. However, the time reference for current satellite navigation systems is predominantly generated by the ground-based main control station, which compromises the system’s ability to provide continuous time services to the equipment and users when the ground station fails. This reliance reveals significant weaknesses in the reliability and robustness of existing systems, particularly in harsh environments or when ground facilities are damaged. For instance, the Galileo global satellite navigation system experienced a 139 h service interruption from 12 to 17 July 2019, severely impacting users. Therefore, next-generation satellite navigation systems must have autonomous onboard timekeeping capabilities to continue providing services even when the ground control center is unavailable [2]. The LEO constellation has the characteristics of high signal power, rapid change of geometric configuration, and low transmission delay, which can be used to accelerate the convergence speed of high-precision point positioning and broadcast navigation enhancement information. Currently, countries across the world are accelerating the deployment of low-Earth-orbit constellations to achieve higher-quality navigation services. The LEO constellation consists of a large number of satellites, and relying on ground infrastructure to establish time references can place a significant load on the satellite–ground links and lead to reliability issues. Establishing and maintaining a space-based time reference, known as LEO time, by utilizing inter-satellite links and clock resources from low-Earth-orbit constellations is therefore important. This system fulfills the time synchronization requirements of LEO constellations and simultaneously serves as a backup for GNSS time, thereby enhancing the overall system reliability [3,4,5]. The German Aerospace Center has conducted preliminary theoretical research on the space-based time reference system by deploying iodine molecular clocks on 4–6 Kepler satellites and establishing laser bidirectional links with MEO satellites to achieve time synchronization, which can contribute to the establishment of more stable time references [6,7].
Currently, numerous scholars have extensively researched autonomous timekeeping technologies based on inter-satellite links, yielding significant theoretical advancements. Studies have proposed the use of rubidium and hydrogen clocks to establish two independent time references, where the hydrogen clocks control the rubidium clocks, thereby fully utilizing the characteristics of the clocks [8,9]. A two-level time reference generation framework has been introduced, employing the simulation of mercury ion optical clocks and passive hydrogen clocks to enhance the time reference stability [10]. It has been highlighted that centralized processing methods are constrained by the onboard computational capacity, prompting the design of a distributed autonomous timekeeping algorithm based on Kalman filtering [11]. Additionally, the optimization of the weight calculation method in the KPW algorithm has been shown to improve long-term stability and provide a novel approach to time scale algorithms [12]. Further exploration of satellite clock data processing methods and time synchronization models has demonstrated the feasibility of establishing a space-based time reference [13,14]. Most of these studies focus on GNSSs, where the number of satellites involved in timekeeping is relatively small. Consequently, they employ Kalman filtering algorithms [15] or their improved versions [16,17,18,19,20] to establish the time reference. However, in low-orbit systems, challenges such as the large number of satellites and complex noise characteristics arise. Traditional Kalman filtering algorithms, which require extensive matrix operations and parameter configurations, are unsuitable for low-orbit constellation scenarios. While the weighted average algorithm [21,22,23] is computationally simple, its noise suppression capability is limited, preventing full utilization of satellite clock characteristics.
In this paper, we first propose a parameter estimation method for the noise matrix of the Kalman filter to ensure accurate and reasonable parameter estimation. Then, to solve the problem that a large number of satellites participate in the synthesis, a D-KPW algorithm is proposed, which estimates each set of the clock error independently and calculates the weights using Allan variance. Finally, to optimize the utilization of clock characteristics, the D-KPW (Control) algorithm is introduced as an enhancement of the original D-KPW framework. Two independent time references with distinct characteristics are constructed: one exhibiting superior short-term stability and the other demonstrating enhanced long-term stability. The short-term stable reference is calibrated by the long-term stable reference to produce the system’s unified time reference. The validity of the proposed algorithm is corroborated through a comparative experimental analysis.
2. Autonomous Timekeeping Framework
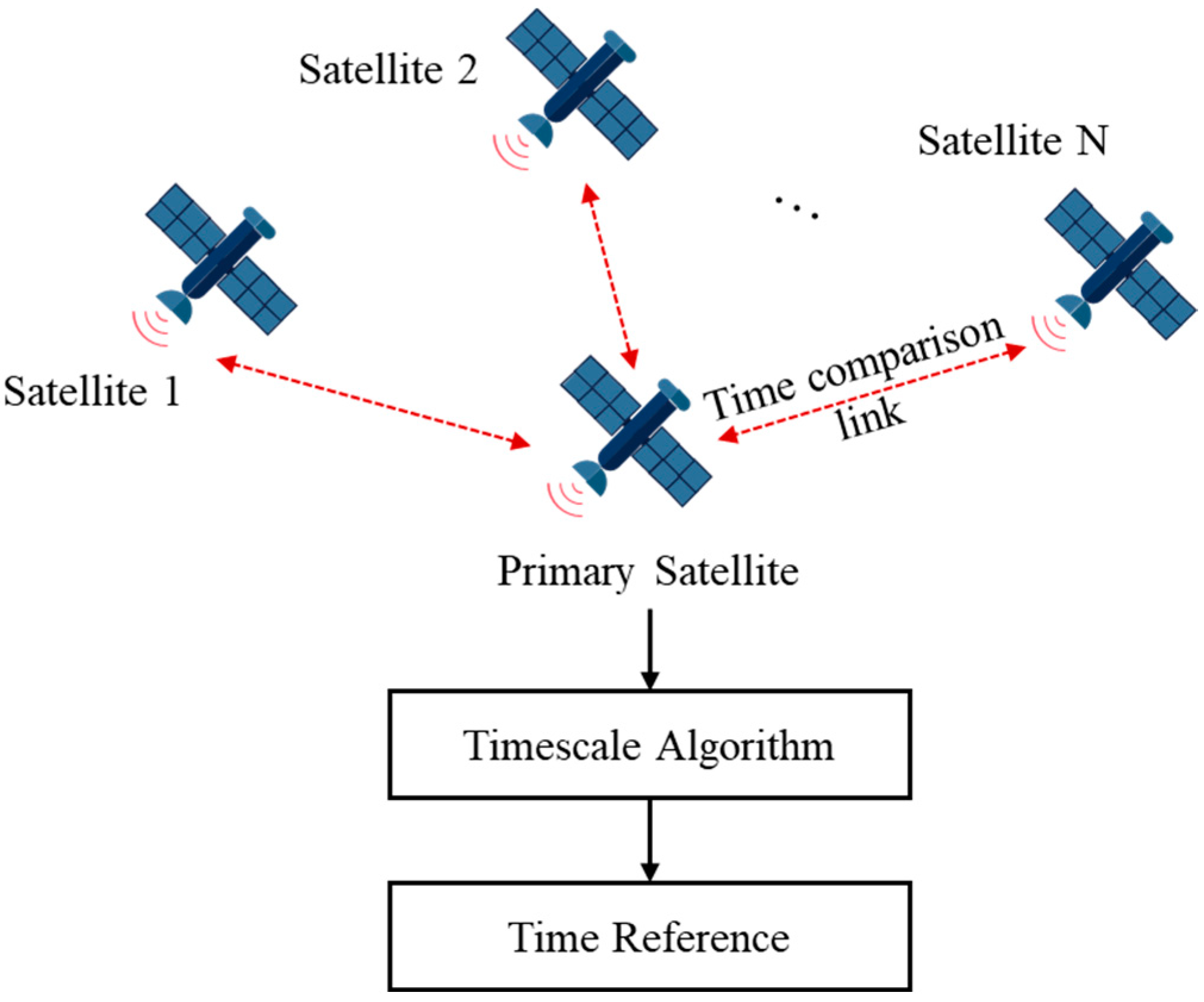
The local time of each satellite is maintained by its onboard atomic clock, and the two-way comparison link between satellites enables high-precision measurements of the time differences between them. The satellite with the best clock performance is designated as the primary satellite, and all satellites in the constellation are compared with the primary satellite to determine clock errors. A system time reference is then established using a timekeeping algorithm. Due to satellite visibility constraints, satellites within the primary satellite’s line of sight identify clock errors through direct comparison, while those outside its visibility calculate clock errors indirectly via relay satellites. At the primary satellite, the system’s time reference is established by synthesizing inter-satellite link measurement data using a timekeeping algorithm. The deviation between each satellite’s time and this reference is computed, and satellite clock parameters are fitted and transmitted to all satellites, enabling network-wide time synchronization.
Figure 1 illustrates the autonomous timing framework based on the inter-satellite link. In this system, N satellites are compared to the primary satellite, resulting in N sets of clock error sequences. The clock error between the satellite and the primary satellite is expressed as follows [8]:
where is the clock reading of the satellite , and is the clock reading of the primary satellite. is the relative clock error between the satellite and the primary satellite. The time reference established in practice is the deviation from the primary node, denoted as . The calculation formula for the time reference is as follows [12]:
where is the predicted value between the satellite and the time reference, which is calculated from historical data to ensure that the system will not change suddenly when the weight changes and when the time is increased or decreased, and is the weight, satisfying the following constraint:
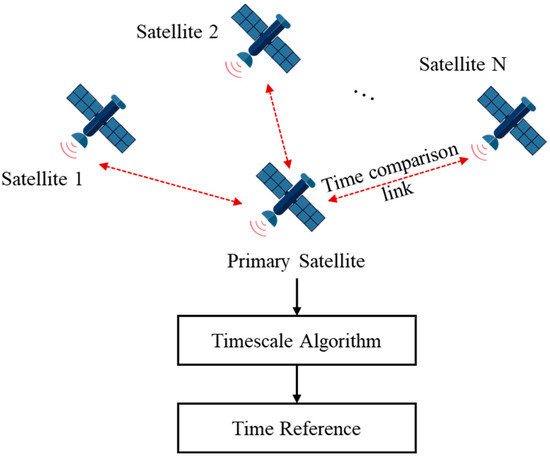
Figure 1.
Autonomous timekeeping framework based on inter-satellite link.
When the satellite-to-ground link is connected, the deviation between the established time reference and GNSS time can be calculated, and then it can be traced back to UTC indirectly:
where is the time deviation between the time reference and the primary satellite established by the inter-satellite link measurement data, is the time deviation between the primary satellite and GNSS time, and is the time deviation between the time reference and GNSS time.
When the system switches to autonomous timekeeping mode, historical data must be used to predict and correct the time accuracy of the system to ensure synchronization with GNSS time. As the autonomous operation duration extends, the prediction error between the time reference and GNSS time will gradually increase. Therefore, the predictability of the time reference serves as a crucial metric for evaluating the autonomous timekeeping performance.
3. Methodology
This section presents the estimation method for the filter noise matrix parameters and redesigns the D-KPW time scale algorithm by integrating the advantages of the Kalman filter and the weighted average algorithm. Based on this, the D-KPW (Control) algorithm is proposed, which reduces computational complexity while improving various performance metrics.
3.1. Parameter Estimation of Filter Noise Matrix
When estimating the clock error using the Kalman filter, the observation noise is typically modeled as white noise, while the internal noise of the atomic clock is treated as colored noise. The autocorrelation function of white noise is an impulse function, indicating no correlation between epochs. In contrast, colored noise shows correlations between epochs, which can be linearly estimated based on the space formed by historical data and described by an model [24] as follows:
where represents the order of the filter, represent the filter coefficients, is the observed data at epoch k, is the white noise sequence at epoch k, and is the frequency domain expression of the filter.
Therefore, an M-order prediction error filter is designed based on the noise model to filter the clock error. The variance of the prediction error derived from the filtered data is used as the estimated value of the observation noise covariance matrix in the Kalman filter. The canonical equation for the M-order prediction error filter is as follows:
or
where is the M-order autocorrelation matrix, is the autocorrelation value with a difference of epochs, is the filter vector, is the minimum value of error energy, and is the error vector. The observed data are passed through the filter, which is expressed as follows:
where is the input data vector, is the prediction error, and is the variance of the prediction error series. The estimated observation noise covariance matrix is as follows:
The discrete state equation of the clock can be characterized as follows [25]:
where is the number of epochs, is the sampling interval between epochs, is the process noise vector, is the clock error at epoch k, and is the frequency deviation. The covariance matrix of the process noise is as follows:
where and are the noise power spectral density of the clock error and frequency offset, respectively, which can be obtained by fitting the Allan variance. The Allan variance is calculated as follows:
where is the number of epochs, and is the calculated Allan variance. The formula for estimating and by the least square method is as follows:
3.2. D-KPW Algorithm
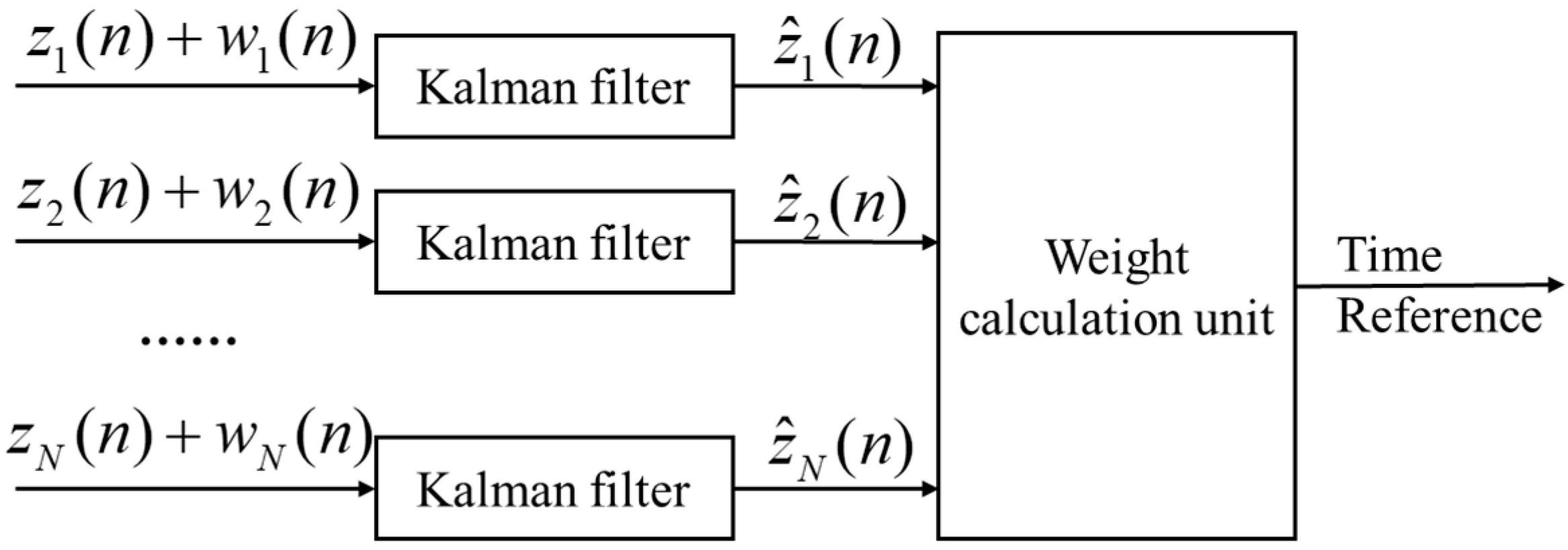
Figure 2 presents a schematic diagram of the D-KPW algorithm framework. For each set of observed clock error series, the Kalman filter is applied to remove frequency white noise and link noise, extracting relevant information. The matrix parameters of the signal and observation models are configured to carry out iterative filtering.
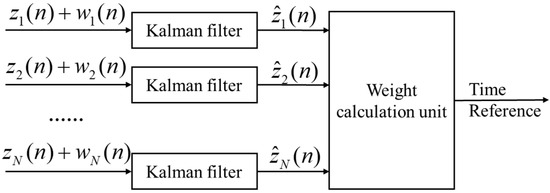
Figure 2.
D-KPW algorithm framework.
The state transition matrix is as follows:
The observation matrix is as follows:
Carrying on the Kalman filter processing, the formula is as follows:
where is the prediction error covariance matrix, is the Kalman gain, is the observation data, is the predicted filter value, is the filter estimate, and is the filter error covariance.
To make the filter converge faster, proper initialization is required as follows:
It is better to use the weight calculated by the Allan variance for weighting, but it needs to accumulate some data, which leads to a lag. To meet the actual demand, the sliding window method is used to calculate and update the dynamic weight. A weight calculation cycle accumulates certain data, and the data are used to calculate the Allan variance .
Further calculation of the weight is carried out as follows:
where is the reciprocal of the Allan variance of satellite , used to determine weights, and is the weight of satellite .
3.3. D-KPW (Control) Algorithm
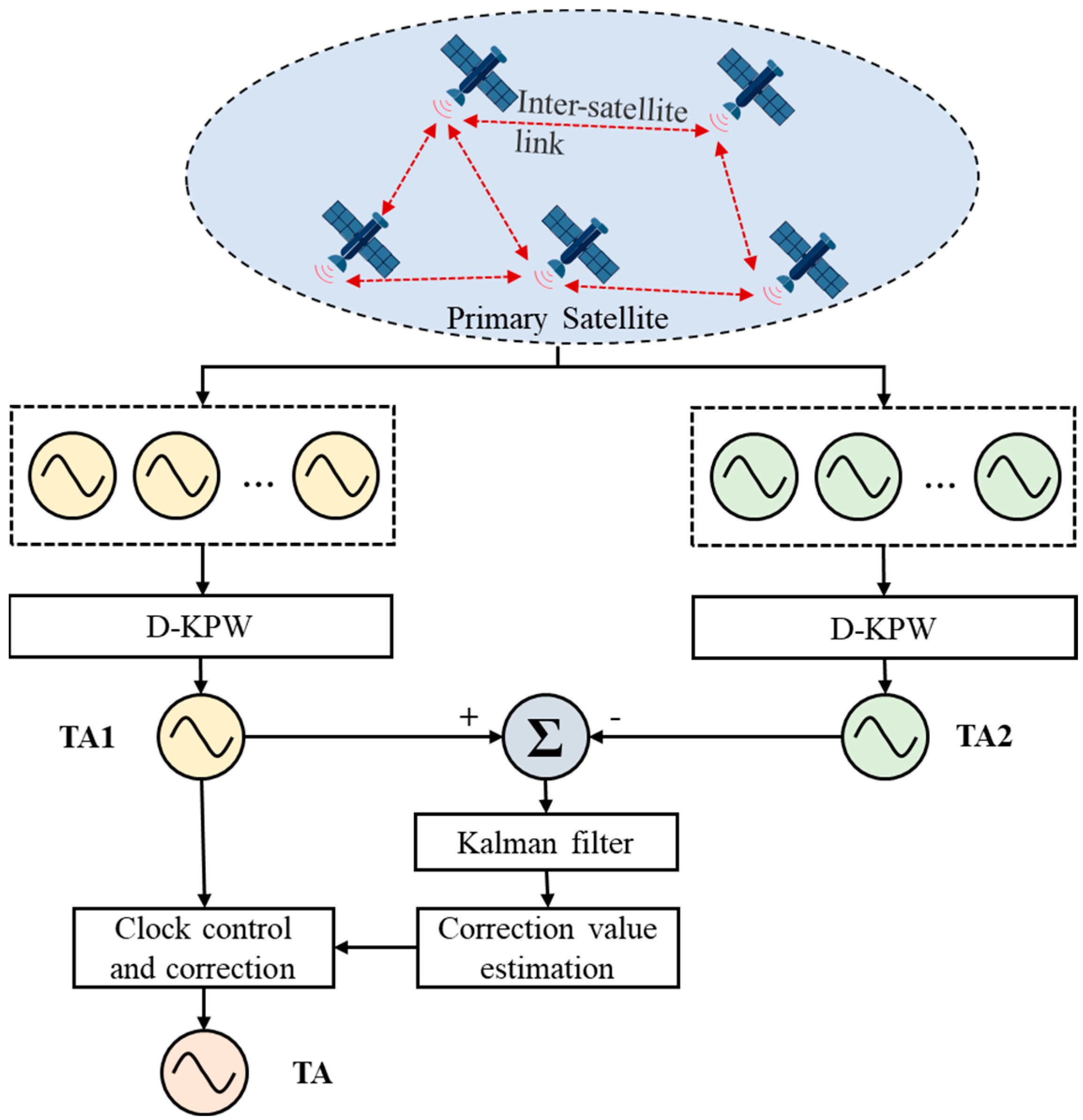
Allan variance is widely employed to assess the stability of a clock, typically using a sampling time of 10,000 s as a demarcation point. An Allan variance with a sampling time less than 10,000 s indicates short-term stability, while an Allan variance with a sampling time exceeding 10,000 s signifies long-term stability. Figure 3 presents the framework of the D-KPW (Control) algorithm, which divides the measured data into two groups according to the long-term stability characteristics. The Euclidean distance of the vector composed of Allan deviations with a sampling period longer than 100,000 s is defined as the evaluation factor, which represents the long-term stability of the satellite clock. The smaller the value is, the better the long-term stability is. The formula to calculate this quantity reads as follows:
where is the evaluation factor of satellite , and is the Allan variance of satellite at sampling time .
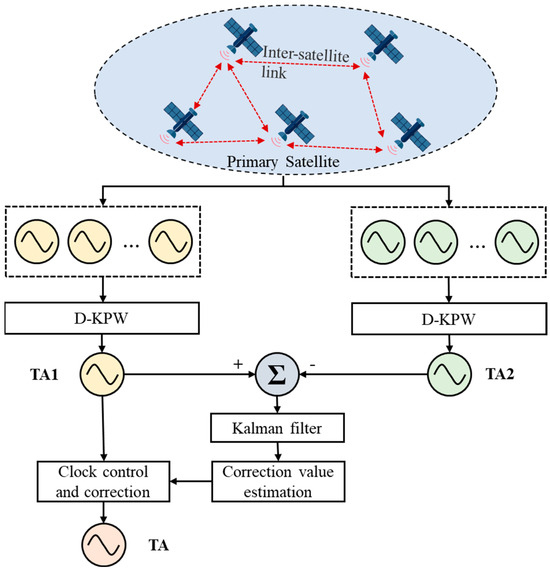
Figure 3.
D-KPW (Control) algorithm framework.
A total of N data groups participate in the calculation, sorted in descending order of . The first L groups are selected to form clock ensemble 1, while the remaining N–L groups form clock ensemble 2.
Clock ensemble 1 is used to establish the time reference with better short-term stability, so is used to calculate the weights. The formula is as follows:
where is the result of the Kalman filtering for the clock error between a satellite and the primary satellite in clock ensemble 1, and is the weight of satellite in clock ensemble 1. Other parameters have the same meaning as in Equation (2).
Clock ensemble 2 is used to establish the time reference with better long-term stability, so is used to calculate the weights. The formula is as follows:
where is the result of Kalman filtering for the clock error between a satellite and the primary satellite in clock ensemble 2, and is the weight of satellite in clock ensemble 2. Other parameters have the same meaning as in Equation (2).
is the clock error between and , calculated as follows:
The real-time difference between and is estimated by the Kalman filter to obtain . The is modified by , and the time reference of the system is established. The established can achieve the same short-term noise characteristics as and the same long-term drift characteristics as .
4. Experiment and Results Analysis
The noise in inter-satellite direct comparison measurements is less than 0.2 ns, having a minimal impact on data accuracy [26]. However, the comparison between invisible satellites through relay satellites will lead to the superposition of the measurement noise. Currently, many GNSS satellites are equipped with rubidium and passive hydrogen clocks, demonstrating the reliability of existing onboard atomic clocks. Therefore, equipping future LEO constellation time-keeping satellites with clocks that have similar characteristics to those on GNSS satellites is a feasible option at this stage. In this paper, we simulate low-orbit satellite scenarios using the clock error products of the GPS and BeiDou system, and we add 0.2 ns to 0.8 ns of white noise to these clock error data to represent the link noise. The settings for the satellite data and the standard deviation (STD) of the link noise are detailed in Table 1. The experimental data were collected using precise clock error data, with a sampling interval of 300 s, provided by the Center for Orbit Determination in Europe (CODE) and were collected from 14 May 2023 to 24 June 2023. In the future, the use of optical links and optical clocks is expected to yield experimental results that surpass those presented in this paper.

Table 1.
The settings for the satellite data and the STD of the link noise.
4.1. Clock Error Estimation and Noise Analysis
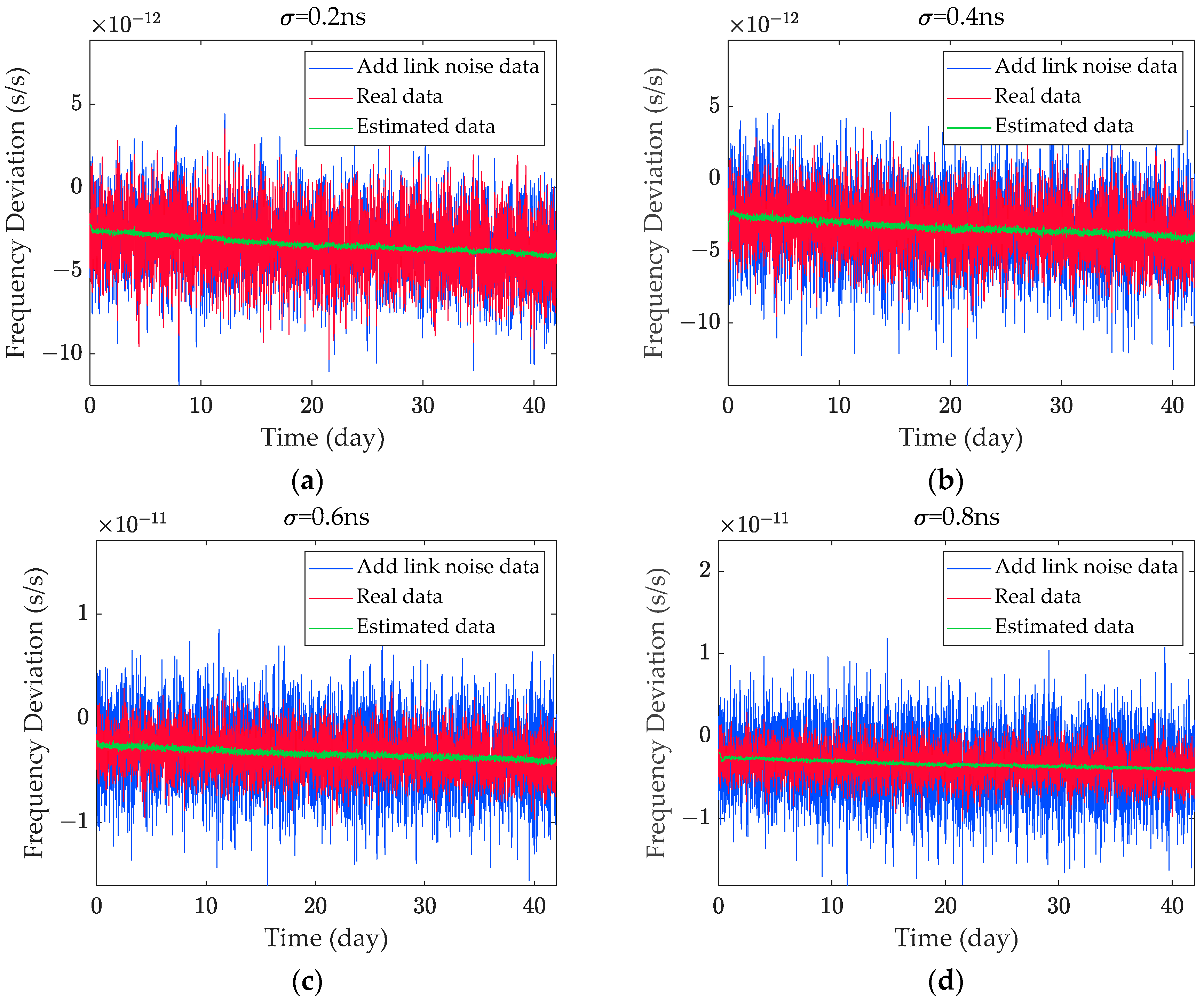
Using the parameter estimation method outlined in Section 3.1, the clock error is filtered under varying noise intensities. To more clearly illustrate the estimation effect, the data with link noise, real data without link noise, and estimation results are converted into frequency deviation data. The frequency deviation is shown in Figure 4, while the Allan deviation is presented in Figure 5.
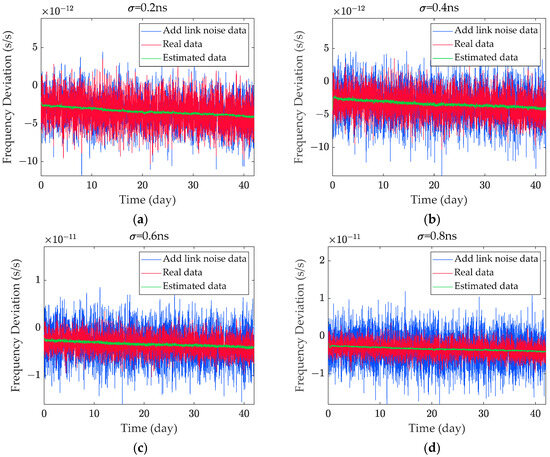
Figure 4.
Filtered frequency deviation. (a) Overlay of 0.2 ns link noise; (b) overlay of 0.4 ns link noise; (c) overlay of 0.6 ns link noise; (d) overlay of 0.8 ns link noise.
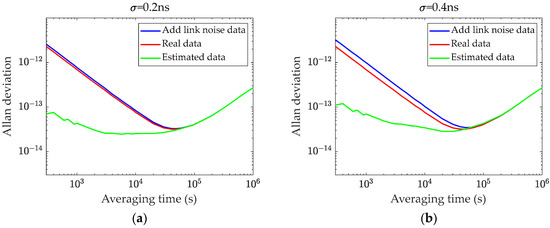
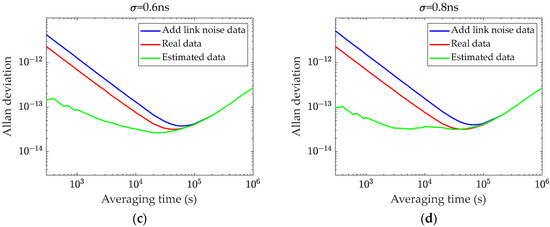
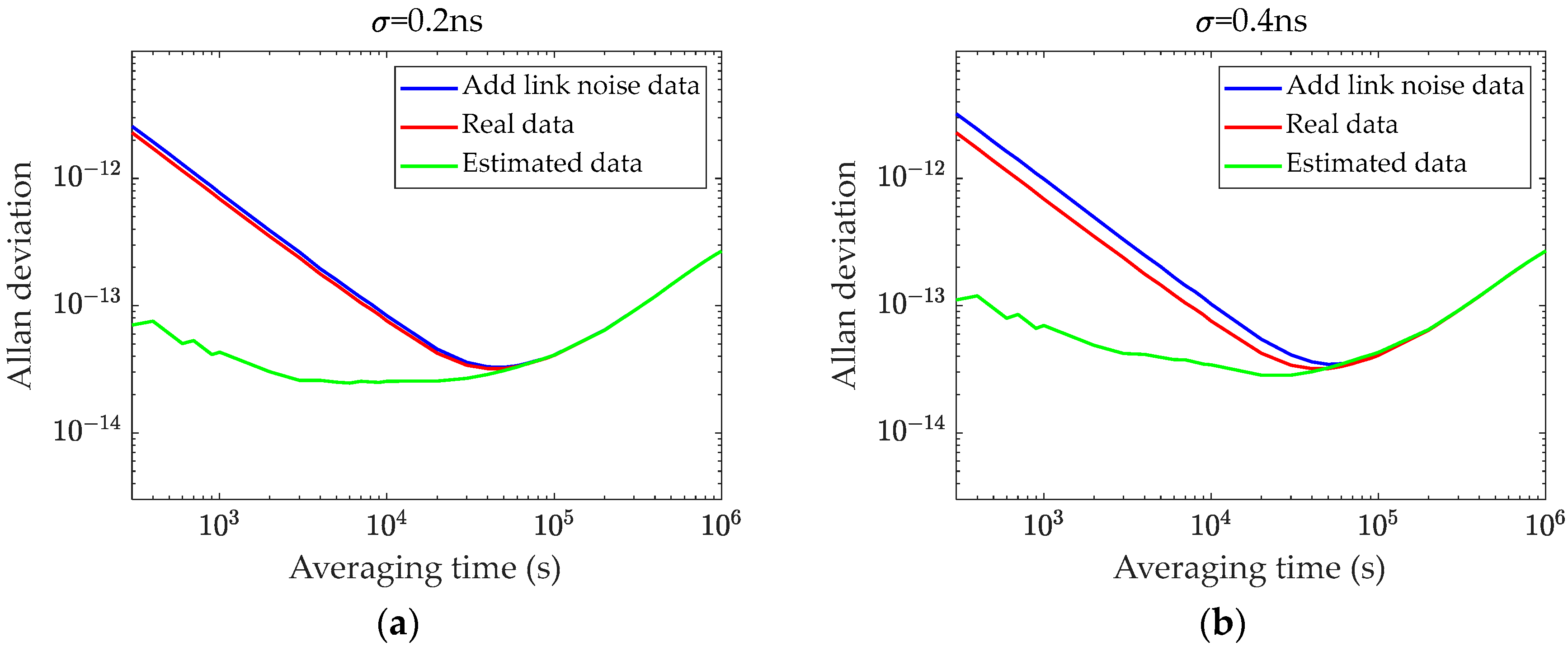
Figure 5.
Allan deviation before and after Kalman filtering. (a) Overlay of 0.2 ns link noise; (b) overlay of 0.4 ns link noise; (c) overlay of 0.6 ns link noise; (d) overlay of 0.8 ns link noise.
The experimental results demonstrate that the Kalman filter effectively reduces noise fluctuations in the frequency deviation and verifies the accuracy of the filter’s parameter estimation. The observation clock error primarily consists of frequency white noise, random walk noise, and link noise. After applying the Kalman filter, most of the link noise and frequency white noise are filtered out, leaving the random walk noise as the dominant component.
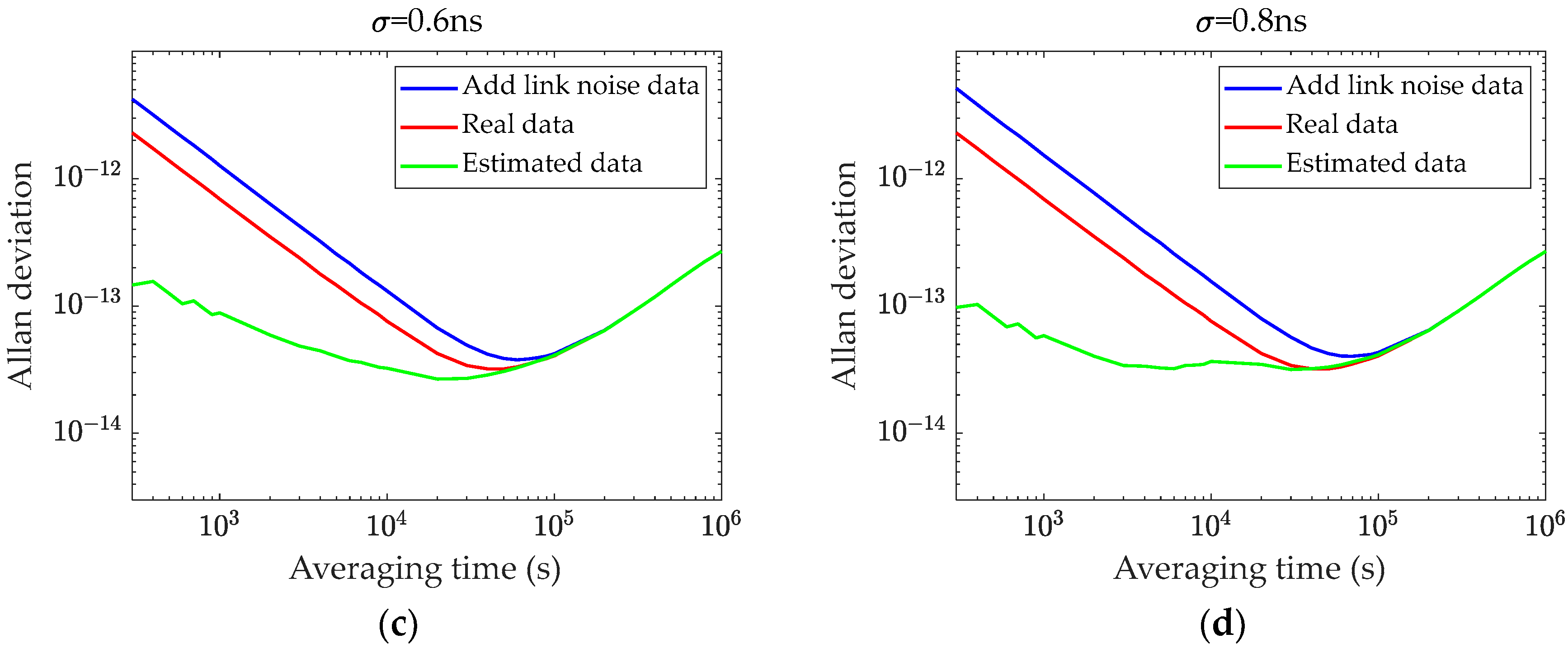
The Allan variance can reflect the magnitude of various types of noise. For short sampling periods, the Allan variance is dominated by white noise, while for long sampling times, it is dominated by random walk noise. Therefore, the weighted average algorithm often uses Allan variance as a weighting factor to reduce the intensity of specific noise types. In practice, to meet real-time requirements, a sliding window is employed to update the observation data and calculate the Allan variance in real time. Similar to the calculation principle of the short-time Fourier transform, the time-varying Allan variance can be obtained, as shown in Figure 6.
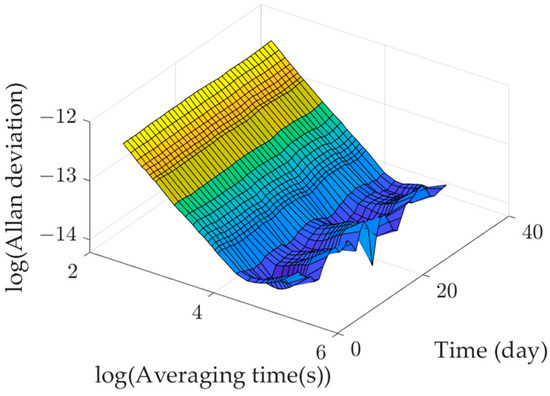
Figure 6.
Allan deviation varies with time.
To reduce weight fluctuations caused by data windowing, an exponential filter is applied to smooth the Allan deviation. The formula is as follows:
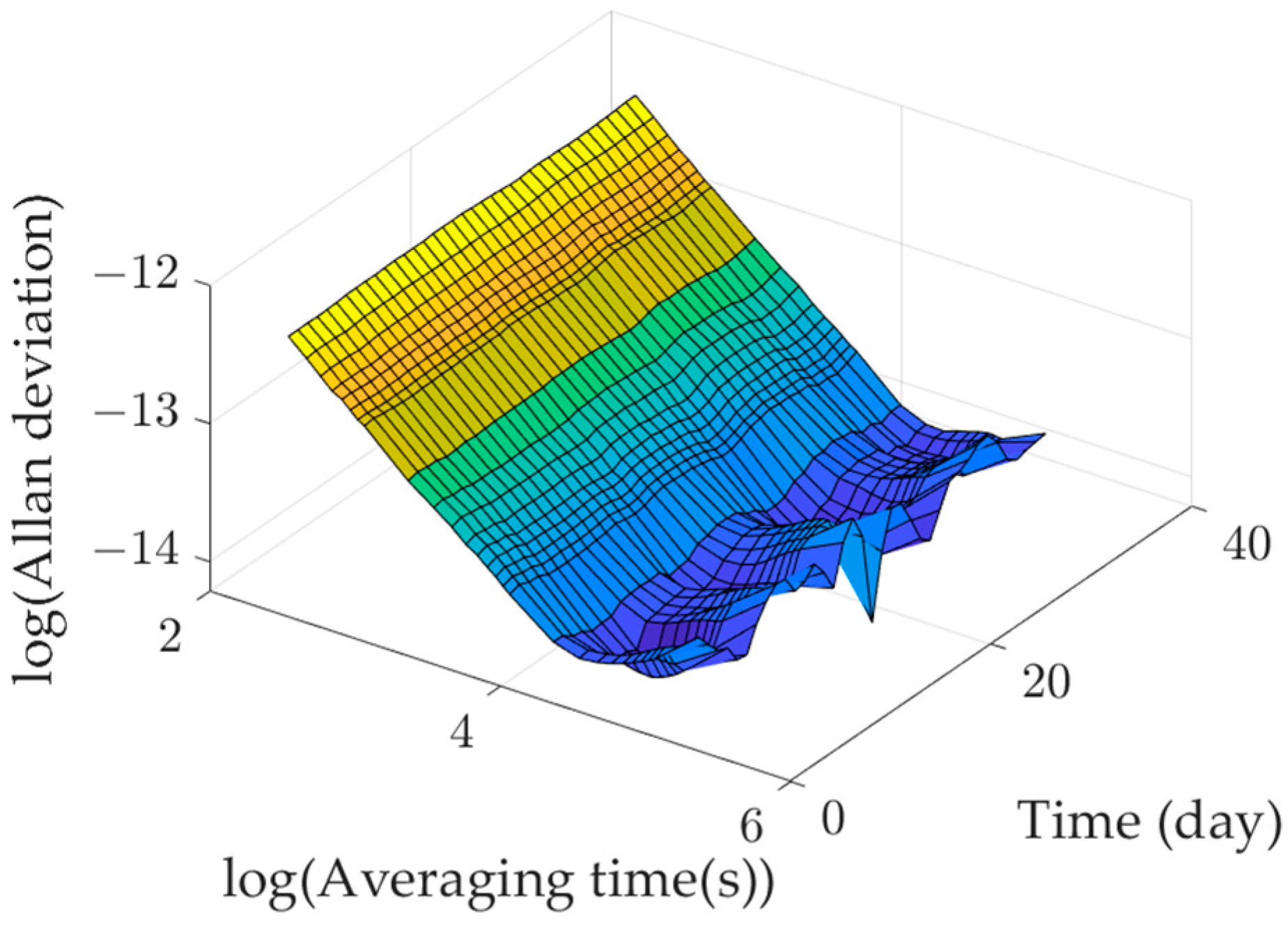
where is the Allan deviation after smoothing filtering at time t, is the Allan deviation calculated by time data, and is the smoothing factor. Figure 7 presents the time variation in the Allan deviation calculated by a satellite for sampling times of 1000 s and 100,000 s at different values. represents the situation without exponential filtering.
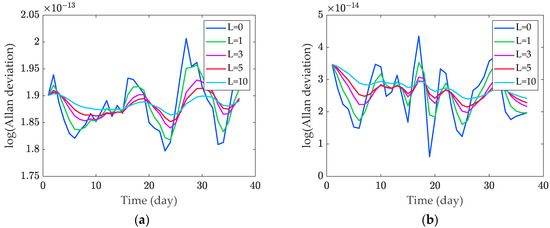
Figure 7.
Allan deviation changes with time at different values. (a) Allan deviation over time with a sampling time of 1000 s; (b) Allan deviation over time with a sampling time of 100,000 s.
With a larger value, the filtering results are less sensitive to current observations, causing the data to change slowly. Conversely, a smaller value makes the filtering results overly sensitive to current observations, leading to faster data changes. To ensure that the Allan deviation does not fluctuate excessively while still reflecting the data trend, a balanced choice is necessary. Thus, this paper sets to 5.
The experimental results show that the Allan variance changes little with time and is a relatively stable statistic. After exponential filtering, there are only small fluctuations, so the weight calculated by the Allan variance will not change significantly over time.
4.2. Frequency Stability Evaluation
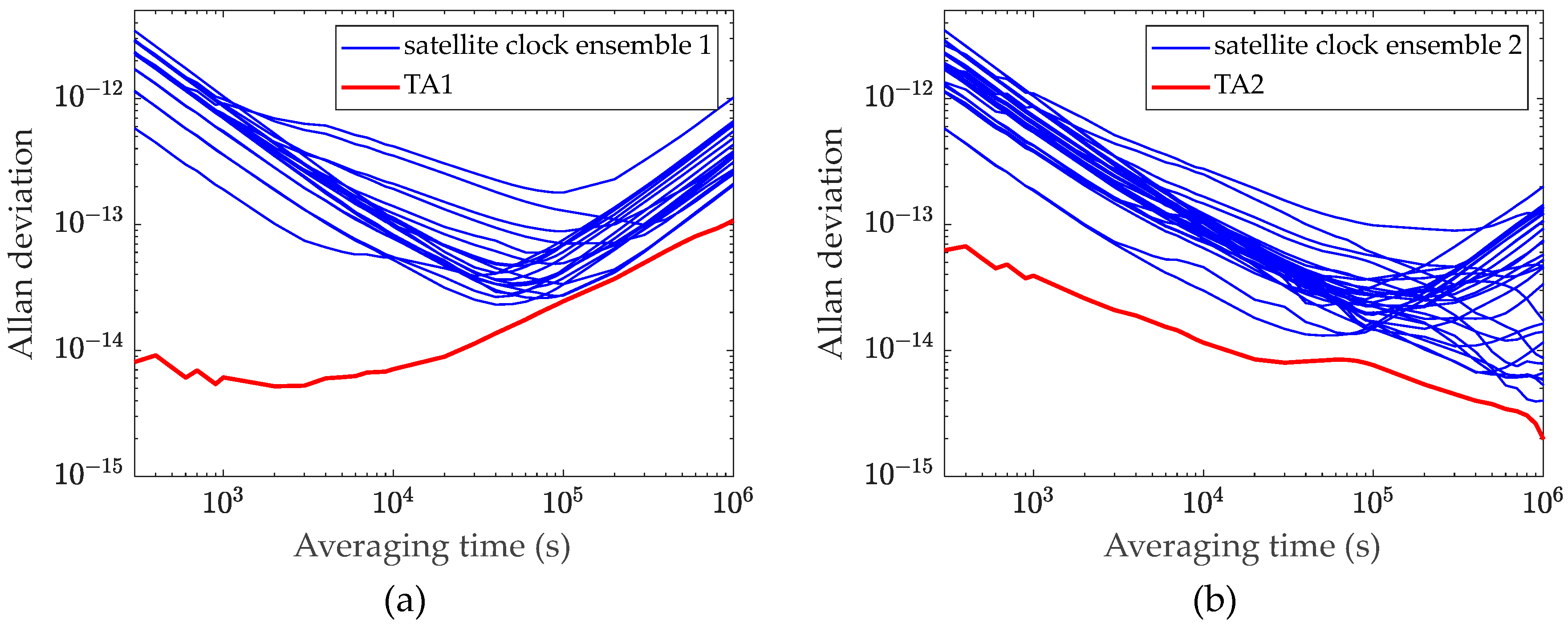
Frequency stability is a critical metric for evaluating time reference performance. All satellite clocks involved in the calculation are divided into clock ensemble 1 and clock ensemble 2, with and established using the D-KPW algorithm, respectively. In Figure 8, the Allan deviations of and are visualized.
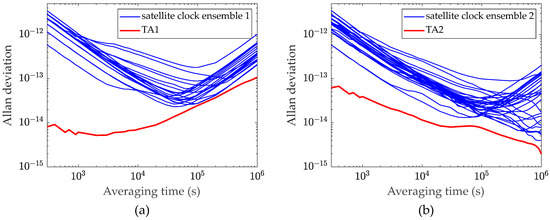
Figure 8.
Allan deviation of and . (a) Allan deviation of each clock in clock ensemble 1 and ; (b) Allan deviation of each clock in clock ensemble 2 and .
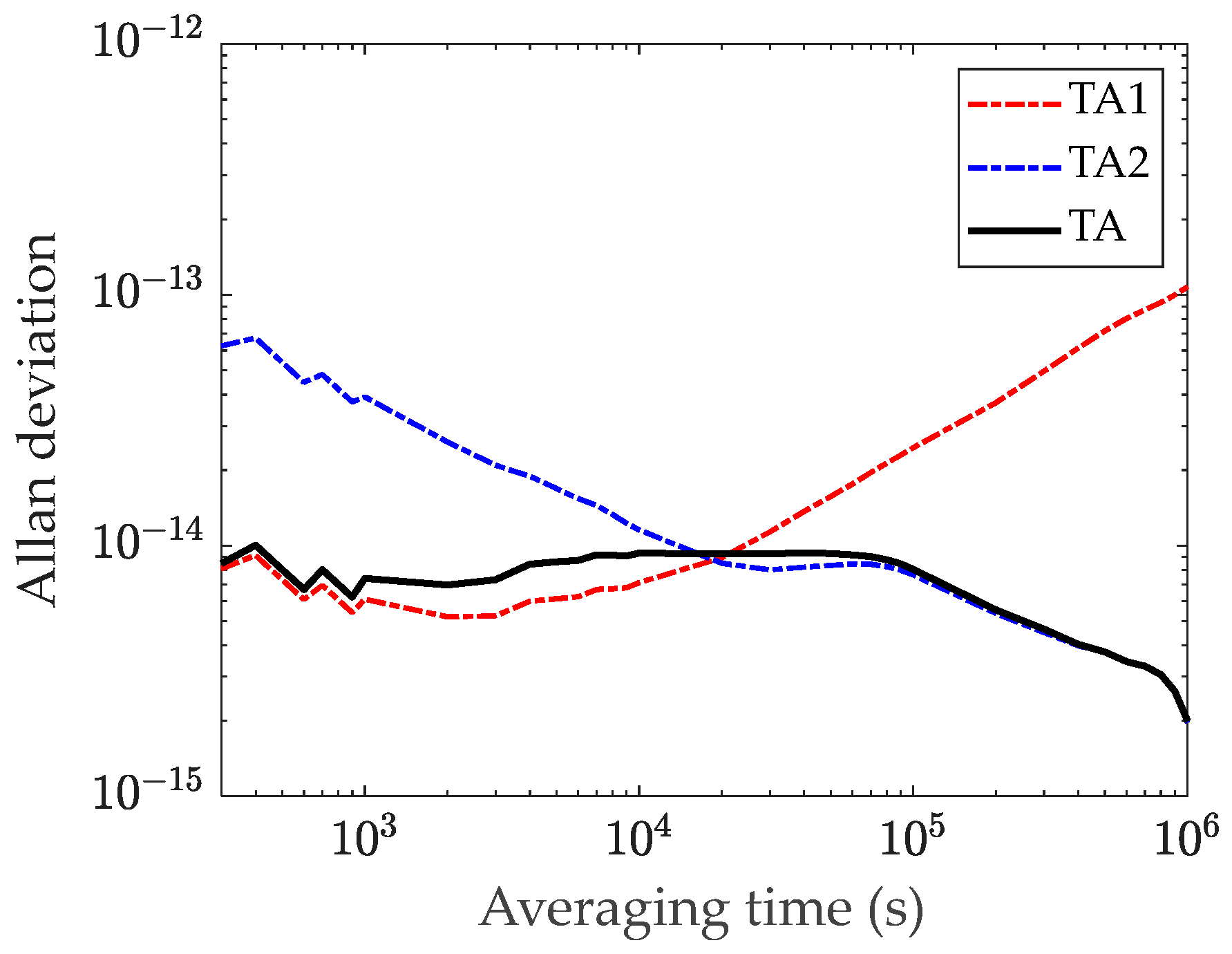
The results indicate that , using short-term stability as the weight index, reduces the impact of frequency white noise but exhibits poor long-term stability. Conversely, , using long-term stability as the weight index, mitigates random walk noise but suffers from poor short-term stability.
Figure 9 demonstrates that the long-term drift of relative to can be predicted and corrected using a Kalman filter, thereby establishing a time reference with improved short-term and long-term stability. To further validate the algorithm’s performance, its stability is compared against the equal weight averaging algorithm, AT1 algorithm, ALGOS algorithm, Kalman filter algorithm, and D-KPW algorithm. The experimental parameters are configured as presented in Table 2.
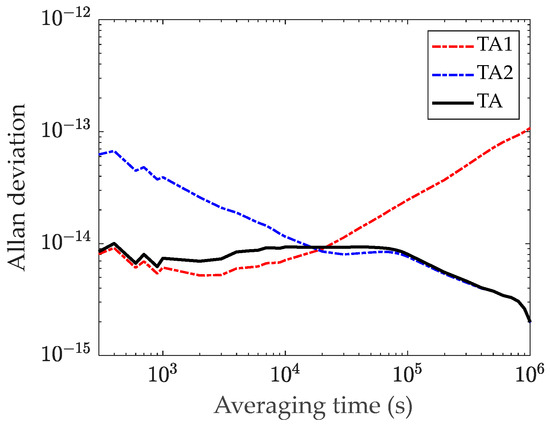
Figure 9.
Allan deviation of calculated by D-KPW (Control).

Table 2.
Experimental parameters of different timescale algorithms.
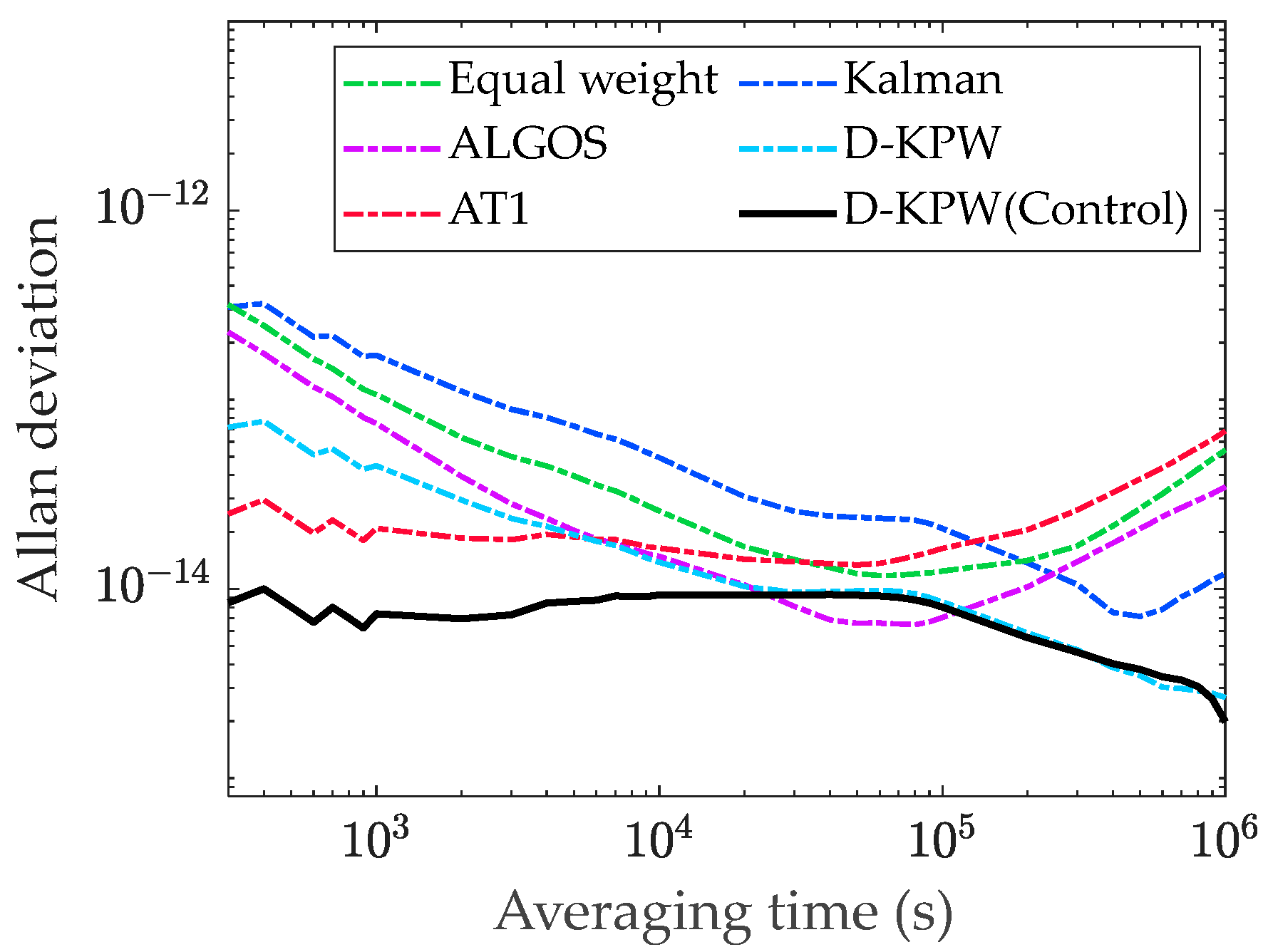
Figure 10 presents the Allan deviation of time references generated by several algorithms, while Table 3 displays the Allan deviation values at different sampling intervals.
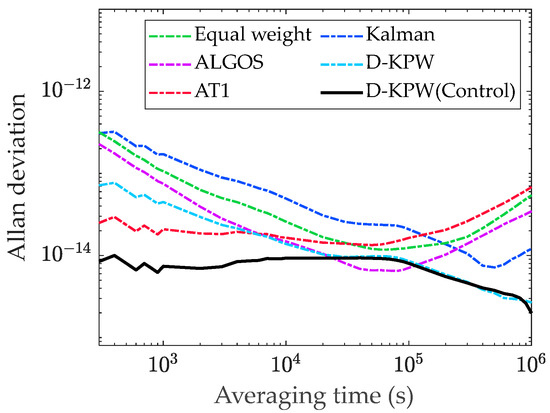
Figure 10.
Allan deviation of time references generated by several algorithms.

Table 3.
Allan deviation under several sampling times.
The experimental results indicate that the frequency stability of the D-KPW (Control) algorithm reaches and at sampling times of 1000 s and 10,000 s, respectively, outperforming all comparative algorithms in terms of short-term stability. At sampling intervals of 100,000 s and 1,000,000 s, the frequency stability reaches and , slightly lower than ALGOS’s at 100,000 s. Overall, the long-term stability surpasses that of all the comparative algorithms. The proposed D-KPW algorithm integrates the strengths of the weighted average algorithm and the Kalman filter. Compared to the Kalman filter, it offers reduced computational complexity and improved performance. In comparison with the weighted average algorithm, it effectively utilizes prior information. D-KPW (Control) further exploits the clock ensemble’s characteristics, effectively suppressing various noise sources, thereby enhancing both the short-term and long-term stability.
4.3. Prediction Error Evaluation
The prediction error between the autonomous time reference and the actual system time is a critical evaluation metric, and different datasets exhibit varying behaviors across different algorithms. The most commonly used statistical prediction models include the linear model, quadratic polynomial model, and gray prediction model [27,28,29], which are suitable for clock error modeling and prediction in cases of small drift terms, large drift terms, and noticeable exponential trends, respectively.
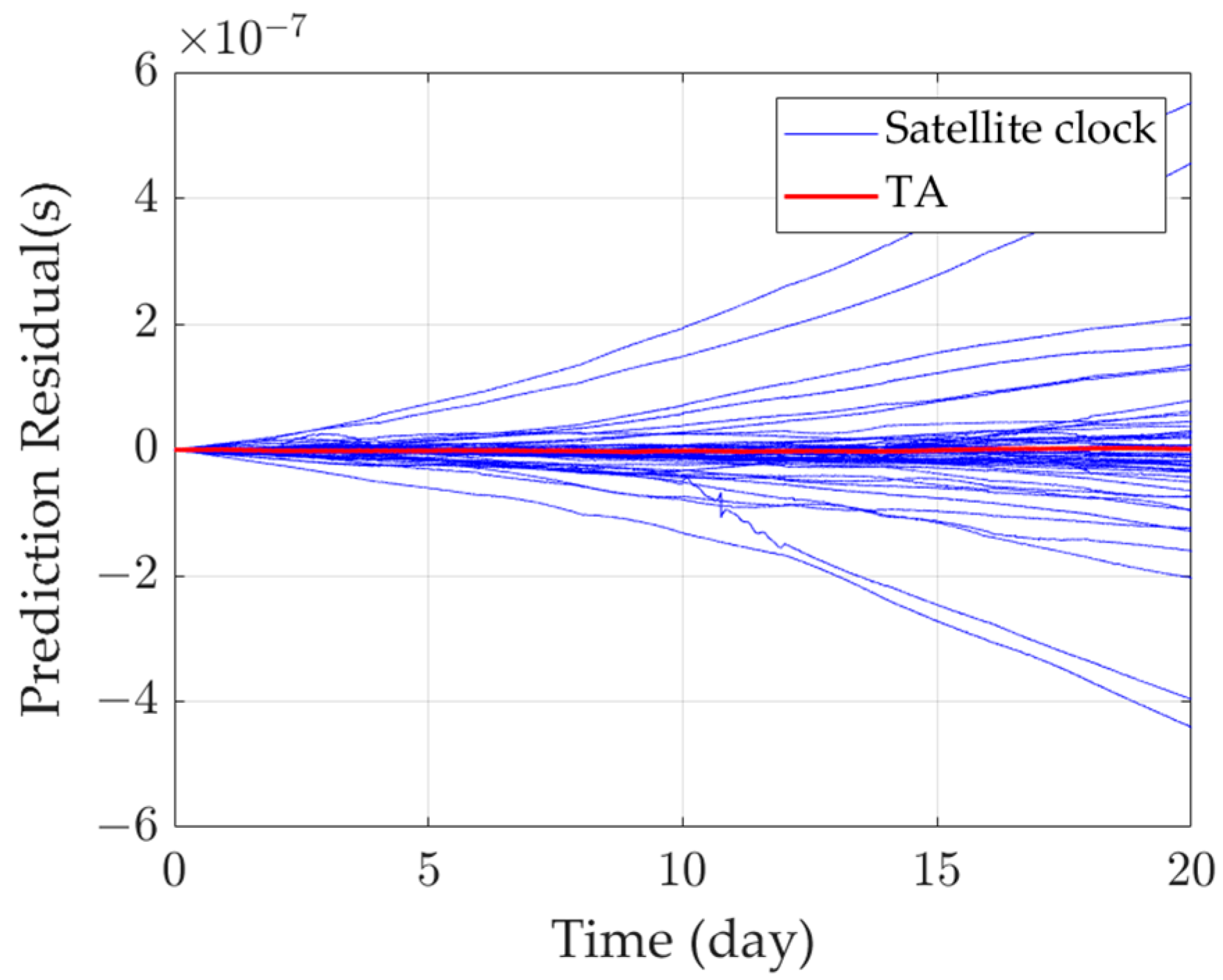
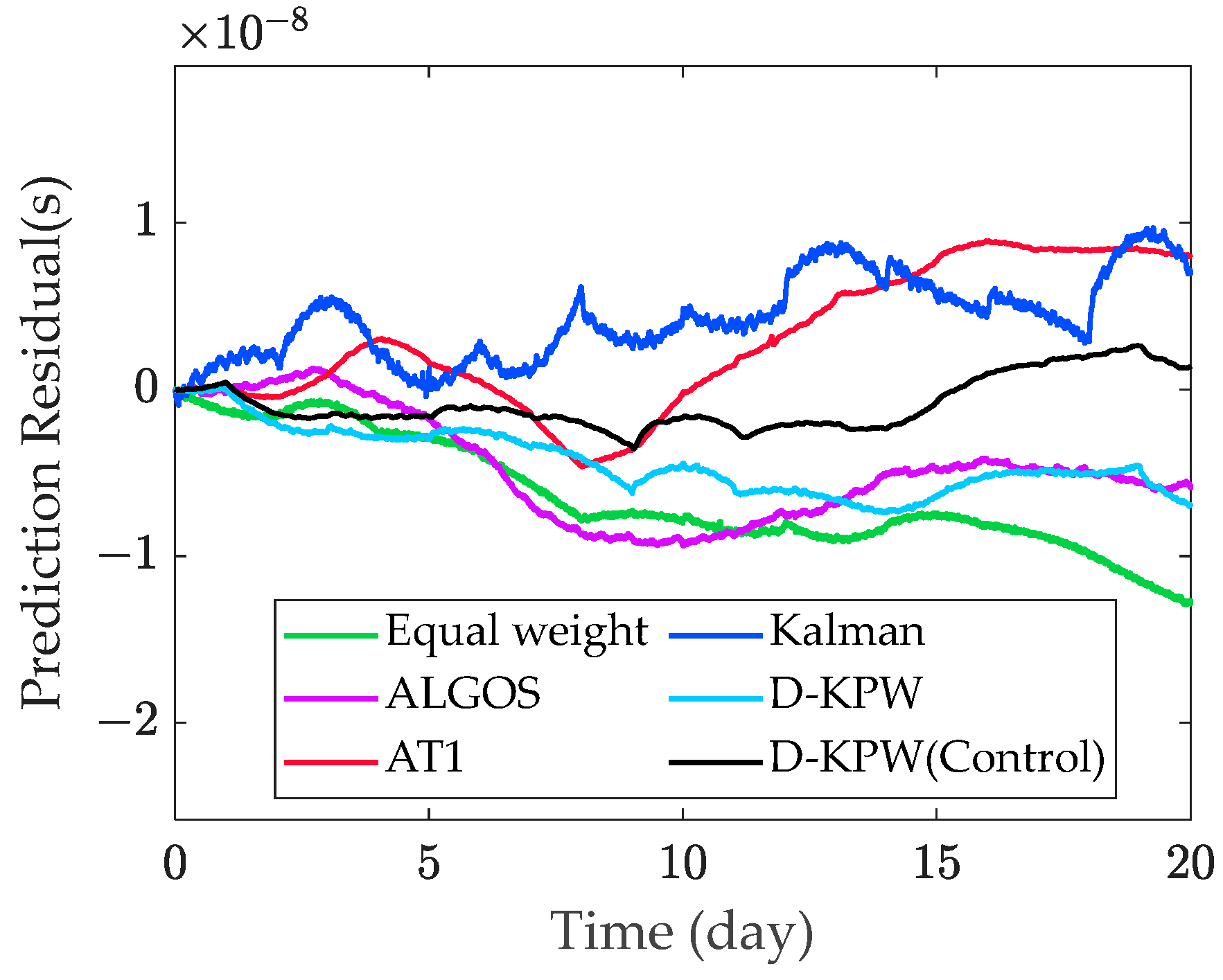
Figure 11 presents the 20-day prediction error curve. The error of an individual atomic clock increases over time, and the 20-day prediction error of a poorly performing satellite clock can reach up to 600 ns. Such an error is intolerable if the system is synchronized to this satellite. In contrast, the 20-day prediction error of the time reference established by the D-KPW (Control) algorithm is only 3.40 ns, allowing the system to synchronize with it and achieve high precision.
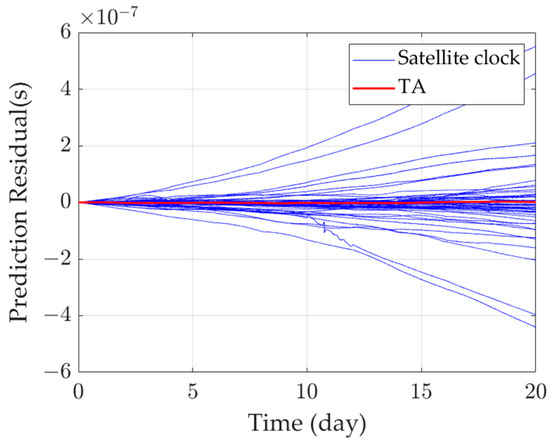
Figure 11.
Twenty-day forecast residual.
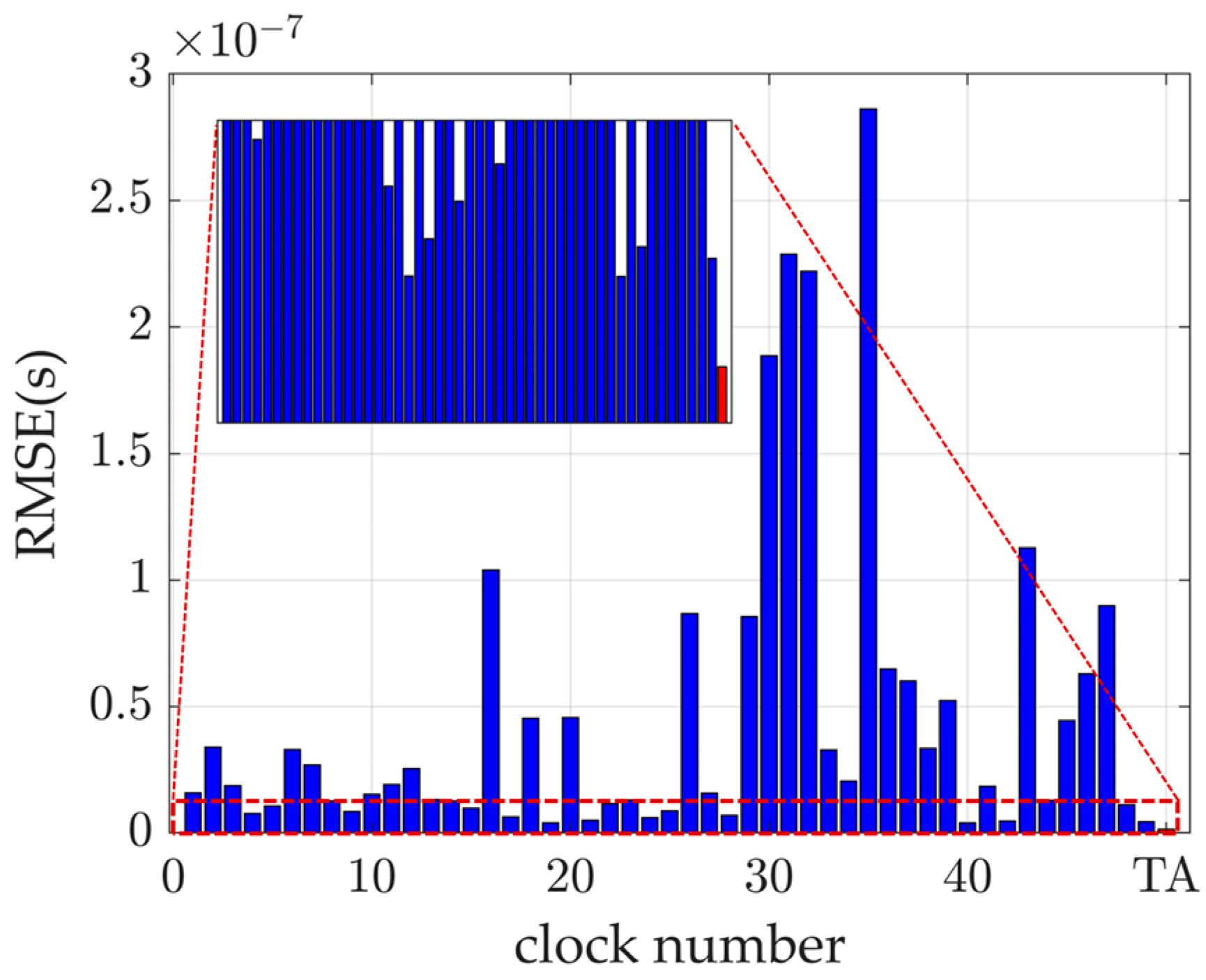
Figure 12 illustrates the root mean square error (RMSE) of the 20-day predictions for the time scale () and all the satellites involved in the calculation. The RMSE of is 1.55 ns, outperforming that of all the individual satellites included in this analysis.
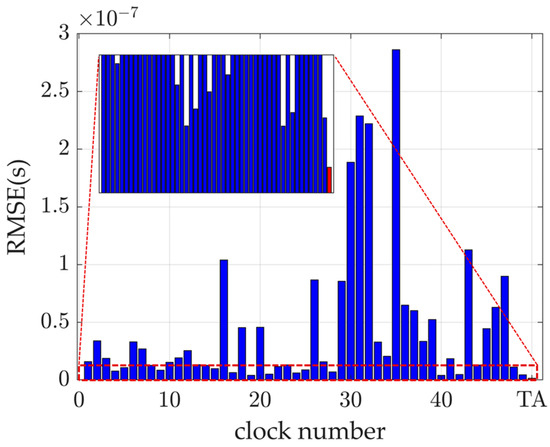
Figure 12.
RMSE of 20-day prediction.
To further verify the prediction performance of the time reference established by the D-KPW (Control) algorithm, a comparison is made with the time references established by the equal weight average algorithm, AT1 algorithm, ALGOS algorithm, Kalman filter algorithm, and D-KPW algorithm.
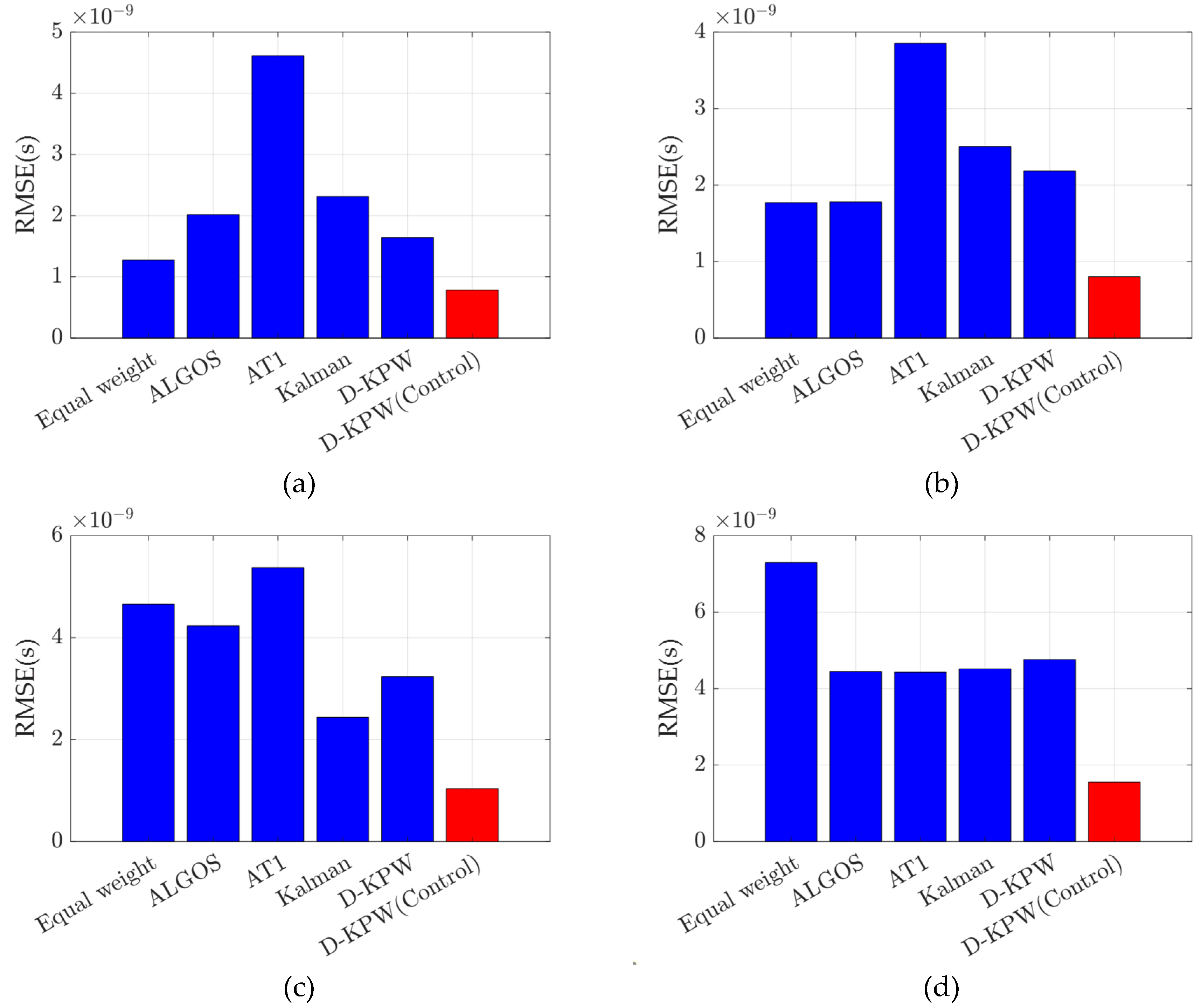
Figure 13 and Figure 14 display the prediction residual curves and the RMSE of the six algorithms for 3 days, 5 days, 10 days, and 20 days, respectively. Table 4 shows that the RMSE of the prediction error for the time reference established by the D-KPW (Control) algorithm reaches s, s, s, and s for 3, 5, 10, and 20 days, respectively, outperforming the other algorithms in comparison. The RMSE of the 20-day prediction residuals generated by the D-KPW (Control) algorithm is 1.55 ns, with a prediction accuracy that is 78%, 65%, 65%, 66%, and 67% higher than those of equal-weight averaging, ALGOS, AT1, the Kalman filter, and D-KPW, respectively. In the system’s independent operation mode, the D-KPW (Control) algorithm achieves the minimum absolute deviation in the time reference, maintaining a high level of synchronization. This indicates that the time reference established by the D-KPW (Control) algorithm offers better predictability.
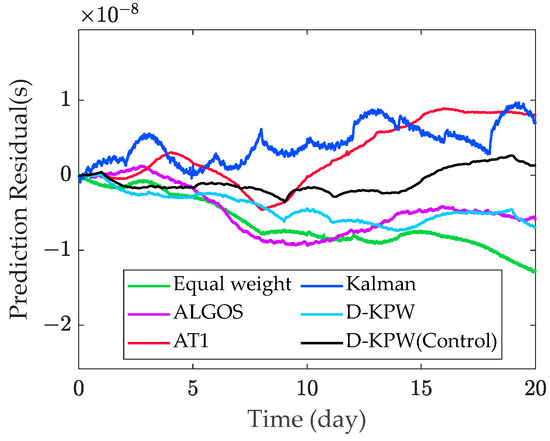
Figure 13.
Twenty-day prediction residual of time reference established by different algorithms.
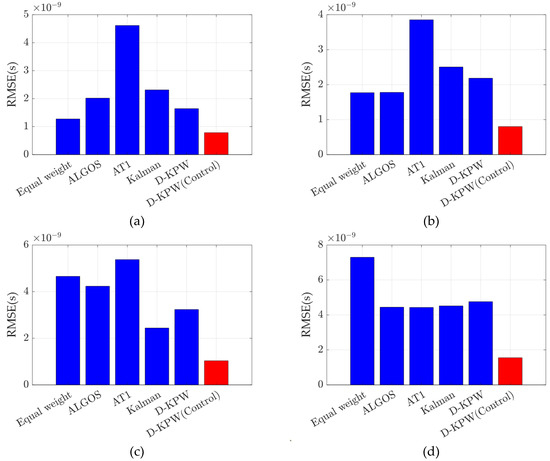
Figure 14.
Prediction residual of time reference established by different algorithms. (a) RMSE of 3-day prediction error; (b) RMSE of 5-day prediction error; (c) RMSE of 10-day prediction error; (d) RMSE of 20-day prediction error.

Table 4.
RMSE of different algorithms’ prediction errors (s).
5. Conclusions
The rapid development of low-Earth-orbit (LEO) constellations will make them an integral part of future satellite navigation systems. To enhance the autonomous timekeeping capabilities of these systems, this paper proposes an autonomous timekeeping algorithm designed specifically for LEO constellations, which optimizes the clock resource utilization in the presence of numerous satellite nodes and complex noise conditions.
The effectiveness of the proposed method is evaluated in terms of stability and predictability, comparing the D-KPW (Control) algorithm with classic methods such as equal-weight averaging, AT1, ALGOS, Kalman filtering, and the D-KPW algorithm introduced in this paper. The D-KPW (Control) algorithm synthesizes clock error data from 48 satellites to establish a time reference. Electing sampling periods of 1000 s, 10,000 s, 100,000 s, and 1,000,000 s, the frequency stability of the time reference is , , , and , respectively. The D-KPW (Control) algorithm generates a time reference with frequency stability that is superior to all other algorithms. The RMSE of the prediction error for the time reference established by the D-KPW (Control) algorithm is s, s, s, and s for 3, 5, 10, and 20 days, respectively, demonstrating superior performance compared to other algorithms.
Due to the lack of publicly available data for LEO satellites, this paper primarily uses GNSS satellite clock error data to simulate LEO spaceborne clocks, only expanding the number of timekeeping nodes. In the future, with the launch of LEO constellations and the deployment of high-performance onboard clocks, sufficient LEO satellite clock data will become available to further validate the algorithm. For LEO satellites, further clock data errors aside from random noise will be introduced, which could affect the accuracy of the LEO constellation time reference. Owing to cost considerations, the large LEO constellation might not be fully equipped with the same high-quality clocks as those in today’s MEOs. In addition, during the transmission of satellite signals, there is a risk of spoofing, so the security of the time information must be taken into account when establishing the time reference. Since time comparison is achieved through the satellite’s bidirectional link, it is possible to incorporate additional authentication information into the link. Addressing these issues will be a key focus in the next phase of research.
Author Contributions
All authors contributed to the study’s conception and design. Conceptualization, S.Y.; Methodology, S.Y., Z.L., and S.N.; Software, S.Y.; Validation, J.P.; Writing—original draft, S.Y.; Writing—review and editing, J.P., M.M., H.G., Z.L., and S.N.; Visualization, M.M.; Funding acquisition, J.P. and H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (grant number 2023YFC2205400), the National Natural Science Foundation of China (grant number U20A0193), and the Science and Technology Innovation Program of Hunan Province (grant number 2021RC3073).
Data Availability Statement
The data used in this study were sourced from the Center for Orbit Determination in Europe (CODE). Readers may download the data from the following address: https://cddis.nasa.gov/archive/gnss/products (accessed on 10 January 2024).
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Tavella, P.; Petit, G. Precise Time Scales and Navigation Systems: Mutual Benefits of Timekeeping and Positioning. Satell. Navig. 2020, 1, 10. [Google Scholar] [CrossRef]
- Pan, J.; Hu, X.; Zhou, S.; Tang, C.; Guo, R.; Zhu, L.; Tang, G.; Hu, G. Time Synchronization of New-Generation BDS Satellites Using Inter-Satellite Link Measurements. Adv. Space Res. 2018, 61, 145–153. [Google Scholar] [CrossRef]
- Meng, Y.; Lei, W.; Bian, L.; Yan, T.; Wang, Y. Clock Tuning Technique for a Disciplined High Medium-Long-Stability GNSS Oscillator with Precise Clock Drifts for LEO Users. GPS Solut. 2020, 24, 110. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, Y.; Ren, X.; Jia, X.; Sun, B. Demand and Key Technology for a LEO Constellation as Augmentation of Satellite Navigation Systems. Satell. Navig. 2024, 5, 11. [Google Scholar] [CrossRef]
- Van Buren, D.; Axelrad, P.; Palo, S. Design of a High-Stability Heterogeneous Clock System for Small Satellites in LEO|GPS Solutions. GPS Solut. 2021, 25, 105. [Google Scholar] [CrossRef]
- Michalak, G.; Neumayer, K.H.; Konig, R. Precise Orbit Determination of the Kepler Navigation System—A Simulation Study. In Proceedings of the 2020 European Navigation Conference (ENC), Dresden, Germany, 23 November 2020; pp. 1–10. [Google Scholar]
- Schmidt, T.D.; Schuldt, T.; Michalak, G.; Surof, J.; Poliak, J.; Giorgi, G.; Braxmaier, C.; Meurer, M.; Günther, C. Optical Technologies for Future Global Navigation Satellite Systems. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24 April 2023; pp. 311–317. [Google Scholar]
- Yang, S.; Yi, X.; Dong, R.; Ren, Q.; Li, X.; Shuai, T.; Zhang, J.; Gong, W. A Method for Autonomous Generation of High-Precision Time Scales for Navigation Constellations. Sensors 2023, 23, 1703. [Google Scholar] [CrossRef]
- Yi, X.; Yang, S.; Dong, R.; Ren, Q.; Shuai, T.; Li, G.; Gong, W. A Composite Clock for Robust Time–Frequency Signal Generation System Onboard a Navigation Satellite. GPS Solut. 2024, 28, 6. [Google Scholar] [CrossRef]
- Yang, S.; Yi, X.; Dong, R.; Wu, Y.; Shuai, T.; Zhang, J.; Ren, Q.; Gong, W. Long-Term Autonomous Time-Keeping of Navigation Constellations Based on Sparse Sampling LSTM Algorithm. Satell. Navig. 2024, 5, 15. [Google Scholar] [CrossRef]
- Zhou, W.; Gao, W.; Pan, J.; Hu, X.; Zhou, S.; Shao, R.; Yuan, Y. Analysis of Preliminary Results from Distributed Autonomous Timekeeping on Beidou-3 Satellites. GPS Solut. 2023, 27, 80. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.; Gao, S.; Li, W.; Guo, X.; Yang, J. Joint Timekeeping of Navigation Satellite Constellation with Inter-Satellite Links. Sensors 2020, 20, 670. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Schoenemann, E.; Hauschild, A.; Hugentobler, U.; Dach, R.; Becker, M. Flight Characterization of New Generation GNSS Satellite Clocks. Navigation 2012, 59, 291–302. [Google Scholar] [CrossRef]
- Ye, X.; Liu, W.; Zuo, Y.; Wang, W.; Wang, H.; Chang, J.; Wang, F. Analysis of BDS-3 Distributed Autonomous Navigation Based on BeiDou System Simulation Platform. Adv. Space Res. 2021, 67, 401–410. [Google Scholar] [CrossRef]
- Greenhall, C.A. Forming Stable Timescales from the Jones–Tryon Kalman Filter. Metrologia 2003, 40, S335–S341. [Google Scholar] [CrossRef]
- Weiss, M.; Weissert, T. AT2, A New Time Scale Algorithm: AT1 Plus Frequency Variance. Metrologia 1991, 28, 65–74. [Google Scholar] [CrossRef][Green Version]
- Jiangmiao, Z.; Di, Y.; Yuhui, Q.; Ye, C.; Wenjuan, W. Kalman Timescale Algorithm Based on Hydrogen Clock Ensemble. In Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; pp. 591–596. [Google Scholar]
- Wang, X.; Yang, Y.; Wang, B.; Lin, Y.; Han, C. Resilient Timekeeping Algorithm with Multi-Observation Fusion Kalman Filter. Satell. Navig. 2023, 4, 25. [Google Scholar] [CrossRef]
- Chen, G.; Xing, N.; Tang, C.; Chang, Z. Clock Ensemble Algorithm Test in the Establishment of Space-Based Time Reference. Remote Sens. 2023, 15, 1227. [Google Scholar] [CrossRef]
- Xue, H.; Nie, W.; Xu, T.; Li, M.; Yang, Y.; Fang, Z.; Gao, F. Establishment of iGMAST Based on Spaceborne Atomic Clocks by Optimizing Kalman plus Weights Algorithm. Measurement 2022, 203, 111998. [Google Scholar] [CrossRef]
- Panfilo, G.; Harmegnies, A.; Tisserand, L. A New Prediction Algorithm for the Generation of International Atomic Time. Metrologia 2012, 49, 49. [Google Scholar] [CrossRef]
- Panfilo, G.; Arias, E. Algorithms for International Atomic Time. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 140–150. [Google Scholar] [CrossRef]
- Parker, T.E.; Levine, J. Impact of New High Stability Frequency Standards on the Performanceof the NIST AT1 Time Scale. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1997, 44, 1239–1244. [Google Scholar] [CrossRef]
- Libal, U.; Johansson, K.H. Yule-Walker Equations Using Higher Order Statistics for Nonlinear Autoregressive Model. In Proceedings of the 2019 Signal Processing Symposium (SPSympo), Krakow, Poland, 1 September 2019; pp. 227–231. [Google Scholar]
- Wang, B.; Chen, J.; Wang, B. Kalman Filter Simulation and Characterization of BDS Satellite Clock. In Proceedings of the 2018 European Frequency and Time Forum (EFTF), Turin, Italy, 10–12 April 2018; pp. 296–299. [Google Scholar]
- Pan, J.; Hu, X.; Zhou, S.; Tang, C.; Wang, D.; Yang, Y.; Dong, W. Full-ISL Clock Offset Estimation and Prediction Algorithm for BDS3. GPS Solut. 2021, 25, 140. [Google Scholar] [CrossRef]
- Ye, Y.; Huijun, Z.; Xiaohui, L. Three Kinds of Algorithm and Its Performance Analysis in the Prediction of Satellite Clocks Bias. In Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; pp. 536–543. [Google Scholar]
- Wang, X.; Chai, H.; Wang, C. A High-Precision Short-Term Prediction Method with Stable Performance for Satellite Clock Bias. GPS Solut. 2020, 24, 105. [Google Scholar] [CrossRef]
- Cai, C.; Liu, M.; Li, P.; Li, Z.; Lv, K. Enhancing Satellite Clock Bias Prediction in BDS with LSTM-Attention Model. GPS Solut. 2024, 28, 92. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).