Infrared Small Target Detection Based on Weighted Improved Double Local Contrast Measure
Abstract
1. Introduction
- A target size estimation method based on double neighborhood gray difference is proposed without using multi-scale operation.
- A weighting coefficient based on the variance difference between the target edge and the neighboring background is proposed to eliminate high-brightness clutter.
- We redefined the local contrast measure for targets of varying sizes by integrating gray and structural characteristics, thereby synchronously enhancing the target and suppressing the background.
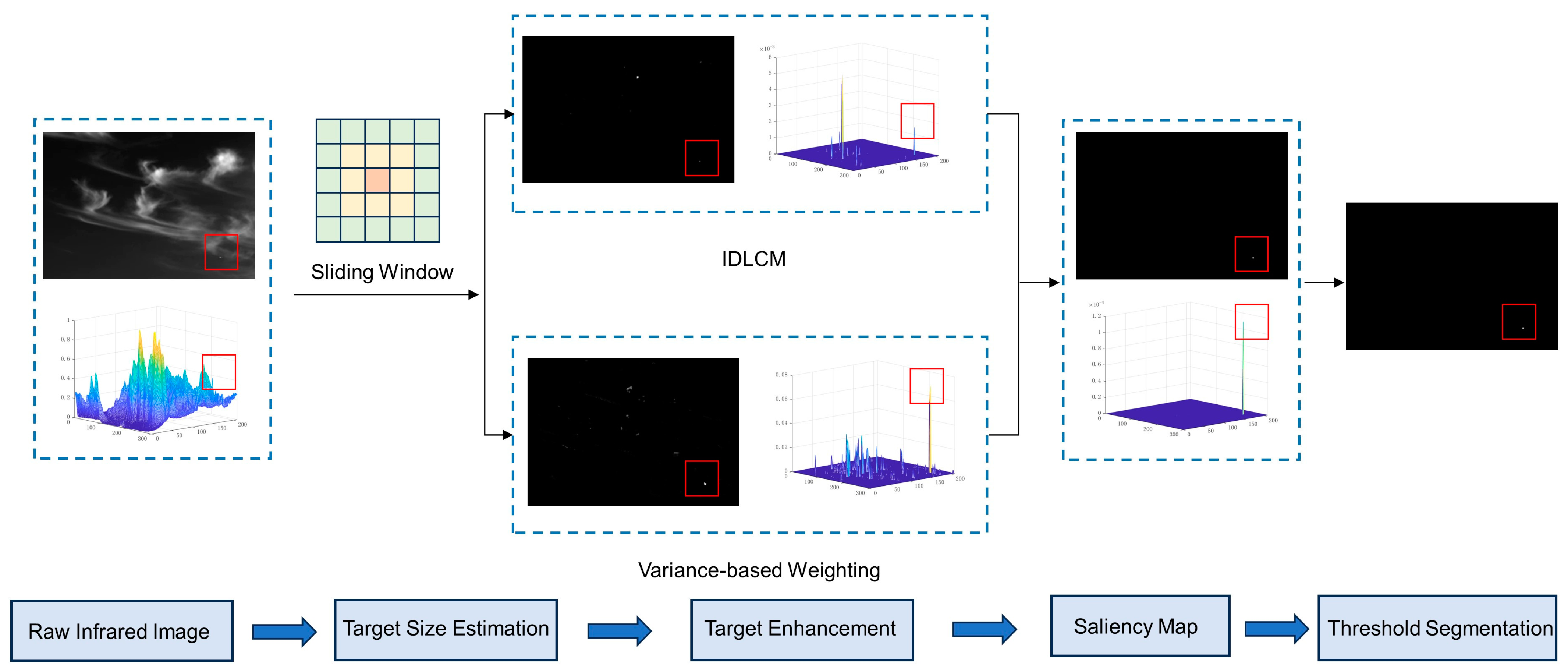
2. Proposed Method
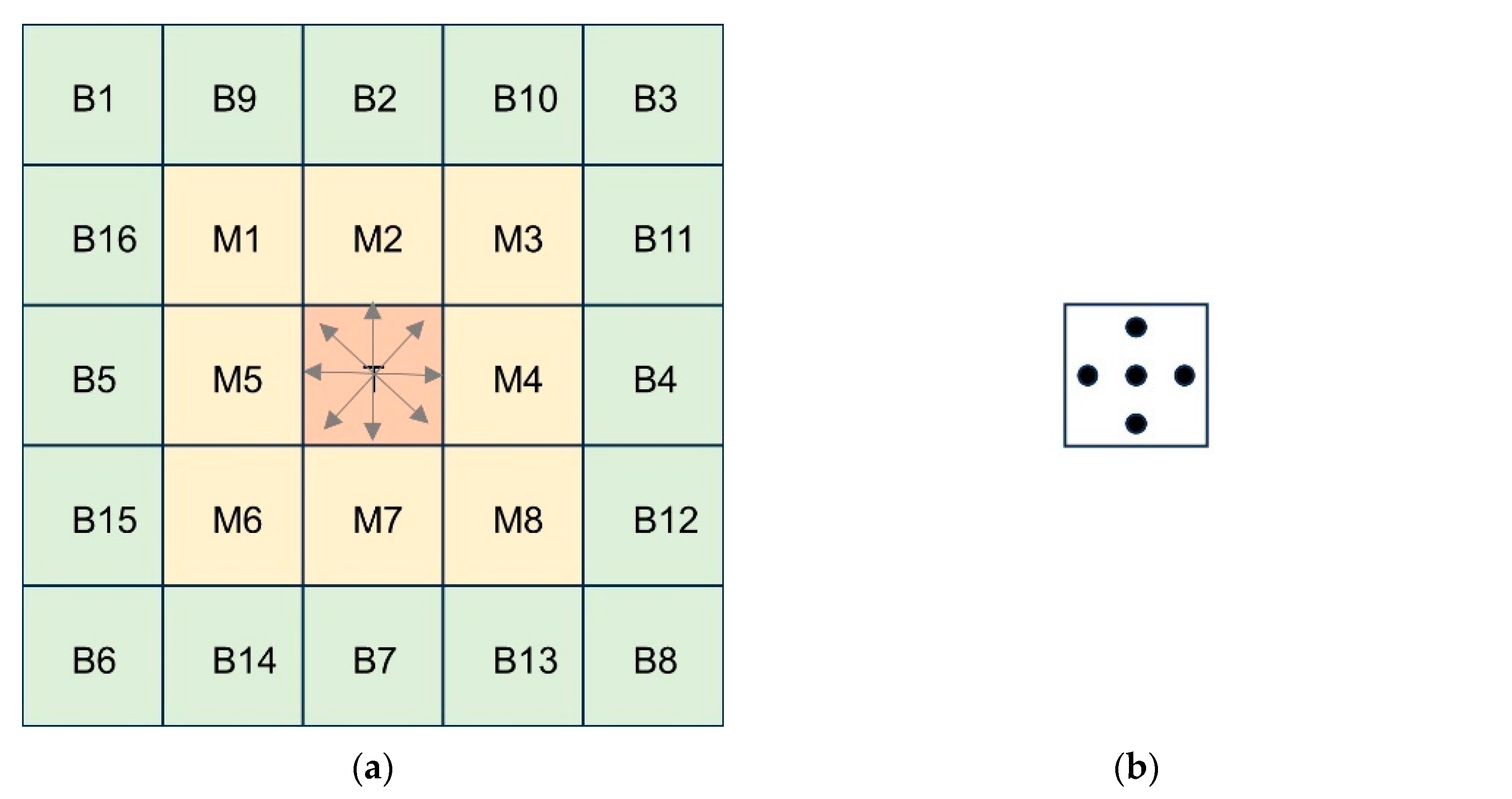
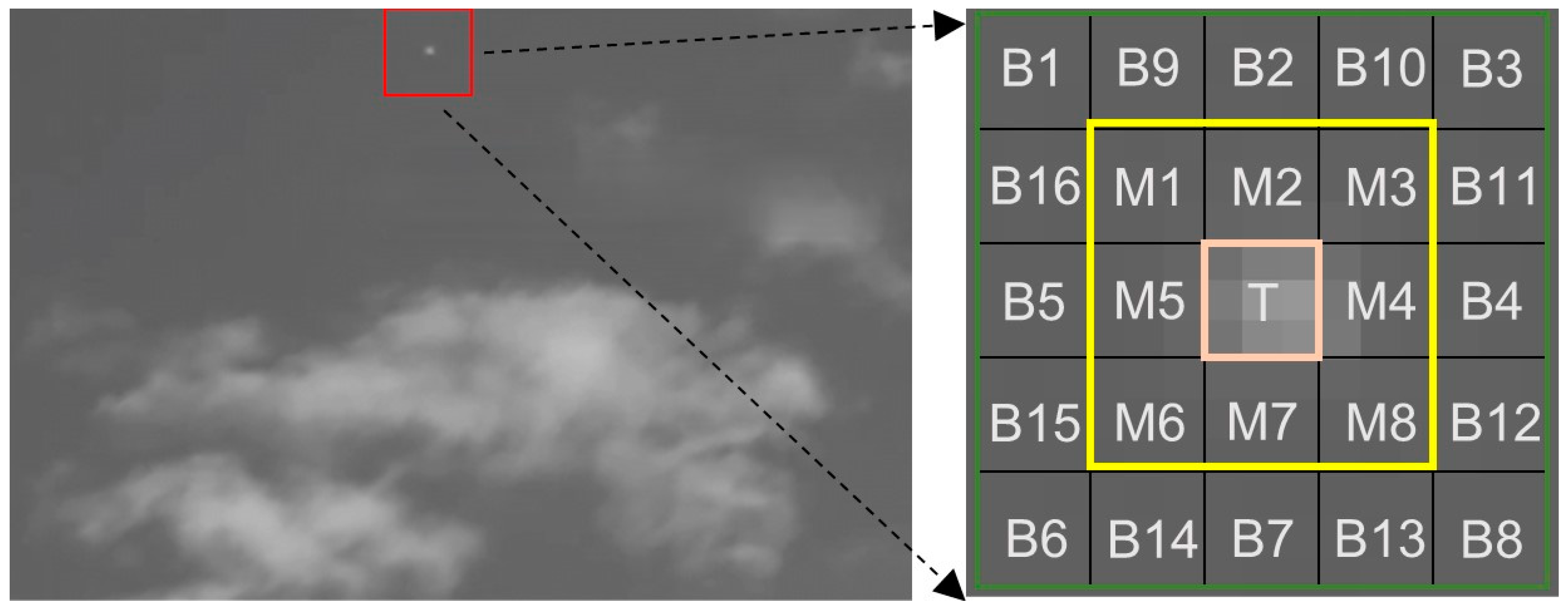
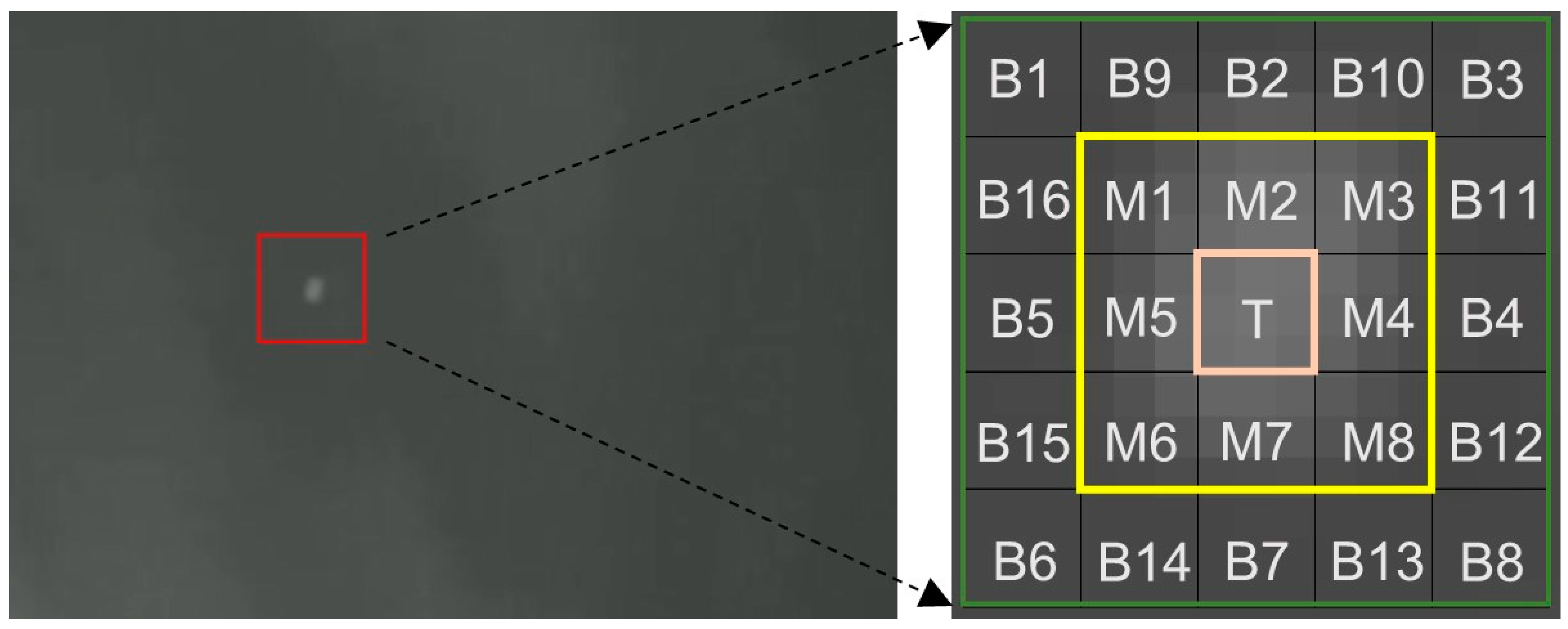
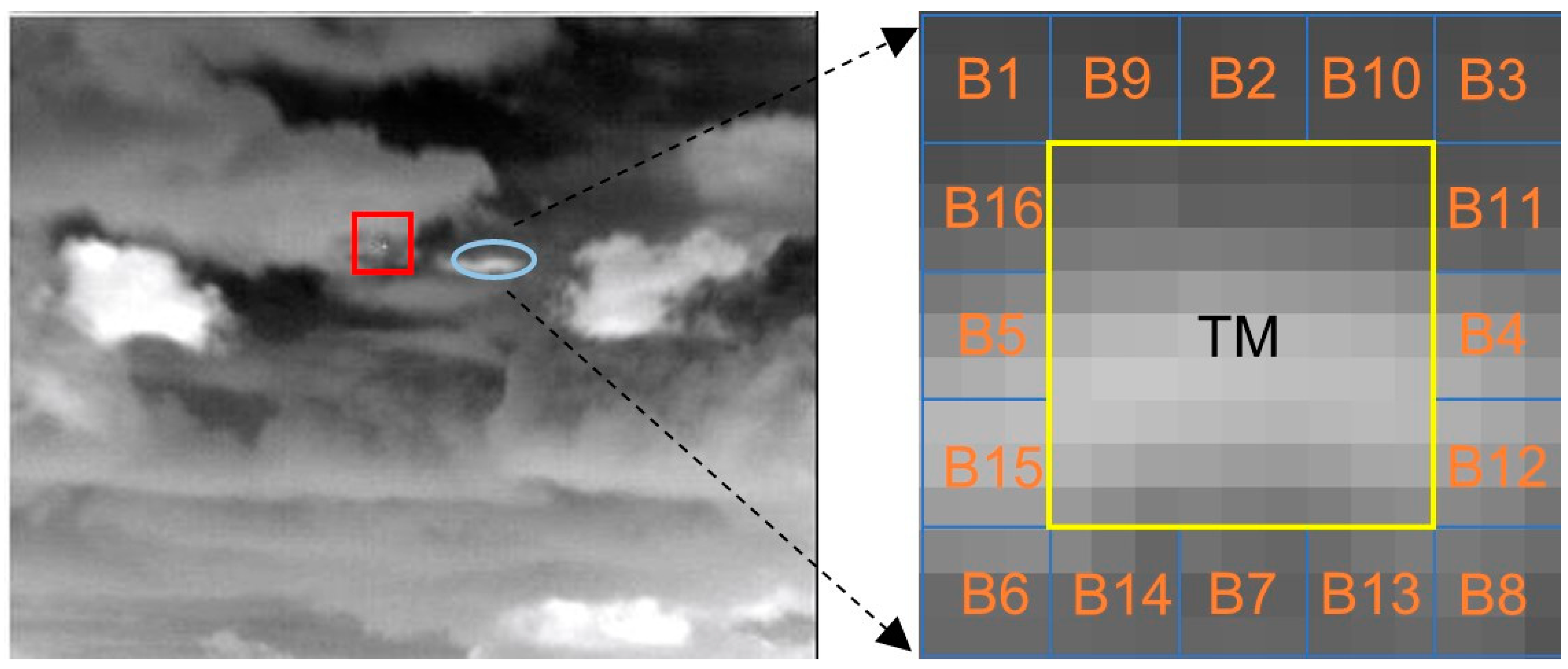
2.1. Candidate Target Pixels’ Screening and Size Estimation
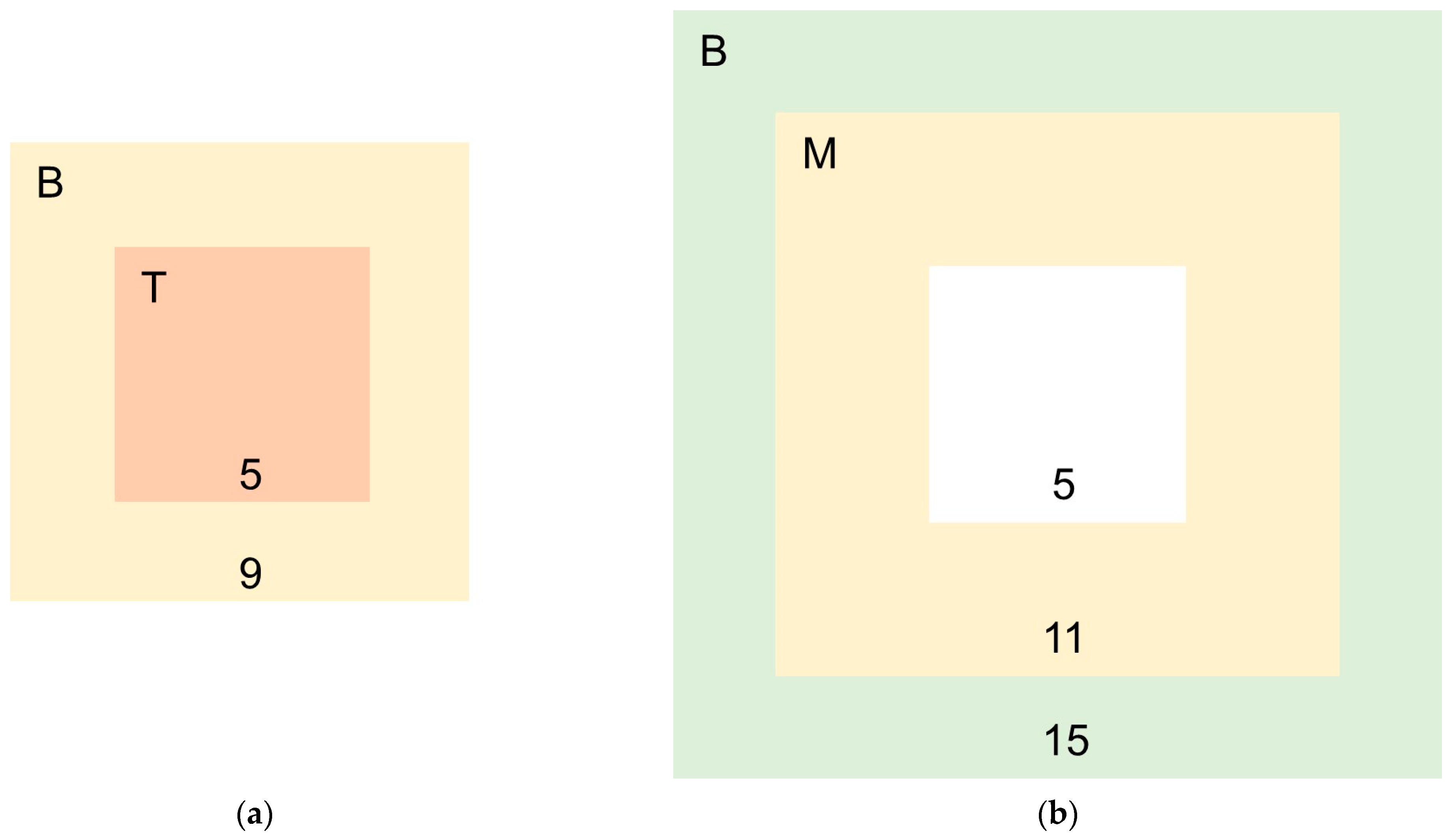
2.2. Calculation of IDLCM
2.3. Calculation of Variance-Based Weighting Coefficient
2.4. Calculation of WIDLCM
2.5. Threshold Operation
3. Experimental Results
3.1. Datasets
3.2. Evaluation Metrics
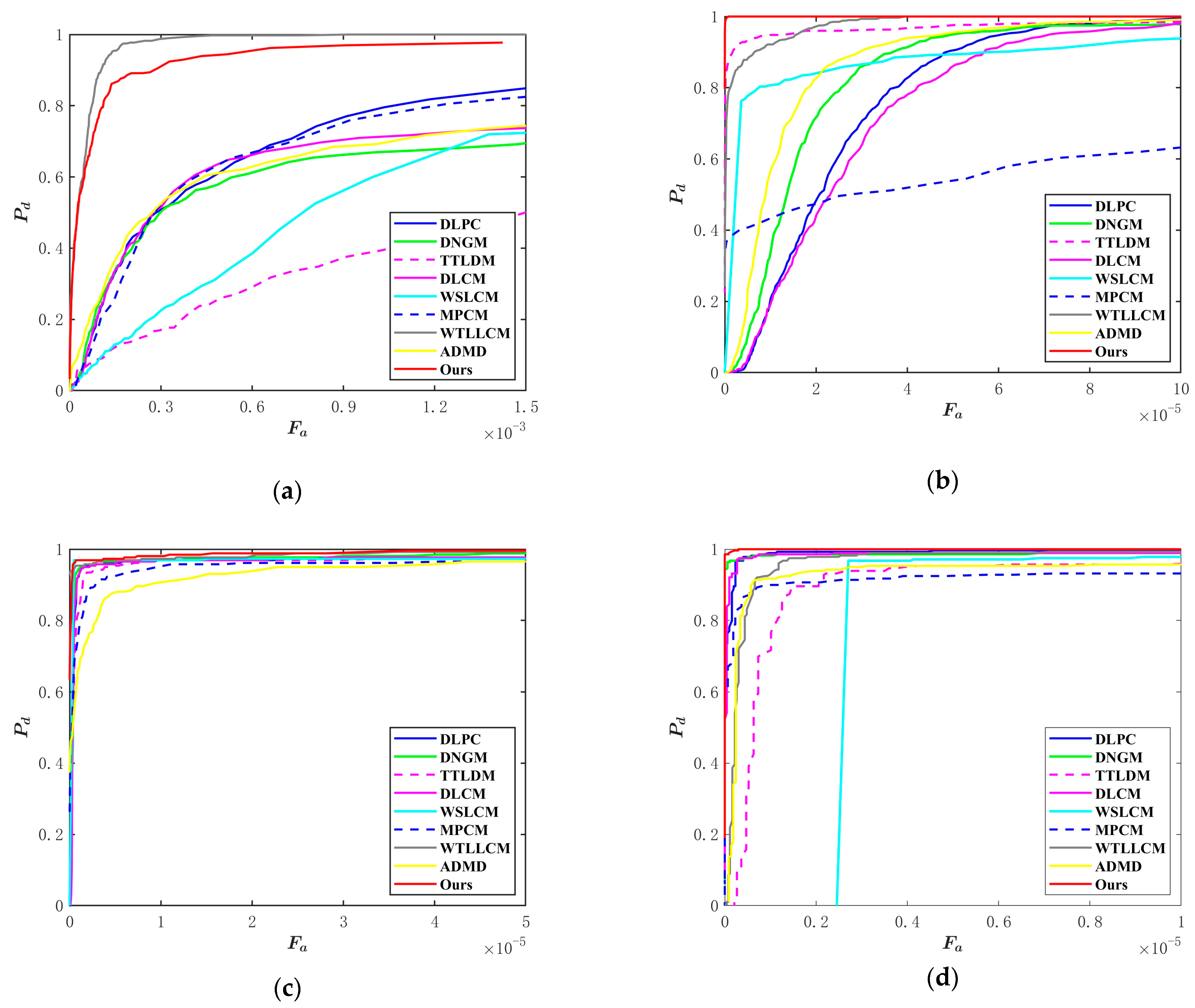
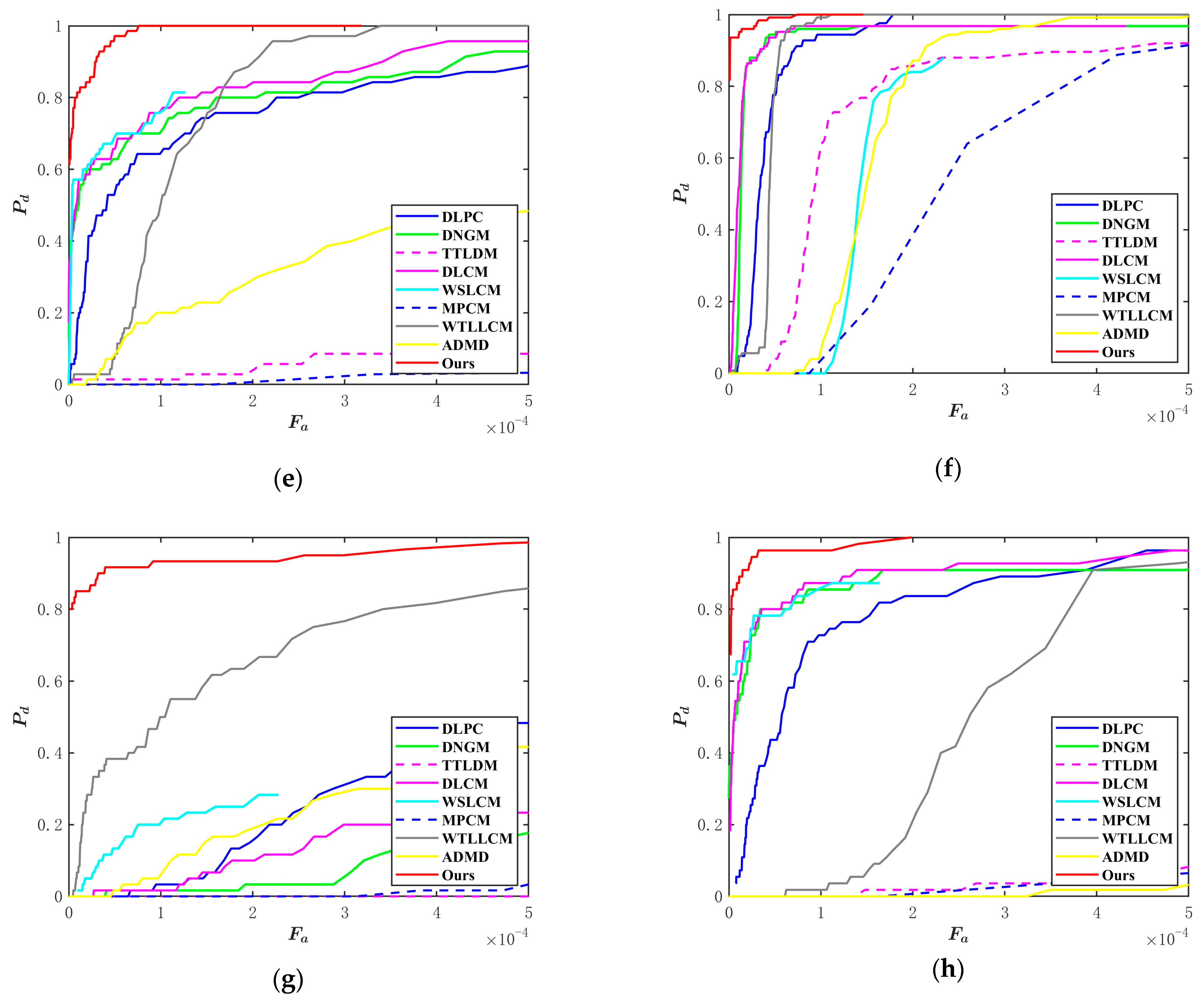
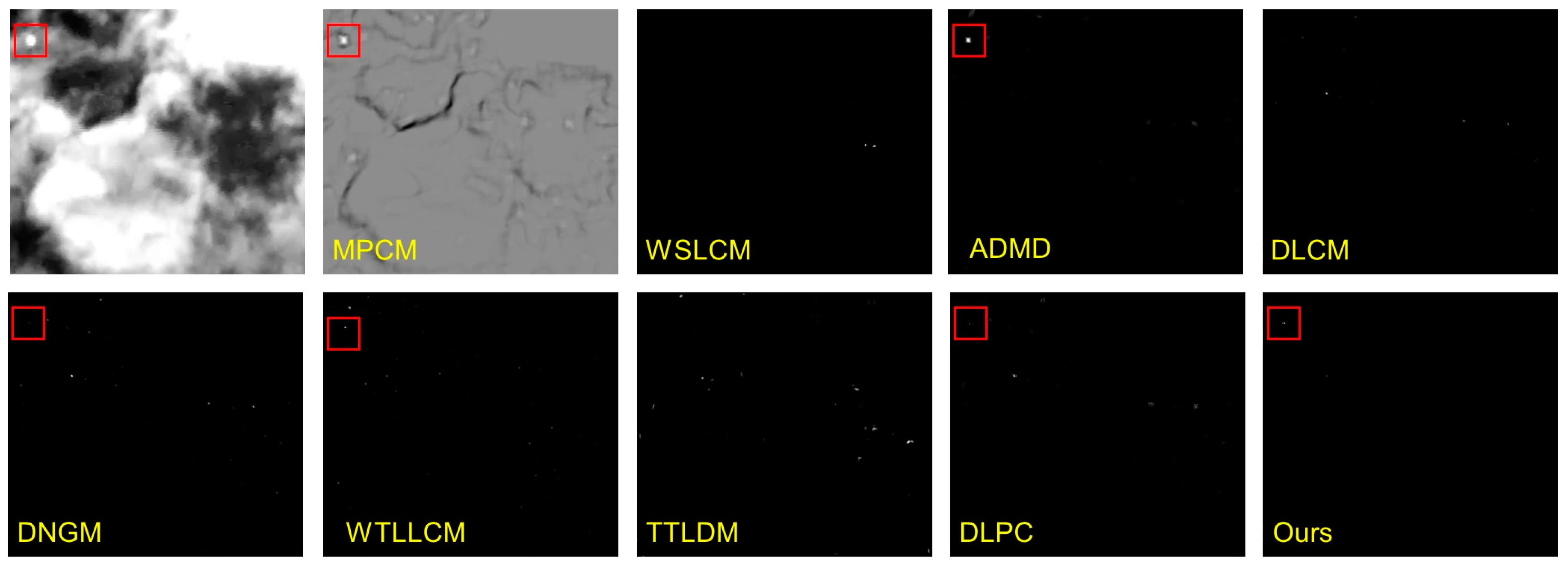
3.3. Qualitative and Quantitative Comparison Results
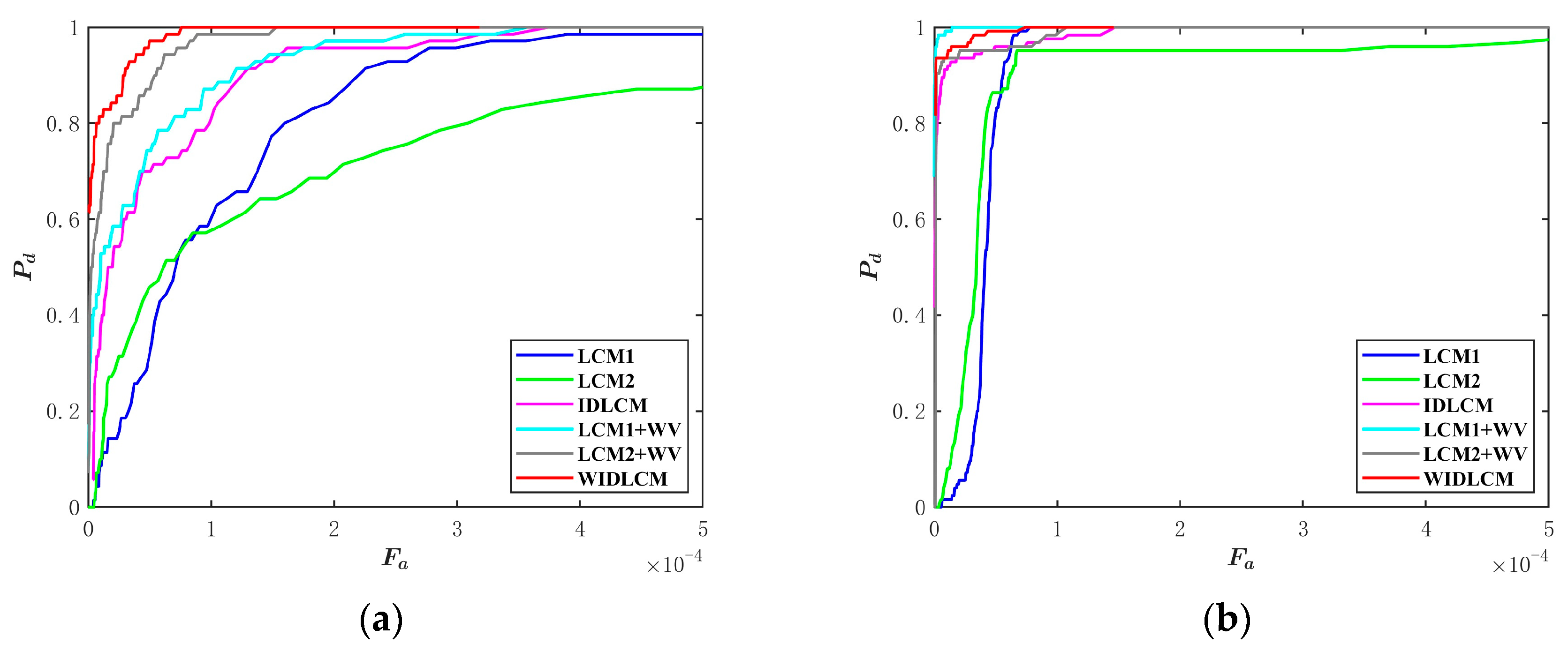
4. Ablation and Validation Experiments
4.1. Ablation Experiments
4.2. Validation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P. Max-mean and Max-median filters for detection of small-targets. In Proceedings of the Signal and Data Processing of Small Targets, Orlando, FL, USA, 20–22 July 1999; Volume 3809, pp. 74–83. [Google Scholar]
- Bai, X.; Zhou, F. Analysis of New Top-Hat Transformation and the Application for Infrared Dim Small Target Detection. Pattern Recognit. 2010, 43, 2145–2156. [Google Scholar] [CrossRef]
- Deng, L.; Zhang, J.; Xu, G.; Zhu, H. Infrared Small Target Detection via Adaptive M-Estimator Ring Top-Hat Transformation. Pattern Recognit. 2021, 112, 107729. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L. Multidirectional ring top-hat transformation for infrared small target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8077–8088. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Li, J.; Yang, J.; Siddique, A. Robust Small Infrared Target Detection Using Weighted Adaptive Ring Top-Hat Transformation. Signal Process. 2023, 217, 109339. [Google Scholar] [CrossRef]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y. Reweighted Infrared Patch-Tensor Model with Both Nonlocal and Local Priors for Single-Frame Small Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3752–3767. [Google Scholar] [CrossRef]
- Kong, X.; Yang, C.; Cao, S.; Li, C.; Peng, Z. Infrared Small Target Detection via Nonconvex Tensor Fibered Rank Approximation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5000321. [Google Scholar] [CrossRef]
- Zhao, E.; Dong, L.; Shi, J. Infrared Maritime Target Detection Based on Iterative Corner and Edge Weights in Tensor Decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 7543–7558. [Google Scholar] [CrossRef]
- Xu, Y.; Wan, M.; Zhang, X.; Wu, J.; Chen, Y.; Chen, Q.; Gu, G. Infrared Small Target Detection Based on Local Contrast-Weighted Multidirectional Derivative. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5000816. [Google Scholar] [CrossRef]
- Zhang, X.; Ru, J.; Wu, C. An Infrared Small Target Detection Method Based on Gradient Correlation Measure. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7507605. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Wei, Y.; Zhang, L. Infrared Small Target Detection Based on Multidirectional Gradient. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6500205. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Attentional Local Contrast Networks for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9813–9824. [Google Scholar] [CrossRef]
- Hou, Q.; Zhang, L.; Tan, F.; Xi, Y.; Zheng, H.; Li, N. ISTDU-Net: Infrared Small-Target Detection U-Net. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7506205. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.; Liu, X.; Su, X. A Multi-Task Framework for Infrared Small Target Detection and Segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5003109. [Google Scholar] [CrossRef]
- Li, B.; Xiao, C.; Wang, L.; Wang, Y.; Lin, Z.; Li, M.; An, W.; Guo, Y. Dense Nested Attention Network for Infrared Small Target Detection. IEEE Trans. Image Process. 2023, 32, 1745–1758. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A Local Contrast Method for Small Infrared Target Detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 574–581. [Google Scholar] [CrossRef]
- Wei, Y.; You, X.; Li, H. Multiscale Patch-Based Contrast Measure for Small Infrared Target Detection. Pattern Recognit. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Pan, S.D.; Zhang, S.; Zhao, M.; An, B.W. Infrared Small Target Detection Based on Double-layer Local Contrast Measure. Acta Photonica Sin. 2020, 49, 110003. [Google Scholar]
- Wu, L.; Ma, Y.; Fan, F.; Wu, M.; Huang, J. A Double-Neighborhood Gradient Method for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1476–1480. [Google Scholar] [CrossRef]
- Lu, X.; Bai, X.; Li, S.; Hei, X. Infrared Small Target Detection Based on the Weighted Double Local Contrast Measure Utilizing a Novel Window. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7507305. [Google Scholar] [CrossRef]
- Chen, C.; Xia, R.; Liu, Y.; Liu, Y. A Simplified Dual-Weighted Three-Layer Window Local Contrast Method for Infrared Small-Target Detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6003705. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, X. Research on High Robust Infrared Small Target Detection Method in Complex Background. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6007705. [Google Scholar] [CrossRef]
- Du, P.; Hamdulla, A. Infrared Small Target Detection Using Homogeneity-Weighted Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2020, 17, 514–518. [Google Scholar] [CrossRef]
- Mu, J.; Li, W.; Rao, J.; Li, F.; Wei, H. Infrared small target detection using tri-layer template local difference measure. Opt. Precis. Eng. 2022, 30, 869–882. [Google Scholar] [CrossRef]
- Liu, L.; Wei, Y.; Wang, Y.; Yao, H.; Chen, D. Using Double-Layer Patch-Based Contrast for Infrared Small Target Detection. Remote Sens. 2023, 15, 3839. [Google Scholar] [CrossRef]
- Wei, H.; Ma, P.; Pang, D.; Li, W.; Qian, J.; Guo, X. Weighted Local Ratio-Difference Contrast Method for Detecting an Infrared Small Target against Ground–Sky Background. Remote Sens. 2022, 14, 5636. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, Y.; Fan, F.; Huang, J.; Wu, L. Global Sparsity-Weighted Local Contrast Measure for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7507405. [Google Scholar] [CrossRef]
- Han, J.; Liu, C.; Liu, Y.; Luo, Z.; Zhang, X.; Niu, Q. Infrared Small Target Detection Utilizing the Enhanced Closest-Mean Background Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 645–662. [Google Scholar] [CrossRef]
- Han, J.; Liu, S.; Qin, G.; Zhao, Q.; Zhang, H.; Li, N. A Local Contrast Method Combined with Adaptive Background Estimation for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1442–1446. [Google Scholar] [CrossRef]
- Guan, X.; Peng, Z.; Huang, S.; Chen, Y. Gaussian Scale-Space Enhanced Local Contrast Measure for Small Infrared Target Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 327–331. [Google Scholar] [CrossRef]
- Jiang, Y.; Xi, Y.; Zhang, L.; Wu, Y.; Tan, F.; Hou, Q. Infrared Small Target Detection Based on Local Contrast Measure with a Flexible Window. IEEE Geosci. Remote Sens. Lett. 2024, 21, 7001805. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, Y.; Fan, F.; Huang, J.; Wu, M. Adaptive Scale Patch-Based Contrast Measure for Dim and Small Infrared Target Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7000305. [Google Scholar] [CrossRef]
- Han, J.; Moradi, S.; Faramarzi, I.; Zhang, H.; Zhao, Q.; Zhang, X.; Li, N. Infrared Small Target Detection Based on the Weighted Strengthened Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1670–1674. [Google Scholar] [CrossRef]
- Cui, H.; Li, L.; Liu, X.; Su, X.; Chen, F. Infrared Small Target Detection Based on Weighted Three-Layer Window Local Contrast. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7505705. [Google Scholar] [CrossRef]
- Tang, Y.; Xiong, K.; Wang, C. Fast Infrared Small Target Detection Based on Global Contrast Measure Using Dilate Operation. IEEE Geosci. Remote Sens. Lett. 2023, 20, 8000105. [Google Scholar] [CrossRef]
- Qin, Y.; Li, B. Effective Infrared Small Target Detection Utilizing a Novel Local Contrast Method. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1890–1894. [Google Scholar] [CrossRef]
- Moradi, S.; Moallem, P.; Sabahi, M.F. Fast and Robust Small Infrared Target Detection Using Absolute Directional Mean Difference Algorithm. Signal Process. 2020, 177, 107727. [Google Scholar] [CrossRef]
- Hui, B.W.; Song, Z.Y.; Fan, H.Q.; Zhong, P.; Hu, W.D.; Zhang, X.F.; Lin, J.G.; Su, H.Y.; Jin, W.; Zhang, Y.J.; et al. A dataset for infrared image dim-small aircraft target detection and tracking under ground/air background. China Sci. Data 2020, 5, 291–302. [Google Scholar]
- Xu, H.; Zhong, S.; Zhang, T.; Zou, X. Multiscale Multilevel Residual Feature Fusion for Real-Time Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5002116. [Google Scholar] [CrossRef]
- Gao, C.; Wang, L.; Xiao, Y.; Zhao, Q.; Meng, D. Infrared Small-Dim Target Detection Based on Markov Random Field Guided Noise Modeling. Pattern Recognit. 2018, 76, 463–475. [Google Scholar] [CrossRef]












| Sequence | Frames | Target Type | Target Size | Target Number | Background Description |
|---|---|---|---|---|---|
| 1 | 396 | aircraft | 2 × 2 to 3 × 3 | 1 | Ground background, forests, high-brightness ground |
| 2 | 600 | aircraft | 2 × 2 to 4 × 3 | 1 | Ground background, forests, high-brightness buildings, high-voltage towers |
| 3 | 260 | aircraft | 3 × 3 to 3 × 4 | 1 | Ground-sky background, forests, high-brightness buildings |
| 4 | 279 | aircraft, vehicle, ship, others | 2 × 2 to 9 × 9 | 1 | Various backgrounds, heavy cloud, high-brightness buildings, heavy noise |
| 5 | 70 | aircraft | 3 × 3 to 5 × 4 | 1 | Sky background, cloud, high-brightness trees |
| 6 | 125 | aircraft | 4 × 4 to 11 × 5 | 1 | Sky background, cloud, high-brightness trees, buildings |
| 7 | 60 | aircraft | 4 × 4 to 5 × 4 | 1 | Sky background, cloud, high-brightness buildings |
| 8 | 55 | aircraft | 4 × 3 to 7 × 6 | 1 | Sky background, cloud, high-brightness trees |
| Sequence | MPCM | WSLCM | ADMD | DLCM | DNGM | WTLLCM | TTLDM | DLPC | Ours |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5.092 | 11.534 | 6.697 | 13.964 | 11.389 | 17.318 | 6.374 | 13.146 | 28.064 |
| 2 | 8.527 | 45.144 | 15.619 | 27.025 | 22.404 | 39.710 | 18.488 | 26.686 | 133.774 |
| 3 | 18.936 | 71.731 | 22.410 | 81.677 | 49.188 | 62.628 | 24.035 | 79.157 | 264.270 |
| 4 | 64.801 | 649.941 | 108.470 | 1025.176 | 583.508 | 888.913 | 219.631 | 585.364 | 1295.452 |
| 5 | 6.924 | 188.473 | 16.147 | 43.573 | 33.999 | 35.790 | 19.783 | 36.764 | 186.746 |
| 6 | 11.562 | 38.832 | 29.420 | 60.389 | 59.629 | 46.942 | 29.638 | 54.500 | 198.082 |
| 7 | 16.597 | 49.607 | 26.668 | 50.195 | 36.296 | 64.373 | 19.713 | 45.090 | 259.731 |
| 8 | 10.379 | 287.512 | 25.399 | 89.992 | 50.595 | 48.914 | 31.947 | 86.308 | 455.925 |
| Sequence | MPCM | WSLCM | ADMD | DLCM | DNGM | WTLLCM | TTLDM | DLPC | Ours |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.603 | 21.412 | 5.772 | 22.178 | 14.105 | 93.389 | 3.381 | 11.613 | 96.219 |
| 2 | 5.030 | 26.757 | 9.727 | 88.520 | 68.345 | 96.105 | 5.214 | 43.879 | 139.744 |
| 3 | 5.172 | 8.712 | 7.434 | 84.331 | 61.507 | 112.061 | 2.851 | 22.194 | 74.232 |
| 4 | 11.854 | 202.296 | 25.688 | 197.243 | 157.745 | 288.923 | 23.279 | 82.363 | 209.836 |
| 5 | 6.443 | 948.813 | 257.987 | 812.916 | 788.141 | 371.758 | 12.754 | 356.311 | 1532.261 |
| 6 | 5.395 | 178.174 | 74.126 | 415.472 | 307.996 | 207.333 | 154.366 | 204.305 | 490.933 |
| 7 | 36.234 | 8470.301 | 3795.154 | 896.055 | 1037.347 | 17,459.412 | 255.534 | 2636.521 | 12,815.916 |
| 8 | 5.039 | 1516.150 | 288.563 | 817.380 | 892.670 | 94.176 | 50.259 | 362.949 | 1218.086 |
| Sequence | MPCM | WSLCM | ADMD | DLCM | DNGM | WTLLCM | TTLDM | DLPC | Ours |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.028 | 1.858 | 0.006 | 0.021 | 0.015 | 0.095 | 0.006 | 0.019 | 0.028 |
| 2 | 0.028 | 1.865 | 0.006 | 0.021 | 0.014 | 0.093 | 0.006 | 0.019 | 0.028 |
| 3 | 0.028 | 1.839 | 0.006 | 0.021 | 0.015 | 0.093 | 0.007 | 0.019 | 0.028 |
| 4 | 0.027 | 1.373 | 0.006 | 0.020 | 0.014 | 0.098 | 0.007 | 0.018 | 0.029 |
| 5 | 0.040 | 2.379 | 0.007 | 0.033 | 0.020 | 0.160 | 0.009 | 0.026 | 0.046 |
| 6 | 0.041 | 2.231 | 0.007 | 0.033 | 0.020 | 0.153 | 0.009 | 0.026 | 0.045 |
| 7 | 0.041 | 2.554 | 0.008 | 0.033 | 0.020 | 0.158 | 0.010 | 0.026 | 0.045 |
| 8 | 0.041 | 2.239 | 0.008 | 0.031 | 0.020 | 0.154 | 0.009 | 0.026 | 0.046 |
| LCM1 | LCM2 | IDLCM | LCM1 + WV | LCM2 + WV | WIDLCM | ||
|---|---|---|---|---|---|---|---|
| BSF | Seq. 5 Seq. 6 | 24.377 | 17.958 | 53.405 | 52.998 | 75.340 | 186.746 |
| 53.372 | 32.149 | 80.076 | 124.285 | 82.408 | 198.082 | ||
| SCRG | Seq. 5 | 380.688 | 486.758 | 478.025 | 1424.573 | 1859.793 | 1532.261 |
| Seq. 6 | 78.363 | 22.835 | 302.626 | 406.900 | 203.348 | 490.933 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Hu, Y.; Wang, Y.; Cheng, L.; Gong, C.; Huang, S.; Zheng, F. Infrared Small Target Detection Based on Weighted Improved Double Local Contrast Measure. Remote Sens. 2024, 16, 4030. https://doi.org/10.3390/rs16214030
Wang H, Hu Y, Wang Y, Cheng L, Gong C, Huang S, Zheng F. Infrared Small Target Detection Based on Weighted Improved Double Local Contrast Measure. Remote Sensing. 2024; 16(21):4030. https://doi.org/10.3390/rs16214030
Chicago/Turabian StyleWang, Han, Yong Hu, Yang Wang, Long Cheng, Cailan Gong, Shuo Huang, and Fuqiang Zheng. 2024. "Infrared Small Target Detection Based on Weighted Improved Double Local Contrast Measure" Remote Sensing 16, no. 21: 4030. https://doi.org/10.3390/rs16214030
APA StyleWang, H., Hu, Y., Wang, Y., Cheng, L., Gong, C., Huang, S., & Zheng, F. (2024). Infrared Small Target Detection Based on Weighted Improved Double Local Contrast Measure. Remote Sensing, 16(21), 4030. https://doi.org/10.3390/rs16214030








