Characterization of Electric Field Fluctuations in the High-Latitude Ionosphere Using a Dynamical Systems Approach: CSES-01 Observations
Abstract
:1. Introduction
2. Data
3. Methods
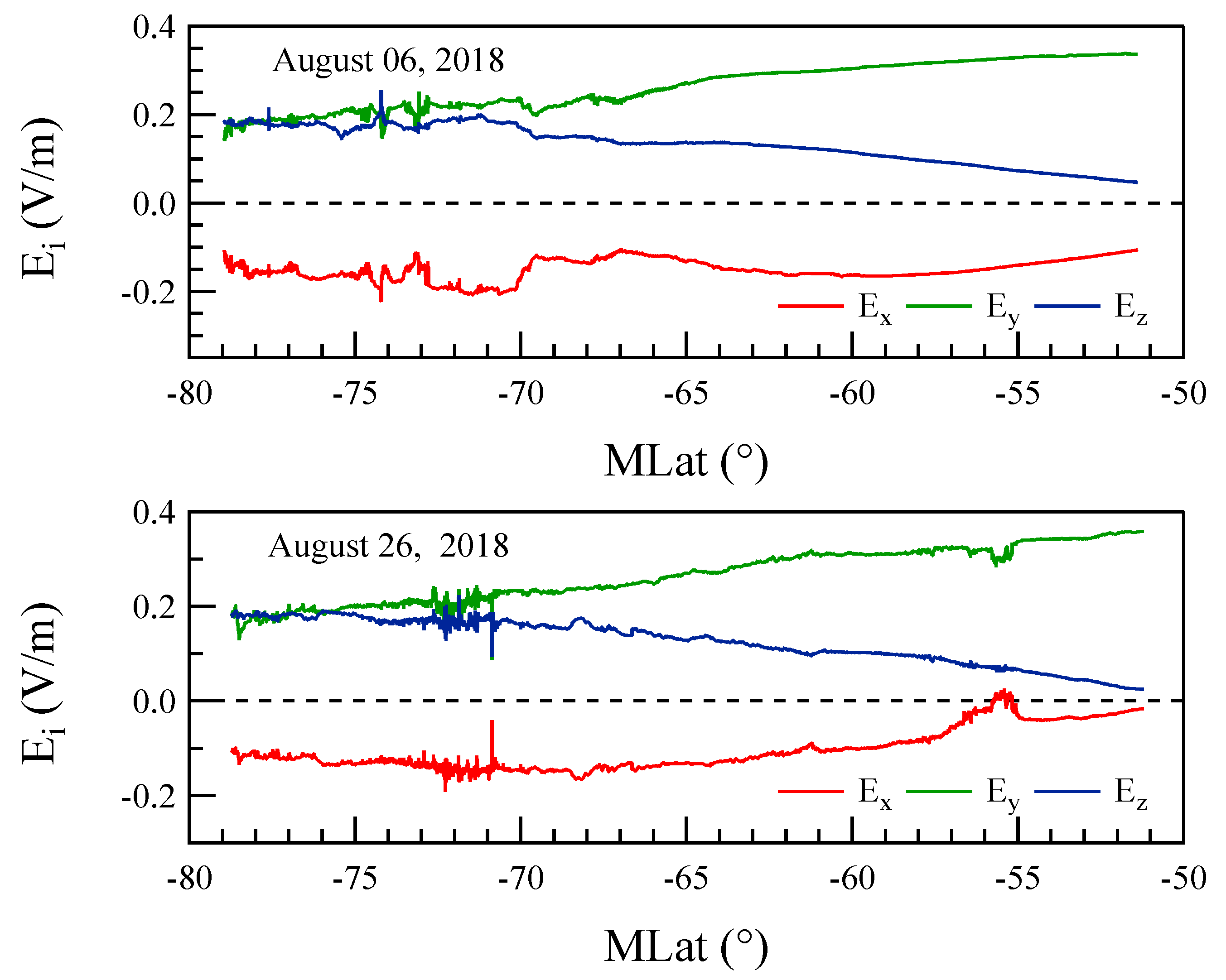
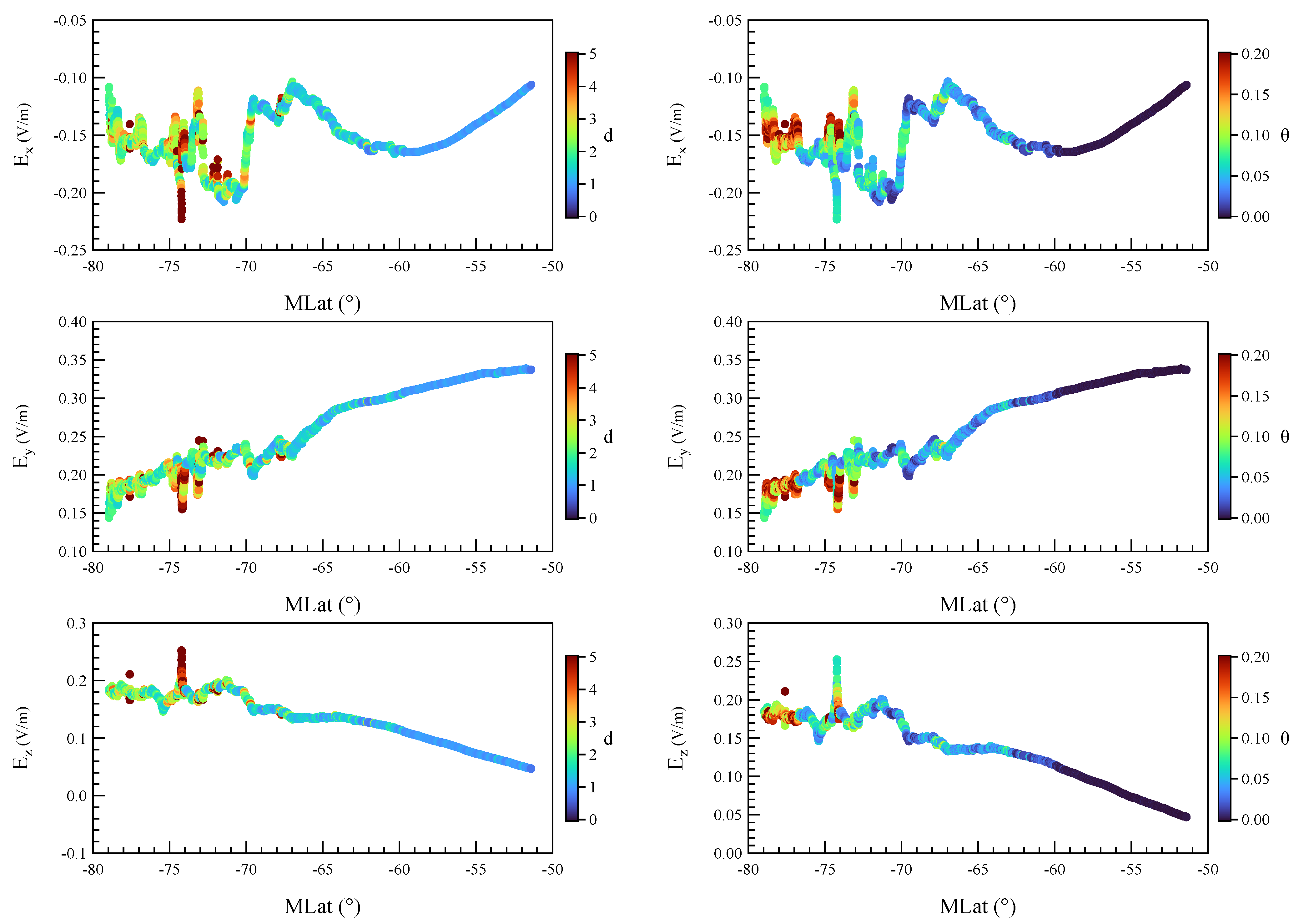
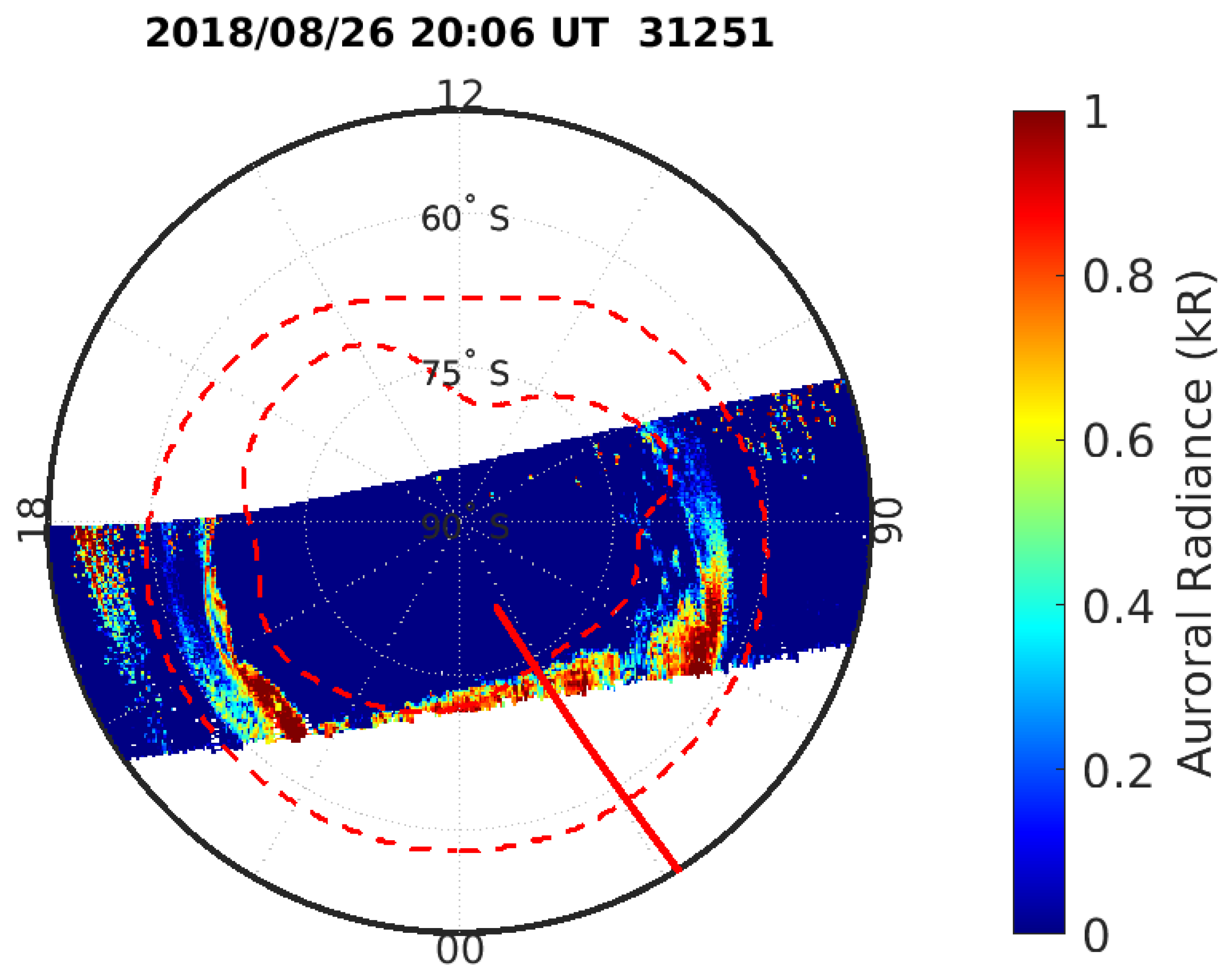
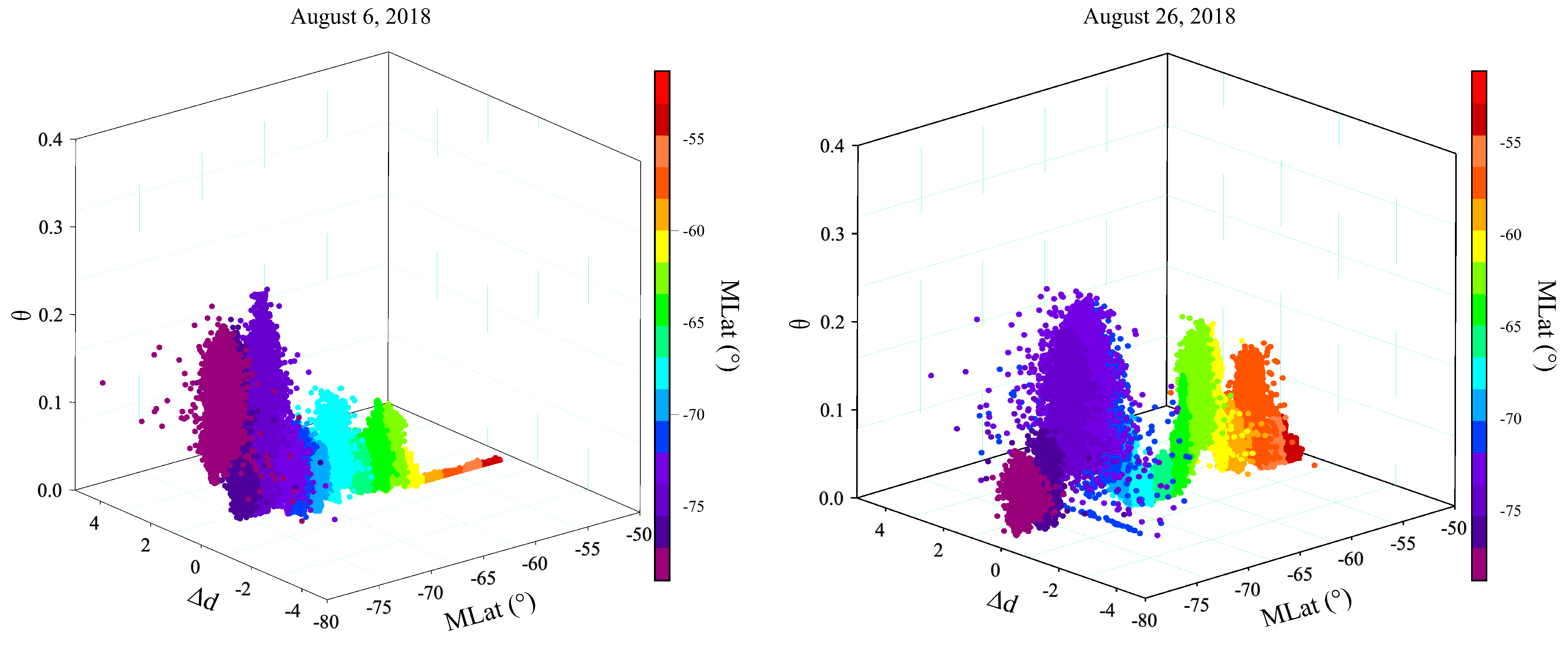
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AACGM | Altitude Adjustment Corrected Geomagnetic |
| AO | auroral oval |
| AE | auroral electrojet |
| CSES | China Seismo-Electromagnetic Satellite |
| DMSP | Defense Meteorological Satellite Program |
| EFD | electric field detector |
| ELF | Extremely-Low-Frequency |
| FACs | field-aligned currents |
| LBHL | Lyman-Birge-Hopfield long |
| LT | local time |
| MLat | magnetic latitude |
| MLT | Magnetic Local Time |
| SSUSI | Special Sensor Ultraviolet Spectrographic Imager |
| ULF | Ultra-Low-Frequency |
| UT | Universal Time |
References
- Liu, J.; Nakamura, T.; Liu, L.; Wang, W.; Balan, N.; Nishiyama, T.; Hairston, M.R.; Thomas, E. Formation of polar ionospheric tongue of ionization during minor geomagnetic disturbed conditions. J. Geophys. Res. Space Phys. 2015, 120, 6860–6873. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Liu, J.; Zheng, Z.; He, Y.; Gao, J.; Sun, L.; Zhong, Y. Dynamics of the tongue of ionizations during the geomagnetic storm on 7 September 2015. J. Geophys. Res. Space Phys. 2021, 126, e2020JA029038. [Google Scholar] [CrossRef]
- Dang, T.; Lei, J.; Wang, W.; Burns, A.; Zhang, B.; Zhang, S.R. Suppression of the polar tongue of ionization during the 21 August 2017 solar eclipse. Geophys. Res. Lett. 2018, 45, 2918–2925. [Google Scholar] [CrossRef]
- Kelly, M.C. The Earth’s Ionosphere: Plasma Physics and Electrodynamics, 2nd ed.; Academic Press Inc.: San Diego, CA, USA, 2009. [Google Scholar]
- Kintner, P.M., Jr. Observations of velocity shear driven plasma turbulence. J. Geophys. Res. 1976, 81, 5114–5122. [Google Scholar] [CrossRef]
- Tam, S.W.Y.; Chang, T.; Kintner, P.M.; Klatt, E. Intermittency analyses on the SIERRA measurements of the electric field fluctuations in the auroral zone. Geophys. Res. Lett. 2005, 32, L05109. [Google Scholar] [CrossRef]
- Golovchanskaya, I.V.; Ostapenko, A.A.; Kozelov, B.V. Relationship between the high-latitude electric and magnetic turbulence and the Birkeland field-aligned currents. J. Geophys. Res. 2006, 111, A12301. [Google Scholar] [CrossRef]
- Abel, G.A.; Freeman, M.P.; Chisham, G. IMF clock angle control of multifractality in ionospheric velocity fluctuations. Geophys. Res. Lett. 2009, 36, L19102. [Google Scholar] [CrossRef]
- Gurnett, D.A.; Huff, R.L.; Menietti, J.D.; Burch, J.L.; Winningham, J.D.; Shawhan, S.D. Correlated low-frequency electric and magnetic noise along the auroral field lines. J. Geophys. Res. 1984, 89, 8971–8985. [Google Scholar] [CrossRef]
- Weimer, D.R.; Goertz, C.K.; Gurnett, D.A.; Maynard, N.C.; Burch, J.L. Auroral zone electric fields from DE 1 and 2 at magnetic conjunctions. J. Geophys. Res. 1985, 90, 7479–7494. [Google Scholar] [CrossRef]
- Parkinson, M.L. Dynamical critical scaling of electric field fluctuations in the greater cusp and magnetotail implied by HF radar observations of F-region Doppler velocity. Ann. Geophys. 2006, 24, 689–705. [Google Scholar] [CrossRef]
- Heppner, J.P.; Liebrecht, M.C.; Maynard, N.C.; Pfaff, R.F. High-latitude distributions of plasma waves and spatial irregularities from DE 2 alternating current electric field observations. J. Geophys. Res. 1993, 98, 1629–1652. [Google Scholar] [CrossRef]
- Abel, G.A.; Freeman, M.P.; Chisham, G.; Watkins, N.W. Investigating turbulent structure of ionospheric plasma velocity using the Halley SuperDARN radar. Nonlinear Process. Geophys. 2007, 14, 799–809. [Google Scholar] [CrossRef]
- Johnson, E.S.; Heelis, R.A. Characteristics of ion velocity structure at high latitudes during steady southward interplanetary magnetic field conditions. J. Geophys. Res. 2005, 110, A12301. [Google Scholar] [CrossRef]
- Golovchanskaya, I.V. On the seasonal variation of electric and magnetic turbulence at high latitudes. Geophys. Res. Lett. 2007, 34, L13103. [Google Scholar] [CrossRef]
- Matsuo, T.; Richmond, A.D. Effects of high-latitude ionospheric electric field variability on global thermospheric Joule heating and mechanical energy transfer rate. J. Geophys. Res. 2008, 113, A07309. [Google Scholar] [CrossRef]
- Consolini, G.; Quattrociocchi, V.; D’Angelo, G.; Alberti, T.; Piersanti, M.; Marcucci, M.F.; De Michelis, P. Electric Field Multifractal Features in the High-Latitude Ionosphere: CSES-01 Observations. Atmosphere 2021, 12, 646. [Google Scholar] [CrossRef]
- Zhang, H.; Zong, Q.; Connor, H.; Delamere, P.; Facskó, G.; Han, D.; Hasegawa, H.; Kallio, E.; Kis, Á.; Le, G.; et al. Dayside Transient Phenomena and Their Impact on the Magnetosphere and Ionosphere. Space Sci. Rev. 2022, 218, 40. [Google Scholar] [CrossRef]
- Faranda, D.; Messori, G.; Yiou, P. Diagnosing concurrent drivers of weather extremes: Application to warm and cold days in North America. Clim. Dyn. 2020, 54, 2187–2201. [Google Scholar] [CrossRef]
- Faranda, D.; Messori, G.; Yiou, P. Dynamical proxies of North Atlantic predictability and extremes. Sci. Rep. 2017, 7, 41278. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Yuan, S.; Wang, L.; Cao, J.; Huang, J.; Zhu, X.; Piergiorgio, P.; Dai, J. The state-of-the-art of the China Seismo-Electromagnetic Satellite mission. Sci. China E Technol. Sci. 2018, 61, 634–642. [Google Scholar] [CrossRef]
- Huang, J.; Lei, J.; Li, S.; Zeren, Z.; Li, C.; Zhu, X.; Yu, W. The Electric Field Detector (EFD) onboard the ZH-1 satellite and first observational results. Earth Planet. Phys. 2018, 2, 469–478. [Google Scholar] [CrossRef]
- Consolini, G.; De Michelis, P.; Alberti, T.; Giannattasio, F.; Coco, I.; Tozzi, R.; Chang, T. On the multifractal features of low-frequency magnetic field fluctuations in the field-aligned current ionospheric polar regions: Swarm observations. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027429. [Google Scholar] [CrossRef]
- Papini, E.; Piersanti, M.; D’Angelo, G.; Cicone, A.; Bertello, I.; Parmentier, A.; Diego, P.; Ubertini, P.; Consolini, G.; Zhima, Z. Detecting the Auroral Oval through CSES-01 Electric Field Measurements in the Ionosphere. Remote Sens. 2023, 15, 1568. [Google Scholar] [CrossRef]
- Davis, T.N.; Sugiura, M. Auroral electrojet activity index AE and its universal time variations. J. Geophys. Res. 1966, 71, 785–801. [Google Scholar] [CrossRef]
- Kamide, Y.; Rostoker, G. What Is the Physical Meaning of the AE Index? EOS Trans. 2004, 85, 188–192. [Google Scholar] [CrossRef]
- Chaston, C.; Salem, C.; Bonnell, J.; Carlson, C.; Ergun, R.; Strangeway, R.; McFadden, J.P. The turbulent Alfvénic aurora. Phys. Rev. Lett. 2008, 100, 175003. [Google Scholar] [CrossRef]
- Tchen, C.; Pecesli, H.; Larsen, S.E. Strong turbulence in low-β plasmas. Plasma Phys. 1980, 22, 817. [Google Scholar] [CrossRef]
- Finlay, C.C.; Kloss, C.; Olsen, N.; Hammer, M.D.; Tøffner-Clausen, L.; Grayver, A.; Kuvshinov, A. The CHAOS-7 geomagnetic field model and observed changes in the South Atlantic Anomaly. Earth Planets Space 2020, 72, 156. [Google Scholar] [CrossRef]
- Lucarini, V.; Faranda, D.; Wouters, J.; Kuna, T. Towards a General Theory of Extremes for Observables of Chaotic Dynamical Systems. J. Stat. Phys. 2014, 154, 723–750. [Google Scholar] [CrossRef]
- Moreira Freitas, A.C.; Milhazes Freitas, J.; Todd, M. Extremal Index, Hitting Time Statistics and periodicity. arXiv 2010, arXiv:1008.1350. [Google Scholar]
- Lucarini, V.; Faranda, D.; Wouters, J. Universal Behaviour of Extreme Value Statistics for Selected Observables of Dynamical Systems. J. Stat. Phys. 2012, 147, 63–73. [Google Scholar] [CrossRef]
- Lucarini, V.; Faranda, D.; de Freitas, A.C.G.M.M.; de Freitas, J.M.M.; Holland, M.; Kuna, T.; Nicol, M.; Todd, M.; Vaienti, S. Extremes and Recurrence in Dynamical Systems; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Faranda, D.; Messori, G.; Alberti, T.; Alvarez-Castro, C.; Caby, T.; Cavicchia, L.; Coppola, E.; Donner, R.; Dubrulle, B.; Galfi, V.M.; et al. A statistical physics and dynamical systems perspective on geophysical extreme events. arXiv 2023, arXiv:2309.15393. [Google Scholar] [CrossRef]
- Alberti, T.; Florindo, F.; Rohling, E.J.; Lucarini, V.; Faranda, D. Dimensional analysis identifies contrasting dynamics of past climate states and critical transitions. arXiv 2023, arXiv:2309.12693. [Google Scholar] [CrossRef]
- Süveges, M. Likelihood estimation of the Extremal index. Extremes 2007, 10, 41–55. [Google Scholar] [CrossRef]
- Moloney, N.R.; Faranda, D.; Sato, Y. An overview of the extremal index. Chaos 2019, 29, 022101. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 2013, 10, 2. [Google Scholar] [CrossRef]
- Shaikh, D.; Shukla, P. 3D simulations of fluctuation spectra in the Hall-MHD plasma. Phys. Rev. Lett. 2009, 102, 045004. [Google Scholar] [CrossRef]
- Galtier, S.; Buchlin, E. Multiscale Hall-magnetohydrodynamic turbulence in the solar wind. Astrophys. J. 2007, 656, 560. [Google Scholar] [CrossRef]
- Alexandrova, O.; Carbone, V.; Veltri, P.; Sorriso-Valvo, L. Small-scale energy cascade of the solar wind turbulence. Astrophys. J. 2008, 674, 1153. [Google Scholar] [CrossRef]
- Basu, S.; Basu, S.; MacKenzie, E.; Coley, W.; Sharber, J.; Hoegy, W. Plasma structuring by the gradient drift instability at high latitudes and comparison with velocity shear driven processes. J. Geophys. Res. Space Phys. 1990, 95, 7799–7818. [Google Scholar] [CrossRef]
- Kintner, P.M.; Seyler, C.E. The status of observations and theory of high latitude ionospheric and magnetospheric plasma turbulence. Space Sci. Rev. 1985, 41, 91–129. [Google Scholar] [CrossRef]
- Paxton, L.J.; Meng, C.I.; Fountain, G.H.; Ogorzalek, B.S.; Darlington, E.H.; Gary, S.A.; Goldsten, J.O.; Kusnierkiewicz, D.Y.; Lee, S.C.; Linstrom, L.A.; et al. SSUSI: Horizon-to-horizon and limb-viewing spectrographic imager for remote sensing of environmental parameters. In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; Ultraviolet Technology IV; Huffman, R.E., Ed.; SPIE: Bellingham, WA, USA, 1993; Volume 1764, pp. 161–176. [Google Scholar] [CrossRef]
- Paxton, L.J.; Schaefer, R.K.; Zhang, Y.; Kil, H. Far ultraviolet instrument technology. J. Geophys. Res. Space Phys. 2017, 122, 2706–2733. [Google Scholar] [CrossRef]
- D’Angelo, G.; Piersanti, M.; Pignalberi, A.; Coco, I.; De Michelis, P.; Tozzi, R.; Pezzopane, M.; Alfonsi, L.; Cilliers, P.; Ubertini, P. Investigation of the physical processes involved in gnss amplitude scintillations at high latitude: A case study. Remote Sens. 2021, 13, 2493. [Google Scholar] [CrossRef]
- Keskinen, M. The structure of the high-latitude ionosphere and magnetosphere. Johns Hopkins Apl Tech. Dig. 1984, 5, 154–158. [Google Scholar]
- Hunsucker, R.D.; Hargreaves, J.K. The High-Latitude Ionosphere and Its Effects on Radio Propagation; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quattrociocchi, V.; De Michelis, P.; Alberti, T.; Papini, E.; D’Angelo, G.; Consolini, G. Characterization of Electric Field Fluctuations in the High-Latitude Ionosphere Using a Dynamical Systems Approach: CSES-01 Observations. Remote Sens. 2024, 16, 3919. https://doi.org/10.3390/rs16213919
Quattrociocchi V, De Michelis P, Alberti T, Papini E, D’Angelo G, Consolini G. Characterization of Electric Field Fluctuations in the High-Latitude Ionosphere Using a Dynamical Systems Approach: CSES-01 Observations. Remote Sensing. 2024; 16(21):3919. https://doi.org/10.3390/rs16213919
Chicago/Turabian StyleQuattrociocchi, Virgilio, Paola De Michelis, Tommaso Alberti, Emanuele Papini, Giulia D’Angelo, and Giuseppe Consolini. 2024. "Characterization of Electric Field Fluctuations in the High-Latitude Ionosphere Using a Dynamical Systems Approach: CSES-01 Observations" Remote Sensing 16, no. 21: 3919. https://doi.org/10.3390/rs16213919
APA StyleQuattrociocchi, V., De Michelis, P., Alberti, T., Papini, E., D’Angelo, G., & Consolini, G. (2024). Characterization of Electric Field Fluctuations in the High-Latitude Ionosphere Using a Dynamical Systems Approach: CSES-01 Observations. Remote Sensing, 16(21), 3919. https://doi.org/10.3390/rs16213919







