Field Programmable Gate Array (FPGA) Implementation of Parallel Jacobi for Eigen-Decomposition in Direction of Arrival (DOA) Estimation Algorithm

Abstract

The eigen-decomposition of a covariance matrix is a key step in the Direction of Arrival (DOA) estimation algorithms such as subspace classes. Eigen-decomposition using the parallel Jacobi algorithm implemented on FPGA offers excellent parallelism and real-time performance. Addressing the high complexity and resource consumption of the traditional parallel Jacobi algorithm implemented on FPGA, this study proposes an improved FPGA-based parallel Jacobi algorithm for eigen-decomposition. By analyzing the relationship between angle calculation and rotation during the Jacobi algorithm decomposition process, leveraging parallelism in the data processing, and based on the concepts of time-division multiplexing and parallel partition processing, this approach effectively reduces FPGA resource consumption. The improved parallel Jacobi algorithm is then applied to the classic DOA estimation algorithm, the MUSIC algorithm, and implemented on Xilinx’s Zynq FPGA. Experimental results demonstrate that this parallel approach can reduce resource consumption by approximately 75% compared to the traditional method but introduces little additional time consumption. The proposed method in this paper will solve the problem of great hardware consumption of eigen-decomposition based on FPGA in DOA applications.

1. Introduction

Spatial spectrum estimation involves arranging multiple antennas or sensors at various spatial locations to form an array, utilizing the array to receive and process spatial signals. By calculating the energy distribution of the signal in various spatial directions, a spatial spectrum is obtained to realize the estimation of wave arrival direction. Therefore, spatial spectrum estimation is also known as Direction of Arrival (DOA) estimation. In recent years, spatial spectrum estimation has been widely applied in communication, radar, exploration, medical treatment, and aerospace systems, playing a crucial role in civilian, defense, and other fields [1,2,3].

The widespread application requirements have promoted the development of DOA estimation, leading to the emergence of numerous algorithms to date. Array-based DOA algorithms primarily include beam forming, nonlinear spectrum estimation, subspace-based methods, subspace fitting methods, etc. [4,5], such as Conventional Beam Forming (CBF), Minimum Variance Distortionless Response (MVDR), Multiple Signal Classification (MUSIC), Estimating Signal Parameter Via Rotational Invariance Techniques (ESPRIT), Maximum Likelihood (ML) methods, and various derivative algorithms. In comparison, CBF algorithms are difficult to implement in practical applications, and nonlinear spectrum estimation techniques have less accuracy. Subspace fitting algorithms are suitable for low Signal-to-Noise Ratio (SNR) and few snapshots, but they require a large amount of computation and numerous fitting optimization algorithms. Subspace-based algorithms have higher accuracy and relatively lower computational demand than subspace fitting algorithms. Therefore, subspace-based algorithms are widely applied in various fields [6,7]. The concept of subspace-based algorithms is to perform eigen-decomposition on the covariance matrix of received signals from an antenna array and divide the array space into signal subspace and noise subspace. Then, by exploiting the orthogonality of these two subspaces, a pencil-shaped spectral peak is constructed to determine the direction of arrival of the signals [8,9,10].

With the development of DOA estimation, real-time processing of array signals imposes high demands for the data processing capabilities of hardware devices. The implementation of high-performance DOA estimation on platforms such as CPU, GPU, FPGA, and DSP has attracted significant attention [11]. FPGA, known for its parallel processing, ease of implementation, high speed, strong flexibility, and abundant resources, has become a major trend in implementing DOA algorithms [12]. Implementing subspace algorithms based on FPGA obtains subspaces utilizing covariance matrix decomposition; thus, covariance matrix decomposition technology is the most complex module in the implementation of subspace algorithms [13,14].

There are two typical methods for the implementation of eigen-decomposition based on FPGA: QR decomposition and Jacobi decomposition [15]. Compared to Jacobi de composition, QR has a faster decomposition speed [16]. However, Jacobi decomposition has higher accuracy [17]. Meanwhile, Jacobi decomposition has high parallelism, which brings significant advantages when implemented on FPGA. The systolic array structure proposed by Brent and Luk [18] is an effective method for implementing the parallel Jacobi algorithm. However, the typical systolic array structure requires significant hardware resources, particularly unfriendly to the decomposition of high-order matrices.

In response to the high complexity of implementing eigen-decomposition on FPGA, many scholars have been conducting related research. Ignacio Bravo, etc. [19] proposed a solution to obtain the eigenvalues and eigenvectors using the reconfigurable hardware on FPGA in the principal component analysis (PCA) technique. This method built on the systolic array structure was independent of the matrix size, reducing the resource consumption in the traditional method. However, the paper did not provide specific hardware resources, time, etc. Gopinath Vasanth Mahale [20] implemented covariance decomposition of a 50 × 50 matrix on the Virtex-5 FPGA platform, but the time consumption was difficult to estimate, and the decomposition accuracy was not high. Chi-Chia Sun and others [21] implemented the parallel unitary-rotate Jacobi method on Network-on-Chip. ZHANG Shuiping and others [22] proposed an implementation scheme for eigenvalue decomposition and compared the area occupied by the implementation schemes under different word lengths, but did not provide the decomposition accuracy. The accelerated Jacobi method proposed by Zhiguo Shi et al. [23] had been experimentally verified to achieve a speed increase of more than two-fold, but at the cost of nearly doubling the resource consumption. Ridha Ghayoula et al. [24] introduced the implementation of the cyclic Jacobi algorithm in terms of hardware architecture implementation. A new low-latency and highly accurate VLSI architecture for computing eigenvalues and eigenvectors of real symmetric matrices was proposed by Rahul Sharma et al. [25]. Chih-Wei Liu et al. [26] used the cyclic Jacobi method with a neural network model to reduce the latency. In addition, Ali Ibrahim and Xiao-Wei Zhang et al. [27,28] carried out a study on one-sided Jacobi algorithm implementation of eigen-decomposition. Uzma M. Butt et al. [9] simplified the implementation complexity of eigen-decomposition and the MUSIC algorithm in terms of algorithmic structure.

To achieve a balance between resources, time, and accuracy, enabling the eigen-decomposition module to be better applied in DOA estimation, this paper proposes an improved parallel Jacobi algorithm. By using time-division multiplexing and parallel partition processing methods, it can significantly reduce hardware resource consumption with minimal time increase. An FPGA-based implementation scheme for the MUSIC algorithm is presented. The proposed method is applied to the MUSIC algorithm. A detailed analysis of the MUSIC algorithm and the proposed feature decomposition method is conducted from the perspectives of resources, time, and accuracy.

The remaining content of this paper is as follows. Section 2 introduces key algorithms and concepts in eigen-decomposition, including the Jacobi algorithm, systolic array structure, and the Coordinate Rotation Digital Computer (CORDIC) algorithm. Section 3 provides a detailed explanation of the improved parallel Jacobi method using time-division multiplexing and parallel partition processing and compares the advantages of our approach over traditional methods. In Section 4, we apply the proposed algorithm to the MUSIC algorithm, validating the feasibility of the approach in terms of resource consumption, execution time, and decomposition accuracy. The final section is a summary of the entire paper.

2. Key Algorithms in Eigen-Decomposition

The Jacobi algorithm is a classic method for the implementation of matrix eigen-decomposition. The principle of Jacobi’s algorithm is to make the matrix tend to be diagonalized by constant orthogonal transformations, and the diagonal elements are the eigenvalues [29]. There are two ways to realize the Jacobi algorithm: serial and parallel decomposition. Serial decomposition can either cyclically scan all non-diagonal elements in sequence or select the largest non-diagonal element each time based on the maximum principle for elimination. Parallel decomposition utilizes a systolic array structure to execute several units processing simultaneously in parallel, fully utilizing the parallel advantages of the Jacobi algorithm [30]. There are nonlinear operations in the orthogonal rotation transformations, and the CORDIC [31] algorithm could be an excellent solution. Therefore, the principle of the Jacobi algorithm, the concept of systolic array structure, and the CORDIC algorithm are introduced in the section.

2.1. Jacobi Algorithm

Assuming A is an n × n order real symmetric matrix, then an orthogonal transformation matrix G exists such that

G^T AG = diag (λ₁, λ₂, ⋯, λ_n)

(1)

where (λ₁, λ₂, ⋯, λ_n) are the eigenvalues. The orthogonal transformation matrix G is composed of the multiplication of many rotation matrices; it can be written as

G = G1 G2 ⋯ Gm

(2)

Assuming that the orthogonal rotation matrix in the (p, q) plane is G_k with an angle of θ, then

G_k^T(θ)A_kG_k (θ) = A_{k + 1}

(3)

G_k is denoted as

$${\mathrm{G}}_k(\theta )=\left[\begin{array}{ccccccc}1& & & & & & 0\\ & \ddots & & & & & \\ & & \cos \theta & & -\sin \theta & & \\ & & & \ddots & & & \\ & & \sin \theta & & \cos \theta & & \\ & & & & & \ddots & \\ 0& & & & & & 1\end{array}\right]$$

(4)

The matrix A after (k − 1) rotations can be written as

$${\mathrm{A}}_k=\left[\begin{array}{ccc}{{\mathrm{a}}_{11}}^{\left(k\right)}& \dots & {{\mathrm{a}}_{1n}}^{\left(k\right)}\\ ⋮& \ddots & ⋮\\ {{\mathrm{a}}_{n1}}^{\left(k\right)}& \dots & {{\mathrm{a}}_{\mathit{nn}}}^{\left(k\right)}\end{array}\right]$$

(5)

Then, the values of the elements of the matrix A will change after the kth orthogonal transformation as follows, where a_pq denotes the elements of the pth row and qth column of the matrix A_{k + 1}.

a_pp^{(k + 1)} = a_pp^(k)cos²θ + a_qq^(k)sin²θ + 2a_pq^(k)sinθcosθ
a_qq^{(k + 1)} = a_qq^(k)cos²θ + a_pp^(k)sin²θ − 2a_pq^(k)sinθcosθ
a_pq^{(k + 1)} = a_qp^{(k + 1)} = a_pq^(k)cos²θ − a_pq^(k)sin²θ + a_qq^(k)sinθcosθ − a_pp^(k)sinθcosθ
a_pi^{(k + 1)} = a_ip^{(k + 1)} = a_ip^(k)cosθ + a_iq^(k)sinθ, i ≠ p,q
a_qi^{(k + 1)} = a_iq^{(k + 1)} = a_iq^(k)cosθ − a_ip^(k)sinθ, i ≠ p,q

(6)

In order to make the non-diagonal elements a_pq^{(k + 1)}, a_qp^{(k + 1)} rotated to 0, θ should be

$$\theta ={\displaystyle \frac{1}{2}}\arctan {\displaystyle \frac{2{{\mathrm{a}}_{\mathit{pq}}}^{\left(k\right)}}{{{\mathrm{a}}_{\mathit{pp}}}^{\left(k\right)}-{{\mathrm{a}}_{\mathit{qq}}}^{\left(k\right)}}}$$

(7)

Therefore, calculating the angle θ and then non-diagonal elements will be removed by rotating the matrix.

2.2. The Systolic Array Structure

The systolic array was proposed by Brent and Luk based on the fact that only the pth and qth row and column elements change in each rotational transformation. Therefore, the matrix can be divided into [n/2] × [n/2] units to compute in parallel. For a matrix A of order 8, the structure of the systolic array is shown in Figure 1. Since A_8×8 is a real symmetric matrix, only the upper triangular elements need to be computed. As shown in the figure, a total of four diagonal units and six non-diagonal units are included; each diagonal unit contains three elements, and each non-diagonal unit contains four elements.

When processing in parallel, the rotation angles of the diagonal units are first calculated, then all units will be rotated with this angle accordingly, which will realize all the non-diagonal elements of the diagonal units removed. Then, through data exchange, transfer the new matrix’s non-diagonal elements into the non-diagonal positions of the diagonal units, iterating to eliminate them until all non-diagonal elements are reduced to 0.

2.3. CORDIC Algorithm

CORDIC is an iterative algorithm for computers and is a good solution to realize the calculation of the arctangent value and matrix rotation as mentioned above [32]. One available approach is using a lookup table to iteratively compute the arctangent values, and using sine and cosine values, which can be obtained easily to compute, and then matrix rotation can be performed by using multipliers. However, this method will need a great deal of Block RAM (BRAM) and multiplier resources, and the computational accuracy is limited. IP cores in FPGA can be a promising method that can realize higher accuracy [14]. Considering the demands of higher accuracy and less resource consumption, the CORDIC IP core provided by Xilinx is adopted in this paper to compute eigen-decomposition for the MUSIC algorithm.

3. Parallel Jacobi Method

3.1. Traditional Parallel Implementation Method

As mentioned earlier, serial implementation of eigen-decomposition requires eliminating each non-diagonal element in a certain order. One iteration round usually cannot meet the accuracy requirements of eigen-decomposition. Iterations also double the time required. For high-order matrix eigen-decomposition with a significant number of non-diagonal elements, the execution time will be a huge disaster.

The parallel implementation of eigen-decomposition can address the time consumption issue in the serial decomposition. Taking an 8-order matrix, for example, Figure 1 shows the systolic array structure of an 8-order matrix. Parallel processing can eliminate four non-diagonal elements at a time, fully leveraging the advantages of parallelism. However, it also brings significant resource consumption issues. Firstly, we need to calculate the arctangent values of four diagonal elements in parallel. This requires four arctangent-mode CORDIC IP cores. Then, we need to rotate 10 units. Each unit’s rotation requires 2 rotation-mode CORDIC IP cores, so rotating 10 units in parallel requires 20 rotation-mode CORDIC IP cores. These are the IP core resources needed to obtain the eigenvalues of an 8-order matrix. In addition, parallel computation of eigenvector rotations is also essential. The resource utilization of the traditional parallel approach is very low. Moreover, it will be worse when implementing high-order eigen-decomposition on FPGA-based platforms.

3.2. Improved Parallel Jacobi Method

To solve this problem, we propose an improved parallel Jacobi implementation method in this paper. By utilizing the concepts of time-division multiplexing and parallel partition processing, resource utilization can be improved. Without introducing additional execution time, the resource pressure of traditional parallel approaches is reduced. The specific approach is as follows.

Firstly, according to the implementation process of the Jacobi algorithm, computation of the arctangent values is necessary for the diagonal elements. The diagonal units use one CORDIC IP core to compute arctangent values serially.

Secondly, matrix rotation of the diagonal units will use IP core resources separately at different times. Another concept for reuse and parallel processing is that the non-diagonal units can also be partitioned based on the arctangent values by analyzing the relationship between the arctangent values and the non-diagonal units. Computation can occur parallelly in different regions, and resources in the same region can be reused at different times.

Thirdly, considering the matching of the timing sequence between the rotation of the eigenvector matrix and the rotation of the covariance matrix, we use a single IP core to serially rotate the eigenvector matrix and execute it in parallel with the two rotations of the covariance matrix.

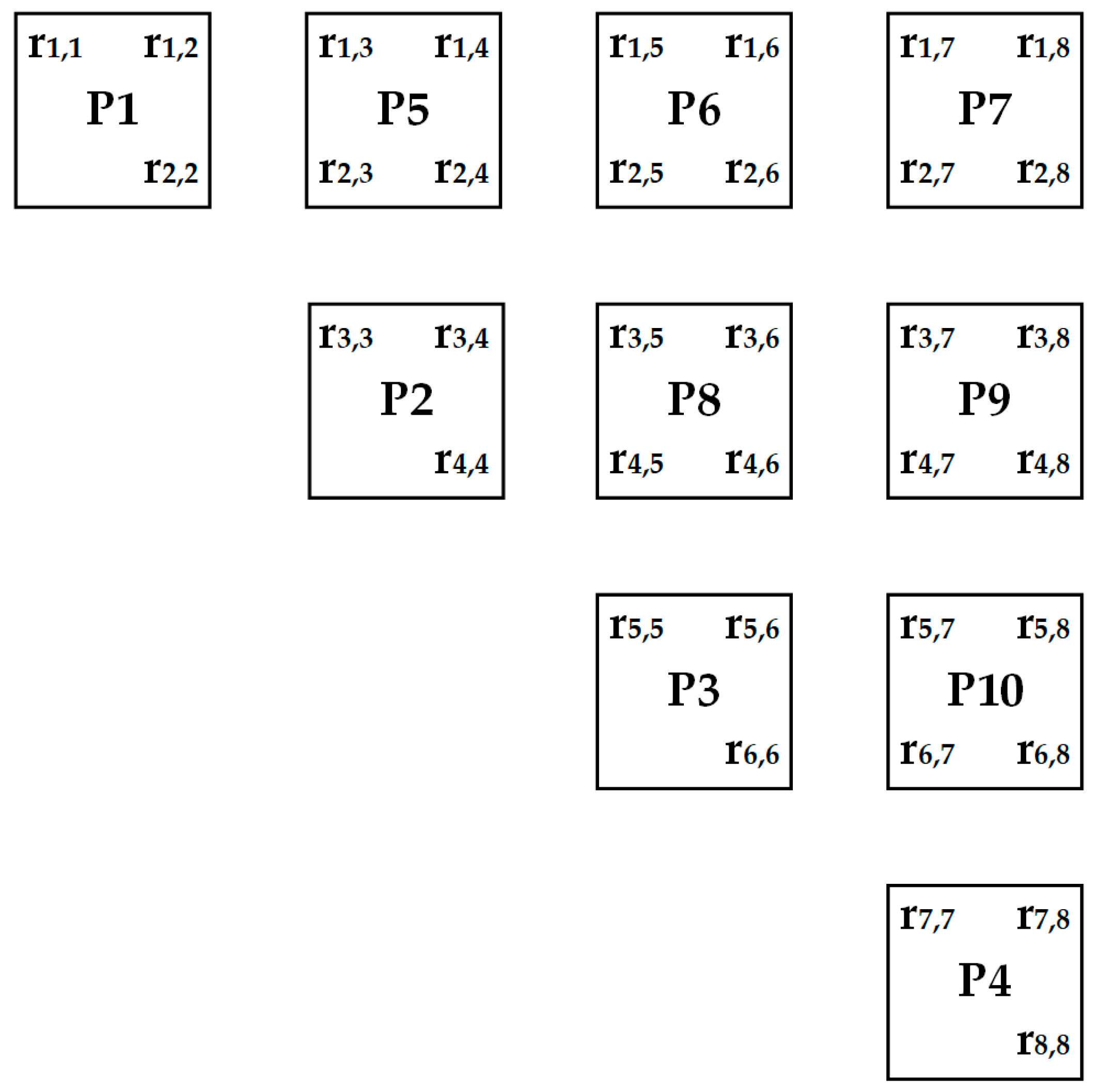
The concept of serially calculating the arctangent values and rotations for diagonal units is straightforward. The specific partition processing for non-diagonal units is described as follows. In the systolic array structure illustrated in Figure 1, taking diagonal element P2 as an example, compute the arctangent value as θ₂. During matrix rotation, not only is the diagonal unit P2 affected, but the elements in the third and fourth rows as well as columns are also involved. Therefore, the P2 unit needs to transmit θ₂ to the non-diagonal units P5/P8/P9. Similarly, the P1 unit needs to transmit θ₁ to the non-diagonal units P5/P6/P7. Obviously, the P5 unit needs to undergo two rotations based on θ₁ and θ₂. This principle is also evident in Equation (5); all units require two rotations, not only the P5 unit. In the first rotation, units P5/P6/P7 need to rotate according to the angle θ₁. Units P8/P9 need to rotate according to the angle θ₂. Unit P10 needs to rotate according to the angle θ₃. Therefore, based on the different rotation angles, the six non-diagonal units are divided into part1/part2/part3 as shown in Figure 2a. In the second rotation, the non-diagonal units adopt different angles. The partitioning is shown in Figure 2b. Although the partitioning is different for the two rotations, the part structure remains symmetrical. This approach avoids complex logic in data transmission; at the same time, the symmetrical structure of parts enables the reuse of CORDIC resources. During each rotation, the units within each part rotate serially, while different parts rotate in parallel. Moreover, the non-diagonal units after partitioning can achieve timing synchronization with the diagonally rotated units (P1, P2, P3, P4) in a serial manner, avoiding the waste of timing resources.

According to the above method, when calculating the arctangent values for the four diagonal units, we only use one arctangent-mode IP core. When performing rotations, the four diagonal units use two rotation-mode IP cores. Each of the six non-diagonal units in each region uses two IP cores. For eigenvector rotation, we only use one IP core.

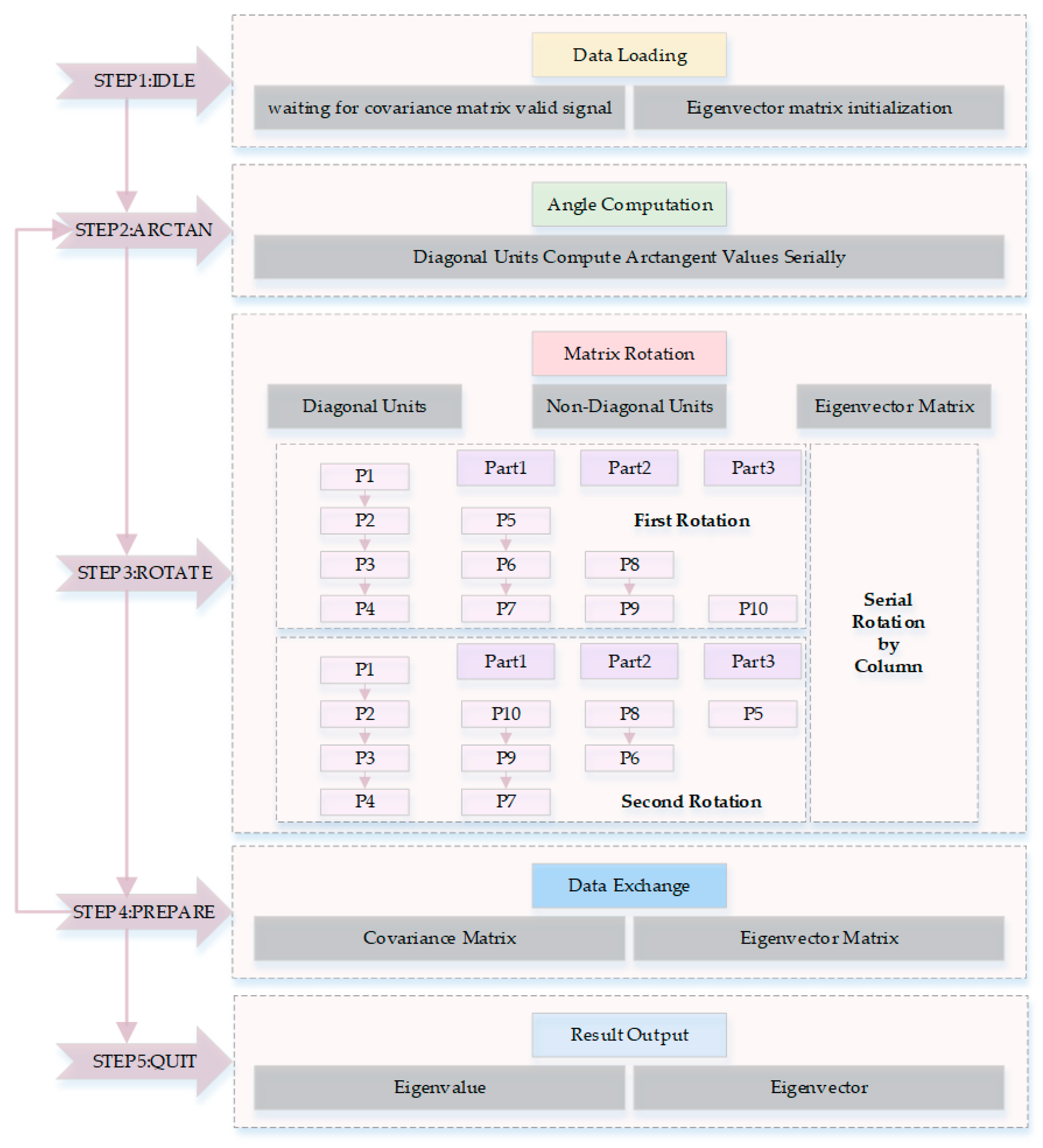
The process of eigen-decomposition of the covariance matrix and computation of eigenvectors is illustrated in Figure 3. The computation is performed in parallel between columns. Specifically, it can be divided into five steps.

• Loading data. Waiting for the computation result of the covariance matrix. When the covariance matrix is valid, initialize the eigenvector matrix to the identity matrix. Switching to the Arctangent State.
• Calculate arctangent values. Compute the arctangent values for the four diagonal units of the matrix sequentially. Store the angle values and Switch to the Rotate State.
• Rotate matrix. Diagonal units, non-diagonal units, and the eigenvector matrix are rotated in parallel. Four diagonal units rotate sequentially, and after the first rotation, the coordinate data input values of the IP core are modified before the second rotation. Non-diagonal units are divided into three parts for parallel rotation. After the first rotation, both the coordinate data and phase data input values of the IP core are modified before the second rotation. The eigenvector matrix only requires one rotation, where column data and arctangent angles are sequentially chosen based on the structure corresponding to the systolic array units of the covariance matrix for rotation. The next step is the Prepare State.
• Exchange Data. The covariance matrix and eigenvector matrix data are updated by using the Round-Robin forward exchange sequence. If the accuracy is not enough, the process continues iterating by transitioning to the Arctangent State; otherwise, it transfers to the Quit State.
• Output Data. Obtain eigenvalues and eigenvector matrix.

3.3. Comparison of Two Methods

Table 1. CORDIC IP core consumption between the traditional systolic array method and our method.

Matrix Order	Method	Eigenvalue			Eigenvector	Difference
		Arctangent-Mode	Rotation-Mode		Rotation-Mode
			Diagonal Units	Non-Diagonal Units
8-order	Traditional	4	8	12	4-32	Almost 75%
	Our	1	2	6	1
12-order	Traditional	6	12	30	6-72	Almost 83.3%
	Our	1	2	10	1-2
16-order	Traditional	8	16	56	8-128	Almost 87.5%
	Our	1	2	14	2

provides a comparison of the usage of IP cores between our method and the traditional method. For an 8-order matrix, it’s obvious that our method can save nearly 75% of resources compared to the traditional parallel Jacobi algorithm. This greatly reduces the burden on FPGA caused by the traditional parallel algorithm.

When facing higher-order covariance matrix decompositions, our method exhibits even greater advantages. Taking an n-order matrix as an example, there would be (n/2) diagonal units and (n²/8 − n/4) non-diagonal units. With our method, we still only use one arctangent mode IP core and two rotation mode IP cores for the selection of diagonal units. The non-diagonal units are partitioned into part1-part(n/2 − 1), with each region utilizing two IP cores. Eigenvector rotation also needs one IP core. In comparison, the traditional parallel structure would require (n/2) arctangent-mode IP cores and (n²/4 + n/2) rotation-mode IP cores. Our method can save approximately 83.3% of resources when applied to 12-order matrices and about 87.5% of resources when applied to 16-order matrices. Therefore, our method will perform better when handling higher-order matrices.

From the perspective of the introduced time resources, it is mainly caused by serialization. Specifically, taking an 8-order matrix as an example, when we use a single IP core to serially calculate the arctangent value, it will take three additional clock cycles compared to the traditional method. The serial rotation of diagonal elements follows the same principle. The serial rotation of non-diagonal unit partitions matches the rotation of diagonal units. Similarly, the serial rotation of eigenvectors and the rotation of covariance matrices match. This means that each rotation round only introduces three clock cycles. Executing one round to eliminate four non-diagonal elements requires an additional 6 clock cycles. Data exchange during one sweep occurs over 7 rounds or 42 clock cycles. In general, performing three or four sweeps will almost bring all non-diagonal elements close to zero, equating to 126 or 168 clock cycles. Although the number of introduced clock cycles may seem substantial, they are negligible for high bit-width and high-order covariance matrix eigen-decomposition or DOA estimation. Compared to the 75% savings in area resources, the introduced time resources can be considered insignificant.

4. Experimentation and Verification

The MUSIC algorithm is a classical algorithm in DOA estimation. We used 8 sensors to form a uniform circular array for signal sampling and implemented two-dimensional DOA estimation using the MUSIC algorithm. We applied the improved parallel Jacobi method to the MUSIC algorithm and implemented it on FPGA to verify its effectiveness and performance. The project is implemented using the Verilog hardware description language for programming, and software tools such as Vivado 2018.3 and Modelsim 10.1c are utilized to develop the MUSIC algorithm, including processes such as RTL coding, simulation, synthesis, implementation, and testing. The analysis mainly focuses on three aspects: hardware resource consumption, execution time, and accuracy.

4.1. Implementation of the MUSIC Algorithm

Firstly, the implementation principle of the MUSIC algorithm is introduced. Assuming there are k narrowband signals incident at different angles in space, on a uniform circular array with n elements, and assuming the signals are independent, noise statistics are independent, and signals and noise are mutually independent, with a noise mean of 0, a variance of σ², and the array received signal X. The array received signal X can be written as

X = AS + N

(8)

where A is the array steering matrix, S is the signal source vector, and N is the noise. The array covariance matrix can be written as

R = E{XX^H} = AE{SS^H}A^H + E{NN^H} = AR_S A^H + σ²I

(9)

where R_S is a diagonal matrix, I is the identity matrix, E and ^H denote expectation and conjugate transpose. And performing eigen-decomposition on the matrix gives

R = U∑U^H = U_S∑_SU_S^H + U_N∑_NU_N^H

(10)

where ∑ = diag(λ₁, λ₂, ⋯, λ_n), arranged in sequential order, we get

λ₁ ≥ λ₂ ≥ ⋯ ≥ λ_k > λ_{k + 1} >⋯> λ_n = σ²

(11)

where U_S = [u₁, u₂, ⋯ u_k] is the signal subspace formed by the eigenvectors corresponding to the k signal eigenvalues, and U_N = [u_{k + 1}, u _{k + 2}, ⋯ u_n] is the noise subspace formed by the eigenvectors corresponding to the n-k noise eigenvalues. It can be proven that the space spanned by the steering vectors of the incoming signals and the signal subspace is the same space, while the signal subspace and noise subspace are orthogonal. However, the actual covariance matrix is obtained from a finite number of samples, denoted as $\tilde{\mathrm{R}}$ instead of R, resulting in

$$\stackrel{\mathrm{~}}{\mathrm{R}}={\displaystyle \frac{1}{L}}{\sum }_1^L\mathrm{X}{\mathrm{X}}^{\mathrm{H}}$$

(12)

where L is the number of sampled snapshots, performing eigen-decomposition on $\tilde{\mathrm{R}}$ results in the signal subspace and noise subspace. However, at this point, the two subspaces are not completely orthogonal, so a two-dimensional spectral scan function is constructed.

$${\mathrm{P}}_{\mathit{MUSIC}}(\theta ,\phi )={\displaystyle \frac{1}{{\mathrm{a}}^{\mathrm{H}}(\theta ,\phi ){\mathrm{U}}_N{\mathrm{U}}_N^{\mathrm{H}}\mathrm{a}(\theta ,\phi )}}$$

(13)

The angle corresponding to its peak value is the direction of arrival of the signal.

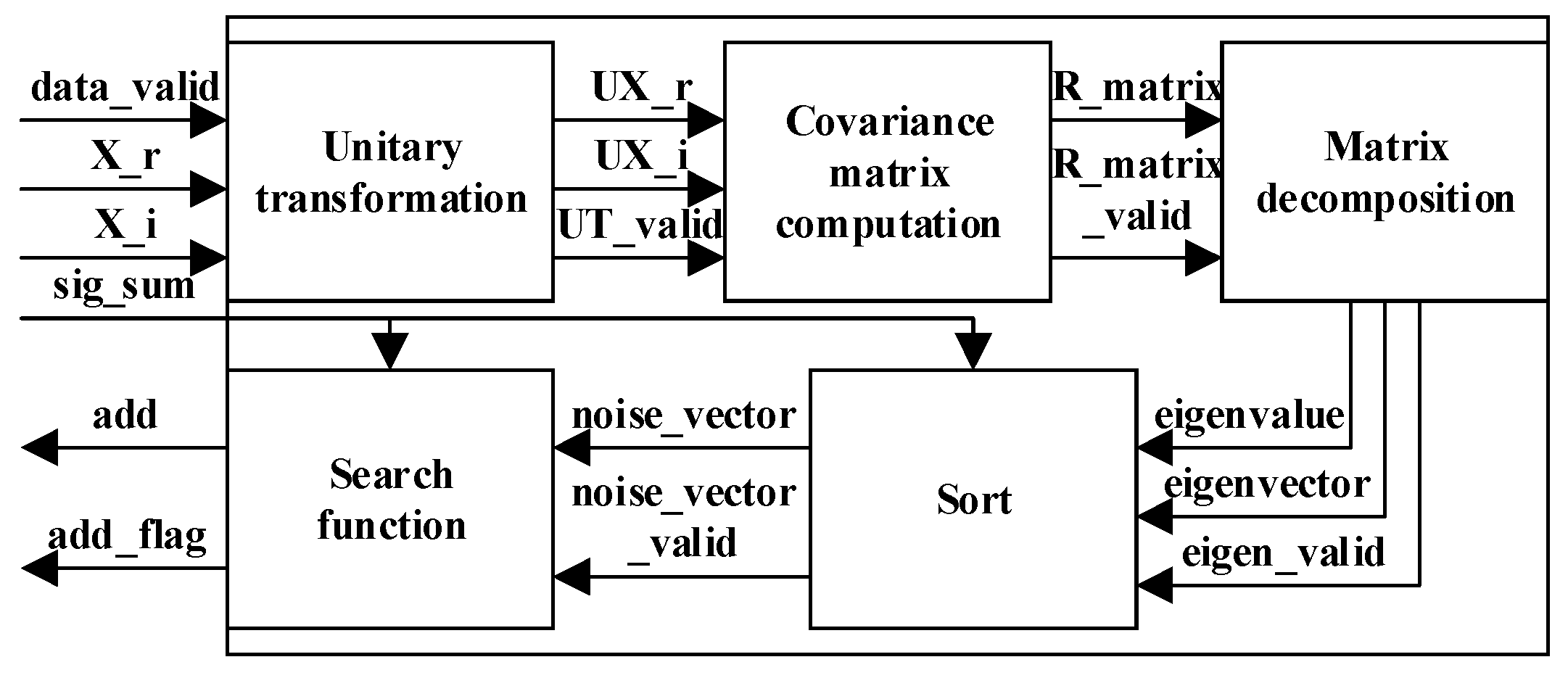
The block diagram of the FPGA-based implementation of the MUSIC algorithm is shown in Figure 4. The specific steps are as follows:

• Receive sampled complex signals and perform the unitary transformation. This enables subsequent covariance matrix decomposition and peak spectrum search to be conducted in the real domain.
• Calculate the 8-order covariance matrix. Real symmetric matrices only need the computation of the upper triangular matrix.
• Use our proposed method to decompose the covariance matrix and obtain eigenvalues and eigenvectors.
• Sort the eigenvalues to obtain the noise subspace.
• Perform spatial spectrum calculation and peak spectrum search to obtain two-dimensional estimated angles.

4.2. Resource Consumption

We perform synthesis of the code using the Vivado development environment.

Table 2. Resource allocation table for each module in the system.

Module	Slice LUTs	Slice Registers
Unitary Transformation	1161	267
Cov_matrix Computation	1506	6052
Matrix Decomposition	49,441	55,313
Sort	8319	4652
Peak Search	5888	4958

lists the resource allocation for each module of the MUSIC algorithm after synthesis. The covariance matrix decomposition module is the most complex in the MUSIC algorithm. As shown in the table, this module consumes the most resources.

We applied the proposed improved parallel Jacobi algorithm to the covariance matrix decomposition module of the MUSIC algorithm.

Table 3. Comparison of the implementation of the MUSIC algorithm and prior reported designs in terms of area.

Metrics	FPGA Series	Matrix Size	Bit-Width	Slice LUTs Resource	Slice Registers Resource
MUSIC in [23]	Virtex-7	8 × 8	32 bit	258,348	113,458
Our Work	Zynq	8 × 8	32 bit	66,315	71,242

shows the comparison of our work with reference [23] in terms of total resources. Both of our schemes used 8 elements to implement the MUSIC algorithm, and the data width was 32 bits. Our solution requires significantly fewer resources than that mentioned in reference [23]. The remaining modules in the MUSIC algorithm are primarily composed of a large number of addition and multiplication operations, so the main difference between our two schemes came from the covariance matrix decomposition module. Therefore, it could be seen that our proposed parallel Jacobi approach had advantages in terms of resources.

Furthermore, we also analyze the resource utilization of our proposed parallel Jacobi method, specifically in the module of covariance matrix decomposition. The covariance matrix decomposition module involves a large number of nonlinear operations and requires the use of the CORDIC algorithm. As mentioned above, our CORDIC algorithm utilizes the IP cores. One reason for this is that modules such as covariance matrix calculation and spatial spectrum computation will employ a significant number of multipliers; thus, the covariance matrix decomposition module should use DSP resources as little as possible. The IP core primarily occupies slice resources. According to the synthesis results, each rotation-mode IP core consumes 4658 slice LUTs and 4782 slice registers, and each arctangent-mode IP core consumes 3573 slice LUTs and 3504 slice registers.

Table 4. Comparison of the proposed method and prior reported designs in terms of area.

Metrics	Traditional Method	Method in [25]	Method in [22]	Our Method
FPGA Series	Zynq	Virtex-7	Virtex-5	Zynq
Matrix Size	8 × 8	8 × 8	8 × 8	8 × 8
Bit-width	32 bit	32 bit	16 bit	32 bit
Work Mode	Eigenvalue and Eigenvector	Eigenvalue and Eigenvector	Only Eigenvalue	Eigenvalue and Eigenvector
DSPs Resource	0	(-)	(-)	0
Slice LUTs Resource	167,294	122,127	50,436 ($)	49,441
Slice Registers Resource	175,811	14,418	67,248 ($)	55,313

($) indicates that the slices given in reference [22] are 8406, calculated based on each slice containing 6 LUTs and 8 registers. (-) indicates that it is not specified in the references.

compares our method, the approaches proposed in recent years, and traditional methods in terms of resource utilization. From Table 4, we can see our implementation and the designs in the traditional method, and [25] have the same matrix size, bit-width, and working mode. Design in reference [22] has less bit-width and only computes eigenvalues without Eigenvectors. Different working modes and bit-widths will have a significant impact on hardware resource consumption. The traditional method utilizes all units for parallel processing, and the eigenvector calculation requires a scheme with 4 rotation-mode IP cores. The approximate resources needed are as shown in the table. Our design employs the concept of partition reuse, saving approximately 75% of the slice resources compared to traditional structures. Using more CORDIC IP cores in the traditional structure would increase resource consumption in the FPGA. Reference [25] utilized a greater number of LUTs and fewer registers because of the extensive use of DSP resources. Our method avoids the use of DSP resources. The slice LUTs resource in our design is only 40% of the LUTs in the Reference [25], but the slice registers in our design are more. That is because the design in Reference [25] also used some hardware multiplexing technology to decrease resources. As is known, the structure of slice LUTs in FPGA is much more complex and occupies more area than the slice registers. Therefore, in the hardware consumption aspects, our design still has an advantage over Reference [25]. The design in Reference [22] only calculates eigenvalues with a 16-bit width, but the resource utilization still exceeds that of our method. Therefore, our approach holds a significant advantage in resource consumption.

4.3. Execution Time

The execution time of the MUSIC algorithm is mainly affected by two modules: the eigen-decomposition of the covariance matrix and the spatial spectrum calculation. The spatial spectrum calculation is mainly influenced by the stepping angle. The smaller the stepping angle, the more spatial spectrum values need to be calculated, resulting in a longer execution time for the MUSIC algorithm. Different direction-finding schemes may have different stepping search angles. Therefore, the execution time of the spatial spectrum calculation module is a subjective and flexible variable. Therefore, we only analyze the execution time of the eigen-decomposition module of the covariance matrix.

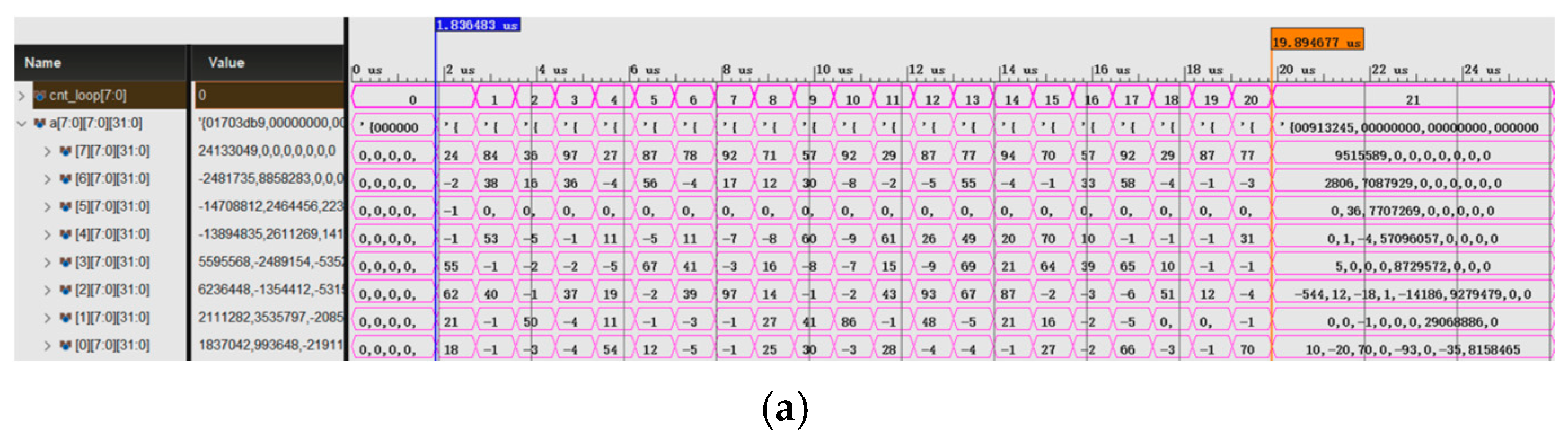
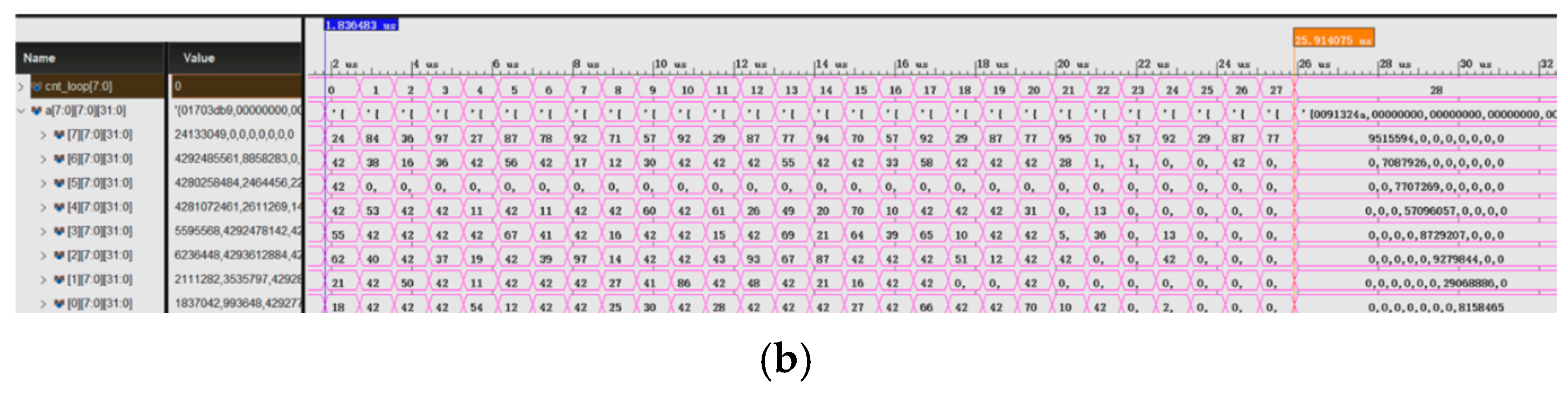
After placement and routing in FPGA, our design in FPGA can operate at the frequency of 150 MHz. Therefore, we simulated our design using the Vivado simulator at the frequency of 150 MHz. In order to balance execution time and decomposition accuracy, we compared the eigen-decomposition results of three sweeps and four sweeps, as shown in the right column in Figure 5. After three sweeps, which are 21 iterations, most of the non-diagonal elements are close to 0, taking 18 microseconds. After four sweeps, which are 28 iterations, the matrix has become a diagonal matrix, requiring 24 µs.

As shown in

Table 5. Comparison of the proposed method and prior reported designs in terms of time.

Metrics	Method in [23]	Method in [25]	Method in [22]	Our Method
Matrix Size	8 × 8	8 × 8	8 × 8	8 × 8
Bit-width	32 bit	32 bit	16 bit	32 bit
Work Mode	Eigenvalue and Eigenvector	Eigenvalue and Eigenvector	Only Eigenvalue	Eigenvalue and Eigenvector
Sweep Number	(-)	3 sweeps	(-)	3 sweeps
Operating frequency	(-)	100 MHz	130 MHz	150 MHz
Execution Time	350 µs	16 µs	6.02 µs	18 µs

(-) indicates that it is not specified in the references.

, we still choose to compare the execution time with the reference literature that was compared in terms of resource consumption, as this may illustrate the trade-off between area and time. The execution time in reference [23] corresponds to the total running time of the MUSIC algorithm, without specifying the running time of the covariance matrix decomposition module. Reference [25] specifies that their decomposition execution time is 16 µs. The possible reason is that there are more slice registers in our design, and time consumption is a little more. Reference [22] reduces computation workload by only calculating 16-bit eigenvalues, resulting in faster execution but less decomposition accuracy. Additionally, it solely computes eigenvalues and cannot be applied to DOA estimation algorithms such as MUSIC. Our method maintains resource efficiency and computing accuracy and introduces little time overhead. Therefore, our method ensures the execution time while using fewer resources.

4.4. Decomposition Accuracy

To analyze the direction-finding accuracy of the MUSIC algorithm implemented on FPGA, a comparison of processing between MATLAB 2017b and FPGA was conducted. Both platforms implemented the MUSIC algorithm using the same procedural steps as described in Section 4.1. In the MATLAB implementation of the MUSIC algorithm, functions are used to compute the covariance matrix, perform decomposition, etc. The MUSIC algorithm implemented on FPGA is entirely self-developed, and the covariance matrix decomposition module employs our proposed method. Additionally, there are some constraints on bit width. The input sampled signal data are 16 bits. The calculated covariance matrix data width is set to 32 bits. The eigenvectors from the covariance matrix decomposition are also taken as 32 bits. In the computation of the spatial spectrum, the steering vectors for each angle are 16 bits, with the highest bit serving as the sign bit.

During testing, both FPGA and MATLAB used the same input data generated by MATLAB, which consisted of 2 signal sources with an SNR of 0 dB randomly in azimuth angles of 0–360° and elevation angles of 0–90°. The azimuth angles were set to 135° and 304°, and the elevation angles were set to 30° and 49°. A total of 256 sets of snapshot data were simulated. The snapshot sampling data were stored in ROM before processing by the FPGA. The VIO virtual button was used as a reset signal, and the system operated at a clock of 100 MHz. The output signals were displayed in real time through ILA core verification.

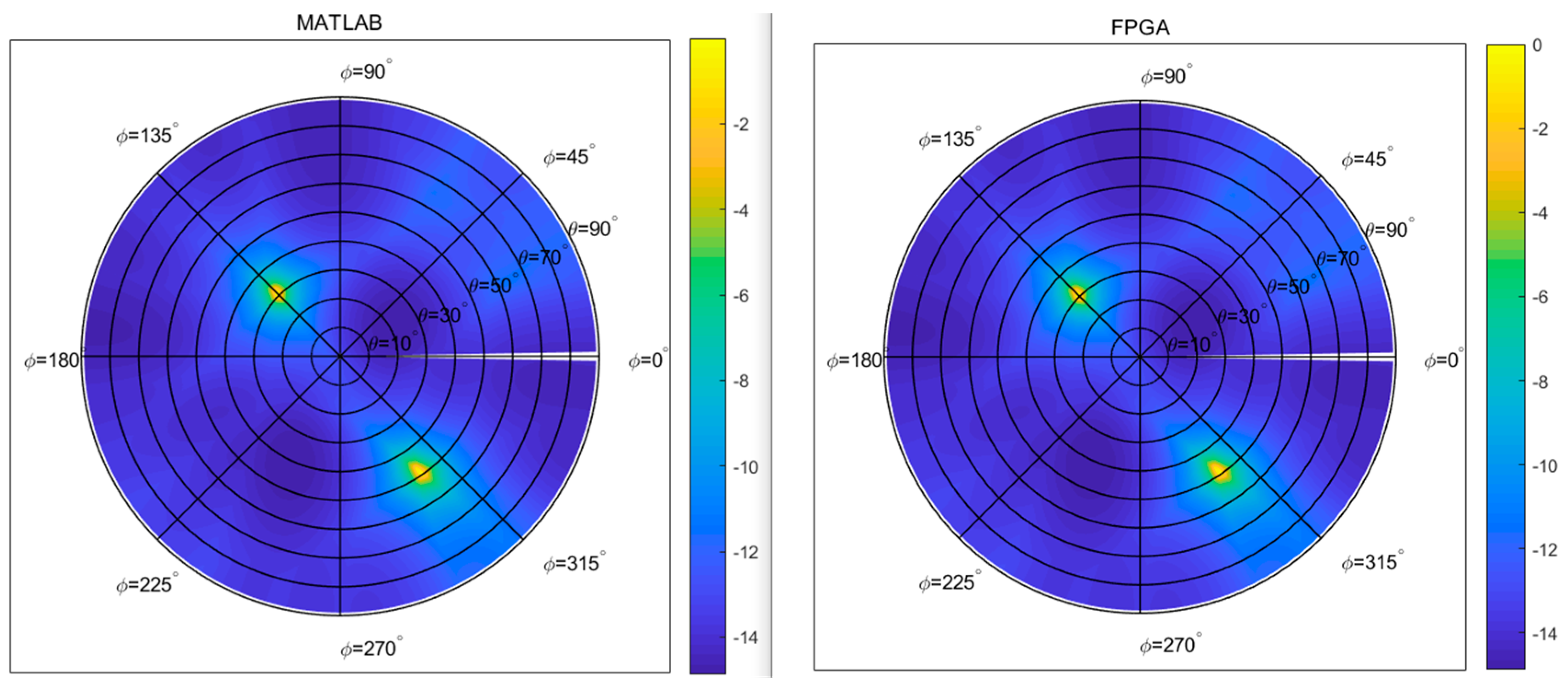
The results from both platforms were compared and visualized on the UV plane in a two-dimensional spatial spectrum as shown in Figure 6. It can be observed from the figure that both directional results are (135°, 30°) and (304°, 49°), indicating that the estimation results are correct. Additionally, it is evident that the main lobe beamwidth and directionality of both are almost identical, making them indistinguishable to the naked eye.

In the case where the number of signal sources, snapshots, SRN, and step angle for spectral peak searching are consistent, the direction-finding accuracy of the system is primarily affected by quantization errors. The FPGA system represents decimal numbers in fixed-point format, and the quantization bit width of the decimal determines the system’s direction-finding accuracy. In addition to truncating the initial system data generated by MATLAB and input into the ROM in FPGA, the main quantization error of the system is caused by the CORDIC algorithm in the covariance matrix decomposition module. When using the CORDIC algorithm for arctangent and rotation modes, if the input data (x, y) is small and the quantization accuracy is low, correct arctangent angles and rotation angles may not be obtained.

Our design employs 32-bit CORDIC IP cores, ensuring the accuracy of the eigen-decomposition to the greatest extent. We recorded the decomposition results of Figure 5 and performed unitary transformation, covariance matrix calculation, and decomposition in MATLAB using the same sample data. The comparison results of the eigenvalue decomposition are shown in

Table 6. Comparison of eigenvalue results for covariance matrix decomposition between MATLAB and FPGA.

		Eigenvalues
MATLAB		7,087,926	7,707,267	8,158,464	8,729,205	9,279,840	9,515,588	29,068,882	57,096,063
FPGA	4 Cycles	7,087,926	7,707,269	8,158,465	8,729,207	9,279,844	9,515,594	29,068,886	57,096,057
	3 Cycles	7,087,929	7,707,269	8,158,465	8,729,572	9,279,479	9,515,589	29,068,886	57,096,057
${∆}_{4 cycles}$		0	2.6 × 10−7	1.2 × 10−7	2.3 × 10−7	4.3 × 10−7	6.3 × 10−7	1.4 × 10−7	1.1 × 10−7
${∆}_{3 cycles}$		4.2 × 10−7	2.6 × 10−7	1.2 × 10−7	4.2 × 10−5	3.9 × 10−7	1.0 × 10−7	1.4 × 10−7	1.1 × 10−7

. Assuming the eigenvalues in the table are denoted as E_MATLAB and E_FPGA, the maximum error between the eigenvalues decomposed by MATLAB and FPGA should be

$$∆=\max {\displaystyle \frac{\left|{\mathrm{E}}_{\mathrm{MATLAB}}\left(\mathrm{i}\right) - {\mathrm{E}}_{\mathrm{FPGA}}\left(\mathrm{i}\right)\right|/2^{30}}{{\mathrm{E}}_{\mathrm{MATLAB}}\left(\mathrm{i}\right)/2^{30}}},\mathrm{i}=1,2,···,8$$

(14)

Experimental comparisons reveal that the maximum error accuracy is within 10⁻⁵ after 21 iterations of the covariance matrix, and within 10⁻⁷ after 28 iterations. The error is mainly from two aspects of our design. One is the quantization of the sampled signal generated by MATLAB and stored in FPGA’s ROM with the 15-bit width. The other is the bit width of IP cores. During the computation of arctangent values and rotations, there are truncation errors due to the bit width. The 32-bit IP cores can ensure the accuracy of eigen-decomposition. Moreover, increasing some iterations can also improve the accuracy of decomposition. After sweeping 4 cycles (iterating 28 rounds), the covariance matrix has already become a diagonal matrix; there is no need for more sweeps. Further increasing the number of iterations will not improve accuracy but increase time consumption. Therefore, in our design, we set the sweeping times as 4 cycles to get high decomposition accuracy and low time consumption.

5. Conclusions

This paper proposes an improved method for covariance matrix decomposition in DOA estimation algorithms. Based on the conventional systolic structure, it optimizes the implementation process of the Jacobi algorithm with time-division multiplexing and parallel partitioning methods. This approach can reduce resource consumption with minimal introduction of time overhead. To improve the accuracy of eigen-decomposition and reduce the utilization of DSP resources, we utilize 32-bit CORDIC IP cores to calculate arctangent values and rotation operations. We conduct an 8-order matrix decomposition on an FPGA to validate the effectiveness and performance of the method. Compared to traditional approaches, our resource consumption can be reduced by approximately 75%. Our method achieves decomposition in just 18 µs at a running clock of 150 MHz. Additionally, the accuracy of eigenvalue decomposition reaches 10⁻⁵ after sweeping 3 cycles and reaches 10⁻⁷ after sweeping 4 cycles. Compared to existing research techniques, our method achieves a better balance in resource consumption, execution time, and decomposition accuracy. Experimental results validate the effectiveness of our approach, meeting the demands for DOA estimation. This approach will provide an effective method for applications such as subspace-based DOA algorithms, which rely on covariance matrix eigen-decomposition. In the future, we will apply this method to DOA estimation scenarios with more antennas, such as a 16-order covariance matrix, which will demonstrate more improvements in hardware resources and computing performances.