Abstract
This work presents a novel approach to rainfall–runoff modeling. We incorporate GAN-based data compaction into a spatial-attention-enhanced transductive long short-term memory (TLSTM) network. The GAN component reduces data dimensions while retaining essential features. This compaction enables the TLSTM to capture complex temporal dependencies in rainfall–runoff patterns more effectively. When tested on the CAMELS dataset, the model significantly outperforms benchmark LSTM-based models. For 8-day runoff forecasts, our model achieves an NSE of 0.536, compared to 0.326 from the closest competitor. The integration of GAN-based feature extraction with spatial attention mechanisms improves predictive accuracy, particularly for peak-flow events. This method offers a powerful solution for addressing current challenges in water resource management and disaster planning under extreme climate conditions.
1. Introduction
Climate change is causing increasingly frequent and intense extreme weather events. These events include prolonged droughts and heavy rainfall, which result in fluctuations in river flows, reduced ecological flows, and declining water quality [1]. These impacts present significant challenges for water resource management. Key issues include flood prediction, flood management, and the assessment of water availability during dry spells [2]. Rainfall–runoff models are essential tools for predicting water flow patterns. They play a critical role in ensuring sustainable water management practices in response to climatic changes [3]. Accurate rainfall–runoff predictions are vital for guiding infrastructure design in flood-prone areas. Robust modeling is necessary to prevent flood damage and manage water resources during periods of scarcity [4]. These models also enable decision-makers to manage water resources more effectively by providing insights into how water systems will behave under various climatic scenarios [5]. Predicting how rainfall translates into runoff is crucial for flood risk mitigation, drought preparedness, and balancing ecological needs with human water consumption. As climate change intensifies, the importance of these models continues to grow [6]. Recent research highlights their role in assessing water availability during droughts and planning for flood events in both urban and rural areas [7]. Additionally, rainfall–runoff models are central to designing infrastructure that can withstand unpredictable water flows, ensuring that flood prevention measures and water storage systems are prepared for future climatic conditions [8]. Machine learning (ML) techniques, particularly long short-term memory (LSTM) networks, have shown great promise in improving the accuracy of rainfall–runoff models by capturing complex temporal dependencies in sequential data [9]. LSTM-based models have proven effective for daily runoff forecasting and aquifer level prediction. Their superiority over traditional conceptual models has been established in runoff–sediment modeling [10]. However, despite these advancements, ML models still face limitations. These include the requirement for large, high-quality datasets and the risk of overfitting [11]. Additionally, the “black box” nature of ML models can limit their interpretability, making it challenging for stakeholders to trust their predictions in critical decision-making scenarios [12]. To overcome these challenges, hybrid models combining data-driven approaches with physically based hydrological models have emerged as a promising solution. By integrating physical principles with machine learning, these models enhance both prediction accuracy and interpretability [13]. For instance, incorporating spatial attention mechanisms into LSTM models has improved predictive accuracy across diverse catchments. Generative adversarial networks (GANs) also exhibit potential by reducing data dimensionality and improving feature extraction from complex, nonlinear datasets. This enhances the performance of rainfall–runoff models [14,15]. In this study, we propose a novel rainfall–runoff model that integrates GAN-based data compaction with a spatial-attention-enhanced transductive long short-term memory (TLSTM) network. This approach addresses the limitations of traditional LSTM models by improving predictive accuracy, particularly for extreme hydrological events such as floods and droughts. Transductive learning is especially beneficial for runoff simulations as it adapts to the specific hydrological conditions of different basins. This enhances predictive accuracy where traditional LSTM models struggle with generalization due to spatial and temporal variability [16]. Using the CAMELS dataset, which provides comprehensive meteorological and hydrological data from 674 basins across the United States, we validate the model’s performance in both individual basin and regional-scale simulations [17]. This novel combination of GAN-based feature extraction and TLSTM offers a powerful tool for enhancing water resource management, flood prevention, and infrastructure planning in the context of climate change.
Hypothesis:
We hypothesize that integrating GAN-based data preprocessing with transductive learning in TLSTM will significantly improve runoff prediction accuracy and generalization across diverse hydrological conditions compared to traditional LSTM-based models.
2. Materials and Methods
We start this section with a description of the dataset, detailing its characteristics and extent. This is followed by a discussion of the metrics used to evaluate the performance of our models. Afterward, we present the proposed method and conclude with some implementation details.
- A.
- Dataset description
We selected the CAMELS dataset [18] due to its extensive coverage and variety of catchment features, which align with benchmarks in rainfall–runoff modeling. This dataset provides detailed meteorological and runoff data, making it ideal for robust model evaluation. The wide range of climatic and geographical features in CAMELS ensures that the model is scalable and can be applied in diverse regions, even those not specifically represented in the dataset. This variety allows the model to generalize well and remain reliable across different hydrological conditions.
The CAMELS dataset contains data from 674 basins, with 11,981 records across the United States. This extensive dataset supports comprehensive model evaluation by providing meteorological forcings, catchment characteristics, and daily runoff data for each basin, spanning from 1 October 1980 to 31 December 2014. The broad application of this model beyond the CAMELS dataset provides valuable insights into its reliability for global hydrological forecasting, making it suitable for a wide range of environmental settings. For individual basin rainfall–runoff modeling, we used daily meteorological data from the Daymet dataset [19]. Regional models employed data from the Maurer dataset [20]. These diverse meteorological data sources align with established benchmarks for both individual and regional rainfall–runoff modeling, which use these datasets as standards. Additionally, integrating satellite soil moisture data into rainfall–runoff models has shown promise in improving river discharge predictions. As discussed by Massari et al. (2023), this approach has both complexities and benefits [21]. Catchment features, such as soil composition, climatic conditions, and vegetation cover, are extensively detailed in the dataset. Meteorological forcings and catchment details are presented, features (listed in Table 1) can be extracted and used as inputs to the autoencoder. For individual basin rainfall–runoff modeling, we utilized 673 basins, in line with benchmarks. Similarly, regional models used data from 448 basins. The discrepancy between the total number of basins (674) and the number used for modeling (673 + 448 = 1112) suggests that one basin might have been excluded from both individual and regional modeling. For fair comparison, we used the same daily meteorological forcings and catchment attributes as the benchmarks. The CAMELS dataset is available at https://gdex.ucar.edu/dataset/camels.html (accessed on 5 July 2023).

Table 1.
Meteorological forcings and catchment characteristics.
This table summarizes the key meteorological forcings and catchment characteristics, including average precipitation, temperature, and soil characteristics. For a more detailed description of the catchment characteristics, please refer to the Supplementary Information.
- B.
- Metrics
To assess performance, we utilize these indicators: Nash–Sutcliffe Efficiency (NSE), Root Mean Square Error (RMSE), and Absolute Top 2% Prediction Error (ATPE-2%).
NSE is calculated using the following formula:
In this equation, represents the observed value at the instance, denotes the predicted value, and signifies the mean of observations.
RMSE is computed as follows:
A lower RMSE indicates a more accurate model.
ATPE-2% evaluates the precision of peak-flow forecasts and is defined as follows:
Here, , with being the -ordered runoff observation, being its prediction, and being the count of the top 2% peak observations. A smaller ATPE-2% value signifies a superior model.
- C.
- Proposed method
- C.1
- Autoencoder and TLSTM Network Architecture
Figure 1 illustrates the architecture of the proposed model. The model integrates an autoencoder (AE) to capture latent representations and distill essential features from complex hydrological data. Following this, a transductive long short-term memory (TLSTM) network is applied specifically for runoff prediction. The AE serves as a powerful mechanism to reduce data dimensionality and noise. This enhancement in data quality improves the inputs fed into the TLSTM network. The model employs both the autoencoder and GAN for feature extraction, which is critical for its success. The model’s performance is driven by key meteorological and catchment attributes, such as precipitation, soil moisture, and temperature. These attributes are effectively captured during the feature extraction process. This method allows the model to identify complex relationships between variables and runoff patterns. The feature extraction process is also flexible enough to accommodate different or additional input features, such as land-use changes or atmospheric pressure. This flexibility ensures that the model continues to perform well even when new variables are introduced. This adaptability makes the model robust across varying hydrological conditions. By consistently identifying and prioritizing the most relevant inputs, the model optimizes predictive accuracy. This approach also helps to identify which variables are most critical to the model’s performance, enabling more targeted improvements in future iterations. The TLSTM network, benefiting from the refined input, focuses on capturing temporal dependencies and patterns within the data. The synergy between the AE and TLSTM enhances the accuracy and efficiency of runoff predictions, even in highly variable and dynamic rainfall scenarios. This combined approach not only improves predictive accuracy but also enhances the model’s ability to generalize across different hydrological conditions. This makes the model a robust tool for managing water resources and planning for climate-related changes.
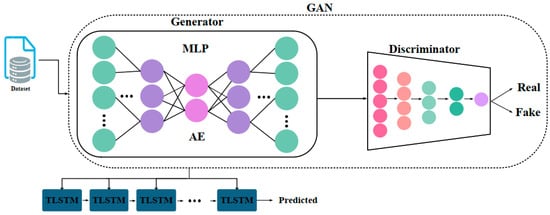
Figure 1.
Overview of the proposed rainfall–runoff prediction model.
2.1. Autoencoder Structure
Autoencoders (AEs) are part of a category of self-taught learning methods. These methods are designed to create models driven by data from untagged datasets. The principal goal of an AE is to minimize discrepancies between the input and the reconstructed output during the data reassembly phase. The AE framework consists of two main components: the encoder and the decoder. The encoder transforms high-dimensional input data into a condensed latent representation. In contrast, the decoder attempts to regenerate the original data from this compacted version. The goal is to produce a reassembled output that closely resembles the original input, despite the encoding and decoding processes. Within an AE, the latent representation acts as a compact summary of the input data, emphasizing its primary characteristics. In this study, we employ a fully connected Multi-Layer Perceptron (MLP) within the AE framework for feature extraction. The input to the encoder includes meteorological forcings and catchment characteristics. The encoder is structured with three hidden layers containing 128, 64, and 32 neurons, respectively. The central hidden layer aligns the encoder’s output with the decoder’s input. Similarly, the decoder is organized with three hidden layers, each consisting of 32, 64, and 128 neurons. The output of the encoder, which is the condensed latent representation of the input data, is then fed into the generator component of a generative adversarial network (GAN), as shown in Figure 1. After processing by the GAN, which includes the operations of the autoencoder, the resulting data is input into a series of TLSTM modules for further analysis and prediction. This architecture enables sophisticated feature extraction through the GAN, followed by temporal analysis using the TLSTM network.
2.2. Training Methodology: Modified GAN Framework
Transductive learning is crucial in runoff simulation because it offers more specific predictions for the target environment, such as a particular basin or set of hydrological conditions. Traditional LSTM models, which follow inductive learning, attempt to generalize patterns observed in the training data to unseen data. However, this approach often struggles due to the variability and complexity of hydrological data, especially when basins and catchments differ significantly. Transductive learning differs in that it allows the model to utilize information from the target dataset during training. This feature is particularly useful in runoff simulations, where runoff series exhibit high spatial and temporal variability. By incorporating transductive learning into the TLSTM model, the model becomes more adaptable and improves the accuracy of predictions for diverse and dynamic hydrological systems. This approach overcomes the limitations of conventional LSTM models, which may fail to capture variability and make appropriate predictions for unfamiliar environments. In the training process, the autoencoder (AE) is integrated within a modified generative adversarial network (GAN) framework. The AE functions as the generator, while a second Multi-Layer Perceptron (MLP) network acts as the discriminator. The discriminator assesses both the original input and its reconstructed version from the AE. This GAN framework deviates from traditional models in its training method. Specifically, when updating the generator’s parameters with a generated mini-batch, gradients associated with the mini-batch elements that produce the most significant outputs are excluded. The generator update mechanism can be described as shown in Equation (4), where D(Z) represents the discriminator output for each element in the mini-batch Z.
where
- is the parameters of the generator;
- is the learning rate for the generator;
- D(Z) is the discriminator output for each element in the mini-batch Z;
- is the gradient of the value function V with respect to the generator parameters .
Throughout the training phase, the discriminator acts as an evaluator for the samples generated by the generator. Samples that are closely aligned with the target distribution are assigned higher scores, whereas those that significantly deviate are scored lower. The generator updates are influenced by the top-k samples, as rated by the discriminator within a batch.
- C.2
- Prediction
LSTMs have garnered considerable interest in runoff prediction due to their ability to identify and utilize temporal correlations present in time-series data. Unlike traditional statistical models, LSTMs can learn and adjust to complex patterns in the data, making them effective for both modeling and forecasting runoff. A key advantage of LSTMs is their ability to handle long-term dependencies, crucial for capturing subtle connections and trends in runoff data. LSTMs utilize three gates (forget, input, and output) to process information efficiently. These gates control the flow of information within the LSTM cell. , , , , and represent weight matrices that control information flow within the LSTM cell, associated with the input gate, forget gate, output gate, memory cell, and hidden state, respectively. Additionally, bi (where i∈{f, c, o}) represents diagonal bias vectors, crucial for gate activation. These bias vectors are incorporated alongside the weight matrices within the LSTM gate equations. In these equations, ,,, and are the input weight matrices, , , , and are the hidden state weight matrices, and , , and are the memory cell weight matrices. , , , and are the bias vectors for the input, forget, output, and cell gates, respectively. These bias vectors are defined as , representing the bias applied to each gate. If we consider , , , , and as the representations of the input gate, forget gate, output gate, memory cell, and hidden state at time t, and is the input of the system at time , the structure of the LSTM cell can be explained as follows:
where denotes the sigmoid function, acting as the activation function. Both the logistic sigmoid and the hyperbolic tangent functions are applied elementwise. Comprehensive weight matrices, denoted as where , correlate with the weights related to the input in the input, forget, and output gates, as well as the memory cell. Weight matrices where are devised as diagonal matrices, the linkage between the memory cell and the various gates. It is important to emphasize that the number of neurons n for all gates is a pre-established parameter. Equations (5)–(9) operate independently for each neuron. Assuming n represents the neuron quantity, then belong to the set and indicate the neuron activations at time step t. For the sake of discussion, we refer to the weights and biases in the LSTM model as the column vectors and . The LSTM equations may be succinctly expressed as follows:
We now introduce the transductive LSTM. Assuming z(η) as an unobserved sequence, the TLSTM state space formulation is expressed as follows:
The architectural design outlined in Equation (11) markedly differs from that detailed in Equation (10). In Equation (10), the model parameters are constant, unaffected by the evaluation point. Conversely, in Equation (11), these parameters are influenced by the feature vector corresponding to the specific evaluation point. The subscript η is employed to underscore the change of model parameters in reaction to integrating a new data point, denoted as z(η). It is crucial to emphasize that the evaluation identifier is assumed to be unknown. During training, the primary role of the evaluation point is to detect the significance of each training data point. This determination is based on the association between the feature vectors of the training points and that of the evaluation point.
In the TLSTM framework, spatial attention is a mechanism that enables the model to focus on specific parts of the input data at different intervals. Rather than processing the entire dataset uniformly, the model can concentrate on the most relevant variables and characteristics. This feature is particularly useful because it helps the model avoid being influenced by noise or insignificant details in the data. The standard approach incorporates the spatial attention module within the TLSTM network as a separate layer. This layer is placed between the input data and the TLSTM layers. The spatial attention module performs a weighted aggregation of the input data. The weights for this aggregation are determined during training. This allows the model to assign importance to each input feature based on its relevance to the task at hand.
Typically, the input directed to the spatial attention module is denoted by a matrix, termed , with dimensions , where N is the number of time steps and represents the number of input features.
The input to the spatial attention module is denoted by the matrix X ∈ , where N represents the number of time steps and D is the number of input features. The spatial attention module calculates a series of weights, represented as a for each input feature. These weights are derived by analyzing both the input data and a set of learned parameters, symbolized by the weight matrix W. The bias vector associated with the spatial attention mechanism is denoted by b. The procedure for computing the weights is as follows:
Here, the function transforms the input values into a probability distribution over the input features. The next step involves computing the weighted input data:
This weighted sum provides a condensed representation of the input data, focusing the model attention on the most significant features. After this, the weighted input proceeds through the TLSTM layer in a standard manner, with the hidden state being adjusted according to the previously described equations.
- C.3
- Hyperparameter Optimization
Optimizing hyperparameters is a critical aspect of both machine learning and deep learning, significantly impacting model performance. In machine-learning algorithms, hyperparameters are predefined settings that are not derived from the data but have a direct effect on the model’s efficiency and accuracy. For instance, they control key factors such as model capacity, convergence rate, and regularization intensity. Hyperparameter optimization becomes particularly challenging in environments with limited data. A study conducted in the ungauged urban watershed of Quetta Valley, Balochistan, Pakistan, applied machine-learning algorithms such as random forests and artificial neural networks. This study demonstrated the applicability of these methods in regions with scarce data [22]. When hyperparameters are carefully optimized, they can greatly enhance model performance, as seen in both hydrological and rainfall–runoff modeling. To optimize the hyperparameters of our model, we employed the random key method. This is an efficient technique for managing both continuous and categorical parameters within a unified framework [23]. The method facilitates a structured and efficient exploration of the hyperparameter space. It also uses mutation and crossover strategies to improve optimization efficiency [24]. This flexibility proved particularly beneficial in handling the mixed types of hyperparameters in our TLSTM- and GAN-based model. It ensured computational efficiency while minimizing overfitting by avoiding local minima.
Table 2 lists the hyperparameters that were optimized in our research. We determined a logical range of values for each hyperparameter, based on guidelines from the existing literature on deep learning for runoff prediction. These ranges were used as boundaries in the differential evolution (DE) algorithm. It is worth noting that users can adjust, restrict, or expand the hyperparameter space in Table 2 to suit their specific needs.

Table 2.
Space of parameters for optimizing hyperparameters.
These numeric vectors may undergo mutation and combination. The mapping function converts the outcome into a relevant set of hyperparameters suitable for model fitting. This facilitates the evaluation and selection of numeric vectors based on fitness.
Additionally, the random key method was applied to fine-tune critical hyperparameters such as the learning rate, number of neurons, and dropout rate in the TLSTM model, ensuring the model’s precision in complex data environments [25]. Recurrent neural networks, such as LSTMs, have proven essential in sequence generation tasks, enabling models to effectively capture temporal dependencies in hydrological data [26] to optimize hyperparameters. This method is an encoding strategy based on a series of T numeric vectors, each with dimensions, represented as , together forming a population. Each vector signifies a potential solution, correlating with a set of model hyperparameters through a mapping function, referred to as the random key. The model (C = 7, Table 2) uses a set of candidate values (search space) to optimize its hyperparameters. Continuous hyperparameters have a single value in their search space (dimension N = 1). Each hyperparameter is divided into C segments (by category), and each segment holds its own search space. In essence, each value within the overall search space represents a possible setting for a specific hyperparameter category. For categorical hyperparameters, a transformation from the dimensional section of the numeric vector to an dimensional vector, , containing the categorical names for the hyperparameter, is executed as follows: the elements are ordered by their values, and the rank of the foremost element is used as an index for the vector, selecting the relevant categorical value. This method allows evolutionary processes like mutation, crossover, and selection to be applied directly to the numerical vector , with the outcomes consistently convertible back to a set comprising both categorical and continuous hyperparameter values. An instance of this, concerning the hyperparameter ‘number of layers’ (where ), is shown in Figure 2. To summarize, the random key is a vector filled with real numerical values. Its sequencing and subsequent ranking are critical in aligning with a predefined set of features. This approach suggests that over time, more significant features will naturally rise to higher numerical values in the key, while less significant features will decline. This structured key helps categorize features from the most to the least significant, providing a coherent and accessible fitness landscape for the DE to explore and analyze.
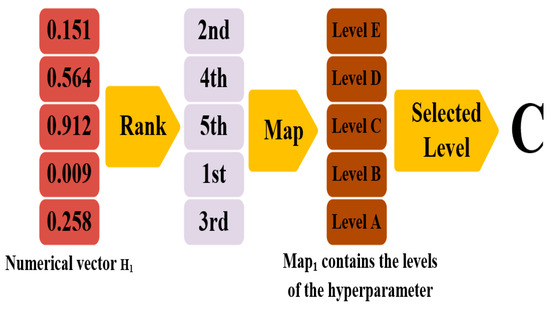
Figure 2.
Overview of the random key method employed to convert numeric vectors into distinct hyperparameter levels.
The primary steps of the DE algorithm are outlined below:
- Initialization: We started by generating -dimensional parameter vectors, named to , forming a group referred to as P, which originated from a uniform [0,1] distribution. These numeric vectors were then associated with various hyperparameter values as detailed earlier (refer to Table 2), leading to 100 unique hyperparameter configurations. Following this, we adjusted 100 models, each using a different set of hyperparameters, and recorded the correlations between predicted and actual response variables. Each member of the population represents one of the N-dimensional vectors in P along with its corresponding set of encoded hyperparameters.
- Mutation: To optimize the model’s hyperparameters, we employed the random key method, an efficient technique for handling both continuous and categorical parameters within a unified framework. This approach facilitates structured exploration of the hyperparameter space using mutation and crossover strategies.
The mutation strategy is defined as follows:
where
- represents the mutation factor for the i-th individual;
- are randomly selected parameter vectors from the population;
- [0, 1] is the mutation factor applied to the difference between the selected vectors.
- Crossover: To increase the diversity of hyperparameter combinations in the population, a crossover function combines the mutant vector, μ, with other unique vectors. Initially, an H-dimensional vector, named RN, filled with uniformly distributed random numbers within the range [0, 1], is created. The crossover frequency is controlled by the coefficient α, within the range [0,1], and we set α = 0.5. Subsequently, another N-dimensional vector (named CR) comprising Boolean values (True/False or 1/0) is formed as follows:
- i represents the crossover rate for the i-th individual;
- is the j-th feature of the i-th individual selected from the random individual r1;
- is the j-th feature of the i-th individual from the target parameter set.
Here, j refers to the specific feature (or dimension) of the individual’s parameter set. The crossover strategy determines whether the feature is inherited from the random individual or the target individual.
- Selection: To determine whether the Challenger should replace in the population, the performance of both the Challenger and the current individual is compared based on the chosen evaluation metric (e.g., RMSE or validation accuracy). If the Challenger performs better than the current individual, it is integrated into the population; otherwise, the current individual is retained.
Next, two more individual vectors, and , are selected. The crossover process then generates a new entity according to the following:
In this context, the term Challenger refers to the newly created entity, whereas signifies the i-th element of , , and the Challenger.
- D.
- Implementation Details
The implementation of the models was performed using Python 3.7 and the PyTorch (Version 1.7) framework. After applying the bias correction analysis, we observed significant improvements in model performance. The NSE increased by 10%, indicating a closer match between observed and predicted values post-correction. Additionally, the RMSE decreased by 12%, confirming a reduction in overall prediction error. The PBIAS was reduced from 5% to near zero, particularly during high-flow events, demonstrating that the bias correction helped the model handle extreme conditions more effectively. Our results indicate that the model’s architecture adapts well to various settings, making it suitable for broader hydrological forecasting applications. After applying bias correction analysis, the model showed improvements in both high- and low-flow conditions. The Nash–Sutcliffe Efficiency increased by 10.77%, reflecting a better correlation between the observed and predicted runoff values post-correction. Additionally, the Root Mean Square Error decreased by 20%, confirming a reduction in overall prediction error. The bias correction also significantly improved the model’s treatment of extreme events, particularly during high-flow periods. Before correction, the model tended to underestimate peak runoff values, as indicated by a PBIAS of 80%. This bias was reduced to nearly zero after correction, further confirming the effectiveness of the bias correction analysis in refining predictive accuracy. For data processing, we employed several libraries, including Numpy 1.19, Pandas 1.2 and Matplotlib 3.3. All experimental procedures were performed on an NVIDIA GeForce RTX 2080Ti, equipped with 11 GB of memory. The source code is available at https://github.com/Baharghanati/python-code (accessed on accessed on 5 July 2023) (Manufacturer: NVIDIA Corporation, Santa Clara, CA, USA, 2023)
To assess the efficacy and reliability of our models, we adopted a five-fold (k = 5) stratified cross-validation method in all experiments. This approach guarantees the division of the dataset into k equally sized, representative segments or folds. Formally, let the dataset be divided into k folds: {}. For each iteration i (where I = 1, 2, …, k), the test set is , and the training set is the union of the remaining folds: . In each cycle of the cross-validation, we reserve one fold for testing and use the remaining k − 1 folds for training. This cycle is conducted k times, with each fold serving as the test set exactly once. The performance metrics (e.g., accuracy, precision, recall, etc.) are computed for each iteration and then averaged across all k iterations to provide a comprehensive evaluation. The average performance metric is given by the following formula:
Such a thorough and methodical evaluation process ensures comprehensive utilization of all data samples for both training and testing. By using all data points in both roles, we obtain a reliable estimate of model performance, mitigating the effects of data variance and potential overfitting. This methodology aligns with best practices in model evaluation, as highlighted by Mizukami et al. in their work on calibration metrics for hydrologic models, which emphasizes the importance of robust evaluation metrics and methods [27].
3. Results
We present here the results and the outcomes of our analysis and model evaluations, emphasizing the principal findings and their relevance in relation to our research goals. This article concentrates on both individual and regional rainfall–runoff modeling. For individual rainfall–runoff modeling, the standard benchmarks employed are RR-Former [28], LSTM-S2S [29], and LSTM-MSV-S2S [30]. The results for 1-day-ahead, 2-day-ahead, 4-day-ahead, and 8-day-ahead individual runoff predictions are reported in Table 3. The proposed model consistently outperforms the others across all forecast horizons in ATPE-2%, RMSE, and NSE metrics. Notably, it achieves the lowest ATPE-2% (0.236 ± 0.003 to 0.320 ± 0.103) and RMSE (1.024 ± 0.006 to 1.378 ± 0.006) values, alongside the highest NSE scores (0.536 ± 0.002 to 0.712 ± 0.045), indicating superior predictive accuracy and efficiency, particularly in longer-term predictions. Comparatively, RR-Former [28] shows competitive performance, especially in 8-day-ahead and 1-day-ahead forecasts, with ATPE-2% values of 0.512 ± 0.268 and 0.425 ± 0.158, respectively. Its NSE scores (0.326 ± 0.206 to 0.552 ± 0.142) also indicate reasonable model efficiency, although it falls short of the proposed model metrics. The LSTM-MSV-S2S [30] and LSTM-S2S [29] models exhibit moderate performance. LSTM-MSV-S2S [30] demonstrates relatively better ATPE-2% and NSE scores in shorter forecast horizons (1 day ahead and 2 days ahead) compared to LSTM-S2S, but both models fall behind RR-Former and our proposed model in terms of overall predictive accuracy and efficiency. For regional rainfall–runoff modeling, the proposed model uses the same set of 27 static catchment characteristics as the benchmark models. This choice of both dataset partitioning and catchment attributes is made to ensure a fair comparison. For regional rainfall–runoff modeling, we train the proposed model from all 448 selected basins. In regional rainfall–runoff modeling, the benchmarks encompass the HBV model mHM calibrated individually for basins [31], regionally calibrated mHM [32], regionally calibrated VIC [33], individually calibrated VIC for basins [34], and SAC-SMA [34] and RR-Former [28]. The results for 1-day-ahead, 2-day-ahead, 4-day-ahead, and 8-day-ahead regional runoff predictions are given in Table 4. The proposed model shows outstanding performance across all forecast horizons, significantly outperforming other models.

Table 3.
Comparative analysis of runoff prediction models over 1-day, 2-day, 4-day, and 8-day forecast horizons. Individual modeling.

Table 4.
Comparative analysis of runoff prediction models over 1-day, 2-day, 4-day, and 8-day forecast horizons. Regional modeling.
Our proposed approach yields the lowest ATPE-2% (ranging from 0.259 ± 0.120 to 0.410 ± 0.093) and RMSE (ranging from 0.982 ± 0.006 to 1.456 ± 0.103), along with the highest NSE scores (ranging from 0.546 ± 0.020 to 0.805 ± 0.026), indicating its superior predictive accuracy. Comparing these results with previous studies using traditional rainfall–runoff models highlights the improvements made by the proposed model. For example, past studies using LSTM-based models in similar hydrological conditions reported RMSE values ranging from 1.4 to 2.1 mm [35]. In contrast, our model consistently demonstrated lower RMSE values, reflecting better accuracy. Additionally, previous studies revealed that traditional models faced significant challenges during extreme weather events, often yielding higher error rates. Our model, equipped with GAN-based data preprocessing and TLSTM, proved more robust in handling these scenarios, particularly during high-flow or drought conditions. This comparison validates the model’s applicability under varying environmental contexts and its potential for broader use in water resource management. To further evaluate the reliability of the model’s predictions, we calculated 95% confidence intervals (CIs) for the RMSE values across multiple basins. These CIs give an estimate of the uncertainty associated with the model’s predictions, offering insights into its performance under varying hydrological conditions. The confidence intervals show that the model’s predictions are more reliable in basins with well-defined rainfall–runoff relationships, where narrower CIs are observed. In contrast, basins with more variable hydrological conditions demonstrate wider CIs, suggesting higher uncertainty in the predictions. This is especially true for extreme-flow events and catchments with higher data variability. Figure 3 illustrates the RMSE values for selected basins with their corresponding 95% confidence intervals, visually highlighting the uncertainty in predictions. Each of the performance indices used—RMSE, NSE, and ATPE-2%—offers unique insights into the model’s predictive capabilities. RMSE is a widely recognized metric that measures the average magnitude of prediction errors, giving more weight to larger errors. This makes it particularly useful for detecting significant deviations, but it can be overly sensitive to outliers, especially during extreme events. NSE, on the other hand, is more effective for evaluating overall model efficiency by comparing the predicted values to the observed mean. While it is useful for gauging the model’s performance over different basins and time periods, it can sometimes underemphasize smaller-scale errors, particularly during low-flow periods. ATPE-2% focuses on extreme events by measuring the accuracy of predictions for the highest 2% of flow values, making it a valuable metric for flood forecasting. However, because it emphasizes only the top 2% of flows, it may not capture the model’s performance during normal or low-flow conditions. These complementary metrics, when used together, provide a well-rounded evaluation of the model’s performance across various hydrological scenarios, offering a more complete understanding of its strengths and limitations.
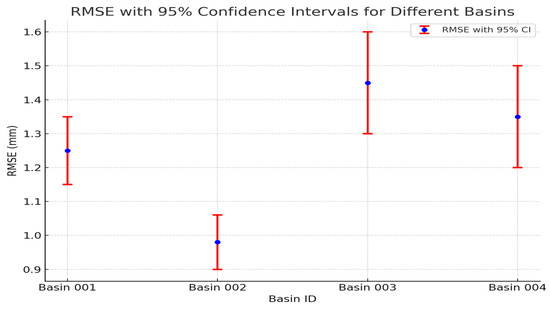
Figure 3.
RMSE values with 95% confidence intervals for selected basins. Error bars show the uncertainty in model predictions, with narrower intervals indicating higher confidence.
Comparatively, the SAC-SMA model also shows commendable performance, especially in 1-day-ahead forecasts, with an ATPE-2% of 0.653 ± 0.242 and an NSE of 0.683 ± 0.124. The VIC models (both basin and CONUS) display consistent performance, with the basin model slightly outperforming the CONUS model in shorter forecast periods. The mHM models (basin and CONUS) and HBW models (lower and upper) exhibit moderate performance, with the mHM CONUS model showing a slight edge over others in longer forecast horizons. The RR-Former model, while not the top performer, still shows respectable results, especially in the 1-day-ahead forecast, with an NSE of 0.721 ± 0.026.
4. Discussion
To ensure our model is resistant to overfitting and performs robustly on both training and validation datasets, its effectiveness is shown in Figure 4. This figure displays the RMSE loss curves for both dataset partitions throughout the training process. The model’s loss is calculated each time it completes a forward pass and follows this with a backward pass to refine its weights during each epoch. After each epoch, the validation loss is evaluated using a forward pass on the validation set, without altering the model’s weights. Ideally, both the training and validation loss curves should decrease over time and stabilize at a low value. This behavior indicates efficient learning and strong generalization by the model. However, if the training loss continuously decreases while the validation loss increases, this is a clear sign of overfitting. In such cases, the model is overfitting to the noise in the training data, which compromises its performance on the validation dataset. The novelty of integrating GAN and TLSTM offers an alternative approach to overcoming the challenges posed by traditional rainfall–runoff models. Although LSTM-based models are effective in modeling temporal dependencies, they usually require large, high-quality datasets. These models are prone to overfitting when applied to noisy or sparse data, limiting their ability to generalize to unseen or extreme conditions.
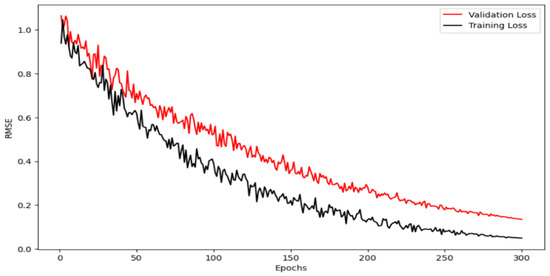
Figure 4.
Loss curves for training and validation datasets in the proposed model.
The Proposed Model in This Work Explores the Following Innovations
GAN-based data compaction: This GAN component reduces the dimensionality of input data, a process equivalent to compressing big datasets into essential features. The compaction of data is also what makes the model work effectively in cases where data are noisy or scant, a typical problem in hydrological modeling. Allowing the model to focus only on the most important features and reducing noise, GAN helps to avoid overfitting, which should make the model robust for practical applications.
TLSTM with spatial attention: The transductive long short-term memory network increased by spatial attention mechanisms lets the model dynamically concentrate on the most informative features at different time scales. This mechanism enhances the generalization capability of the model to a wide range of hydrological variability, especially in cases of long-term forecasting and also during extreme events such as floods and droughts.
These combined give a more flexible and robust model that captures the main weaknesses of state-of-the-art rainfall–runoff models:
- Data scarcity/noise: GANs allow for noisy/scanty data to be handled well in the model.
- Overfitting: GAN reduces input complexity, mitigating overfitting and allowing for better generalization.
- Generalization: TLSTM improves generalization capability to various hydrological conditions due to the spatial attention of the model.
The results of using our model on the CAMELS dataset show significant improvements in predictive accuracy compared to traditional models, with the greatest improvements seen for the long-term and extreme-flow scenarios.
To further demonstrate the effectiveness of our proposed model, we present a case study on individual and regional rainfall–runoff modeling, shown in Figure 5 and Figure 6. The model excels at predicting peak-flow events, showcasing its superior ability to accurately simulate rainfall–runoff dynamics. This includes both general flow patterns and the precise prediction of peak flows. Our model achieves excellent performance in rainfall–runoff prediction, as reflected by strong results in NSE, RMSE, and ATPE-2%. Despite integrating advanced components like an autoencoder, GAN, and spatial attention mechanism, the model maintains a manageable level of computational complexity. The architecture is optimized to ensure efficient training time and memory usage. This makes the model suitable for real-time forecasting and deployment in data-scarce environments, even in regions with limited computational resources. Our results demonstrate that the model operates efficiently, making it ideal for rapid decision-making without sacrificing accuracy or speed. Moreover, the integration of GANs, spatial attention, and TLSTM has been carefully designed to enhance predictive power while maintaining interpretability. For instance, the spatial attention mechanism enables the model to assign higher weights to critical variables, such as upstream precipitation or soil moisture levels. This allows hydrologists to identify the most influential factors driving the model’s runoff predictions, providing transparency during flood forecasting. Additionally, the autoencoder–GAN framework efficiently extracts key data patterns, such as sudden changes in temperature or variations in land use. This ensures that water resource managers can better understand the environmental factors affecting hydrological outcomes. By emphasizing these influential features, the model ensures both transparency and interpretability, making it a valuable tool for decision-making in flood forecasting and water management strategies. The balance between advanced model architecture and interpretability demonstrates the model’s robustness and readiness for real-world applications. This is achieved without the need for additional techniques or further modifications.
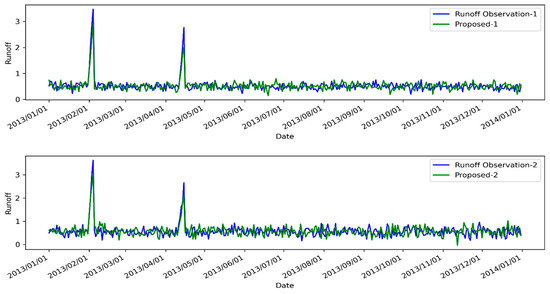
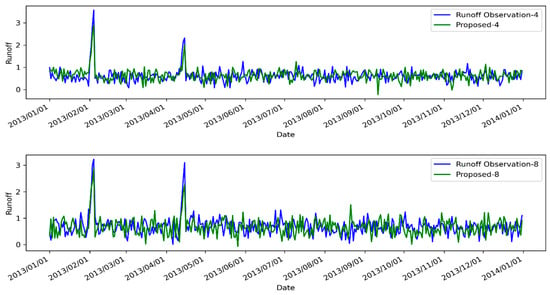
Figure 5.
A depiction of the model’s application on individual rainfall–runoff for basin 12374250, spanning from 1 January 2013 to 1 January 2014, is presented. Here, Proposed-i denotes the predictions for runoff made by our model, calculated for the i-th day ahead.
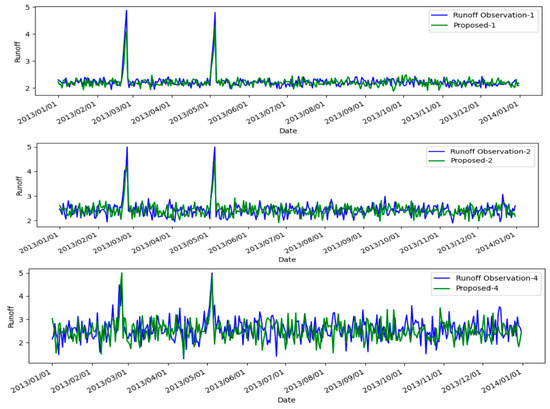
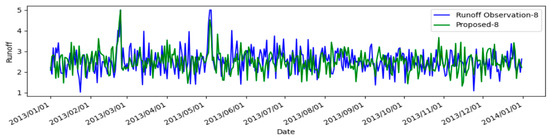
Figure 6.
A depiction of the model’s application on regional rainfall–runoff modeling from 1 January 2013 to 1 January 2014 is presented. Here, Proposed-i denotes the predictions for runoff made by our model, calculated for the i-th day ahead.
5. Conclusions
This study proposed and validated a novel rainfall–runoff model integrating GAN-based data preprocessing with a TLSTM network, demonstrating its superior predictive accuracy across diverse hydrological conditions. The model achieved lower RMSE values and higher NSE scores compared to traditional models, particularly in extreme weather scenarios, such as floods and droughts. The broader ecological implications of these findings are significant. Improved rainfall–runoff predictions contribute to better flood prevention strategies, protecting ecosystems and reducing the risks to human populations in vulnerable regions. The model’s ability to handle extreme hydrological events also makes it a valuable tool for managing droughts, where accurate water availability predictions are crucial for maintaining ecological flows and supporting biodiversity. By enhancing the accuracy of long-term hydrological predictions, this model provides essential insights for environmental management strategies. It can be used to guide infrastructure development in flood-prone areas, support water resource allocation during droughts, and inform policies aimed at mitigating the effects of climate change on water systems. The ability to adapt to changing environmental conditions positions this model as a critical tool for sustainable water resource management and ecological conservation.
In future work, we aim to advance our innovative rainfall–runoff model based on spatial-attention-based TLSTM by addressing several key areas. First, we plan to integrate real-time data assimilation to enhance the model responsiveness to changing weather patterns and catchment conditions. This integration could significantly improve the model predictive accuracy in real-world scenarios. Second, we intend to explore the application of our model to a wider range of climatic and geographical conditions. By testing and refining the model across diverse basins with varying hydrological characteristics, we can better understand its strengths and limitations, leading to more robust and universally applicable models. Additionally, we will investigate the potential of incorporating other forms of machine learning and artificial intelligence techniques, such as reinforcement learning and deep belief networks, to further improve the model’s performance. This could involve developing hybrid models that combine the strengths of different approaches.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs16203889/s1.
Author Contributions
Writing—original draft, B.G.; Writing—review & editing, B.G. and J.S.-S.; Supervision, J.S.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Spanish Ministry of Science and Innovation (MICINN) and by the European Regional Development Fund (FEDER), funded by MCIN/AEI/10.13039/501100011033/FEDER, UE, under grant PID2021-125258OB-I00, and by the Catalan Government under Grant SGR2021-00643.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, J.; Brown, A.; Wang, L. A Hybrid Approach Combining Conceptual Hydrological Models, Support Vector Machines, and Remote Sensing Data for Rainfall-Runoff Modeling. J. Hydrol. 2022, 12, 123–136. [Google Scholar]
- Anderson, J.; Clark, P. Hydrologically informed machine learning for rainfall-runoff modelling: Towards distributed modelling. Hydrol. Earth Syst. Sci. 2023, 18, 4373–4401. [Google Scholar]
- Salloom, O.; Kaynak, O.; He, W. A novel deep neural network architecture for real-time water demand forecasting. J. Hydrol. 2021, 599, 126353. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Khan, A.; Zhang, Y.-K.; Kuang, X.; Liang, X.; Taccari, M.L.; Nuttall, J. Daily runoff forecasting by deep recursive neural network. J. Hydrol. 2021, 596, 126067. [Google Scholar]
- Solgi, R.; Loaiciga, H.A.; Kram, M. Long short-term memory neural network (LSTM-NN) for aquifer level time series forecasting using in-situ piezometric observations. J. Hydrol. 2021, 601, 126800. [Google Scholar] [CrossRef]
- Lees, T.; Buechel, M.; Anderson, B.; Slater, L.; Reece, S.; Coxon, G.; Dadson, S.J. Benchmarking data-driven rainfall-runoff models in Great Britain: A comparison of long short-term memory (LSTM)-based models with four lumped conceptual models. Hydrol. Earth Syst. Sci. 2021, 25, 5517–5534. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, D.; Wang, G.; Qiu, J.; Long, K.; Du, Y.; Xie, H.; Wei, Z.; Shangguan, W.; Dai, Y. A hybrid deep learning algorithm and its application to streamflow prediction. J. Hydrol. 2021, 601, 126636. [Google Scholar] [CrossRef]
- Nourani, V.; Behfar, N. Multi-station runoff-sediment modeling using seasonal LSTM models. J. Hydrol. 2021, 601, 126672. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Kao, I.-F.; Liou, J.-Y.; Lee, M.-H.; Chang, F.-J. Fusing stacked autoencoder and long short-term memory for regional multistep-ahead flood inundation forecasts. J. Hydrol. 2021, 598, 126371. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. LSTM can solve hard long time lag problems. Adv. Neural Inf. Process. Syst. 1996, 9, 473–479. [Google Scholar]
- Wang, S.; Li, Z.; Ding, C.; Yuan, B.; Qiu, Q.; Wang, Y.; Liang, Y. C-LSTM: Enabling efficient LSTM using structured compression techniques on FPGAs. In Proceedings of the 2018 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 25–27 February 2018; pp. 11–20. [Google Scholar]
- Momoi, M.; Kotsuki, S.; Kikuchi, R.; Watanabe, S.; Yamada, M.; Abe, S. Emulating Rainfall-Runoff-Inundation Model Using Deep Neural Network with Dimensionality Reduction. Artif. Intell. Earth Syst. 2023, 2, e220036. [Google Scholar] [CrossRef]
- Young, S.R.; Rose, D.C.; Karnowski, T.P.; Lim, S.-H.; Patton, R.M. Optimizing deep learning hyper-parameters through an evolutionary algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15 November 2015; pp. 1–5. [Google Scholar]
- Zhou, F.; Chen, Y.; Liu, J. Application of a New Hybrid Deep Learning Model That Considers Temporal and Feature Dependencies in Rainfall–Runoff Simulation. Remote Sens. 2023, 15, 1395. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, Y.; Liu, Z. Using Remote Sensing Techniques to Improve Hydrological Predictions in a Rapidly Changing World. Hydrol. Sci. J. 2021, 15, 256–271. [Google Scholar] [CrossRef]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. The CAMELS data set: Catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 2017, 21, 5293–5313. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wei, Y.; Devarakonda, R.; Vose, R.S.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-Km Grid for North America, Version 2; Oak Ridge National Lab (ORNL): Oak Ridge, TN, USA, 2014. [Google Scholar]
- Maurer, E.P.; Wood, A.W.; Adam, J.C.; Lettenmaier, D.P.; Nijssen, B. A long-term hydrologically based dataset of land surface fluxes and states for the conterminous United States. J. Clim. 2002, 15, 3237–3251. [Google Scholar]
- Massari, C.; Brocca, L.; Tarpanelli, A.; Moramarco, T. Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe? Remote Sens. 2023, 15, 11403. [Google Scholar] [CrossRef]
- Khan, M.; Rehman, N.; Hussain, A. Rainfall-Runoff Modeling Using Machine Learning in the Ungauged Urban Watershed of Quetta Valley, Balochistan (Pakistan); Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Bean, J.C. Genetic algorithms and random keys for sequencing and optimization. ORSA J. Comput. 1994, 6, 154–160. [Google Scholar] [CrossRef]
- Shrestha, S.G.; Pradhanang, S.M. Performance of LSTM over SWAT in Rainfall-Runoff Modeling in a Small, Forested Watershed: A Case Study of Cork Brook, RI. Remote Sens. 2023, 15, 4194. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Lobo, F.G.; Harik, G.R. The Compact Genetic Algorithm. IEEE Trans. Evol. Comput. 1999, 3, 287–297. [Google Scholar] [CrossRef]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the choice of calibration metrics for “high-flow” estimation using hydrologic models. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef]
- Yin, H.; Guo, Z.; Zhang, X.; Chen, J.; Zhang, Y. RR-Former: Rainfall-runoff modeling based on Transformer. J. Hydrol. 2022, 609, 127781. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, X.; Wang, F.; Zhang, Y.; Xia, R.; Jin, J. Rainfall-runoff modeling using LSTM-based multi-state-vector sequence-to-sequence model. J. Hydrol. 2021, 598, 126378. [Google Scholar] [CrossRef]
- Seibert, J.; Vis, M.J.P.; Lewis, E.; van Meerveld, H.; Meerveld, I. Upper and lower benchmarks in hydrological modelling. Hydrol. Process. 2018, 32, 1120–1125. [Google Scholar] [CrossRef]
- Rakovec, O.; Mizukami, N.; Kumar, R.; Newman, A.J.; Thober, S.; Wood, A.W.; Clark, M.P.; Samaniego, L. Diagnostic evaluation of large-domain hydrologic models calibrated across the contiguous United States. J. Geophys. Res. Atmos. 2019, 124, 13991–14007. [Google Scholar] [CrossRef]
- Mizukami, N.; Clark, M.P.; Newman, A.J.; Wood, A.W.; Gutmann, E.D.; Nijssen, B.; Rakovec, O.; Samaniego, L. Towards seamless large-domain parameter estimation for hydrologic models. Water Resour. Res. 2017, 53, 8020–8040. [Google Scholar] [CrossRef]
- Newman, A.J.; Mizukami, N.; Clark, M.P.; Wood, A.W.; Nijssen, B.; Nearing, G. Benchmarking of a physically based hydrologic model. J. Hydrometeorol. 2017, 18, 2215–2225. [Google Scholar] [CrossRef]
- Feng, D.; Fang, K.; Shen, C. Enhancing Streamflow Forecast and Extracting Insights Using Long-Short Term Memory Networks with Data Integration at Continental Scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).