CDP-MVS: Forest Multi-View Reconstruction with Enhanced Confidence-Guided Dynamic Domain Propagation
Abstract
1. Introduction
- (1)
- To reduce the impact of plot slope on image quality and to efficiently acquire image datasets, we designed a novel method for creating forest image datasets. This method involves filming a video around the forest plot twice—once inside and once outside the plot—and then using batch processing code to extract video frames at a custom frequency, achieving the goal of semi-automated dataset creation.
- (2)
- We proposed a multi-view reconstruction algorithm, CDP-MVS, tailored for forest surveys. This algorithm aims to reduce the interference of sky information on forest reconstruction, minimize reconstruction errors caused by uneven lighting, and alleviate the issue of prolonged reconstruction times for large plots. As a result, it significantly enhances both the accuracy and efficiency of forest reconstruction.
2. Materials and Methods
2.1. Study Area
2.2. Method
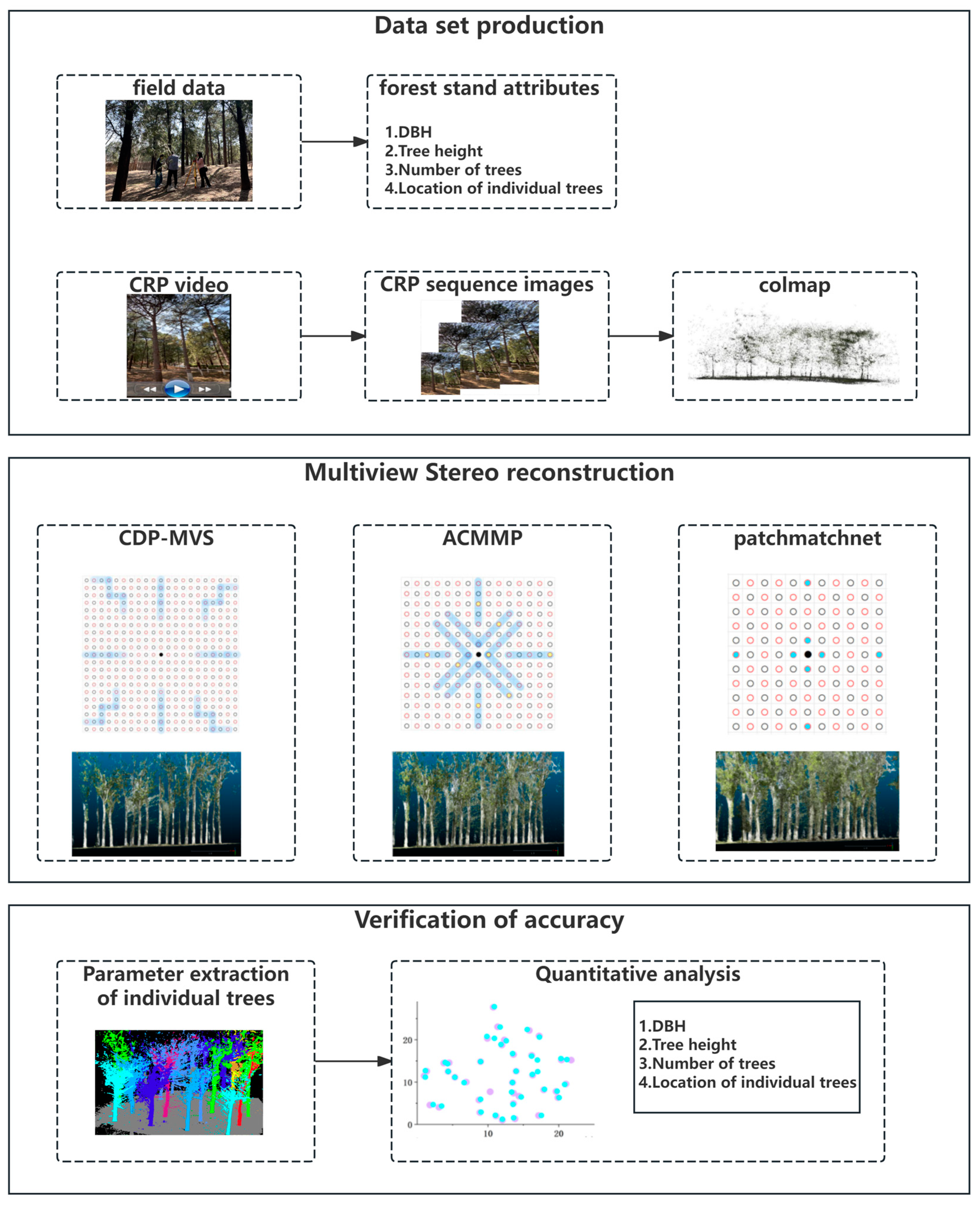
2.2.1. Dataset Creation
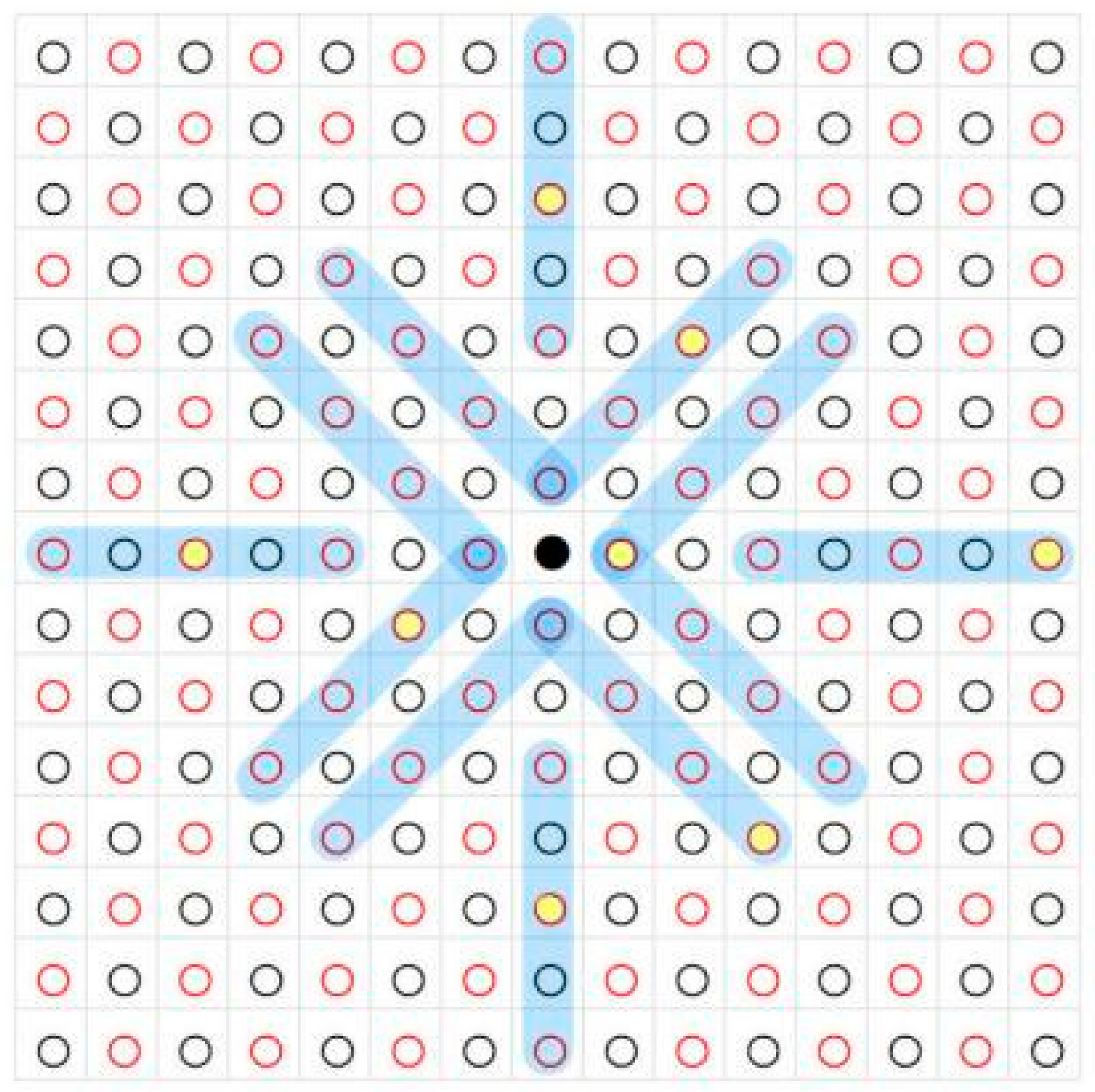
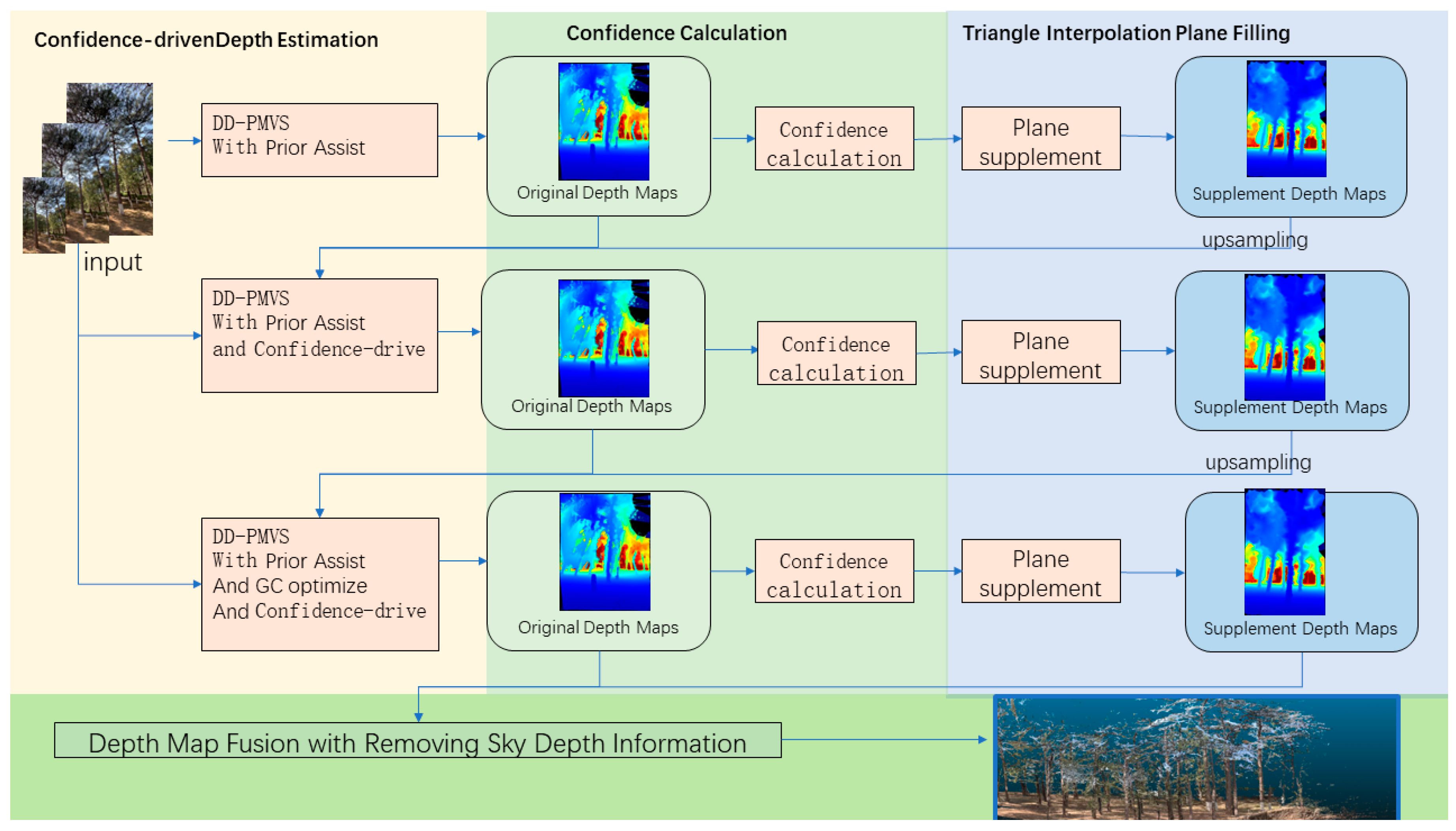
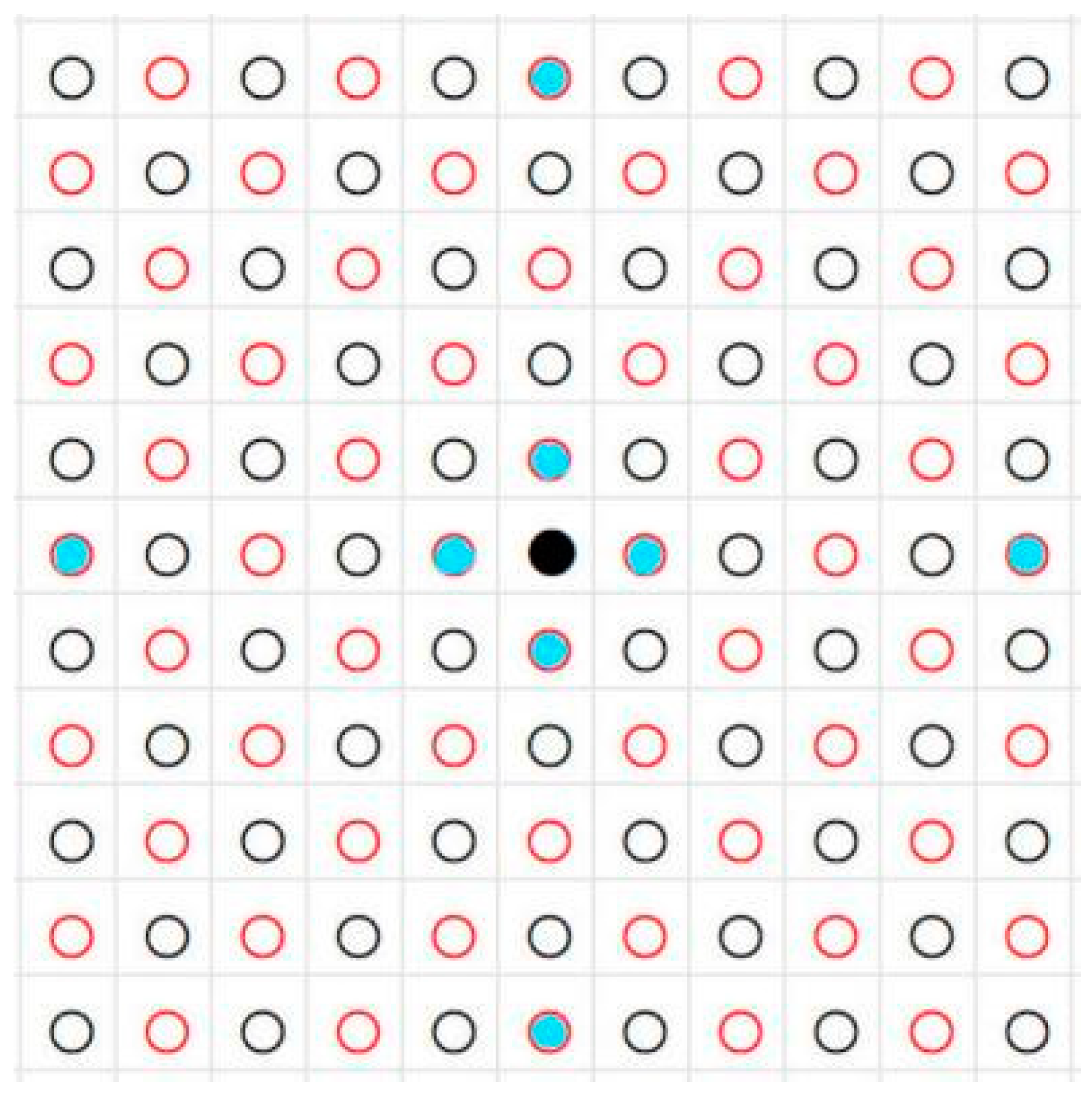
2.2.2. Multi-View Reconstruction
- i.
- ACMMP
- ii.
- CDP-MVS
- iii.
- PatchMatchNet
2.2.3. Accuracy Validation
3. Results
3.1. Visualization Results
3.2. Reconstruction Time Performance
3.3. Reconstructed Tree Quantity
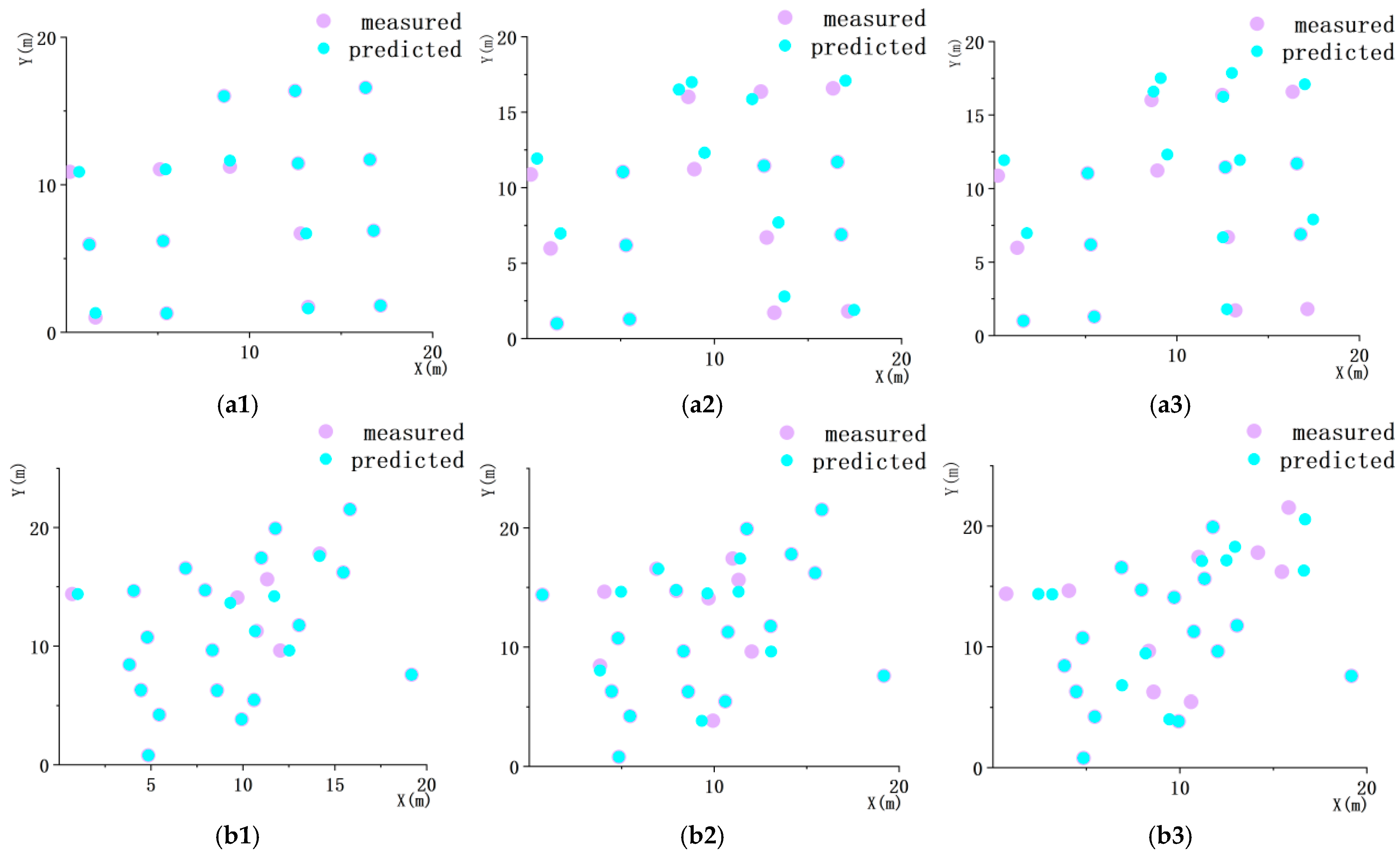
3.4. Reconstructed Tree Positions
3.5. Reconstructed Tree DBH
3.6. Reconstructed Tree Height
4. Discussion
4.1. Impact of Different Terrains on Reconstruction Results
4.2. Comparison between Traditional Block-Matching Geometric Reconstruction Models and Deep Learning Models
4.3. Research Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- You, L.; Tang, S.; Song, X.; Lei, Y.; Zang, H.; Lou, M.; Zhuang, C. Precise Measurement of Stem Diameter by Simulating the Path of Diameter Tape from Terrestrial Laser Scanning Data. Remote Sens. 2016, 8, 717. [Google Scholar] [CrossRef]
- Zhu, R.; Guo, Z.; Zhang, X. Forest 3D Reconstruction and Individual Tree Parameter Extraction Combining Close-Range Photo Enhancement and Feature Matching. Remote Sens. 2021, 13, 1633. [Google Scholar] [CrossRef]
- Yu, R.; Ren, L.; Luo, Y. Early Detection of Pine Wilt Disease in Pinus Tabuliformis in North China Using a Field Portable Spectrometer and UAV-Based Hyperspectral Imagery. For. Ecosyst. 2021, 8, 44. [Google Scholar] [CrossRef]
- Akay, A.E.; Oğuz, H.; Karas, I.R.; Aruga, K. Using LiDAR Technology in Forestry Activities. Environ. Monit. Assess. 2009, 151, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Zhang, X.; Zhou, X.; Yin, T. Extraction of topographic information of larch plantation by oblique photogrammetry. J. Beijing For. Univ. 2019, 41, 1–12. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Photo Tourism: Exploring Photo Collections in 3D. In Proceedings of the SIGGRAPH, Boston, MA, USA, 30 July–3 August 2006; pp. 835–846. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Heinly, J.; Schonberger, J.L.; Dunn, E.; Frahm, J.M. Reconstructing the World in Six Days (as Captured by the Yahoo 100 Million Image Dataset). In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3287–3295. [Google Scholar]
- Schönberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Cui, H. Fast and Robust Large-Scale 3D Reconstruction. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2016. [Google Scholar]
- Slocum, R.K.; Parrish, C.E. Simulated Imagery Rendering Workflow for Uas-Based Photogrammetric 3d Reconstruction Accuracy Assessments. Remote Sens. 2017, 9, 396. [Google Scholar] [CrossRef]
- Moulon, P.; Monasse, P.; Marlet, R. Adaptive Structure from Motion with a Contrario Model Estimation. In Proceedings of the Asian Conference on Computer Vision (ACCV), Taipei, Taiwan, 20–24 November 2016; pp. 257–272. [Google Scholar] [CrossRef]
- Wu, C. Towards Linear-Time Incremental Structure from Motion. In Proceedings of the 3DV 2013—International Conference on 3D Vision, Seattle, WA, USA, 29 June–1 July 2013; pp. 127–134. [Google Scholar] [CrossRef]
- Xu, H.; Tao, W.; Gao, X. ACMMP: Adaptive Checkerboard Matching and Multi-scale Planar Prior for Multi-view Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 6638–6647. [Google Scholar] [CrossRef]
- Yan, X.; Chai, G.; Han, X.; Lei, L.; Wang, G.; Jia, X.; Zhang, X. SA-Pmnet: Utilizing Close-Range Photogrammetry Combined with Image Enhancement and Self-Attention Mechanisms for 3D Reconstruction of Forests. Remote Sens. 2024, 16, 416. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y.; Kang, S.B.; Shum, H.-Y. Symmetric Stereo Matching for Occlusion Handling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; pp. 399–406. [Google Scholar]
- Kang, S.B.; Szeliski, R.; Chai, J. Handling Occlusions in Dense Multi-view Stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001; p. I-I. [Google Scholar]
- Strecha, C.; Fransens, R.; Van Gool, L. Wide-baseline Stereo from Multiple Views: A Probabilistic Account. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, WA, USA, 27 June–2 July 2004; p. I-I. [Google Scholar]
- Xu, Q.; Tao, W. Multi-Scale Geometric Consistency Guided Multi-View Stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Cheng, S.; Xu, Z.; Zhu, S.; Li, Z.; Li, L.E.; Ramamoorthi, R.; Su, H. Deep Stereo using Adaptive Thin Volume Representation with Uncertainty Awareness. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2524–2534. [Google Scholar]
- Aanæs, H.; Jensen, R.R.; Vogiatzis, G.; Tola, E.; Dahl, A.B. Large-Scale Data for Multiple-View Stereopsis. Int. J. Comput. Vis. 2016, 120, 153–168. [Google Scholar] [CrossRef]
- Keskar, N.S.; Mudigere, D.; Nocedal, J.; Smelyanskiy, M.; Tang, P.T.P. On Large-batch Training for Deep Learning: Generalization Gap and Sharp Minima. arXiv 2016, arXiv:1609.04836. [Google Scholar]
- Collins, A.R. A space-sweep approach to true multi-image matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 358–363. [Google Scholar]
- Baillard, C.; Zisserman, A. A plane-sweepstrategy for the 3d reconstruction of buildings from multiple images. Int. Arch. Photogramm. Remote Sens. 2000, 33, 56–62. [Google Scholar]
- Gallup, D.; Frahm, J.-M.; Mordohai, P.; Yang, Q.; Pollefeys, M. Real-time planesweeping stereo with multiple sweeping directions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Galliani, S.; Lasinger, K.; Schindler, K. Massively parallel multiview stereopsis by surface normal diffusion. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 873–881. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Frahm, J.-M.; Pollefeys, M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the IEEE European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 501–518. [Google Scholar]
- Wang, Z.; Galliani, J.; Vogel, S.; Rhemann, C.; Tankovich, V.; Theobalt, C. PatchMatchNet: Learned Multi-View PatchMatch Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14194–14203. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Fu, C.; Huang, N.; Huang, Z.; Liao, Y.; Xiong, X.; Zhang, X.; Cai, S. Confidence-Guided Planar-Recovering Multiview Stereo for Weakly Textured Plane of High-Resolution Image Scenes. Remote Sens. 2023, 15, 2474. [Google Scholar] [CrossRef]
- Yu, A.; Bi, H.; Jing, L. Scene-aware refinement network for unsupervised monocular depth estimation in ultra-low altitude oblique photography of UAV. ISPRS J. Photogramm. Remote Sens. 2023, 205, 284–300. [Google Scholar] [CrossRef]
- Germain, H.; Lepetit, V.; Bourmaud, G. Neural Reprojection Error: Merging Feature Learning and Camera Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar] [CrossRef]
- Ren, C.; Xu, Q.; Zhang, S.; Yang, J. Hierarchical Prior Mining for Non-local Multi-View Stereo. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023. [Google Scholar] [CrossRef]
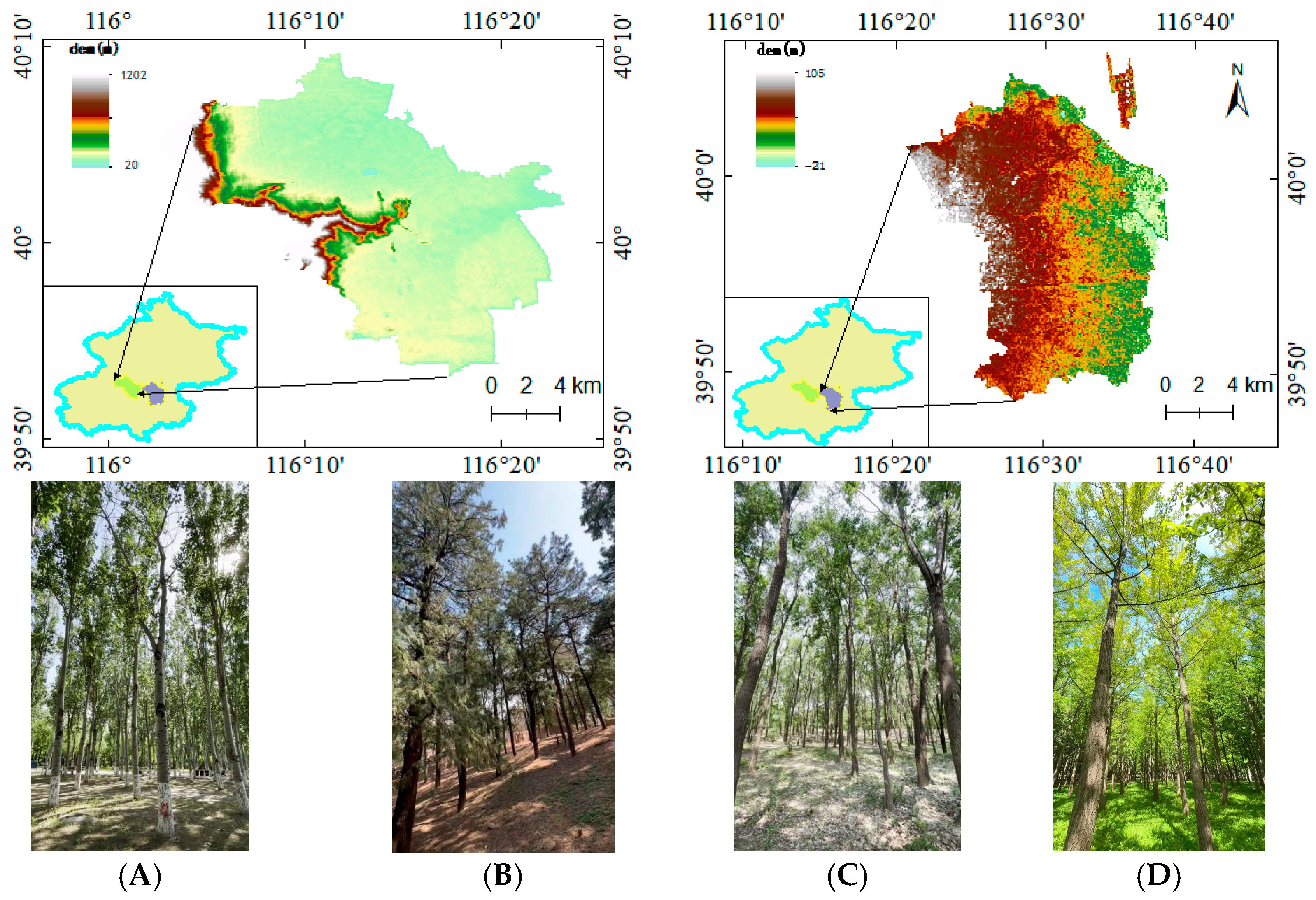











| Sample Plot | Stand Type | Region | Slope (◦) | Tree Count |
|---|---|---|---|---|
| A | Poplar | Dongsheng Bajia Park | 6 | 16 |
| B | Pine | Jiufeng | 36 | 24 |
| C | Elm | Olympic Forest Park | 11 | 38 |
| D | Ginkgo | Olympic Forest Park | 21 | 23 |
| Method | Poplar | Pine | Elm | Ginkgo |
|---|---|---|---|---|
| CDP-MVS | 3.1 | 1.8 | 2.5 | 2.1 |
| ACMMP | 3.2 | 1.8 | 2.68 | 2.23 |
| PatchMatchNet | 8.35 | 6.43 | 6.03 | 6.57 |
| Stand Type | Method | Reconstructed Count | Surveyed Count | QAE |
|---|---|---|---|---|
| Poplar | CDP-MVS | 16 | 16 | 100.00% |
| ACMMP | 17 | 93.75% | ||
| PatchMatchNet | 19 | 81.25% | ||
| Pine | CDP-MVS | 24 | 24 | 100.00% |
| ACMMP | 24 | 100.00% | ||
| PatchMatchNet | 25 | 95.83% | ||
| Elm | CDP-MVS | 38 | 38 | 100.00% |
| ACMMP | 41 | 92.11% | ||
| PatchMatchNet | 44 | 84.21% | ||
| Ginkgo | CDP-MVS | 23 | 23 | 100.00% |
| ACMMP | 25 | 91.30% | ||
| PatchMatchNet | 26 | 86.97% |
| Method | Poplar | Pine | Elm | Ginkgo |
|---|---|---|---|---|
| CDP-MVS | 0.14 | 0.25 | 0.19 | 0.13 |
| ACMMP | 0.51 | 0.32 | 0.37 | 0.46 |
| PatchMatchNet | 0.52 | 0.45 | 0.67 | 0.57 |
| Stand Type | Method | Reconstructed Mean DBH | Measured Mean DBH | AE |
|---|---|---|---|---|
| Poplar | CDP-MVS | 22.13 | 22.23 | 96.27% |
| ACMMP | 22.08 | 95.85% | ||
| PatchMatchNet | 23.17 | 94.44% | ||
| Pine | CDP-MVS | 19.52 | 20.68 | 90.00% |
| ACMMP | 19.43 | 89.76% | ||
| PatchMatchNet | 21.5 | 93.78% | ||
| Elm | CDP-MVS | 21.3 | 19.62 | 90.64% |
| ACMMP | 21.07 | 88.55% | ||
| PatchMatchNet | 21.82 | 90.09% | ||
| Ginkgo | CDP-MVS | 19.27 | 20.37 | 93.62% |
| ACMMP | 18.58 | 90.25% | ||
| PatchMatchNet | 22.05 | 89.27% |
| Stand Type | Method | Reconstructed Mean Height | Measured Mean Height | HAE |
|---|---|---|---|---|
| Poplar | CDP-MVS | 17.88 | 22.23 | 4.35 |
| ACMMP | 18.07 | 4.16 | ||
| PatchMatchNet | 17.67 | 4.56 | ||
| Pine | CDP-MVS | 8.89 | 11.05 | 2.16 |
| ACMMP | 8.79 | 2.26 | ||
| PatchMatchNet | 8.44 | 2.61 | ||
| Elm | CDP-MVS | 20.76 | 26.31 | 5.55 |
| ACMMP | 21.09 | 5.22 | ||
| PatchMatchNet | 21.52 | 4.79 | ||
| Ginkgo | CDP-MVS | 17.07 | 21.65 | 4.58 |
| ACMMP | 17.19 | 4.46 | ||
| PatchMatchNet | 17.42 | 4.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Chen, Z.; Zhang, X.; Cheng, S. CDP-MVS: Forest Multi-View Reconstruction with Enhanced Confidence-Guided Dynamic Domain Propagation. Remote Sens. 2024, 16, 3845. https://doi.org/10.3390/rs16203845
Liu Z, Chen Z, Zhang X, Cheng S. CDP-MVS: Forest Multi-View Reconstruction with Enhanced Confidence-Guided Dynamic Domain Propagation. Remote Sensing. 2024; 16(20):3845. https://doi.org/10.3390/rs16203845
Chicago/Turabian StyleLiu, Zitian, Zhao Chen, Xiaoli Zhang, and Shihan Cheng. 2024. "CDP-MVS: Forest Multi-View Reconstruction with Enhanced Confidence-Guided Dynamic Domain Propagation" Remote Sensing 16, no. 20: 3845. https://doi.org/10.3390/rs16203845
APA StyleLiu, Z., Chen, Z., Zhang, X., & Cheng, S. (2024). CDP-MVS: Forest Multi-View Reconstruction with Enhanced Confidence-Guided Dynamic Domain Propagation. Remote Sensing, 16(20), 3845. https://doi.org/10.3390/rs16203845







