Retrieval of Solar Shortwave Irradiance from All-Sky Camera Images
Abstract
1. Introduction
2. Instrumentation and Sites
2.1. Instruments
2.2. Sites
3. Method
3.1. Dataset
3.1.1. Initial Dataset and Data Filtering
3.1.2. CMF Calculation and Data Classification
3.2. Model
3.3. Test Set
4. Results
4.1. SW Irradiance
4.2. Daily SW Irradiation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Acronyms
| AEMet | Meteorological State Agency of Spain |
| AERONET | Aerosol Robotic Network |
| BRDF | Bi-directional Reflectance Distribution Function |
| BSRN | Baseline Surface Radiation Network |
| CC | Cloud Cover |
| CMF | Cloud Modification Factor |
| CMFGHI | Cloud Modification Factor for Global Horizontal Irradiance |
| CNN | Convolutional Neural Network |
| CNN-CC | Convolutional Neural Network-Cloud Cover |
| CNN-CMF | Convolutional Neural Network-Cloud Modification Factor |
| DNA | Argentinian National Direction of the Antarctic |
| DWD | Deutscher Wetterdienst—Germany Weather Service |
| FMI | Finnish Meteorological Institute |
| GHI | Global Horizontal Irradiance |
| GHIcf | Global Horizontal Irradiance under cloud-free conditions |
| GHId | Daily Global Horizontal Irradiation |
| GHImeas | Global Horizontal Irradiance under cloudy conditions |
| GOA-UVa | Group of Atmospheric Optics of the University of Valladolid |
| GRUAN | The Global Climate Observing System (GCOS) Reference Upper-Air Network |
| HDR | High Dynamic Range |
| LW | Longwave |
| MBE | Mean Bias Error |
| MODIS | Moderate-Resolution Imaging Spectroradiometer |
| MOL-RAO | Meteorologisches Observatorium Lindenberg—Richard-Aßmann-Observatorium |
| OMI-DOAS | Ozone Monitoring System Differential Optical Absorption Spectroscopy |
| RGGB | Red Green Green Blue |
| RTM | Radiative Transfer Models |
| SBDART | Santa Barbara DISORT Atmospheric Radiative Transfer |
| SD | Standard Deviation |
| SMN | National Meteorological Service of Argentina |
| SW | Shortwave |
| SZA | Solar Zenith Angle |
| WCRP | World Climate Research Program |
| WMO | World Meteorological Organization |
References
- de La Casiniere, A.; Cachorro, V. La Radiación Solar en el Sistema Tierra-Atmósfera; Ediciones Universidad de Valladolid: Valladolid, Spain, 2008. [Google Scholar]
- Liou, K.N. An Introduction to Atmospheric Radiation, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Stone, R.; Mefford, T.; Dutton, E.; Longenecker, D.; Halter, B.; Endres, D. Surface Radiation and Meteorological Measurements: January 1992 to December 1994; NOAA Data Report ERL-CMDL-11; Climate Monitoring and Diagnosis Laboratory: Boulder, CO, USA, 1996; p. 81. [Google Scholar]
- Goosse, H.; Kay, J.; Armour, K.; Bodas-Salcedo, A.; Chepfer, H.; Docquier, D.; Jonko, A.; Kushner, P.; Lecomte, O.; Massonnet, F.; et al. Quantifying climate feedbacks in polar regions. Nat. Commun. 2018, 9, 1919. [Google Scholar] [CrossRef] [PubMed]
- Korevaar, M.A.N. Measuring Solar Irradiance for Photovoltaics. In Solar Radiation—Measurement, Modeling and Forecasting Techniques for Photovoltaic Solar Energy Applications; IntechOpen: London, UK, 2022; Chapter 2. [Google Scholar] [CrossRef]
- Calbó, J.; Pagès, D.; González, J.A. Empirical studies of cloud effects on UV radiation: A review. Rev. Geophys. 2005, 43, RG2002. [Google Scholar] [CrossRef]
- Stanhill, G.; Cohen, S. Global dimming: A review of the evidence for a widespread and significant reduction in global radiation. Agric. For. Meteorol. 2001, 107, 255–278. [Google Scholar] [CrossRef]
- Wild, M.; Gilgen, H.; Roesch, A.; Ohmura, A.; Long, C.N.; Dutton, E.G.; Forgan, B.; Kallis, A.; Russak, V.; Tsvetkov, A. From dimming to brightening: Decadal changes in solar radiation at Earth’s surface. Science 2005, 308, 847–850. [Google Scholar] [CrossRef] [PubMed]
- Wild, M. Global dimming and brightening: A review. J. Geophys. Res. 2009, 114, D00D16. [Google Scholar] [CrossRef]
- Wild, M.; Trüssel, B.; Ohmura, A.; Long, C.N.; Dutton, E.G.; König Langlo, G.; Tsvetkov, A. Global dimming and brightening: An update beyond 2000. J. Geophys. Res. 2009, 114, D00D13. [Google Scholar] [CrossRef]
- Wild, M. Enlightening global dimming and brightening. Bull. Amer. Meteor. Soc. 2012, 93, 27–37. [Google Scholar] [CrossRef]
- Sánchez-Lorenzo, A.; Calbó, J.; Brunetti, M.; Deser, C. Dimming/brightening over the Iberian Peninsula: Trends in sunshine duration and cloud cover and their relations with atmospheric circulation. J. Geophys. Res. 2009, 114, D00D09. [Google Scholar] [CrossRef]
- Román, R.; Cazorla, A.; Toledano, C.; Olmo, F.; Cachorro, V.; de Frutos, A.; Alados-Arboledas, L. Cloud cover detection combining high dynamic range sky images and ceilometer measurements. Atmos. Res. 2017, 196, 224–236. [Google Scholar] [CrossRef]
- Román, R.; Antuña Sánchez, J.C.; Cachorro, V.E.; Toledano, C.; Torres, B.; Mateos, D.; Fuertes, D.; López, C.; González, R.; Lapionok, T.; et al. Retrieval of aerosol properties using relative radiance measurements from an all-sky camera. Atmos. Meas. Tech. 2022, 15, 407–433. [Google Scholar] [CrossRef]
- González-Fernández, D.; Román, R.; Antuña-Sánchez, J.C.; Cachorro, V.E.; Copes, G.; Herrero-Anta, S.; Herrero-del Barrio, C.; Barreto, A.; González, R.; Ramos; et al. A neural network to retrieve cloud cover from all-sky cameras: A case of study over Antarctic. Q. J. R. Meteorol. Soc. 2024. under review. [Google Scholar] [CrossRef]
- Antuña-Sánchez, J.C.; Román, R.; Bosch, J.; Toledano, C.; Mateos, D.; González, R.; Cachorro, V.E.; de Frutos, A.M. ORION software tool for the geometrical calibration of all-sky cameras. PLoS ONE 2022, 17, e0265959. [Google Scholar] [CrossRef] [PubMed]
- Alcor System. OMEA “All Sky” Camera Installation and User Manual; Alcor System: Lyon, France, 2022. [Google Scholar]
- Antuña-Sánchez, J.C.; Román, R.; Cachorro, V.E.; Toledano, C.; López, C.; González, R.; Mateos, D.; Calle, A.; de Frutos, A.M. Relative sky radiance from multi-exposure all-sky camera images. Atmos. Meas. Tech. 2021, 14, 2201–2217. [Google Scholar] [CrossRef]
- Antuña-Sánchez, J.C. Configuración y Metodología para el Uso de Cámaras de Todo Cielo en la Obtención de Parámetros Atmosféricos. Ph.D. Thesis, School of the University of Valladolid, Valladolid, Spain, 2022. [Google Scholar]
- Kipp & Zonen. Instruction Manual CMP Series Pyranometer/CMA Series Albedometer; Kipp & Zonen: Delft, The Netherlands, 2013. [Google Scholar]
- Kipp & Zonen. Instruction Manual CM21 Precision Pyranometer; Kipp & Zonen: Delft, The Netherlands, 2004. [Google Scholar]
- Kipp & Zonen. Instruction Manual CM22 Precision Pyranometer; Kipp & Zonen: Delft, The Netherlands, 2004. [Google Scholar]
- García, R.D.; Cuevas, E.; Ramos, R.; Cachorro, V.E.; Redondas, A.; Moreno-Ruiz, J.A. Description of the Baseline Surface Radiation Network (BSRN) station at the Izaña Observatory (2009–2017): Measurements and quality control/assurance procedures. Geosci. Instrum. Methods Data Syst. 2019, 8, 77–96. [Google Scholar] [CrossRef]
- Eko Instruments Co. Instruction Manual Pyranometer MS-802/402/410/602 with Ventilator: MS-802F/402F Version: 9; Eko Instruments Co., Ltd.: Tokyo, Japan, 2015. [Google Scholar]
- Bennouna, Y.; Cachorro, V.; Mateos, D.; Burgos, M.; Toledano, C.; Torres, B.; de Frutos, A. Long-term comparative study of columnar and surface mass concentration aerosol properties in a background environment. Atmos. Environ. 2016, 140, 261–272. [Google Scholar] [CrossRef]
- Román, R.; Bilbao, J.; de Miguel, A. Uncertainty and variability in satellite-based water vapor column, aerosol optical depth and Angström exponent, and its effect on radiative transfer simulations in the Iberian Peninsula. Atmos. Environ. 2014, 89, 556–569. [Google Scholar] [CrossRef]
- Cachorro, V.E.; Burgos, M.A.; Mateos, D.; Toledano, C.; Bennouna, Y.; Torres, B.; de Frutos, A.M.; Herguedas, A. Inventory of African desert dust events in the north-central Iberian Peninsula in 2003–2014 based on sun-photometer–AERONET and particulate-mass–EMEP data. Atmos. Chem. Phys. 2016, 16, 8227–8248. [Google Scholar] [CrossRef]
- Herrero-Anta, S.; Román, R.; Mateos, D.; González, R.; Antuña-Sánchez, J.C.; Herreras-Giralda, M.; Almansa, A.F.; González-Fernández, D.; del Barrio, C.H.; Toledano, C.; et al. Retrieval of aerosol properties from zenith sky radiance measurements. Atmos. Meas. Tech. 2023, 16, 4423–4443. [Google Scholar] [CrossRef]
- del Barrio, C.H.; Mateos, D.; Román, R.; González, R.; Herrero-Anta, S.; González-Fernández, D.; Calle, A.; Toledano, C.; Cachorro, V.E.; De Frutos Baraja, Á.M. Analysis of Daytime and Night-Time Aerosol Optical Depth from Solar and Lunar Photometry in Valladolid (Spain). Remote Sens. 2023, 15, 5362. [Google Scholar] [CrossRef]
- Toledano, C.; González, R.; Fuertes, D.; Cuevas, E.; Eck, T.F.; Kazadzis, S.; Kouremeti, N.; Gröbner, J.; Goloub, P.; Blarel, L.; et al. Assessment of Sun photometer Langley calibration at the high-elevation sites Mauna Loa and Izaña. Atmos. Chem. Phys. 2018, 18, 14555–14567. [Google Scholar] [CrossRef]
- Román, R.; González, R.; Toledano, C.; Barreto, A.; Pérez-Ramírez, D.; Benavent-Oltra, J.A.; Olmo, F.J.; Cachorro, V.E.; Alados-Arboledas, L.; de Frutos, A.M. Correction of a lunar-irradiance model for aerosol optical depth retrieval and comparison with a star photometer. Atmos. Meas. Tech. 2020, 13, 6293–6310. [Google Scholar] [CrossRef]
- Barreto, A.; García, R.D.; Guirado-Fuentes, C.; Cuevas, E.; Almansa, A.F.; Milford, C.; Toledano, C.; Expósito, F.J.; Díaz, J.P.; León-Luis, S.F. Aerosol characterisation in the subtropical eastern North Atlantic region using long-term AERONET measurements. Atmos. Chem. Phys. 2022, 22, 11105–11124. [Google Scholar] [CrossRef]
- Cuevas, E.; Milford, C.; Barreto, A.; Bustos, J.J.d.; García, O.E.; García, R.D.; Marrero, C.; Prats, N.; Ramos, R.; Redondas, A.; et al. Izaña Atmospheric Research Center. Activity Report 2021–2022; NIPO: 666-24-002-7; State Meteorological Agency (AEMet): Madrid, Spain; WMO/GAW: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]
- González, R.; Toledano, C.; Román, R.; Mateos, D.; Asmi, E.; Rodríguez, E.; Lau, I.C.; Ferrara, J.; D’Elia, R.; Antuña-Sánchez, J.C.; et al. Characterization of Stratospheric Smoke Particles over the Antarctica by Remote Sensing Instruments. Remote Sens. 2020, 12, 3769. [Google Scholar] [CrossRef]
- Debevec, P.E.; Malik, J. Recovering High Dynamic Range Radiance Maps from Photographs; Siggraph 97; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 1997. [Google Scholar]
- Reinhard, E.; Stark, M.; Shirley, P.; Ferwerda, J. Photographic tone reproduction for digital images. ACM Trans. Graph. 2002, 21, 267–276. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—Description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Kylling, A.; Stamnes, K.; Tsay, S. A reliable and efficient two-stream algorithm for spherical radiative transfer: Documentation of accuracy in realistic layered media. J. Atmos. Chem. 1995, 21, 115–150. [Google Scholar] [CrossRef]
- Kurucz, R.L. Synthetic Infrared Spectra. Symp. Int. Astron. Union 1994, 154, 523–531. [Google Scholar] [CrossRef]
- Schaaf, C.; Liu, J.; Gao, F.; Strahler, A.H. MODIS albedo and reflectance anisotropy products from Aqua and Terra. Land Remote Sens. Glob. Environ. Chang. NASA’s Earth Obs. Syst. Sci. ASTER MODIS 2011, 11, 549–561. [Google Scholar]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. SBDART: A Research and Teaching Software Tool for Plane-Parallel Radiative Transfer in the Earth’s Atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Román, R.; Bilbao, J.; de Miguel, A. Solar radiation simulations in the Iberian Peninsula: Accuracy and sensitivity to uncertainties in inputs of a radiative transfer model. J. Quant. Spectrosc. Radiat. Transf. 2014, 145, 95–109. [Google Scholar] [CrossRef]
- Piedehierro, A.; Antón, M.; Cazorla, A.; Alados-Arboledas, L.; Olmo, F. Evaluation of enhancement events of total solar irradiance during cloudy conditions at Granada (Southeastern Spain). Atmos. Res. 2014, 135–136, 1–7. [Google Scholar] [CrossRef]
- Pfister, G.; McKenzie, R.L.; Liley, J.B.; Thomas, A.; Forgan, B.W.; Long, C.N. Cloud Coverage Based on All-Sky Imaging and Its Impact on Surface Solar Irradiance. J. Appl. Meteorol. 2003, 42, 1421–1434. [Google Scholar] [CrossRef]
- Schade, N.H.; Macke, A.; Sandmann, H.; Stick, C. Enhanced solar global irradiance during cloudy sky conditions. Meteorol. Z. 2007, 16, 295–303. [Google Scholar] [CrossRef]
- Mateos, D.; Antón, M.; Valenzuela, A.; Cazorla, A.; Olmo, F.J.; Alados-Arboledas, L. Short-wave radiative forcing at the surface for cloudy systems at a midlatitude site. Tellus Ser. B Chem. Phys. Meteorol. 2013, 65, 21069. [Google Scholar] [CrossRef]
- Tzoumanikas, P.; Nikitidou, E.; Bais, A.; Kazantzidis, A. The effect of clouds on surface solar irradiance, based on data from an all-sky imaging system. Renew. Energy 2016, 95, 314–322. [Google Scholar] [CrossRef]


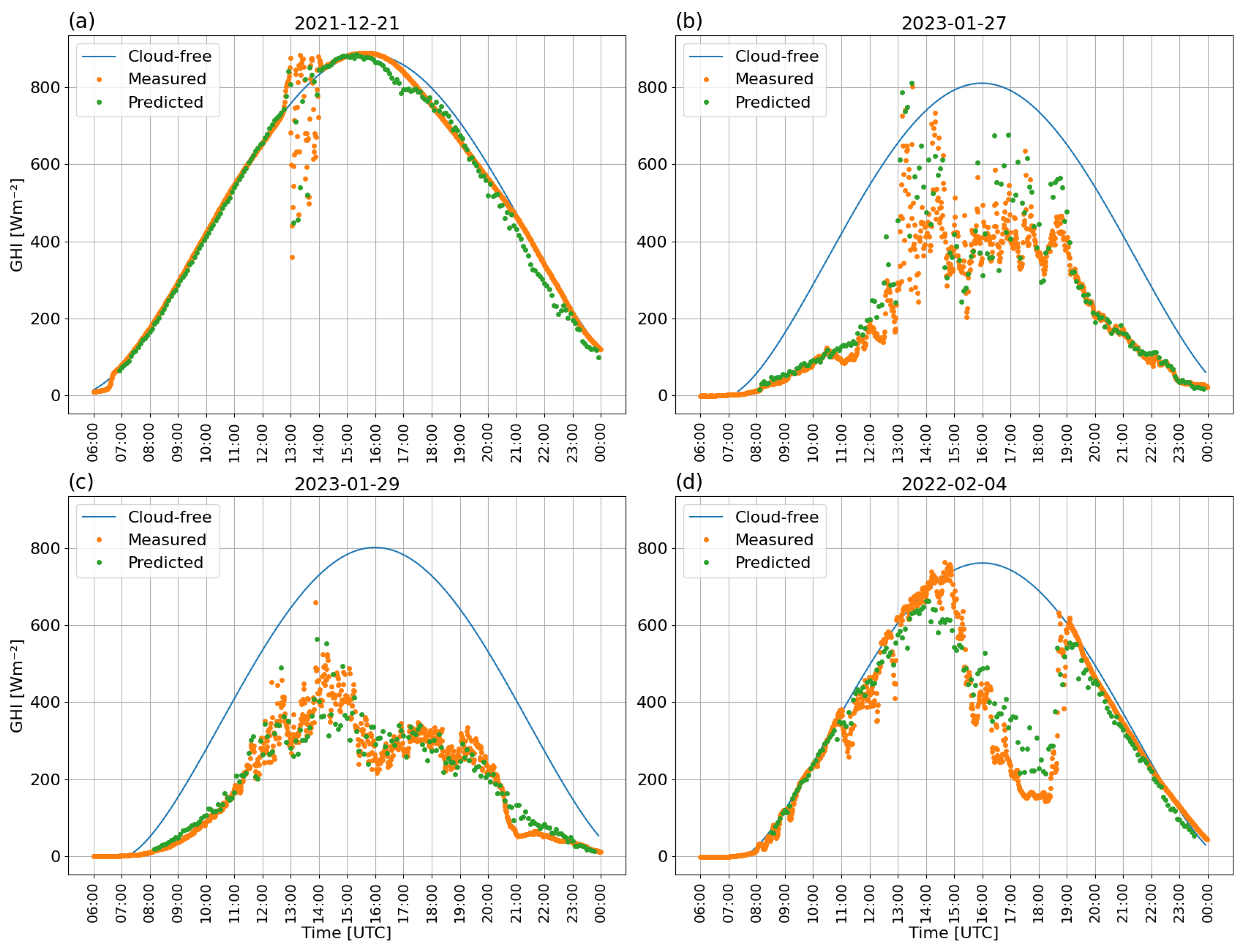
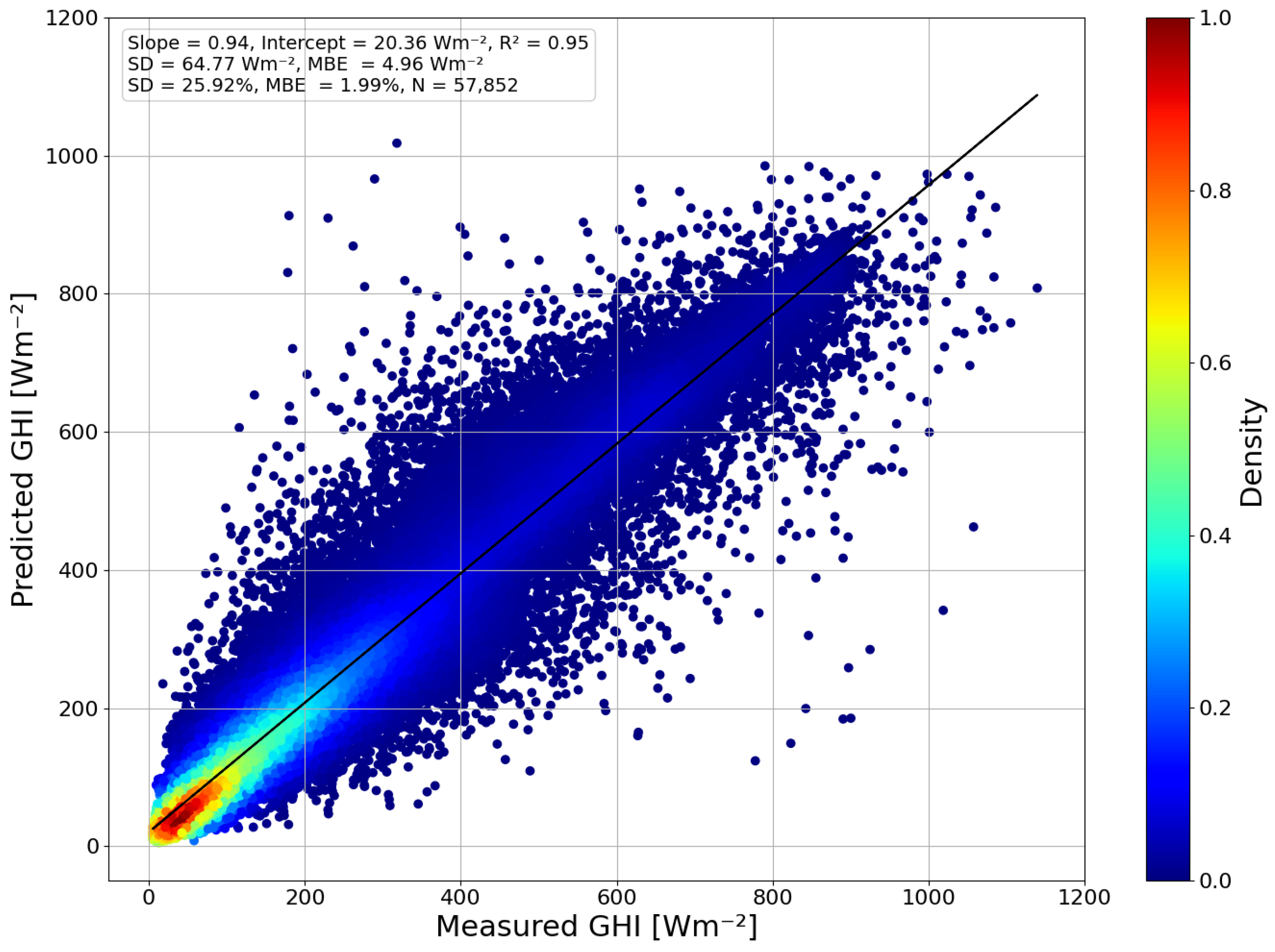

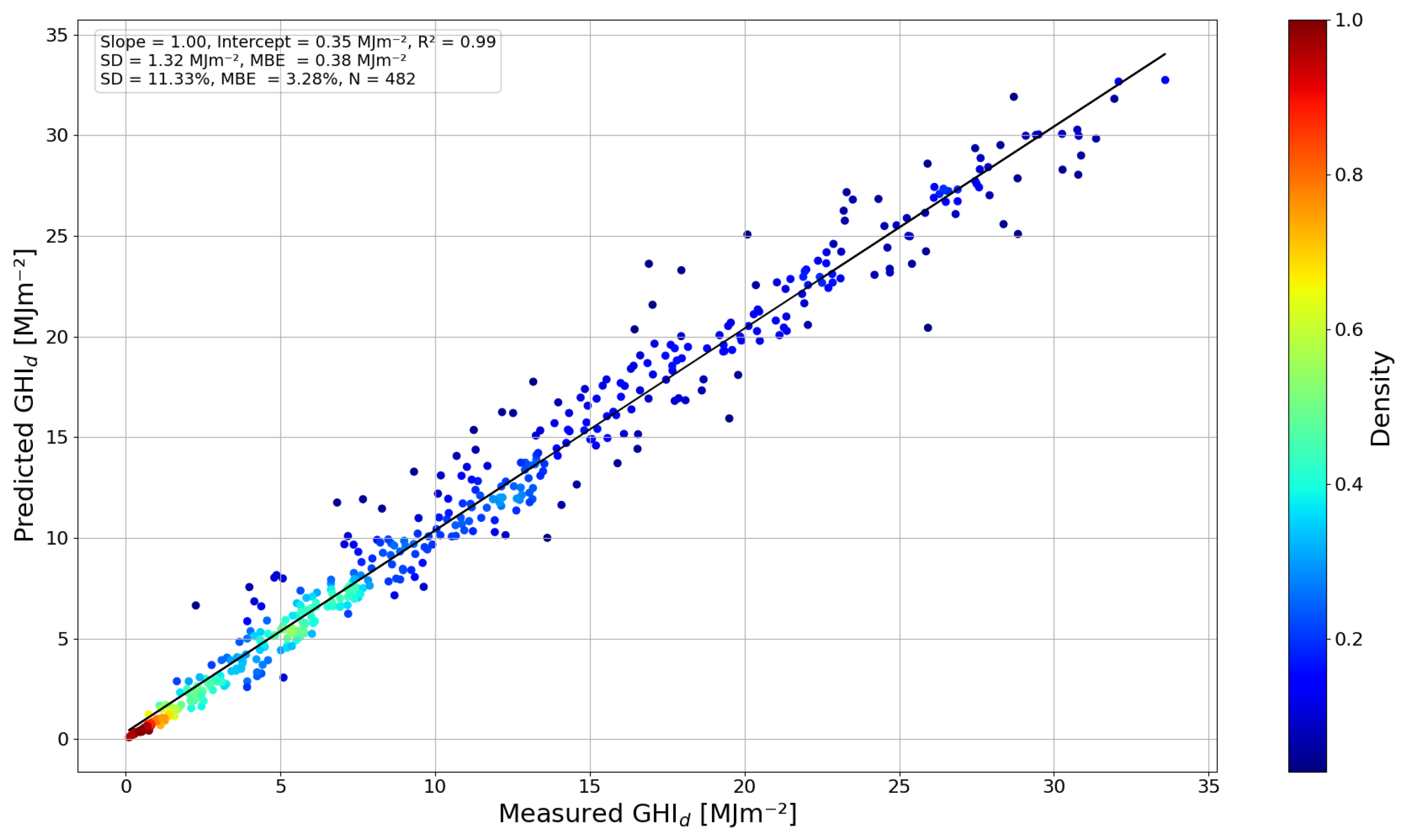
| Site | Initial Dataset | Filtered Dataset | Train Dataset | Validation Dataset | Test Dataset |
|---|---|---|---|---|---|
| Valladolid | 82,865 | 70,962 | 25,654 | 7096 | 38,212 |
| Izaña | 46,509 | 41,327 | 6104 | 4133 | 31,090 |
| Lindenberg | 146,575 | 125,380 | 54,679 | 12,539 | 58,072 |
| Total | 275,949 | 237,669 | 86,527 | 23,768 | 127,374 |
| SZA [°] | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
|---|---|---|---|---|---|---|---|---|---|
| oktas | MBE ± SD [%] | MBE ± SD [%] | MBE ± SD [%] | MBE ± SD [%] | MBE ± SD [%] | MBE ± SD [%] | MBE ± SD [%] | MBE ± SD [%] | MBE ± SD [%] |
| 0 | −1.1 ± 4.1 | 0.4 ± 6.4 | 1.3 ± 6.7 | −0.5 ± 6.4 | −0.7 ± 7.7 | −1.9 ± 10.1 | −1.8 ± 13.0 | −6.5 ± 15.1 | −12.8 ± 22.8 |
| 1 | −2.8 ± 7.5 | 0.4 ± 11.1 | −1.3 ± 9.8 | −0.1 ± 12.1 | −0.2 ± 14.3 | −1.9 ± 15.7 | −3.6 ± 20.4 | −11.8 ± 23.8 | −18.2 ± 26.8 |
| 2 | −0.9 ± 11.3 | −2.1 ± 17.2 | −0.8 ± 13.9 | −1.0 ± 17.3 | −2.0 ± 19.4 | −1.9 ± 22.2 | −2.5 ± 22.8 | −6.1 ± 27.9 | −8.6 ± 29.4 |
| 3 | −0.0 ± 16.8 | −0.4 ± 18.2 | 6.3 ± 18.2 | 2.9 ± 15.7 | −0.0 ± 20.1 | 2.7 ± 20.1 | 3.5 ± 21.8 | −4.5 ± 29.6 | −10.5 ± 31.7 |
| 4 | −3.2 ± 26.3 | −2.4 ± 19.3 | 0.0 ± 21.7 | 1.8 ± 23.8 | 3.9 ± 21.0 | 4.1 ± 22.9 | −4.6 ± 29.8 | −3.7 ± 25.6 | −9.7 ± 28.6 |
| 5 | −1.0 ± 23.6 | 2.8 ± 23.4 | 3.8 ± 18.8 | 2.7 ± 24.1 | 3.9 ± 26.2 | 5.4 ± 25.1 | −0.5 ± 26.8 | −1.3 ± 27.0 | −9.4 ± 32.7 |
| 6 | 3.0 ± 22.6 | 1.3 ± 25.9 | 6.3 ± 21.1 | 2.6 ± 23.4 | 3.7 ± 25.2 | −1.3 ± 24.2 | −1.5 ± 28.6 | −5.9 ± 27.0 | −10.6 ± 32.9 |
| 7 | 5.4 ± 24.1 | 8.9 ± 22.3 | 6.7 ± 22.7 | 2.0 ± 24.9 | 2.0 ± 27.0 | −3.9 ± 28.7 | −0.9 ± 28.5 | −3.7 ± 27.8 | −11.7 ± 31.4 |
| 8 | −0.8 ± 29.1 | 4.7 ± 29.1 | 4.1 ± 28.4 | 4.1 ± 28.5 | 5.1 ± 26.4 | 3.8 ± 27.4 | 3.0 ± 31.8 | 3.8 ± 29.5 | −5.2 ± 37.4 |
| All | −0.0 ± 27.1 | 3.5 ± 21.8 | 3.3 ± 19.8 | 2.7 ± 21.8 | 3.3 ± 22.1 | 1.7 ± 23.4 | 0.9 ± 26.1 | −0.7 ± 27.3 | −8.5 ± 33.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Fernández, D.; Román, R.; Mateos, D.; Herrero del Barrio, C.; Cachorro, V.E.; Copes, G.; Sánchez, R.; García, R.D.; Doppler, L.; Herrero-Anta, S.; et al. Retrieval of Solar Shortwave Irradiance from All-Sky Camera Images. Remote Sens. 2024, 16, 3821. https://doi.org/10.3390/rs16203821
González-Fernández D, Román R, Mateos D, Herrero del Barrio C, Cachorro VE, Copes G, Sánchez R, García RD, Doppler L, Herrero-Anta S, et al. Retrieval of Solar Shortwave Irradiance from All-Sky Camera Images. Remote Sensing. 2024; 16(20):3821. https://doi.org/10.3390/rs16203821
Chicago/Turabian StyleGonzález-Fernández, Daniel, Roberto Román, David Mateos, Celia Herrero del Barrio, Victoria E. Cachorro, Gustavo Copes, Ricardo Sánchez, Rosa Delia García, Lionel Doppler, Sara Herrero-Anta, and et al. 2024. "Retrieval of Solar Shortwave Irradiance from All-Sky Camera Images" Remote Sensing 16, no. 20: 3821. https://doi.org/10.3390/rs16203821
APA StyleGonzález-Fernández, D., Román, R., Mateos, D., Herrero del Barrio, C., Cachorro, V. E., Copes, G., Sánchez, R., García, R. D., Doppler, L., Herrero-Anta, S., Antuña-Sánchez, J. C., Barreto, Á., González, R., Gatón, J., Calle, A., Toledano, C., & de Frutos, Á. (2024). Retrieval of Solar Shortwave Irradiance from All-Sky Camera Images. Remote Sensing, 16(20), 3821. https://doi.org/10.3390/rs16203821






