Analysis of the Influence of Different Reference Models on Recovering Gravity Anomalies from Satellite Altimetry
Abstract
1. Introduction
2. Research Area and Data
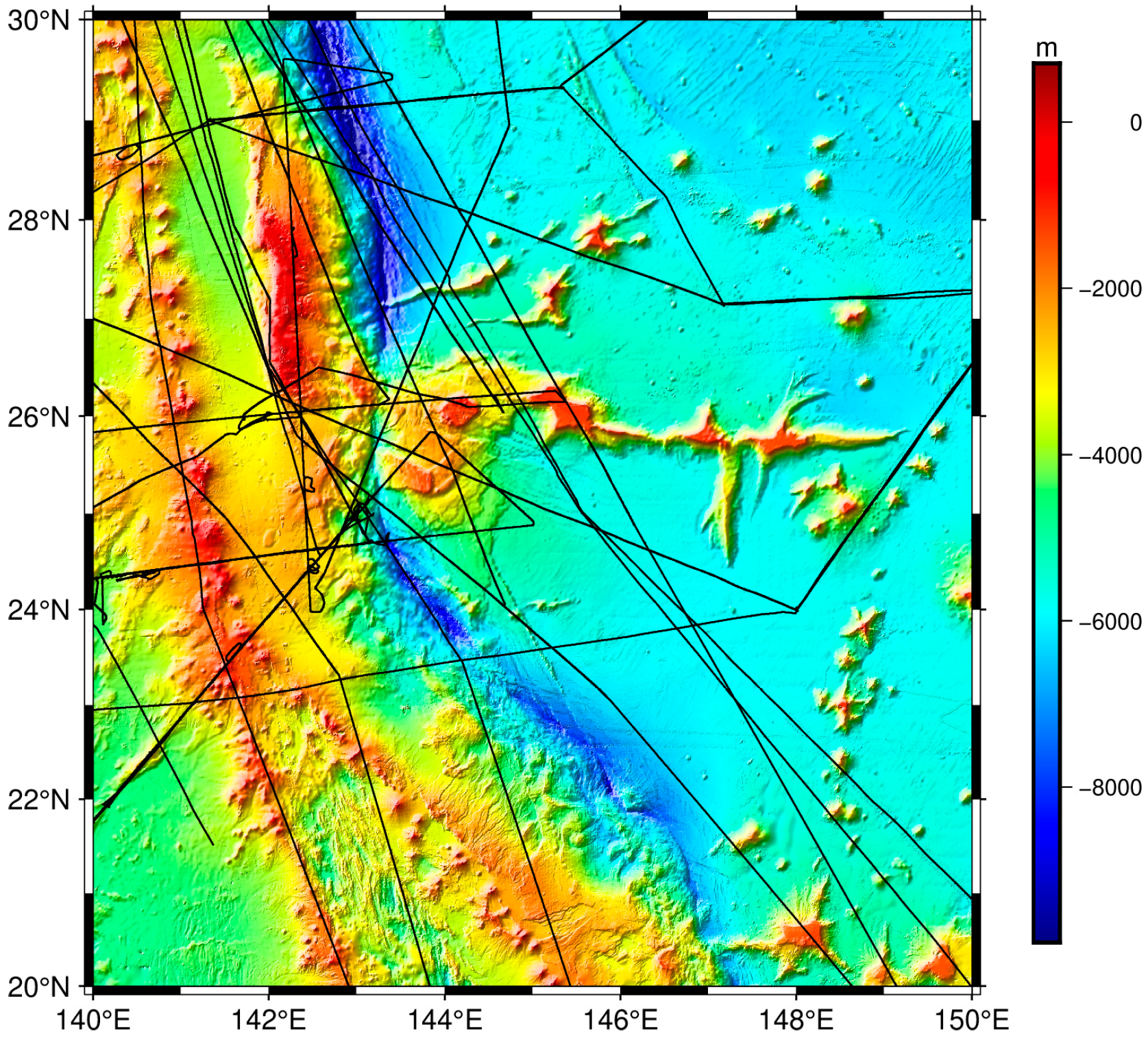
2.1. Research Area
2.2. Data Description and Models
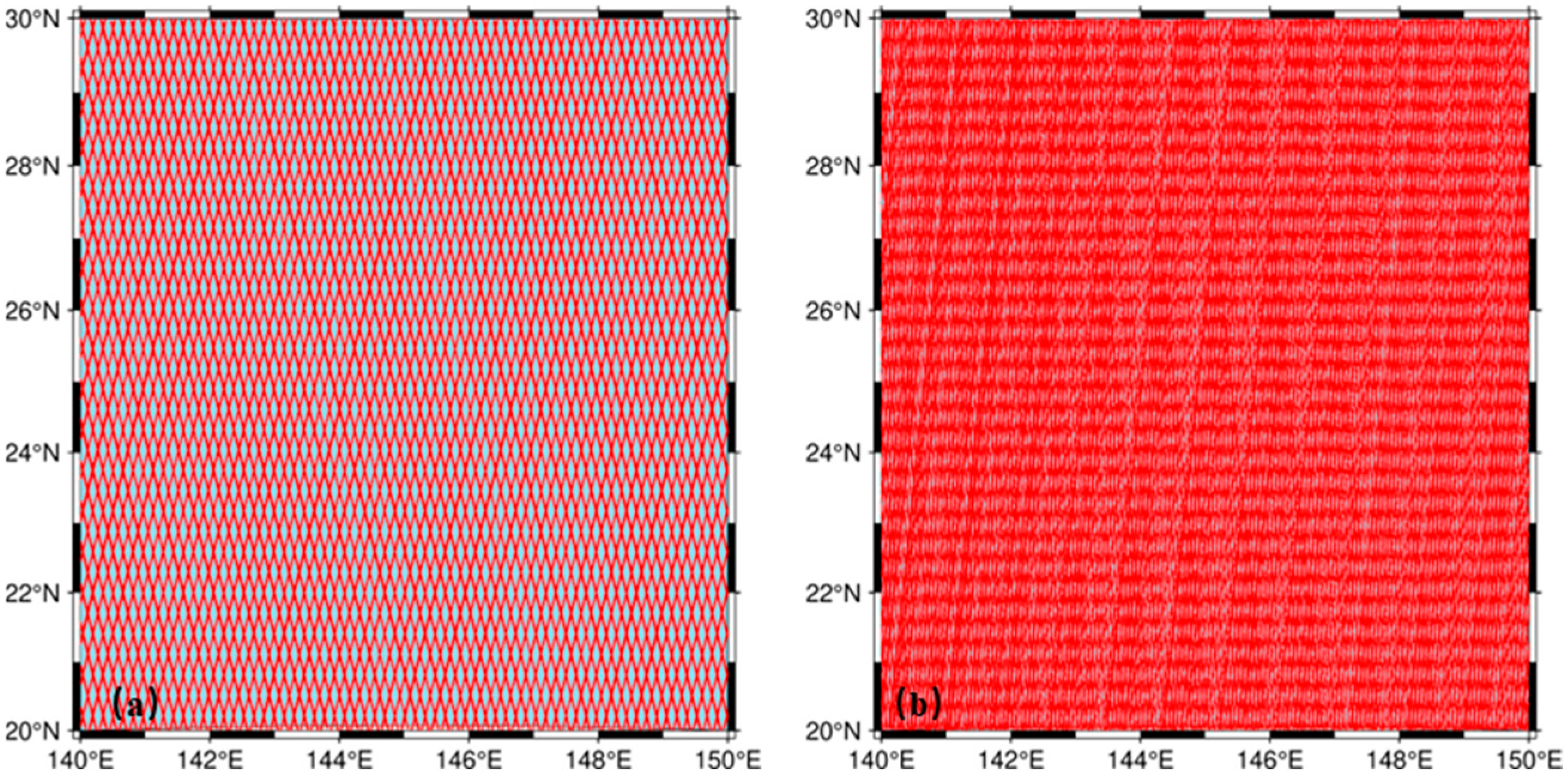
2.2.1. Satellite Altimetry Data
2.2.2. Shipborne Gravity Data
2.2.3. Marine Gravity Anomaly Model
2.2.4. Reference Gravity Field Model
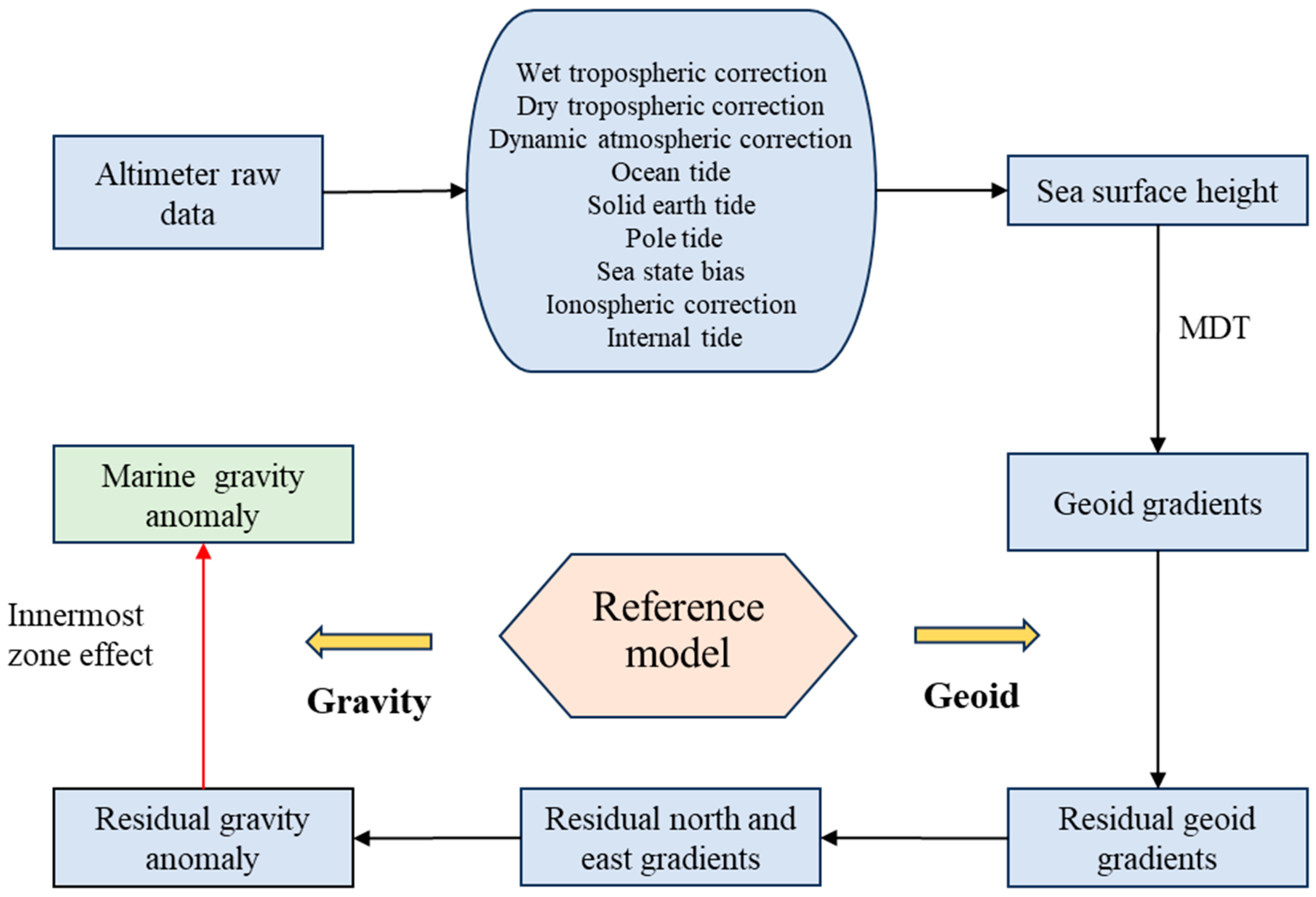
3. Method
3.1. Shipborne Gravity Preprocessing Method
3.2. Processing Method of the Altimeter Data
4. Results and Discussion
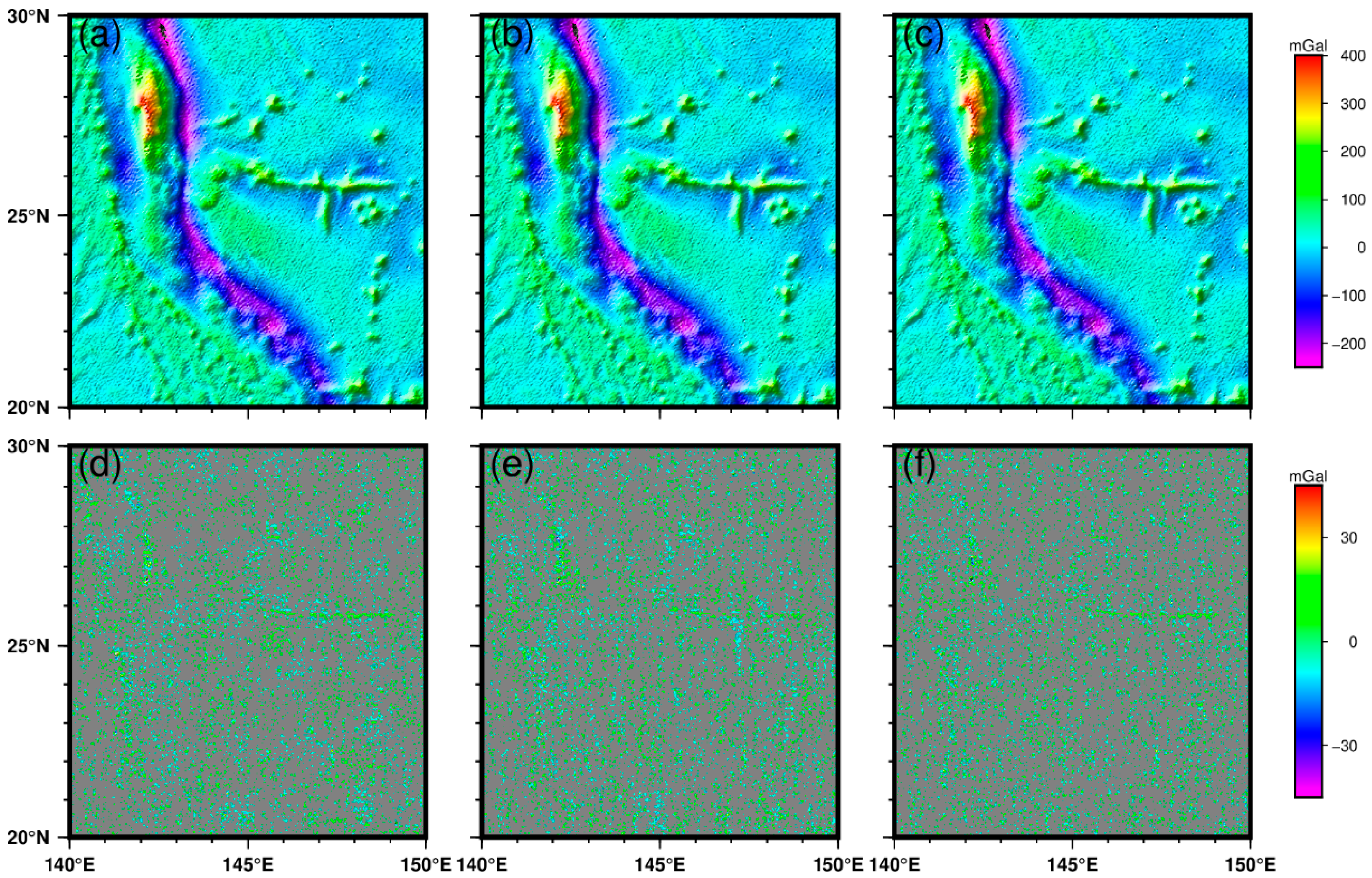
4.1. Different-Degree Reference Gravity Models
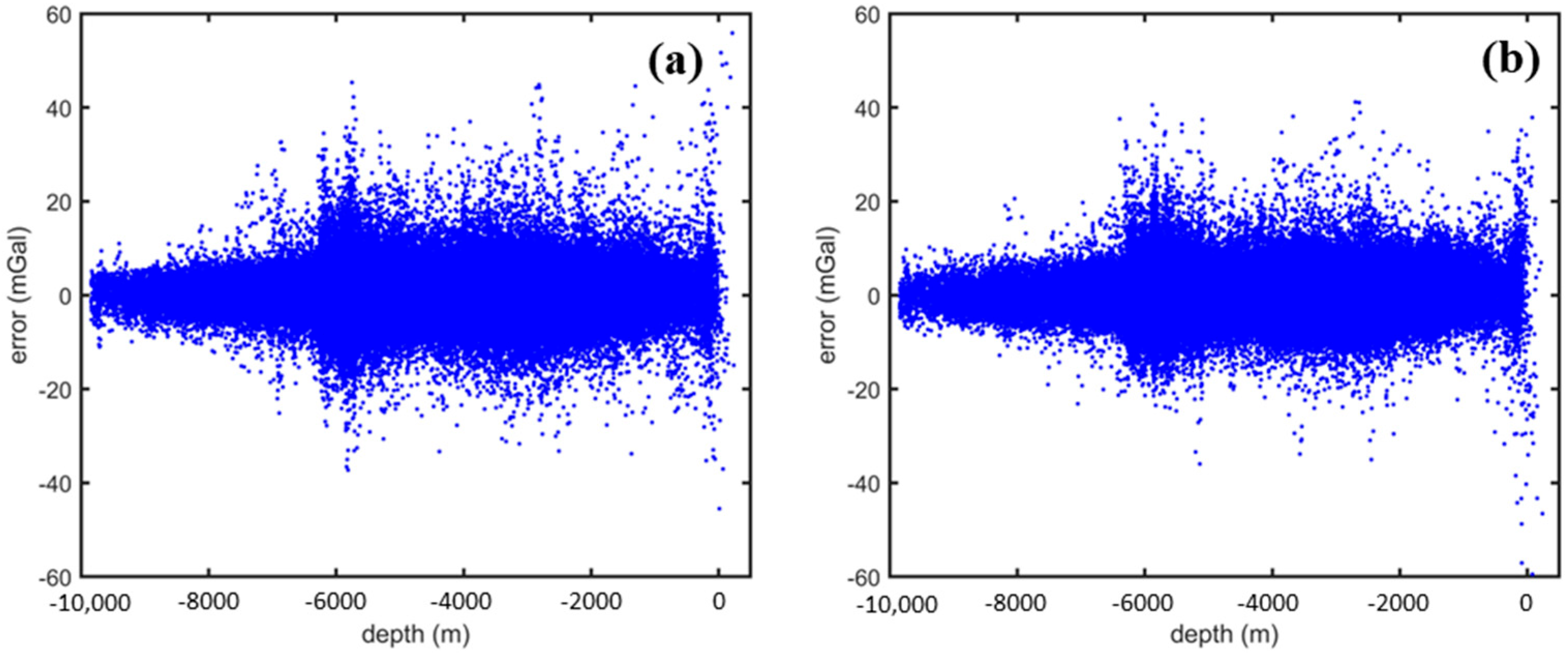
4.2. The Influence of the High-Degree Reference Model and Its Relationship with Marine Bathymetry
4.3. Weighted Fusion of Different Reference Models
5. Conclusions
- HUST-Grace2016s, WHU-SWPU-GOGR2022S, and EGM2008 are utilized as reference fields to assess the accuracy of altimeter-derived gravity anomalies. The STD of the gravity anomalies for the two types of satellites is observed to decrease successively from 49 mGal to 31 mGal, and ultimately to 4 mGal. It is concluded that when recovering the marine gravity field using altimeter data, high-degree gravity field models should be prioritized as reference fields.
- The effects of four different high-degree reference gravity field models on the recovery of gravity anomalies using altimeter data are analyzed. The results reveal that the utilization of these different high-degree models exerts minimal influence on the outcomes of the recovered gravity anomalies. In contrast, the evaluation based on shipborne data and DTU17 confirms that the XGM2019e_2159 model is optimal, which aligns with the reference gravity anomaly employed by the SDUST gravity anomaly model released by Shandong University of Science and Technology.
- When using the same high-degree reference gravity field model, the gravity anomalies inverted by HY-2A are similar to those of CryoSat-2, which proves that HY-2A reached the world’s most advanced level. Under the same conditions, the STD of gravity anomalies retrieved by CryoSat-2 is approximately 0.2 mGal smaller than that of HY-2A.
- The accuracy of the altimeter data in restoring the marine gravity field on the shallow shore is low. When the marine depth is less than 2000 m, both CryoSat-2 and HY-2A using the XGM2019e_2159 model to restore the gravity field obtain the highest accuracies. Compared with EGM2008, the accuracy is improved by 0.6747 mGal and 0.6165 mGal, respectively. The weighted fusion method proposed in this paper can further improve the problem of the poor inversion accuracy of altimeter satellites in shallow water areas.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, W.; Xu, H.; Zhong, M.; Yuan, M.; Peng, B.; Zhou, X. Progress and Present Status of Research on Earth’s Gravitational Field Models. J. Geod. Geodyn. 2010, 30, 83–91. [Google Scholar]
- Sandwell, D.T.; Mueller, R.D.; Smith, W.H.F.; Garcia, E.; Francis, R. New Global Marine Gravity Model from CryoSat-2 and Jason-1 Reveals Buried Tectonic Structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Bao, L.; Shum, C. Altimeter-Derived Marine Gravity Variations Reveal the Magma Mass Motions within the Subaqueous Nishinoshima Volcano, Izu-Bonin Arc, Japan. J. Geod. 2021, 95, 46. [Google Scholar] [CrossRef]
- Hwang, C.; Chang, E.T.Y. Seafloor Secrets Revealed. Science 2014, 346, 32–33. [Google Scholar] [CrossRef]
- Zehentner, N.; Mayer-Guerr, T. Precise Orbit Determination Based on Raw GPS Measurements. J. Geod. 2016, 90, 275–286. [Google Scholar] [CrossRef]
- Mao, N.; Li, A.; Xu, J.; Qin, F.; Wu, M.; He, H.; Li, J. Marine Gravity Anomaly from Satellite Altimetry: Interpolation and Matching Navigation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5918919. [Google Scholar] [CrossRef]
- Huang, M.; Liu, M.; Deng, K.; Ouyang, Y.; Lu, X.; Zhai, G.; Wu, T.; Chen, X. Test and correction of scale values for air-sea gravimeters using repeated survey lines. Chin. J. Geophys.-Chin. Ed. 2018, 61, 3160–3169. [Google Scholar]
- Wang, B.; Wu, L.; Wu, P.; Li, Q.; Bao, L.; Wang, Y. Multidimensional Evaluation of Altimetry Marine Gravity Models with Shipborne Gravity Data from a New Platform Marine Gravimeter. J. Mar. Sci. Eng. 2024, 12, 1314. [Google Scholar] [CrossRef]
- Chen, X.; Kong, X.; Zhou, R.; Zhang, S. Fusion of Altimetry-Derived Model and Ship-Borne Data in Preparation of High-Resolution Marine Gravity Determination. Geophys. J. Int. 2024, 236, 1262–1274. [Google Scholar] [CrossRef]
- Wan, X.; Zhang, R.; Sui, X.; Chen, L. Analysis of Earth Gravity Field Detection Based on Satellite Data. Spacecr. Eng. 2017, 26, 121–129. [Google Scholar]
- Li, A.; Che, H.; Qin, F.; Huang, C.; Gong, W. Development and Prospect of Cold Atom Interferometry Gravimetry Measurement. J. Nav. Univ. Eng. 2021, 33, 1–7. [Google Scholar]
- Che, H.; Li, A.; Fang, J.; Ge, G.; Gao, W.; Zhang, Y.; Liu, C.; Xu, J.; Chang, L.; Huang, C.; et al. Ship-borne dynamic absolute gravity measurement based on cold atom gravimeter. Acta Phys. Sin. 2022, 71, 113701. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H.F. Marine Gravity Anomaly from Geosat and ERS 1 Satellite Altimetry. J. Geophys. Res. 1997, 102, 10039–10054. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H.F. Global Marine Gravity from Retracked Geosat and ERS-1 Altimetry: Ridge Segmentation versus Spreading Rate. J. Geophys. Res. 2009, 114, B1. [Google Scholar] [CrossRef]
- Andersen, O.B.; Knudsen, P. Global Marine Gravity Field from the ERS-1 and Geosat Geodetic Mission Altimetry. J. Geophys. Res. 1998, 103, 8129–8137. [Google Scholar] [CrossRef]
- Andersen, O.B. The DTU10 Global Gravity Field and Mean Sea Surface—Improvements in the Arctic. In Proceedings of the 2nd IGFS Meeting, Fairbanks, AK, USA, 20–22 September 2010. [Google Scholar]
- Wan, X.; Annan, R.; Wang, W. Assessment of HY-2A GM Data by Deriving the Gravity Field and Bathymetry over the Gulf of Guinea. Earth Planets Space 2020, 72, 151. [Google Scholar] [CrossRef]
- Zhu, C.; Guo, J.; Hwang, C.; Gao, J.; Yuan, J.; Liu, X. How HY-2A/GM Altimeter Performs in Marine Gravity Derivation: Assessment in the South China Sea. Geophys. J. Int. 2019, 219, 1056–1064. [Google Scholar] [CrossRef]
- Li, J.; Sideris, M.G. Marine Gravity and Geoid Determination by Optimal Combination of Satellite Altimetry and Shipborne Gravimetry Data. J. Geod. 1997, 71, 209–216. [Google Scholar] [CrossRef]
- Zhu, C.; Yang, L.; Bian, H.; Li, H.; Guo, J.; Liu, N.; Lin, L. Recovering Gravity from Satellite Altimetry Data Using Deep Learning Network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5911311. [Google Scholar] [CrossRef]
- Liu, Q.; Xu, K.; Jiang, M.; Wang, J. Preliminary Marine Gravity Field from HY-2A/GM Altimeter Data. Acta Oceanol. Sin. 2020, 39, 127–134. [Google Scholar] [CrossRef]
- Zaki, A.; Mansi, A.H.; Selim, M.; Rabah, M.; El-Fiky, G. Comparison of Satellite Altimetric Gravity and Global Geopotential Models with Shipborne Gravity in the Red Sea. Mar. Geod. 2018, 41, 258–269. [Google Scholar] [CrossRef]
- Li, Q.; Bao, L.; Wang, Y. Accuracy Evaluation of Altimeter-Derived Gravity Field Models in Offshore and Coastal Regions of China. Front. Earth Sci. 2021, 9, 722019. [Google Scholar] [CrossRef]
- Wang, B.; Wu, L.; Li, Q.; Bao, L.; Wang, Y. Estimating the True Spatial Resolution of Satellite Altimeter-Derived Gravity Field Models with Shipborne Data in the South China Sea. Appl. Geophys. 2023, 20, 51–61. [Google Scholar] [CrossRef]
- Annan, R.F.; Wan, X. Recovering Marine Gravity Over the Gulf of Guinea From Multi-Satellite Sea Surface Heights. Front. Earth Sci. 2021, 9, 700873. [Google Scholar] [CrossRef]
- Zhang, W.; Zheng, W.; Wu, F.; Li, Z.; Liu, Z. Research Progress and Prospect of Global Marine Gravity Field Model. Sci. Surv. Mapp. 2020, 45, 16–30. [Google Scholar]
- Hwang, C.; Hsu, H.-Y.; Jang, R.-J. Global Mean Sea Surface and Marine Gravity Anomaly from Multi-Satellite Altimetry: Applications of Deflection-Geoid and Inverse Vening Meinesz Formulae. J. Geod. 2002, 76, 407–418. [Google Scholar] [CrossRef]
- Hwang, C. Inverse Vening Meinesz Formula and Deflection-Geoid Formula: Applications to the Predictions of Gravity and Geoid over the South China Sea. J. Geod. 1998, 72, 304–312. [Google Scholar] [CrossRef]
- Wan, X.; Yu, J. Accuracy Analysis of the Remove-Restore Process in Inverse Stokes Formula. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 77–80. [Google Scholar]
- Li, Z.; Guo, J.; Ji, B.; Wan, X.; Zhang, S. A Review of Marine Gravity Field Recovery from Satellite Altimetry. Remote Sens. 2022, 14, 4790. [Google Scholar] [CrossRef]
- Li, Z. Satellite Radar Altimeter Waveform Retracking of Waveform Derivative Method and Derivation of Gravity Anomalies. Mater’s Dissertation, Shandong University of Science and Technology, Qingdao, China, 2020. [Google Scholar]
- Zhang, S. Research on Determination of Marine Gravity Anomalies from Multi-Satellite Altimeter Data. Ph.D. Dissertation, Wuhan University, Wuhan, China, 2016. [Google Scholar]
- Along-Track Level-2+ (L2P) SLA Product Handbook; CNES Paris: Paris, France, 2017.
- Zhu, C.; Guo, J.; Yuan, J.; Li, Z.; Liu, X.; Gao, J. SDUST2021GRA: Global Marine Gravity Anomaly Model Recovered from Ka-Band and Ku-Band Satellite Altimeter Data. Earth Syst. Sci. Data 2022, 14, 4589–4606. [Google Scholar] [CrossRef]
- Zhang, S.; Sandwell, D.T.; Jin, T.; Li, D. Inversion of Marine Gravity Anomalies over Southeastern China Seas from Multi-Satellite Altimeter Vertical Deflections. J. Appl. Geophys. 2017, 137, 128–137. [Google Scholar] [CrossRef]
- Zhu, C.; Guo, J.; Gao, J.; Liu, X.; Hwang, C.; Yu, S.; Yuan, J.; Ji, B.; Guan, B. Marine Gravity Determined from Multi-Satellite GM/ERM Altimeter Data over the South China Sea: SCSGA V1.0. J. Geod. 2020, 94, 50. [Google Scholar] [CrossRef]
- Tscherning, C.C.; Rapp, R.H. Closed Covariance Expressions for Gravity Anomalies, Geoid Undulations, and Deflections of the Vertical Implied by Anomaly Degree Variance Models; Division of Geodetic Science: Columbus, OH, USA, 1974. [Google Scholar]



| Satellite | CryoSat-2 | HY-2A/GM |
|---|---|---|
| Product | L2P | L2P |
| Inclination (°) | 92 | 99.34 |
| Cycle Duration (days) | 369 | 168 |
| Time Period | cycle 007–cycle 130 | cycle 067–cycle 288 |
| Cruise | Period (UTC) | Max | Min | Number | Gravimeter | Accuracy |
|---|---|---|---|---|---|---|
| KR05-01 | 05/01/2005~24/01/2005 | 126.9 | −264.9 | 4511 | Shipboard gravimeter: KSS 31Portable gravimeter: CG-3M | 1.0 |
| KR05-14 | 05/10/2005~18/10/2005 | 115.8 | −249.7 | 5389 | ||
| KR05-16 | 11/11/2005~04/12/2005 | 134.6 | −209.3 | 10,612 | ||
| KR05-17 | 10/12/2005~25/12/2005 | 151.6 | −224.6 | 4750 | ||
| KR06-01 | 05/01/2006~26/01/2006 | 129.9 | −99.0 | 9488 | ||
| KR06-07 | 05/07/2006~26/07/2006 | 371.8 | −263.5 | 69,821 | ||
| KR06-12 | 13/09/2006~22/09/2006 | 111.6 | −166.9 | 10,926 | ||
| KR06-14 | 29/10/2006~19/11/2006 | 193.6 | −249.0 | 37,468 | ||
| KR06-15 Leg1 | 24/11/2006~26/11/2006 | 124.8 | −236.2 | 7791 | ||
| KR06-16 | 15/12/2006~27/12/2006 | 133.6 | −14.4 | 4738 | ||
| KR07-03 | 03/03/2007~29/03/2007 | 212.5 | −214.3 | 81,603 | ||
| KR07-16 | 26/11/2007~01/12/2007 | 215.7 | −116.3 | 6814 |
| Model | Year | Degree | Data | Institution |
|---|---|---|---|---|
| HUST-Grace2016s | 2016 | 160 | Grace | HUST |
| WHU-SWPU-GOGR2022S | 2023 | 300 | Goce, Grace | WHU/SWPU |
| SGG-UGM-2 | 2020 | 2190 | Altimetry, EGM2008, Goce, Grace | WHU |
| EGM2008 | 2008 | 2190 | Altimetry, Ground data, Grace | NGS/NASA |
| EIGEN-6C4 | 2014 | 2190 | Altimetry, Ground data, Goce, Grace, Lageos | GFZ/GRGS |
| XGM2019e_2159 | 2019 | 2190 | Altimetry, GOCO06s, Ground data, topography | GFZ |
| Satellite | Reference Model | Min | Max | Mean | Std |
|---|---|---|---|---|---|
| CryoSat-2 | HUST-Grace2016s | −200.7411 | 280.2770 | 0.2918 | 49.2385 |
| WHU-SWPU-GOGR2022S | −111.9221 | 236.5845 | −0.0351 | 31.5660 | |
| EGM2008 | −49.5802 | 62.6038 | 0.0284 | 3.6133 | |
| HY-2A | HUST-Grace2016s | −203.4208 | 255.7436 | 0.2904 | 49.2219 |
| WHU-SWPU-GOGR2022S | −112.6769 | 232.8994 | −0.0378 | 31.2331 | |
| EGM2008 | −52.9798 | 62.7806 | 0.0249 | 3.8634 |
| Satellite | Gravity Field | Reference Model | Min | Max | Mean | Std |
|---|---|---|---|---|---|---|
| HY-2A | DTU17 | EGM2008 | −52.9798 | 62.7806 | 0.0249 | 3.8634 |
| EIGEN-6C4 | −49.8846 | 60.9428 | 0.0250 | 3.8290 | ||
| SGG-UGM-2 | −48.7438 | 56.7438 | 0.0183 | 3.9429 | ||
| XGM2019e_2159 | −45.5058 | 55.8648 | 0.0247 | 3.7725 | ||
| Shipborne data | EGM2008 | −23.4470 | 30.4806 | 0.1554 | 4.6973 | |
| EIGEN-6C4 | −23.7071 | 31.3502 | 0.3181 | 4.5655 | ||
| SGG-UGM-2 | −24.6165 | 30.9431 | 0.2225 | 4.4339 | ||
| XGM2019e_2159 | −24.3792 | 30.3459 | 0.1370 | 4.4088 | ||
| CryoSat-2 | DTU17 | EGM2008 | −49.5802 | 62.6038 | 0.0284 | 3.6133 |
| EIGEN-6C4 | −45.0850 | 57.7311 | 0.0277 | 3.6382 | ||
| SGG-UGM-2 | −50.8154 | 41.2329 | 0.0212 | 3.7366 | ||
| XGM2019e_2159 | −59.4770 | 41.1555 | 0.0281 | 3.5706 | ||
| Shipborne data | EGM2008 | −27.5854 | 30.4129 | −0.0026 | 4.3275 | |
| EIGEN-6C4 | −26.8541 | 31.8181 | 0.1434 | 4.2647 | ||
| SGG-UGM-2 | −29.6454 | 30.5549 | 0.0531 | 4.1959 | ||
| XGM2019e_2159 | −27.7187 | 28.9465 | −0.0227 | 4.1903 |
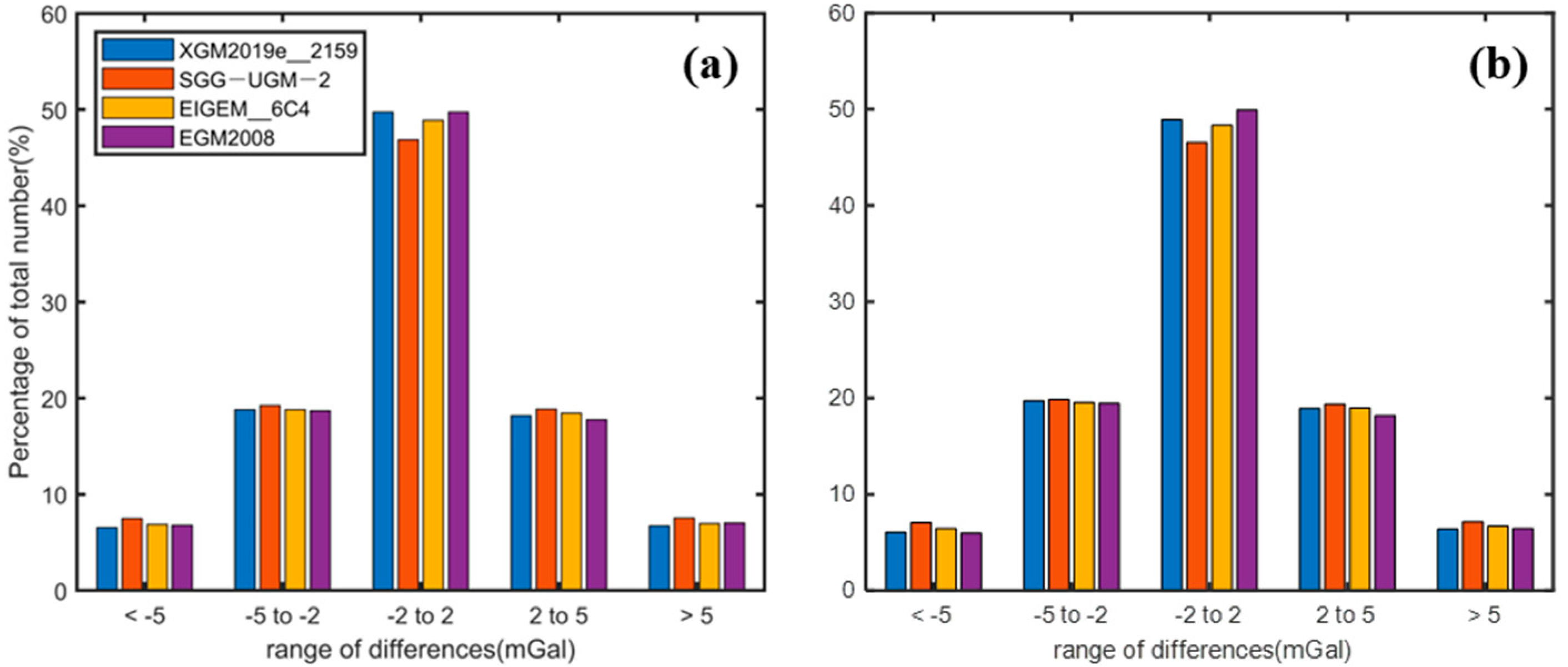
| Satellite | Reference Model | <2 (%) | 2~5 (%) | 5~10 (%) | >10 (%) | STD (mGal) |
|---|---|---|---|---|---|---|
| CryoSat-2 | EGM2008 | 53.80 | 36.95 | 8.12 | 1.14 | 3.2130 |
| EIGEN-6C4 | 51.79 | 38.10 | 9.03 | 1.08 | 3.2890 | |
| SGG-UGM-2 | 49.88 | 38.96 | 9.96 | 1.20 | 3.4065 | |
| XGM2019e_2159 | 52.02 | 37.66 | 9.20 | 1.12 | 3.3065 | |
| HY-2A | EGM2008 | 53.67 | 36.08 | 8.82 | 1.43 | 3.3809 |
| EIGEN-6C4 | 52.30 | 37.17 | 9.18 | 1.35 | 3.3941 | |
| SGG-UGM-2 | 49.92 | 38.14 | 10.48 | 1.46 | 3.5323 | |
| XGM2019e_2159 | 52.26 | 37.07 | 9.29 | 1.38 | 3.4199 |
| Satellite | Reference Model | <2 (%) | 2~5 (%) | 5~10 (%) | >10 (%) | STD (mGal) |
|---|---|---|---|---|---|---|
| CryoSat-2 | EGM2008 | 36.83 | 36.32 | 20.74 | 6.11 | 5.3276 |
| EIGEN-6C4 | 37.22 | 37.72 | 20.37 | 4.69 | 4.9708 | |
| SGG-UGM-2 | 36.45 | 38.44 | 20.43 | 4.68 | 5.0912 | |
| XGM2019e_2159 | 40.04 | 39.08 | 17.28 | 3.61 | 4.6529 | |
| HY-2A | EGM2008 | 36.43 | 36.16 | 20.54 | 6.87 | 5.7078 |
| EIGEN-6C4 | 38.55 | 36.71 | 19.20 | 5.54 | 5.3721 | |
| SGG-UGM-2 | 36.42 | 37.13 | 20.74 | 5.70 | 5.5554 | |
| XGM2019e_2159 | 40.69 | 37.59 | 17.03 | 4.69 | 5.0913 |
| Satellite | Component | Average STD (mGal) | Weight |
|---|---|---|---|
| CryoSat-2 | EGM2008 | 5.3276 | 0.2195 |
| EIGEN-6C4 | 4.9708 | 0.2522 | |
| SGG-UGM-2 | 5.0912 | 0.2404 | |
| XGM2019e_2159 | 4.6529 | 0.2878 | |
| HY-2A | EGM2008 | 5.7078 | 0.2252 |
| EIGEN-6C4 | 5.3721 | 0.2541 | |
| SGG-UGM-2 | 5.5554 | 0.2377 | |
| XGM2019e_2159 | 5.0913 | 0.2830 |
| Difference | Satellite | Min | Max | Mean | STD |
|---|---|---|---|---|---|
| Fusion-DTU17 | CryoSat-2 | −51.5867 | 45.9602 | 0.9729 | 4.6214 |
| HY-2A | −49.0245 | 57.3946 | 0.7653 | 5.0686 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Qin, F.; Wei, H.; Zhu, F.; Qian, L. Analysis of the Influence of Different Reference Models on Recovering Gravity Anomalies from Satellite Altimetry. Remote Sens. 2024, 16, 3758. https://doi.org/10.3390/rs16203758
Han Y, Qin F, Wei H, Zhu F, Qian L. Analysis of the Influence of Different Reference Models on Recovering Gravity Anomalies from Satellite Altimetry. Remote Sensing. 2024; 16(20):3758. https://doi.org/10.3390/rs16203758
Chicago/Turabian StyleHan, Yu, Fangjun Qin, Hongwei Wei, Fengshun Zhu, and Leiyuan Qian. 2024. "Analysis of the Influence of Different Reference Models on Recovering Gravity Anomalies from Satellite Altimetry" Remote Sensing 16, no. 20: 3758. https://doi.org/10.3390/rs16203758
APA StyleHan, Y., Qin, F., Wei, H., Zhu, F., & Qian, L. (2024). Analysis of the Influence of Different Reference Models on Recovering Gravity Anomalies from Satellite Altimetry. Remote Sensing, 16(20), 3758. https://doi.org/10.3390/rs16203758




