A Comprehensive Comparison of Far-Field and Near-Field Imaging Radiometry in Synthetic Aperture Interferometry
Abstract
1. Introduction
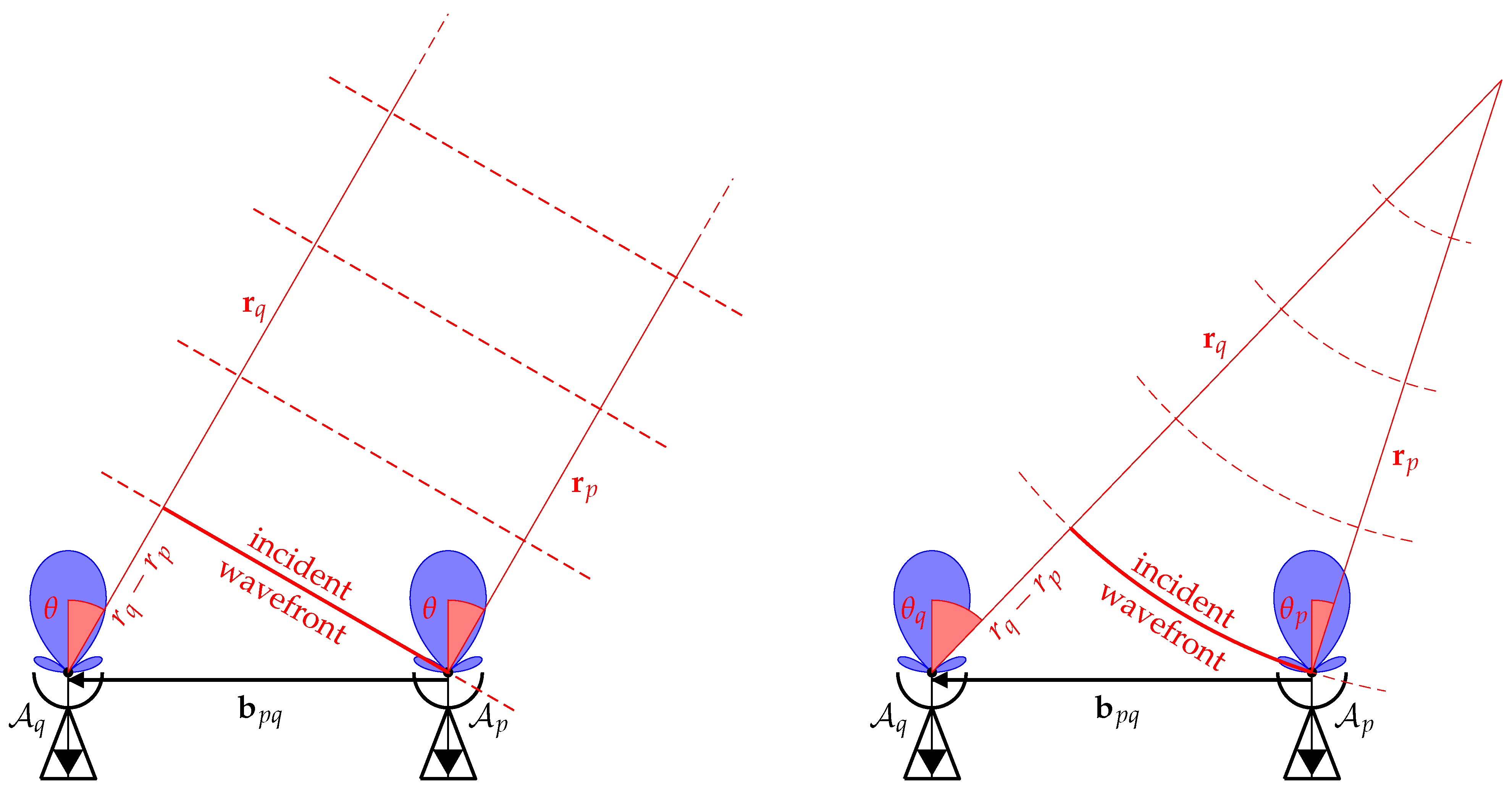
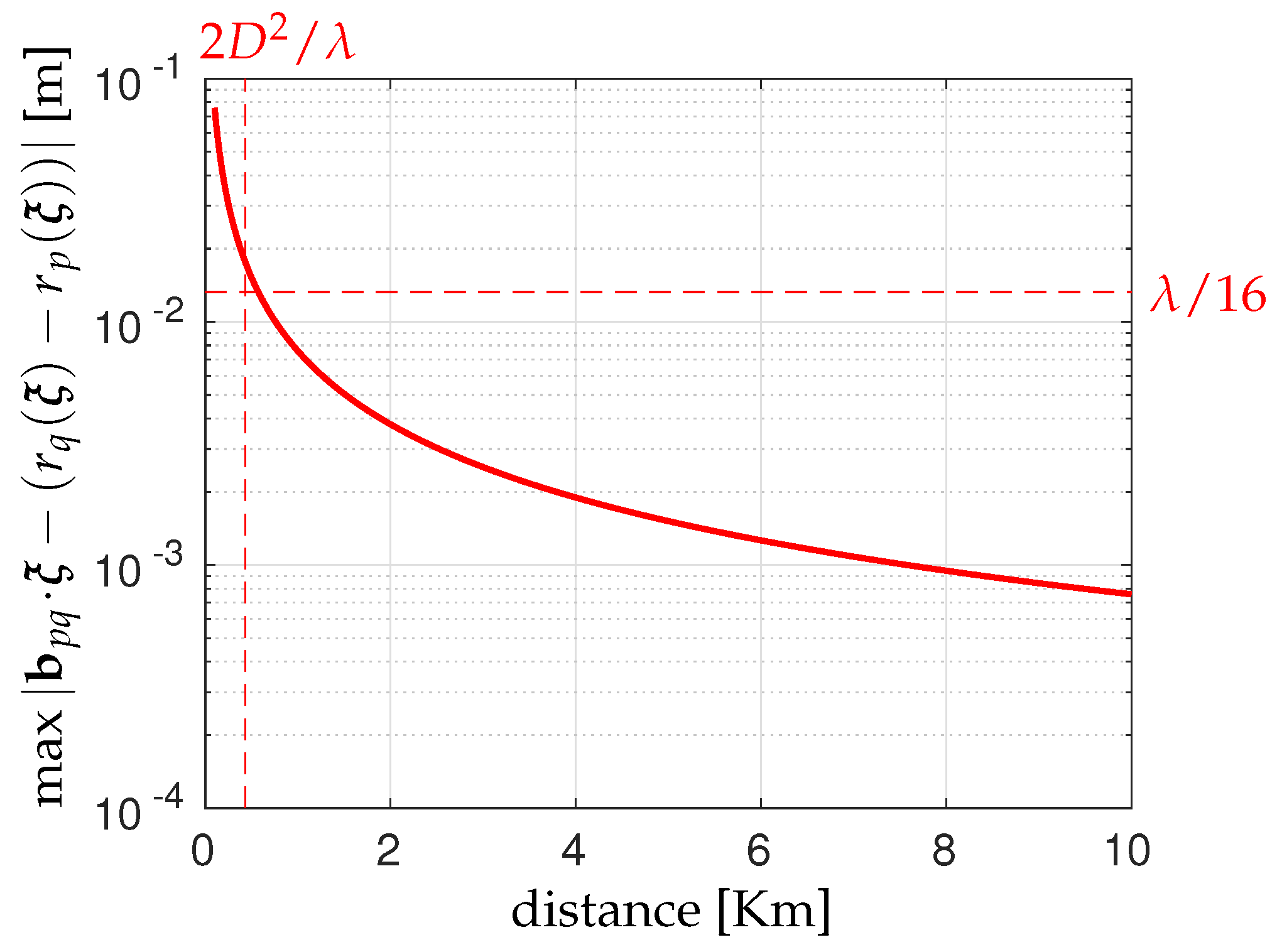
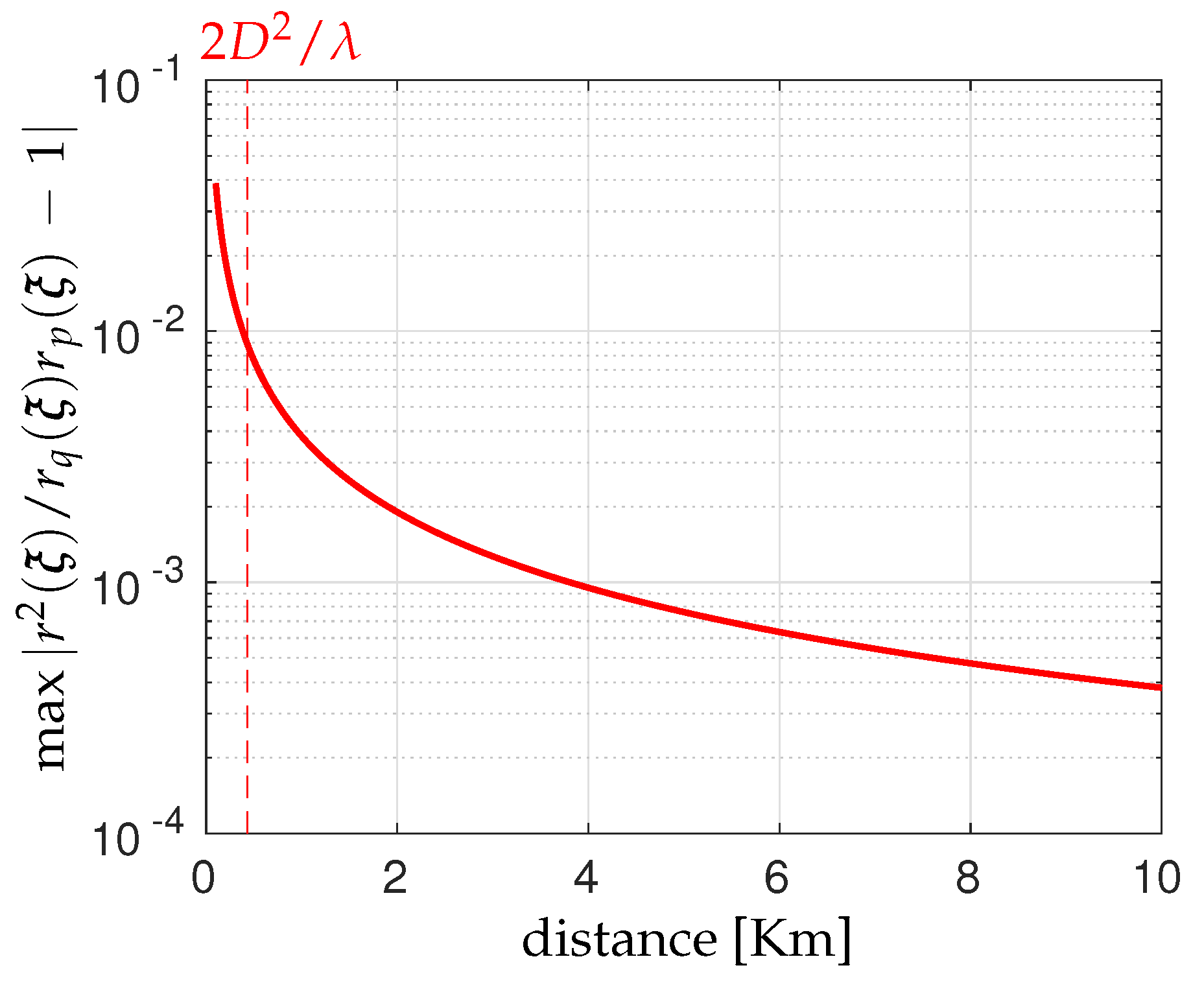
2. Far-Field vs. Near-Field: A Geometrical Comparison
3. Instrument Modeling
- The third and last dissemblance is found in the antenna voltage patterns and where local directions and of the local spherical angles and are assumed to be equal to in the far-field approximation.
4. Regularized Inversion
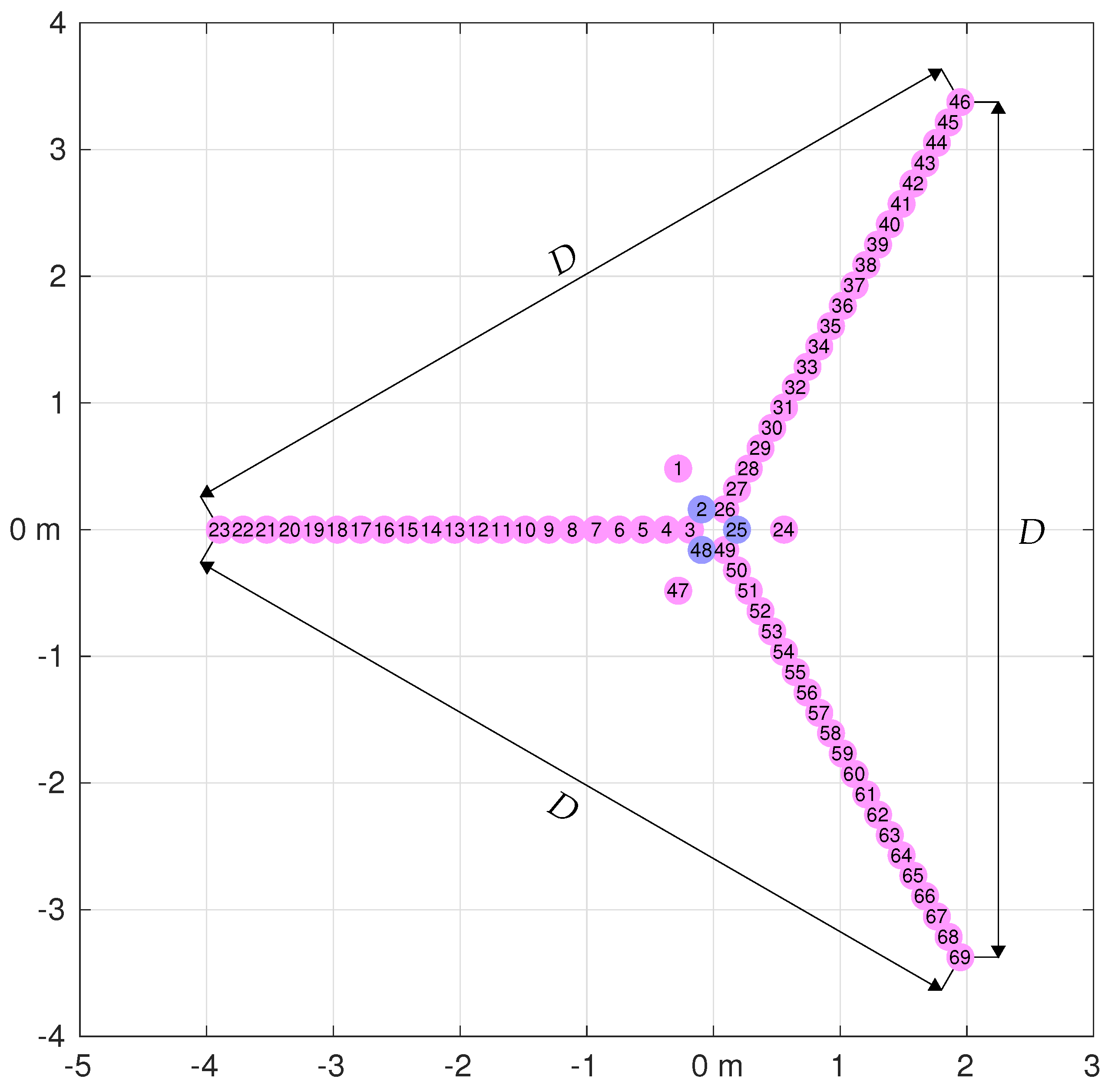
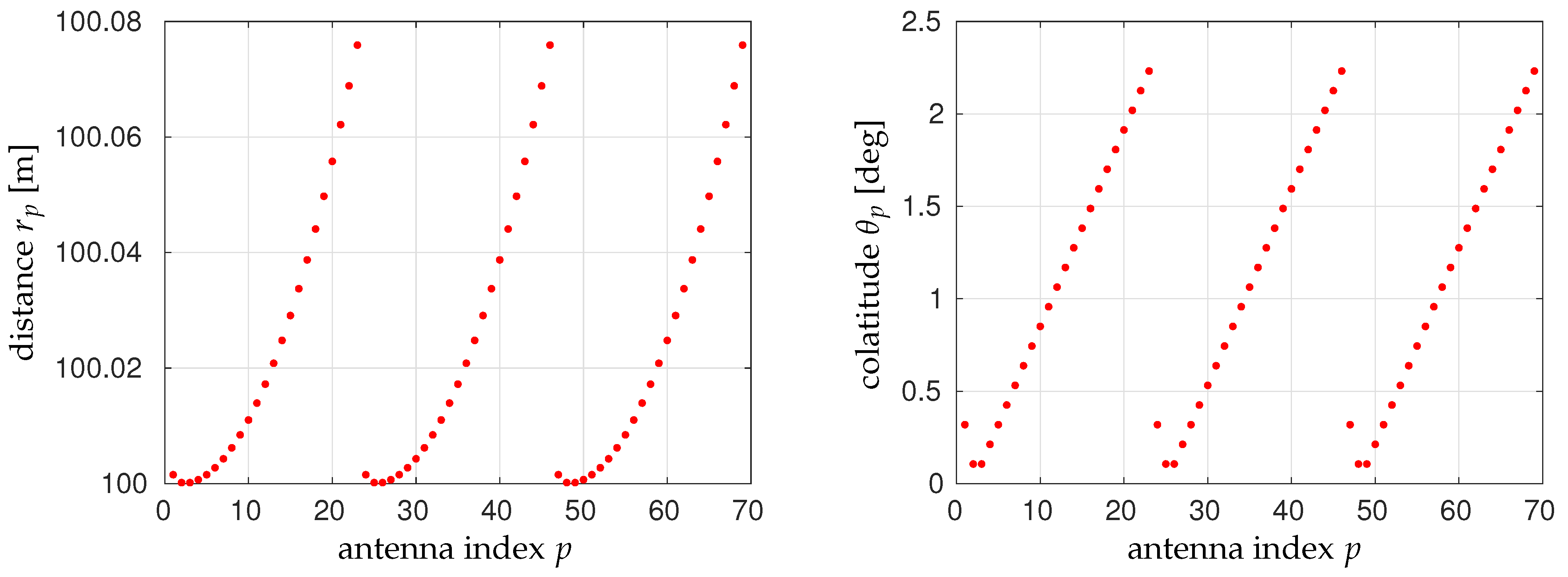
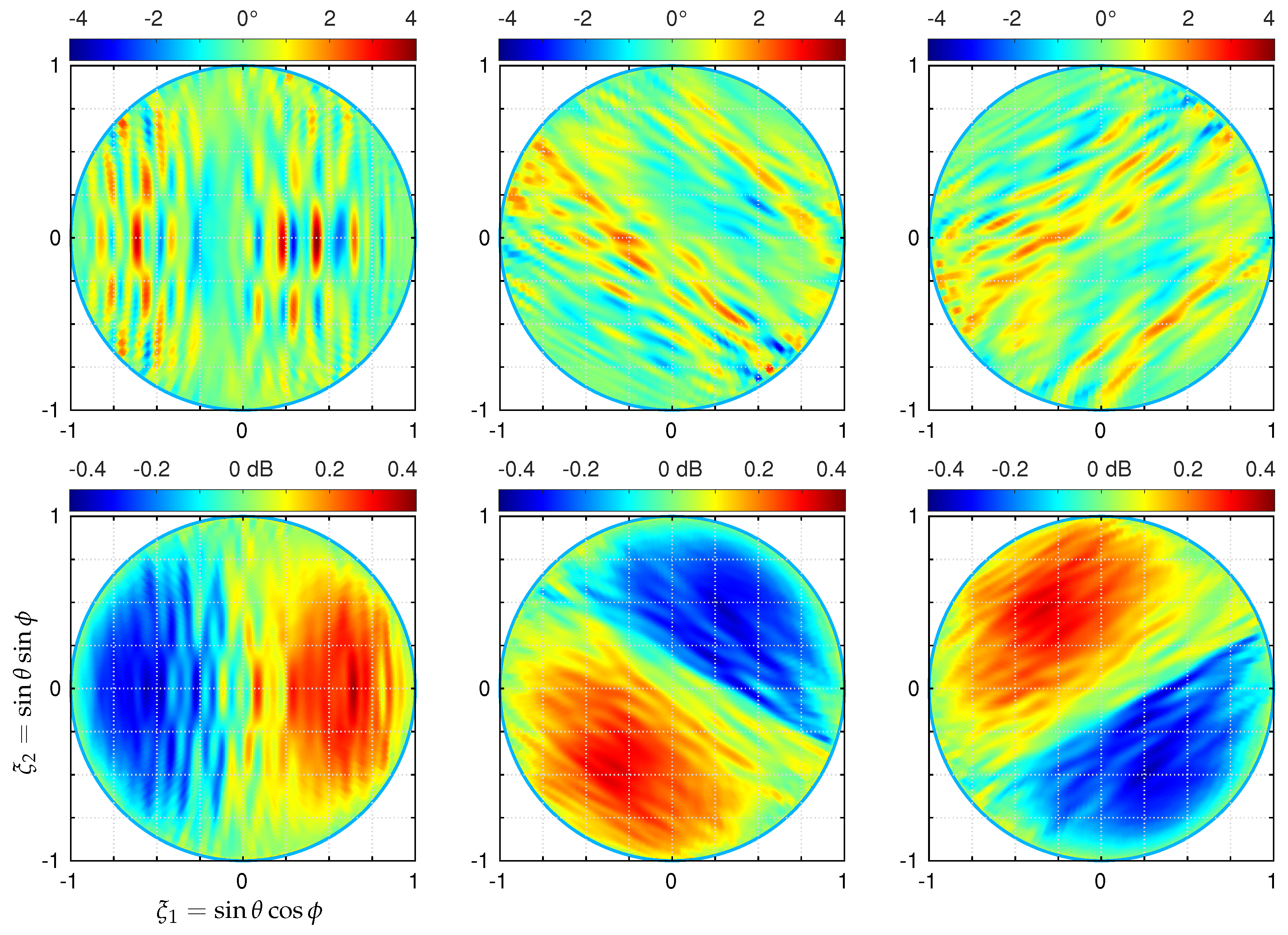
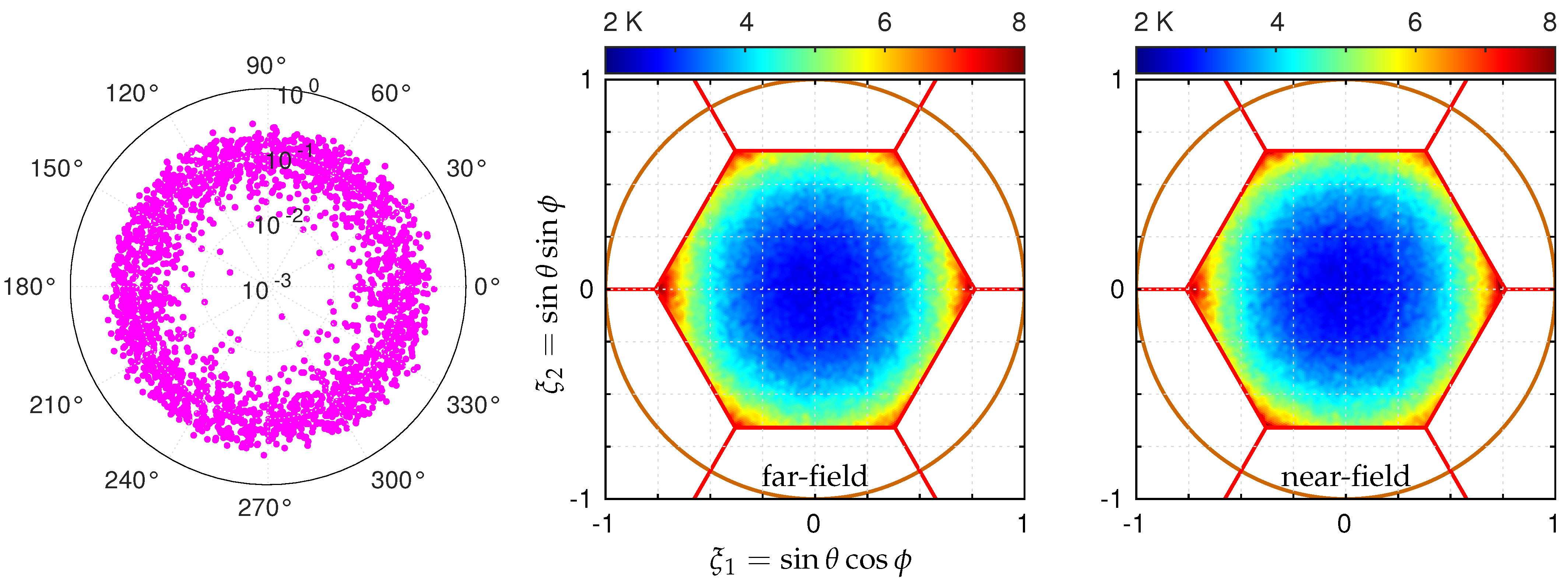
5. Numerical Simulations and Comparison
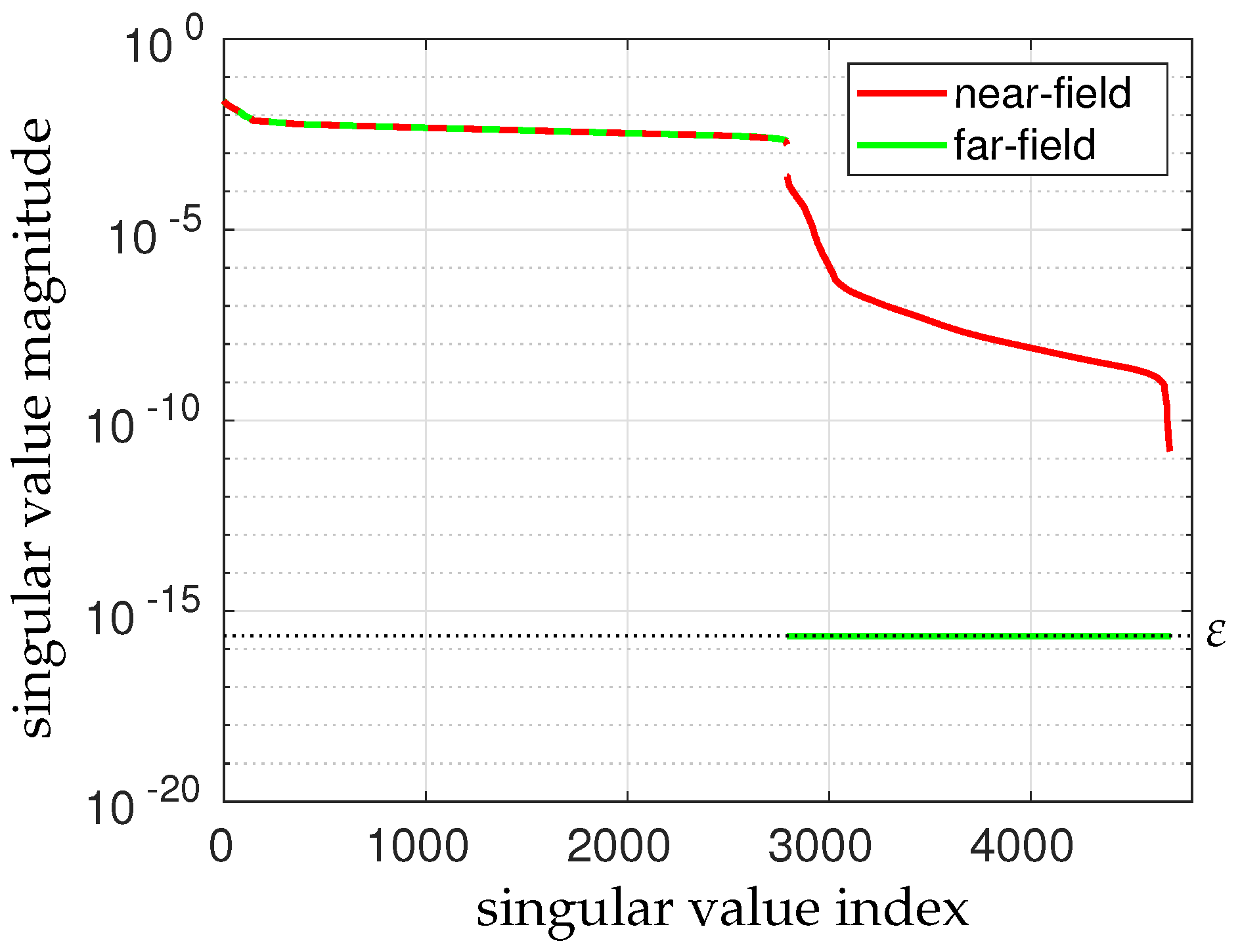
5.1. Singular Values
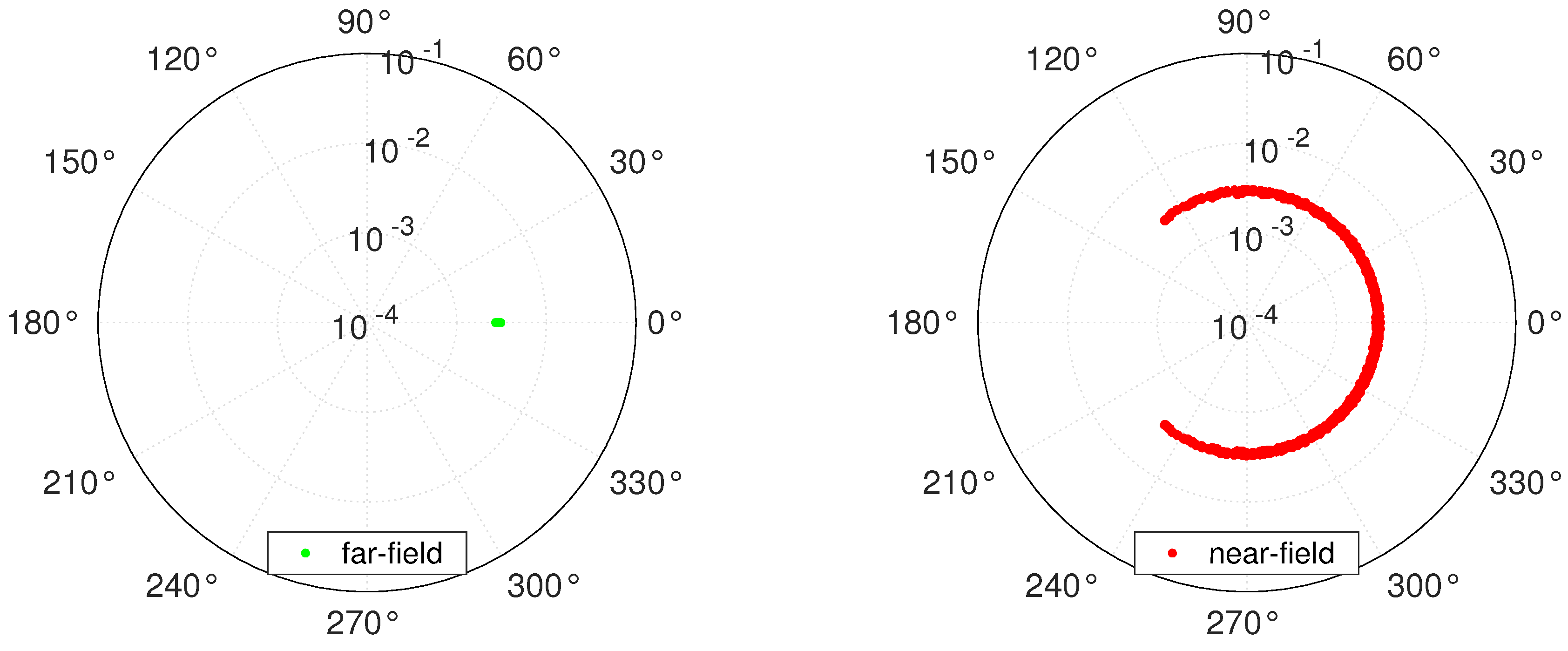
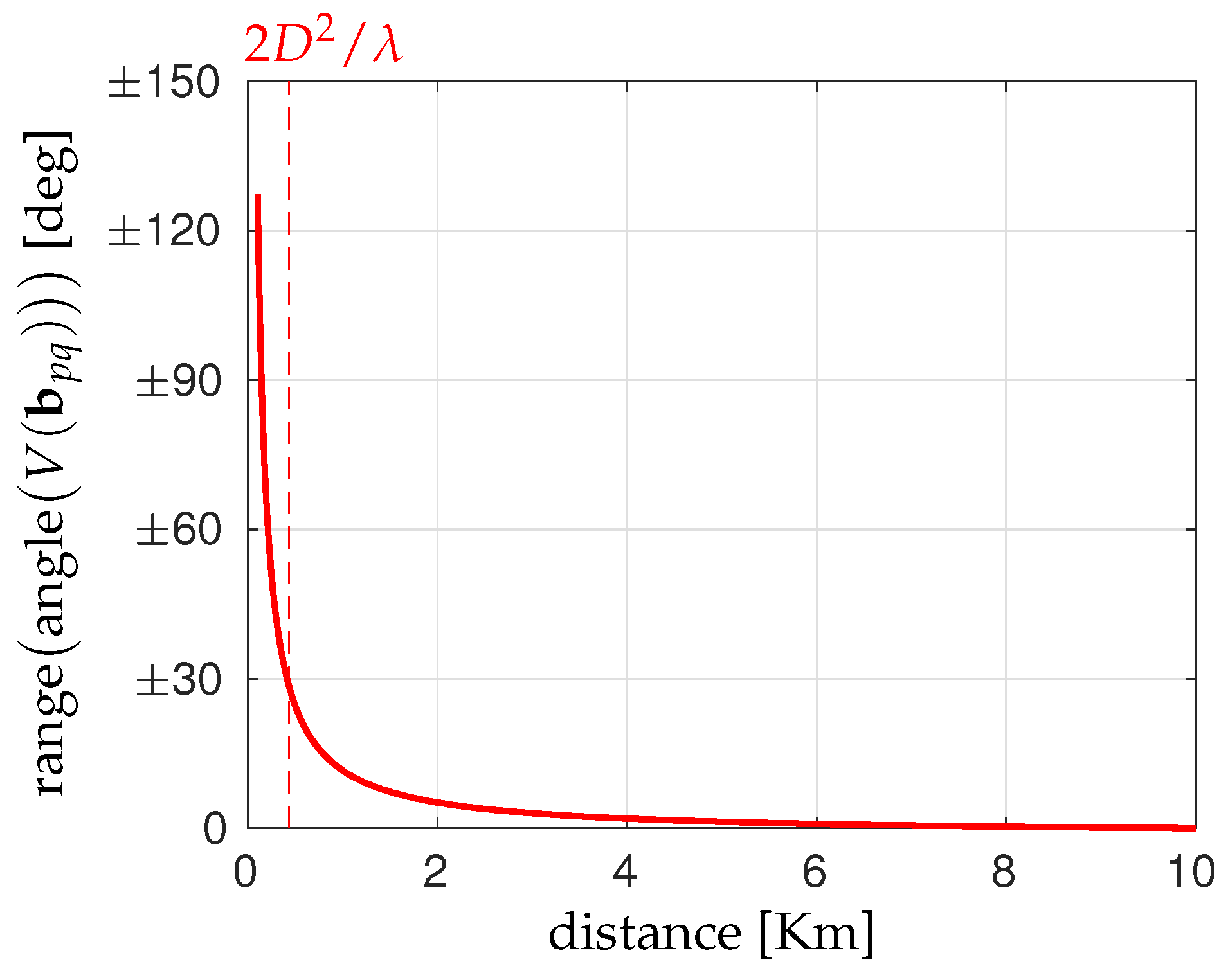
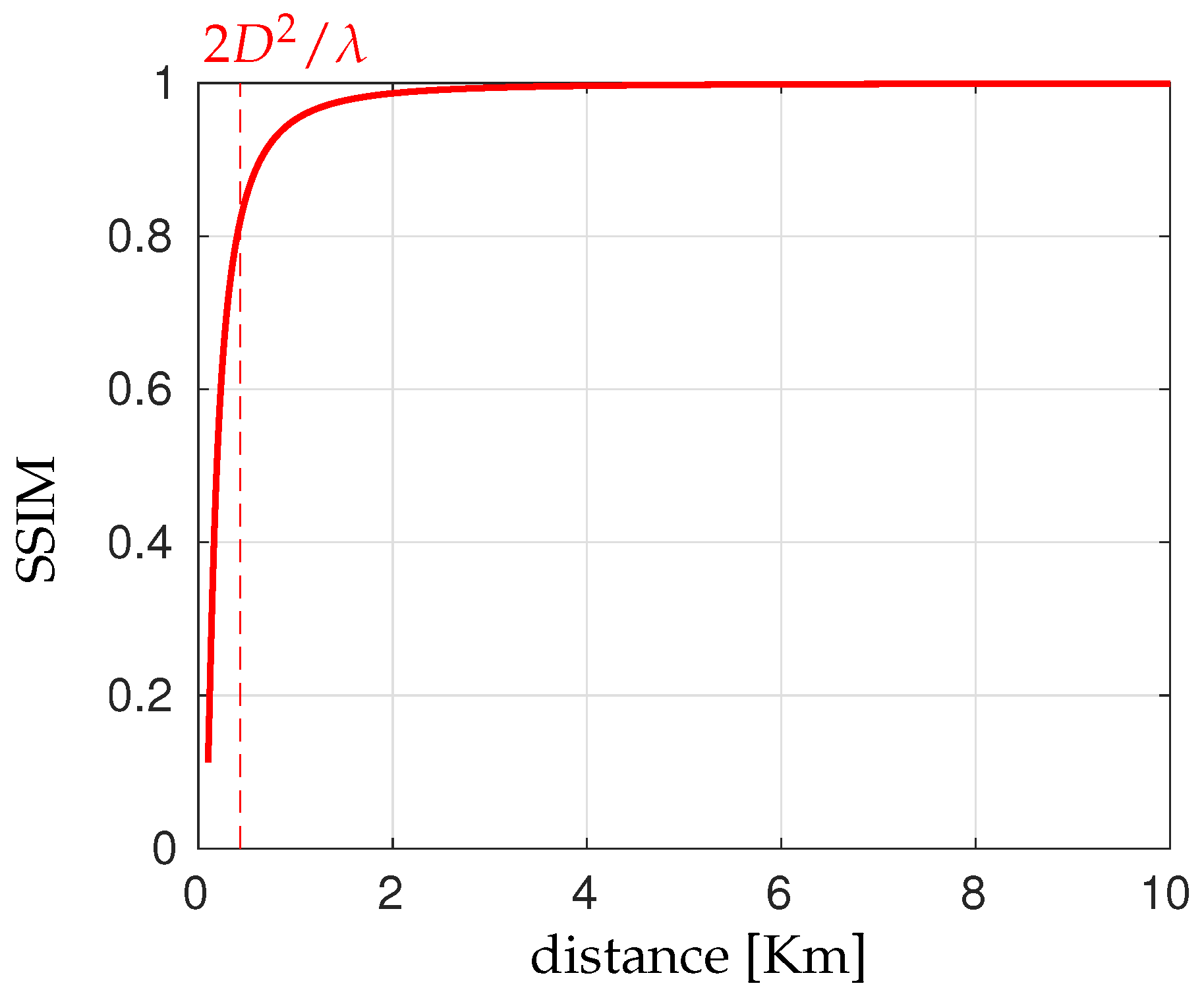
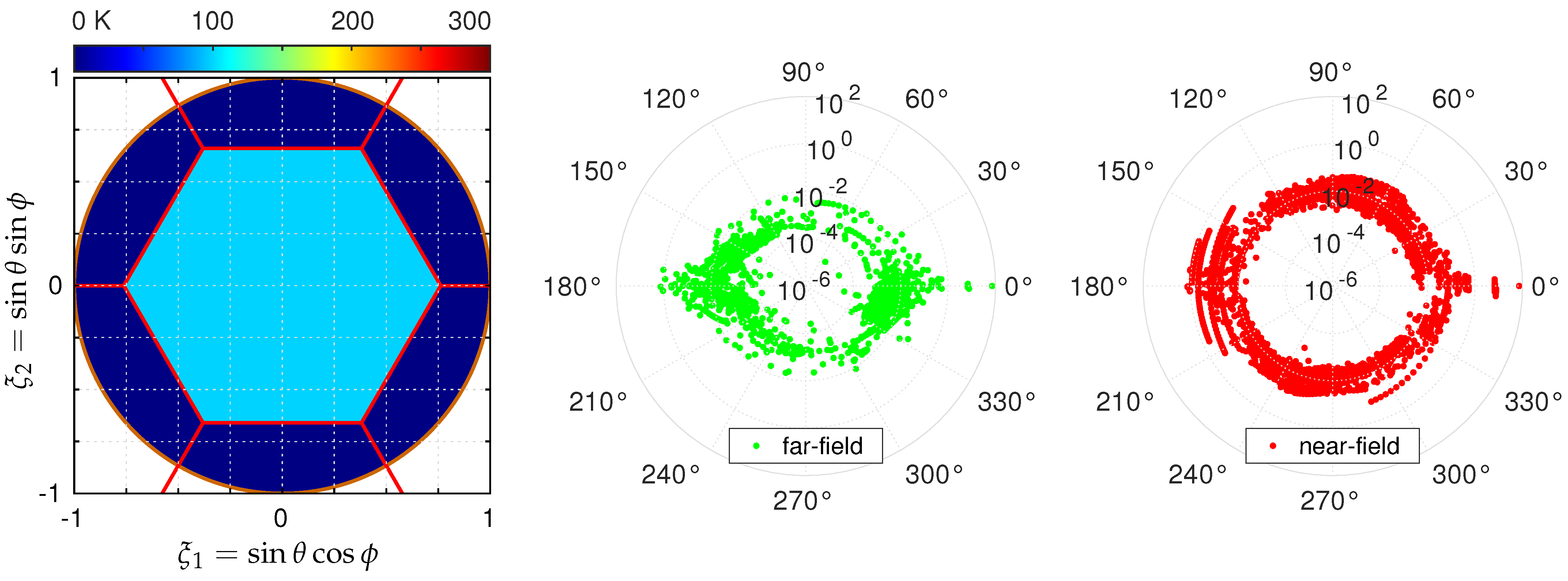
5.2. Far-Field vs. Near-Field
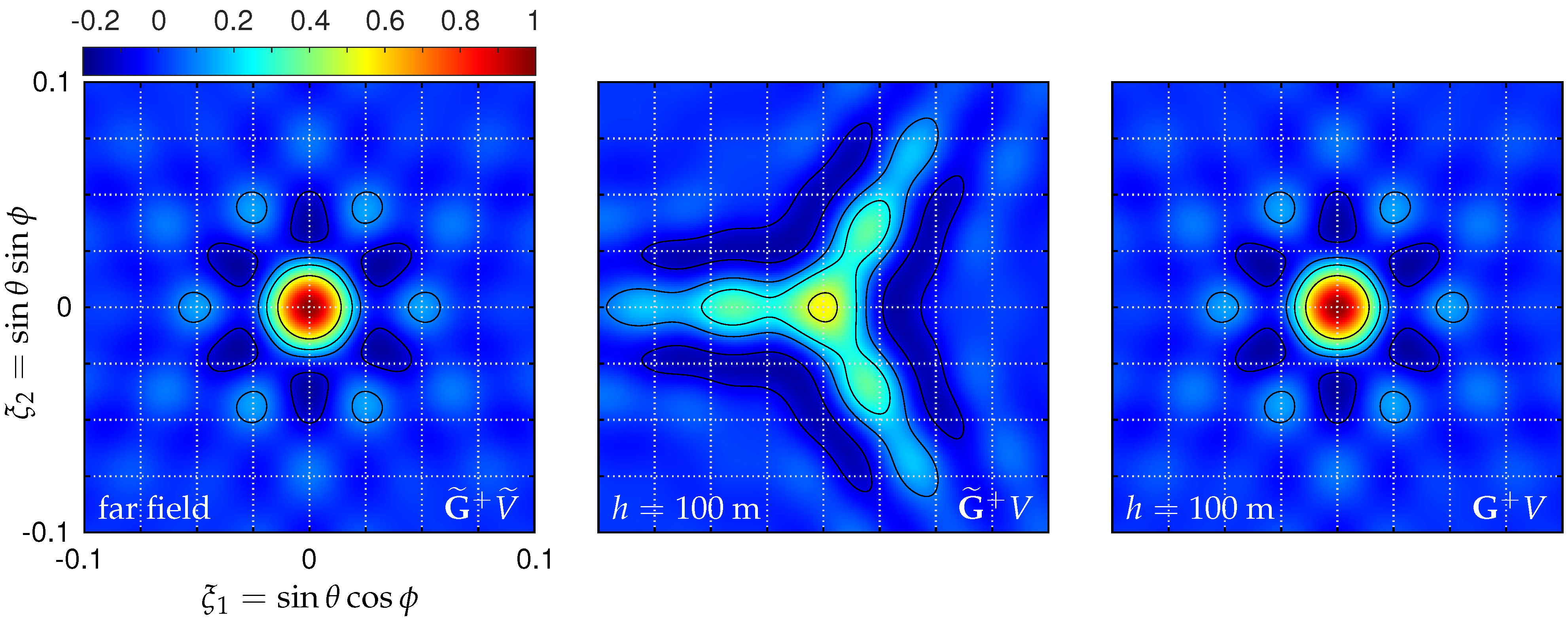
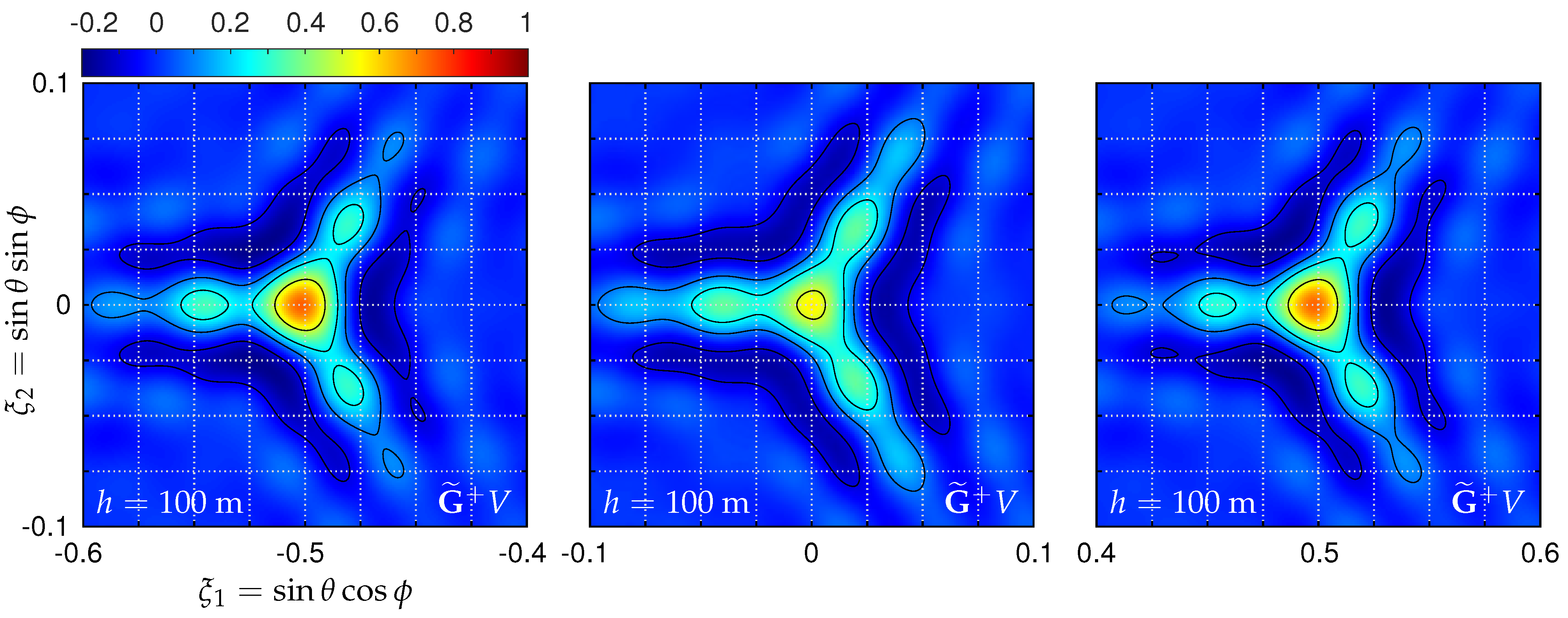
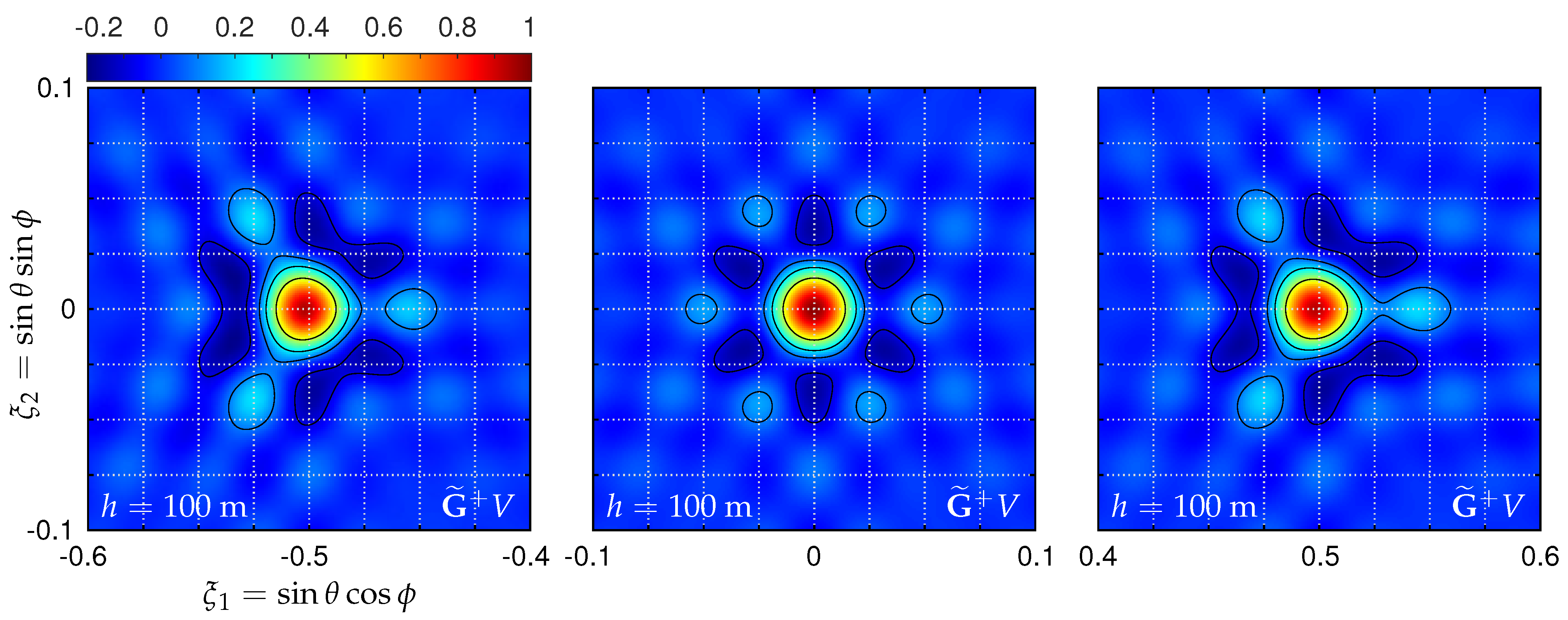
5.3. Point Source
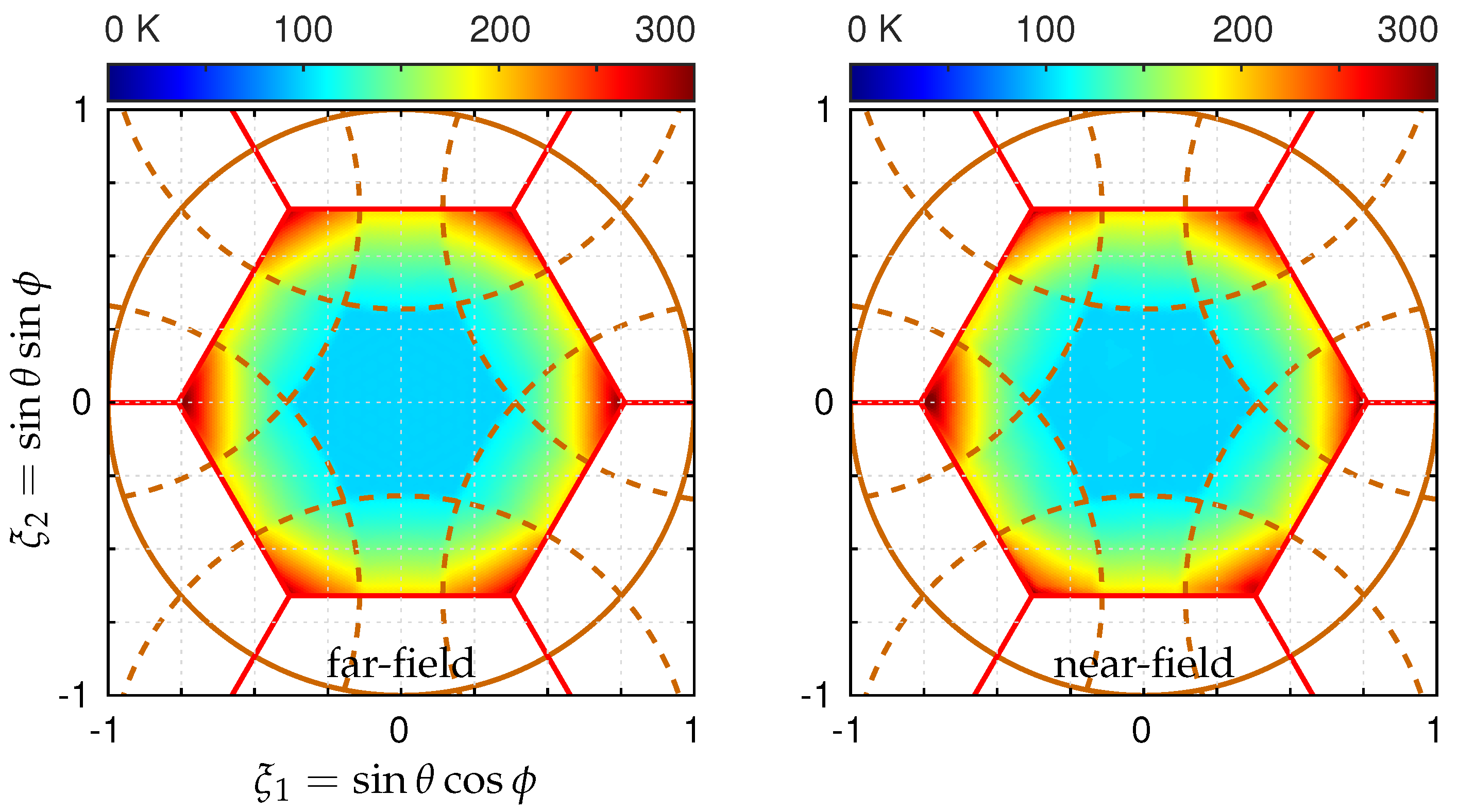
5.4. Extended Source
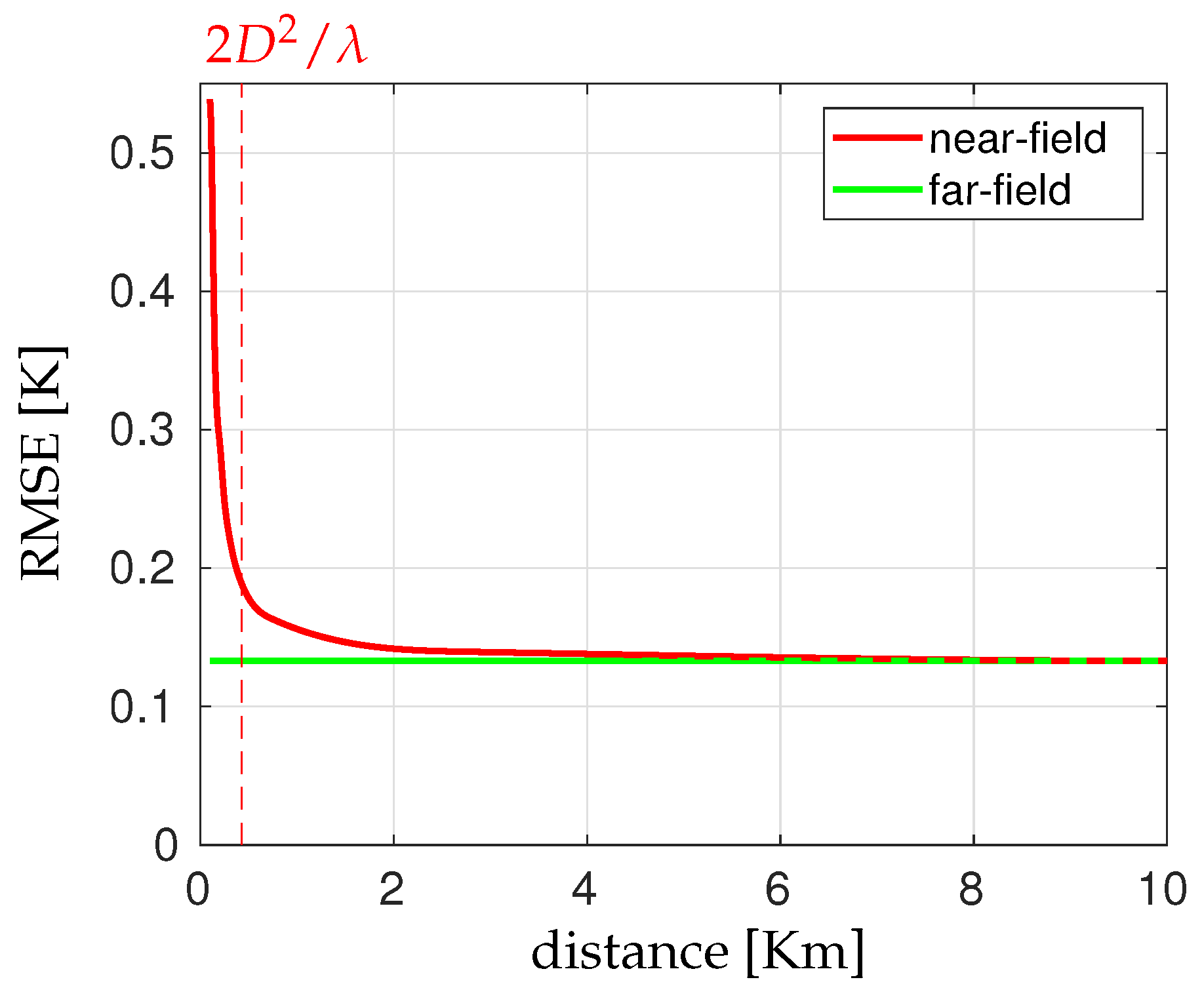
5.5. Radiometric Sensitivity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mutual Coherence of an Incoherent Source
References
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Selvan, K.T.; Janaswamy, R. Fraunhofer and Fresnel Distances: Unified Derivation for Aperture Antennas. IEEE Antennas Propag. Mag. 2017, 59, 12–15. [Google Scholar] [CrossRef]
- Haupt, R.L. Antenna Arrays: A Computational Approach, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Laursen, B.; Skou, N. Synthetic Aperture Radiometry Evaluated by a Two-Channel Demonstration Model. IEEE Trans. Geosci. Remote Sens. 1998, 36, 822–832. [Google Scholar] [CrossRef]
- van Cittert, P.H. Die Wahrscheinliche Schwingungsverteilung in Einer von Einer Lichtquelle Direkt Oder Mittels Einer Linse Beleuchteten Ebene. Physica 1934, 1, 201–210. [Google Scholar] [CrossRef]
- Zernike, F. The Concept of Degree of Coherence and its Application to Optical Problems. Physica 1934, 5, 785–795. [Google Scholar] [CrossRef]
- Anterrieu, É.; Lafuma, P.; Jeannin, N. An Algebraic Comparison of Synthetic Aperture Interferometry and Digital Beam Forming in Imaging Radiometry. Remote Sens. 2022, 14, 2285. [Google Scholar] [CrossRef]
- Bará, J.; Camps, A.; Torres, F.; Corbella, I. Angular resolution of two-dimensional, hexagonally sampled interferometric radiometers. Radio Sci. 1998, 33, 1459–1473. [Google Scholar] [CrossRef]
- Duran, I.; Lin, W.; Corbella, I.; Torres, F.; Duffo, N.; Martín-Neira, M. SMOS floor error impact and migation on ocean imaging. In Proceedings of the IEEE International Geoscience And Remote Sensing Symposium (IGARSS 2015), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Camps, A.; Corbella, I.; Bará, J.; Torres, F. Radiometric sensitivity computation in aperture synthesis interferometric radiometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 680–685. [Google Scholar] [CrossRef]
- Ryle, M.; Vonberg, D.D. Solar Radiation at 175 Mc/s. Nature 1946, 158, 339–340. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press and Assessment: Cambridge, UK, 1999. [Google Scholar]
- Thompson, A.R.; Moran, J.W.; Swenson, G.W. Interferometry and Synthesis in Radio Astronomy, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Fischman, M.A.; England, A.W. A technique for Reducing Fringe Washing Effects in L-Band Aperture Synthesis Radiometry. In Proceedings of the IEEE International Geoscience And Remote Sensing Symposium (IGARSS 2000), Honolulu, HI, USA, 24–28 July 2000. [Google Scholar]
- Zatman, M. How Narrow is Narrowband? IEE Proc.-Radar Sonar Navig. 1998, 145, 85–91. [Google Scholar] [CrossRef]
- Tanner, A.B.; Lambrigsten, B.H.; Gaier, T.M.; Torres, F. Near Field Characterization of the GeoSTAR Demonstrator. In Proceedings of the IEEE International Geoscience And Remote Sensing Symposium (IGARSS 2006), Denver, CO, USA, 31 July–4 August 2006. [Google Scholar]
- Peichl, M.; Suess, H.; Suess, M.; Kern, S. Microwave Imaging of the Brightness Temperature Distribution of Extended Areas in the Near and Far Field Using Two-Dimensional Aperture Synthesis with High Spatial Resolution. Radio Sci. 1998, 33, 781–801. [Google Scholar] [CrossRef]
- Liangbing, C.; Qingxia, L.; Zubiao, X.; Ke, C.; Yaoting, Z. Near-Field Imaging of One-Dimensional Aperture Synthesis Radiometers. In Proceedings of the IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications (MAPE 2009), Beijing, China, 27–29 October 2009. [Google Scholar]
- Zhang, C.; Wu, J.; Liu, H.; Yan, J. Imaging Algorithm for Synthetic Aperture Interferometric Radiometer in Near Field. Sci. China Technol. Sci. 2011, 54, 2224–2231. [Google Scholar] [CrossRef]
- Díez-García, R.; Martín-Neira, M. Antenna spacing and pattern differences: Their impact in MIRAS reconstruction error. In Proceedings of the 14th Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment (MicroRad 2016), Espoo, Finland, 11–14 April 2016. [Google Scholar]
- Fu, P.; Hu, F.; Hu, H.; Zheng, T. A Wavenumber Domain Imaging Algorithm for Synthetic Aperture Interferometric Radiometry in Near-Field. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2020), Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Fu, P.; Zhu, D.; Hu, F.; Xu, Y.; Xia, H. A Near-Field Imaging Algorithm Based on Angular Spectrum Theory for Synthetic Aperture Interferometric Radiometer. IEEE Trans. Microw. Theory Tech. 2022, 70, 3606–3616. [Google Scholar] [CrossRef]
- Hu, H.; Zhu, D.; Hu, F. A Novel Imaging Method Using Fractional Fourier Transform for Near-Field Synthetic Aperture Radiometer Systems. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wu, Y.; Li, Y.; Song, G.; Dou, H.; Li, H. A Near-Field Imaging Method Based on the Near-Field Distance for an Aperture Synthesis Radiometer. Remote Sens. 2024, 16, 767. [Google Scholar] [CrossRef]
- Feigenbaum, L. Brook Taylor and the method of increments. Arch. Hist. Exact Sci. 1985, 34, 1–140. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Wang, J.; Li, Y.; Zhang, Y. Regularization Imaging Algorithm with Accurate G Matrix for Near-Field MMW Synthetic Aperture Imaging Radiometer. Prog. Electromagn. Res. B 2014, 58, 193–203. [Google Scholar] [CrossRef]
- Schnoering, G.; Kawaguchi, T.; Höller, C. Mixed Near-and Far-Field 2D Imaging with Sparse Arrays. In Proceedings of the IEEE Radar Conference (RadarConf24), Denver, CO, USA, 6–10 May 2024. [Google Scholar]
- Corbella, I.; Duffo, N.; Vall-llossera, M.; Camps, A.; Torres, A. The Visibility Function in Interferometric Aperture Synthesis Radiometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1677–1682. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Suess, M.; Kainulainen, J.; Martin-Porqueras, F. The Flat Target Transformation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 613–620. [Google Scholar] [CrossRef]
- Anterrieu, É. A Resolving Matrix Approach for Synthetic Aperture Imaging Radiometers. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1649–1656. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.; Zhang, S.; Chen, X. General G-matrix imaging method for near-field millimeter-wave SAIR with any arrays. In Proceedings of the IEEE International Wireless Symposium (IWS 2018), Chengdu, China, 6–10 May 2018. [Google Scholar]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems, 1st ed.; Society for Industrial & Applied Mathematics: Philadelphia, PA, USA, 1998. [Google Scholar]
- Goodberlet, M.A. Improved Image Reconstruction Techniques for Synthetic Aperture Radiometers. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1362–1366. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Hansen, P.C. The Truncated SVD as a Method for Regularization. BIT Numer. Math. 1987, 27, 534–553. [Google Scholar] [CrossRef]
- Fay, T.H.; Kloppers, P.H. The Gibbs’ Phenomenon. Int. J. Math. Educ. Sci. Technol. 2001, 32, 73–89. [Google Scholar] [CrossRef]
- Anterrieu, É.; Waldteufel, P.; Lannes, A. Apodization Functions for 2D Hexagonally Sampled Synthetic Aperture Imaging Radiometers. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2531–2542. [Google Scholar] [CrossRef]
- McMullan, K.D.; Brown, M.A.; Martín-Neira, M.; Rits, W.; Ekholm, S.; Lemanczyk, J. SMOS: The Payload. IEEE Trans. Geosci. Remote Sens. 2008, 46, 594–605. [Google Scholar] [CrossRef]
- Barré, H.; Duesmann, B.; Kerr, Y.H. SMOS: The Mission and the System. IEEE Trans. Geosci. Remote Sens. 2008, 46, 587–593. [Google Scholar] [CrossRef]
- Pivnenko, S.; Nielsen, J.M.; Cappellin, C.; Lemanczyk, G.; Breinbjerg, O. High-Accuracy Calibration of the SMOS Radiometer Antenna Patterns at the DTU-ESA Spherical Near-Field Antenna Test Facility. In Proceedings of the IEEE International Geoscience And Remote Sensing Symposium (IGARSS 2007), Barcelona, Spain, 23–28 July 2007. [Google Scholar]
- Bayle, F.; Wigneron, J.-P.; Kerr, Y.H.; Waldteufel, P.; Anterrieu, E.; Orlhac, J.-C.; Chanzy, A.; Marloie, O.; Bernardini, M.; Sobjaerg, S.; et al. Two-dimensional synthetic aperture images over a land surface scene. IEEE Trans. Geosci. Remote Sens. 2002, 40, 710–714. [Google Scholar] [CrossRef]
- Talone, M.; Gourrion, J.; Sabia, R.; Gabarró, C.; Gonzalez, V.; Camps, A.; Corbella, I.; Monerris, A.; Font, J. SMOS’ brightness temperatures validation: First results after the commisioning phase. In Proceedings of the IEEE International Geoscience And Remote Sensing Symposium (IGARSS 2010), Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.-P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Enache Juglea, S.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Zine, S.; Boutin, J.; Font, J.; Reul, N.; Waldteufel, P.; Gabarró, C.; Tenerelli, J.; Petitcolin, F.; Vergely, J.-L.; Talone, M.; et al. Overview of the SMOS Sea Surface Salinity Prototype Processor. IEEE Trans. Geosci. Remote Sens. 2008, 46, 621–645. [Google Scholar]
- Thompson, A.R.; Clark, B.G.; Wade, C.M.; Napier, P.J. The Very Large Array. Astrophys. J. Suppl. Ser. 1980, 44, 151–167. [Google Scholar] [CrossRef]
- Padin, S.; Shepherd, M.C.; Cartwright, J.K.; Keeney, R.G.; Mason, B.S.; Pearson, T.J.; Readhead, A.C.S.; Schaal, W.A.; Sievers, J.; Udomprasert, P.S.; et al. The Cosmic Background Imager. Publ. Astron. Soc. Pac. 2002, 114, 83–97. [Google Scholar]
- Colliander, A.; Tauriainen, S.; Auer, T.I.; Kainulainen, J.; Uusitalo, J.; Toikka, M.; Hallikainen, M.T. MIRAS Reference Radiometer: A fully polarimetric noise injection radiometer. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1135–1143. [Google Scholar] [CrossRef]
- The MathWorks Inc.: Help Center. Available online: https://fr.mathworks.com/help/matlab/ref/eps.html (accessed on 1 August 2023).
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Torres, F.; Abril, J.; Nova, E.; Broquetas, A.; Jofre, L. Far field condition in passive interferometry for security screening applications. Proceedings of IEEE the European Conference on Antennas and Propagation (EuCAP 2010), Barcelona, Spain, 12–16 April 2010. [Google Scholar]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Khazâal, A.; Carfantan, H.; Anterrieu, É. On the reduction of the systematic error in imaging radiometry by aperture synthesis: A new approach for the SMOS space mission. IEEE Geosci. Remote Sens. Lett. 2009, 6, 47–51. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Vol. II: Mainly Electromagnetism and Matter, New Millennium ed.; Basic Books: New-York, NY, USA, 2011. [Google Scholar]
- Bracewell, R. The Fourier Transform and Its Applications, 3rd ed.; McGraw-Hill: New-York, NY, USA, 1999. [Google Scholar]
- Planck, M. Ueber das Gesetz der Energieverteilung im Normalspectrum. Ann. Phys. 1901, 309, 553–563. [Google Scholar] [CrossRef]
- Rayleigh, J. Remarks upon the Law of Complete Radiation. Philos. Mag. 1900, 49, 539–540. [Google Scholar] [CrossRef]
- Jeans, J. On the Partition of Energy between Matter and Aether. Philos. Mag. 1905, 10, 91–98. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anterrieu, E.; Yu, L.; Jeannin, N. A Comprehensive Comparison of Far-Field and Near-Field Imaging Radiometry in Synthetic Aperture Interferometry. Remote Sens. 2024, 16, 3584. https://doi.org/10.3390/rs16193584
Anterrieu E, Yu L, Jeannin N. A Comprehensive Comparison of Far-Field and Near-Field Imaging Radiometry in Synthetic Aperture Interferometry. Remote Sensing. 2024; 16(19):3584. https://doi.org/10.3390/rs16193584
Chicago/Turabian StyleAnterrieu, Eric, Louise Yu, and Nicolas Jeannin. 2024. "A Comprehensive Comparison of Far-Field and Near-Field Imaging Radiometry in Synthetic Aperture Interferometry" Remote Sensing 16, no. 19: 3584. https://doi.org/10.3390/rs16193584
APA StyleAnterrieu, E., Yu, L., & Jeannin, N. (2024). A Comprehensive Comparison of Far-Field and Near-Field Imaging Radiometry in Synthetic Aperture Interferometry. Remote Sensing, 16(19), 3584. https://doi.org/10.3390/rs16193584





