Evaluation of the Operational Global Ocean Wave Forecasting System of China
Abstract
1. Introduction
2. Wave Model, Data, and Method
2.1. Wave Model
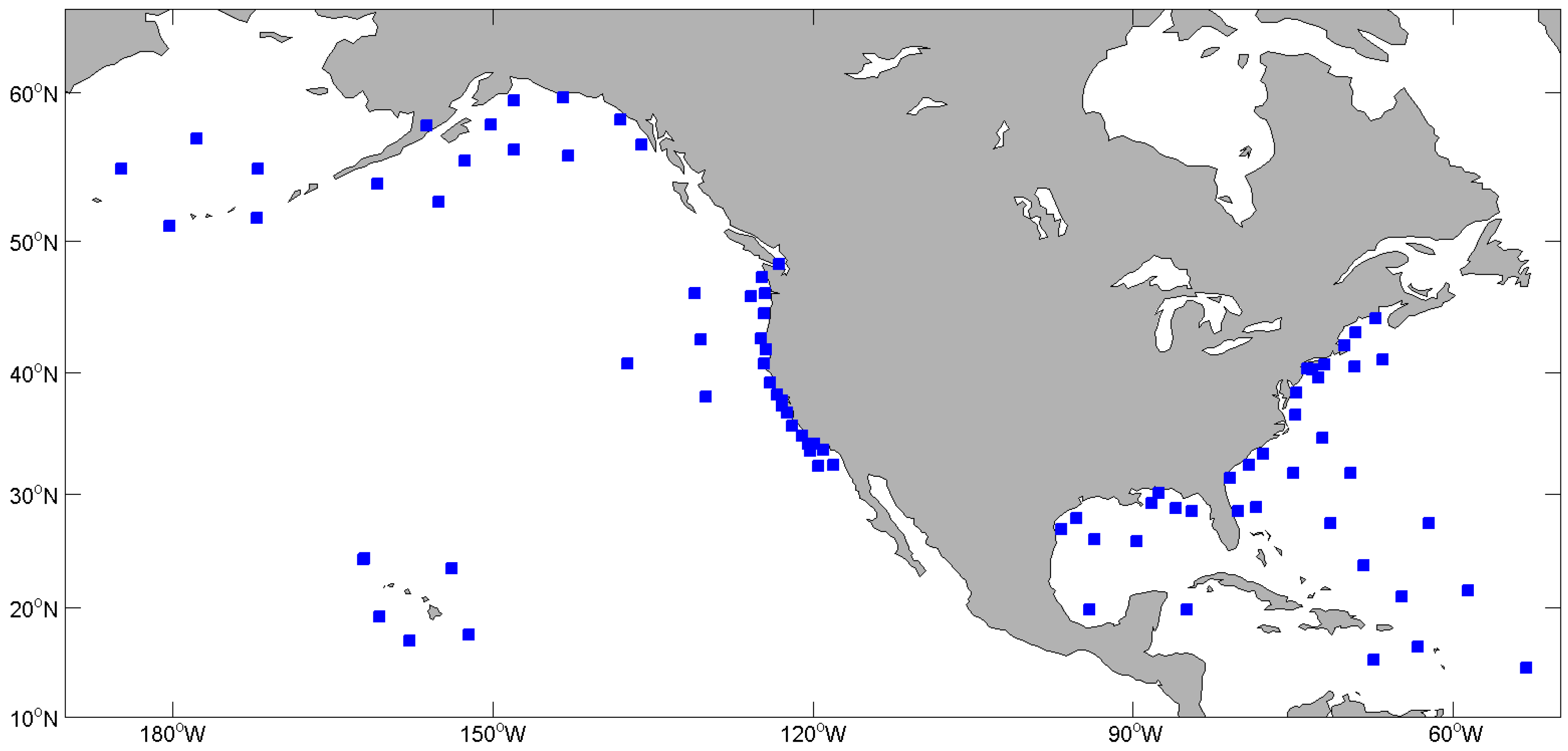
2.2. Data
2.3. Method
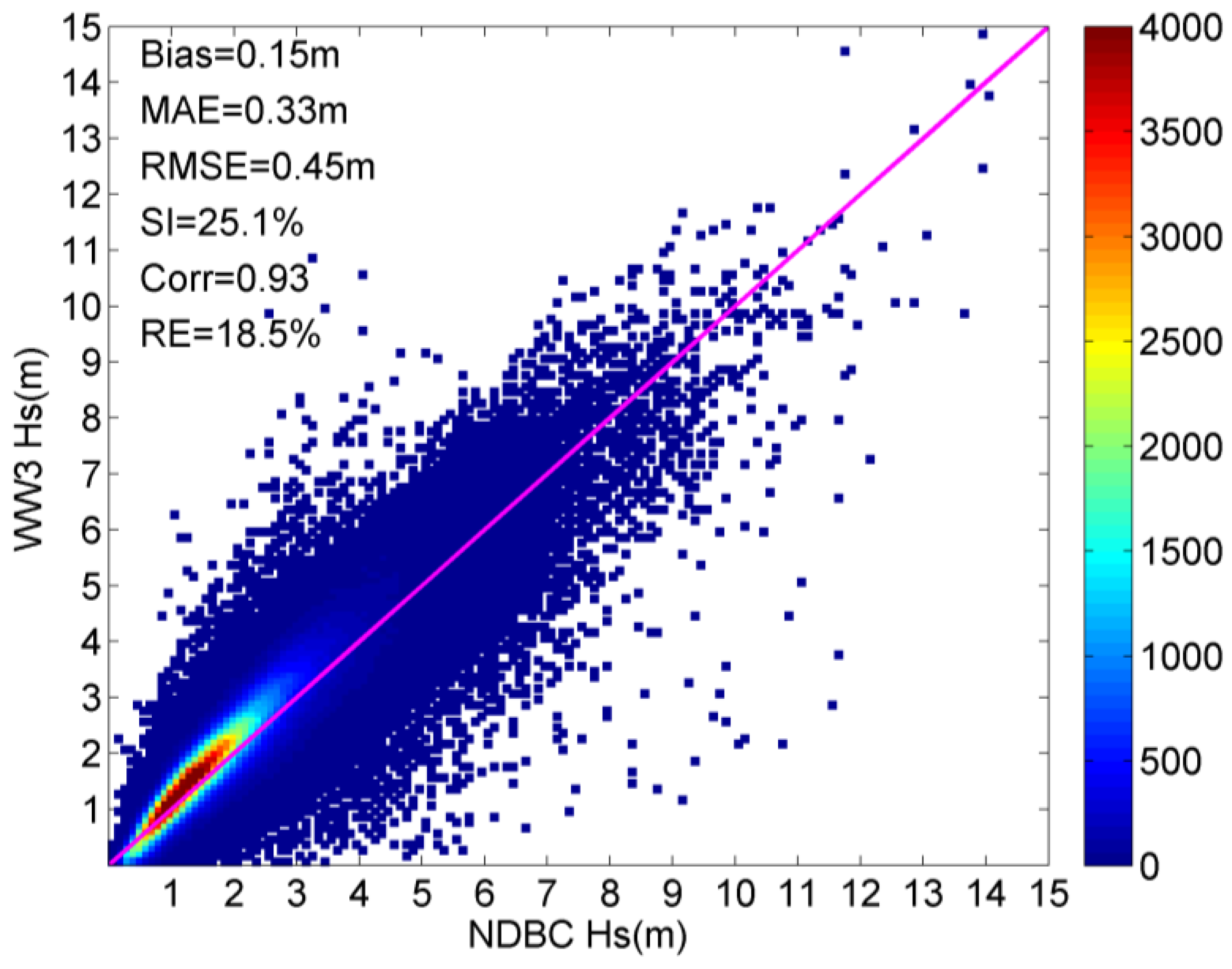
3. Results
3.1. Evaluation of Forecasting Performance in China’s Offshore Areas
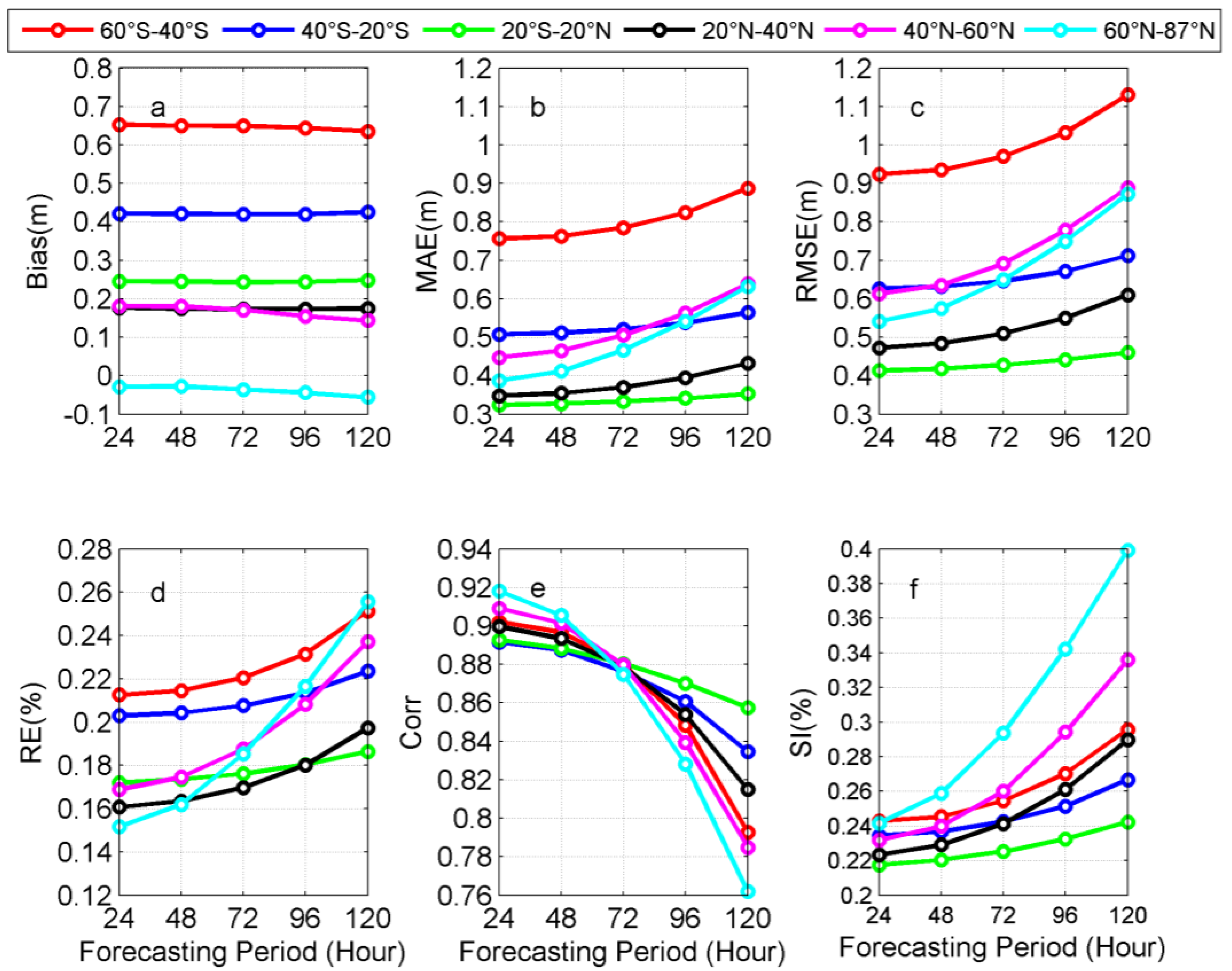
3.2. Evaluation of Forecasting Performance in Global Ocean Waters
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WAMDI Group. The WAM Model—A Third Generation Ocean Wave Prediction Model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P.A.E.M. Dynamics and Modelling of Ocean Waves; Cambridge University Press: Cambridge, UK, 1994; ISBN 0-521-47047-1. [Google Scholar]
- Tolman, H.L. A Third-Generation Model for Wind Waves on Slowly Varying, Unsteady and Inhomogeneous Depth and Currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Tolman, H.L. User Manual and System Documentation of WAVEWATCH IIITM version 3.14. Tech. Note MMAB Contrib. 2009, 276, 194. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A Third-Generation Wave Model for Coastal Regions: 1. Model Description and Validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Bidlot, J.R. Present Status of Wave Forecasting at ECMWF. In Workshop on Ocean Waves; ECMWF: Reading, UK, 2012. [Google Scholar]
- Janssen, P.A.E.M.; Bidlot, J.R. Progress in Operational Wave Forecasting. Procedia IUTAM 2018, 26, 14–29. [Google Scholar] [CrossRef]
- ECMWF. IFS Documentation CY45R1—Part VII: ECMWF Wave Model; ECMWF: Reading, UK, 2018. [Google Scholar] [CrossRef]
- Campos, R.M.; Alves, J.H.G.M.; Penny, S.G.; Krasnopolsky, V. Assessments of Surface Winds and Waves from the NCEP Ensemble Forecast System. Weather Forecast. 2018, 33, 1533–1546. [Google Scholar] [CrossRef]
- Chen, H.S. Ensemble Prediction of Ocean Waves at NCEP. In Proceedings of the 28th Ocean Engineering Conference, Taipei, Taiwan, China, 30 November–2 December 2006; pp. 25–37. [Google Scholar]
- Cao, D.; Chen, H.S.; Tolman, H. Verification of Ocean Wave Ensemble Forecasts at NCEP. In Proceedings of the 10th International Workshop on Wave Hindcasting and Forecasting and Coastal Hazard Symposium, Oahu, HI, USA, 11–16 November 2007; Available online: http://www.waveworkshop.org/10thWaves/ProgramFrameset.htm (accessed on 18 July 2023).
- Alves, J.H.G.M.; Chawla, A.; Tolman, H.L.; Schwab, D.; Lang, G.; Mann, G. The Operational Implementation of a Great Lakes Wave Forecasting System at NOAA/NCEP. Weather Forecast. 2014, 29, 1473–1497. [Google Scholar] [CrossRef]
- Aouf, L.; Lefèvre, J.M. On the Impact of the Assimilation of SARAL/AltiKa Wave Data in the Operational Wave Model MFWAM. Mar. Geod. 2015, 38, 381–395. [Google Scholar] [CrossRef]
- Li, J.G.; Saulter, A. Unified Global and Regional Wave Model on a Multi-Resolution Grid. Ocean Dyn. 2014, 64, 1657–1670. [Google Scholar] [CrossRef]
- Seemanth, M.; Remya, P.G.; Bhowmick, S.A.; Sharma, R.; Balakrishnan Nair, T.M.; Kumar, R.; Chakraborty, A. Implementation of Altimeter Data Assimilation on a Regional Wave Forecasting System and Its Impact on Wave and Swell Surge Forecast in the Indian Ocean. Ocean Eng. 2021, 237, 109585. [Google Scholar] [CrossRef]
- Wan, L.; Liu, Y.; Ling, T. Development of a Global High-Resolution Marine Dynamic Environmental Forecasting System. Atmos. Ocean. Sci. Lett. 2018, 11, 379–387. [Google Scholar] [CrossRef]
- Wang, H.; Wan, L.; Qin, Y.; Wang, Y.; Yang, X.; Liu, Y.; Xing, J.; Chen, L.; Wang, Z.; Zhang, T.; et al. Development and Application of the Chinese Global Operational Oceanography Forecasting System. Adv. Earth Sci. 2016, 31, 1090–1104. [Google Scholar]
- Wang, Y.; Yu, Z. Validation of Impact of Assimilation of Altimeter Satellite Significant Wave Height on Wave Forecast in the Northwest Pacific. Acta Oceanol. Sin. 2009, 31, 1–8. [Google Scholar] [CrossRef]
- Bidlot, J.R.; Holmes, D.J.; Wittmann, P.A.; Lalbeharry, R.; Chen, H.S. Inter-comparison of the Performance of Operational Ocean Wave Forecasting Systems with Buoy Data. Weather Forecast. 2002, 17, 287–310. [Google Scholar] [CrossRef]
- Bidlot, J.R.; Holt, M. Verification of Operational Global and Regional Wave Forecasts Systems against Measurements from Moored Buoys; JCOMM Tech. Rep. 2006, 30, WMO-TD-1333; WMO: Geneva, Switzerland; IOC: Geneva, Switzerland, 2006; 11p.
- Bidlot, J.R.; Li, J.G.; Wittmann, P.; Fauchon, M.; Chen, H.; Lefevre, J.M.; Bruns, T.; Greenslade, D.; Ardhuin, F.; Kohno, N.; et al. Inter-Comparison of Operational Wave Forecasting Systems. In Proceedings of the 10th International Workshop on Wave Hindcasting and Forecasting and Coastal Hazard Symposium, Oahu, HI, USA, 11–16 November 2007. Available online: http://www.waveworkshop.org/10thWaves/ProgramFrameset.htm (accessed on 19 July 2023).
- WMO Lead Centre for Wave Forecast Verification. Intercomparison of Operational Wave Forecasting Systems Against In-Situ Observations for JJA 2023—00 and 12UTC Runs, Part I: Significant Wave Height; ECMWF: Reading, UK, 2023; 61p, Available online: https://confluence.ecmwf.int/display/WLW/Significant+wave+height?prview=/116958920/348807936/LCWFV_swh_report_12_JJA2023.pdf (accessed on 19 December 2023).
- Valiente, N.G.; Saulter, A.; Gomez, B.; Bunney, C.; Li, J.G.; Palmer, T.; Pequignet, C. The Met Office Operational Wave Forecasting System: The Evolution of the Regional and Global Models. Geosci. Model Dev. 2023, 16, 2515–2538. [Google Scholar] [CrossRef]
- Bernier, N.B.; Alves, J.H.; Tolman, H.; Chawla, A.; Peel, S.; Pouliot, B.; Bélanger, J.M.; Pellerin, P.; Lépine, M.; Roch, M. Operational Wave Prediction System at Environment Canada: Going Global to Improve Regional Forecast Skill. Weather Forecast. 2016, 31, 353–370. [Google Scholar] [CrossRef]
- Michalis, R.; Anna, Z.; Gerasimos, K. Implementation and Validation of a New Operational Wave Forecasting System of the Mediterranean Monitoring and Forecasting Centre in the framework of the Copernicus Marine Environment Monitoring Service. Nat. Hazards Earth Syst. Sci. 2018, 18, 2675–2695. [Google Scholar] [CrossRef]
- Remya, P.G.; Rabi Ranjan, T.; Sirisha, P.; Harikumar, R.; Balakrishnan Nair, T.M. Indian Ocean Wave Forecasting System for Wind Waves: Development and Its Validation. J. Oper. Oceanogr. 2020, 14, 1–16. [Google Scholar] [CrossRef]
- The WAVEWATCH III Development Group (WW3DG). User Manual and System Documentation of WAVEWATCH III Version 6.07; Tech. Note 333; NOAA/NWS/NCEP/MMAB: College Park, MD, USA, 2019; Appendices, 465p. [Google Scholar]
- Yang, J.; Zhang, J.; Jia, Y.; Fan, C.; Cui, W. Validation of Sentinel-3A/3B and Jason-3 Altimeter Wind Speeds and Significant Wave Heights Using Buoy and ASCAT Data. Remote Sens. 2020, 12, 2079. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.; Liu, B.; Lin, W.; He, Y.; Liu, J. Validation and Calibration of Nadir SWH Products from CFOSAT and HY-2B with Satellites and In Situ Observations. J. Geophys. Res. Ocean. 2021, 126, e2020JC016689. [Google Scholar] [CrossRef]
- Sepulveda, H.H.; Queffeulou, P.; Ardhuin, F. Assessment of SARAL/AltiKa Wave Height Measurements Relative to Buoy, Jason-2, and Cryosat-2 Data. Mar. Geod. 2015, 38, 449–465. [Google Scholar] [CrossRef]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global Trends in Wind Speed and Wave Height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef]
- WMO Lead Centre for Wave Forecast Verification. Intercomparison of Operational Wave Forecasting Systems Against In-Situ Observations for JJA 2023—00 and 12UTC Runs, Part III: 10 Meter Wind Speed; ECMWF: Reading, UK, 2023; 61p, Available online: https://confluence.ecmwf.int/display/WLW/Wind+speed?preview=/116958928/373758446/LCWFV_10ff_report_12_SON2023.pdf (accessed on 20 December 2023).
- Wang, J.; Li, B.; Gao, Z.; Wang, J. Comparison of ECMWF Significant Wave Height Forecasts in the China Sea with Buoy Data. Weather Forecast. 2019, 34, 1693–1704. [Google Scholar] [CrossRef]
- Ardhuin, F.; Orfila, A. Wind waves. In New Frontiers in Operational Oceanography; Chassignet, E.P., Pascual, A., Tintoré, J., Verron, J., Eds.; GODAE: Mallorca, Spain, 2018; pp. 393–422. [Google Scholar]
- Tolman, H.L. Treatment of Unresolved Islands and Ice in Wind Wave Models. Ocean Model. 2003, 5, 219–231. [Google Scholar] [CrossRef]
- Wu, M.; Wang, H.; Wan, L.; Wang, J.; Wang, Y.; Wang, J. The Impacts of the Application of the Ensemble Optimal Interpolation Method in Global Ocean Wave Data Assimilation. Atmosphere 2023, 14, 818. [Google Scholar] [CrossRef]
- Li, J.G. Global Transport on a Spherical Multiple-Cell Grid. Mon. Weather Rev. 2011, 139, 1536–1555. [Google Scholar] [CrossRef]
- Li, J.G. Propagation of Ocean Surface Waves on a Spherical Multiple-Cell Grid. J. Comput. Phys. 2012, 231, 8262–8277. [Google Scholar] [CrossRef]
- Li, J.G. Hybrid Multi-Grid Parallelisation of WAVEWATCH III Model on Spherical Multiple-Cell Grids. J. Parallel Distr. Com. 2022, 167, 187–198. [Google Scholar] [CrossRef]
- Hou, F.; Gao, Z.; Li, J.; Yu, F. An Efficient Algorithm for Generating a Spherical Multiple-Cell Grid. Acta Oceanol. Sin. 2022, 41, 41–50. [Google Scholar] [CrossRef]
- Saulter, A.; Bunney, C.; Li, J.G.; Palmer, T. Process and Resolution Impacts on UK Coastal Wave Predictions from Operational Global-Regional Wave Models. In Proceedings of the 1st International Workshop on Waves, Storm Surges and Coastal Hazards Incorporating the 15th International Waves Workshop, Liverpool, UK, 10–15 September 2017. Available online: http://www.waveworkshop.org/15thWaves/index.htm (accessed on 19 July 2023).

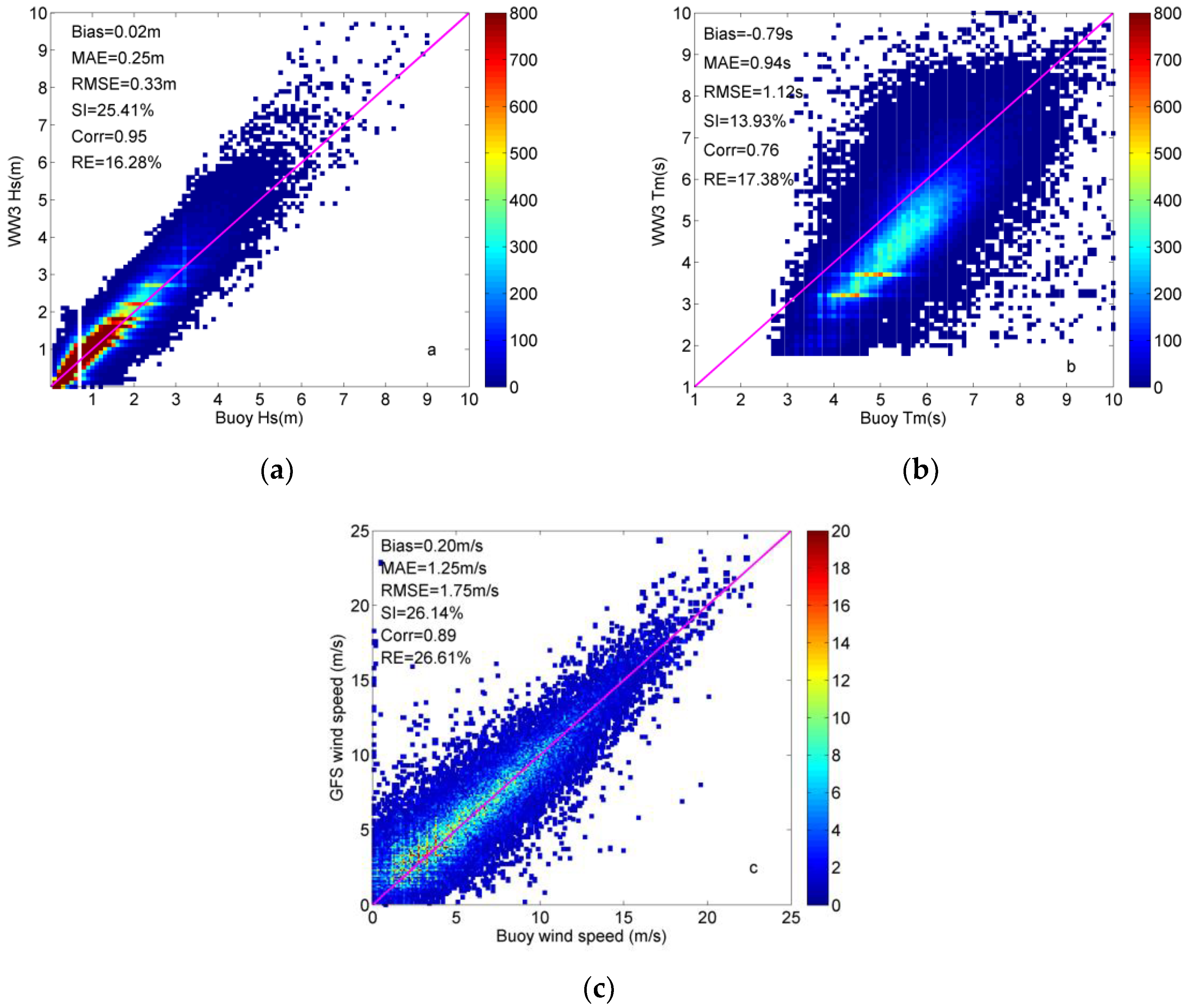
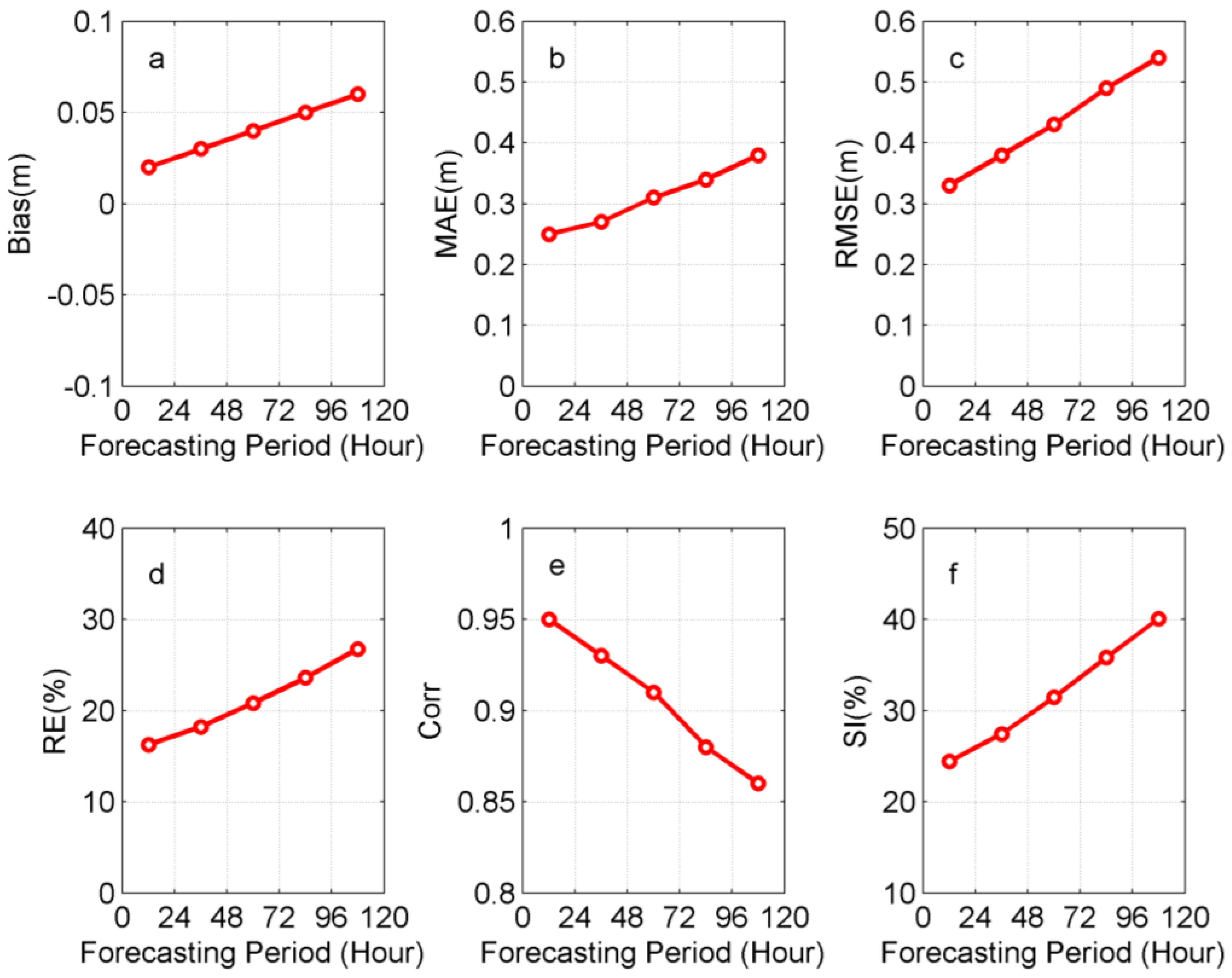
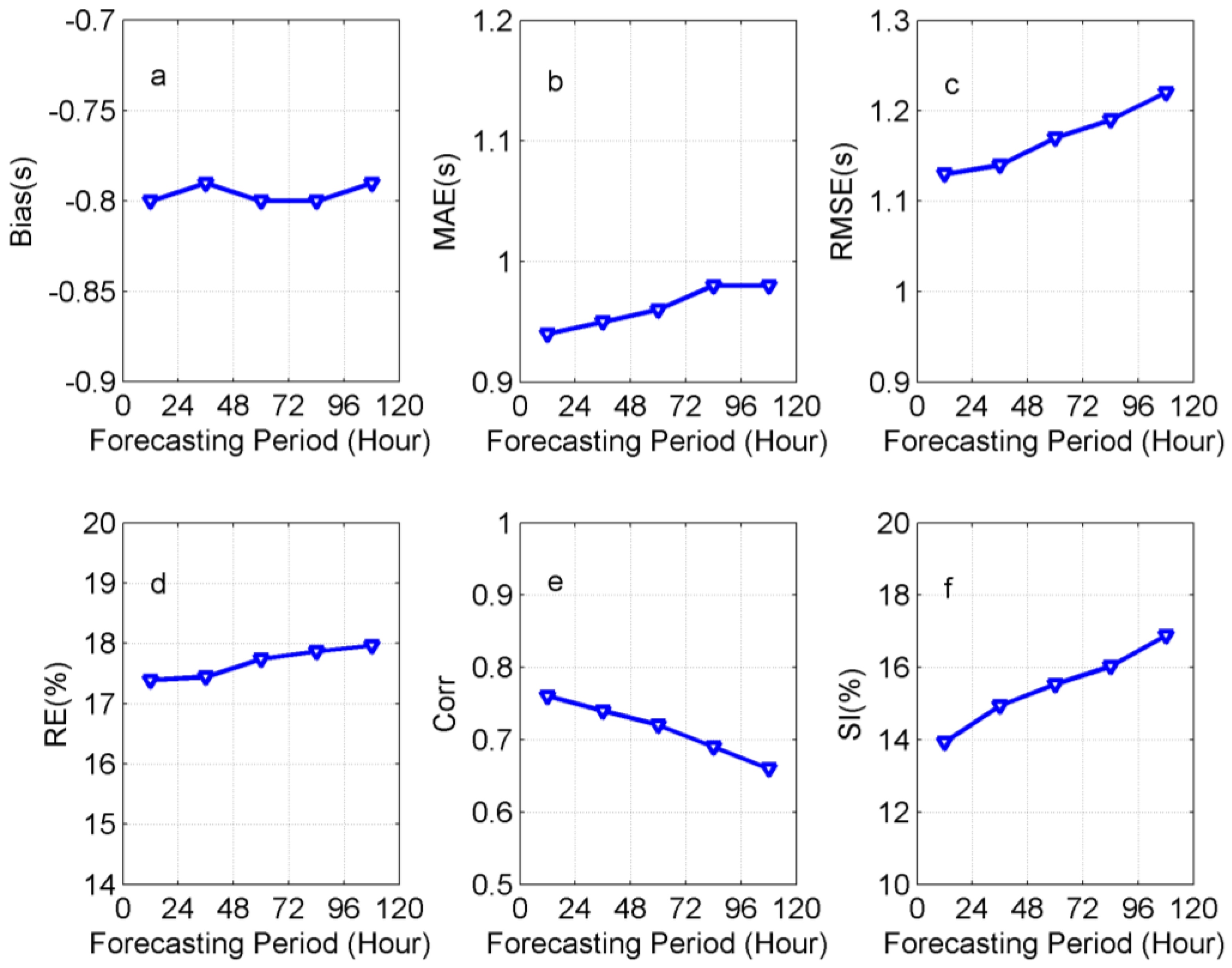
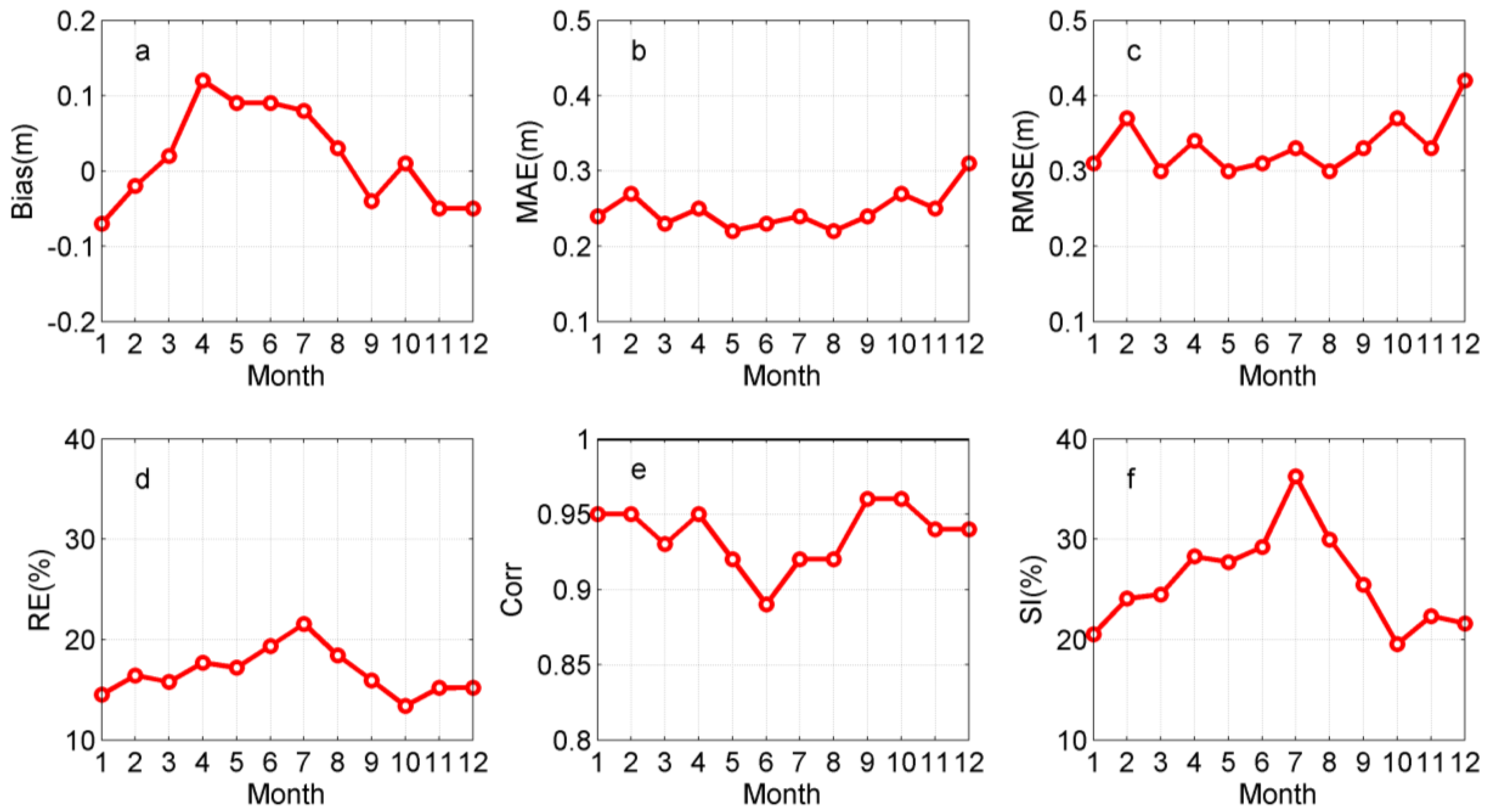
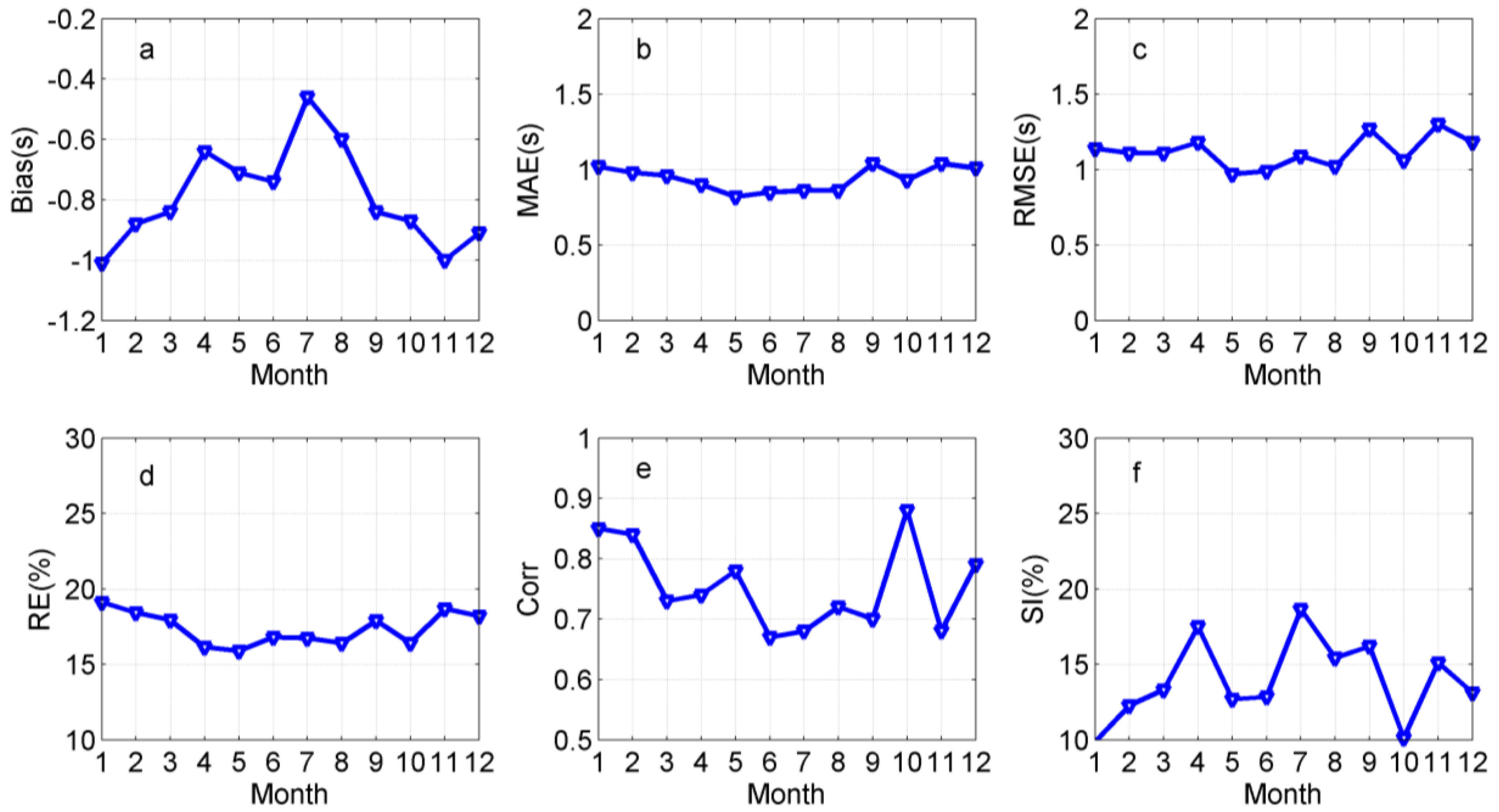
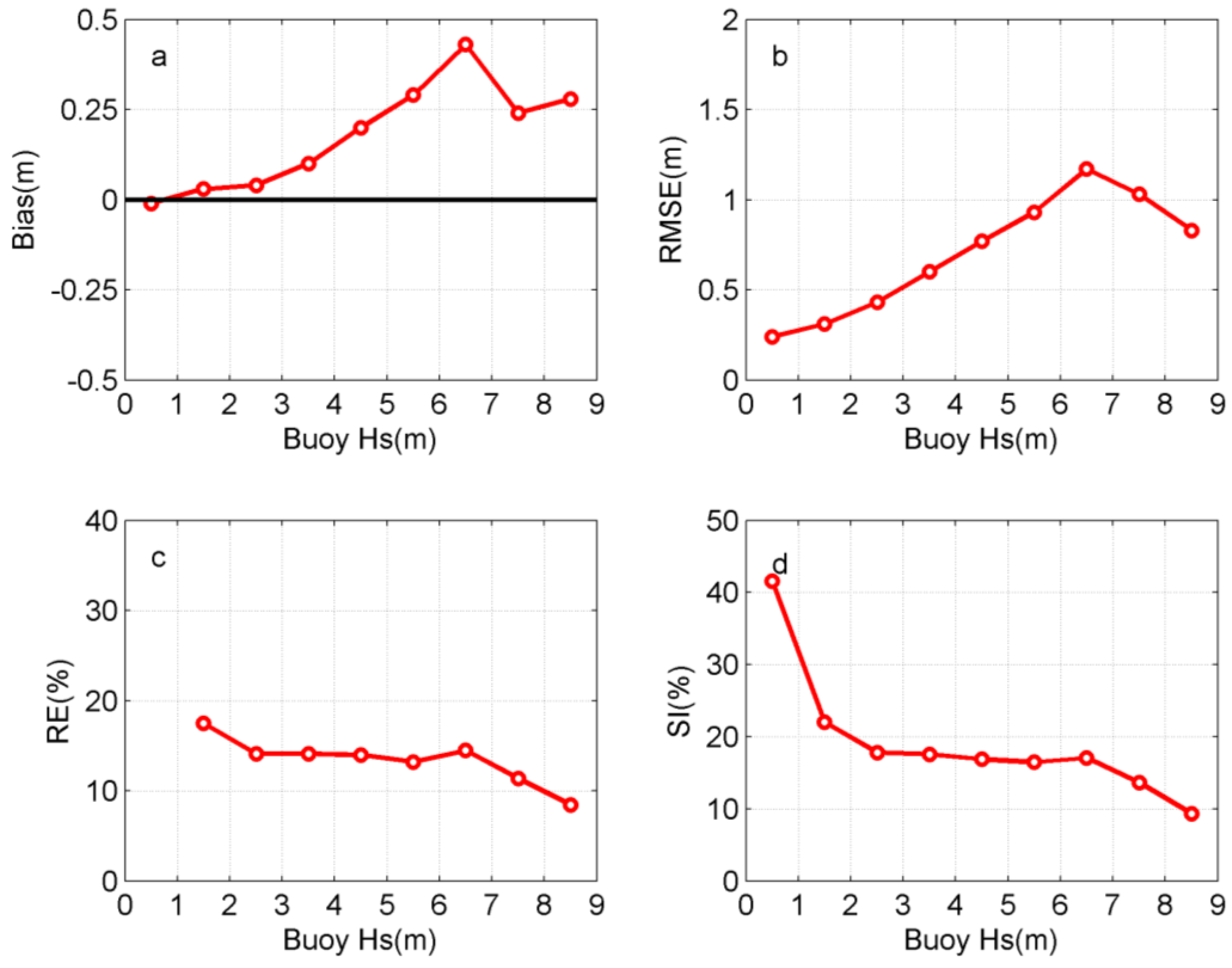
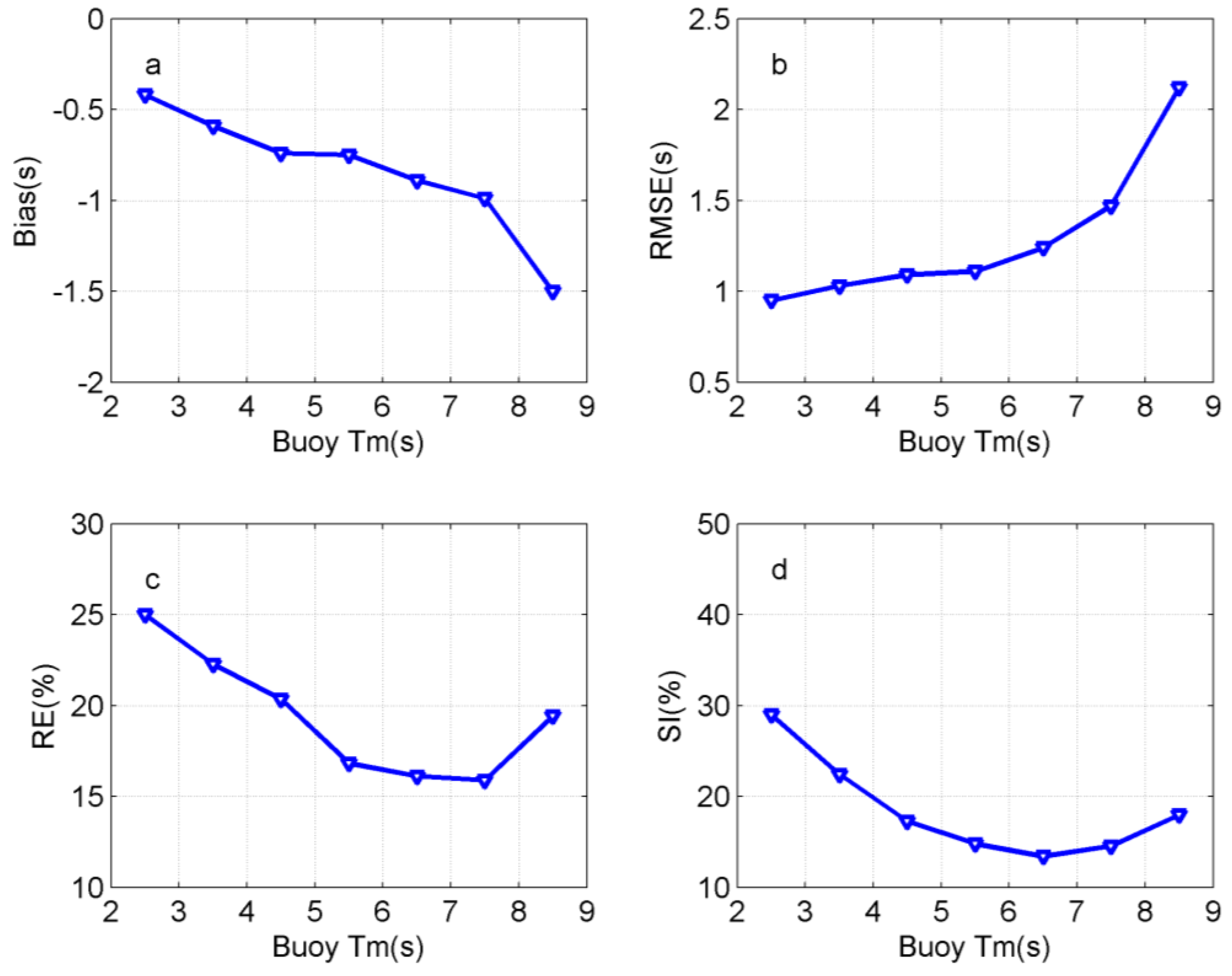

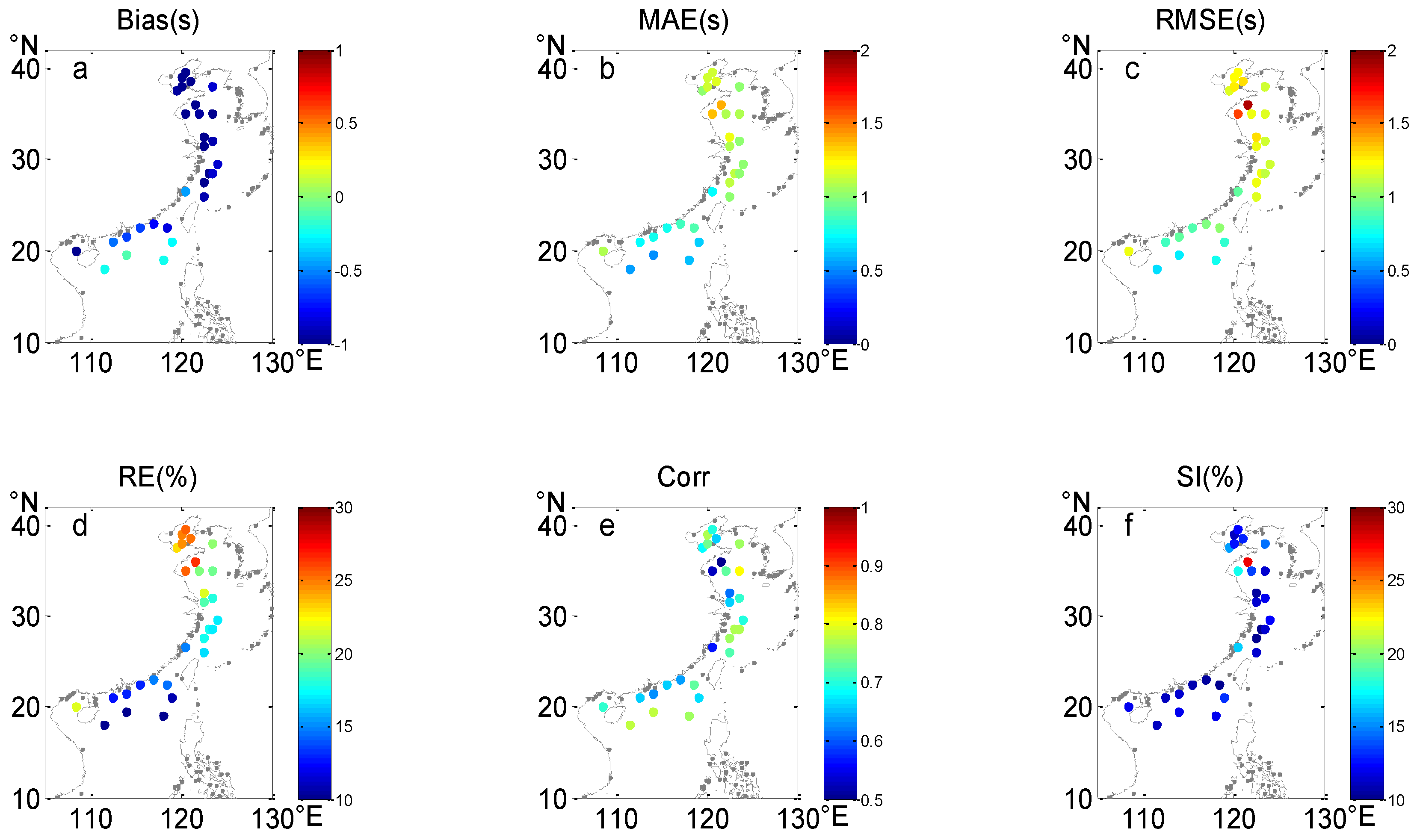

| Entries | Buoy Hs (m) | WW3 Hs (m) | Bias (m) | MAE (m) | RMSE (m) | RE (%) | Corr | SI (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Entire year | 187,052 | 1.32 | 1.34 | 0.02 | 0.25 | 0.33 | 16.28 | 0.95 | 25.41 |
| Spring | 47,092 | 1.12 | 1.19 | 0.07 | 0.23 | 0.31 | 16.49 | 0.94 | 26.53 |
| Summer | 47,693 | 0.96 | 1.03 | 0.07 | 0.23 | 0.31 | 19.37 | 0.91 | 31.52 |
| Autumn | 48,303 | 1.56 | 1.53 | −0.03 | 0.25 | 0.34 | 14.44 | 0.96 | 22.14 |
| Winter | 43,964 | 1.64 | 1.59 | −0.05 | 0.27 | 0.37 | 14.95 | 0.95 | 21.75 |
| Entries | Buoy Tm (s) | WW3 Tm (s) | Bias (s) | MAE (s) | RMSE (s) | RE (%) | Corr | SI (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Entire year | 125,361 | 5.52 | 4.73 | −0.79 | 0.94 | 1.12 | 17.38 | 0.76 | 13.93 |
| Spring | 29,520 | 5.44 | 4.71 | −0.73 | 0.89 | 1.09 | 16.65 | 0.75 | 14.50 |
| Summer | 30,650 | 5.25 | 4.65 | −0.60 | 0.86 | 1.03 | 16.65 | 0.69 | 15.64 |
| Autumn | 34,203 | 5.78 | 4.88 | −0.90 | 1.00 | 1.21 | 17.65 | 0.75 | 13.80 |
| Winter | 30,988 | 5.59 | 4.67 | −0.92 | 1.00 | 1.14 | 18.57 | 0.83 | 11.75 |
| Entries | Buoy Hs (m) | WW3 Hs (m) | Bias (m) | MAE (m) | RMSE (m) | RE (%) | Corr | SI (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Bohai Sea | 27,150 | 0.71 | 0.62 | −0.09 | 0.21 | 0.28 | 19.10 | 0.88 | 37.57 |
| Yellow Sea | 50,668 | 0.95 | 0.87 | −0.08 | 0.21 | 0.27 | 17.22 | 0.91 | 28.02 |
| East China Sea | 41,579 | 1.54 | 1.55 | 0.01 | 0.22 | 0.29 | 14.07 | 0.93 | 19.45 |
| South China Sea | 60,295 | 1.79 | 1.96 | 0.17 | 0.29 | 0.38 | 16.05 | 0.96 | 18.33 |
| Beibu Gulf | 7772 | 0.92 | 0.87 | −0.05 | 0.2 | 0.28 | 18.22 | 0.92 | 29.74 |
| Entries | Buoy Tm (s) | WW3 Tm (s) | Bias (s) | MAE (s) | RMSE (s) | RE (%) | Corr | SI (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Bohai Sea | 13,086 | 4.43 | 3.38 | −1.05 | 1.08 | 1.21 | 23.20 | 0.76 | 13.32 |
| Yellow Sea | 29,230 | 5.18 | 4.09 | −1.09 | 1.18 | 1.39 | 21.80 | 0.68 | 16.30 |
| East China Sea | 30,821 | 5.83 | 4.90 | −0.93 | 1.03 | 1.15 | 16.68 | 0.74 | 11.23 |
| South China Sea | 47,867 | 5.9 | 5.43 | −0.47 | 0.70 | 0.84 | 12.00 | 0.74 | 11.21 |
| Beibu Gulf | 4326 | 4.8 | 3.76 | −1.04 | 1.07 | 1.19 | 21.81 | 0.72 | 12.02 |
| Bias (m) | MAE (m) | RMSE (m) | RE (%) | Corr | SI (%) | |
|---|---|---|---|---|---|---|
| Gulf of Mexico | −0.08 | 0.22 | 0.31 | 16.88 | 0.91 | 28.98 |
| East Coast | −0.05 | 0.24 | 0.35 | 16.38 | 0.91 | 25.55 |
| Atlantic Ocean | 0.10 | 0.22 | 0.31 | 12.04 | 0.92 | 17.25 |
| West Coast | 0.28 | 0.43 | 0.56 | 21.15 | 0.91 | 26.04 |
| Hawaii | 0.29 | 0.33 | 0.42 | 15.91 | 0.92 | 19.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Wang, J.; Cai, Q.; Wang, Y.; Wang, J.; Wang, H. Evaluation of the Operational Global Ocean Wave Forecasting System of China. Remote Sens. 2024, 16, 3535. https://doi.org/10.3390/rs16183535
Wu M, Wang J, Cai Q, Wang Y, Wang J, Wang H. Evaluation of the Operational Global Ocean Wave Forecasting System of China. Remote Sensing. 2024; 16(18):3535. https://doi.org/10.3390/rs16183535
Chicago/Turabian StyleWu, Mengmeng, Juanjuan Wang, Qiongqiong Cai, Yi Wang, Jiuke Wang, and Hui Wang. 2024. "Evaluation of the Operational Global Ocean Wave Forecasting System of China" Remote Sensing 16, no. 18: 3535. https://doi.org/10.3390/rs16183535
APA StyleWu, M., Wang, J., Cai, Q., Wang, Y., Wang, J., & Wang, H. (2024). Evaluation of the Operational Global Ocean Wave Forecasting System of China. Remote Sensing, 16(18), 3535. https://doi.org/10.3390/rs16183535




