Response of Upper Ocean to Parameterized Schemes of Wave Breaking under Typhoon Condition
Abstract
1. Introduction
2. Methodology
2.1. Descriptions of the Modeling System
2.2. Wave Breaking Parameterization
2.2.1. Classical Boundary Layer Scheme
2.2.2. Wave Age Parameterization
2.2.3. Breaking Wave Parameter Parameterization
3. Materials and Methods
3.1. Typhoon Introduction
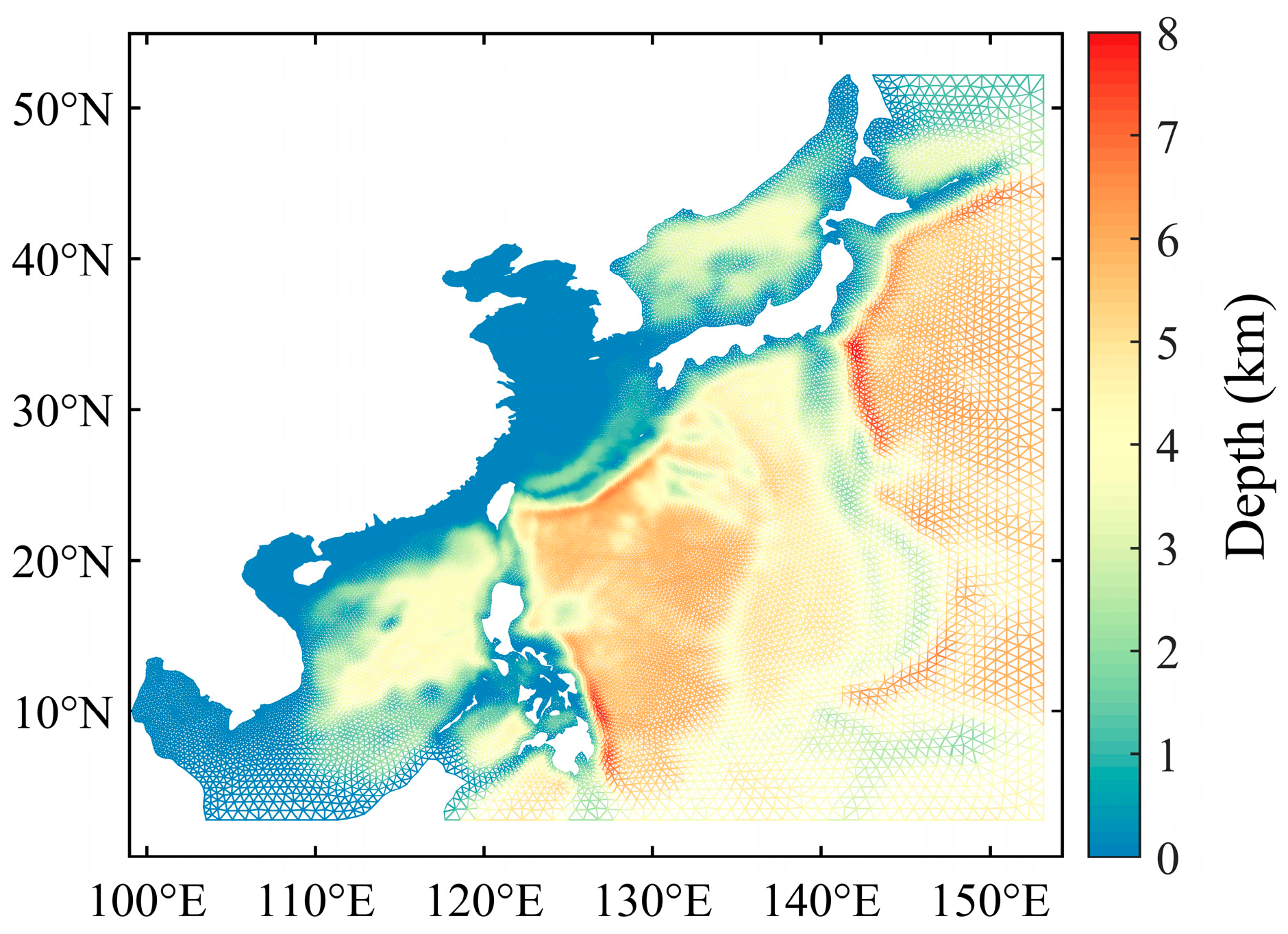
3.2. Model Setup
4. Results and Discussion
4.1. Wave Simulation Result
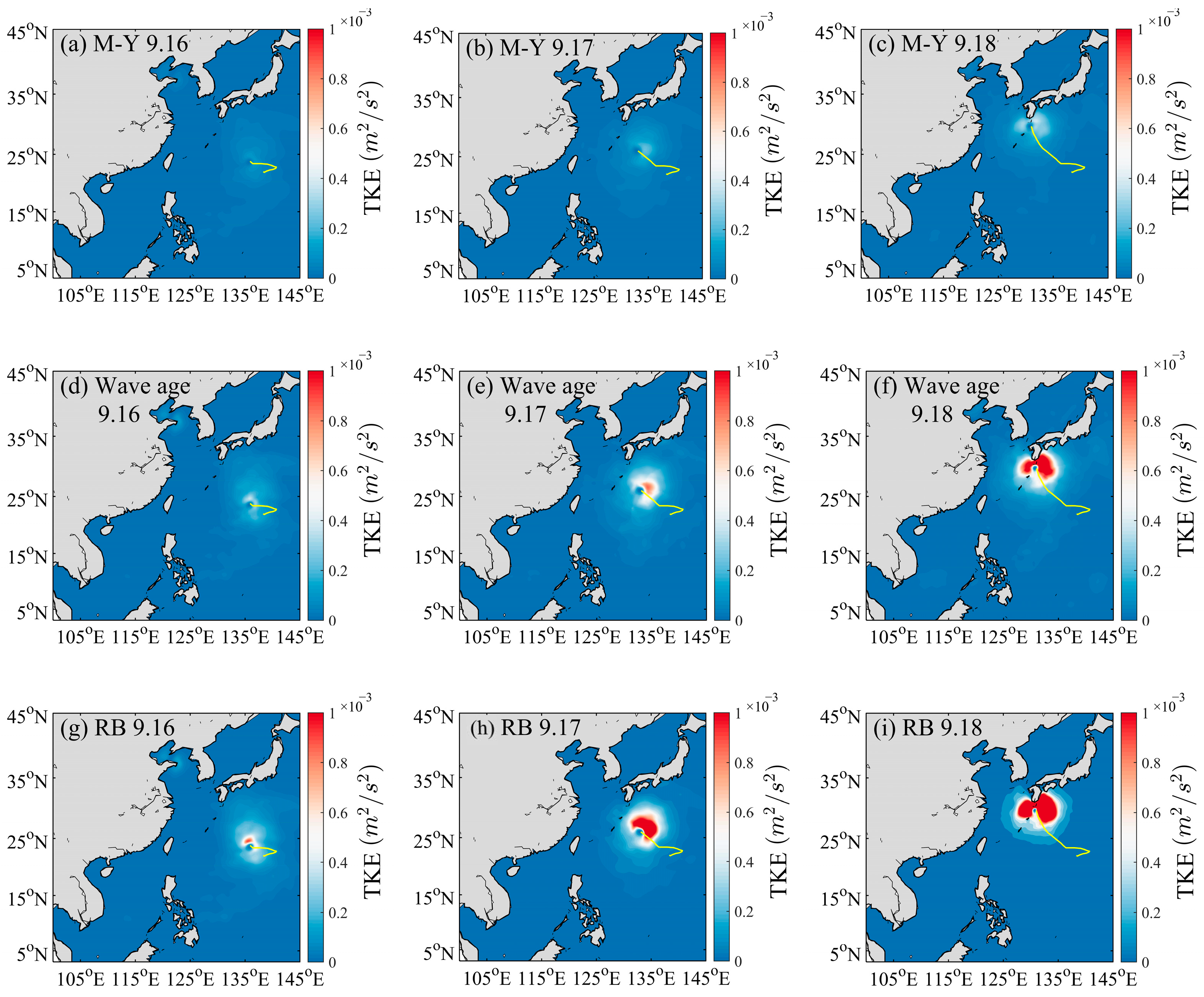
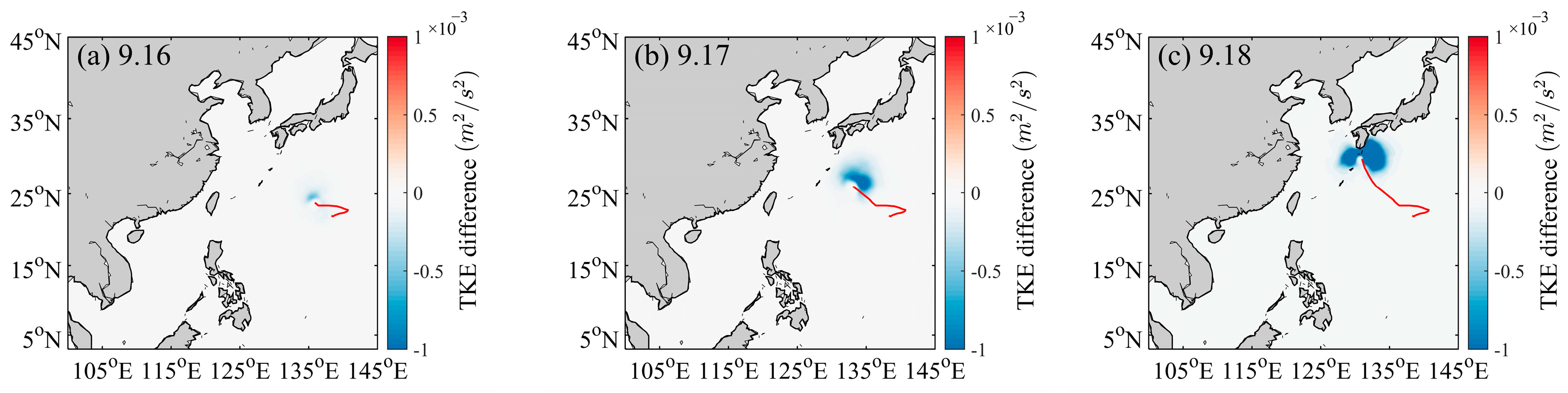
4.2. Simulation Results of Turbulent Kinetic Energy
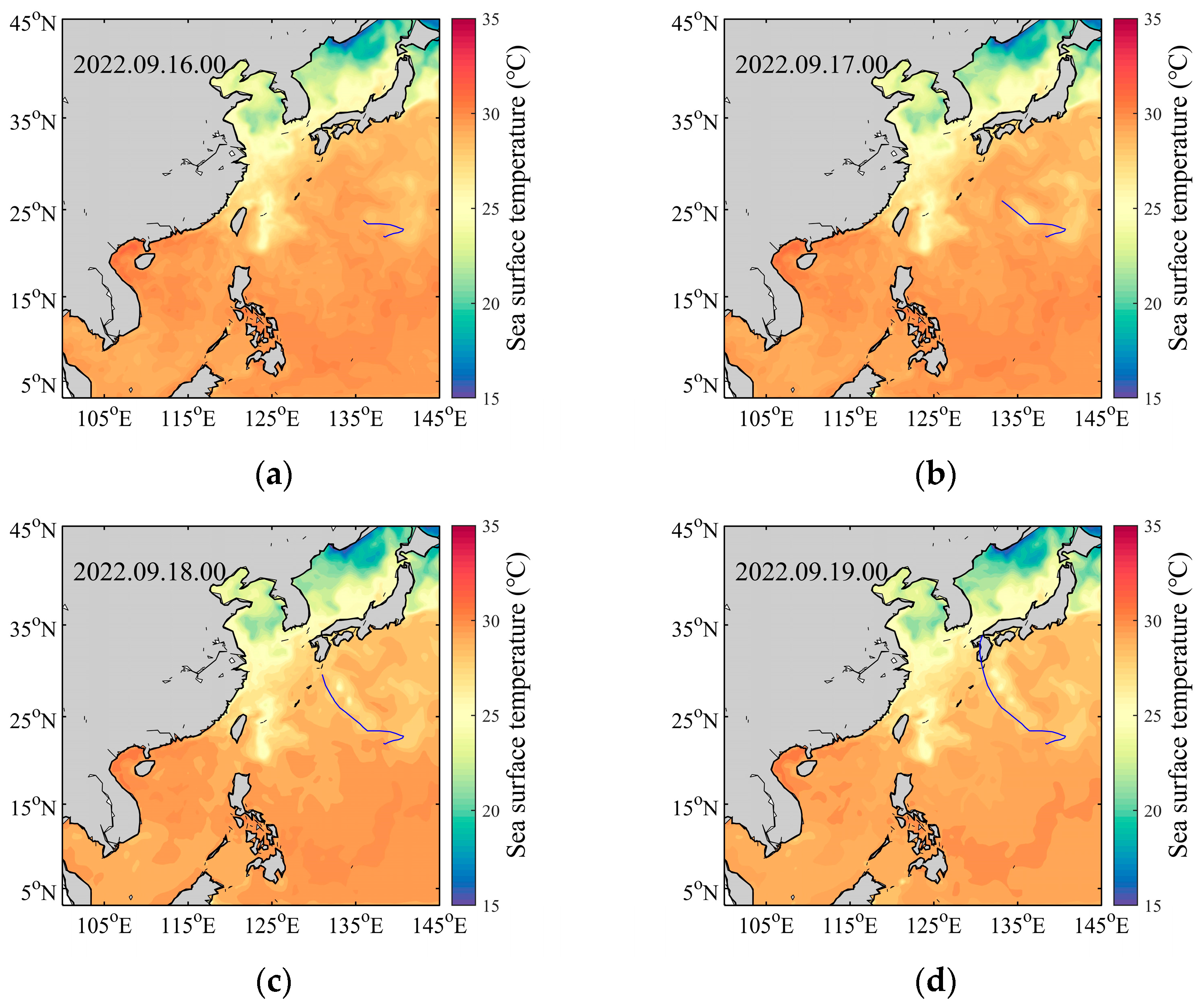
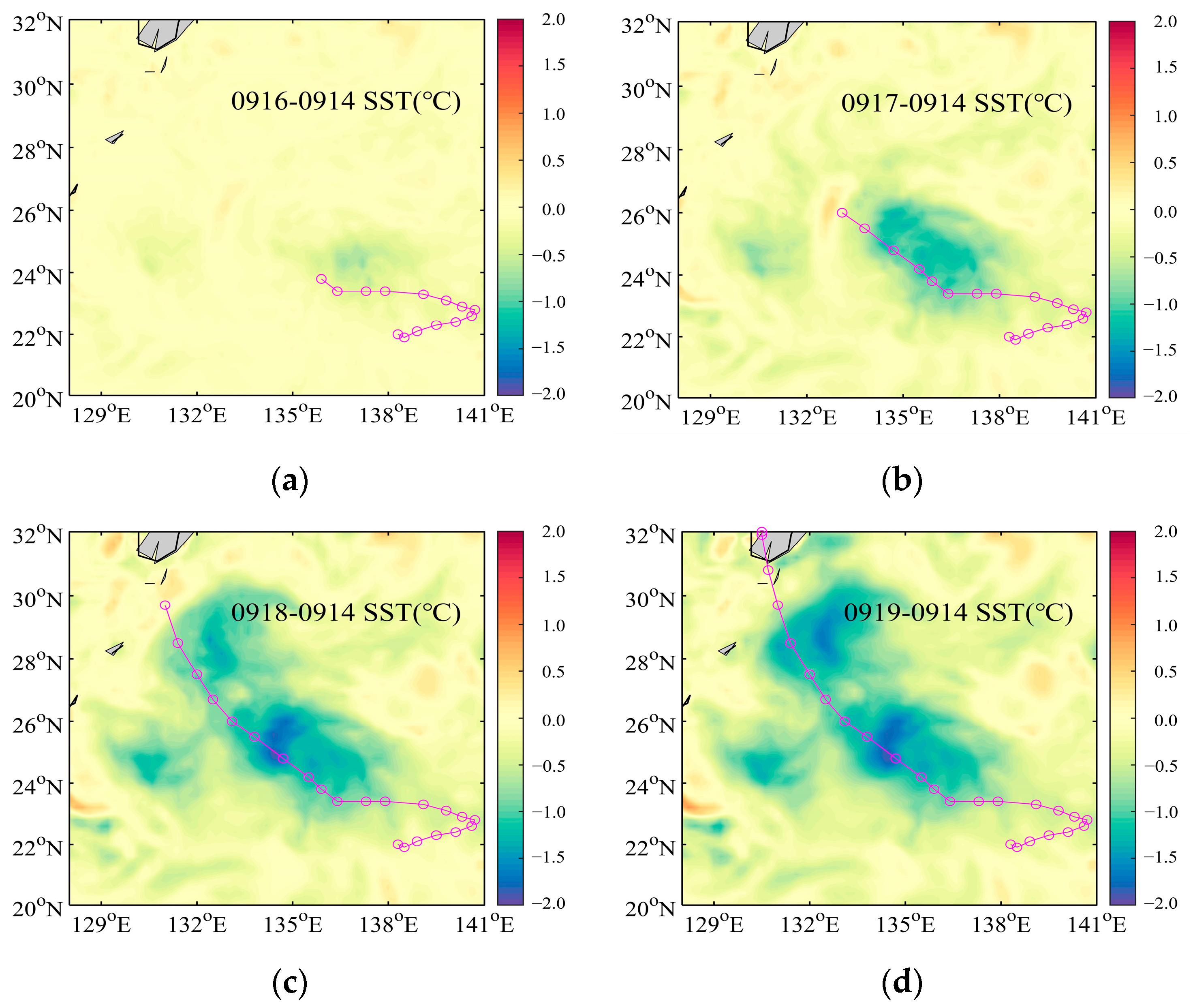
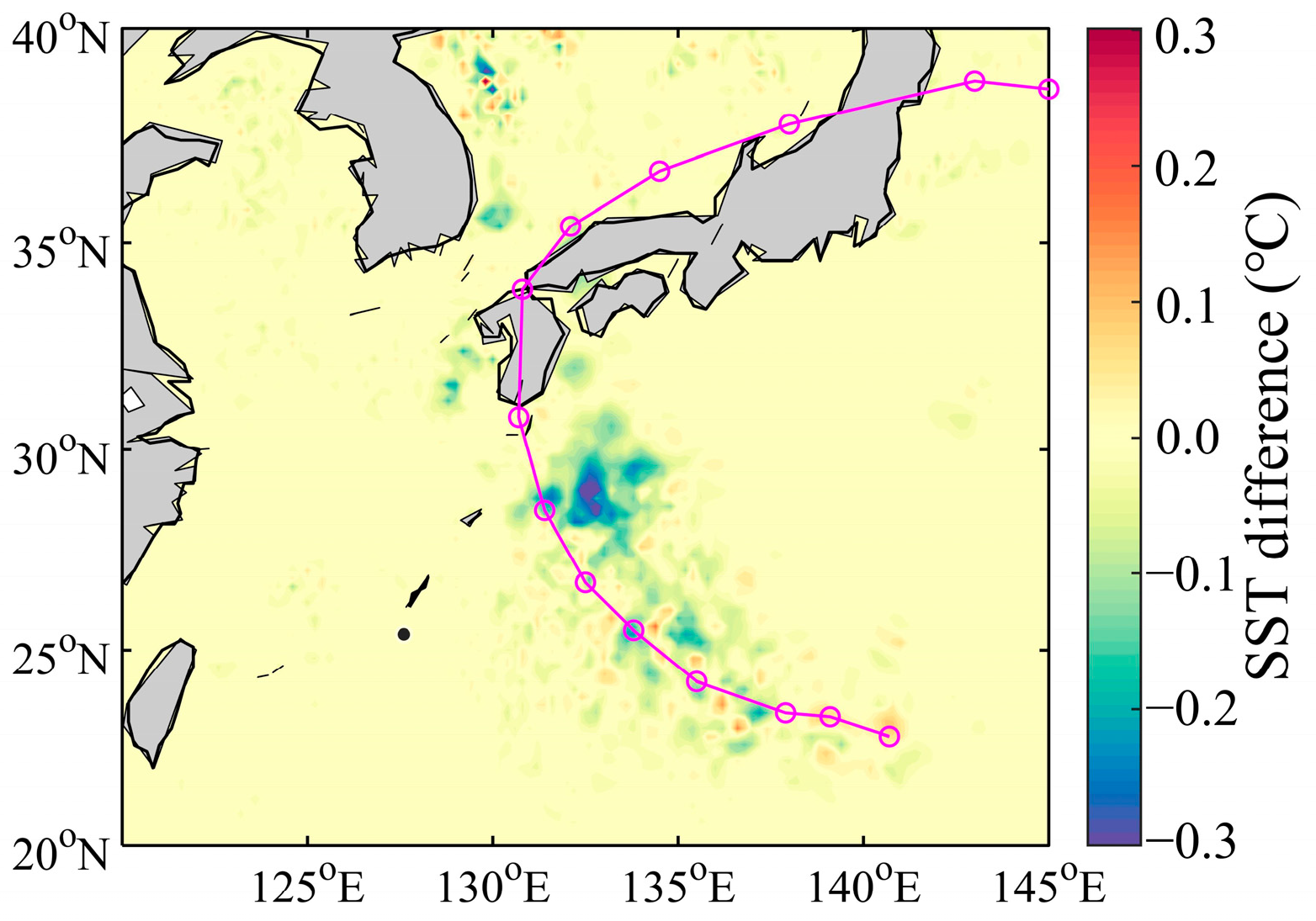
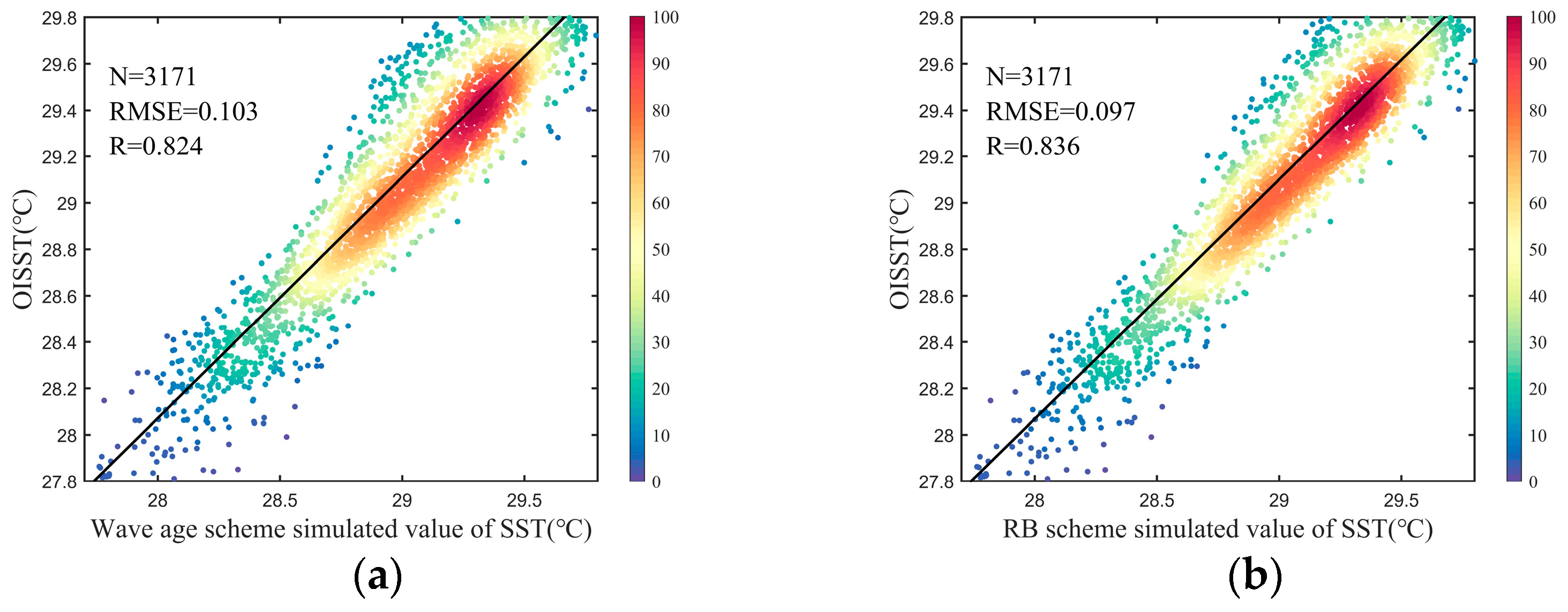
4.3. Sea Surface Temperature Simulation Results
4.4. Mixed Layer Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, L.; Rutgersson, A.; Sahlée, E. Upper-ocean mixing due to surface gravity waves. J. Geophys. Res. Oceans 2015, 120, 8210–8228. [Google Scholar] [CrossRef]
- Qiao, F.; Yuan, Y.; Yang, Y.; Zheng, Q.; Xia, C.; Ma, J. Wave-induced mixing in the upper ocean: Distribution and application to a global ocean circulation model. Geophys. Res. Lett. 2004, 31, 11. [Google Scholar] [CrossRef]
- Rascle, N.; Chapron, B.; Ardhuin, F.; Soloviev, A. A note on the direct injection of turbulence by breaking waves. Ocean Model. 2013, 70, 145–151. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, Y.; Sun, Z.; Chang, Y. Laboratory study on the evolution of waves parameters due to wave breaking in deep water. Wave Motion 2017, 68, 31–42. [Google Scholar] [CrossRef]
- Cai, Y.; Wen, Y.; Wu, L.; Zhou, C.; Zhang, F. Impact of wave breaking on upper-ocean turbulence. J. Geophys. Res. Oceans 2017, 122, 1513–1528. [Google Scholar] [CrossRef]
- Agrawal, Y.C.; Terray, E.A.; Donelan, M.A.; Hwang, P.A.; Williams, A.J.; Drennan, W.M.; Kahma, K.K.; Krtaigorodskii, S.A. Enhanced dissipation of kinetic energy beneath surface waves. Nature 1992, 359, 219–220. [Google Scholar] [CrossRef]
- Ardhuin, F.; Orfila, A. Wind Waves. In New Frontiers in Operational Oceanography; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2018; pp. 393–422. [Google Scholar]
- Wada, A.; Niino, H.; Nakano, H. Roles of vertical turbulent mixing in the ocean response to Typhoon Rex (1998). J. Oceanogr. 2009, 65, 373–396. [Google Scholar] [CrossRef]
- Carniel, S.; Warner, J.C.; Chiggiato, J.; Sclavo, M. Investigating the impact of surface wave breaking on modeling the trajectories of drifters in the northern Adriatic Sea during a wind-storm event. Ocean Model. 2009, 30, 225–239. [Google Scholar] [CrossRef]
- Thomson, J.; Schwendeman, M.S.; Zippel, S.F.; Moghimi, S.; Gemmrich, J.; Rogers, W.E. Wave-Breaking Turbulence in the Ocean Surface Layer. J. Phys. Oceanogr. 2016, 46, 1857–1870. [Google Scholar]
- Alari, V.; Staneva, J.; Breivik, O.; Bidlot, J.R.; Mogensen, K.; Janssen, P. Surface wave effects on water temperature in the Baltic Sea: Simulations with the coupled NEMO-WAM model. Ocean Dyn. 2016, 66, 917–930. [Google Scholar]
- Breivik, Y.; Mogensen, K.; Bidlot, J.R.; Balmaseda, M.A.; Janssen, P.A.E.M. Surface Wave Effects in the NEMO Ocean Model: Forced and Coupled Experiments. J. Geophys. Res. Ocean. 2015, 120, 135–143. [Google Scholar] [CrossRef]
- Guan, C.; Zhang, W.; Zhu, D.; Wei, L. A review of research on wave-induced mixing in the upper ocean: Research progress and existing problems. Period. Ocean. Univ. China 2014, 44, 20–24. [Google Scholar]
- Mellor, G.; Blumberg, A. Wave Breaking and Ocean Surface Layer Thermal Response. J. Phys. Oceanogr. 2004, 34, 693–698. [Google Scholar] [CrossRef]
- Sun, Q.; Song, G.J. Wave breaking on turbulent energy budget in the ocean surface mixed layer. Chin. J. Oceanol. Limnol. 2008, 26, 9–13. [Google Scholar] [CrossRef]
- Toba, Y. A parameter describing overall conditions of wave breaking, whitecapping, sea-spray production and wind stress. In Oceanic Whitecaps; Springer: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Zhao, D.; Toba, Y.; Suzuki, Y.; Komori, S. Effect of wind waves on air-sea gas exchange: Proposal of an overall CO2 transfer velocity formula as a function of breaking-wave parameter. Tellus Ser. B Chem. Phys. Meteorol. 2003, 55, 478–487. [Google Scholar] [CrossRef]
- Toba, Y.; Komori, S.; Suzuki, Y.; Zhao, D. Similarity and dissimilarity in air-sea momentum and CO2 transfers: The nondimensional transfer coefficients in light of the windsea Reynolds number. In Atmosphere-Ocean Interactions; WIT Press: Southampton, UK, 2006; pp. 53–82. [Google Scholar]
- Shi, J.; Zhao, D.L.; Xun-Qiang, L.I.; Zhong, Z. New wave-dependent formulae for sea spray flux at air-sea interface. J. Hydrodyn. 2009, 21, 573–581. [Google Scholar] [CrossRef]
- Zhao, D.; Toba, Y.; Sugioka, K.I.; Komori, S. New sea spray generation function for spume droplets. J. Geophys. Res. Oceans 2006, 111, C2. [Google Scholar] [CrossRef]
- Zhao, D.; Toba, Y. Dependence of Whitecap Coverage on Wind and Wind-Wave Properties. J. Oceanogr. 2001, 57, 603–616. [Google Scholar] [CrossRef]
- Craig, P.D.; Banner, M.L. Modeling Wave-Enhanced Turbulence in the Ocean Surface Layer. J. Phys. Oceanogr. 1994, 24, 2546–2559. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An Unstructured Grid, Finite-Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Niu, Q.; Xia, M.; Rutherford, E.S.; Mason, D.M.; Anderson, E.J.; Schwab, D.J. Investigation of interbasin exchange and interannual variability in Lake Erie using an unstructured-grid hydrodynamic model. J. Geophys. Res. Ocean. 2015, 120, 2212–2232. [Google Scholar] [CrossRef]
- Jiang, L.; Xia, M. Dynamics of the Chesapeake Bay outflow plume: Realistic plume simulation and its seasonal and interannual variability. J. Geophys. Res. Oceans 2016, 121, 1424–1445. [Google Scholar] [CrossRef]
- Kang, X.; Xia, M.; Pitula, J.S.; Chigbu, P. Dynamics of water and salt exchange at Maryland Coastal Bays. Estuar. Coast. Shelf Sci. 2017, 189, 1–16. [Google Scholar] [CrossRef]
- Chen, J.; Weisberg, R.H.; Liu, Y.; Zheng, L.; Zhu, J. On the Momentum Balance of Tampa Bay. J. Geophys. Res. Oceans 2019, 124, 4492–4510. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Zheng, L. Impacts of Hurricane Irma on the Circulation and Transport in Florida Bay and the Charlotte Harbor Estuary. Estuaries Coasts 2020, 43, 1194–1216. [Google Scholar] [CrossRef]
- Galperin, B.; Kantha, L.H.; Hassid, S.; Rosati, A. A Quasi-equilibrium Turbulent Energy Model for Geophysical Flows. J. Atmos. Sci. 1988, 45, 55–62. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations: I The Basic Experiment. Mon. Weather. Rev. 1962, 91, 99–164. [Google Scholar] [CrossRef]
- Niu, Q.; Xia, M. Wave climatology of Lake Erie based on an unstructured-grid wave model. Ocean Dyn. 2016, 66, 1271–1284. [Google Scholar] [CrossRef]
- Mao, M.; Xia, M. Dynamics of wave–current–surge interactions in Lake Michigan: A model comparison. Ocean Model. 2016, 110, 1–20. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Beardsley, R.C.; Perrie, W.; Lin, H. Applications of an unstructured grid surface wave model (FVCOM-SWAVE) to the Arctic Ocean: The interaction between ocean waves and sea ice. Ocean Model. 2019, 145, 101532. [Google Scholar] [CrossRef]
- Qi, J.; Chen, C.; Beardsley, R.C.; Perrie, W.; Lai, Z. An unstructured-grid finite-volume surface wave model (FVCOM-SWAVE): Implementation, validations and applications. Ocean Model. 2009, 28, 153–166. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Terray, E.A.; Donelan, M.A.; Agrawal, Y.C.; Drennan, W.M.; Kahma, K.K.; Williams, A.J.; Hwang, P.A.; Kitaigorodskii, S.A. Estimates of Kinetic Energy Dissipation under Breaking Waves. J. Phys. Oceanogr. 1996, 26, 792–807. [Google Scholar] [CrossRef]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P. Dynamics and Modelling of Ocean Waves. Dyn. Atmos. Ocean. 1994, 25, 276–278. [Google Scholar]
- Xiong, J.; Yu, F.; Fu, C. Evaluation and improvement of the ERA5 wind field in typhoon storm surge simulations. Appl. Ocean. Res. 2022, 118, 103000. [Google Scholar] [CrossRef]
- Zhai, R.; Huang, C.; Yang, W. Applicability evaluation of ERA5 wind and wave reanalysis data in the South China Sea. J. Oceanol. Limnol. 2023, 41, 495–517. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Zheng, Z.H. Interaction of Cloud Dynamics and Microphysics during the Rapid Intensification of Super-Typhoon Nanmadol (2022) Based on Multi-Satellite Observations. Geophys. Res. Lett. 2023, 50, e2023GL104541. [Google Scholar] [CrossRef]
- Wang, Z. Stokes-Drift Effect on the Upper Ocean. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2012. [Google Scholar]
- Lai, Q.-Z.; Wu, L.-G.; Xie, Z.-L. Sea Surface Temperature Response to Typhoon Morakot(2009) and Its Influence. J. Trop. Meteorol. 2015, 21, 111–120. [Google Scholar]
- Yin, K.; Xu, S.; Zhao, Q.; Zhang, N.; Li, M. Effects of sea surface warming and sea-level rise on tropical cyclone and inundation modeling at Shanghai coast. Nat. Hazards 2021, 109, 755–784. [Google Scholar] [CrossRef]
- Li, X.; Zhao, D.; Zou, Z. A numerical study of Stokes drift and thermal effects on the oceanic mixed layer. Acta Oceanol. Sin. 2020, 39, 39–49. [Google Scholar] [CrossRef]
- Chuanjiang, H.; Fangli, Q. Effects of horizontal mixing on the upper ocean temperature in the equatorial Pacific Ocean. Acta Oceanol. Sin. 2012, 31, 16–23. [Google Scholar]
- Yu, C.; Yang, Y.; Yin, X.; Sun, M.; Shi, Y. Impact of Enhanced Wave-Induced Mixing on the Ocean Upper Mixed Layer during Typhoon Nepartak in a Regional Model of the Northwest Pacific Ocean. Remote Sens. 2020, 12, 2808. [Google Scholar] [CrossRef]
- Price, J.F.; Weller, R.A.; Pinkel, R. Diurnal Cycling: Observations and Models of the Upper Ocean Response to Diurnal Heating, Cooling, and Wind Mixing. J. Geophys. Res. Ocean. JGR 1986, 91, 8411–8427. [Google Scholar] [CrossRef]
- Watanabe, M.; Hibiya, T. Global estimates of the wind-induced energy flux to inertial motions in the surface mixed layer. Geophys. Res. Lett. 2002, 29, 64-1–64-3. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Xie, Q.; Meng, W.-G.; Yuan, J.-N.; Wang, X.-D. An Experiment Study on the Influence of Different Sea Surface Temperature on Typhoon Dujuan Over the South China Sea. J. Trop. Meteorol. 2009, 25, 401–406. [Google Scholar]
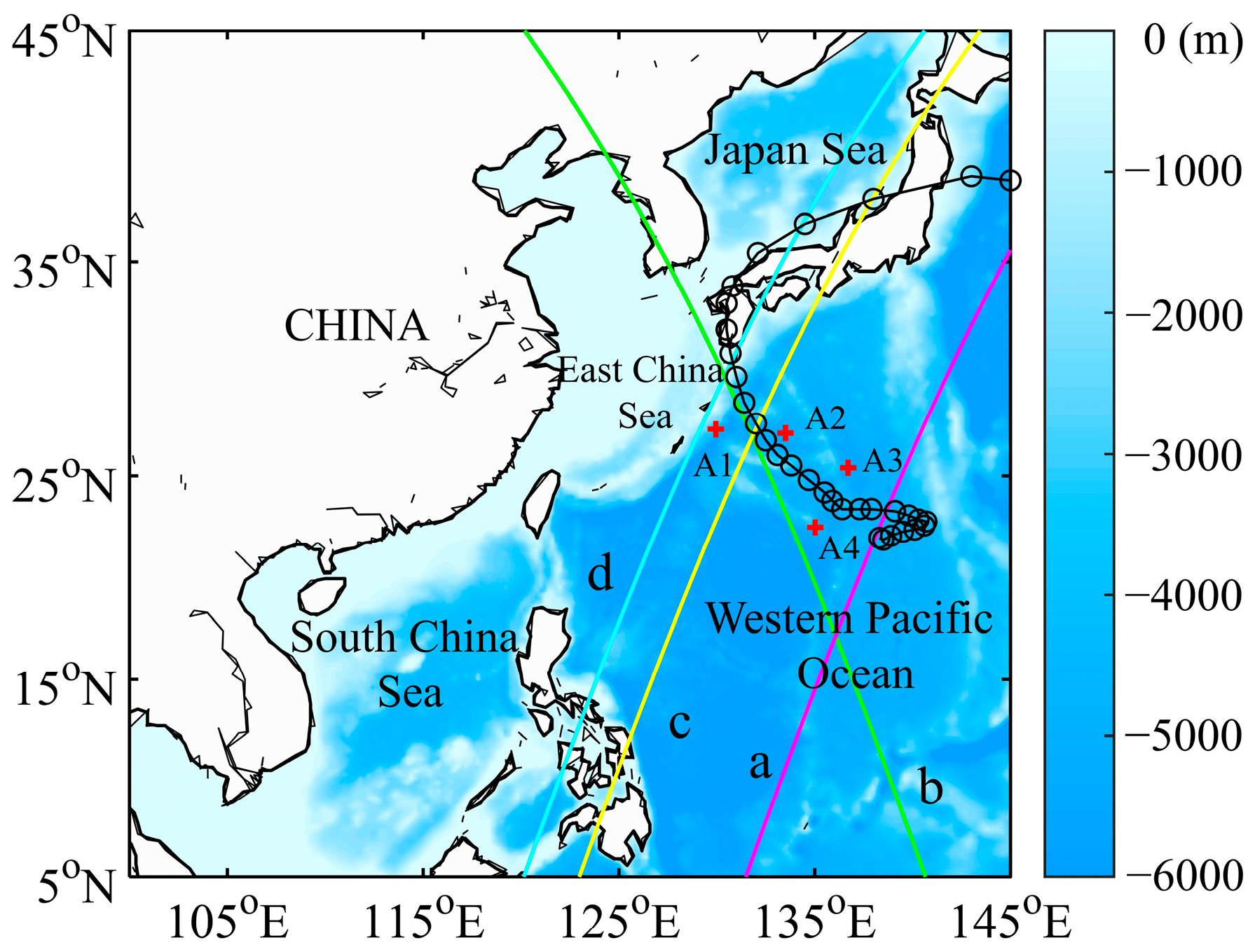

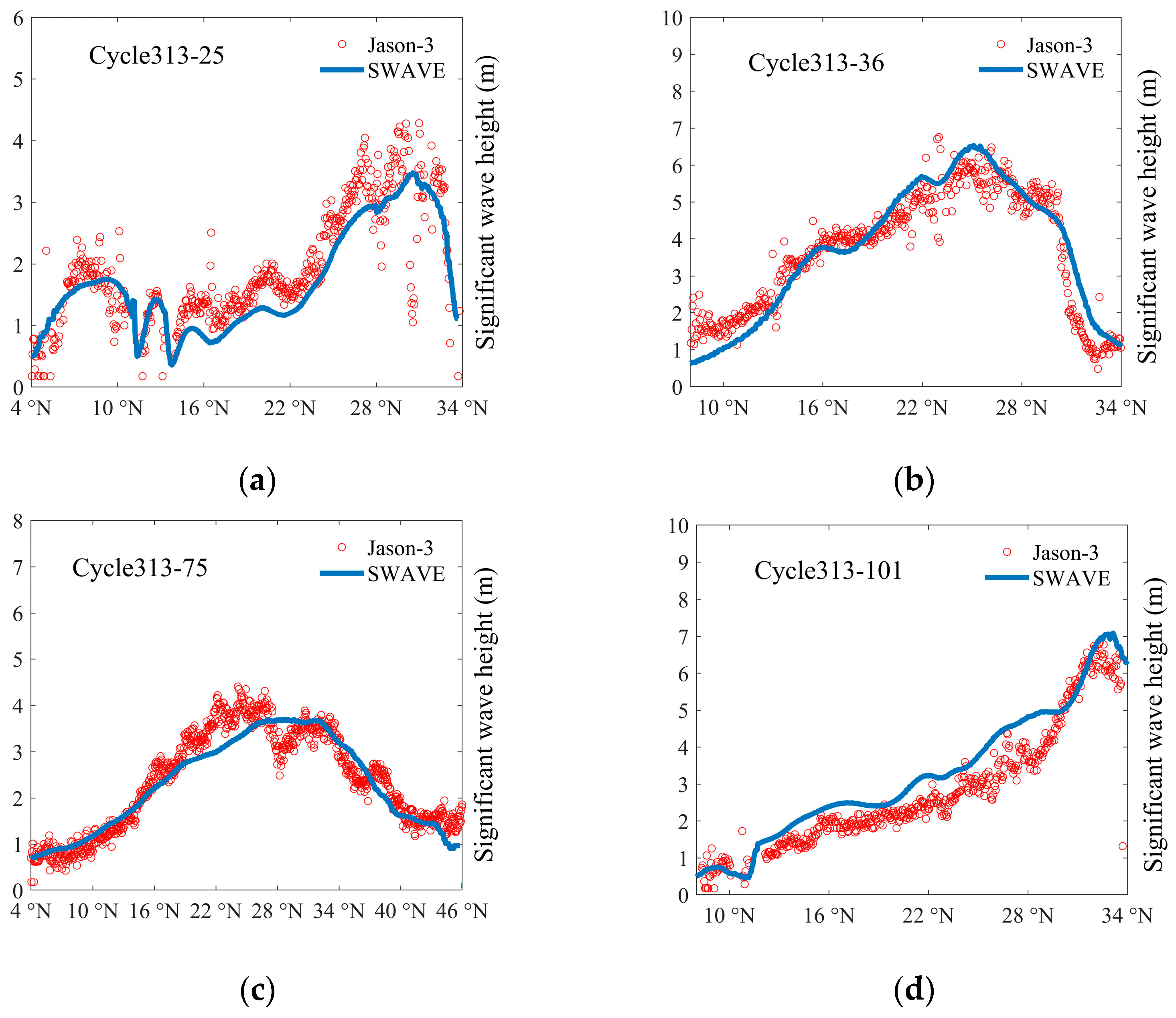



| Track | COR | MAE (m) | RMSE (m) |
|---|---|---|---|
| a | 0.85 | 0.22 | 0.50 |
| b | 0.91 | 0.26 | 0.59 |
| c | 0.92 | 0.12 | 0.23 |
| d | 0.87 | 0.43 | 0.64 |
| Average | 0.89 | 0.26 | 0.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Chen, J.; Shi, J.; Xia, J.; Zhang, W.; Yi, Z.; Wang, H.; Zhang, S.; Lv, J.; Zhao, Z.; et al. Response of Upper Ocean to Parameterized Schemes of Wave Breaking under Typhoon Condition. Remote Sens. 2024, 16, 3524. https://doi.org/10.3390/rs16183524
Cao X, Chen J, Shi J, Xia J, Zhang W, Yi Z, Wang H, Zhang S, Lv J, Zhao Z, et al. Response of Upper Ocean to Parameterized Schemes of Wave Breaking under Typhoon Condition. Remote Sensing. 2024; 16(18):3524. https://doi.org/10.3390/rs16183524
Chicago/Turabian StyleCao, Xuhui, Jie Chen, Jian Shi, Jingmin Xia, Wenjing Zhang, Zhenhui Yi, Hanshi Wang, Shaoze Zhang, Jialei Lv, Zeqi Zhao, and et al. 2024. "Response of Upper Ocean to Parameterized Schemes of Wave Breaking under Typhoon Condition" Remote Sensing 16, no. 18: 3524. https://doi.org/10.3390/rs16183524
APA StyleCao, X., Chen, J., Shi, J., Xia, J., Zhang, W., Yi, Z., Wang, H., Zhang, S., Lv, J., Zhao, Z., & Wang, Q. (2024). Response of Upper Ocean to Parameterized Schemes of Wave Breaking under Typhoon Condition. Remote Sensing, 16(18), 3524. https://doi.org/10.3390/rs16183524





