Complex Permittivity of Adobe Verses Frequency and Water Content
Abstract
1. Introduction
2. Materials and Methods
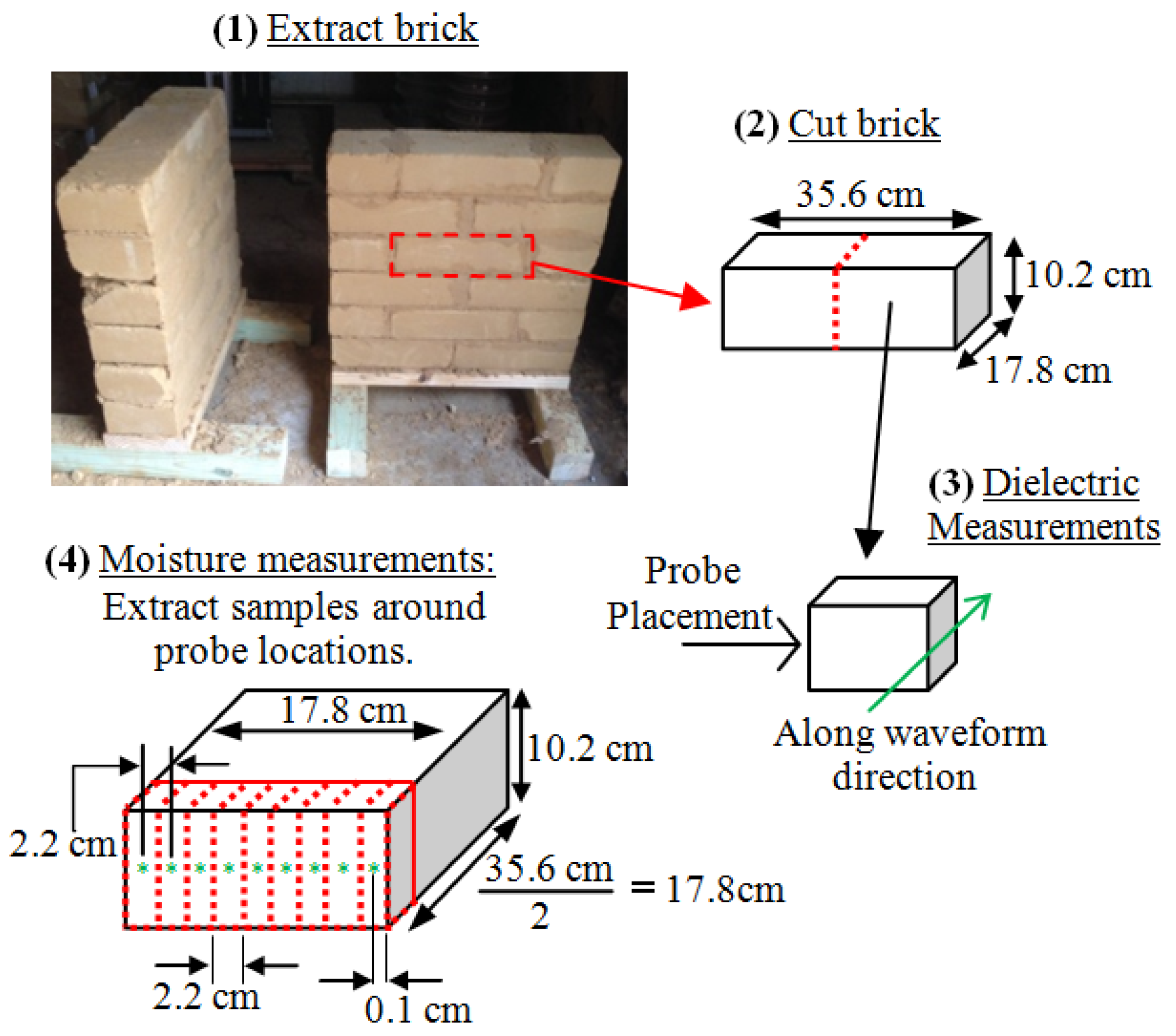
2.1. Adobe Test Articles
2.2. Details of Measurement Procedures
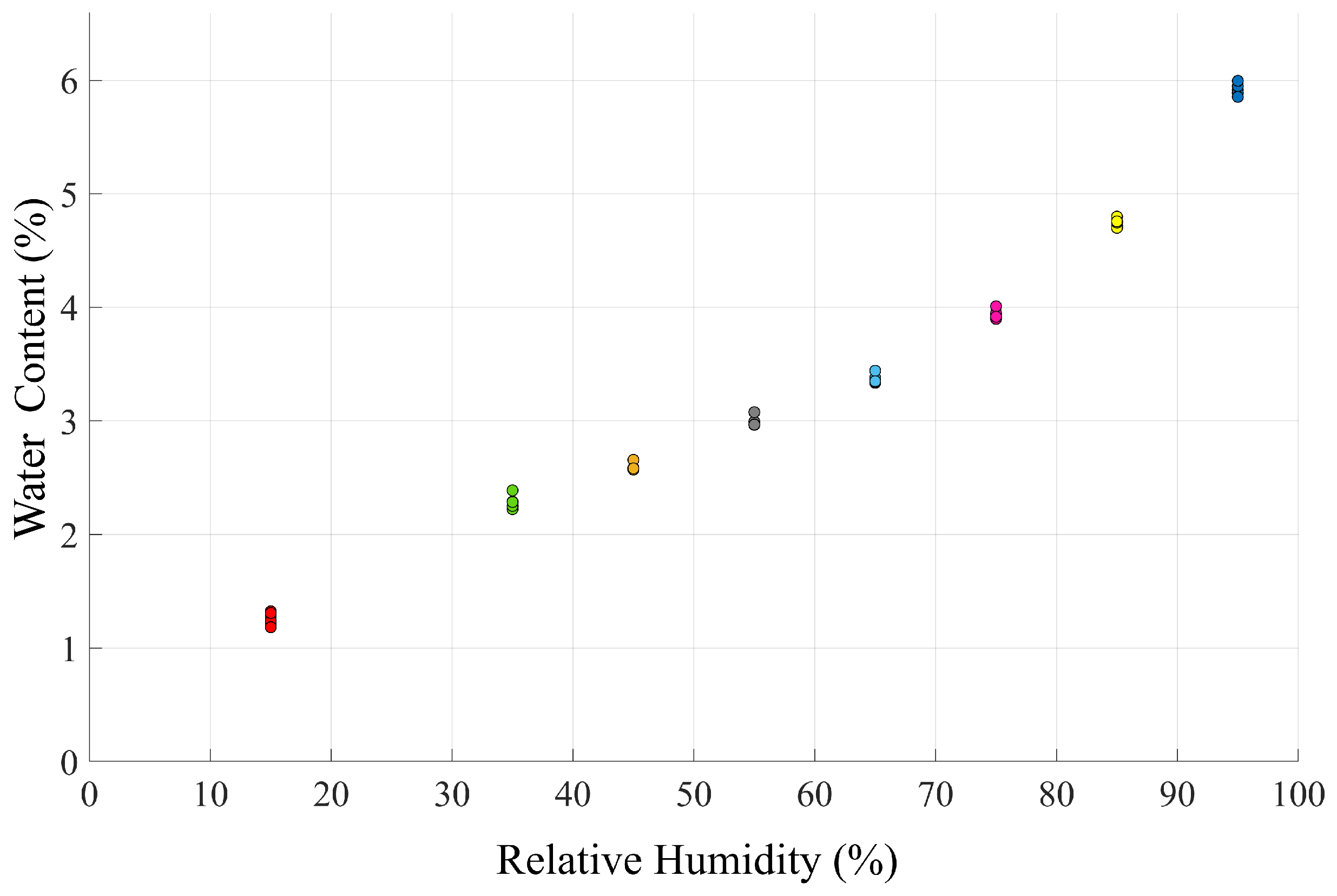
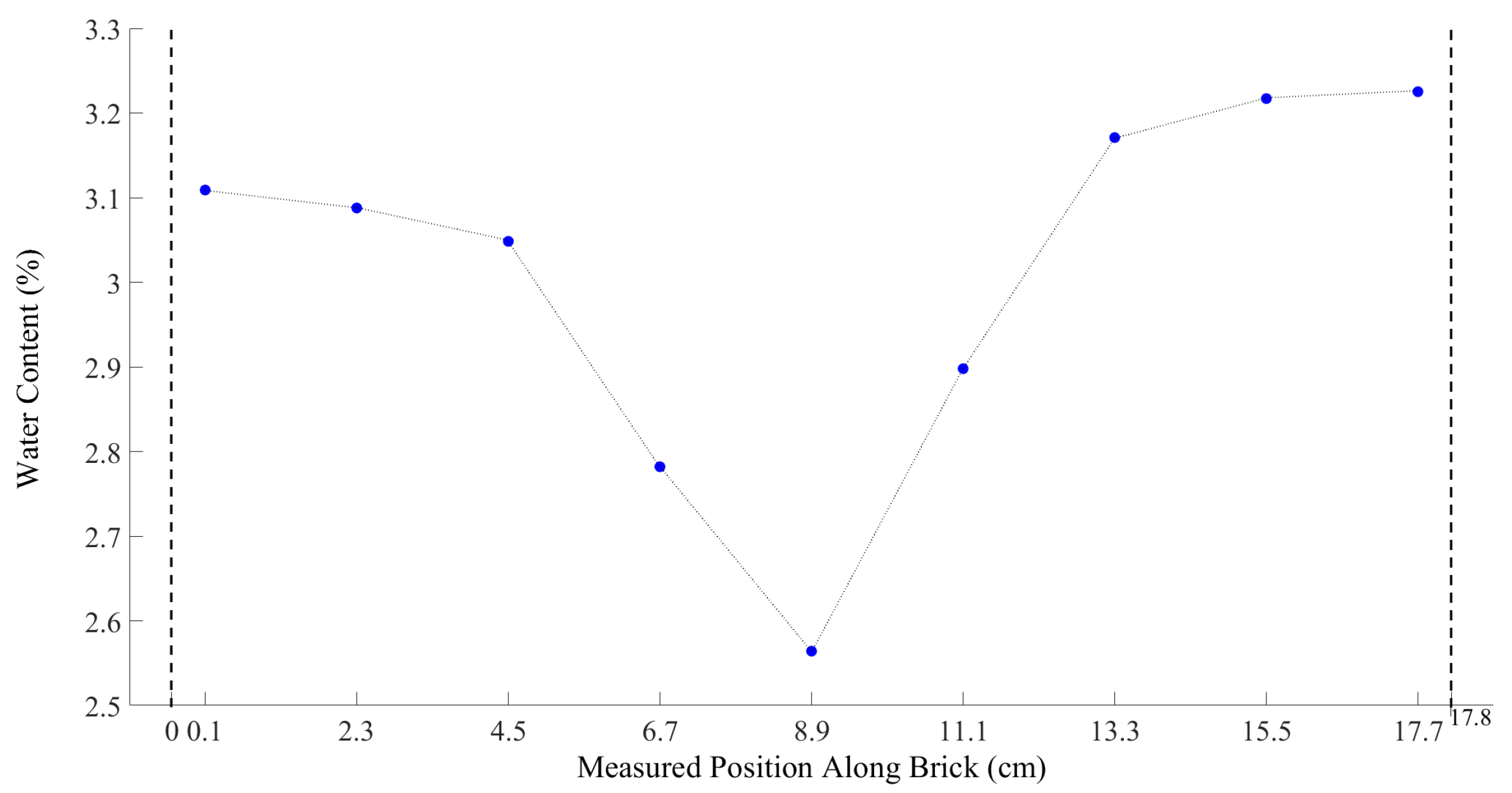
2.2.1. Validation of Water Content Homogeneity within the Adobe Samples
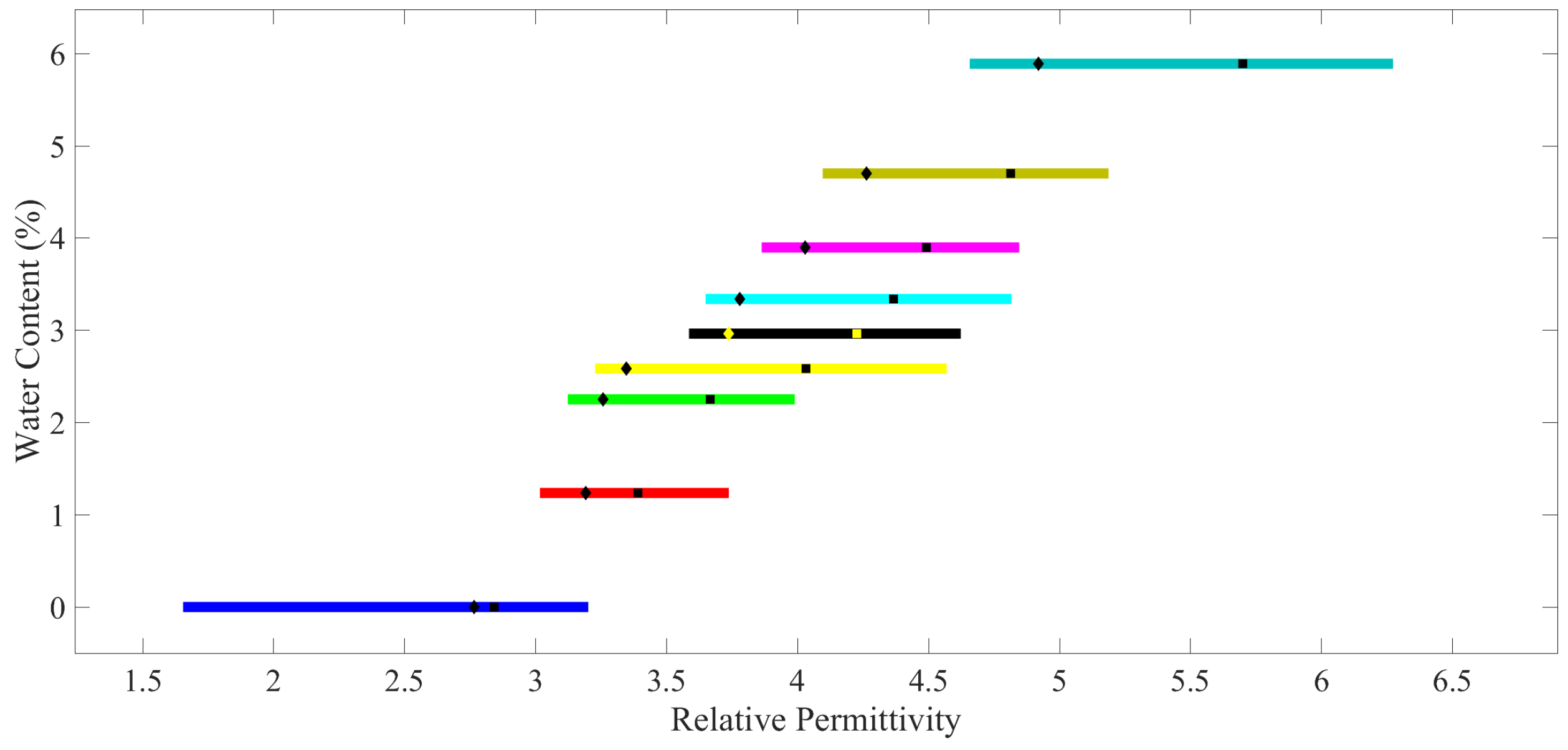
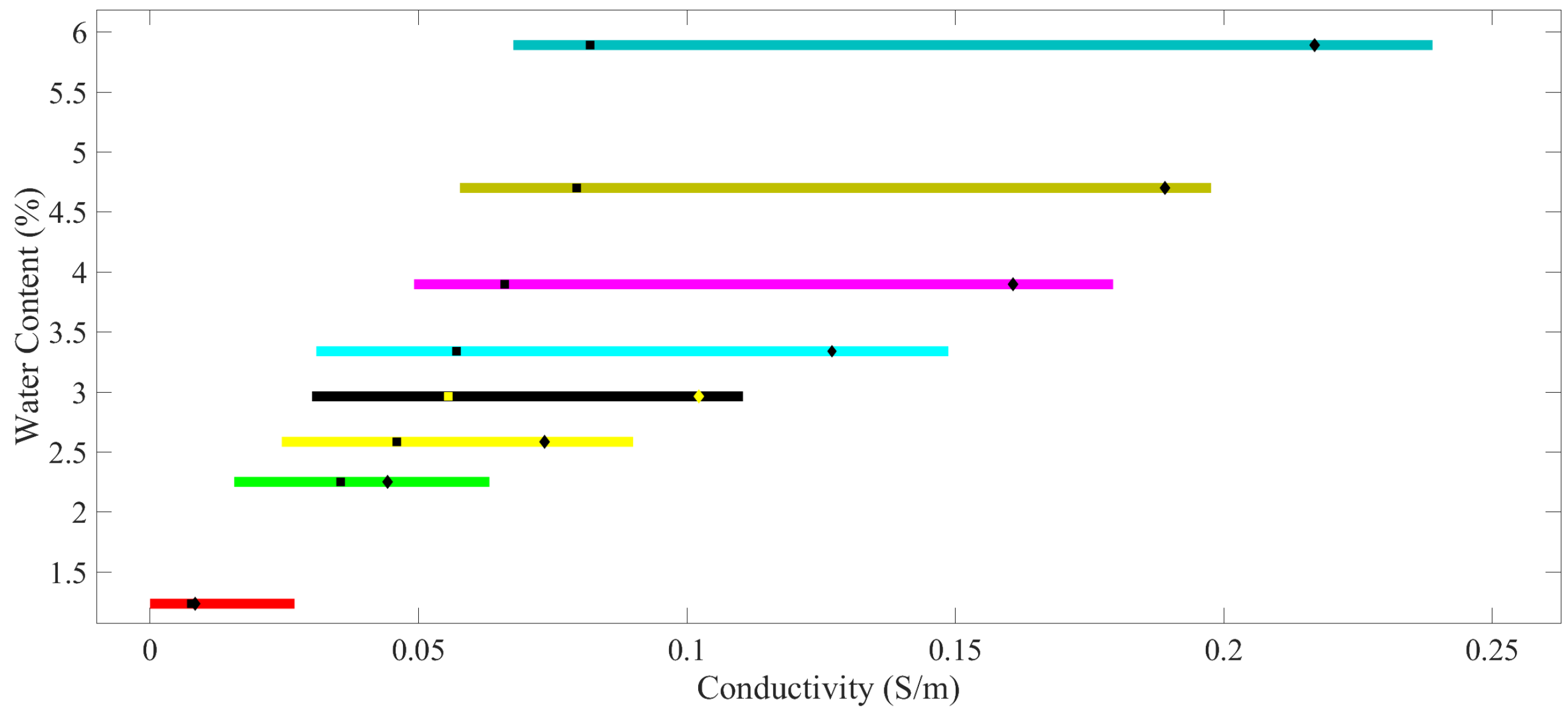
2.2.2. Complex Permittivity Measurements
2.2.3. Measurement of Adobe Brick Water Content Profile
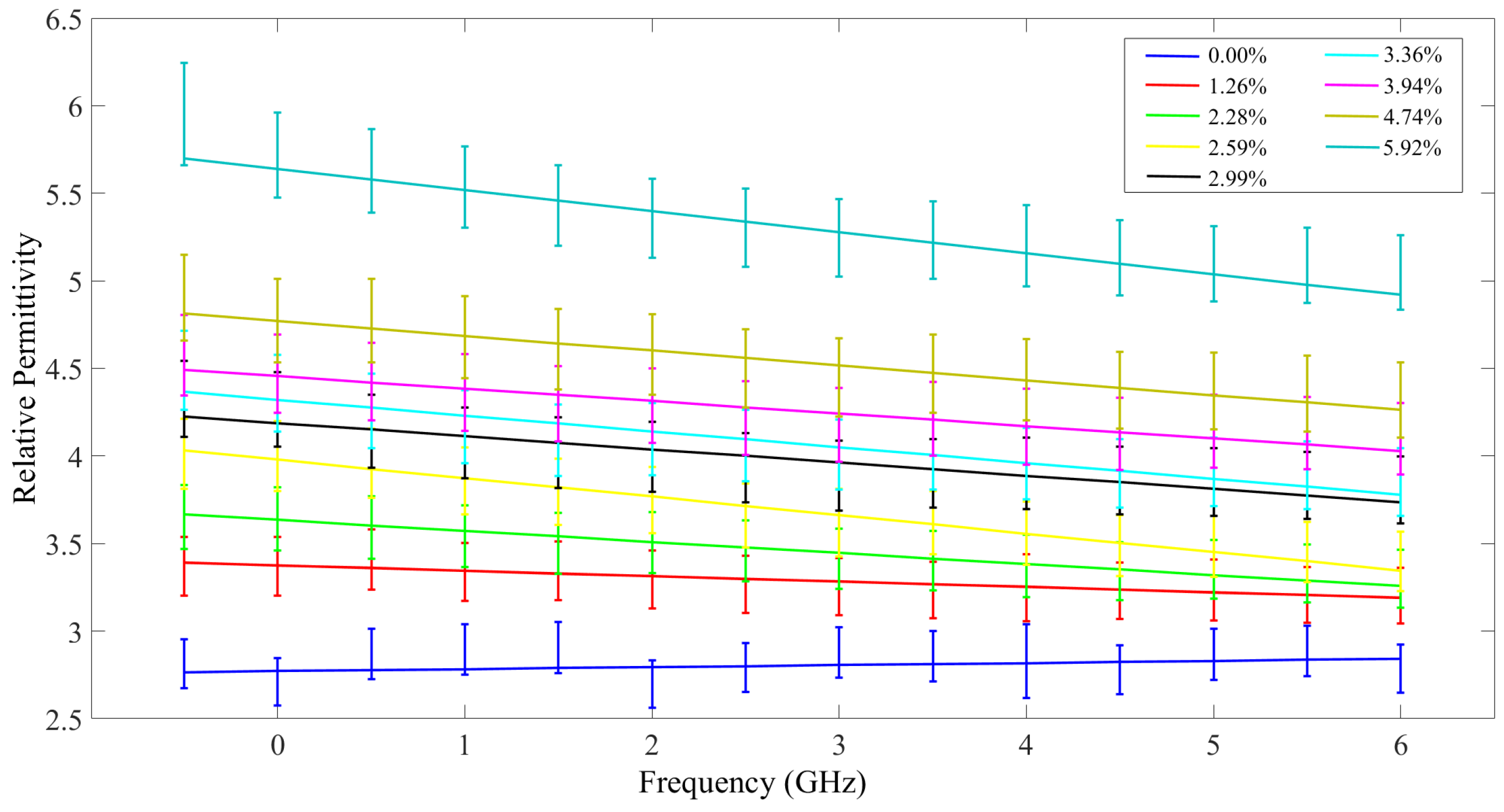
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Farwell, M.; Ross, J.; Luttrell, R.; Cohen, D.; Chin, W.; Dogaru, T. Sense through the wall system development and design considerations. J. Frankl. Inst. 2008, 345, 570–591. [Google Scholar]
- Baranoski, E. Through-wall sensing; radar signal processing; model-based reasoning; propagation effects. J. Frankl. Inst. 2008, 345, 556–569. [Google Scholar]
- Withington, P.; Fluhler, H.; Nag, S. Enhancing homeland security with advanced UWB sensors. IEEE Microw. Mag. 2003, 4, 51–58. [Google Scholar]
- Ferris, D.D., Jr.; Currie, N.C. Survey of current technologies for through-the-wall surveillance (TWS). In Proceedings of the Sensors, C3I, Information, and Training Technologies for Law Enforcement, Boston, MA, USA, 3–5 November 1998; SPIE: San Francisco, CA, USA, 1999; Volume 3577, pp. 62–72. [Google Scholar]
- Price, S.; Donohoe, J.P.; Fairley, J.R. Effects of wall moisture profiles on matched illumination waveforms—Simulation and measurement. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 0597–0601. [Google Scholar]
- Price, S.R.; Donohoe, J.P.; Fairley, J. Impacts of wall–target interaction on matched illumination waveforms for twri. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1402–1405. [Google Scholar]
- Beyea, S.; Balcom, B.; Bremner, T.; Prado, P.; Green, D.; Armstrong, R.; Grattan-Bellew, P. Magnetic resonance imaging and moisture content profiles of drying concrete. Cem. Concr. Res. 1998, 28, 453–463. [Google Scholar]
- Thajudeen, C.; Hoorfar, A.; Ahmad, F.; Dogaru, T. Measured complex permittivity of walls with different hydration levels and the effect on power estimation of TWRI target returns. Prog. Electromagn. Res. B 2011, 30, 177–199. [Google Scholar]
- Menke, F.; Knochel, R.; Boltze, T.; Hauenschild, C.; Leschnik, W. Moisture measurement in walls using microwaves. In Proceedings of the 1995 IEEE MTT-S International Microwave Symposium, Orlando, FL, USA, 15–20 May 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1147–1150. [Google Scholar]
- Huizinga, R. Assessment on the Moisture Content in the Brick Walls of the Church in Bergeijk with the Use of a Microwave Meter. Master’s Thesis, University of Groningen, Groningen, The Netherlands, 2012. [Google Scholar]
- Kääriäinen, H.; Rudolph, M.; Schaurich, D.; Tulla, K.; Wiggenhauser, H. Moisture measurements in building materials with microwaves. NDT E Int. 2001, 34, 389–394. [Google Scholar]
- Maierhofer, C.; Wöstmann, J. Investigation of dielectric properties of brick materials as a function of moisture and salt content using a microwave impulse technique at very high frequencies. NDT E Int. 1998, 31, 259–263. [Google Scholar]
- Soutsos, M.; Bungey, J.; Millard, S.; Shaw, M.; Patterson, A. Dielectric properties of concrete and their influence on radar testing. NDT E Int. 2001, 34, 419–425. [Google Scholar]
- Robert, A. Dielectric permittivity of concrete between 50 MHz and 1 GHz and GPR measurements for building materials evaluation. J. Appl. Geophys. 1998, 40, 89–94. [Google Scholar]
- Sandrolini, F.; Franzoni, E. An operative protocol for reliable measurements of moisture in porous materials of ancient buildings. Build. Environ. 2006, 41, 1372–1380. [Google Scholar]
- Hauschild, T.; Menke, F. Moisture measurement in masonry walls using a non-invasive reflectometer. Electron. Lett. 1998, 34, 2413–2414. [Google Scholar]
- Sbartaï, Z.; Laurens, S.; Viriyametanont, K.; Balayssac, J.; Arliguie, G. Non-destructive evaluation of concrete physical condition using radar and artificial neural networks. Constr. Build. Mater. 2009, 23, 837–845. [Google Scholar]
- Reckhow, D.A. Gravimetric Methods. Available online: www.ecs.umass.edu/cee/reckhow/courses/572/572bk15/572BK15.html (accessed on 1 June 2023).
- Agilent 805070E Dielectric Probe Kit 200 MHz to 50 GHz. Available online: http://literature.cdn.keysight.com/litweb/pdf/5989-0222EN.pdf (accessed on 12 May 2023).
- Technical Overview—N1501A Dielectric Probe Kit. Available online: https://www.keysight.com/us/en/assets/7018-04631/technical-overviews/5992-0264.pdf (accessed on 1 July 2024).
- Price, S.R.; Price, S.R.; Anderson, D.T. Introducing fuzzy layers for deep learning. In Proceedings of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LA, USA, 23–26 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Lindsay, M.; Veal, C.; Kovaleski, S.; Anderson, D.T.; Price, S.R. Artificial intelligence supported material design for tailored image transformations. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XXXI, Online, 27 April–8 May 2020; SPIE: San Francisco, CA, USA, 2020; Volume 11406, pp. 31–42. [Google Scholar]



| Gravel | |||
| Coarse (%) | Medium (%) | Fine (%) | Total (%) |
| Sand | |||
| Coarse (%) | Medium (%) | Fine (%) | Total (%) |
| Fines | |||
| Silt (%) | Clay (%) | Total (%) | |
| Distance from Brick Edge (cm) | Water Content (%) | (500 MHz, 7 GHz) | (S/m) (500 MHz, 7 GHz) |
|---|---|---|---|
| 0.1 | 3.11 | 4.61, 3.86 | 0.073, 0.13 |
| 2.3 | 3.09 | 4.38, 3.74 | 0.071, 0.11 |
| 4.5 | 3.04 | 4.23, 3.63 | 0.069, 0.10 |
| 6.7 | 2.78 | 3.90, 3.42 | 0.054, 0.10 |
| 8.9 | 2.56 | 3.87, 3.35 | 0.048, 0.075 |
| 11.1 | 2.98 | 4.00, 3.45 | 0.062, 0.082 |
| 13.3 | 3.17 | 4.64, 3.89 | 0.063, 0.11 |
| 15.5 | 3.22 | 4.69, 3.92 | 0.071, 0.12 |
| 17.7 | 3.25 | 4.70, 3.92 | 0.075, 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Price, S.R.; Donohoe, J.P.; Price, S.R.; Fairley, J.; Robert, S. Complex Permittivity of Adobe Verses Frequency and Water Content. Remote Sens. 2024, 16, 3445. https://doi.org/10.3390/rs16183445
Price SR, Donohoe JP, Price SR, Fairley J, Robert S. Complex Permittivity of Adobe Verses Frequency and Water Content. Remote Sensing. 2024; 16(18):3445. https://doi.org/10.3390/rs16183445
Chicago/Turabian StylePrice, Steven R., J. Patrick Donohoe, Stanton R. Price, Josh Fairley, and Stephanie Robert. 2024. "Complex Permittivity of Adobe Verses Frequency and Water Content" Remote Sensing 16, no. 18: 3445. https://doi.org/10.3390/rs16183445
APA StylePrice, S. R., Donohoe, J. P., Price, S. R., Fairley, J., & Robert, S. (2024). Complex Permittivity of Adobe Verses Frequency and Water Content. Remote Sensing, 16(18), 3445. https://doi.org/10.3390/rs16183445






