Error Analysis of Non-Time-Synchronized Lightning Positioning Method
Abstract
1. Introduction
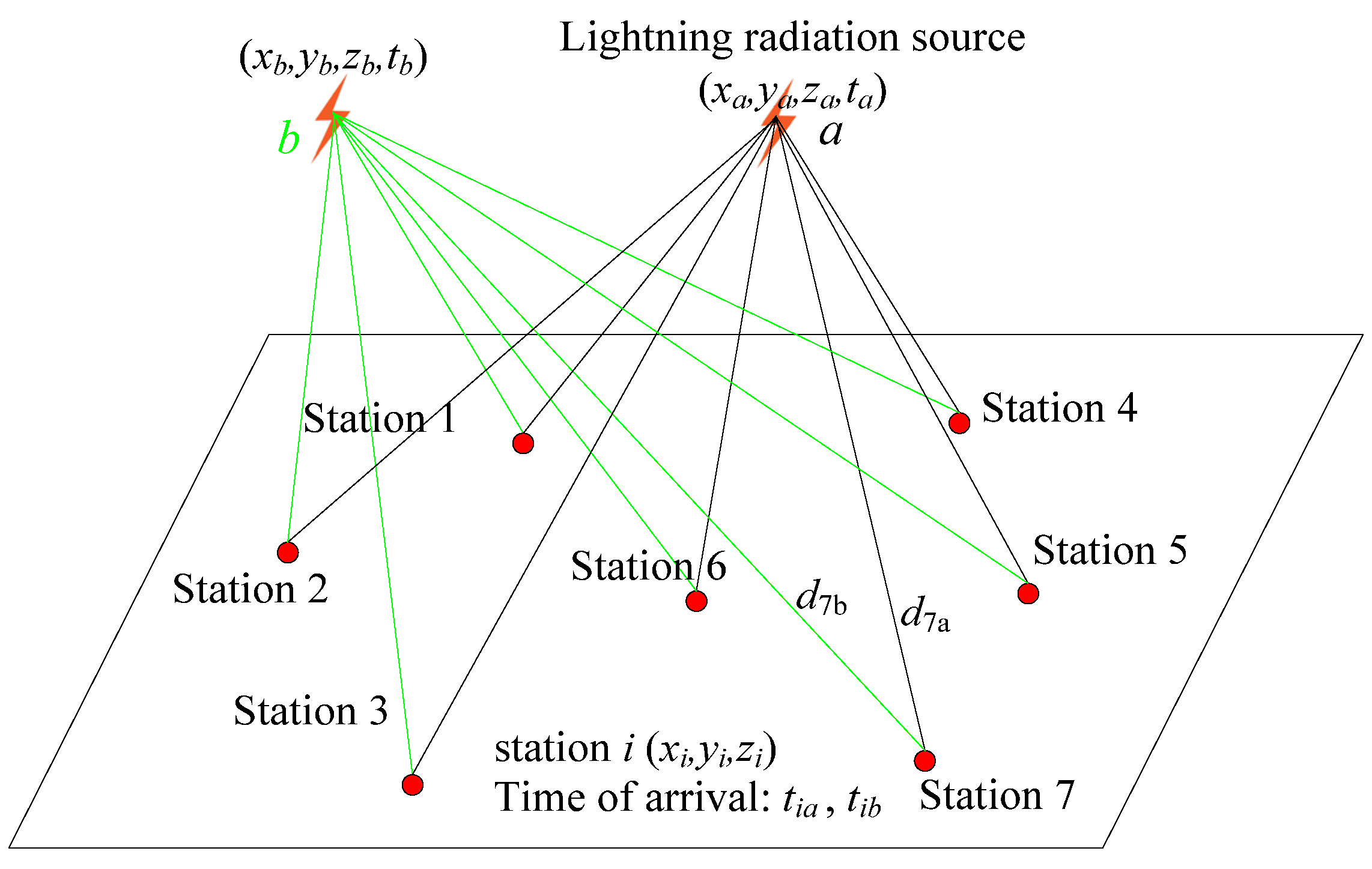
2. The Principle of the Non-Time-Synchronized Lightning Positioning Method
3. Introduction to Positioning System Errors
3.1. Extraction Errors of Lightning Pulse Signals
3.2. Tropospheric Delay Errors
3.3. Position Error of the Lightning Detection Station Itself
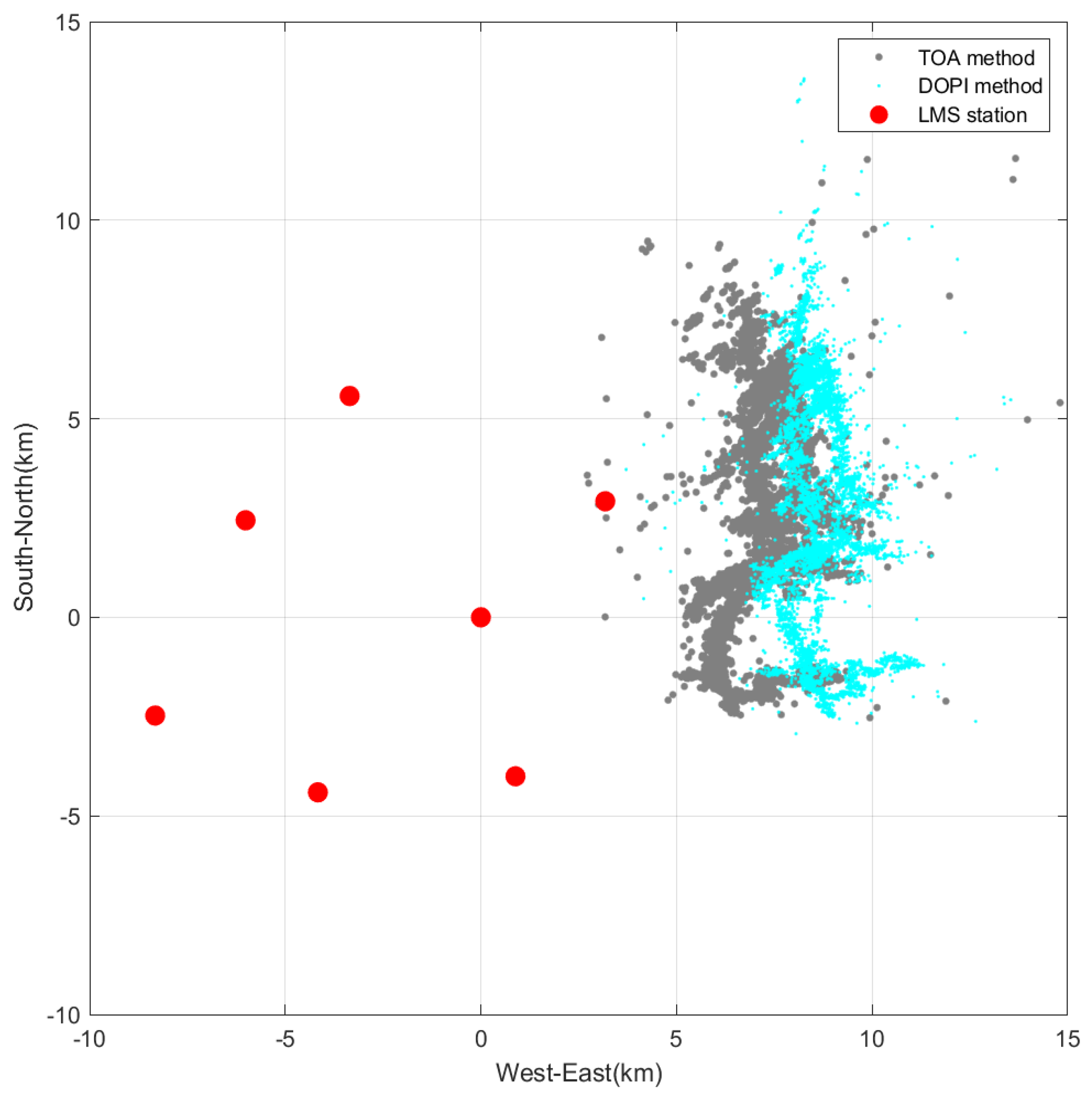
4. Lightning Positioning Results Based on Non-Time-Synchronized Positioning Method
5. Error Analysis of the Non-Time-Synchronized Positioning Method
5.1. Position Error Based on Non-Fixed-Coordinate Beacon Point
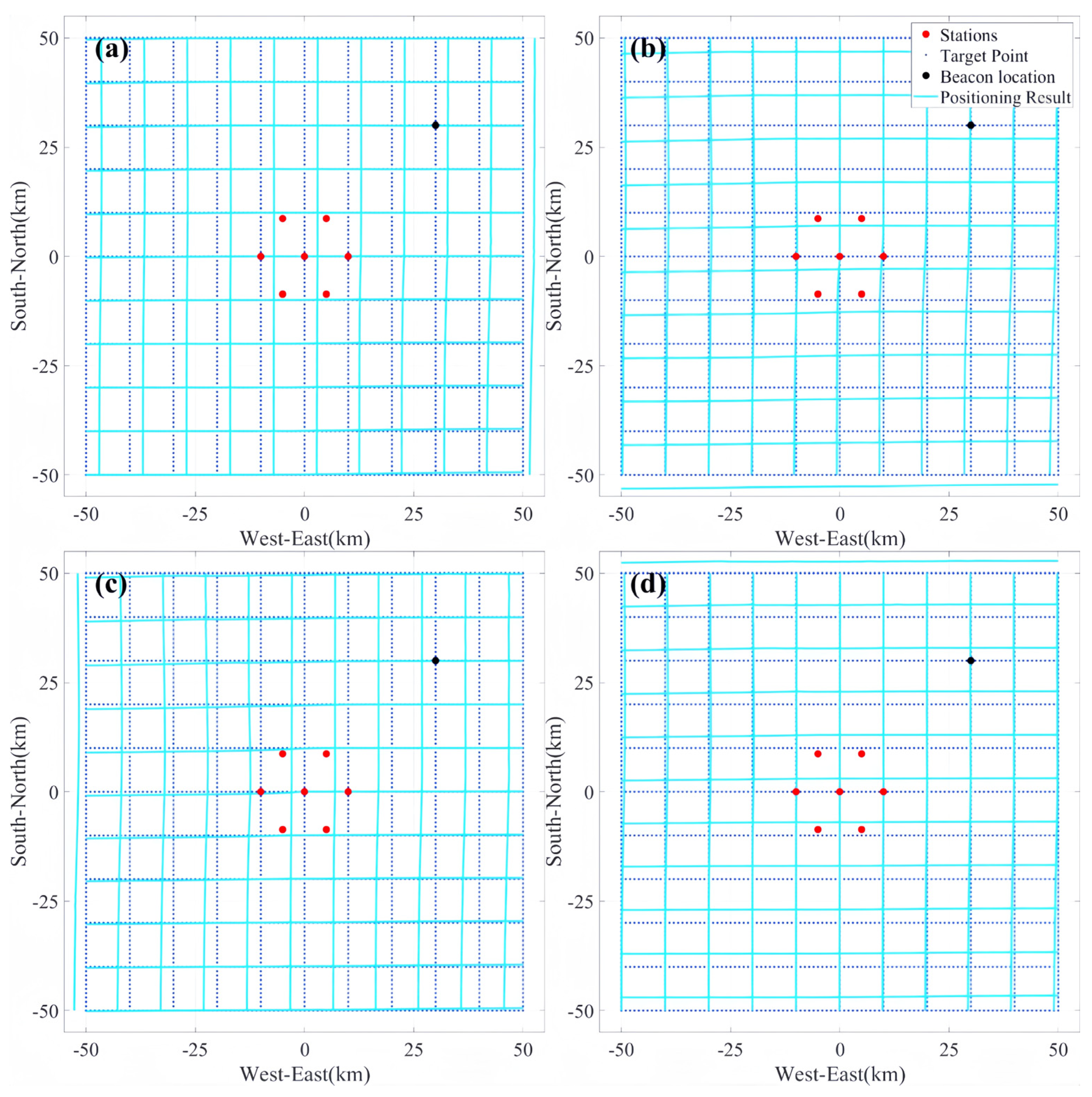
5.2. Positioning Error Based on Fixed-Coordinate Beacon Point
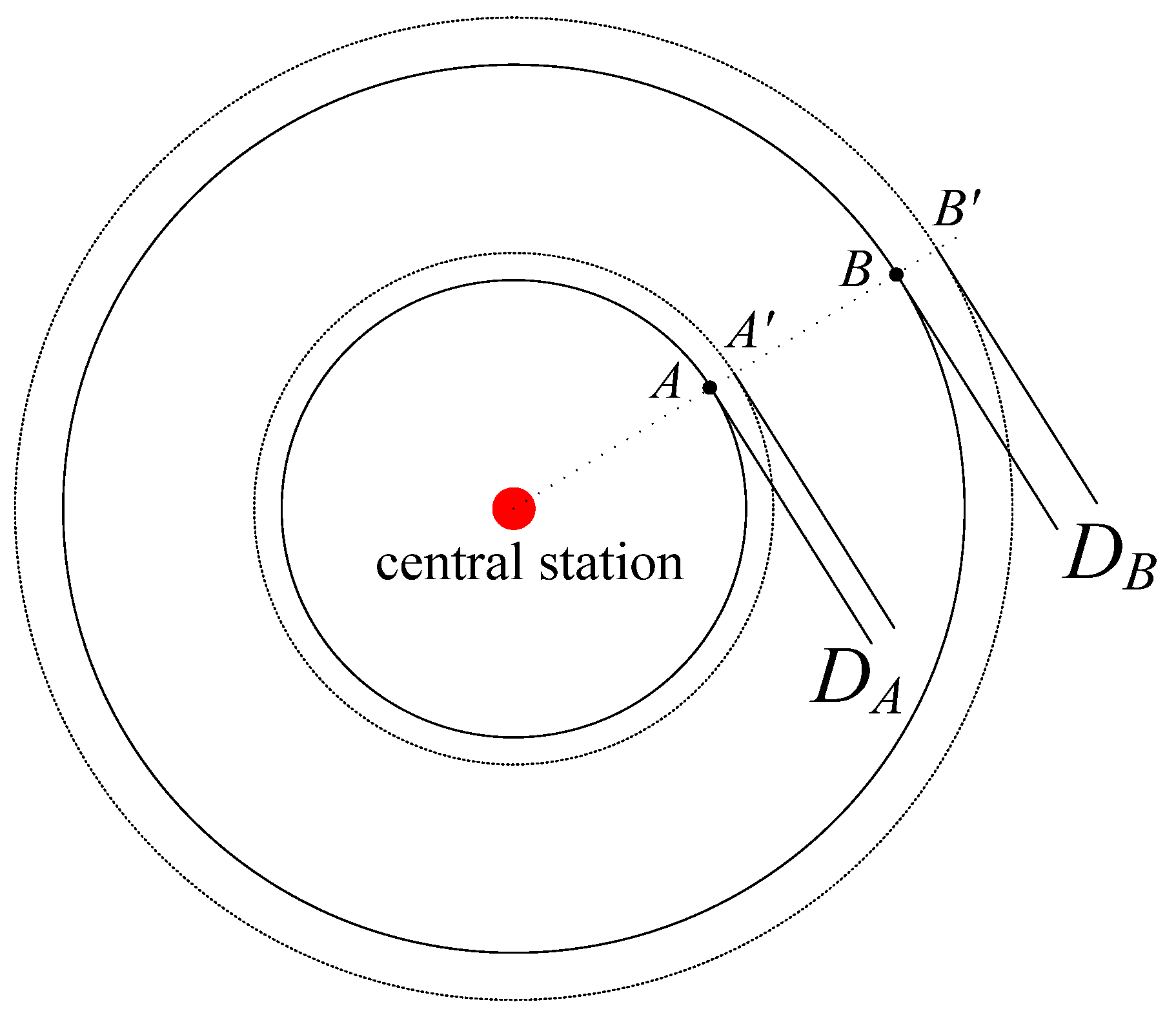
5.2.1. Effect of Positional Error of Fixed-Coordinate Beacon Point on Positioning Results
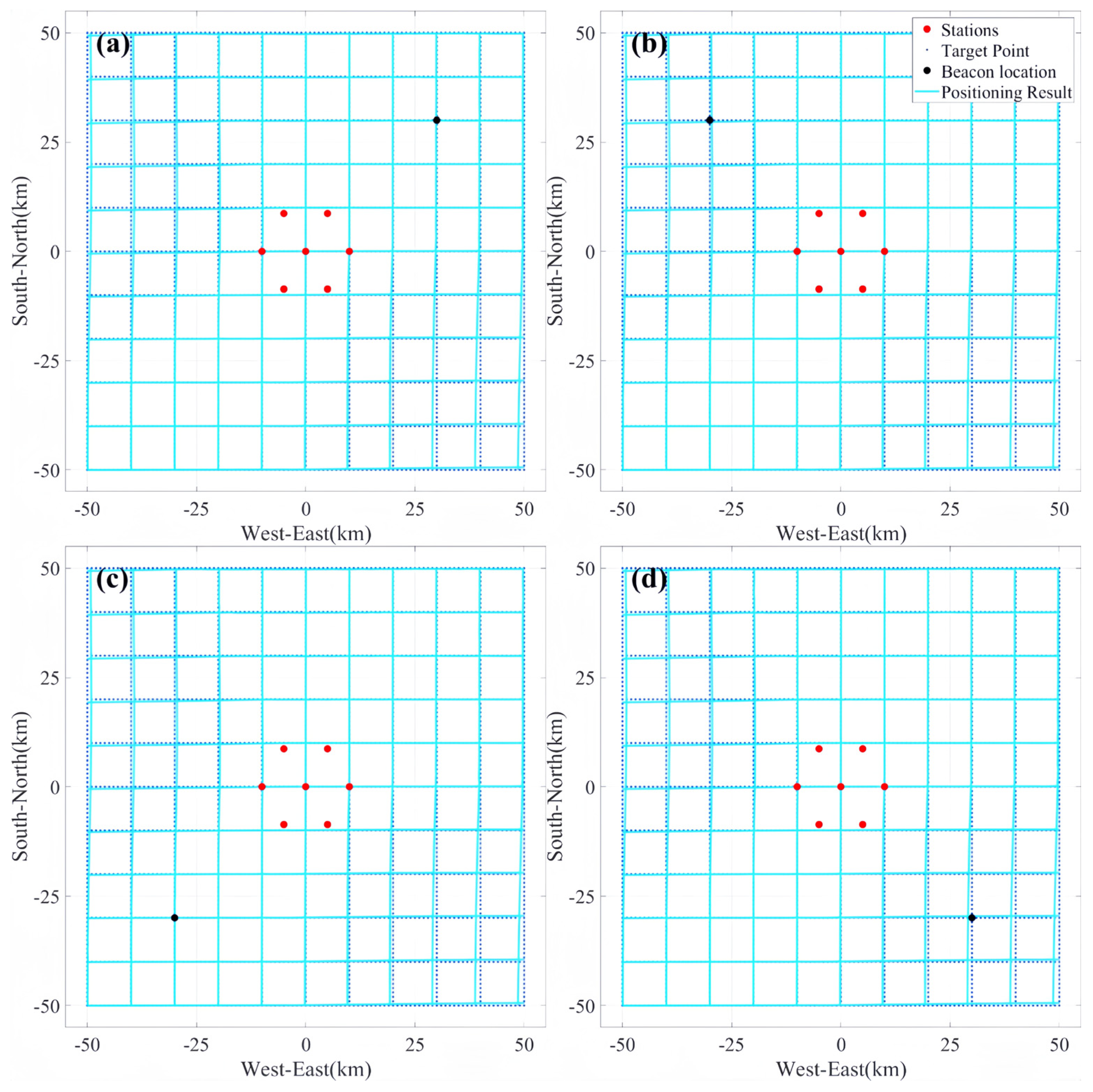
5.2.2. Effect of Relative Position of Fixed-Coordinate Beacon Point on Positioning Results
6. Conclusions
- In the non-time-synchronized lightning positioning method using two random radiation sources for joint positioning, there are uneven errors in the positioning results, and the positioning results can roughly reflect the lightning contours.
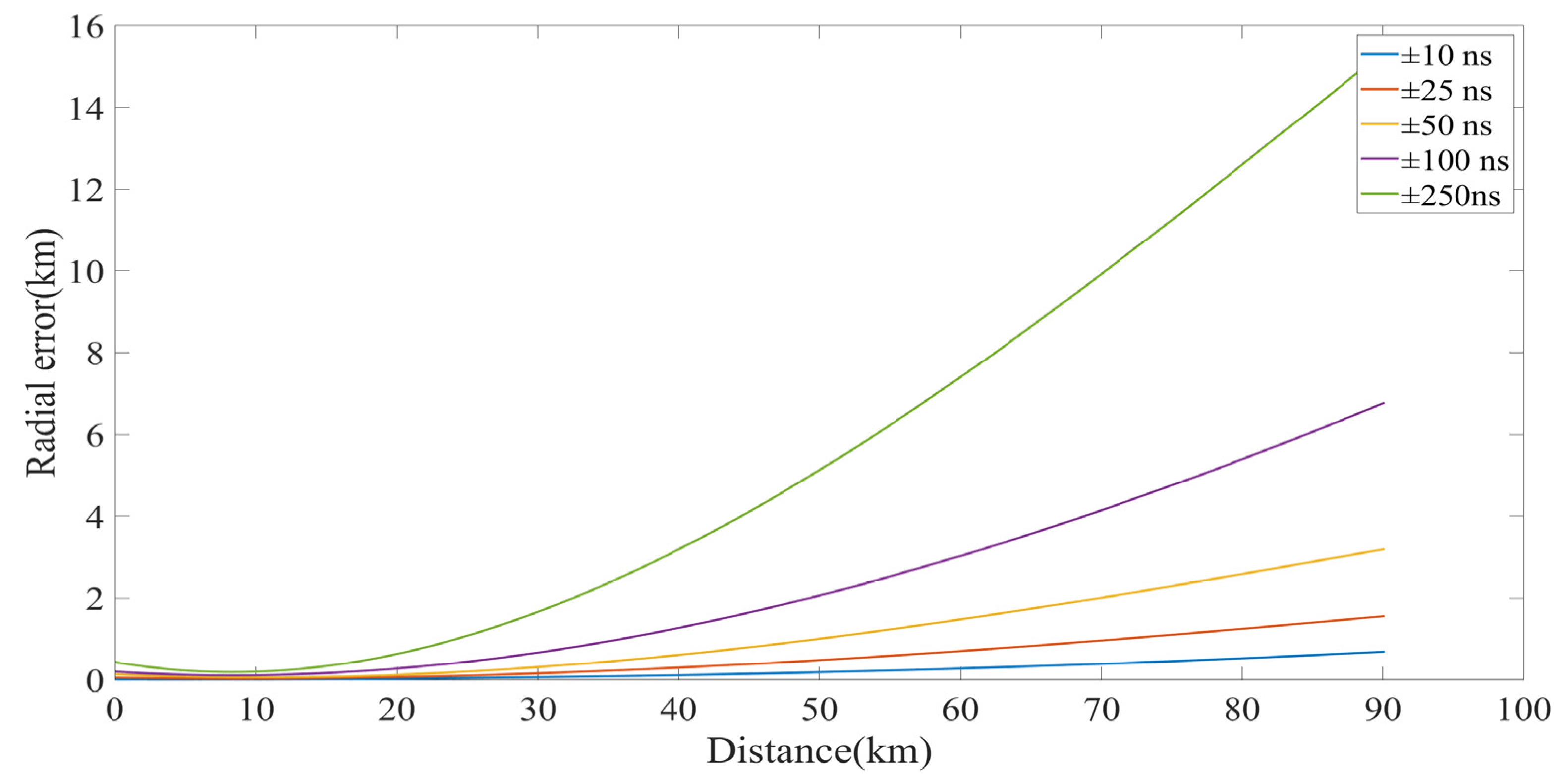
- Similarly to the traditional positioning method, the farther away from the center of the positioning network, the larger the radial error of the positioning results. For a positioning network with a baseline length of 10 km, when the measurement error of the pulse interval is less than ±50 ns, the radial error is less than 2 km within 90 km from the center of the positioning network.
- The positioning results when using a fixed-coordinate beacon point for joint positioning are similar to those of the traditional method, and the positional error of the beacon point affects the accuracy of positioning and is positively correlated with the positional error of the beacon point in terms of orientation and size.
- The simulated positioning errors are basically the same when the joint beacon points are centrosymmetric about the center coordinates. In other words, when the non-time-synchronized lightning positioning method is utilized for radiation source positioning, the positioning accuracy is essentially unaffected when the coordinates of the beacon point are transformed.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rison, W.; Thomas, R.J.; Krehbiel, P.R.; Hamlin, T.; Harlin, J. A GPS-based three-dimensional lightning mapping system: Initial observations in central New Mexico. Geophys. Res. Lett. 1999, 26, 3573–3576. [Google Scholar] [CrossRef]
- Smith, D.A.; Eack, K.B.; Harlin, J.; Heavner, M.J.; Jacobson, A.R.; Massey, R.S.; Shao, X.M.; Wiens, K.C. The Los Alamos Sferic Array: A research tool for lightning investigations. J. Geophys. Res. Atmos. 2002, 107, ACL 5-1–ACL 5-14. [Google Scholar] [CrossRef]
- Dowden, R.L.; Holzworth, R.H.; Rodger, C.J.; Lichtenberger, J.; Thomson, N.R.; Jacobson, A.R.; Lay, E.; Brundell, J.B.; Lyons, T.J.; O’Keefe, S.; et al. World-wide lightning location using VLF propagation in the Earth-ionosphere waveguide. IEEE Antennas Propag. Mag. 2008, 50, 40–60. [Google Scholar] [CrossRef]
- Betz, H.D.; Schmidt, K.; Laroche, P.; Blanchet, P.; Oettinger, W.P.; Defer, E.; Dziewit, Z.; Konarski, J. LINET—An international lightning detection network in Europe. Atmos. Res. 2009, 91, 564–573. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Y.; Qie, X.; Zhang, T.; Zhao, Y.; Li, Y.; Cao, D. Using lightning locating system based on time-of-arrival technique to study three-dimensional lightning discharge processes. Sci. China Earth Sci. 2010, 53, 591–602. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Y.; Wang, Y.; Zhang, T.; Wu, B.; Liu, Y. Experimental study on location accuracy of a 3D VHF lightning-radiation-source locating network. Sci. China Earth Sci. 2015, 58, 2034–2048. [Google Scholar] [CrossRef]
- Sun, Z.; Qie, X.; Liu, M.; Cao, D.; Wang, D. Lightning VHF radiation location system based on short-baseline TDOA technique—Validation in rocket-triggered lightning. Atmos. Res. 2013, 129–130, 58–66. [Google Scholar] [CrossRef]
- Qie, X.; Liu, D.; Sun, Z. Recent advances in research of lightning meteorology. J. Meteorol. Res. 2014, 28, 983–1002. [Google Scholar] [CrossRef]
- Wang, D.; Xiushu, Q.; Tie, Y.; Guangshu, Z.; Tong, Z.; Tinglong, Z.; Qilin, Z. Analysis of the initial stage intracloud lightning using the pulse location technique based on the fast electric field change. J. Meteorol. Res. 2009, 23, 772–781. [Google Scholar]
- Wang, Y.; Qie, X.; Wang, D.; Liu, M.; Su, D.; Wang, Z.; Liu, D.; Wu, Z.; Sun, Z.; Tian, Y. Beijing Lightning Network (BLNET) and the observation on preliminary breakdown processes. Atmos. Res. 2016, 171, 121–132. [Google Scholar] [CrossRef]
- Srivastava, A.; Tian, Y.; Qie, X.; Wang, D.; Sun, Z.; Yuan, S.; Wang, Y.; Chen, Z.; Xu, W.; Zhang, H.; et al. Performance assessment of Beijing Lightning Network (BLNET) and comparison with other lightning location networks across Beijing. Atmos. Res. 2017, 197, 76–83. [Google Scholar] [CrossRef]
- Shi, D.; Zheng, D.; Zhang, Y.; Zhang, Y.; Huang, Z.; Lu, W.; Chen, S.; Yan, X. Low-frequency E-field Detection Array (LFEDA)—Construction and preliminary results. Sci. China Earth Sci. 2017, 60, 1896–1908. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Zheng, D.; Zhang, Y.; Fan, X.; Fan, Y.; Xu, L.; Lyu, W. A Method of Three-Dimensional Location for LFEDA Combining the Time of Arrival Method and the Time Reversal Technique. J. Geophys. Res. Atmos. 2019, 124, 6484–6500. [Google Scholar] [CrossRef]
- Yuan, S.; Qie, X.; Jiang, R.; Wang, D.; Sun, Z.; Srivastava, A.; Williams, E. Origin of an Uncommon Multiple-Stroke Positive Cloud-to-Ground Lightning Flash with Different Terminations. J. Geophys. Res. Atmos. 2020, 125, e2019JD032098. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Tan, Y.; Chen, Z.; Zheng, D.; Zhang, Y.; Fan, Y. Fast and Fine Location of Total Lightning from Low Frequency Signals Based on Deep-Learning Encoding Features. Remote Sens. 2021, 13, 2212. [Google Scholar] [CrossRef]
- Wang, Y.; Min, Y.; Liu, Y.; Zhao, G. A New Approach of 3D Lightning Location Based on Pearson Correlation Combined with Empirical Mode Decomposition. Remote Sens. 2021, 13, 3883. [Google Scholar] [CrossRef]
- Wang, Y.; Min, Y.; Liu, Y.; Yao, L.; Liu, Y.; Guo, Z. A non-time-synchronized lightning positioning method and its preliminary application. Atmos. Res. 2023, 285, 106641. [Google Scholar] [CrossRef]
- Thomas, R.J.; Krehbiel, P.R.; Rison, W.; Hunyady, S.J.; Winn, W.P.; Hamlin, T.; Harlin, J. Accuracy of the Lightning Mapping Array. J. Geophys. Res. Atmos. 2004, 109, D14207. [Google Scholar] [CrossRef]
- Bitzer, P.M.; Christian, H.J.; Stewart, M.; Burchfield, J.; Podgorny, S.; Corredor, D.; Hall, J.; Kuznetsov, E.; Franklin, V. Characterization and applications of VLF/LF source locations from lightning using the Huntsville Alabama Marx Meter Array. J. Geophys. Res. Atmos. 2013, 118, 3120–3138. [Google Scholar] [CrossRef]
- Sun, Z.; Qie, X.; Liu, M. Characteristics of a Negative Cloud-to-Ground Lightning Discharge Based on Locations of VHF Radiation Sources. Atmos. Ocean. Sci. Lett. 2014, 7, 248–253. [Google Scholar] [CrossRef]
- Sun, Z.; Qie, X.; Liu, M.; Jiang, R.; Wang, Z.; Zhang, H. Characteristics of a negative lightning with multiple-ground terminations observed by a VHF lightning location system. J. Geophys. Res. Atmos. 2016, 121, 413–426. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, G.; Zhang, T.; Li, Y.; Fan, X.; Wu, B. Error Correction in Three-Dimension Location System of Lightning VHF Radiation. Plateau Meteorol. 2012, 31, 1407–1413. [Google Scholar]
- Zhao, J.Y.; Song, S.L.; Chen, Q.M.; Zhou, W.L.; Zhu, W.Y. Establishment of a new global model for zenith tropospheric delay based on functional expression for its vertical profile. Chin. J. Geophys. 2014, 57, 3140–3153. [Google Scholar] [CrossRef]
- Li, W.; Yuan, Y.; Ou, J.; Li, H.; Li, Z. A new global zenith tropospheric delay model IGGtrop for GNSS applications. Chin. Sci. Bull. 2012, 57, 2132–2139. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yao, L.; Min, Y.; Liu, Y.; Zhao, G. Error Analysis of Non-Time-Synchronized Lightning Positioning Method. Remote Sens. 2024, 16, 3443. https://doi.org/10.3390/rs16183443
Wang Y, Yao L, Min Y, Liu Y, Zhao G. Error Analysis of Non-Time-Synchronized Lightning Positioning Method. Remote Sensing. 2024; 16(18):3443. https://doi.org/10.3390/rs16183443
Chicago/Turabian StyleWang, Yanhui, Lijie Yao, Yingchang Min, Yali Liu, and Guo Zhao. 2024. "Error Analysis of Non-Time-Synchronized Lightning Positioning Method" Remote Sensing 16, no. 18: 3443. https://doi.org/10.3390/rs16183443
APA StyleWang, Y., Yao, L., Min, Y., Liu, Y., & Zhao, G. (2024). Error Analysis of Non-Time-Synchronized Lightning Positioning Method. Remote Sensing, 16(18), 3443. https://doi.org/10.3390/rs16183443




