Abstract
Understanding the water and carbon cycles within terrestrial ecosystems is crucial for effective monitoring and management of regional water resources and the ecological environment. However, physical models like the SEB- and LUE-based ones can be complex and demand extensive input data. In our study, we leveraged multiple variables (vegetation growth, surface moisture, radiative energy, and other relative variables) as inputs for various regression algorithms, including Multiple Linear Regression (MLR), Random Forest Regression (RFR), and Backpropagation Neural Network (BPNN), to estimate water (ET) and carbon fluxes (NEE) in the Haihe River Basin, and compared the estimated results with the observations from six eddy covariance flux towers. We aimed to (1) assess the impacts of different input variables on the accuracy of ET and NEE estimations, (2) compare the accuracy of the three regression methods, including three machine learning algorithms and Multiple Linear Regression, and (3) evaluate the performance of ET and NEE estimation models across various regions. The key findings include: (1) Increasing the number of input variables typically improved the accuracy of ET and NEE estimations. (2) RFR proved to be the most accurate for both ET and NEE estimations among the three regression algorithms. Of these, the four types of variables used together with RFR resulted in the best accuracy for ET (R2 of 0.81 and an RMSE of 1.13 mm) and NEE (R2 of 0.83 and an RMSE of 2.83 gC/m2) estimations. (3) Vegetation growth variables (i.e., VIs) are the most important inputs for ET and NEE estimation. (4) The proposed ET and NEE estimation models exhibited some variation in accuracy across different validation sites. Despite these variations, the accuracy levels across all six validation sites remained relatively high. Overall, this study lays the groundwork for an efficient approach to agricultural water resources and ecosystem monitoring and management.
1. Introduction
The water cycle and carbon cycle constitute two pivotal components of terrestrial ecosystems, directly influencing vegetation transpiration and photosynthesis, respectively [1]. Evapotranspiration (ET), a crucial component of the water cycle, contributes significantly to returning approximately 60% of precipitation back to the atmosphere [2]. Furthermore, the majority of organic carbon in terrestrial ecosystems is sequestered through vegetation photosynthesis, serving as the primary source of vegetation biomass [3]. Consequently, the precise and efficient monitoring of water and carbon fluxes holds utmost importance in agriculture, ecology, environmental science, and hydrology studies. Instruments such as the eddy covariance system (EC) [4] and large aperture scintillator (LAS) [5] have emerged for use in observing water and carbon fluxes in the field. Despite their ability to cover areas spanning several square kilometers, these instruments cannot provide distributed results or result maps. Remote sensing (RS) offers a remarkable tool for monitoring ecosystem processes at a regional scale. Many RS-based models have been proposed for water and carbon fluxes, broadly categorized into physical and empirical models.
The Surface Energy Balance (SEB)-based algorithm stands as a widely accepted physical model for ET estimation. Prominent examples include the Surface Energy Balance Algorithm for Land (SEBAL) [6,7], Two Source Energy Balance (TSEB) [8], and Surface Energy Balance System (SEBS) [9]. These algorithms have found extensive application in ET estimation across various ecosystems [10,11,12,13,14]. For carbon flux estimation, the Light Use Efficiency (LUE)-based algorithm is a commonly used physical model for gross primary productivity (GPP) assessment [1,15,16,17,18,19]. The LUE model determines GPP by multiplying the photosynthesis-absorbed radiation with the actual LUE to calculate the carbon fixed via photosynthesis [20]. These physical models, be they used for ET or GPP, bridge the gap between remote sensing data and target variables. However, they require a significant number of parameters and computations, adding to their complexity [20,21]. Furthermore, these models [11,21] often rely on meteorological data, but the current spatial resolution of such data is often too coarse to align with high-resolution satellite imagery like Landsat (30 m) or Sentinel (10 m).
On the other hand, empirical models offer simplicity but with less interpretability. They are typically based on relationships between remote sensing data and in-situ observations of water or carbon fluxes [22,23,24,25,26]. The advent of machine learning algorithms has facilitated better alignments between remote sensing data and in situ observations [4,27]. It is worth noting that empirical models often exhibit limited spatial universality; models trained on samples from a specific area might not perform well in other regions [4]. Additionally, semi-empirical equations like Penman–Monteith [28,29] and Priestley–Taylor [30] have also been employed in remote sensing model development. In summary, both model types possess distinct strengths and weaknesses.
Although numerous scholars have delved into the use of the remote sensing model for water or carbon fluxes, most of their investigations into these two flux estimation models have been independent. However, it is crucial to recognize the intricate interaction and coupling between transpiration and photosynthesis, as highlighted by Sun et al. [31]. Photosynthesis and transpiration primarily facilitate the exchange of water and carbon with the atmosphere through leaf stomata. The aperture of these stomata is modulated by various abiotic and biotic factors inherent to plants [32]. For instance, during drought conditions characterized by increased evaporation and decreased precipitation, leaf stomata tend to shrink, thereby impacting carbon exchange.
Moreover, soil serves as an additional hub for the exchange of water and carbon within the ecosystem. Soil water can either evaporate directly into the atmosphere or be absorbed by plants, and soil moisture levels also influence soil microbial respiration [33]. Additionally, carbon assimilated by plants contributes to the formation of soil organic carbon [34], while the soil organic carbon content, in turn, affects the soil water transport process [35]. In essence, the exchange of water and carbon fluxes in terrestrial ecosystems is an intricately linked and complex process. Therefore, incorporating this interaction into water and carbon flux estimation models has the potential to significantly enhance accuracy. In general, the transpiration and photosynthetic capacity of vegetation are determined by various factors, including vegetation growth, radiative energy, and soil conditions. However, it remains unclear which type of factor has the greatest impact on vegetation transpiration and photosynthesis, and which indicators are most critical when constructing models.
Remote sensing technology offers a spatially and temporally continuous and efficient means of gathering information. Nevertheless, handling the vast amounts of remote sensing data in terms of acquisition, storage, and computation demands high-performance computing resources. Google Earth Engine (GEE), a cloud-based platform, stores petabytes of earth observation data and serves as a cost-effective solution for online data processing [36]. GEE has found applications in diverse fields such as global forest mapping [37], surface water mapping and analysis [38,39], cropland mapping [40], and crop yield prediction [41,42]. Consequently, GEE holds the potential to serve as an efficient platform for the co-estimation of water and carbon fluxes.
In this study, we utilized multiple variables, including vegetation growth, surface moisture, radiative energy, and other pertinent variables, as inputs for various regression algorithms. Specifically, we employed Multiple Linear Regression (MLR), Random Forest Regression (RFR), and Backpropagation Neural Network (BPNN) to estimate water (ET) and carbon fluxes (NEE). The estimated results were then compared with observations from six eddy covariance flux towers. The objectives of this study were threefold: (1) to assess the impacts of different input variables on the accuracy of evapotranspiration (ET) and net ecosystem exchange (NEE) estimations, (2) to compare the accuracy of the three regression methods, encompassing three machine learning algorithms and Multiple Linear Regression, and (3) to evaluate the performance of ET and NEE estimation models across various regions.
2. Study Area and Data Collection
2.1. Study Area
In this study, we focused on the Haihe River Basin (HRB), one of China’s nine primary river basins, as our study area for estimating water and carbon fluxes. Based on ground-observed data, our study period primarily spanned from 2003 to 2020. Located in northern China, the HRB covers an area of 3.18 × 105 km2, encompassing Beijing, Tianjin, as well as portions of Hebei, Shanxi, Shandong, Henan, Inner Mongolia, and Liaoning provinces (refer to Figure 1). The basin’s terrain slopes down from northwest to southeast, featuring three distinct geomorphic types: plateau, mountain, and plain. The HRB is typically characterized by a temperate East Asian monsoon climate, with an average annual temperature ranging from 1.5 °C to 14 °C. The annual average relative humidity lies between 50% and 70%. With an annual precipitation average of 539 mm, land surface evaporation averaging 470 mm, and water surface evaporation at 1100 mm, the region is classified as semi-humid to semi-arid. Notably, cropland dominates the land use in the HRB, covering a vast area of 1.47 × 105 km2, making it a significant source of food production in China. Consequently, gaining insights into the water and carbon fluxes of these croplands is crucial for effective agricultural water management and production strategies in the HRB.
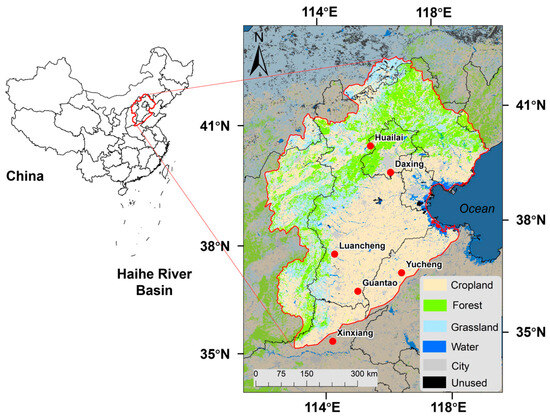
Figure 1.
Study area. Note: the land use type data were obtained from the Resource and Environment Science and Data Center (RESDC), China Academy of Science (https://www.resdc.cn/).
2.2. Satellite Data
In this study, we utilized surface reflectance and surface temperature data from Landsat 7 and Landsat 8 (specifically, Level 2, Collection 2, Tier 1 data) for the estimation of water and carbon fluxes. The surface reflectance data encompassed six spectral bands: blue, green, red, near-infrared, shortwave infrared 1, and shortwave infrared 2. Detailed information on these bands is provided in Table 1. These datasets underwent geometric correction, radiometric calibration, and atmospheric correction. Additionally, we employed the Quality Assurance (QA) band from both Landsat 7 and Landsat 8 for cloud masking prior to data analysis. The entire satellite data processing was carried out using the Google Earth Engine (GEE) platform. Among them, due to sensor issues, Landsat 7′s observation data suffer from stripe missing problems. This study employs the focal statistics-based method provided by the GEE platform for interpolation. For specifics, please refer to https://code.earthengine.google.com/16e86cfbd845a7b583100cb8c27348e9, accessed on 25 January 2024.

Table 1.
Satellite data description.
2.3. Flux Data
In this study, the flux tower observations obtained from ChinaFLUX (http://www.chinaflux.org) were used for the model evaluation, and the six flux tower sites located exclusively within the cropland ecosystem were used for estimating water and carbon fluxes. Figure 1 illustrates the positions of these six sites, while Table 2 provides detailed information about them. For in situ carbon flux measurements, we relied on the net ecosystem exchange (NEE, measured in gC/m2) recorded by the flux towers. Similarly, the latent heat flux (LE, measured in W/m2) observed by the flux towers served as our in situ water flux, which we converted to evapotranspiration (ET, in mm) using Equation (1).
where λ is the latent heat vaporization. For the EC observation system, it should be noted that the energy balance closure issue was often found, i.e., the available energy (net radiation (Rn, W/m2) minus ground heat flux (G, W/m2)) is not equal to the sum of LE and sensible heat flux (H, W/m2). Therefore, the energy balance closure ratio (EBCR, Equation (2)) was used to filter the flux data [1]:
where the energy fluxes were all calculated at the daily scale. Only the measurements with EBCR more than 80% were used in this study. Moreover, the Bowen ratio method was used to forcing the energy closure of the selected measurements (Equation (3)) [43]:
where LEcor is the corrected latent heat flux. After matching the satellite data (after cloud mask) and filtering using EBCR, totally 411 samples of ET and 490 samples of NEE were used in this study. The flux observation sensors were installed at the 40 m height, and the observation frequency is 30 min, while the observation data were taken at the statistic to daily scale to match the results from the proposed model. Figure 2a,b shows the histogram of observed ET and NEE.

Table 2.
The details of flux tower sites.
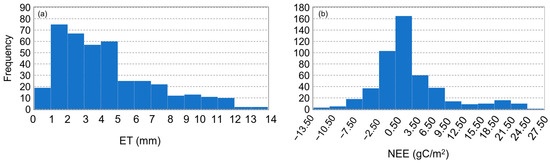
Figure 2.
The histograms of observed (a) ET and (b) NEE.
3. Methodology
3.1. Machine Learning Methods
The relationship between remote sensing data and target variables may often be nonlinear, making machine learning algorithms particularly suitable for addressing such complexities. These algorithms excel at handling nonlinear, heteroscedastic problems and extracting valuable insights from vast amounts of remote sensing data [44,45]. In our study, we employed two machine learning algorithms—Random Forest Regression (RFR), and Backpropagation Neural Network (BPNN)—for fitting and estimating water (ET) and carbon (NEE) fluxes. These algorithms have been extensively utilized in establishing remote sensing models, including crop yield estimation [46], soil moisture estimation [4], leaf area index estimation [47], plant biomass estimation [48], and soil organic matter content estimation [49]. Additionally, we used Multiple Linear Regression (MLR) as a traditional fitting algorithm for comparison with these machine learning methods.
- (1)
- Random forest regression (RFR)
RFR is an ensemble learning method primarily used for regression problems. It is based on the ensemble of decision trees and improves the accuracy and robustness of predictions by constructing multiple decision trees and averaging or majority voting on their prediction results. The following are the main steps and characteristics of the Random Forest Regression algorithm:
- Random Sampling—Using the bootstrap sampling method to randomly extract multiple sample sets from the original training data set, with each sample set having the same size as the original data set;
- Decision Tree Construction—For each sample set, construct a decision tree. During the tree construction process, introduce randomness to increase the diversity of the trees, such as randomly selecting features for splitting;
- Each decision tree independently predicts new data;
- Ensemble Prediction—Averaging the prediction results of all decision trees to obtain the final prediction result.
- (2)
- Backpropagation Neural Network (BPNN)
The BP Neural Network regression algorithm is a multi-layer feedforward network trained using the error backpropagation algorithm, widely applied to various regression prediction problems. The main steps of the BP neural network regression algorithm include:
- Network Initialization—Randomly set the weights and biases between neurons in each layer;
- Forward Propagation of Input Signals—Propagate the input signals forward through the network and calculate the output of neurons in each layer;
- Error Calculation—Calculate the error based on the network’s output and the desired output;
- Error Backpropagation—Propagate the error signal backward and adjust the weights and biases of neurons in each layer according to the gradient descent method or other optimization algorithms;
- Iterative Training—Repeat steps b to d until the maximum number of iterations.
In this study, we employed Python and SkLearn to program the selected regression algorithms. The parameters of the two machine learning algorithms are presented in Table 3.

Table 3.
Definitions of input variables extracted from Landsat observations.
3.2. Input Variables
This study selected four types of variables as input indicators for the model: vegetation growth, surface moisture, radiative energy, and others.
- (1)
- Vegetation growth
Vegetation growth is characterized by spectral indices constructed with reference to the relevant literature. Here, 11 commonly used spectral indices are selected, as shown in Table 4. Through correlation analysis, it can be seen that these indices have varying degrees of correlation with ET and NEE, demonstrating their potential for accurately estimating ET and NEE. All the VIs were derived from the six optical bands—blue, green, red, near-infrared, and two shortwave infrared bands captured by both Landsat 7 and Landsat 8. A Pearson correlation (Equation (4)) analysis was conducted between ET and NEE, utilizing vegetation indices (VIs) derived from satellite observations to prove the potential of the Vis:
where X and Y are the variables, as illustrated in Figure 3. Divergent outcomes emerged for ET and NEE. Among them, SAVI exhibited the strongest correlation with ET, achieving a correlation coefficient (r) of 0.66. CVI, NDVI, AFRI, GCI, ENDVI, and LSWI followed, all demonstrating comparable r values exceeding 0.5. Conversely, EVI, NPCI, and MDWI showed a weak correlation with r values below 0.1. When considering NEE, the correlations with VIs were generally weaker compared to those with ET. The majority of the correlations between various VIs and NEE were less than 0.2, with MNDVI, EVI, NPCI, and MDWI falling below 0.1.

Table 4.
Definitions of input variables extracted from Landsat observations.
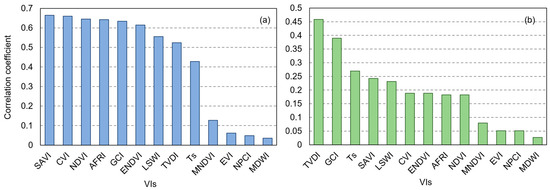
Figure 3.
The correlation of VIs with (a) ET and (b) NEE.
- (2)
- Surface moisture
Surface moisture conditions can influence vegetation transpiration and photosynthesis to some extent, as well as soil evaporation. Here, surface temperature (Ts), Temperature Vegetation Drought Index (TVDI), and Surface–Air Temperature Difference (SATD) are selected to represent surface moisture conditions. Ts were obtained from Landsat 7/8 thermal band [27]. TVDI was calculated based on Ts-NDVI space (Equation (5)) [61]. SATDs were calculated as the difference between Ts with air temperature (Ta), Ta values were obtained from the study of Fang et al. [62], and the nearest algorithm was employed to resample the Ta dataset from 1 km spatial resolution to 30 m.
where Tsmax and Tsmin is the surface temperature of dry edge and wet edge.
- (3)
- Radiation energy
Solar radiation is the primary energy source for water evaporation and plant photosynthesis. In this paper, four indicators are selected: downward shortwave radiation (Rs_down, Equation (6)); upward shortwave radiation (Rs_up, Equations (7) and (8)); downward longwave radiation (Rl_down, Equation (9)); and upward longwave radiation (Rl_up, Equation (10)).
where GSC represents the solar constant, taken as 1376 W/m2; θ represents the solar zenith angle; τsw represents the atmospheric transmittance; dr represents the astronomical distance between the sun and the Earth; α represents surface albedo; αp represents the influence of atmospheric path radiation, which is generally taken as 0.03; B, R, NIR, SWIR1, SWIR2 represent Blue band, Red band, Near infrared band, Shortwave infrared 1 band and Shortwave infrared 2 band observed by Landsat; εa and ε represent the atmospheric emissivity and surface emissivity, respectively; σ represents the Stefan–Boltzmann constant, taken as 5.67 × 10−8 W/m2K4. The specific calculation methods for these parameters can be referenced from the study of Cheng et al. [21].
- (4)
- Others
Considering the seasonal variations in phenology and climate that can influence plant physiological processes [2], we incorporated the Julian day (i.e., the day of the year, DOY) as one of the input variables. Figure 4 presents the ET and NEE variation with DOY. DOY was introduced as a non-VIs factor to capture the seasonal variations in radiation and temperature. Analysis revealed a binomial relationship between ET and DOY, with an R-squared value of 0.31. However, no significant correlation was observed between NEE and DOY. Additionally, the position (longitude and latitude) and elevation (DEM) were also employed as the inputs. The DEM data (ASTER GDEM, 30 m) were obtained from Geospatial Data Cloud (https://www.gscloud.cn, accessed on 15 August 2022.).
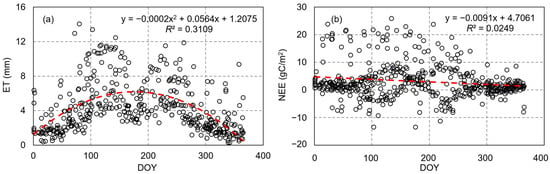
Figure 4.
The scatter plot of DOY with (a) ET and (b) NEE.
3.3. Modeling and Validation
3.3.1. Modeling Methods
The flux tower footprint is typically influenced by various factors, including the instrument’s height, land surface conditions, turbulence intensity, and terrain features [63]. This study determines the observation range of the flux tower through the footprint function proposed by Kljun et al. [64], in order to match the corresponding pixels of ET and NEE observed by remote sensing. This footprint is considered as a function of variables such as height, wind speed, wind direction, etc. For specific calculation methods, please refer to the study of Kljun et al. [64].
Furthermore, to facilitate a rigorous and unbiased comparison among the four regression methods (MLR, RFR, BPNN) using the selected input variables, we randomly allocated 80% of the samples and corresponding in situ ET/NEE measurements for model training. The remaining 20% were reserved to assess model accuracy. Figure 5 provides a detailed flowchart illustrating this process.
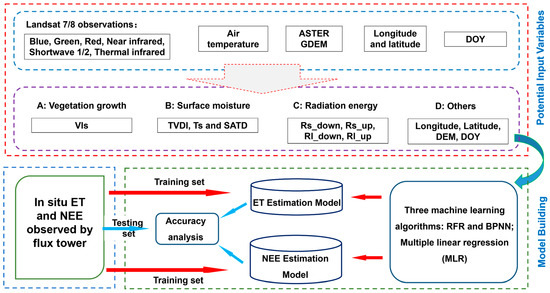
Figure 5.
The flowchart of the data preprocessing, model building and validation.
3.3.2. Validation Methods
A fivefold cross-validation was employed for an objective and reliable assessment of model accuracy, as it expands the testing dataset. The final accuracy was determined by calculating the average of the results obtained from the fivefold cross-validation. Moreover, we also evaluate the accuracy in different flux tower sites. Specifically, observations from a designated site were used as the testing set while data from the other five sites served as the training set.
Additionally, to quantify the model’s performance, we utilized two metrics: the coefficient of determination (R2) and the root mean square error (RMSE). These metrics were calculated using the following formulae:
where VarMi is the estimated ET or NEE given by the proposed model and VarObi is the observed ET or NEE by flux tower. n is the number of samples, which is 428 for ET estimation and 509 for NEE estimation.
4. Results
4.1. Modeling and Validation of ET and NEE Estimation
4.1.1. Contributions of Different Input Variables
This study evaluates the impacts of different types of input variables (vegetation growth, surface moisture, radiative energy, and others) and their combinations on the estimation of ET (evapotranspiration) and NEE (net ecosystem exchange). The results (fivefold cross-validation) are shown in Figure 6. The combination of four types of variables inputs, along with the Random Forest Regression (RFR) algorithm, achieved the highest estimation accuracy, with an R2 of 0.81 and an RMSE of 1.13 mm for ET estimation, and an R2 of 0.83 and an RMSE of 2.83 gC/m2 for NEE estimation. The accuracy for the combination of three types of variables was ET—R2 = 0.61–0.78, RMSE = 1.18–1.62 mm; NEE—R2 = 0.26–0.81, RMSE = 2.90–5.91 gC/m2. The accuracy for the combination of two types of variables was ET—R2 = 0.53–0.79, RMSE = 1.28–1.82 mm; NEE—R2 = 0.01–0.77, RMSE = 3.08–6.34 gC/m2. When using a single type of input variable, vegetation growth variables (R2 = 0.50, RMSE = 1.87 mm) and other variables (R2 = 0.52, RMSE = 1.93 mm) combined with the RFR algorithm provided the most accurate ET estimation. Similarly, vegetation growth (R2 = 0.49, RMSE = 4.58 gC/m2) combined with the RFR algorithm also yielded the most accurate NEE estimation. Overall, vegetation growth has more potential when used in estimating ET and NEE. Given the distinct seasonal variation in ET (Figure 4a), the RFR algorithm effectively captures the nonlinear relationship between ET and DOY (Day of Year). In summary, for both ET and NEE estimation, the combination of multiple types of input variables enhances the accuracy of machine learning models, and different combinations of variables provide more informative data on ET and NEE.
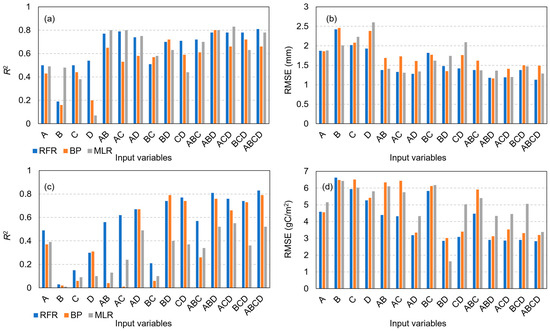
Figure 6.
The accuracy metrics of ET and NEE estimation: (a) R2 (b) RMSE for ET and (c) R2 (d) RMSE for NEE. Note: A, B, C and D represents the input variables of vegetation growth, surface moisture, radiative energy, and others.
4.1.2. The Performance of Different Regression Methods
The accuracy levels of the three algorithms differed significantly, whether for ET or NEE estimation (Figure 7). Based on variance analysis, Random Forest Regression (RFR) demonstrated superior accuracy for both ET (R2 = 0.19–0.81, RMSE = 1.13–2.42 mm) and NEE (R2 = 0.03–0.83, RMSE = 2.83–6.63 gC/m2) estimation compared to the other algorithms. Conversely, Backpropagation Neural Network (BPNN) and Multiple Linear Regression (MLR) exhibited relatively low accuracy for ET prediction. MLR exhibited the lowest accuracy for NEE prediction.
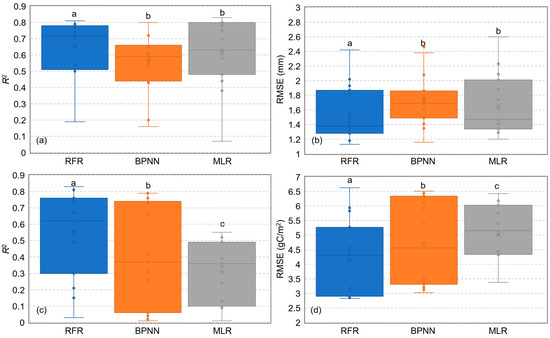
Figure 7.
The box plots of different algorithms for ET and NEE estimation: (a) R2; (b) RMSE for ET and (c) R2; (d) RMSE for NEE. The letters “a”, “b” and “c” on the boxes indicate significant differences based on ANOVA (p < 0.05).
Considering only the optimal cases for each algorithm (i.e., four types of variables combinedly input), RFR achieved an R2 of 0.81 and an RMSE of 1.13 mm for ET estimation, and an R2 of 0.83 and an RMSE of 2.83 gC/m2 for NEE estimation. There are differences in the accuracy of ET and NEE estimation between the BPNN and MLR algorithms. For ET estimation, the highest accuracy of the MLR algorithm (R2 = 0.78, RMSE = 1.29 mm) is slightly better than that of BPNN (R2 = 0.66, RMSE = 1.49 mm), while for NEE estimation, the highest accuracy of the MLR algorithm (R2 = 0.52, RMSE = 3.38 gC/m2) is significantly lower (p < 0.05) than that of BPNN (R2 = 0.78, RMSE = 3.20 gC/m2).
4.1.3. The Stability of the Model in Different Sites
To assess the spatial robustness of our proposed model, validation was performed across multiple sites. Specifically, observations from a designated site were used as the testing set, while data from the other five sites served as the training set. Utilizing the optimal conditions (RFR with four types of variables together as inputs for both ET and NEE estimation), the results were modeled and are presented in Figure 8 and Table 5. Although the validation results were generally slightly higher to those obtained through five-fold cross-validation for both ET and NEE estimation, the differences were not pronounced. Specifically, for ET estimation, we achieved an R2 of 0.86 and an RMSE of 1.12 mm, while for NEE estimation, the R2 was 0.83 and the RMSE was 2.74 gC/m2. However, there were notable variations in accuracy across different sites. For ET estimation, the R2 ranged from 0.51 to 0.87, and the RMSE fluctuated between 0.94 and 2.28 mm across the six sites. Similarly, for NEE estimation, the R2 spanned from 0.35 to 0.80, with the RMSE varying from 1.42 to 5.48 gC/m2. These discrepancies can be attributed to several factors. Firstly, the spatial accuracy differences inherent in our proposed model contribute to these variations. Secondly, the differing number of samples observed at each site also influences the validation results.
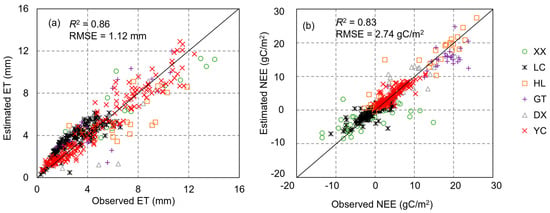
Figure 8.
The validation conducted in different sites: (a) ET and (b) NEE.

Table 5.
Statistics of the validation conducted in different sites.
4.2. Spatial Distribution
Figure 9 shows the estimated ET (Figure 9a) and NEE (Figure 9c) maps of a case region, which are compared with the MODIS 8-day composite products (with a spatial resolution of 1 km). From the perspective of spatial distribution trends, the ET and NEE obtained in this study show good consistency with the MODIS data. From a detailed perspective, this study, based on Landsat data (with a spatial resolution of 30 m), can provide more detailed information. Moreover, high-resolution temporal images offer deeper insights into crop phenological changes. Overall, our ET and NEE estimation model serves as a valuable tool for regional water resource management, crop growth monitoring, as well as ecological and environmental field surveillance.
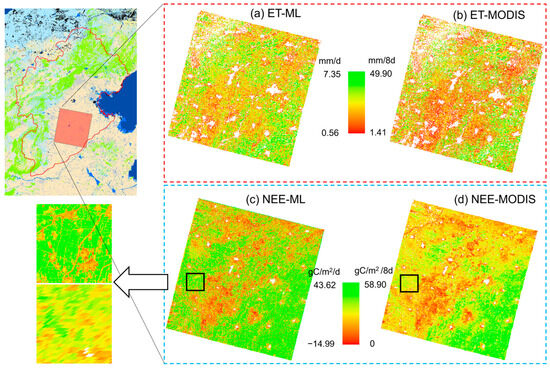
Figure 9.
The spatial distribution of estimated ET based on this study (a) MODIS (b); NEE based on this study (c) and MODIS (d).
5. Discussion
Based on the findings of this study, it can be inferred that utilizing remote sensing Vegetation Indices (VIs) to correlate with ET and NEE yields reasonably accurate results. In comparison to the SEB-based and LUE-based models, these empirical models offer a simpler, more efficient approach while reducing the dependency on meteorological data. Typically, widely used distributed meteorological datasets like GLDAS and MERRA possess relatively low spatial resolutions (ranging from 0.25° to 0.625°), necessitating a spatial downscaling procedure before they can be effectively paired with high-resolution remote sensing data. This downscaling process, however, introduces additional uncertainties to data accuracy, as noted by Rudiger et al. [65], and subsequently increases the uncertainties inherent in SEB-based and LUE-based models [21,26]. Furthermore, previous research has confirmed the limited accuracy of these distributed meteorological datasets [66,67,68]. In contrast, empirical models circumvent these errors, but they have a drawback in terms of limited explanatory power [69,70].
In this study, we employed three regression algorithms (MLR, RFR, and BPNN) to fit multiple types of variables with ET and NEE, observing varying fitting accuracies (refer to Figure 7). Among them, RFR consistently achieved the highest accuracy. As a representative ensemble learning algorithm, RFR derives its final estimates by averaging multiple decision trees. This approach ensures more stable results and effectively mitigates the impact of anomalous samples [71]. Consequently, RFR has been widely used in remote sensing applications for various indicators, such as soil water content estimation [4], crop yield prediction [45,46], and remote sensing image classification [72], often outperforming other machine learning algorithms. MLR also demonstrated considerable accuracy in estimating ET and NEE, particularly when highly correlated variables were included. Furthermore, MLR exhibited stability even with the introduction of additional variables with lower correlation. These less informative variables for ET or NEE estimation could be downweighted by assigning smaller fitting coefficients in MLR. It should be noted that MLR struggles with handling complex nonlinear problems, and from the results, we see that the estimation of NEE is even more challenging, thus the accuracy of MLR is quite limited. In contrast, BPNN struggled more with processing irrelevant input variables. As a neural network algorithm, BPNN typically requires a substantial sample size and is sensitive to anomalous samples or variables with limited explanatory power [4,73].
In general, the regression algorithms employed in this study exhibited satisfactory fitting, but some errors persisted. Firstly, while the empirical models minimized uncertainties from input variables, such as by foregoing meteorological data, the geographical registration, radiometric calibration, and atmospheric correction processes inherent to Landsat data cannot fully guarantee the absolute accuracy and objectivity of the obtained Vegetation Indices (VIs) or surface temperature in portraying the actual situation [74,75]. Secondly, the precision of in situ measurements also impacts model performance, although the Eddy Covariance (EC) method is widely used for measuring water and carbon fluxes [76]. Previous studies have proven that EC suffers a typical error of ET estimation of about 5–20% [77,78]. Furthermore, discrepancies arise from the mismatch between the spatial resolution of satellite observations and the flux tower footprint [21]. Additionally, it is crucial to note that estimating ET and NEE often necessitates temporal up-scaling, unlike status-describing indicators like leaf area or canopy coverage. Converting instantaneous satellite observation data to daily-scale ET or NEE is essential. When it comes to physical models, the up-scaling process based on energy ratios incurs errors ranging from approximately 16.27 to 26.33% [4,79]. Although empirical models bypass this process, treating it as a “black box”, this does not signify the elimination of errors.
From Figure 8 and Table 5, it is evident that the proposed model still faces the challenge of uneven spatial accuracy. Apart from the varying observation sample sizes across the six sites, this issue may also stem from regional indicators that have not been taken into account. From the perspective of model input variables, vegetation indices that describe vegetation growth remain the most effective indicators for estimating ET (Evapotranspiration) and NEE (Net Ecosystem Exchange). The physiological activities of plants, such as transpiration and photosynthesis, are largely determined by their growth status. Multiple studies have shown the potential of using surface temperature to estimate air temperature or net radiation [80,81,82,83]. However, surface water conditions and solar radiation energy primarily serve as supplementary variables to vegetation growth, enhancing the accuracy of remote sensing models in estimating ET and NEE. Additionally, it is important to note that there are potential correlations among the input variables, allowing for some degree of substitution between them. For example, solar radiation exhibits seasonal characteristics and thus has a certain correlation with the Day of Year (DOY). The albedo of vegetation is highly correlated with vegetation growth and water status. Therefore, even without radiation-related variables as model inputs, the accuracy of ET and NEE remains relatively high. In general, the combination of multiple variables can effectively improve the accuracy of the model, as well as enhance its stability [45].
The combination of remote sensing and machine learning has gained increasing popularity in recent times, offering a streamlined and cost-effective approach for monitoring land surface indicators. Furthermore, the perception of machine learning algorithms as inscrutable “black boxes” has diminished [69]. In the context of ET and NEE estimation, we propose three potential avenues for future research: (1) developing down-scaling techniques to acquire more precise meteorological data, or devising algorithms to retrieve meteorological indicators from satellite observations; (2) exploring more dependable in situ measurement methods that align with the spatial resolution of satellite observations, such as integrating unmanned aerial vehicle observations with the EC system; (3) creating a more robust up-scaling method, independent of specific NEE or ET estimation algorithms, to accurately translate instantaneous satellite data to a daily scale.
6. Conclusions
This study examined the use of multiple variables (vegetation growth, surface moisture, radiative energy, and other relative variables) as inputs for various regression algorithms, including Multiple Linear Regression (MLR), Random Forest Regression (RFR), and Backpropagation Neural Network (BPNN), to estimate water (ET) and carbon fluxes (NEE). The key findings can be summarized as follows:
- (1)
- Increasing the number of input variables typically improved the accuracy of ET and NEE estimations. Here, four types of variables used together (RFR) resulted in the best accuracy for ET (R2 of 0.81 and an RMSE of 1.13 mm) and NEE (R2 of 0.83 and an RMSE of 2.83 gC/m2) estimations. Moreover, vegetation growth variables (i.e., VIs) are the most important inputs for ET and NEE estimation;
- (2)
- Among the three regression algorithms tested, each demonstrated different levels of accuracy in estimating ET and NEE. Overall, RFR proved to be the most accurate for both ET and NEE estimations;
- (3)
- The proposed ET and NEE estimation models exhibited some variation in accuracy across different validation sites. Specifically, the R2 for ET estimation ranged from 0.51 to 0.87, and the RMSE fluctuated between 0.94 and 2.28 mm across the six sites. Similarly, for NEE estimation, the R2 spanned from 0.35 to 0.80, with the RMSE varying from 1.42 to 5.48 gC/m2. Despite these variations, the accuracy levels across all six validation sites remained relatively high.
The findings presented in this study demonstrate the potential of using Landsat observations in combination with machine learning techniques to simultaneously estimate ET and NEE. This approach lays the groundwork for an efficient method in agricultural water resource and ecosystem monitoring and management.
Author Contributions
Methodology, M.C.; Resources, Z.L. and C.S.; Writing—original draft, M.C.; Writing—review & editing, J.X., K.L. and C.S.; Visualization, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by National Natural Science Foundation of China (Grant No. 42301366), China Postdoctoral Science Foundation (Grant No. 2023M733001), Basic Research Program Natural Science Foundation of Jiangsu Province (Grant No. SBK2023043261) and A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, S.; Garcia, M.; Bauer-Gottwein, P.; Jakobsen, J.; Zarco-Tejada, P.J.; Bandini, F.; Paz, V.S.; Ibrom, A. High spatial resolution monitoring land surface energy, water and CO2 fluxes from an Unmanned Aerial System. Remote Sens. Environ. 2019, 229, 14–31. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, X.; Jin, X.; Li, B.; Liu, K.; Shi, L. Satellite time series data reveal interannual and seasonal spatiotemporal evapotranspiration patterns in China in response to effect factors. Agric. Water Manag. 2021, 255, 107046. [Google Scholar] [CrossRef]
- Heimann, M.; Reichstein, M. Terrestrial ecosystem carbon dynamics and climate feedbacks. Nature 2008, 451, 289–292. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Jiao, X.; Liu, Y.; Shao, M.; Yu, X.; Bai, Y.; Wang, Z.; Wang, S.; Tuohuti, N.; Liu, S. Estimation of soil moisture content under high maize canopy coverage from UAV multimodal data and machine learning. Agric. Water Manag. 2022, 264, 107530. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.C.; Er-Raki, S.; Chehbouni, A.; Boulet, G.; Bonnefond, J.-M.; De Bruin, H. The use of the scintillation technique for monitoring seasonal water consumption of olive orchards in a semi-arid region. Agric. Water Manag. 2007, 89, 173–184. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL).: Part 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.; Roerink, G.; Van der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL).: Part 2: Validation. J. Hydrol. 1998, 212, 213–229. [Google Scholar] [CrossRef]
- Anderson, M.; Norman, J.; Diak, G.; Kustas, W.; Mecikalski, J. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Awada, H.; Di Prima, S.; Sirca, C.; Giadrossich, F.; Marras, S.; Spano, D.; Pirastru, M. A remote sensing and modeling integrated approach for constructing continuous time series of daily actual evapotranspiration. Agric. Water Manag. 2022, 260, 107320. [Google Scholar] [CrossRef]
- Laipelt, L.; Bloedow Kayser, R.H.; Fleischmann, A.S.; Ruhoff, A.; Bastiaanssen, W.; Erickson, T.A.; Melton, F. Long-term monitoring of evapotranspiration using the SEBAL algorithm and Google Earth Engine cloud computing. ISPRS J. Photogramm. Remote Sens. 2021, 178, 81–96. [Google Scholar] [CrossRef]
- Peddinti, S.R.; Kisekka, I. Estimation of turbulent fluxes over almond orchards using high-resolution aerial imagery with one and two-source energy balance models. Agric. Water Manag. 2022, 269, 107671. [Google Scholar] [CrossRef]
- Wolff, W.; Francisco, J.P.; Flumignan, D.L.; Marin, F.R.; Folegatti, M.V. Optimized algorithm for evapotranspiration retrieval via remote sensing. Agric. Water Manag. 2022, 262, 107390. [Google Scholar] [CrossRef]
- Xue, J.; Fulton, A.; Kisekka, I. Evaluating the role of remote sensing-based energy balance models in improving site-specific irrigation management for young walnut orchards. Agric. Water Manag. 2021, 256, 107132. [Google Scholar] [CrossRef]
- Dong, J.; Li, L.; Li, Y.; Yu, Q. Inter-comparisons of mean, trend and interannual variability of global terrestrial gross primary production retrieved from remote sensing approach. Sci. Total Environ. 2022, 822, 153343. [Google Scholar] [CrossRef]
- Guo, H.; Li, S.; Kang, S.; Du, T.; Liu, W.; Tong, L.; Hao, X.; Ding, R. Comparison of several models for estimating gross primary production of drip-irrigated maize in arid regions. Ecol. Model. 2022, 468, 109928. [Google Scholar] [CrossRef]
- Shu, Y.; Liu, S.; Wang, Z.; Xiao, J.; Shi, Y.; Peng, X.; Gao, H.; Wang, Y.; Yuan, W.; Yan, W.; et al. Effects of Aerosols on Gross Primary Production from Ecosystems to the Globe. Remote Sens. 2022, 14, 2759. [Google Scholar] [CrossRef]
- Xiao, F.; Liu, Q.; Xu, Y. Estimation of Terrestrial Net Primary Productivity in the Yellow River Basin of China Using Light Use Efficiency Model. Sustainability 2022, 14, 7399. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Ju, W.; Zhou, Y.; Cheng, X. Improved estimation of global gross primary productivity during 1981–2020 using the optimized P model. Sci. Total Environ. 2022, 838, 156172. [Google Scholar] [CrossRef]
- Pei, Y.; Dong, J.; Zhang, Y.; Yuan, W.; Doughty, R.; Yang, J.; Zhou, D.; Zhang, L.; Xiao, X. Evolution of light use efficiency models: Improvement, uncertainties, and implications. Agric. For. Meteorol. 2022, 317, 108905. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, X.; Li, B.; Yu, X.; Shao, M.; Jin, X. Long time series of daily evapotranspiration in China based on the SEBAL model and multisource images and validation. Earth Syst. Sci. Data 2021, 13, 3995–4017. [Google Scholar] [CrossRef]
- Dechant, B.; Ryu, Y.; Badgley, G.; Kohler, P.; Rascher, U.; Migliavacca, M.; Zhang, Y.; Tagliabue, G.; Guan, K.; Rossini, M.; et al. NIRvP: A robust structural proxy for sun-induced chlorophyll fluorescence and photosynthesis across scales. Remote Sens. Environ. 2022, 268, 112763. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martinez, A.; Walther, S.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Munoz-Mari, J.; Javier Garcia-Haro, F.; Guanter, L.; et al. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef]
- Dou, X.; Yang, Y. Evapotranspiration estimation using four different machine learning approaches in different terrestrial ecosystems. Comput. Electron. Agric. 2018, 148, 95–106. [Google Scholar] [CrossRef]
- Carter, C.; Liang, S. Evaluation of ten machine learning methods for estimating terrestrial evapotranspiration from remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 86–92. [Google Scholar] [CrossRef]
- Lees, K.J.; Quaife, T.; Artz, R.R.E.; Khomik, M.; Clark, J.M. Potential for using remote sensing to estimate carbon fluxes across northern peatlands—A review. Sci. Total Environ. 2018, 615, 857–874. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Li, B.; Jiao, X.; Huang, X.; Fan, H.; Lin, R.; Liu, K. Using multimodal remote sensing data to estimate regional-scale soil moisture content: A case study of Beijing, China. Agric. Water Manag. 2022, 260, 107298. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.; De Jeu, R.; Gash, J.; Meesters, A.; Dolman, A. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Sun, P.; Wu, Y.; Xiao, J.; Hui, J.; Hu, J.; Zhao, F.; Qiu, L.; Liu, S. Remote sensing and modeling fusion for investigating the ecosystem water-carbon coupling processes. Sci. Total Environ. 2019, 697, 134064. [Google Scholar] [CrossRef] [PubMed]
- Gago, J.; Daloso, D.d.M.; Figueroa, C.M.; Flexas, J.; Fernie, A.R.; Nikoloski, Z. Relationships of Leaf Net Photosynthesis, Stomatal Conductance, and Mesophyll Conductance to Primary Metabolism: A Multispecies Meta-Analysis Approach. Plant Physiol. 2016, 171, 265–279. [Google Scholar] [CrossRef] [PubMed]
- Orchard, V.A.; Cook, F. Relationship between soil respiration and soil moisture. Soil Biol. Biochem. 1983, 15, 447–453. [Google Scholar] [CrossRef]
- Kuzyakov, Y.; Domanski, G. Carbon input by plants into the soil. Review. J. Plant Nutr. Soil Sci. 2000, 163, 421–431. [Google Scholar] [CrossRef]
- Murray, S.J.; Foster, P.N.; Prentice, I.C. Evaluation of global continental hydrology as simulated by the Land-surface Processes and eXchanges Dynamic Global Vegetation Model. Hydrol. Earth Syst. Sci. 2011, 15, 91–105. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S.J.N. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, J.; Guo, L.; Fang, S.; Zhang, J.; Sun, B.; Mao, J.; Sheng, Z.; Li, L. Long-term detection and spatiotemporal variation analysis of open-surface water bodies in the Yellow River Basin from 1986 to 2020. Sci. Total Environ. 2022, 845, 157152. [Google Scholar] [CrossRef]
- Gumma, M.K.; Thenkabail, P.S.; Panjala, P.; Teluguntla, P.; Yamano, T.; Mohammed, I. Multiple agricultural cropland products of South Asia developed using Landsat-8 30 m and MODIS 250 m data using machine learning on the Google Earth Engine (GEE) cloud and spectral matching techniques (SMTs) in support of food and water security. Giscience Remote Sens. 2022, 59, 1048–1077. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Tao, F.; Zhang, L.; Luo, Y.; Zhang, J.; Han, J.; Xie, J. Integrating Multi-Source Data for Rice Yield Prediction across China using Machine Learning and Deep Learning Approaches. Agric. For. Meteorol. 2021, 297, 108275. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Luo, Y.; Zhang, L.; Zhang, J.; Li, Z.; Tao, F. Wheat yield predictions at a county and field scale with deep learning, machine learning, and google earth engine. Eur. J. Agron. 2021, 123, 126204. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, J.; Liang, S.; Feng, J.; Fisher, J.B.; Li, X.; Li, X.; Liu, S.; Ma, Z.; Miyata, A.; et al. Comparison of satellite-based evapotranspiration models over terrestrial ecosystems in China. Remote Sens. Environ. 2014, 140, 279–293. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Deep neural network algorithm for estimating maize biomass based on simulated Sentinel 2A vegetation indices and leaf area index. Crop J. 2020, 8, 87–97. [Google Scholar] [CrossRef]
- Cheng, M.; Penuelas, J.; McCabe, M.F.; Atzberger, C.; Jiao, X.; Wu, W.; Jin, X. Combining multi-indicators with machine-learning algorithms for maize yield early prediction at the county-level in China. Agric. For. Meteorol. 2022, 323, 109057. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. Environ. 2020, 237, 111599. [Google Scholar] [CrossRef]
- Liu, S.B.; Jin, X.L.; Nie, C.W.; Wang, S.Y.; Yu, X.; Cheng, M.H.; Shao, M.C.; Wang, Z.X.; Tuohuti, N.; Bai, Y.; et al. Estimating leaf area index using unmanned aerial vehicle data: Shallow vs. deep machine learning algorithms. Plant Physiol. 2021, 187, 1551–1576. [Google Scholar] [CrossRef]
- Yu, D.; Zha, Y.; Sun, Z.; Li, J.; Jin, X.; Zhu, W.; Bian, J.; Ma, L.; Zeng, Y.; Su, Z. Deep convolutional neural networks for estimating maize above-ground biomass using multi-source UAV images: A comparison with traditional machine learning algorithms. Precis. Agric. 2022, 24, 92–113. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Kung, H.-t.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Widlowski, J.L. Advanced vegetation indices optimized for up-coming sensors: Design, performance, and applications. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2489–2505. [Google Scholar]
- Ranjan, R.; Chopra, U.K.; Sahoo, R.N.; Singh, A.K.; Pradhan, S. Assessment of plant nitrogen stress in wheat (Triticum aestivum L.) through hyperspectral indices. Int. J. Remote Sens. 2012, 33, 6342–6360. [Google Scholar] [CrossRef]
- Bajgain, R.; Xiao, X.; Wagle, P.; Basara, J.; Zhou, Y. Sensitivity analysis of vegetation indices to drought over two tallgrass prairie sites. ISPRS J. Photogramm. Remote Sens. 2015, 108, 151–160. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Qian, B.; Zhao, T.; Jing, Q.; Geng, X.; Wang, J.; Huffman, T.; Shang, J. Estimating winter wheat biomass by assimilating leaf area index derived from fusion of Landsat-8 and MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 63–74. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, G.; Li, Y.; Wang, D.; Ma, Y. Monitoring the seasonal dynamics of soil salinization in the Yellow River delta of China using Landsat data. Nat. Hazards Earth Syst. Sci. 2019, 19, 1499–1508. [Google Scholar] [CrossRef]
- Vincini, M.; Frazzi, E.; D’Alessio, P. A broad-band leaf chlorophyll vegetation index at the canopy scale. Precis. Agric. 2008, 9, 303–319. [Google Scholar] [CrossRef]
- Gilbertson, J.K.; Kemp, J.; van Niekerk, A. Effect of pan-sharpening multi-temporal Landsat 8 imagery for crop type differentiation using different classification techniques. Comput. Electron. Agric. 2017, 134, 151–159. [Google Scholar] [CrossRef]
- Tang, Z.; Li, Y.; Gu, Y.; Jiang, W.; Xue, Y.; Hu, Q.; LaGrange, T.; Bishop, A.; Drahota, J.; Li, R. Assessing Nebraska playa wetland inundation status during 1985–2015 using Landsat data and Google Earth Engine. Environ. Monit. Assess. 2016, 188, 654. [Google Scholar] [CrossRef]
- Morton, D.C.; DeFries, R.S.; Nagol, J.; Souza, C.M., Jr.; Kasischke, E.S.; Hurtt, G.C.; Dubayah, R. Mapping canopy damage from understory fires in Amazon forests using annual time series of Landsat and MODIS data. Remote Sens. Environ. 2011, 115, 1706–1720. [Google Scholar] [CrossRef]
- Balogun, A.-L.; Yekeen, S.T.; Pradhan, B.; Althuwaynee, O.F. Spatio-Temporal Analysis of Oil Spill Impact and Recovery Pattern of Coastal Vegetation and Wetland Using Multispectral Satellite Landsat 8-OLI Imagery and Machine Learning Models. Remote Sens. 2020, 12, 1225. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Fang, S.; Mao, K.; Xia, X.; Wang, P.; Shi, J.; Bateni, S.M.; Xu, T.; Cao, M.; Heggy, E.; Qin, Z. Dataset of daily near-surface air temperature in China from 1979 to 2018. Earth Syst. Sci. Data 2022, 14, 1413–1432. [Google Scholar] [CrossRef]
- Damm, A.; Paul-Limoges, E.; Kukenbrink, D.; Bachofen, C.; Morsdorf, F. Remote sensing of forest gas exchange: Considerations derived from a tomographic perspective. Glob. Chang. Biol. 2020, 26, 2717–2727. [Google Scholar] [CrossRef] [PubMed]
- Kljun, N.; Calanca, P.; Rotach, M.; Schmid, H. The simple two-dimensional parameterisation for Flux Footprint Predictions FFP. Geosci. Model Dev. Discuss. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Rudiger, C.; Su, C.H.; Ryu, D.; Wagner, W. Disaggregation of Low-Resolution L-Band Radiometry Using C-Band Radar Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1425–1429. [Google Scholar] [CrossRef]
- Wang, W.; Cui, W.; Wang, X.J.; Chen, X. Evaluation of GLDAS-1 and GLDAS-2 Forcing Data and Noah Model Simulations over China at the Monthly Scale. J. Hydrometeorol. 2016, 17, 2815–2833. [Google Scholar] [CrossRef]
- Ji, L.; Senay, G.B.; Verdin, J.P. Evaluation of the Global Land Data Assimilation System (GLDAS) Air Temperature Data Products. J. Hydrometeorol. 2015, 16, 2463–2480. [Google Scholar] [CrossRef]
- Du, Y.F.; Shi, H.R.; Zhang, J.Q.; Xia, X.A.; Yao, Z.D.; Fu, D.S.; Hu, B.; Huang, C.L. Evaluation of MERRA-2 hourly surface solar radiation across China. Sol. Energy 2022, 234, 103–110. [Google Scholar] [CrossRef]
- Hancox-Li, L. Robustness in machine learning explanations: Does it matter? In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 640–647. [Google Scholar]
- Zhou, J.; Gandomi, A.H.; Chen, F.; Holzinger, A. Evaluating the Quality of Machine Learning Explanations: A Survey on Methods and Metrics. Electronics 2021, 10, 593. [Google Scholar] [CrossRef]
- Webb, G.I.; Zheng, Z.J. Multistrategy ensemble learning: Reducing error by combining ensemble learning techniques. IEEE Trans. Knowl. Data Eng. 2004, 16, 980–991. [Google Scholar] [CrossRef]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine Versus Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- He, L.; Ren, X.; Wang, Y.; Liu, B.; Zhang, H.; Liu, W.; Feng, W.; Guo, T. Comparing methods for estimating leaf area index by multi-angular remote sensing in winter wheat. Sci. Rep. 2020, 10, 13943. [Google Scholar] [CrossRef] [PubMed]
- Ilori, C.O.; Pahlevan, N.; Knudby, A. Analyzing performances of different atmospheric correction techniques for Landsat 8: Application for coastal remote sensing. Remote Sens. 2019, 11, 469. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Vickers, D.; Gockede, M.; Law, B.E. Uncertainty estimates for 1-h averaged turbulence fluxes of carbon dioxide, latent heat and sensible heat. Tellus Ser. B-Chem. Phys. Meteorol. 2010, 62, 87–99. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z. The accuracy of temporal upscaling of instantaneous evapotranspiration to daily values with seven upscaling methods. Hydrol. Earth Syst. Sci. 2021, 25, 4417–4433. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Phan Thanh, N.; Kappas, M.; Degener, J. Estimating Daily Maximum and Minimum Land Air Surface Temperature Using MODIS Land Surface Temperature Data and Ground Truth Data in Northern Vietnam. Remote Sens. 2016, 8, 2. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Zhang, G.; Ma, Y.; Yang, K.; Ye, M. Daily air temperature estimation on glacier surfaces in the Tibetan Plateau using MODIS LST data. J. Glaciol. 2018, 64, 132–147. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).